Integrating Machine Learning Ensembles for Landslide Susceptibility Mapping in Northern Pakistan
Abstract
1. Introduction
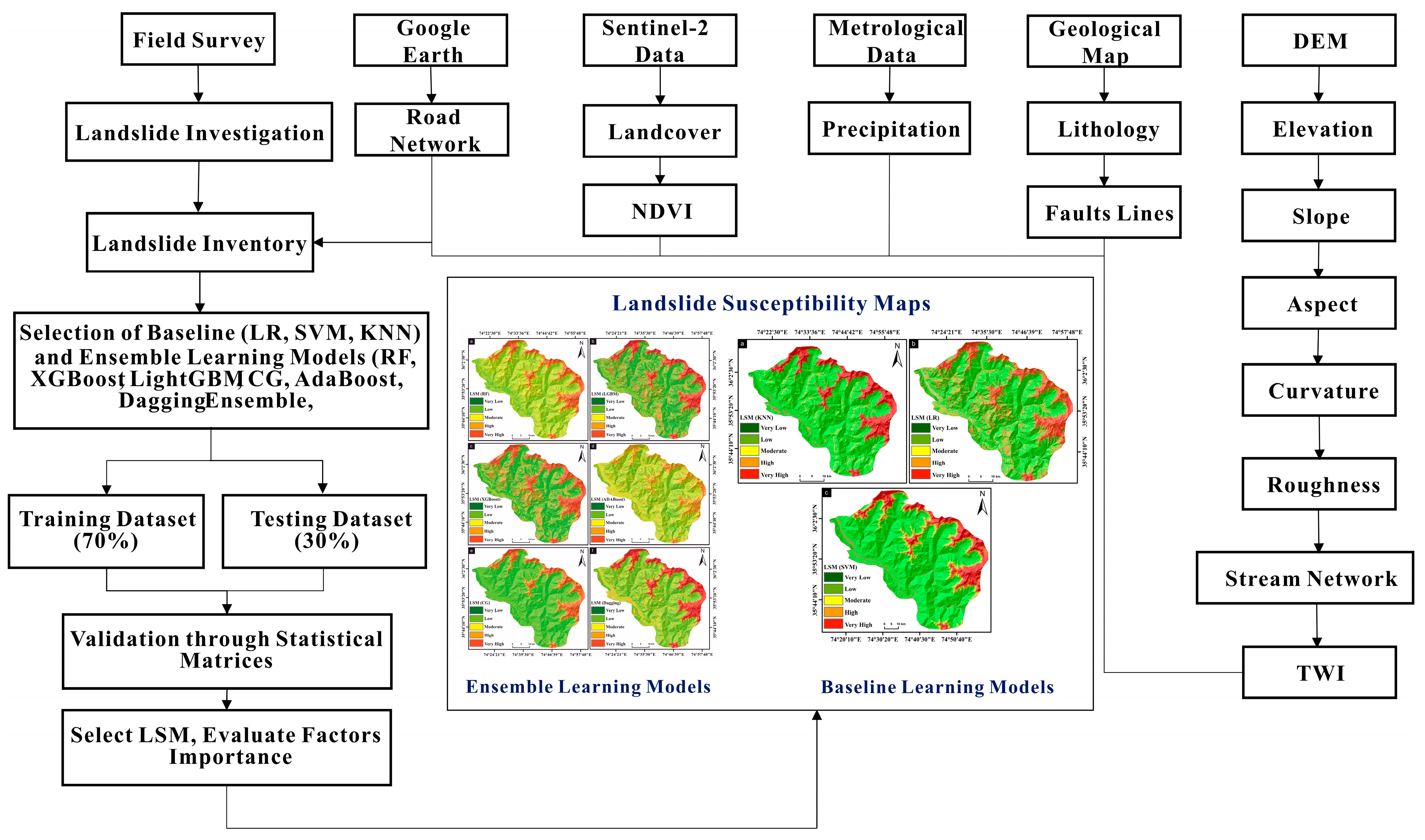
2. Materials and Methods
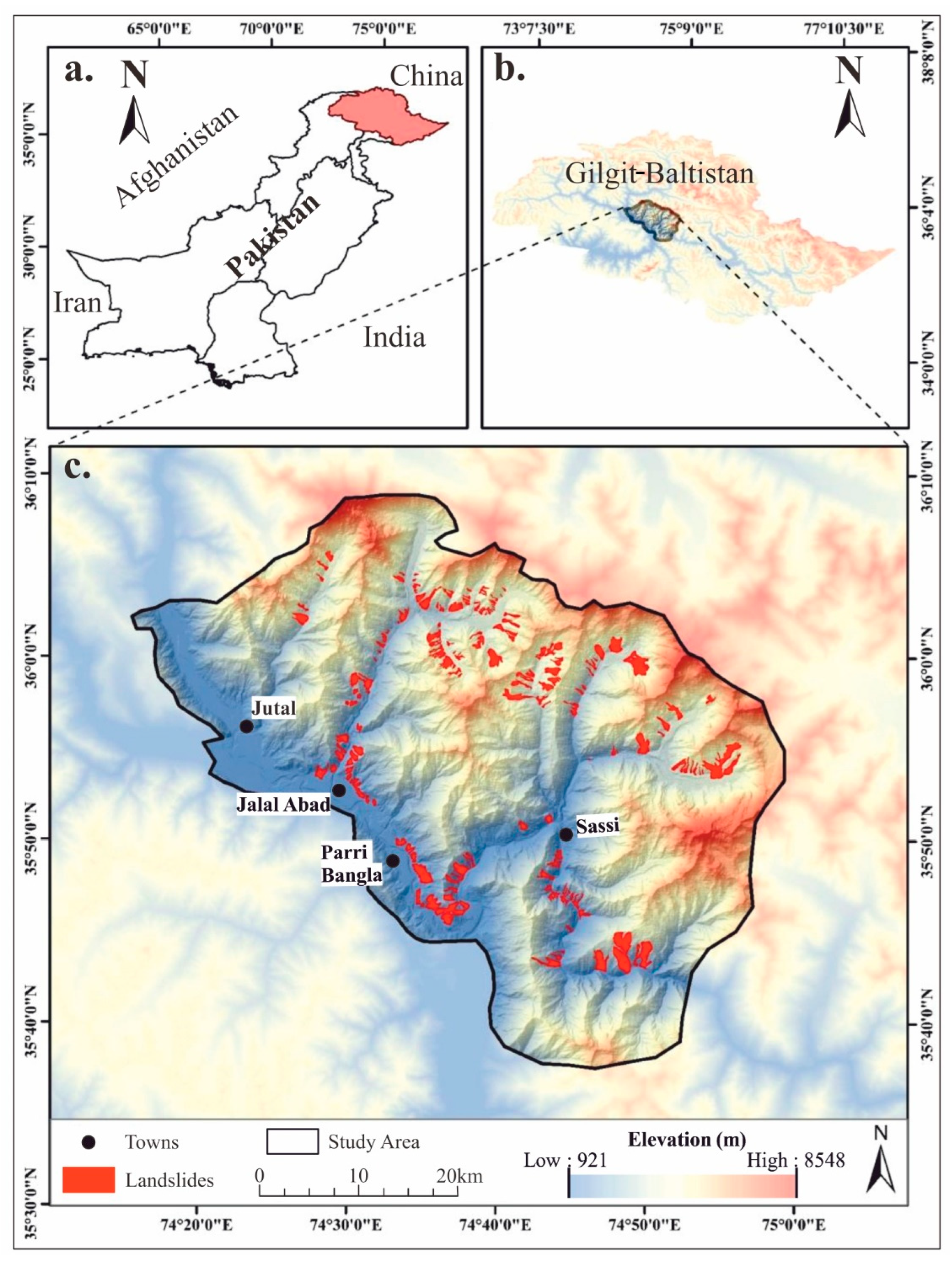
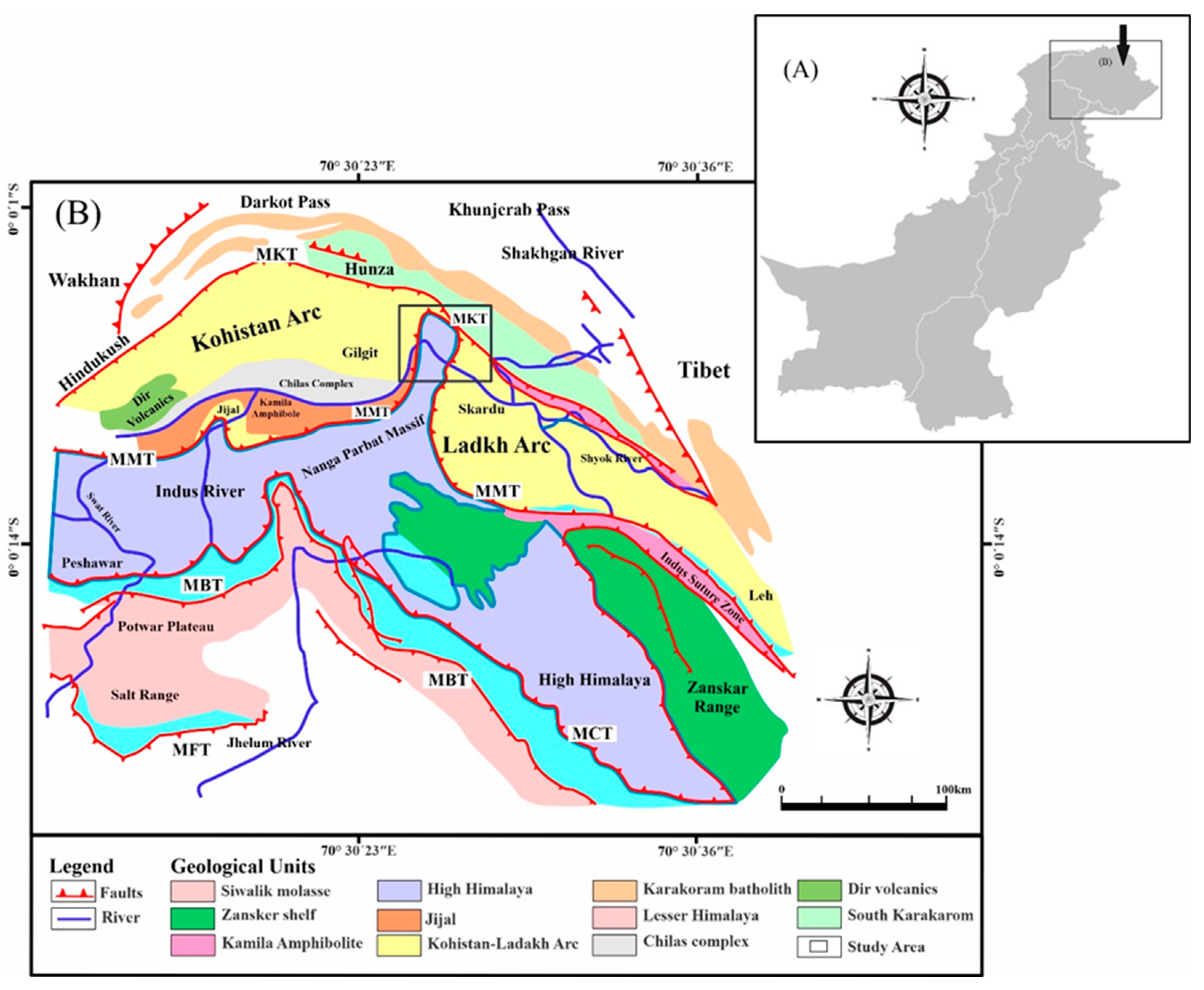
2.1. Study Area and Geological Setting
2.2. Dataset
2.3. Landslide Inventory
2.4. Landslide Causative Factors (LCFs)
2.5. Baseline Learning Algorithms
2.5.1. Logistic Regression
2.5.2. K-Nearest Neighbors (KNN)
2.5.3. Support Vector Machine
2.6. Ensemble Learning Algorithms
2.6.1. Random Forest (RF)
2.6.2. LightGBM
2.6.3. Extreme Gradient Boosting (XGBoost)
2.6.4. AdaBoost
2.6.5. Dagging Ensemble
2.6.6. Cascade Generalization (CG) Ensemble
2.7. Validation Methods
2.8. Determining Key Factors with Correlation-Based Features and a Random Forest Classifier
3. Results
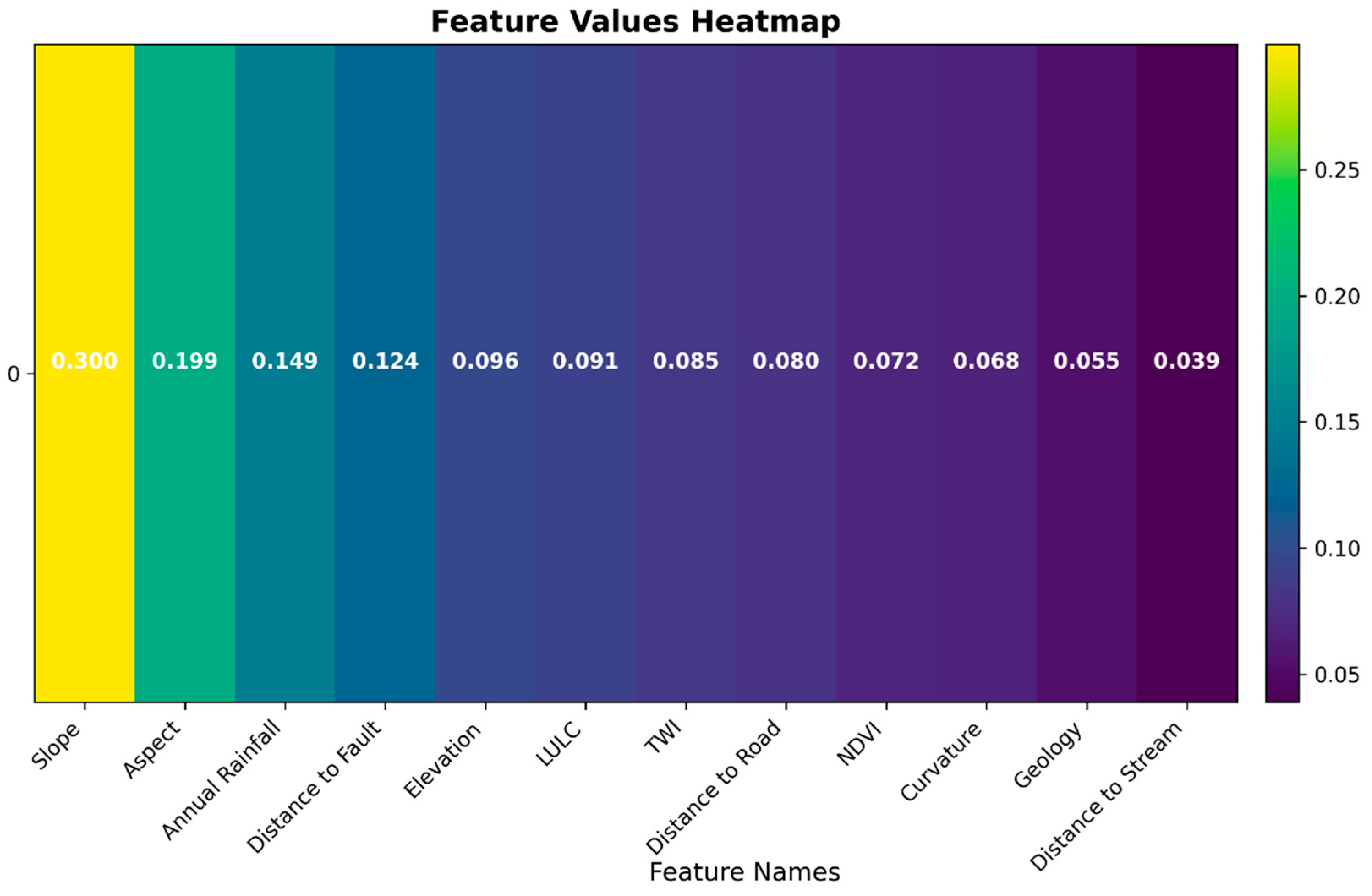
3.1. Feature Importance Evaluation with Correlation-Based Feature Selection and Random Forest Classifier
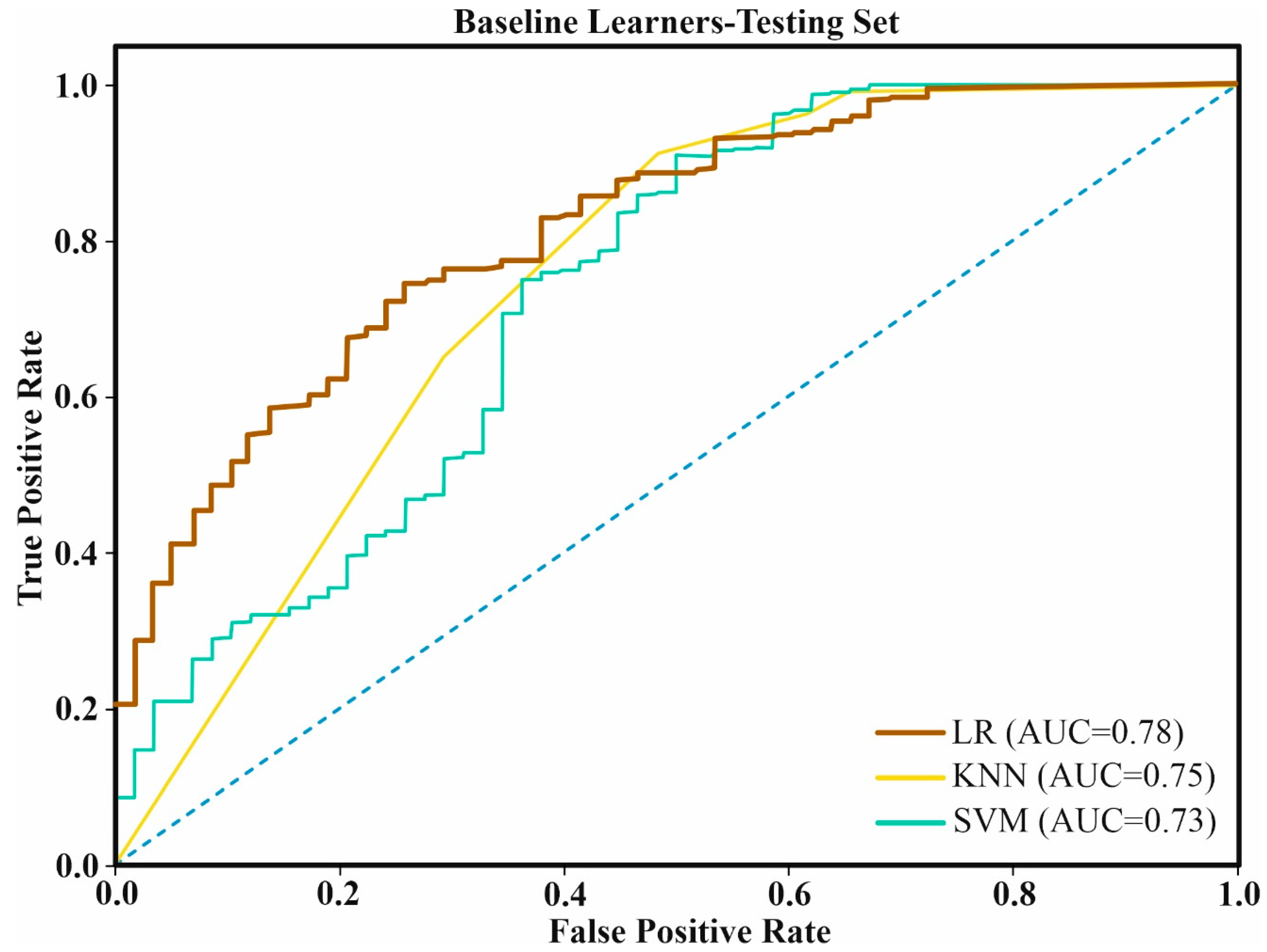
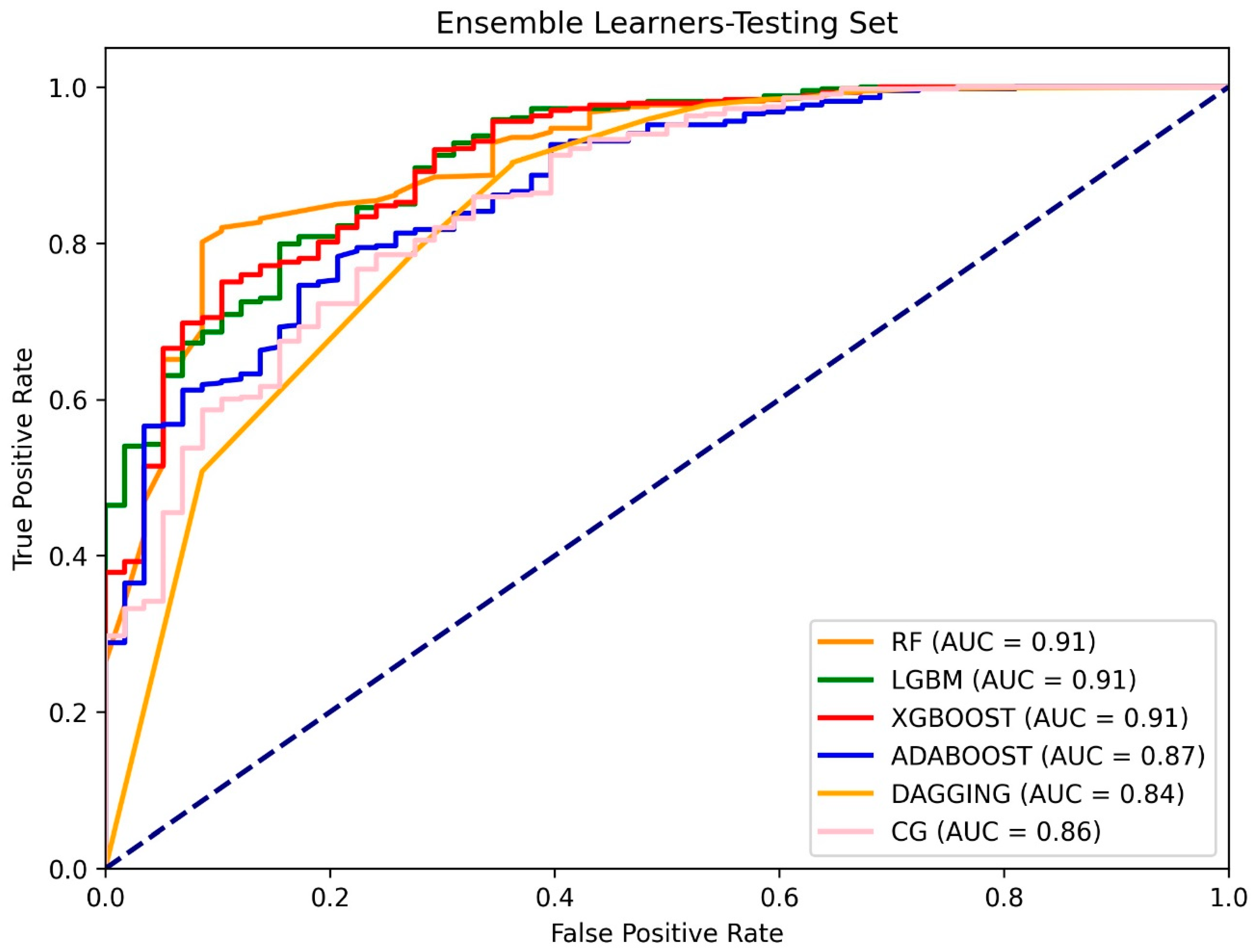
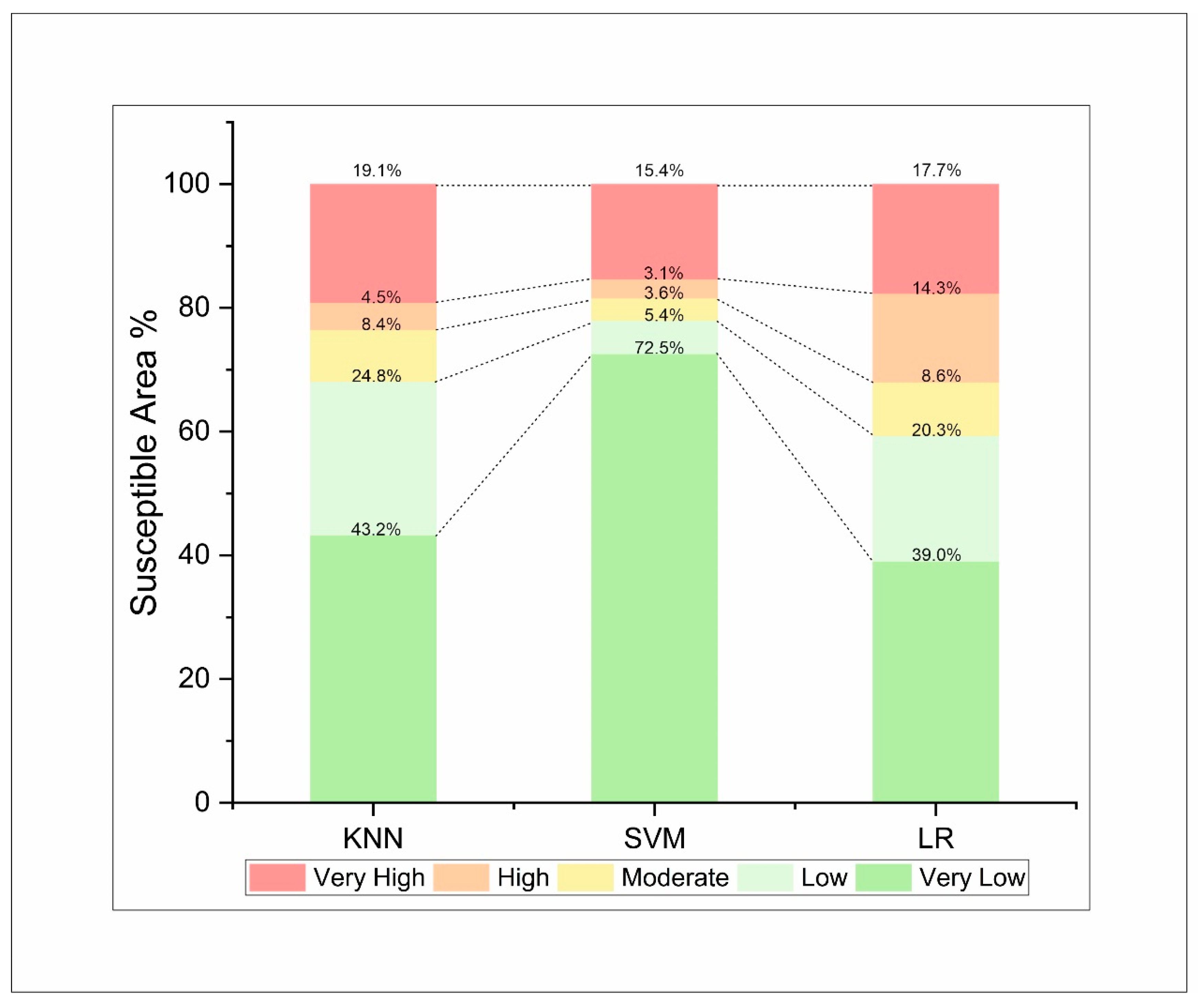
3.2. Model Validation and Comparison for Landslide Susceptibility
3.3. Construction and Validation of LSM
4. Discussion
4.1. Feature Selection
4.2. Validation of the Models
4.3. Use of LSM in Landslide Management
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, J.; Cui, Y.; Xu, W.; Yin, Y.; Li, Y.; Jin, W. Numerical Investigation of the Landslide-Debris Flow Transformation Process Considering Topographic and Entrainment Effects: A Case Study. Landslides 2022, 19, 773–788. [Google Scholar] [CrossRef]
- Xiong, H.; Ma, C.; Li, M.; Tan, J.; Wang, Y. Landslide Susceptibility Prediction Considering Land Use Change and Human Activity: A Case Study under Rapid Urban Expansion and Afforestation in China. Sci. Total Environ. 2023, 866, 161430. [Google Scholar] [CrossRef] [PubMed]
- Gómez, D.; García, E.F.; Aristizábal, E. Spatial and Temporal Landslide Distributions Using Global and Open Landslide Databases. Nat. Hazards 2023, 117, 25–55. [Google Scholar] [CrossRef]
- Khan, A.; Shitao, Z.; Khan, G. Comparative Analysis and Landslide Susceptibility Mapping of Hunza and Nagar Districts, Pakistan. Arab. J. Geosci. 2022, 15, 1644. [Google Scholar] [CrossRef]
- Sökefeld, M. The Power of Lists: IDPs and Disaster Governmentality after the Attabad Landslide in Northern Pakistan. Ethnos 2022, 87, 365–383. [Google Scholar] [CrossRef]
- Cheema, A.R. Disaster Management in Pakistan. In The Role of Mosque in Building Resilient Communities; Springer: Berlin/Heidelberg, Germany, 2022; pp. 51–93. [Google Scholar]
- Sestras, P.; Bilașco, Ștefan; Roșca, S.; Veres, I.; Ilies, N.; Hysa, A.; Spalević, V.; Cîmpeanu, S.M. Multi-Instrumental Approach to Slope Failure Monitoring in a Landslide Susceptible Newly Built-Up Area: Topo-Geodetic Survey, UAV 3D Modelling and Ground-Penetrating Radar. Remote Sens. 2022, 14, 5822. [Google Scholar] [CrossRef]
- Yu, H.; Arabameri, A.; Costache, R.; Anca, C.; Arora, A. Land Subsidence Susceptibility Assessment Using Advanced Artificial Intelligence Models. Geocarto Int. 2022, 37, 18067–18093. [Google Scholar] [CrossRef]
- Goswami, A.; Sen, S.; Sanyal, R. Delineation of Landslide Hazard Zones of a Part of Sutlej Basin in Himachal Pradesh through Frequency Ratio Model. In Convergence of Deep Learning and Artificial Intelligence in Internet of Things; CRC Press: Boca Raton, FL, USA, 2022; pp. 211–229. ISBN 100335596X. [Google Scholar]
- Arabameri, A.; Chandra Pal, S.; Rezaie, F.; Chakrabortty, R.; Saha, A.; Blaschke, T.; Di Napoli, M.; Ghorbanzadeh, O.; Thi Ngo, P.T. Decision Tree Based Ensemble Machine Learning Approaches for Landslide Susceptibility Mapping. Geocarto Int. 2022, 37, 4594–4627. [Google Scholar] [CrossRef]
- Naceur, H.A.; Abdo, H.G.; Igmoullan, B.; Namous, M.; Almohamad, H.; Al Dughairi, A.A.; Al-Mutiry, M. Performance Assessment of the Landslide Susceptibility Modelling Using the Support Vector Machine, Radial Basis Function Network, and Weight of Evidence Models in the N’fis River Basin, Morocco. Geosci. Lett. 2022, 9, 39. [Google Scholar] [CrossRef]
- Mao, Z.; Shi, S.; Li, H.; Zhong, J.; Sun, J. Landslide Susceptibility Assessment Using Triangular Fuzzy Number-Analytic Hierarchy Processing (TFN-AHP), Contributing Weight (CW) and Random Forest Weighted Frequency Ratio (RF Weighted FR) at the Pengyang County, Northwest China. Environ. Earth Sci. 2022, 81, 86. [Google Scholar] [CrossRef]
- Eitvandi, N.; Sarikhani, R.; Derikvand, S. Landslide Susceptibility Mapping by Integrating Analytical Hierarchy Process, Frequency Ratio, and Fuzzy Gamma Operator Models, Case Study: North of Lorestan Province, Iran. Environ. Monit. Assess. 2022, 194, 600. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Huang, F.; Fan, X.; Shahabi, H.; Shirzadi, A.; Wang, D.; Peng, C.; Zhao, X.; Chen, W. Improving the Performance of Artificial Intelligence Models Using the Rotation Forest Technique for Landslide Susceptibility Mapping. Int. J. Environ. Sci. Technol. 2023, 20, 11239–11254. [Google Scholar] [CrossRef]
- Sahin, E.K. Implementation of Free and Open-Source Semi-Automatic Feature Engineering Tool in Landslide Susceptibility Mapping Using the Machine-Learning Algorithms RF, SVM, and XGBoost. Stoch. Environ. Res. Risk Assess. 2023, 37, 1067–1092. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Jebur, M.N.; Bui, D.T.; Xu, C.; Akgun, A. Spatial Prediction of Landslide Hazard at the Luxi Area (China) Using Support Vector Machines. Environ. Earth Sci. 2016, 75, 40. [Google Scholar] [CrossRef]
- Chen, W.; Chai, H.; Zhao, Z.; Wang, Q.; Hong, H. Landslide Susceptibility Mapping Based on GIS and Support Vector Machine Models for the Qianyang County, China. Environ. Earth Sci. 2016, 75, 474. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, W.; Peng, C.; Wang, D.; Xue, W.; Bian, H. Modeling Landslide Susceptibility Using an Evidential Belief Function-Based Multiclass Alternating Decision Tree and Logistic Model Tree. Environ. Earth Sci. 2022, 81, 404. [Google Scholar] [CrossRef]
- Abedini, M.; Ghasemian, B.; Shirzadi, A.; Bui, D.T. A Comparative Study of Support Vector Machine and Logistic Model Tree Classifiers for Shallow Landslide Susceptibility Modeling. Environ. Earth Sci. 2019, 78, 560. [Google Scholar] [CrossRef]
- SS, V.C.; Shaji, E. Landslide Identification Using Machine Learning Techniques: Review, Motivation, and Future Prospects. Earth Sci. Inform. 2022, 15, 2063–2090. [Google Scholar] [CrossRef]
- Pradhan, B.; Lee, S. Landslide Risk Analysis Using Artificial Neural Network Model Focusing on Different Training Sites. Int. J. Phys. Sci. 2009, 3, 1–15. [Google Scholar]
- Zhao, Z.; Xu, Z.; Hu, C.; Wang, K.; Ding, X. Geographically Weighted Neural Network Considering Spatial Heterogeneity for Landslide Susceptibility Mapping: A Case Study of Yichang City, China. Catena 2024, 234, 107590. [Google Scholar] [CrossRef]
- Pham, B.T.; van Phong, T.; Nguyen-Thoi, T.; Parial, K.; Singh, S.K.; Ly, H.-B.; Nguyen, K.T.; Ho, L.S.; van Le, H.; Prakash, I. Ensemble Modeling of Landslide Susceptibility Using Random Subspace Learner and Different Decision Tree Classifiers. Geocarto Int. 2022, 37, 735–757. [Google Scholar] [CrossRef]
- Park, I.; Lee, S. Spatial Prediction of Landslide Susceptibility Using a Decision Tree Approach: A Case Study of the Pyeongchang Area, Korea. Int. J. Remote Sens. 2014, 35, 6089–6112. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Landslide Susceptibility Mapping Using a Modified Decision Tree Classifier in the Xanthi Perfection, Greece. Landslides 2016, 13, 305–320. [Google Scholar] [CrossRef]
- Duan, G.; Hu, J.; Deng, L.; Fu, J. Landslide Susceptibility Prediction by Gray Wolf Optimized Support Vector Machine Model under Different Factor States. J. Appl. Remote Sens. 2023, 17, 44510. [Google Scholar] [CrossRef]
- Ballabio, C.; Sterlacchini, S. Support Vector Machines for Landslide Susceptibility Mapping: The Staffora River Basin Case Study, Italy. Math. Geosci. 2012, 44, 47–70. [Google Scholar] [CrossRef]
- Luu, C.; Ha, H.; Bui, Q.D.; Luong, N.-D.; Khuc, D.T.; Vu, H.; Nguyen, D.Q. Flash Flood and Landslide Susceptibility Analysis for a Mountainous Roadway in Vietnam Using Spatial Modeling. Quat. Sci. Adv. 2023, 11, 100083. [Google Scholar] [CrossRef]
- Wolpert, D.H. The Lack of a Priori Distinctions between Learning Algorithms. Neural Comput. 1996, 8, 1341–1390. [Google Scholar] [CrossRef]
- Sharma, B.; Pandey, A. Mapping of Erosion Hazard in and around Kharagpur Hills, Bihar Using Hydrological Indices. In MOL2NET’22, Conference on Molecular, Biomed., Comput. & Network Science and Engineering, 8th ed.; MDPI: Basel, Switzerland, 2022. [Google Scholar]
- Zafar, S.; Zafar Khan, M.; Mehmood, T.; Begum, F.; Sadiq, M. Role of Community-Based Conservation and Natural Resource Management in Building Climate Resilience among Vulnerable Mountain Societies. Clim. Dev. 2022, 15, 608–621. [Google Scholar] [CrossRef]
- Hussain, J.; Zhang, J.; Saleem, A.; Luo, Y.; Afaq Hussain, M.; Hussain, J.; Fitria, F.; Akram, W.; Arifullah; Hussain, H. Suitability Assessment Constraints of Potential Aggregate Resources Using an Integrated GIS Approach. J. Mater. Civ. Eng. 2023, 35, 4023307. [Google Scholar] [CrossRef]
- Hussain, J.; Zhang, J.; Iqbal, S.M.; Hussain, J.; Fitria, F.; Lina, X.; Ali, N.; Hussain, S.; Akram, W.; Ali, M. Exploring the Potential of Late Permian Aggregate Resources for Utilization in Engineering Structures through Geotechnical, Geochemical and Petrographic Analyses. Sci. Rep. 2023, 13, 5088. [Google Scholar] [CrossRef]
- Bahram, I. Analysis of Seismicity and Related Seismic Risk in Muslim Countries: Case Studies from Afghanistan and Pakistan. Ph.D. Thesis, University of Arkansas, Fayetteville, AR, USA, 2022. [Google Scholar]
- Madin, I.P.; Lawrence, R.D.; Ur-Rehman, S. The Northwestern Nanga Parbat–Haramosh Massif: Evidence for Crustal Uplift at the Northwestern Corner of the Indian Craton. Tecton. West. Himalayas Geol. Soc. Am. Spec. Pap. 1989, 232, 169–182. [Google Scholar]
- Searle, M.P.; Khan, M.A.; Fraser, J.E.; Gough, S.J.; Jan, M.Q. The Tectonic Evolution of the Kohistan-Karakoram Collision Belt along the Karakoram Highway Transect, North Pakistan. Tectonics 1999, 18, 929–949. [Google Scholar] [CrossRef]
- Petterson, M.G.; Windley, B.F. RbSr Dating of the Kohistan Arc-Batholith in the Trans-Himalaya of North Pakistan, and Tectonic Implications. Earth Planet. Sci. Lett. 1985, 74, 45–57. [Google Scholar] [CrossRef]
- Khan, H.; Shafique, M.; Khan, M.A.; Bacha, M.A.; Shah, S.U.; Calligaris, C. Landslide Susceptibility Assessment Using Frequency Ratio, a Case Study of Northern Pakistan. Egypt. J. Remote Sens. Sp. Sci. 2019, 22, 11–24. [Google Scholar] [CrossRef]
- Scaioni, M.; Longoni, L.; Melillo, V.; Papini, M. Remote Sensing for Landslide Investigations: An Overview of Recent Achievements and Perspectives. Remote Sens. 2014, 6, 9600–9652. [Google Scholar] [CrossRef]
- Su, X.; Zhang, Y.; Meng, X.; Yue, D.; Ma, J.; Guo, F.; Zhou, Z.; Rehman, M.U.; Khalid, Z.; Chen, G.; et al. Landslide Mapping and Analysis along the China-Pakistan Karakoram Highway Based on SBAS-InSAR Detection in 2017. J. Mt. Sci. 2021, 18, 2540–2564. [Google Scholar] [CrossRef]
- Deng, N.; Li, Y.; Ma, J.; Shahabi, H.; Hashim, M.; de Oliveira, G.; Chaeikar, S.S. A Comparative Study for Landslide Susceptibility Assessment Using Machine Learning Algorithms Based on Grid Unit and Slope Unit. Front. Environ. Sci. 2022, 10, 1009433. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation-Based Feature Selection for Machine Learning. Ph.D. Thesis, The University of Waikato, Hamilton, New Zealand, 1999. [Google Scholar]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid Artificial Intelligence Models Based on a Neuro-Fuzzy System and Metaheuristic Optimization Algorithms for Spatial Prediction of Wildfire Probability. Agric. For. Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]
- Sahrane, R.; Bounab, A.; Kharim, Y.E.L. Investigating the Effects of Landslides Inventory Completeness on Susceptibility Mapping and Frequency-Area Distributions: Case of Taounate Province, Northern Morocco. Catena 2023, 220, 106737. [Google Scholar] [CrossRef]
- Hussain, M.A.; Chen, Z.; Zheng, Y.; Zhou, Y.; Daud, H. Deep Learning and Machine Learning Models for Landslide Susceptibility Mapping with Remote Sensing Data. Remote Sens. 2023, 15, 4703. [Google Scholar] [CrossRef]
- Hussain, S.; Pan, B.; Afzal, Z.; Ali, M.; Zhang, X.; Shi, X.; Ali, M. Landslide Detection and Inventory Updating Using the Time-Series InSAR Approach along the Karakoram Highway, Northern Pakistan. Sci. Rep. 2023, 13, 7485. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.; Huang, J.; Huang, F.; Bhuyan, K.; Meena, S.R.; Catani, F. Uncertainty Analysis of Non-Landslide Sample Selection in Landslide Susceptibility Prediction Using Slope Unit-Based Machine Learning Models. Gondwana Res. 2023, 117, 307–320. [Google Scholar] [CrossRef]
- Sukristiyanti, S.; Wikantika, K.; Sadisun, I.A.; Yayusman, L.F.; Soebowo, E. Preliminary Study of Landslide Susceptibility Modeling with Random Forest Algorithm Using R (Case Study: The Cisangkuy Sub-Watershed). In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 936, p. 12015. [Google Scholar]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Li, T.; Guo, C.; Hong, H.; Li, W.; Pan, D.; Hui, J.; Ma, M.; et al. A Novel Ensemble Approach of Bivariate Statistical-Based Logistic Model Tree Classifier for Landslide Susceptibility Assessment. Geocarto Int. 2018, 33, 1398–1420. [Google Scholar] [CrossRef]
- Ali, A.; Akhtar, R.; Hussain, J. Unveiling High Mountain Communities’ Perception of Climate Change Impact on Lives and Livelihoods in Gilgit-Baltistan: Evidence from People-Centric Approach. Environ. Commun. 2023, 17, 602–617. [Google Scholar] [CrossRef]
- Shah, N.A.; Shafique, M.; Ishfaq, M.; Faisal, K.; van der Meijde, M. Integrated Approach for Landslide Risk Assessment Using Geoinformation Tools and Field Data in Hindukush Mountain Ranges, Northern Pakistan. Sustainability 2023, 15, 3102. [Google Scholar] [CrossRef]
- Hussain, S.; Hongxing, S.; Ali, M.; Ali, M. PS-InSAR Based Validated Landslide Susceptibility Modelling: A Case Study of Ghizer Valley, Northern Pakistan. Geocarto Int. 2022, 37, 3941–3962. [Google Scholar] [CrossRef]
- Hussain, S.; Hongxing, S.; Ali, M.; Sajjad, M.M.; Ali, M.; Afzal, Z.; Ali, S. Optimized Landslide Susceptibility Mapping and Modelling Using PS-InSAR Technique: A Case Study of Chitral Valley, Northern Pakistan. Geocarto Int. 2022, 37, 5227–5248. [Google Scholar] [CrossRef]
- Zárate, B.A.; El Hamdouni, R.; Fernández del Castillo, T. Characterization and Analysis of Landslide Evolution in Intramountain Areas in Loja (Ecuador) Using RPAS Photogrammetric Products. Remote Sens. 2023, 15, 3860. [Google Scholar] [CrossRef]
- Shang, H.; Su, L.; Chen, W.; Tsangaratos, P.; Ilia, I.; Liu, S.; Cui, S.; Duan, Z. Spatial Prediction of Landslide Susceptibility Using Logistic Regression (LR), Functional Trees (FTs), and Random Subspace Functional Trees (RSFTs) for Pengyang County, China. Remote Sens. 2023, 15, 4952. [Google Scholar] [CrossRef]
- Shahabi, H.; Ahmadi, R.; Alizadeh, M.; Hashim, M.; Al-Ansari, N.; Shirzadi, A.; Wolf, I.D.; Ariffin, E.H. Landslide Susceptibility Mapping in a Mountainous Area Using Machine Learning Algorithms. Remote Sens. 2023, 15, 3112. [Google Scholar] [CrossRef]
- Searle, M.P.; Kahn, M.A. Geological Map of North Pakistan and Adjacent Areas of Northern Ladakh and Western Tibet. (Western Himalaya, Salt Ranges, Kohistan, Karakoram, Hindu Kush), 1: 650 000; British Geological Service (BGS): Nottingham, UK, 1996. [Google Scholar]
- Feng, H.; Miao, Z.; Hu, Q. Study on the Uncertainty of Machine Learning Model for Earthquake-Induced Landslide Susceptibility Assessment. Remote Sens. 2022, 14, 2968. [Google Scholar] [CrossRef]
- Fan, X.; Liu, B.; Luo, J.; Pan, K.; Han, S.; Zhou, Z. Comparison of Earthquake-Induced Shallow Landslide Susceptibility Assessment Based on Two-Category LR and KDE-MLR. Sci. Rep. 2023, 13, 833. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, P.; Liu, J.; He, J.; Yang, H.; Zeng, Y.; He, Y.; Yang, C. Comparison of LR, 5-CV SVM, GA SVM, and PSO SVM for Landslide Susceptibility Assessment in Tibetan Plateau Area, China. J. Mt. Sci. 2023, 20, 979–995. [Google Scholar] [CrossRef]
- Yuan, X.; Liu, C.; Nie, R.; Yang, Z.; Li, W.; Dai, X.; Cheng, J.; Zhang, J.; Ma, L.; Fu, X. A Comparative Analysis of Certainty Factor-Based Machine Learning Methods for Collapse and Landslide Susceptibility Mapping in Wenchuan County, China. Remote Sens. 2022, 14, 3259. [Google Scholar] [CrossRef]
- Hussain, M.A.; Chen, Z.; Wang, R.; Shah, S.U.; Shoaib, M.; Ali, N.; Xu, D.; Ma, C. Landslide Susceptibility Mapping Using Machine Learning Algorithm. Civ. Eng. J. 2022, 8, 209–224. [Google Scholar] [CrossRef]
- Al-Aizari, A.R.; Al-Masnay, Y.A.; Aydda, A.; Zhang, J.; Ullah, K.; Islam, A.R.M.T.; Habib, T.; Kaku, D.U.; Nizeyimana, J.C.; Al-Shaibah, B.; et al. Assessment Analysis of Flood Susceptibility in Tropical Desert Area: A Case Study of Yemen. Remote Sens. 2022, 14, 4050. [Google Scholar] [CrossRef]
- Ullah, K.; Wang, Y.; Fang, Z.; Wang, L.; Rahman, M. Multi-Hazard Susceptibility Mapping Based on Convolutional Neural Networks. Geosci. Front. 2022, 13, 101425. [Google Scholar] [CrossRef]
- Hussain, M.A.; Chen, Z.; Kalsoom, I.; Asghar, A.; Shoaib, M. Landslide Susceptibility Mapping Using Machine Learning Algorithm: A Case Study along Karakoram Highway (KKH), Pakistan. J. Indian Soc. Remote Sens. 2022, 50, 849–866. [Google Scholar] [CrossRef]
- Sheng, Y.; Xu, G.; Jin, B.; Zhou, C.; Li, Y.; Chen, W. Data-Driven Landslide Spatial Prediction and Deformation Monitoring: A Case Study of Shiyan City, China. Remote Sens. 2023, 15, 5256. [Google Scholar] [CrossRef]
- Vapnik, V.; Vapnik, V. Statistical Learning Theory Wiley. New York 1998, 1, 2. [Google Scholar]
- Miao, F.; Ruan, Q.; Wu, Y.; Qian, Z.; Kong, Z.; Qin, Z. Landslide Dynamic Susceptibility Mapping Base on Machine Learning and the PS-InSAR Coupling Model. Remote Sens. 2023, 15, 5427. [Google Scholar] [CrossRef]
- Ali, S.A.; Parvin, F.; Pham, Q.B.; Khedher, K.M.; Dehbozorgi, M.; Rabby, Y.W.; Anh, D.T.; Nguyen, D.H. An Ensemble Random Forest Tree with SVM, ANN, NBT, and LMT for Landslide Susceptibility Mapping in the Rangit River Watershed, India. Nat. Hazards 2022, 113, 1601–1633. [Google Scholar] [CrossRef]
- Tang, H.; Wang, C.; An, S.; Wang, Q.; Jiang, C. A Novel Heterogeneous Ensemble Framework Based on Machine Learning Models for Shallow Landslide Susceptibility Mapping. Remote Sens. 2023, 15, 4159. [Google Scholar] [CrossRef]
- Al-Aizari, A.R.; Alzahrani, H.; AlThuwaynee, O.F.; Al-Masnay, Y.A.; Ullah, K.; Park, H.J.; Al-Areeq, N.M.; Rahman, M.; Hazaea, B.Y.; Liu, X. Uncertainty Reduction in Flood Susceptibility Mapping Using Random Forest and EXtreme Gradient Boosting Algorithms in Two Tropical Desert Cities, Shibam and Marib, Yemen. Remote Sens. 2024, 16, 336. [Google Scholar] [CrossRef]
- Deng, H.; Wu, X.; Zhang, W.; Liu, Y.; Li, W.; Li, X.; Zhou, P.; Zhuo, W. Slope-Unit Scale Landslide Susceptibility Mapping Based on the Random Forest Model in Deep Valley Areas. Remote Sens. 2022, 14, 4245. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Zhang, Y.; Xu, J.; Zhang, W. Landslide Susceptibility Mapping Using Hybrid Random Forest with GeoDetector and RFE for Factor Optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Tang, L.; Gu, X.; Wang, L. Efficient Time-Variant Reliability Analysis of Bazimen Landslide in the Three Gorges Reservoir Area Using XGBoost and LightGBM Algorithms. Gondwana Res. 2023, 123, 41–53. [Google Scholar] [CrossRef]
- Sun, D.; Chen, D.; Zhang, J.; Mi, C.; Gu, Q.; Wen, H. Landslide Susceptibility Mapping Based on Interpretable Machine Learning from the Perspective of Geomorphological Differentiation. Land 2023, 12, 1018. [Google Scholar] [CrossRef]
- Sun, D.; Wu, X.; Wen, H.; Gu, Q. A LightGBM-Based Landslide Susceptibility Model Considering the Uncertainty of Non-Landslide Samples. Geomat. Nat. Hazards Risk 2023, 14, 2213807. [Google Scholar] [CrossRef]
- Hindarto, D. Case Study: Gradient Boosting Machine vs. Light GBM in Potential Landslide Detection. J. Comput. Netw. Archit. High Perform. Comput. 2024, 6, 169–178. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Y.; Xu, S.; He, Y.; Li, Z.; Yu, X.; Liang, Y.; Wu, W.; Wang, Y. Combining a Class-Weighted Algorithm and Machine Learning Models in Landslide Susceptibility Mapping: A Case Study of Wanzhou Section of the Three Gorges Reservoir, China. Comput. Geosci. 2022, 158, 104966. [Google Scholar] [CrossRef]
- Wang, S.; Zhuang, J.; Zheng, J.; Fan, H.; Kong, J.; Zhan, J. Application of Bayesian Hyperparameter Optimized Random Forest and XGBoost Model for Landslide Susceptibility Mapping. Front. Earth Sci. 2021, 9, 712240. [Google Scholar] [CrossRef]
- Al-Masnay, Y.A.; Al-Areeq, N.M.; Ullah, K.; Al-Aizari, A.R.; Rahman, M.; Wang, C.; Zhang, J.; Liu, X. Estimate Earth Fissure Hazard Based on Machine Learning in the Qa’ Jahran Basin, Yemen. Sci. Rep. 2022, 12, 21936. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, L.; Han, Y.; Sun, Y.; Zang, Y.; Zhou, M. Landslide Hazard Assessment in Highway Areas of Guangxi Using Remote Sensing Data and a Pre-Trained XGBoost Model. Remote Sens. 2023, 15, 3350. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into Geospatial Heterogeneity of Landslide Susceptibility Based on the SHAP-XGBoost Model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y.; Wang, L.; Liu, S.; Meng, X. Landslide Susceptibility Mapping Using Random Forest and Extreme Gradient Boosting: A Case Study of Fengjie, Chongqing. Geol. J. 2023, 58, 2372–2387. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Teke, A. Predictive Performances of Ensemble Machine Learning Algorithms in Landslide Susceptibility Mapping Using Random Forest, Extreme Gradient Boosting (XGBoost) and Natural Gradient Boosting (NGBoost). Arab. J. Sci. Eng. 2022, 47, 7367–7385. [Google Scholar] [CrossRef]
- Yavuz Ozalp, A.; Akinci, H.; Zeybek, M. Comparative Analysis of Tree-Based Ensemble Learning Algorithms for Landslide Susceptibility Mapping: A Case Study in Rize, Turkey. Water 2023, 15, 2661. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Yu, H.; Pei, W.; Zhang, J.; Chen, G. Landslide Susceptibility Mapping and Driving Mechanisms in a Vulnerable Region Based on Multiple Machine Learning Models. Remote Sens. 2023, 15, 1886. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, M.; Liu, K. Comparisons of Convolutional Neural Network and Other Machine Learning Methods in Landslide Susceptibility Assessment: A Case Study in Pingwu. Remote Sens. 2023, 15, 798. [Google Scholar] [CrossRef]
- Wu, Y.; Ke, Y.; Chen, Z.; Liang, S.; Zhao, H.; Hong, H. Application of Alternating Decision Tree with AdaBoost and Bagging Ensembles for Landslide Susceptibility Mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
- Ting, K.M.; Witten, I.H. Stacking Bagged and Dagged Models; University of Waikato, Department of Computer Science: Hamilton, New Zealand, 1997. [Google Scholar]
- Sahana, M.; Pham, B.T.; Shukla, M.; Costache, R.; Thu, D.X.; Chakrabortty, R.; Satyam, N.; Nguyen, H.D.; van Phong, T.; Le, H. Van Rainfall Induced Landslide Susceptibility Mapping Using Novel Hybrid Soft Computing Methods Based on Multi-Layer Perceptron Neural Network Classifier. Geocarto Int. 2022, 37, 2747–2771. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Tran, T.H.; Ha, N.A.; Ngo, V.L.; Nadhir, A.A.; Tran, V.P.; Nguyen, H.D.; Malek, M.A.; Amini, A.; Prakash, I.; et al. GIS Based Novel Hybrid Computational Intelligence Models for Mapping Landslide Susceptibility: A Case Study at Da Lat City, Vietnam. Sustainability 2019, 11, 7118. [Google Scholar] [CrossRef]
- Mallick, J.; Alqadhi, S.; Talukdar, S.; Sarkar, S.K.; Roy, S.K.; Ahmed, M. Modelling and Mapping of Landslide Susceptibility Regulating Potential Ecosystem Service Loss: An Experimental Research in Saudi Arabia. Geocarto Int. 2022, 37, 10170–10198. [Google Scholar] [CrossRef]
- Yan, X.; Jiao, J.; LI, M.; QI, H.; Liang, Y.; XU, Q.; Zhang, Z.; Jiang, X.; Li, J.; Zhang, Z. Lateral Connectivity of Landslides and Its Influence on Sediment Yield of Slope-Channel Cascade Under Heavy Rainstorm on the Loess Plateau. CATENA 2022, 216, 106378. [Google Scholar] [CrossRef]
- Hang, H.T.; Tung, H.; Hoa, P.D.; Phuong, N.V.; van Phong, T.; Costache, R.; Nguyen, H.D.; Amiri, M.; Le, H.-A.; Le, H. Van Spatial Prediction of Landslides along National Highway-6, Hoa Binh Province, Vietnam Using Novel Hybrid Models. Geocarto Int. 2022, 37, 5201–5226. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen-Thoi, T.; Qi, C.; van Phong, T.; Dou, J.; Ho, L.S.; van Le, H.; Prakash, I. Coupling RBF Neural Network with Ensemble Learning Techniques for Landslide Susceptibility Mapping. Catena 2020, 195, 104805. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Chen, W.; Ly, H.-B.; Ho, L.S.; Omidvar, E.; Tran, V.P.; Tien Bui, D. A Novel Intelligence Approach of a Sequential Minimal Optimization-Based Support Vector Machine for Landslide Susceptibility Mapping. Sustainability 2019, 11, 6323. [Google Scholar] [CrossRef]
- Thai Pham, B.; Shirzadi, A.; Shahabi, H.; Omidvar, E.; Singh, S.K.; Sahana, M.; Talebpour Asl, D.; Bin Ahmad, B.; Kim Quoc, N.; Lee, S. Landslide Susceptibility Assessment by Novel Hybrid Machine Learning Algorithms. Sustainability 2019, 11, 4386. [Google Scholar] [CrossRef]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Hong, H.; Akgun, A.; Tian, Y.; Liu, J.; Zhu, A.; Li, S. Novel Hybrid Artificial Intelligence Approach of Bivariate Statistical-Methods-Based Kernel Logistic Regression Classifier for Landslide Susceptibility Modeling. Bull. Eng. Geol. Environ. 2019, 78, 4397–4419. [Google Scholar] [CrossRef]
- Costache, R.; Pham, Q.B.; Avand, M.; Linh, N.T.T.; Vojtek, M.; Vojteková, J.; Lee, S.; Khoi, D.N.; Nhi, P.T.T.; Dung, T.D. Novel Hybrid Models between Bivariate Statistics, Artificial Neural Networks and Boosting Algorithms for Flood Susceptibility Assessment. J. Environ. Manag. 2020, 265, 110485. [Google Scholar] [CrossRef] [PubMed]
- Pham, B.T.; Jaafari, A.; Prakash, I.; Bui, D.T. A Novel Hybrid Intelligent Model of Support Vector Machines and the MultiBoost Ensemble for Landslide Susceptibility Modeling. Bull. Eng. Geol. Environ. 2019, 78, 2865–2886. [Google Scholar] [CrossRef]
- Nguyen, V.V.; Pham, B.T.; Vu, B.T.; Prakash, I.; Jha, S.; Shahabi, H.; Shirzadi, A.; Ba, D.N.; Kumar, R.; Chatterjee, J.M. Hybrid Machine Learning Approaches for Landslide Susceptibility Modeling. Forests 2019, 10, 157. [Google Scholar] [CrossRef]
- Peng, T.; Chen, Y.; Chen, W. Landslide Susceptibility Modeling Using Remote Sensing Data and Random SubSpace-Based Functional Tree Classifier. Remote Sens. 2022, 14, 4803. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Singh, S.K.; Al-Ansari, N.; Clague, J.J.; Jaafari, A.; Chen, W.; Miraki, S.; Dou, J. Shallow Landslide Susceptibility Mapping: A Comparison between Logistic Model Tree, Logistic Regression, Naïve Bayes Tree, Artificial Neural Network, and Support Vector Machine Algorithms. Int. J. Environ. Res. Public Health 2020, 17, 2749. [Google Scholar] [CrossRef]
- Ageenko, A.; Hansen, L.C.; Lyng, K.L.; Bodum, L.; Arsanjani, J.J. Landslide Susceptibility Mapping Using Machine Learning: A Danish Case Study. ISPRS Int. J. Geo-Inf. 2022, 11, 324. [Google Scholar] [CrossRef]
- Lee, C.; Lee, G.G. Information Gain and Divergence-Based Feature Selection for Machine Learning-Based Text Categorization. Inf. Process. Manag. 2006, 42, 155–165. [Google Scholar] [CrossRef]
- Ozcift, A.; Gulten, A. Classifier Ensemble Construction with Rotation Forest to Improve Medical Diagnosis Performance of Machine Learning Algorithms. Comput. Methods Programs Biomed. 2011, 104, 443–451. [Google Scholar] [CrossRef]
- Provost, F.; Hibert, C.; Malet, J. Automatic Classification of Endogenous Landslide Seismicity Using the Random Forest Supervised Classifier. Geophys. Res. Lett. 2017, 44, 113–120. [Google Scholar] [CrossRef]
- Nhu, V.-H.; Shirzadi, A.; Shahabi, H.; Chen, W.; Clague, J.J.; Geertsema, M.; Jaafari, A.; Avand, M.; Miraki, S.; Talebpour Asl, D. Shallow Landslide Susceptibility Mapping by Random Forest Base Classifier and Its Ensembles in a Semi-Arid Region of Iran. Forests 2020, 11, 421. [Google Scholar] [CrossRef]
- Dang, V.-H.; Dieu, T.B.; Tran, X.-L.; Hoang, N.-D. Enhancing the Accuracy of Rainfall-Induced Landslide Prediction along Mountain Roads with a GIS-Based Random Forest Classifier. Bull. Eng. Geol. Environ. 2019, 78, 2835–2849. [Google Scholar] [CrossRef]
- Aslam, B.; Maqsoom, A.; Khalil, U.; Ghorbanzadeh, O.; Blaschke, T.; Farooq, D.; Tufail, R.F.; Suhail, S.A.; Ghamisi, P. Evaluation of Different Landslide Susceptibility Models for a Local Scale in the Chitral District, Northern Pakistan. Sensors 2022, 22, 3107. [Google Scholar] [CrossRef] [PubMed]
- Abbas, F.; Zhang, F.; Abbas, F.; Ismail, M.; Iqbal, J.; Hussain, D.; Khan, G.; Alrefaei, A.F.; Albeshr, M.F. Landslide Susceptibility Mapping: Analysis of Different Feature Selection Techniques with Artificial Neural Network Tuned by Bayesian and Metaheuristic Algorithms. Remote Sens. 2023, 15, 4330. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide Susceptibility Mapping Using GIS-Based Statistical Models and Remote Sensing Data in Tropical Environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef]
- Ma, Z.; Mei, G.; Piccialli, F. Machine Learning for Landslides Prevention: A Survey. Neural Comput. Appl. 2021, 33, 10881–10907. [Google Scholar] [CrossRef]
- Rahmati, O.; Kornejady, A.; Samadi, M.; Deo, R.C.; Conoscenti, C.; Lombardo, L.; Dayal, K.; Taghizadeh-Mehrjardi, R.; Pourghasemi, H.R.; Kumar, S. PMT: New Analytical Framework for Automated Evaluation of Geo-Environmental Modelling Approaches. Sci. Total Environ. 2019, 664, 296–311. [Google Scholar] [CrossRef]
- Lombardo, L.; Opitz, T.; Ardizzone, F.; Guzzetti, F.; Huser, R. Space-Time Landslide Predictive Modelling. Earth-Sci. Rev. 2020, 209, 103318. [Google Scholar] [CrossRef]
- Hong, H.; Panahi, M.; Shirzadi, A.; Ma, T.; Liu, J.; Zhu, A.-X.; Chen, W.; Kougias, I.; Kazakis, N. Flood Susceptibility Assessment in Hengfeng Area Coupling Adaptive Neuro-Fuzzy Inference System with Genetic Algorithm and Differential Evolution. Sci. Total Environ. 2018, 621, 1124–1141. [Google Scholar] [CrossRef] [PubMed]
- Kalantar, B.; Pradhan, B.; Amir Naghibi, S.; Motevalli, A.; Mansor, S. Assessment of the Effects of Training Data Selection on the Landslide Susceptibility Mapping: A Comparison between Support Vector Machine (SVM), Logistic Regression (LR) and Artificial Neural Networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
- Kulsoom, I.; Hua, W.; Hussain, S.; Chen, Q.; Khan, G.; Shihao, D. SBAS-InSAR Based Validated Landslide Susceptibility Mapping along the Karakoram Highway: A Case Study of Gilgit-Baltistan, Pakistan. Sci. Rep. 2023, 13, 3344. [Google Scholar] [CrossRef] [PubMed]
- Shirzadi, A.; Soliamani, K.; Habibnejhad, M.; Kavian, A.; Chapi, K.; Shahabi, H.; Chen, W.; Khosravi, K.; Thai Pham, B.; Pradhan, B. Novel GIS Based Machine Learning Algorithms for Shallow Landslide Susceptibility Mapping. Sensors 2018, 18, 3777. [Google Scholar] [CrossRef] [PubMed]


| S.NO | Parameters | Data Origins | Comprehensive Details |
|---|---|---|---|
| 1 | Elevation Slope Aspect Curvature TWI Distance to River | DEM 12.5 m | https://search.asf.alaska.edu/#/, accessed on 29 June 2023 |
| 2 | LULC | Sentinel-2 images 10 m | https://earthexplorer.usgs.gov/#/, accessed on 30 August 2023 |
| 3 | Lithology Distance to Road Distance to Fault | Geological map scale: 1:650,000 | Geological Map of Pakistan (Searle & Khan 1996) [57] |
| 4 | Rainfall | GIOVANNI | https://gpm.nasa.gov/data/sources/giovanni#/, accessed on 19 September 2023 |
| Attribute | Average Merit (AM) | Average Rank (AR) | Rank Error (AR) |
|---|---|---|---|
| Slope | 29.92 | 1 | 0.0 |
| Elevation | 24.82 | 2 | 0.0 |
| Aspect | 17.61 | 3 | 0.0 |
| Annual Rainfall | 14.85 | 4 | 0.0 |
| Distance to Fault | 11.32 | 5 | 0.0 |
| LULC | 6.08 | 6 | 0.0 |
| TWI | 5.164 | 7 | 0.0 |
| Distance to Road | 5.141 | 8 | 0.0 |
| NDVI | 5.139 | 9 | 0.0 |
| Geology | 4.291 | 10 | 0.0 |
| Curvature | 0.141 | 11 | 0.0 |
| Distance to Stream | 0.218 | 12 | 0.0 |
| Testing Set | |||
|---|---|---|---|
| KNN | SVM | LR | |
| ACC | 0.896 | 0.910 | 0.912 |
| AUC | 0.750 | 0.734 | 0.784 |
| K | 0.409 | 0.359 | 0.394 |
| Testing Set | ||||||
|---|---|---|---|---|---|---|
| RF | LGBM | XGBoost | AdaBoost | Dagging | CG | |
| ACC | 0.914 | 0.925 | 0.927 | 0.898 | 0.916 | 0.923 |
| AUC | 0.909 | 0.907 | 0.910 | 0.870 | 0.843 | 0.863 |
| K | 0.481 | 0.579 | 0.620 | 0.445 | 0.525 | 0.530 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, N.; Chen, J.; Fu, X.; Ali, R.; Hussain, M.A.; Daud, H.; Hussain, J.; Altalbe, A. Integrating Machine Learning Ensembles for Landslide Susceptibility Mapping in Northern Pakistan. Remote Sens. 2024, 16, 988. https://doi.org/10.3390/rs16060988
Ali N, Chen J, Fu X, Ali R, Hussain MA, Daud H, Hussain J, Altalbe A. Integrating Machine Learning Ensembles for Landslide Susceptibility Mapping in Northern Pakistan. Remote Sensing. 2024; 16(6):988. https://doi.org/10.3390/rs16060988
Chicago/Turabian StyleAli, Nafees, Jian Chen, Xiaodong Fu, Rashid Ali, Muhammad Afaq Hussain, Hamza Daud, Javid Hussain, and Ali Altalbe. 2024. "Integrating Machine Learning Ensembles for Landslide Susceptibility Mapping in Northern Pakistan" Remote Sensing 16, no. 6: 988. https://doi.org/10.3390/rs16060988
APA StyleAli, N., Chen, J., Fu, X., Ali, R., Hussain, M. A., Daud, H., Hussain, J., & Altalbe, A. (2024). Integrating Machine Learning Ensembles for Landslide Susceptibility Mapping in Northern Pakistan. Remote Sensing, 16(6), 988. https://doi.org/10.3390/rs16060988









