A Priori Knowledge Based Ground Moving Target Indication Technique Applied to Distributed Spaceborne SAR System
Abstract
:1. Introduction
2. Signal Model and Adaptive Clutter Cancellation
3. Problem Statements and A Priori Knowledge Integration
3.1. Moving Target Steering Vector Mismatch
3.2. Integration of A Priori Knowledge
4. Multiple Hypothesis Testing Technique
4.1. Adaptive Detection Techniques
4.2. Multiple Hypothesis Testing Technique
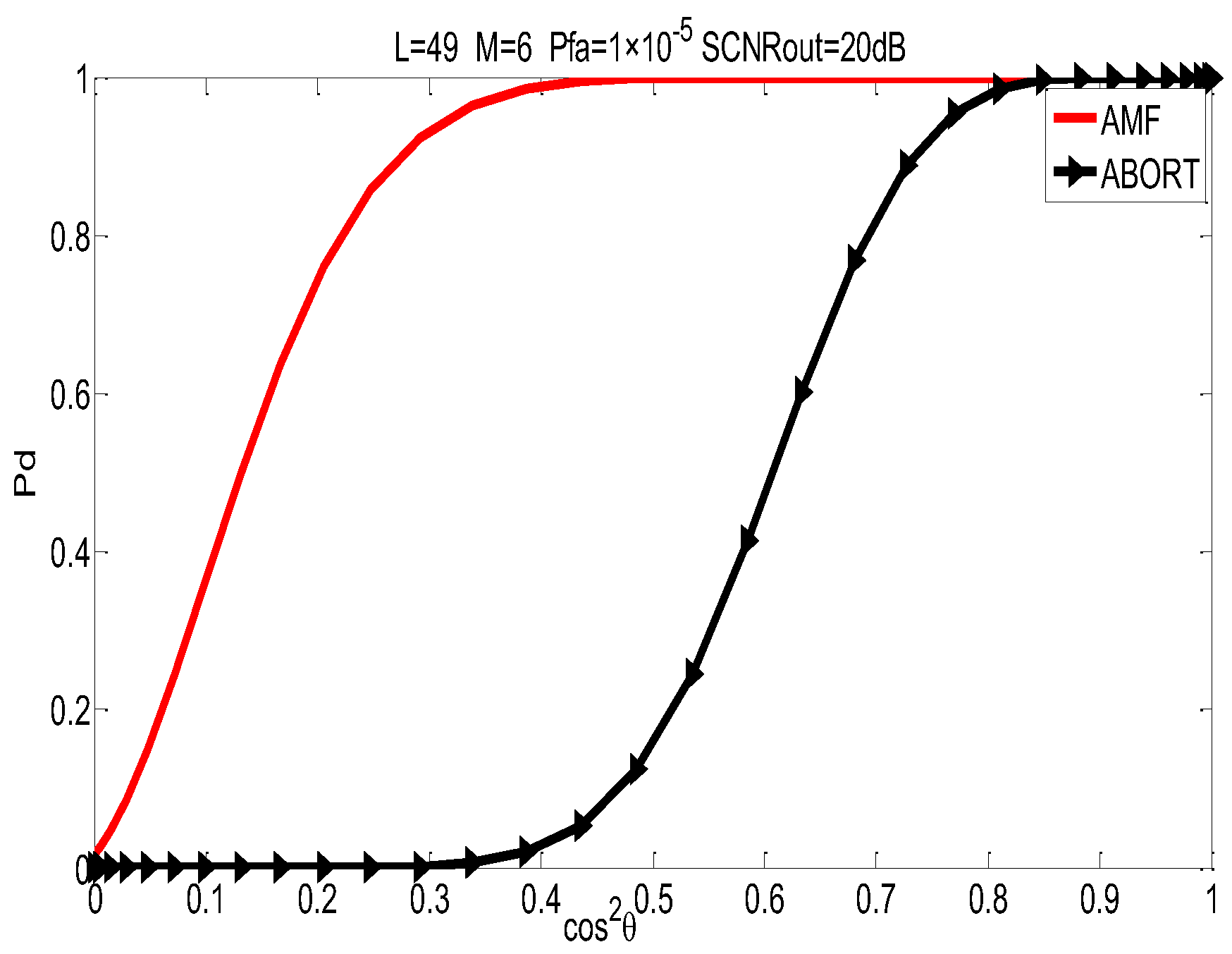
5. Simulation Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAR | synthetic aperture radar |
| GMTI | ground moving target indication |
| DOF | degreeoffreedoms |
| AMF | adaptive matched filter |
| ABORT | adaptive beamformer orthogonalrejection test |
| MHT | multiple hypothesis testing |
| MDV | minimum detectable velocity |
| ATI | along track interferometric |
| DPCA | displaced phase center antenna |
| TSX | TerraSAR-X |
| TDX | TanDEM-X |
| SCNR | signal-to-clutter plus noise ratio |
| SBRAS | SpaceBorne Radar Advanced Simulator |
| i.i.d. | independent and identically distributed |
| ML | maximum likelihood |
| STAP | space time adaptive processing |
| RCS | radar cross-section |
| GLRT | generalized likelihood ratio test |
| ACE | adaptive coherence estimator |
| ROC | Receiver Operating Characteristic |
| Pd | probability of detection |
| Pfa | probability of false alarm |
| LRT | likelihood ratios test |
| Pc | probability of correct classification |
| InSAR | interferometric synthetic aperture radar |
| DEM | digital elevation model |
References
- Paul Aguttes, J. The SAR Train Concept: An Along-Track Formation of Sar Satellites for Diluting the Antenna Area over N Smaller Satellites, While Increasing Performance by N. Acta Astronaut. 2005, 57, 197–204. [Google Scholar] [CrossRef]
- Budillon, A.; Schirinzi, G. Performance Evaluation of a GLRT Moving Target Detector for TerraSAR-X Along-Track Interferometric Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3350–3360. [Google Scholar] [CrossRef]
- Suwa, K.; Yamamoto, K.; Tsuchida, M.; Nakamura, S.; Wakayama, T.; Hara, T. Image-Based Target Detection and Radial Velocity Estimation Methods for Multichannel SAR-GMTI. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1325–1338. [Google Scholar] [CrossRef]
- Sikaneta, I.C.; Gierull, C.H. Adaptive CFAR for Space-Based Multichannel SAR–GMTI. IEEE Trans. Geosci. Remote Sens. 2012, 50, 5004–5013. [Google Scholar] [CrossRef]
- Rashid, M.; Dansereau, R.M. Cramér–Rao Lower Bound Derivation and Performance Analysis for Space-Based SAR GMTI. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6031–6043. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Spaceborne Bi- and Multistatic SAR: Potential and Challenges. IEEE Proc. Radar Sonar Navig. 2006, 153, 184–198. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A Satellite Formation for High-Resolution SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Li, Z.F.; Bao, Z.; Yang, F.F. Ground Moving Target Detection and Location Based on SAR Images for Distributed Spaceborne SAR. Sci. China Ser. F 2005, 48, 632–646. [Google Scholar] [CrossRef]
- Yang, Z.W.; Liao, G.S.; Zeng, C. Reduced-Dimensional Processing for Ground Moving Target Detection in Distributed Space-Based Radar. IEEE Geosci. Remote Sens. Lett. 2007, 4, 256–259. [Google Scholar] [CrossRef]
- He, X.P.; Liao, G.S.; Xu, J.W.; Zhu, S.Q. Robust Radial Velocity Estimation Based on Joint-Pixel Normalized Sample Covariance Matrix and Shift Vector for Moving Targets. IEEE Geosci. Remote Sens. Lett. 2019, 16, 221–225. [Google Scholar] [CrossRef]
- Meyer, F.; Hinz, S.; Laika, A.; Weihing, D.; Bamler, R. Performance Analysis of the TerraSAR-X Traffic Monitoring Concept. ISPRS J. Photogramm. Remote Sens. 2006, 61, 225–242. [Google Scholar] [CrossRef]
- Hinz, S.; Meyer, F.; Laika, A.; Bamler, R. Spaceborne Traffic Monitoring with Dual Channel Synthetic Aperture Radar Theory and Experiments. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05)—Workshops, San Diego, CA, USA, 21–23 September 2005; pp. 89–94. [Google Scholar] [CrossRef]
- Meyer, F.; Hinz, S.; Laika, A.; Bamler, R. A-Priori Information Driven Detection of Moving Objects for Traffic Monitoring by SAR. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Republic of Korea, 25–29 July 2005; Volume 4, pp. 2932–2936. [Google Scholar] [CrossRef]
- Meyer, F.; Hinz, S. The Feasibility of Traffic Monitoring with TerraSAR-X–Analyses and Consequences. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; IGARSS’04. IEEE: Anchorage, AK, USA, 2004; Volume 2, pp. 1502–1505. [Google Scholar] [CrossRef]
- Cai, B.; Dong, Z.; Zhang, Y.; Chen, Q. Integrating a Prior Information to Spaceborne Dual-Channel SAR-GMTI. In Proceedings of the IET Conference Publications, Guilin, China, 20–22 April 2009; pp. 444–448. [Google Scholar] [CrossRef]
- Baumgartner, S.V.; Krieger, G. Fast GMTI Algorithm For Traffic Monitoring Based On A Priori Knowledge. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4626–4641. [Google Scholar] [CrossRef]
- Baumgartner, S.V.; Krieger, G. A priori knowledge based GMTI algorithm for traffic monitoring applications. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 469–472. [Google Scholar]
- Baumgartner, S.V.; Krieger, G. Real-Time Road Traffic Monitoring Using a Fast a Priori Knowledge Based SAR-GMTI Algorithm. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1843–1846. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, X.; Zou, Z.; Liu, X.; Liao, G.; Fan, H. Road-Aided Along-Track Baseline Estimation in a Multichannel SAR-GMTI System. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1416–1420. [Google Scholar] [CrossRef]
- Budillon, A.; Gierull, C.H.; Pascazio, V.; Schirinzi, G. Along-Track Interferometric SAR Systems for Ground-Moving Target Indication: Achievements, Potentials, and Outlook. IEEE Geosci. Remote Sens. Mag. 2020, 8, 46–63. [Google Scholar] [CrossRef]
- Song, C.; Wang, B.; Xiang, M.; Li, W. Extended GLRT Detection of Moving Targets for Multichannel SAR Based on Generalized Steering Vector. Sensors 2021, 21, 1478. [Google Scholar] [CrossRef]
- Pan, W.; Cai, B. Robust Adaptive Ground Moving Target Indication Technique Applied to Distributed Spaceborne SAR System. In Proceedings of the 2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 22–24 October 2010; pp. V5-289–V5-293. [Google Scholar] [CrossRef]
- Cai, B. Research on Signal Processing of Distributed Spaceborne InSAR and SAR-GMTI. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2009. [Google Scholar] [CrossRef]
- Wang, M.; Huang, H.; Dong, Z. SBRAS—An Advanced Simulator of Spaceborne Radar. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 4942–4944. [Google Scholar] [CrossRef]
- He, Z.H.; He, F.; Dong, Z.; Liang, D.N. Real-Time Raw-Signal Simulation Algorithm for InSAR Hardware-in-the-Loop Simulation Applications. IEEE Geosci. Remote Sens. Lett. 2012, 9, 134–138. [Google Scholar] [CrossRef]
- Gierull, C.H. Digital Channel Balancing of Along-Track Interferometric SAR Data; Technical Memorandum TM 2003-024; Defence Research Establishment Ottawa (DREO): Ottawa, ON, Canada, 2003. [Google Scholar]
- Chiu, S.; Livingstone, C. A Comparison of Displaced Phase Centre Antenna and Along-Track Interferometry Techniques for RADARSAT-2 Ground Moving Target Indication. Can. J. Remote Sens. 2005, 31, 37–51. [Google Scholar] [CrossRef]
- McDonald, K.F.; Blum, R.S. Exact Performance of STAP Algorithms with Mismatched Steering and Clutter Statistics. IEEE Trans. Signal Process. 2000, 48, 2750–2763. [Google Scholar] [CrossRef]
- Pulsone, N.B.; Rader, C.M. Adaptive Beamformer Orthogonal Rejection Test. IEEE Trans. Signal Process. 2001, 49, 521–529. [Google Scholar] [CrossRef]
- Richmond, C.D. Performance of the Adaptive Sidelobe Blanker Detection Algorithm in Homogeneous Environments. IEEE Trans. Signal Process. 2000, 48, 1235–1247. [Google Scholar] [CrossRef]
- Robey, F.C.; Fuhrmann, D.R.; Kelly, E.J.; Nitzberg, R.A. A CFAR adaptive matched filter detector. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 208–216. [Google Scholar] [CrossRef]
- Kelly, E.J. An adaptive detection algorithm. IEEE Trans. Aerosp. Electron. Syst. 1986, AES-22, 115–127. [Google Scholar] [CrossRef]
- Gini, F.; Farina, A.; Greco, M.S. Radar Detection and Preclassification Based on Multiple Hypothesis Testing. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1046–1059. [Google Scholar] [CrossRef]
- Green, M.; Zoubir, A.M. Multiple hypothesis testing for time-varying nonlinear system identification. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; Volume 1, pp. 560–563. [Google Scholar] [CrossRef]
- Fomin, F.V.; Kratsch, D. Exact Exponential Algorithms; Texts in Theoretical Computer Science. In An EATCS Series; Springer: Berlin/Heidelberg, Germany, 2010; pp. 49–72. ISBN 978-3-642-16532-0. [Google Scholar]
- Lodhi, M.A.; Bajwa, W.U. Detection Theory for Union of Subspaces. IEEE Trans. Signal Process. 2018, 66, 6347–6362. [Google Scholar] [CrossRef]
- Grzegorzewski, P. The Inclusion–Exclusion Principle for IF-Events. Inf. Sci. 2011, 181, 536–546. [Google Scholar] [CrossRef]
- Gaffney, C.T. The Application of the Inclusion-Exclusion Principle in Learning Monotone Boolean Functions. Master’s Thesis, University of Nevada, Reno, NV, USA, 2009. [Google Scholar]
- Roberts, F.S.; Tesman, B. Applied Combinatorics. In A Chapman & Hall Book, 2nd ed.; CRC Press: Boca Raton, FA, USA, 2009; ISBN 978-1-4200-9982-9. [Google Scholar]
- Pastina, D.; Turin, F. Exploitation of the COSMO-SkyMed SAR System for GMTI Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 966–979. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, B.; Hao, X.; Chen, L.; Liang, J.; Cheng, T.; Luo, Y. A Priori Knowledge Based Ground Moving Target Indication Technique Applied to Distributed Spaceborne SAR System. Remote Sens. 2023, 15, 2467. https://doi.org/10.3390/rs15092467
Cai B, Hao X, Chen L, Liang J, Cheng T, Luo Y. A Priori Knowledge Based Ground Moving Target Indication Technique Applied to Distributed Spaceborne SAR System. Remote Sensing. 2023; 15(9):2467. https://doi.org/10.3390/rs15092467
Chicago/Turabian StyleCai, Bin, Xiaolong Hao, Li Chen, Jia Liang, Tianhao Cheng, and Ying Luo. 2023. "A Priori Knowledge Based Ground Moving Target Indication Technique Applied to Distributed Spaceborne SAR System" Remote Sensing 15, no. 9: 2467. https://doi.org/10.3390/rs15092467





