Accurate Discharge Estimation Based on River Widths of SWOT and Constrained At-Many-Stations Hydraulic Geometry
Abstract
1. Introduction
2. Materials and Methods
2.1. SWOT-River-Width Extraction
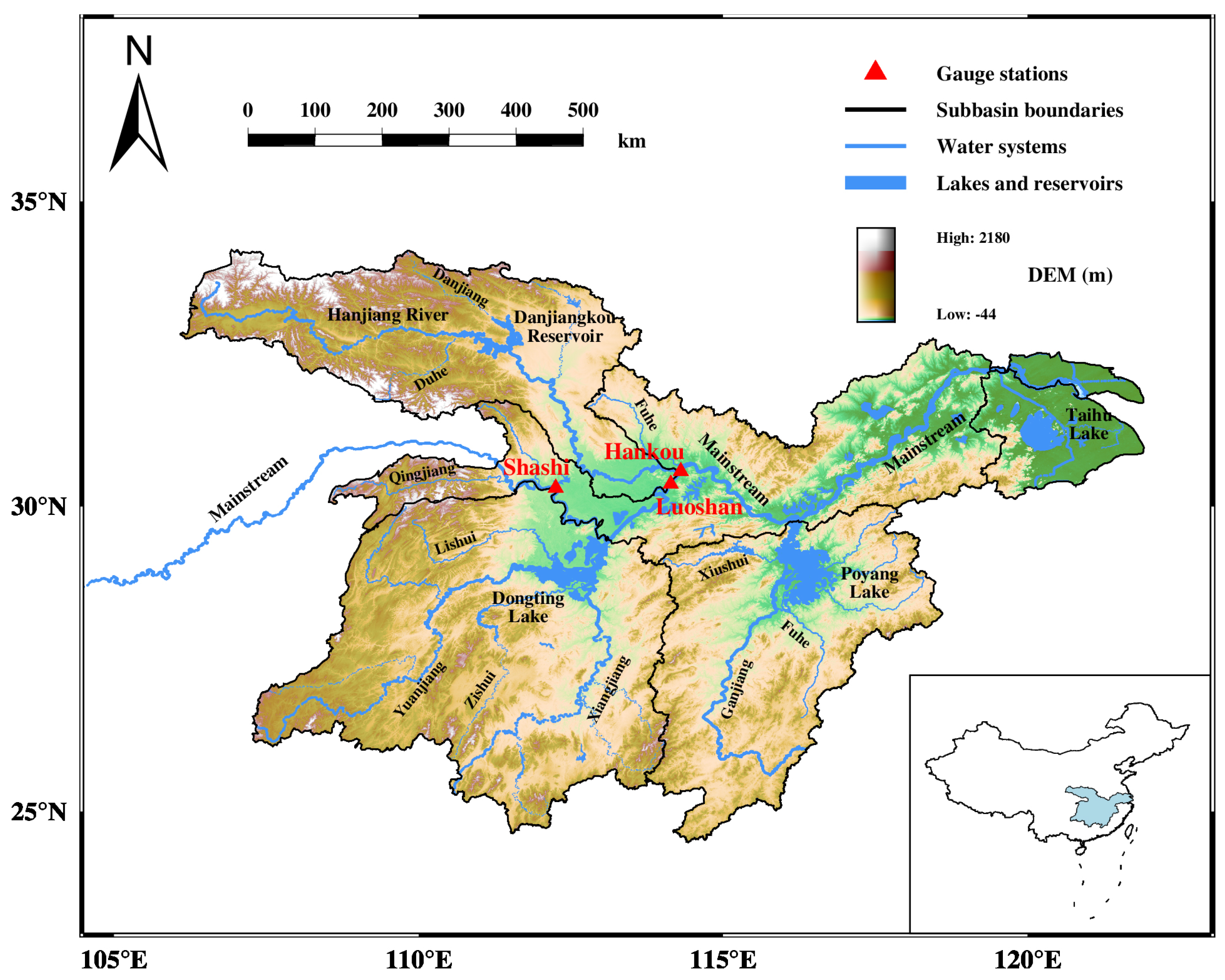
2.1.1. Study Region and Datasets
2.1.2. SWOT-River-Product Simulation
2.1.3. River-Width Extraction from SWOT River Product
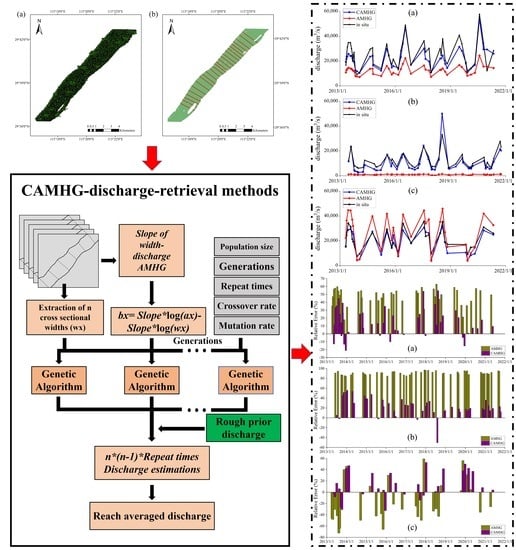
2.2. AMHG-Discharge-Retrieval Methods
2.2.1. At-Many-Stations Hydraulic Geometry
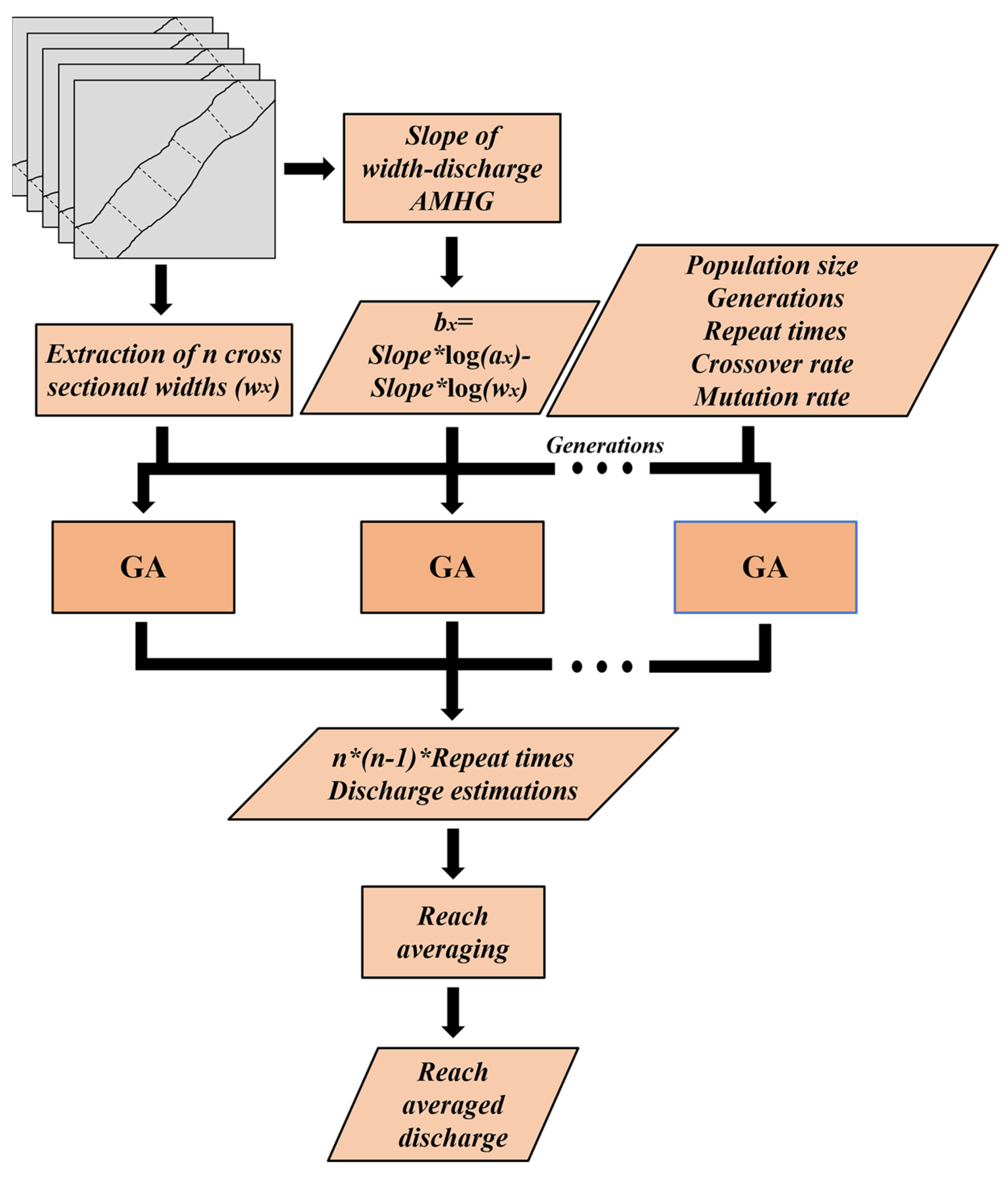
2.2.2. Discharge-Calculation Workflow Based on AMHG and SWOT River Width
2.2.3. Constrained At-Many-Stations Hydraulic Geometry-Discharge-Retrieval Approach
2.2.4. Performance Metrics
3. Results
3.1. Discharge Estimation of Original AMHG-Discharge-Retrieval Method
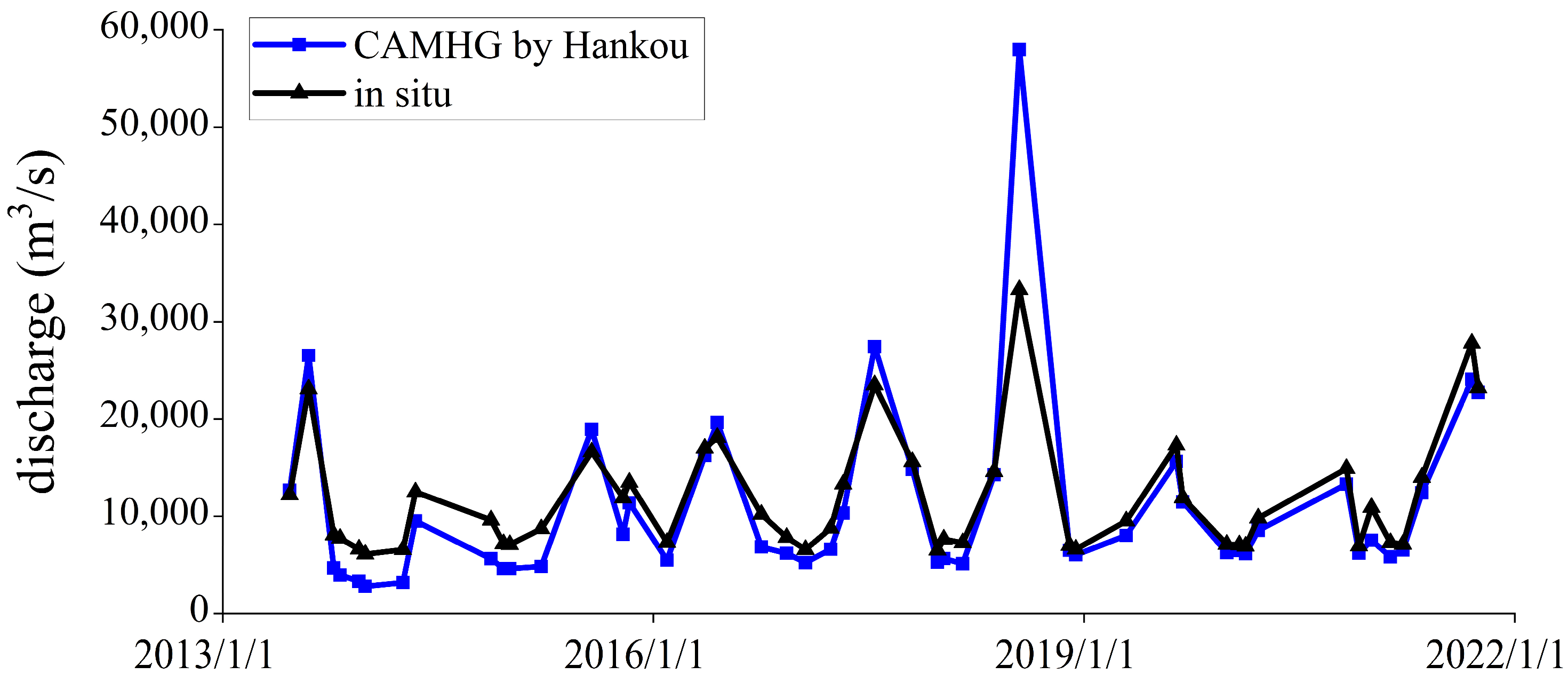
3.2. Discharge Estimation of CAMHG-Discharge-Retrieval Approach
4. Discussion
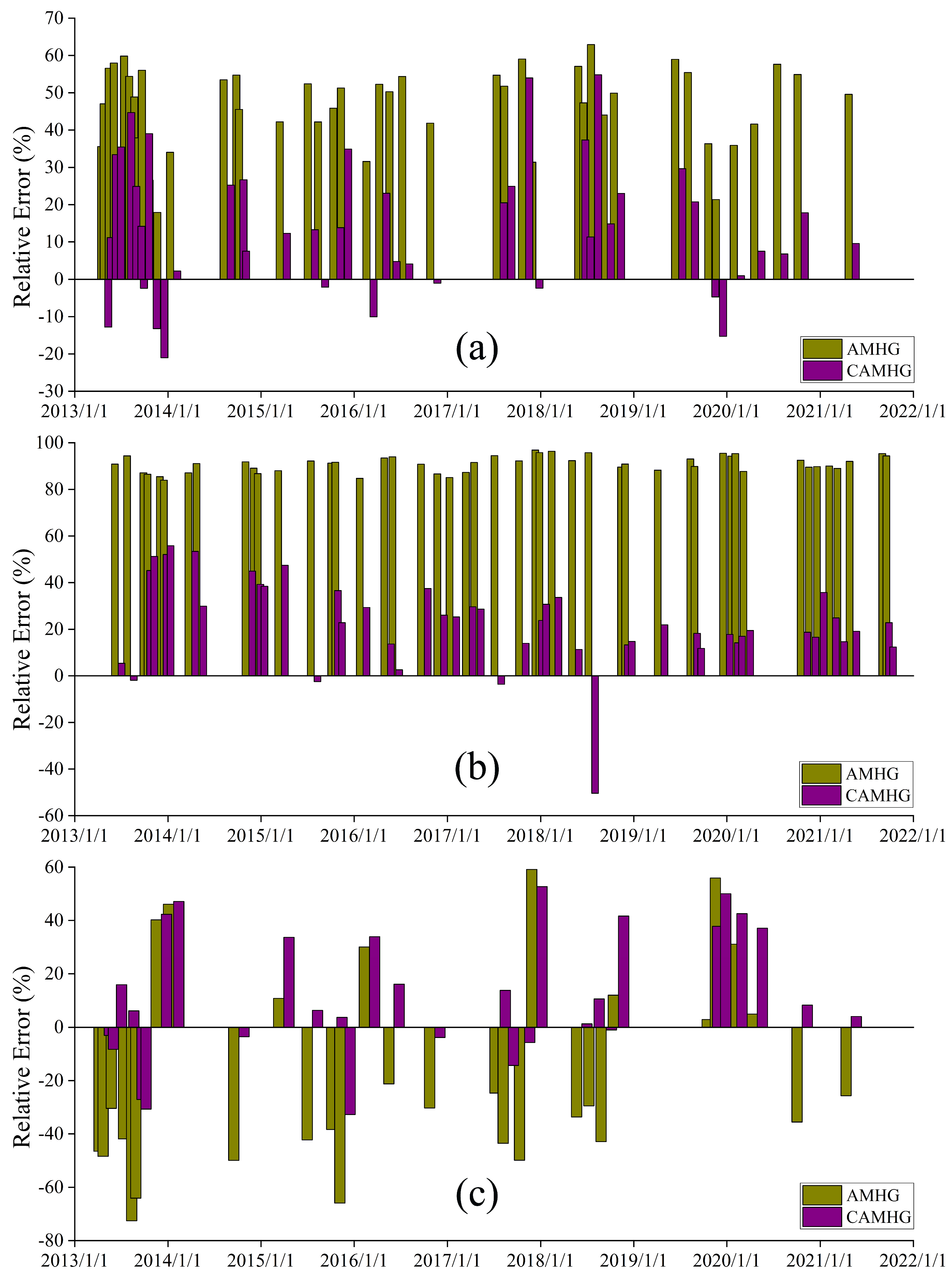
4.1. Analysis the Results of Original AMHG-Discharge-Retrieval Method
4.2. Analysis of the Results of the CAMHG-Discharge-Retrieval Approach
4.3. Influence of Prior Discharge and Threshold Selection on Discharge Calculation
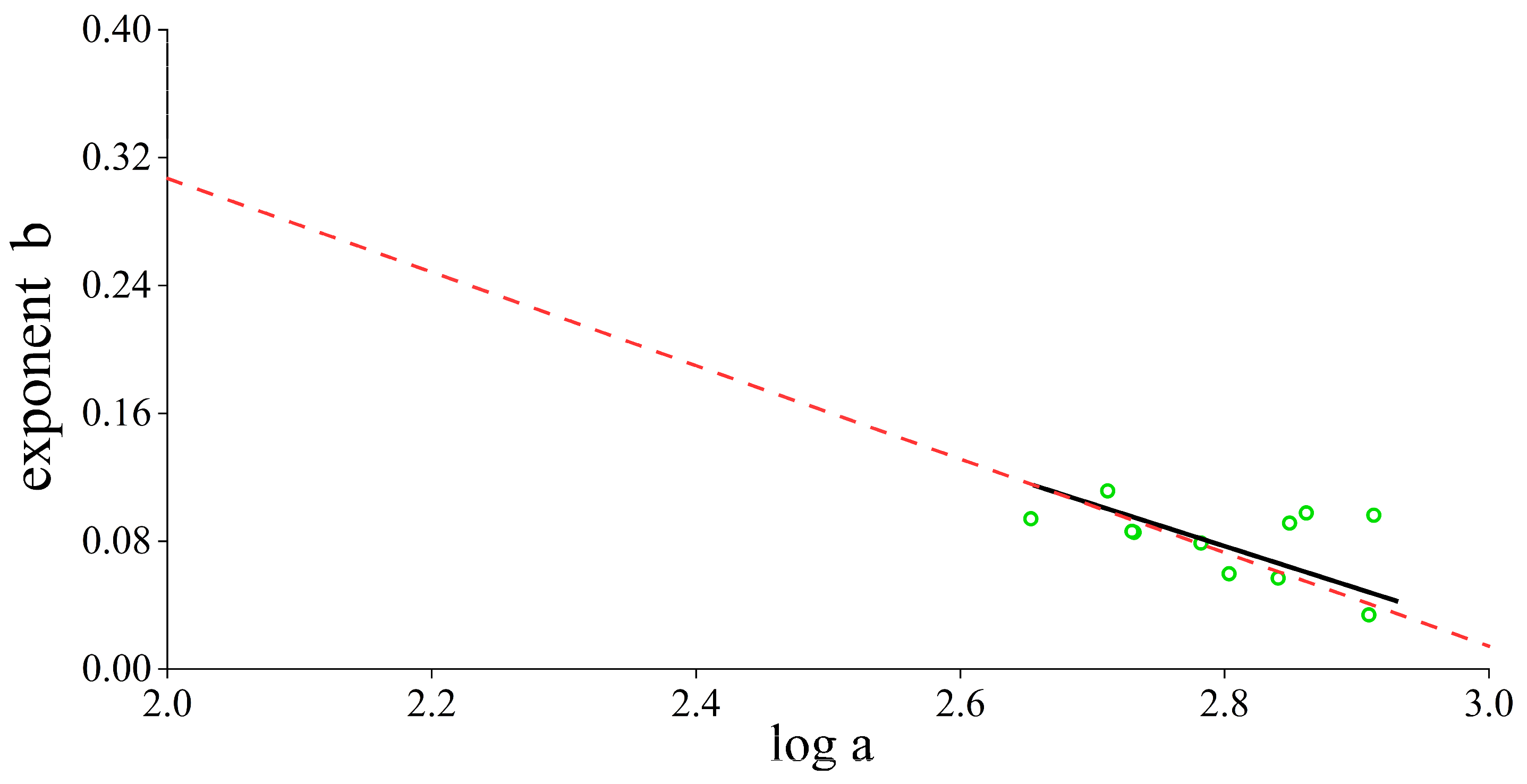
4.4. The Feasibility of Establishing AMHG Relationship Solely Using River-Width Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An Intercomparison of Remote Sensing River Discharge Estimation Algorithms from Measurements of River Height, Width, and Slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Oki, T.; Kanae, S. Global hydrological cycles and world water resources. Science 2006, 313, 1068–1072. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Fekete, B.M.; Meybeck, M.; Lammers, R.B. Global System of Rivers: Its Role in Organizing Continental Land Mass and Defining Land-to-Ocean Linkages. Glob. Biogeochem. Cycles 2000, 14, 599–621. [Google Scholar] [CrossRef]
- Turnipseed, D.P.; Sauer, V.B. Discharge Measurements at Gaging Stations; Techniques and Methods; US Geological Survey: Reston, VA, USA, 2010; pp. 2–8.
- Absi, R. Reinvestigating the Parabolic-Shaped Eddy Viscosity Profile for Free Surface Flows. Hydrology 2021, 8, 126. [Google Scholar] [CrossRef]
- Lin, H.; Cheng, X.; Zheng, L.; Li, T.; Peng, F.; Zhang, Z.; Tao, J. Discharge Estimation with Improved Methods Using MODIS Data in Greenland: An Application in the Watson River. IEEE J. Sel Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7576–7588. [Google Scholar] [CrossRef]
- Huntington, T.G. Evidence for Intensification of the Global Water Cycle: Review and Synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring Surface Water from Space. Surv. Geophys. 2007, 45, RG2002. [Google Scholar] [CrossRef]
- Biancamaria, S.; Durand, M.; Andreadis, K.M.; Bates, P.D.; Boone, A.; Mognard, N.M.; Rodríguez, E.; Alsdorf, D.E.; Lettenmaier, D.P.; Clark, E.A. Assimilation of Virtual Wide Swath Altimetry to Improve Arctic River Modeling. Remote Sens. Environ. 2011, 115, 373–381. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating Discharge in Rivers Using Remotely Sensed Hydraulic Information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.A.; Fulton, J.W.; Garambois, P.-A. Satellite Remote Sensing Estimation of River Discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using Satellite Altimetry Data to Augment Flow Estimation Techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Huang, Q.; Long, D.; Du, M.; Zeng, C.; Qiao, G.; Li, X.; Hou, A.; Hong, Y. Discharge Estimation in High-Mountain Regions with Improved Methods Using Multisource Remote Sensing: A Case Study of the Upper Brahmaputra River. Remote Sens. Environ. 2018, 219, 115–134. [Google Scholar] [CrossRef]
- Revel, M.; Ikeshima, D.; Yamazaki, D.; Kanae, S. A Framework for Estimating Global-Scale River Discharge by Assimilating Satellite Altimetry. Water Resour. Res. 2021, 57, e2020WR027876. [Google Scholar] [CrossRef]
- Ashmore, P.; Sauks, E. Prediction of Discharge from Water Surface Width in a Braided River with Implications for At-a-Station Hydraulic Geometry. Water Resour. Res. 2006, 42, 85. [Google Scholar] [CrossRef]
- Smith, L.C.; Pavelsky, T.M. Estimation of River Discharge, Propagation Speed, and Hydraulic Geometry from Space: Lena River, Siberia. Water Resour. Res. 2008, 44, 165. [Google Scholar] [CrossRef]
- Nathanson, M.; Kean, J.W.; Grabs, T.J.; Seibert, J.; Laudon, H.; Lyon, S.W. Modelling Rating Curves Using Remotely Sensed LiDAR Data. Hydrol. Process. 2012, 26, 1427–1434. [Google Scholar] [CrossRef]
- Pavelsky, T.M. Using Width-Based Rating Curves from Spatially Discontinuous Satellite Imagery to Monitor River Discharge. Hydrol. Process. 2014, 28, 3035–3040. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Clark, E.A.; Lettenmaier, D.P.; Alsdorf, D.E. Prospects for River Discharge and Depth Estimation through Assimilation of Swath-Altimetry into a Raster-Based Hydrodynamics Model. Geophys. Res. Lett. 2007, 34, L10403. [Google Scholar] [CrossRef]
- Durand, M.; Rodriguez, E.; Alsdorf, D.E.; Trigg, M. Estimating River Depth From Remote Sensing Swath Interferometry Measurements of River Height, Slope, and Width. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 20–31. [Google Scholar] [CrossRef]
- Durand, M.; Neal, J.; Rodríguez, E.; Andreadis, K.M.; Smith, L.C.; Yoon, Y. Estimating Reach-Averaged Discharge for the River Severn from Measurements of River Water Surface Elevation and Slope. J. Hydrol. 2014, 511, 92–104. [Google Scholar] [CrossRef]
- Gejadze, I.; Malaterre, P.-O. Discharge Estimation under Uncertainty Using Variational Methods with Application to the Full Saint-Venant Hydraulic Network Model. Int. J. Numer. Meth. Fluids 2017, 83, 405–430. [Google Scholar] [CrossRef]
- Brisset, P.; Monnier, J.; Garambois, P.-A.; Roux, H. On the Assimilation of Altimetric Data in 1D Saint–Venant River Flow Models. Adv. Water Resour. 2018, 119, 41–59. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Schumann, G.J.-P.; Frasson, R.P.M.; Wei, R.; Pavelsky, T.M.; Castellarin, A.; Brath, A.; Durand, M.T. Characterizing Water Surface Elevation under Different Flow Conditions for the Upcoming SWOT Mission. J. Hydrol. 2018, 561, 848–861. [Google Scholar] [CrossRef]
- Uebbing, B.; Kusche, J.; Forootan, E. Waveform Retracking for Improving Level Estimations From TOPEX/Poseidon, Jason-1, and Jason-2 Altimetry Observations Over African Lakes. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2211–2224. [Google Scholar] [CrossRef]
- Gleason, C.J.; Smith, L.C. Toward Global Mapping of River Discharge Using Satellite Images and At-Many-Stations Hydraulic Geometry. Proc. Natl. Acad. Sci. USA 2014, 111, 4788–4791. [Google Scholar] [CrossRef] [PubMed]
- Gleason, C.J.; Smith, L.C.; Lee, J. Retrieval of River Discharge Solely from Satellite Imagery and At-Many-Stations Hydraulic Geometry: Sensitivity to River Form and Optimization Parameters. Water Resour. Res. 2014, 50, 9604–9619. [Google Scholar] [CrossRef]
- Gleason, C.J.; Wang, J. Theoretical Basis for At-many-stations Hydraulic Geometry. Geophys. Res. Lett. 2015, 42, 7107–7114. [Google Scholar] [CrossRef]
- Gleason, C.J.; Hamdan, A.N. Crossing the (Watershed) Divide: Satellite Data and the Changing Politics of International River Basins: Crossing the (Watershed) Divide. Geogr. J. 2017, 183, 2–15. [Google Scholar] [CrossRef]
- Dingman, S.L.; Afshari, S. Field Verification of Analytical At-a-Station Hydraulic-Geometry Relations. J. Hydrol. 2018, 564, 859–872. [Google Scholar] [CrossRef]
- Mengen, D.; Ottinger, M.; Leinenkugel, P.; Ribbe, L. Modeling River Discharge Using Automated River Width Measurements Derived from Sentinel-1 Time Series. Remote Sens. 2020, 12, 3236. [Google Scholar] [CrossRef]
- Biancamaria, S.; Andreadis, K.M.; Durand, M.; Clark, E.A.; Rodriguez, E.; Mognard, N.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Oudin, Y. Preliminary Characterization of SWOT Hydrology Error Budget and Global Capabilities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2010, 3, 6–19. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Durand, M.T.; Andreadis, K.M.; Beighley, R.E.; Paiva, R.C.D.; Allen, G.H.; Miller, Z.F. Assessing the Potential Global Extent of SWOT River Discharge Observations. J. Hydrol. 2014, 519, 1516–1525. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Durand, M.T.; Hossain, F. Spatiotemporal Interpolation of Discharge across a River Network by Using Synthetic SWOT Satellite Data. Water Resour. Res. 2015, 51, 430–449. [Google Scholar] [CrossRef]
- Bonnema, M.G.; Sikder, S.; Hossain, F.; Durand, M.; Gleason, C.J.; Bjerklie, D.M. Benchmarking Wide Swath Altimetry-Based River Discharge Estimation Algorithms for the Ganges River System. Water Resour. Res. 2016, 52, 2439–2461. [Google Scholar] [CrossRef]
- Brinkerhoff, C.B.; Gleason, C.J.; Ostendorf, D.W. Reconciling At-a-Station and At-Many-Stations Hydraulic Geometry Through River-Wide Geomorphology. Geophys. Res. Lett. 2019, 46, 9637–9647. [Google Scholar] [CrossRef]
- Barber, C.A.; Gleason, C.J. Verifying the Prevalence, Properties, and Congruent Hydraulics of at-Many-Stations Hydraulic Geometry (AMHG) for Rivers in the Continental United States. J. Hydrol. 2018, 556, 625–633. [Google Scholar] [CrossRef]
- Hagemann, M.W.; Gleason, C.J.; Durand, M.T. BAM: Bayesian AMHG-Manning Inference of Discharge Using Remotely Sensed Stream Width, Slope, and Height. Water Resour. Res. 2017, 53, 9692–9707. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Statistical Methods in Water Resources; USGS Techniques and Methods; Elsevier Science Publishers B.V.: New York, NY, USA, 1992; Book 4, Chapter A3. [Google Scholar]
- Duan, N. Smearing Estimate: A Nonparametric Retransformation Method. J. Am. Stat. Assoc. 1983, 78, 605–610. [Google Scholar] [CrossRef]
- Fernandez, D.E. Swot Project Mission Performance and Error Budget. Available online: https://swot.jpl.nasa.gov/system/documents/files/2178_2178_SWOT_D-79084_v10Y_FINAL_REVA__06082017.pdf (accessed on 2 November 2022).
- Elmer, N.J.; Hain, C.; Hossain, F.; Desroches, D.; Pottier, C. Generating Proxy SWOT Water Surface Elevations Using WRF-Hydro and the CNES SWOT Hydrology Simulator. Water Resour. Res. 2020, 56, e2020WR027464. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications; US Geological Survey: Washington, DC, USA, 1953; pp. 1–2.
- Smith, L.C.; Isacks, B.L.; Bloom, A.L.; Murray, A.B. Esti.imation of Discharge From Three Braided Rivers Using Synthetic Aperture Radar Satellite Imagery: Potential Application to Ungaged Basins. Water Resour. Res. 1996, 32, 2021–2034. [Google Scholar] [CrossRef]
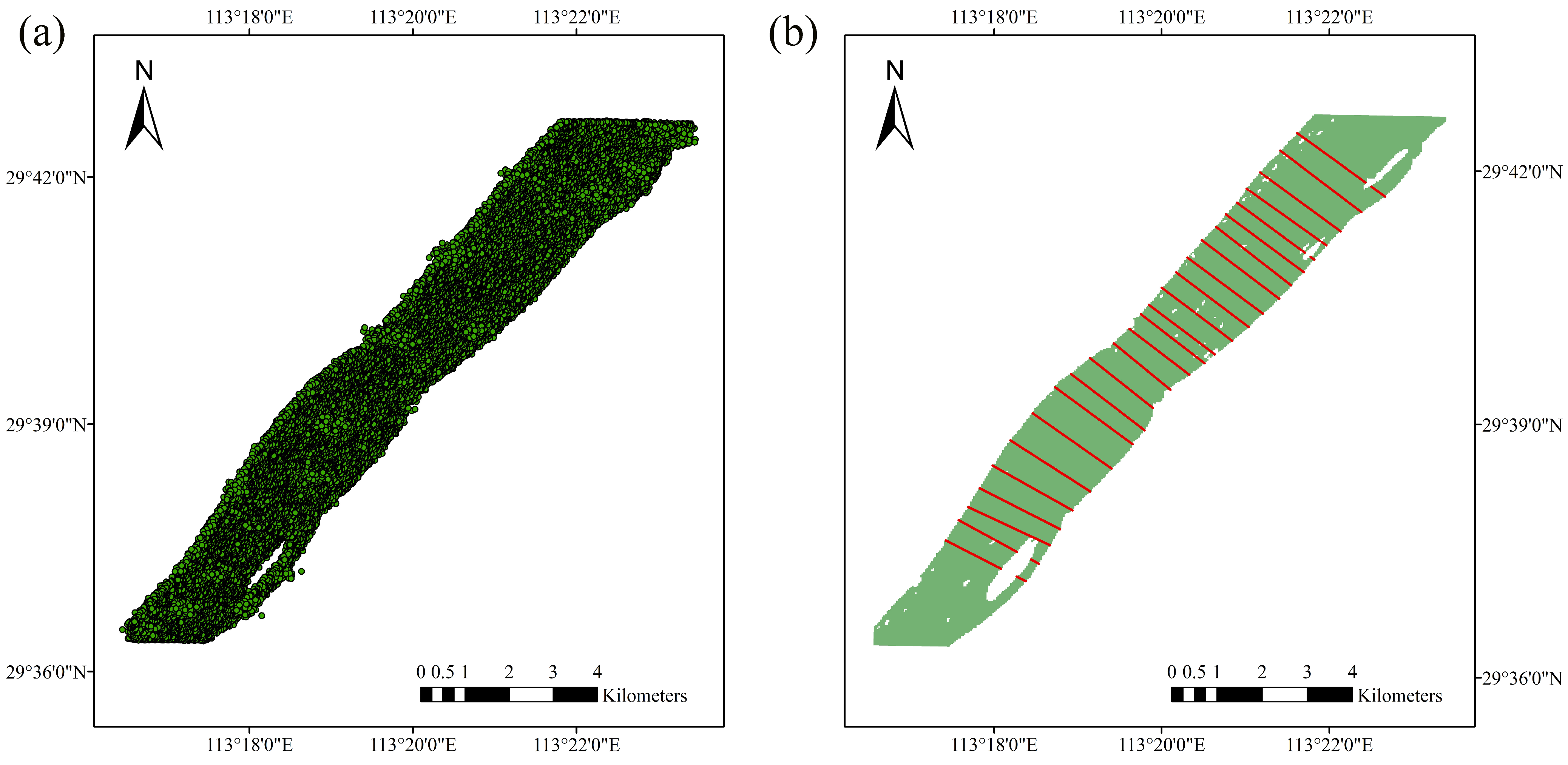





| Cross-Section No. | Width (m) | Cross-Section No. | Width (m) |
|---|---|---|---|
| 1 | 2028.23 | 14 | 1490.06 |
| 2 | 2027.54 | 15 | 1490.46 |
| 3 | 1922.89 | 16 | 1625.91 |
| 4 | 1875.83 | 17 | 1877.38 |
| 5 | 1758.96 | 18 | 1941.77 |
| 6 | 1967.31 | 19 | 1938.64 |
| 7 | 1882.49 | 20 | 1901.33 |
| 8 | 1966.83 | 21 | 1822.39 |
| 9 | 1899.51 | 22 | 1790.99 |
| 10 | 1840.87 | 23 | 1764.48 |
| 11 | 1740.1 | 24 | 1447.5 |
| 12 | 1648.15 | 25 | 1439.12 |
| 13 | 1590.08 |
| Parameter | Value |
|---|---|
| Population size | 10 |
| Generations | 50 |
| Minimum value of coefficient a | 10 |
| Maximum value of coefficient a | 1000 |
| Minimum value of exponent b | 0.01 |
| Maximum value of exponent b | 0.31 |
| Crossover rate | 0.8 |
| Mutation rate | 0.1 |
| Minimum allowable discharge | 5000 m3/s |
| Maximum allowable discharge | 60,000 m3/s |
| Repeat times | 50 |
| Description | Abbreviation | Definition |
|---|---|---|
| Relative error | RE | |
| Root-mean-square error | RMSE | |
| Relative-root-mean-square error | RRMSE | |
| Correlation coefficient | CC | 1 |
| Reach | AMHG | Optimized AMHG | ||||
|---|---|---|---|---|---|---|
| RMSE (m3/s) | RRMSE | CC | RMSE (m3/s) | RRMSE | CC | |
| Hankou | 14,628.958 | 100.1% | 0.9157 | 5784.471 | 24.4% | 0.8925 |
| Shashi | 12,298.872 | 1137.1% | 0.6484 | 4131.544 | 49.9% | 0.9487 |
| Luoshan | 8852.526 | 48.6% | 0.9489 | 4143.641 | 45.5% | 0.9179 |
| Reach | RMSE_Wet (m3/s) | RMSE_Dry (m3/s) | ||
|---|---|---|---|---|
| Before | After | Before | After | |
| Hankou | 17,967.503 | 6047.949 | 6183.772 | 3857.448 |
| Shashi | 18,475.323 | 5295.306 | 6923.751 | 2510.011 |
| Luoshan | 11,221.269 | 3529.366 | 4177.478 | 4647.384 |
| Threshold | RMSE (m3/s) | CC |
|---|---|---|
| 50% | 4411.595 | 0.9504 |
| 20% | 3649.598 | 0.9412 |
| 10% | 3798.167 | 0.9398 |
| 5% | 3864.888 | 0.9394 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, B.; Jin, T.; Liu, D.; Wang, Y.; Wu, X. Accurate Discharge Estimation Based on River Widths of SWOT and Constrained At-Many-Stations Hydraulic Geometry. Remote Sens. 2023, 15, 1672. https://doi.org/10.3390/rs15061672
Du B, Jin T, Liu D, Wang Y, Wu X. Accurate Discharge Estimation Based on River Widths of SWOT and Constrained At-Many-Stations Hydraulic Geometry. Remote Sensing. 2023; 15(6):1672. https://doi.org/10.3390/rs15061672
Chicago/Turabian StyleDu, Bin, Taoyong Jin, Dong Liu, Youkun Wang, and Xuequn Wu. 2023. "Accurate Discharge Estimation Based on River Widths of SWOT and Constrained At-Many-Stations Hydraulic Geometry" Remote Sensing 15, no. 6: 1672. https://doi.org/10.3390/rs15061672
APA StyleDu, B., Jin, T., Liu, D., Wang, Y., & Wu, X. (2023). Accurate Discharge Estimation Based on River Widths of SWOT and Constrained At-Many-Stations Hydraulic Geometry. Remote Sensing, 15(6), 1672. https://doi.org/10.3390/rs15061672