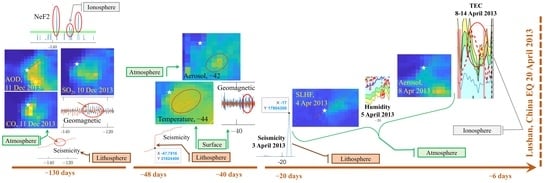
Are There One or More Geophysical Coupling Mechanisms before Earthquakes? The Case Study of Lushan (China) 2013

Abstract

Several possible lithosphere–atmosphere–ionosphere coupling mechanisms before earthquake occurrence are presented in the literature. They are described by several models with different interaction channels (e.g., electromagnetic, mechanics, chemical, thermal), sometimes in conflict with each other. In this paper, we search for anomalies six months before the Lushan (China) 2013 earthquake in the three geo-layers looking for a possible view of the couplings and testing if one or another is more reliable to describe the observations. The Lushan earthquake occurred in China’s Sichuan province on 20 April 2013, with a magnitude of Mw = 6.7. Despite the moderate magnitude of the event, it caused concern because its source was localized on the southwest side of the same fault that produced the catastrophic Wenchuan event in 2008. This paper applies a geophysical multi-layer approach to search for possible pre-earthquake anomalies in the lithosphere, atmosphere, and ionosphere. In detail, six main increases in the accumulated seismic stress were depicted. Anomalous geomagnetic pulsations were recorded in the Chengdu observatory, sometimes following the increased stress. Atmosphere status and composition were found to be anomalous in several periods before the earthquake, and, spatially, the anomalies seem to appear firstly far from the upcoming earthquakes and later approaching the Longmenshan fault where the Lushan earthquakes nucleated. The Formosat-3 data identified interesting anomalies in the altitude or electron content of the ionospheric F2 peak in correspondence with seismic and atmospheric anomalies 130 days before the earthquake. In addition, the total electron content showed high anomalous values from 12 to 6 days before the earthquake. We compared the anomalies and tried to explain their correspondences in different geo-layers by the lithosphere–atmosphere–ionosphere coupling models. In particular, we identified three possible couplings with different mechanisms: a first, about 130 days before the earthquake, with a fast (order of one day) propagation delay; a second, about 40 days before the earthquake occurrence, with a propagation delay of few days and a third from 2.5 weeks until one week before the event. Such evidence suggests that the geo-layers could interact with different channels (pure electromagnetic or a chain of physical-chemical processes) with specific propagation delays. Such results support the understanding of the preparation for medium and large earthquakes globally, which is necessary (although not sufficient) knowledge in order to mitigate their impact on human life.

1. Introduction

The Lushan earthquake occurred in China on 20 April 2013 at 00:02:47 UT (8:02:47 Chinese time). The hypocenter was localized at 30.308° N, 102.888° E, and a 14 km depth. The largest city close to the epicenter was Chengdu (120 km East-North-East), the capital of Sichuan province with about 20 million inhabitants. Xie et al. [1] determined the source parameters with several techniques estimating a moment magnitude Mw of about 6.66. From a tectonic point of view, the earthquake occurred due to a thrust fault on the Longmenshan fault, which was where the catastrophic Mw = 7.9 Wenchuan 2008 earthquake occurred five years before [2].

The possibility that there are precursors to earthquakes is a debated scientific question. Concerning the recent past in China, it is paradoxical that the successful prediction of the M7.3 Haicheng earthquake that occurred on 4 February 1975 was followed in the next year by a wholly unexpected and tragic M7.5 Tangshan earthquake on 27 July 1976 [3]. These predictions have been based mainly on observing strange animal behavior, which has also been observed before more recent earthquakes, for example, the Mw = 6.1 earthquake in Colfiorito, Central Italy, in 1997 [4]. If the animals, in some cases, feel some alteration of the environment that humans cannot perceive, the instrumentations developed in the last decades, especially remote sensing satellites, must be able to catch these possible alterations before an earthquake. So, the right research path for a future prediction of earthquakes is firstly to understand the possible environmental changes that typically occur before their occurrence. This is the topic of this paper.

Several pieces of evidence have been provided in the last few decades showing possible candidates for earthquake precursors. Preliminary studies focused on the investigation of one parameter before one earthquake, such as Frase-Smith et al. [5], who reported Ultra Low Frequency (ULF) electromagnetic emissions before the M7.1 Loma-Prieta (US) 1989 earthquake. Other studies, such as Piscini et al. [6], applied a multi-parametric approach to study the atmosphere in the specific case of Skin Temperature, Total Column Water Vapour, and Total Column Ozone before the Italian Seismic sequence of 2016–2017. The advantage of a multi-parametric approach is a better understanding of the physical phenomenon, in this case, in the atmosphere. Still, to have a complete picture of the Earth, a multi-layer approach applied to the lithosphere, atmosphere, and ionosphere is required. Such an approach can better understand the possible interactions between the geo-layers in the preparation phase of an earthquake. Interesting claiming of chains of the possible lithosphere–atmosphere–ionosphere couplings before the Mw = 9.1 great Tohoku (Japan) 2011, Mw = 7.8 Gorkha (Nepal) 2015, Mw = 6.0 Amatrice (Italy) 2016, Mw = 7.5 Indonesia 2018, Mw = 7.1 Ridgecrest (USA), and Mw = 7.2 Kermadec (New Zealand) 2019 earthquakes were reported, respectively, by Chen et al. [7], Han et al. [8], Ouzounov et al. [9], Fan et al. [10], Marchetti et al. [11,12], and De Santis et al. [13,14]. A similar approach with further interesting findings was applied before the La Palma 2021 and Hunga Tonga-Hunga-Ha’Apai 2022 volcano eruptions by Marchetti et al. [15,16] and D’Arcangelo et al. [17]. This multi-layer and multi-parametric approach is the one we followed in the present study.

Some single parameters used in such studies were statistically investigated in specific areas or worldwide. In particular, Hattori et al. [18] propose a 10-years statistical investigation of ULF electromagnetic signals from ground geomagnetic observatories in Japan. Genzano et al. [19] instead made a statistical assessment of Thermal InfraRed (TIR) anomalies detected from satellites, including Japan. The worldwide ionospheric perturbations detected by DEMETER, Swarm, and China Seismo Electromagnetic Satellite were systematically correlated with earthquakes of magnitude 4.8+, 5.5+, or 6.0+ by Yan et al. [20], Ouyang et al. [21], De Santis et al. [22,23], He et al. [24], and Marchetti et al. [16,25]. These studies demonstrated statistically that ionospheric perturbations preceded some earthquakes by days, weeks, or even months. They also identified that the anticipation time increases with the magnitude of the upcoming events and that the location under the sea or on land can influence the frequency of the electromagnetic signal [22,25].

The existence of pre-earthquake processes is also supported by different Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) models [26]. Unfortunately, the different models contradict each other, describing the coupling with different physical and chemical mechanisms. Essentially, we can outline three coupling mechanisms:

• Pure electromagnetic channel. In this case, the electromagnetic pre-earthquake disturbances propagate using the Maxwell equations of electromagnetism. These models include the ULF electromagnetic waves induced by the separation of charges at the fault level as predicted by Molchanov and Hayakawa [27,28] or an induced current in the ionosphere for variation of resistivity in the ground as indicated by Enomoto [29].
• Chain of mechanical, chemical, thermal, and electromagnetic phenomena. In this mechanism, one process induces another. For example, an increase in mechanical stress can release some radon gas at the Earth’s surface that increases the temperature, drops the humidity, ionizes the air, creates aerosols and clouds, and perturbs electric circuits as proposed by Pulinets and Ouzounov [30], Pulinets and Khachikyan [31], and Pulinets et al. [32,33].
• Acoustic gravity waves. Hayakawa et al. [34] proposed that thermal heating of the ground for the accumulation of the stress on the fault could induce some air pressure oscillations that generate acoustic gravity waves potentially reaching the ionosphere.

It is necessary to note that the above classification is a simplification even of the cited theories. Still, it could help to discriminate in observing what is more likely due to one coupling mechanism rather than another Finally, it is important to note that other explanations are also possible; for example, Freund et al. [35,36] proposed that increased stress can break peroxy-links in the rock, releasing free positive charges (positive-holes or simply p-holes) as the electron can quickly recombine in other ways. These p-holes can potentially explain all the pre-earthquake processes, even the increase in the thermal infrared (IR) radiation detected in several cases before earthquakes. Still, in this theory, such emission would be due to IR photons emitted during p-holes recombination just under the Earth’s surface. If this assumption is valid, the IR emission will not correspond to an Earth’s surface temperature increase. To confirm or exclude such a hypothesis, high-resolution spectra from satellites would be required to discriminate if the IR radiation comes from a “black body” or line emissions, as proposed by Freund et al. [36].

In this paper, we investigate the preparation phase of the Lushan 2013 earthquake through a multi-parametric and multi-layer study. In particular, data from the lithosphere, atmosphere, and ionosphere were analyzed to search for possible geophysical couplings between the geo-layers in the preparation phase of the seismic event.

2. Materials and Methods

This section presents the source and processing of the lithospheric, atmospheric (from the climatological archive), geomagnetic ground observatories, and ionospheric datasets.

2.1. Lithosphere

To study the variations in the lithosphere, we acquired an earthquake catalog. We analyzed cumulative Benioff strain and the released energy as the function of the distance, i.e., the Es parameter as defined by Hattori et al. [18] and Han et al. [37]. The earthquake catalog was retrieved from China National Earthquake Data Center (http://data.earthquake.cn, last accessed on 7 January 2023) and covered the period from 22 October 2012 to 20 April 2013 (i.e., a period of six months before the Lushan earthquake). We selected the seismic events that occurred within the Dobrovolsky radius D (𝐷 = 10^0.43𝑀 km, where M is the earthquake magnitude) [38], and their geographical localization is shown in Figure 1.

We first used the ZMap toolbox provided by ETH (Zurich, Switzerland) [39] to calculate the completeness magnitude Mc and found that Mc was equal to 0.6 within the Dobrovolsky radius, as shown in Figure 2. The completeness magnitude Mc is the minimum magnitude of a seismic event that can be surely detected by a particular seismic network in a specific space-time scale [40]. Only the seismic events with magnitude M ≥ Mc were considered in the following lithospheric analyses.

We calculated the cumulative Benioff strain “S” and “Es” parameter to analyze the lithospheric activity before the Lushan earthquake. The Benioff cumulative strain [41] can be estimated as follows:

$$S\left(t\right)={\displaystyle \sum }_{i=1}^{N\left(t\right)}\sqrt{{10}^{\left(1.5·M_i+4.8\right)}}$$

where “Mi” is the magnitude of the “i-th” seismic event and “N(t)” is the total number of seismic events that occurred until the time “t”. The “Es” parameter is the daily sum of the local earthquake energy ($E_s^{\prime }$) defined by the following equation:

$$E_s\left(t\right)={\displaystyle \sum }_{i=1}^{N\left(t\right)}{E}_s^{\prime }\left(t,i\right)$$

$$E_s^{\prime }\left(t,i\right)=\sqrt{\frac{{10}^{\left(1.5·M_i+4.8\right)}}{r_i^2}}$$

where “r_i” and Es’ are the epicentral distance in km and the local energy in J/km² of the “i-th” seismic event, respectively.

2.2. Geomagnetic Ground Data Processing

We investigated ground geomagnetic data from an observatory station relatively close to the Lushan earthquake, Chengdu FGM01 (CDP), and compared it with the far observatory station, Beijing Ming Tombs (BMT), which was more than 1500 km away from CDP and the epicenter. In particular, CDP was inside the Lushan Dobrovolsky area and near the epicenter, 653.3 m above sea level, while BMT (116.2°E and 40.3°N, 183 m above sea level) was outside the Dobrovolsky area. BMT was taken as a reference, as it was unlikely to be influenced by the Lushan earthquake.

Despite previous studies reporting seismo-induced electromagnetic phenomena from geomagnetic ground stations, as Ultra Low Frequency (ULF) electromagnetic waves recorded from the Z-Vertical component of the geomagnetic field from ground observatories (e.g., [37]), we think that, in this case, the geographical location of the CDP observatory could be not optimal to study this component. We note that Han et al. [37] and Zhuang et al. [42] analyzed statistically the geomagnetic data selecting the closest earthquake to the observatory (in the function of their magnitude). In this paper, we explored one earthquake, the Lushan 2013 seismic event, and the closest geomagnetic observatory was about 106.6 km away. Considering the hypocentral depth of the earthquake was about 14 km, a seismo-induced disturbance coming from the source zone of this earthquake would impact more the horizontal components of the geomagnetic field at the CDP observatory than the vertical one. Consequently, we provide a full analysis of the horizontal and vertical components at the CDP observatory compared with the recording at BMT observatory taking into account the geometry constraints from the earthquake and the geographical position of the geomagnetic observatories.

To avoid inevitable gaps in the data, the original data were cleaned of invalid samples (labeled −99,999) and interpolated by a Piecewise Cubic Hermite Interpolating Polynomial [43]. In addition, the data from CDP obtained from the China Earthquake Networks Center, National Earthquake Data Center (http://data.earthquake.cn) consists of relative values of the total horizontal ($∆\mathrm{H}$), declination ($∆\mathrm{D}$), and vertical ($∆\mathrm{Z}$) components with a sampling rate of 1 Hz. Conversely, the data from BMT (INTERMAGNET) contains absolute values of the north (X), east (Y), and vertical (Z) components with 1 min sampling. Thus, mean values of the CDP data were calculated within a window of 1 min and unified (added baseline and rotated in the other reference frame) by data format conversion:

$$\begin{gathered} \mathrm{H}\left(\mathrm{t}\right)=∆\mathrm{H}\left(\mathrm{t}\right)-∆\mathrm{H}\left(0\right)+\mathrm{H}\left(0\right) \\ \mathrm{D}\left(\mathrm{t}\right)=∆\mathrm{D}\left(\mathrm{t}\right)/60-∆\mathrm{D}\left(0\right)/60+\mathrm{D}\left(0\right) \\ \mathrm{Z}\left(\mathrm{t}\right)=∆\mathrm{Z}\left(\mathrm{t}\right)-∆\mathrm{Z}\left(0\right)+\mathrm{Z}\left(0\right) \\ \mathrm{X}\left(\mathrm{t}\right)=\mathrm{H}\left(\mathrm{t}\right)*\cos \left[D\left(t\right)\right] \\ \mathrm{Y}\left(\mathrm{t}\right)=\mathrm{H}\left(\mathrm{t}\right)*\sin \left[D\left(t\right)\right] \end{gathered}$$

where $∆\mathrm{H}(\mathrm{t}$), $∆\mathrm{D}\left(\mathrm{t}\right)$, $∆\mathrm{Z}\left(\mathrm{t}\right)$ are relative values of the total horizontal, declination ($∆\mathrm{D}$), and vertical ($∆\mathrm{Z}$) components, respectively, detected by CDP. “$∆\mathrm{H}\left(0\right)$”, “$∆\mathrm{D}\left(0\right)$”, “$∆\mathrm{Z}\left(0\right)$” are the original data in the research period. “$\mathrm{H}\left(0\right)$”, “$\mathrm{D}\left(0\right)$”, “$\mathrm{Z}\left(0\right)$” are magnetic field components estimated for CDP location on the first research day (22 October 2012) by the International Geomagnetic Reference Field (IGRF [44]) model (acquired from NCEI Geomagnetic Calculators, https://www.noaa.gov/, last accessed on 30 November 2022), $\mathrm{H}\left(0\right)=34018.8\mathrm{nT}$, $\mathrm{D}\left(0\right)=-1.8661°$, $\mathrm{Z}\left(0\right)=37519.9\mathrm{nT}$.

We filtered the geomagnetic data by five frequency filters, which are defined as A: a high-pass filter of 1 h; B: a band-pass filter between 1 h and 6 h; C: a band-pass filter between 6 h and 1 day; D: a band-pass filter between 1 day and 1 week; and E: a low-pass filter of 1 week analogous to [15]. We compared the CDP and BMT observatories for X, Y, and Z geomagnetic field components based on five frequency bands divided by these filters. We considered that, if CDP and BMT were in accordance, it should be a response to a global perturbation. At the same time, we suggest a local effect for differences between the two observatories.

2.3. Atmosphere: Climatological Archive Data Analysis

In this paper, six parameters were selected to monitor the status of the atmosphere before the Lushan earthquake. They are surface Air temperature, sulfur dioxide, aerosol optical thickness (AOT), carbon monoxide, surface total latent energy flux, and surface specific humidity. Several authors have reported surface total latent energy flux as a possible earthquake precursor [45,46,47]. The relative (or specific) humidity at the surface level is predicted to decrease by the LAIC model of Pulinets and Ouzounov [30], so we also included it to complete our framework of atmospheric analyses.

The data were retrieved from the Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2) climatological model provided by NASA [48]. The dataset was conceived to investigate possible variations in the Earth’s climate. Still, it constitutes a precious resource of data that has extended from 1980 to the present, updated monthly based on several atmospheric parameters interpolated on a regular grid in space and time. Its spatial resolution is 0.625° in longitude, 0.50° in latitude, and 1 h in time. Among the other purposes for which MERRA-2 can be used, it has already been used in the study of the pre-earthquake processes in several cases (the Mw = 6.0 & 6.5 Italy 2016 [11], Mw = 7.8 Ecuador 2016 [45], Mw = 7.3 Iran-Iraq border 2017 [46], Mw = 7.5 Indonesia 2018 [12], Mw = 7.2 Kermadec Islands 2019 [14], and Mw = 7.1 Japan 2021 [47] earthquakes) by the CAPRI and MEANS algorithms defined by Piscini et al. [6,49]. The main difference between the two algorithms is that CAPRI considers possible global warming, performs a linear fit over the data, and removes the obtained slope, correcting the time series. Here, checking the original data for atmospheric parameters in Sichuan, as reported in Figure 3, it can be seen that SO₂ and CO substantially increased between 2000 and 2010, and CO became low after 2020. The decrease in CO after 2020 could be due to ecological policies implemented by China to reduce pollution (for example, promoting electric vehicles instead of combustion-engined vehicles) or an effect of a reduction in production in factories due to COVID pandemic prevention rules. It is out of the scope of this manuscript to determine the cause of such trends, but we want to remove them from the original data as they look to be related to air pollution and not to possible pre-earthquake phenomena. At the same time, the trends are very different from a linear trend, so a polynomial of sufficient degree could fit better such trends.

In Figure 4, it is possible to see the residual sum of the square of a polynomial with a degree from 1 (linear) to 11. Initially, only odd degrees were tested, and then, the even degrees were added around the minimum. Degree 6 is a minimum of the residuals for almost all the parameters and was selected as the best fit for all the atmospheric analyses presented in this paper. The time series are again represented after subtracting the 6-degree polynomial in Figure 3 with red lines. The value of the first year was added to the full-time series to have a real absolute value. We noted that the absolute value of these curves doesn’t influence the classification of a particular day as anomalous or not. In fact, the anomaly criterium is based on the standard deviation, and, thus, is independent of the mean absolute value of the whole time series.

After this data pre-processing, the standard MEANS algorithm [49] was applied, the process of which can be briefly summarized as:

• Calculation of preliminary historical mean and exclusion of years that contain some outliers, i.e., one or more values greater than the mean plus 10 standard deviations of all the data.
• Calculation of historical time series (from 1980 to 2021), in terms of mean and standard deviations of the values of a 3-degree side square centered on the epicenter excluding the year of the earthquakes (2013).
• Overplot of the year of the earthquake (2013) above the mean plus or minus 1.0, 1.5, and 2.0 standard deviations of each specific day of the historical time series.
• Defining the values outside the 2-standard deviation thresholds as anomalous and, for such days, extracting the map and spatial information of locations of high values of the investigated quantity.

The calculation of the mean and standard deviation day-by-day assures that the result is independent of any seasonal trends.

2.4. Ionosphere

At the time of the occurrence of the Lushan earthquake, the Low Earth Orbit (LEO) satellites, usually used for pre-earthquake study, were unavailable. In fact, the DEMETER and CHAMP satellites were decommissioned some years before (in 2010), Swarm was launched only at the end of 2013, and the China Seismo Electromagnetic satellite (CSES) in 2018. For this reason, we relied on the Total Electron Content (TEC) global maps obtained from ground stations and vertical electron density profiles measured by the FormoSat-3 satellite to investigate the ionosphere.

2.4.1. TEC

TEC data was retrieved from the Global Ionospheric Map (GIM). This dataset is available worldwide with a spatial resolution of 5° longitude, 2.5° latitude, and 2 h in time at precise UT. The data are available systematically from 2000, and we retrieved up to 2022 to construct a background. Only the six months before the earthquake for each year were selected from 22 October (of the year before) until 20 April. The data processing here applied was initially prepared to analyze another natural hazard: the “La Palma” volcano eruption of 19 September 2021 by Marchetti et al. [15]. In that paper, the solar cycle modulation of TEC was removed by normalization using a sinusoidal curve. Even if the accordance of the sine curve with the TEC data was found to be good (with a correlation coefficient greater than 0.9), the sine curve could not follow the variations in the maxima and minima of the solar cycle that are different cycle-by-cycle. This paper introduces the daily Sunspot number to follow the solar cycle trend better. The use of Sunspot number improved the remotion of the TEC modulation induced by solar activity, surely not due to eventual pre-earthquake processes. Three different TEC dependencies as a function of Sunspot number were tested: linear, 2-order polynomial (Figure S5 in Supplementary Materials), and exponential (Figure 5B). Considering the minimum residual balanced with the degrees of freedom of the fits, i.e., the maximum adjusted coefficient of determination, the exponential fit was selected.

The following steps can summarise the procedure of the algorithm:

• Select a couple of TEC maps: one preceding, and the other following, the selected local time to be analyzed.
• Spatially interpolate the value of TEC at the epicenter latitude and longitude for each map by a cubic surface.
• Temporal linear interpolate the TEC at the selected local time with the previous two values from step 2.
• Check the geomagnetic conditions by Dst and ap indexes rejecting the samples recorded during disturbed conditions (|Dst| > 20 nT or ap > 10 nT).
• Repeat this process for each day/year to be analyzed, contributing to the background or the time series to be analyzed if inside the period of six months preceding the Lushan earthquake.
• For each year, the average TEC and Sun Spot Number index (also selected in quiet geomagnetic time, i.e., the same days used for TEC) is calculated and reported in Figure 5A.
• An exponential fit of the TEC versus the Sunspot number is performed and shown in Figure 5B.
• The TEC is finally normalized by dividing each value for the value estimated for that year by the fit calculated in Step 7.
• For each day, the background mean and standard deviation of the normalized TEC are calculated, excluding the six months before the Lushan earthquake
• A time series graph is produced, and the values before the Lushan earthquake that overpassed the background mean plus two standard deviations are defined as anomalous.

2.4.2. Vertical Electron Density profiles from FormoSat-3

In addition to TEC data, we retrieved the available electron density ionospheric profiles measured by the FormoSat-3/COSMIC-1 (Formosa Satellite 3/Constellation Observing System for Meteorology, Ionosphere, and Climate) satellite during the same six months before the Lushan 2013 earthquake. FormoSat-3/COSMIC-1 was launched on 14 April 2006 and worked until 6 May 2020. Previous authors have used FormoSat satellites to search for possible pre-earthquake ionospheric disturbances [50,51].

The vertical electron density profiles were retrieved within the Dobrovoslky radius and a comparison annular surrounding region. Figure 6 shows two examples of electron density profiles from FormoSat, the first (Figure 6A) shows only the typical electron density peak F2. The second (Figure 6B) presents a second peak, i.e., a small inversion of the vertical profile at around 100 km altitude, known as the sporadic E layer, formed under particular circumstances, including pre-seismic activity [52,53]. In the electron density profile of Figure 6B, there are some negative electron density values under the F2 peak. Such values are obviously physically impossible as the electron density cannot be physically negative as the minimum possible value is zero. However, as the quantity is not directly measured but indirectly estimated by inversion of GNSS Radio Occultations data, the result of the calculation could provide some negative data. In addition, visible from the figure, the shape of the Ne profile is still reliable, and probably it is just underestimated. Such a weakness in the inversion technique for Formosat is known in the literature, and some improved methods were proposed, for example, by Pedatella et al. [54]. They provided an upgraded electron density profile starting from 2015 data, so we still rely on this paper’s original electron density profiles. Furthermore, the analysis proposed in this paper compares the measurements inside the Dobrovolsky area with a surrounding area observed by the same satellite, so an underestimation of the values would not affect the results of this paper as the data and background are based on the same dataset.

The process of elaboration of electron density profiles consists of the following steps:

• Smoothing of the original Ne vertical profile with a moving average calculated sample-by-sample in a window of 11 samples. This operation assures that any spike in the original vertical profiles can be removed.
• Rejection of the profile below 50 km altitude as the F2 peak cannot be under such an altitude. However, the satellite often measured very high electron density values close to the ground, which were probably some bias in the measurements or data inversion.
• Extraction of the F2 maximum electron density value (NmF2), its altitude (hmF2), and its geographical position. It is important to note that the vertical profile is inclined, and any point corresponds to a different latitude and longitude, and we obtained the F2 value.
• Using the International Reference Ionosphere Model IRI-2016 [55], the information was reported to the epicentral coordinates by the proportion of the model computed at the measurement point and the epicenter.

3. Results

3.1. Lithosphere

The earthquake catalog data from six months before the Lushan earthquake were systematically analyzed using the method described in the previous section. According to the cumulative result of Benioff strain “S” shown in Figure 7, there are five accelerations in the trend, especially ~92 and ~48 days before the earthquake, and particularly notable is the last growth three days before the earthquake. The accelerated increases could be connected to activities of the fault system before the Lushan earthquake. Calculating the Es parameter, we obtained the graph shown in Figure 8.

3.2. Geomagnetic Data from Earth’s Surface

Figure 9, Figure 10, and Figure S1 in Supplementary Materials show the North (X), East (Y), and vertical (Z) components of geomagnetic data measured by CDP and BMT ground observatories, respectively. The data were filtered into five frequency bands. These figures demonstrate that the two observatories were generally consistent with each other, especially in terms of the Z component. At the same time, we indicate some differences between CDP and BMT with red circles, which may be produced by the preparation phase of the Lushan earthquake. We applied correlation analysis numerically based on Spearman rank correlation coefficient estimation to validate the uncorrelation between two datasets of CDP and BMT. The window used to compute correlation coefficient r is shifted by 20% of its length for every step. The lengths were selected as twice the higher cut-off period or longer, 2 h, 12 h, 2 days, 14 days, and 35 days, respectively, for the five filters. Then we defined quiet geomagnetic conditions as |Dst| ≤ 20 nT and ap ≤ 10 nT. Only windows with more than 10 samples in quiet geomagnetic conditions were considered in this research. Moreover, because of invalid samples without information, labeled −99,999 in the data, we rejected windows with more than 10% invalid samples. Figure S2 in Supplementary Materials shows the behavior of the correlation coefficient r, whose values range from −1 to +1. When the r value is close to 0 inside the window, it demonstrates that the datasets from CDP and BMT presented different trends; when r is a positive value (close to 1), it implies proportional trends in the two datasets, while 1 means 100% concordance; when r is a negative value (close to −1), it designates negative correlation. Furthermore, uncorrelated data were selected as candidate pre-earthquake anomalous signals by the window with |r|≤ 0.3. In fact, as we judge those differences between the two observatories will appeal to local phenomena, hopefully, these are possible pre-earthquake anomalies.

3.3. Atmospheric Temperature and Composition

The atmospheric composition was investigated by analyzing surface Air temperature, sulfur dioxide mixing ratio, Aerosol Optical Thickness (AOT), carbon monoxide surface concentration, surface total latent energy flux, and surface specific humidity.

The temperature time series is shown in Figure 11, and three anomalies (i.e., values above the two-standard deviation of the historical mean) are depicted by red ovals. Two of these have persistence as defined by Piscini et al. [6], i.e., their occurrence lasts at least two consecutive days. The temperature is very high on the day before the earthquake but inside the two standard deviation thresholds for just 0.1 K.

The time series in the six months before the Lushan earthquake of carbon monoxide surface concentration is shown in Figure 12. Two consecutive anomalous days are depicted and highlighted by a red circle on 10 and 11 December 2012 (i.e., −130 and −129 days with respect to the earthquake). Several days show negative anomalies underlined by blue circles. Still, no LAIC models predict a decrease in CO in the atmosphere as a precursor of earthquakes; consequently, we don’t consider these events further.

In Figure 13, we show the time series of aerosol levels in the six months before the Lushan 2013 earthquake. The anomalous values are greater than the previous time series and are highlighted by red circles. In particular, some anomalies were persistent for three days on 4–6 November 2012 (about −165 days with respect to the earthquake), for two days plus one close day on 8, 9, and 11 December 2012 (about −130 days with respect to the earthquake), for three days plus one close day on 9, 11–13 March 2013 (about −40 days with respect to the earthquake) and two days on 8–9 April 2013, so just 10 days before the earthquake. The aerosol level on 10 April 2013 is a little inside the 2 standard deviations, so it cannot be considered an anomalous day, even though its value is very much higher than the normal value and following two anomalous days. The AOD abnormal value is about 1.5 on the earthquake day. This result is consistent with the study of Liu et al. [56].

The time series for the six months before the Lushan 2013 earthquake of sulfur dioxide levels is shown in Figure 14, and red circles depict the positive anomalous values. In particular, one value (7 February 2013, 71 days before the earthquake) is exceptionally high but doesn’t persist for more than one day. Other days present persistent anomalies, such as 1–2 November 2012 (−169 days with respect to the earthquake), 9–10 December 2012 (−130 days with respect to the earthquake), and 19 and 20 February 2013 (−59 days with respect to the earthquake).

In Figure 15, a map for each atmospheric parameter on an anomalous day is reported. In particular, CO levels showed two anomalous days: 10 and 11 December, and both are reported. It is possible to see that on the first day, the highest pixels were located on the main plate boundary and closer to the future epicenter. In contrast, only the anomaly closest to the future epicenter persisted on the second day, suggesting a possible relation with the upcoming seismic event.

For temperature, aerosol, and SO₂, three closer and anomalous days (8, 13, and 14 March 2013) were selected, respectively.

In addition to the previous parameters, in Figure 16 and Figure 17, we analyzed the time series of the surface total latent energy flux and the surface specific humidity in the six months prior to the Lushan earthquake. The total latent heat flux is more commonly known as surface latent heat flux, but in the label, we used the parameter’s name used in the MERRA-2 archive. It is possible to note that total latent energy flux has multiple anomalous days: 29 October, 15 and 24 November, 22, 28, and 29 December 2012, 2 January, 7 February (the most anomalous), 28 February, 9, 25 and 30 March and 4 April 2013. They are, respectively, −173, −156, −147, −119, −113, −112, −108, −72, −51, −42, −26, −21, and −16 days with respect to the event. It is striking that, among all the anomalous days (see Figure S4 in the Supplementary Materials), the closer to the time of the upcoming earthquake, i.e., the 4 April 2013 anomaly (16 days prior to the event), the higher the values of total latent energy flux (see Figure 18) aligned with the Longmenshan fault where the seismic source was located.

For the specific humidity, we extracted the negative anomalies (i.e., the values lower than the mean minus two standard deviations), which are four values: 3 and 16 November, 23 December 2012 and 5 April 2013 (−168, −155, −118, −15 days with respect to the earthquake day). We further note that 17 November 2012 is lower than 1.5 standard deviations as well as 6 April 2013, so both of these anomalies could be considered as partially persistent for two consecutive days.

3.4. Ionosphere

The ionosphere was investigated by Total Electron Content (TEC) data and electron density profiles measured by FormoSat-3 (also known as COSMIC-1). Figure 19 shows the time series of normalized TEC interpolated above the Lushan earthquake at 2:00 local time. This time was chosen to directly compare the results with the present China Seismo Electromagnetic Satellite (CSES), even though it was not yet launched at the time of the Lushan earthquake occurrence. Despite this, it is interesting to repeat the technique for natural hazards occurring during CSES fly time like the La Palma 19 September 2021 volcanic eruption [15].

The time series depicted one small anomaly (slightly above the threshold) on 23 October 2012 and a more interesting group of anomalies from 12 to 6 days before the Lushan earthquake. In particular, five consecutive anomalous days were recorded from 8 to 12 April 2013 and 14 April 2014, i.e., a little more than one week in advance of the seismic event, which agrees with the study by Dai et al. [57]. It is worth noting that the TEC value on 13 April 2013 is high, but it did not overpass the threshold of 2 standard deviations, so from the objective point of view, it cannot be classified as an anomalous day. On these days, geomagnetic conditions were extremely quiet, as visible from the lower panel (−1 nT ≤ Dst ≤ 7 nT and 2nT ≤ ap ≤ 3nT). This group of three days with a high TEC value (including two anomalous days) followed the increased aerosol levels in the atmosphere detected by the previous analysis.

The electron density profiles of Formosat-3 were investigated as described in Section 2.4, extracting the altitude of the electron density peak (hmF2) and its electron density (NeF2) for all the profiles acquired in the circle investigation area centered on the earthquake and with a radius r_max defined by the following equation:

$$r_{max}=\sqrt{2·{\left(r_{Dob}\right)}^2+{\left(r_{Dob}+g\right)}^2}$$

where r_Dob is the Dobrovolsky radius [38] and g is a gap set equal to 300 km. The scope is to have two areas separated by this gap: the inner is the Dobrovolsky area to search for possible pre-earthquake effects, and the outer is an annulus surrounding the epicenter of an equivalent area of two times the Dobrovoslky area used to define a background value. Six months before the Lushan 2013 earthquake, 2465 points were selected in the above-selected area. The histogram of the distribution of hmF2 is reported in Figure 20. The samples below 200 km are not only unrealistic but also not expected, and from the investigation of the original profiles, they are clearly due to unrealistic electron density profiles. Consequently, we reject all the points below 200 km, reducing the dataset to 2352 samples.

For each sample, the local time LT was calculated from the UT time and the longitude “lon” of acquisition:

$$LT=UT+\frac{lon}{15}$$

Factor 15 is the ratio between the degree and hours, considering that half circumference is 180° and 12 h. For each day, the samples acquired in the Dobrovoslky area with a maximum difference of 1 h in local time with the samples in the background area are selected. Finally, such samples are compared with the closer sample in the background area, obtaining a total of 281 relative estimations of the variations of F2 reported in Figure 21 and defined as:

$$∆hmF2=\frac{hmF{2}_{Dob}-hmF{2}_{bg}}{hmF{2}_{bg}},∆NeF2=\frac{NeF{2}_{Dob}-NeF{2}_{bg}}{NeF{2}_{bg}}$$

As can be seen, the variations in the altitude of the F2 peak follow a more Gaussian distribution than the electron density variation, which is biased toward positive values. Some values are clearly anomalous and are highlighted by red circles in Figure 21. The precise values are provided in

Table 1. Anomalous values of the F2 ionospheric peak as extracted from the time series shown in Figure 21. In the first rows, the anomalous altitude days of the F2 peak are presented, and in the following rows, the anomalous days for an increase in electron density in the F2 peak are listed.

Date and Time UT	Days with Respect to the EQ	hmF2 in the Dobrovolsky [km]	hmF2 in the Background [km]	Δ hmF2	Local Time	Geomagnetic Indexes
31 October 2012 13:08:24	−170.5	202. 5	333.1	−39.2%	20:00	Dst = 12 nT, ap = 4 nT, AE = 44 nT
14 November 2012 14:47:09	−156.4	372.8	294.6	26.6%	21:39	Dst = − 64nT, ap = 7 nT, AE = 83 nT
24 December 2012 18:59:09	−116.2	348.1	256.4	35.7%	1:51	Dst = 2 nT, ap = 2 nT, AE = 84 nT
26 December 2012 18:14:25	−114.2	334.4	250.5	33.5%	1:06	Dst = 7 nT, ap = 0 nT, AE = 17 nT
14 February 2012 4:56:41	−64.8	258.0	391.6	-34.1%	11:48	Dst = −21 nT, ap = 18 nT, AE = 338 nT
Date	Days with Respect to the EQ	NeF2 in the Dobrovolsky [e−/cm3]	NeF2 in the Background [e−/cm3]	Δ NeF2	Local Time	Geomagnetic Indexes
31 October 2012 13:08:24	−170.5	1.48 × 106	5.18 × 105	187%	20:00	Dst = 12 nT, ap = 4 nT, AE = 44 nT
3 December 2012 11:13:45	−137.5	9.13 × 105	2.54 × 105	260%	18:05	Dst = 8 nT, ap = 4 nT, AE = 35 nT
11 December 2012 0:08:34	−130.0	3.22 × 105	1.29 × 105	150%	7:00	Dst = 10 nT, ap = 5 nT, AE = 12 nT
16 December 2012 8:28:51	−124.6	2.35 × 106	7.22 × 105	226%	15:20	Dst = −7 nT, ap = 6 nT, AE = 239 nT
31 December 2012 23:49:33	−109.0	3.06 × 105	7.57 × 104	304%	6:41	Dst = 8 nT, ap = 2 nT, AE = 26 nT

, and the electron density vertical profiles of the most representative are shown in Figure 22. In particular, the geomagnetic indexes Dst, ap, and AE recorded during each anomalous value are also reported in Table 1. For all the anomalies, it can be excluded that they could be induced by the geomagnetic activity, except for the one recorded on 22 February 2013, as it could be induced by penetrating electric currents from the high poles where high activity was measured (AE = 634 nT). Contrariwise, the anomalies observed on 31 October, 8,10,12 December 2012, and 5 January 2013 cannot be explained by geomagnetic activity and could be, in principle, induced by the preparation phase of the earthquake. The high value of NeF2 recorded in the Dobrovolsky on 20 December 2012 with respect to the one in the background is unlikely to be due to geomagnetic activity even if at pole auroral electrojet was a little high with AE = 208 nT.

4. Discussion

4.1. Three Possible Lithosphere–Atmosphere–Ionosphere Couplings before the Earthquake

Comparing the results in the analyzed three geo-layers, it is possible to depict a common anomalous time about 130 days before the earthquake. In fact, the lithosphere presents a very slight increase in stress, while the aerosol, sulfur dioxide, and carbon monoxide levels, and surface total latent energy flux are increased in the atmosphere; at around the same time, the Chengdu geomagnetic station recorded more magnetic pulses between 6 and 24 h in the X component and the electron density of the F2 ionospheric peak was higher. Furthermore, the atmospheric aerosol level became anomalous three days before the ionospheric anomaly suggesting a bottom-up coupling mechanism.

To investigate better the possible coupling 130 days before the earthquake, Figure 23 represents the difference in surface air temperature on 11 December 2012 with respect to the typical values of the region. In addition, Figure 23 shows higher temperature values in the mountain region, northwest of the upcoming epicenter. Higher temperature values at the high-altitude area are explainable by Freund et al. [36], which predicts that positive holes migrate towards geographical high peak regions and emit infrared radiation due to charges recombination at or just below the Earth’s surface. Even though this would not be a real increase in temperature, ’it’s impossible to distinguish from present satellite remote sensing observations without spectra of the radiation. Despite this possible explanation, ’it is important to note that no pixels reached an increase in temperature greater than 2 standard deviations, so according to our definition of “anomaly”, there was no temperature anomaly on 11 December 2012 inside the Dobrovolsky area.

The almost synchronous increase in these quantities requires a fast-coupling mechanism. Due to the absence of surface air temperature anomalies, we would exclude the possibility of an acoustic gravity wave to describe this possible lithosphere–atmosphere–ionosphere coupling as proposed in other cases [34,58]. Similar synchronous anomalies in the atmosphere and ionosphere in coincidence with some foreshocks of the Mw = 7.5 Indonesia 2018 were reported by Marchetti et al. [12], even though the anticipation time was different (slightly less than two months before the Indonesia 2018 earthquake).

A second possible coupling between the lithosphere and atmosphere was identified about forty days before the earthquake. A strong increase in the Benioff cumulative stress curve and Es parameter happened 47~48 days before the seismic event. This was followed by an increase in temperature and surface total latent energy flux after a large emission of aerosol, SO₂, and, finally, geomagnetic anomalies about 40 days before the Lushan earthquake. We would underline that this possible coupling has a longer propagation delay than the previous case; in fact, it requires about a week, while the first eventual coupling involved all the layers on the same day, so this is about 7/8 times slower.

Comparing the results in the last few weeks before the earthquake, it is very interesting to note that seismicity recorded a peak on about 3 April 2013, followed, on 4 April (see Figure 17), by a high surface total energy flux, the day after by a decrease in humidity, then the atmosphere showed a high increase in aerosol from 8 to 10 April 2013, and, finally, the ionosphere TEC was high from 8 to 14 April 2013. As discussed in the Section 3, 10 April 2013 is high but not anomalous for aerosol and 13 April for TEC. Nevertheless, we could explain the detected increase in aerosol as a potential sign of air ionization that, in about two days, propagates in the ionosphere, inducing an increase in total electron content as predicted by the Pulinets and Ouzounov [30] model. Their model suggests that radon release induces air ionization if this is the case. Ye et al. [59] investigated radon concentration in water at six stations around the Longmenshan fault from 2003 to 2014, including the Wenchuan 2008 and Lushan 2013 earthquakes. The authors claimed that long-term variations in radon concentrations are associated with seismic trends, while short-term variations produced contradictory results. However, we notice that the Ganzi station showed high radon concentrations from about 1 March 2013 until the Lushan 2013 earthquake, followed by a gradual decrease immediately afterward [59]. A small peak was identified around 1 April 2013, just one week before the increase in aerosol and TEC that we identified, possibly explaining it. Unfortunately, we cannot draw a final conclusion due to the unconfirmed radon results from the other stations.

4.2. Space-Time Distribution of the Anomalies in Lithosphere Atmosphere and Ionosphere

In order to better show the identified anomalies or events in the lithosphere, atmosphere, and ionosphere, we provide a four-dimensional map (longitude, latitude, depth, and time) and a three-dimensional map (longitude, time, and latitude) in Figure 24 and Figure 25. We divided the depth of the anomalies in the ionosphere by 10 to avoid large vertical distances in the figure. In both Figure 24 and Figure 25, a triangle represents anomalies in the atmosphere; a square indicates anomalies in the ionosphere and geomagnetic ground data; dots depict anomalies in the lithosphere; and the Lushan earthquake is marked with a diamond. It could be seen that there are a large number of anomalies in three geo-layers clustered along the Longmenshan fault, which is the seismogenic fault zone of the Lushan earthquake. While this is expected for earthquakes in the lithosphere, it is remarkable for atmospheric and ionospheric anomalies. From Figure 24, it is also possible to depict a suggested space-time order of anomalies and interactions between the three geo-layers that we marked with ellipses and arrows and numbered from 1 to 4. In addition, we circled small areas where anomalies appeared in all three geo-layers in Figure 25.

4.3. Possible Explanation from the LAIC Models for the Identified Anomalies

The anomalies identified about 130 days before the Lushan earthquake could be explained with a degassing induced by fluid migrations as proposed for other earthquakes by Ventura and Di Giovambattista [60] together with a release of p-holes [36] at the Earth’s surface. The release of p-holes can explain the anomalous pulsations recorded by the geomagnetic ground stations. Their accumulation could have induced the formation of plasma bubbles up to the ionosphere, as numerically simulated by Kuo et al. [61]. Such a simulation opened a scientific debate about its validity [62,63], but also other authors supported the theoretical existence of pre-earthquake ionospheric plasma irregularities [26]. At the same time, the degassing could explain the anomalous concentrations of SO₂ and CO in the atmosphere, which could have facilitated the formation of aerosol [30] and ionized the air increasing the free charges in the atmosphere and contributing to the eventual p-holes. Figure 26A presents a graphic sketch of these mechanisms.

A similar explanation could explain the possible coupling, identified about 40 days before the Lushan earthquake, probably without p-holes, due to the lack of evidence for ionospheric anomalies. The magnetic anomalies detected at the end of this possible coupling could be produced by electrical alteration of the atmosphere for a slower air ionization with respect to the previous coupling. We notice a crucial difference between the possible coupling 130 days and the one 40 days before the Lushan earthquake: the lithospheric source of the first seems to be a parallel fault located South-East of the first fault. Instead, the second group of anomalies seems to have been induced by the Longmenshan fault, which is responsible for the upcoming earthquake. This also shows how the anomalies could approach the upcoming event of interested fault as the event is closer in time, as proposed by Wu et al. [64].

The last group of anomalies starting about 2.5 weeks before the earthquakes could be well explained with a release of radon and following implications in the atmosphere and ionosphere proposed by the Pulinets and Ouzounov model [30] and represented in Figure 26B. The lithospheric source of these anomalies seems to be located Southwest on the same Longmenshan fault system; even though it was spatially not so close, it was the one responsible for the upcoming Lushan earthquake. The fact that the place of the upcoming earthquake was placed in the gap between the previous events is also well in agreement with other seismological simulations and investigations for other tectonic contexts [65,66].

5. Conclusions

In this paper, anomalies in the lithosphere, atmosphere, and ionosphere in the six months before the Mw6.7 Lushan (China) 2013 earthquake were extracted. In particular, increases in seismic stress were depicted 160, 92, 60, 48, 17, and 3 days before the Lushan earthquake. The geomagnetic ground station at Chengdu displayed anomalous signals not seen at the Beijing station, 140, 130, 100, and 35 days before the main shock. Surface air temperature, CO, Aerosol, and SO₂ levels, total latent energy flux, and specific humidity displayed several anomalies in the investigated period. The most interesting feature is their spatial organization, which converged toward the Longmenshan fault where the Lushan earthquake nucleated. The Formosat-3 satellite detected anomalies in the F2 ionospheric peak 170, 140, 130, and 110 days before the earthquake. TEC increased above the two standard deviations of its historical value from 12 to 6 days prior to the seismic event. The identified anomalies were further discussed, and possible couplings between the three geo-layers are presented in the view of the several lithosphere–atmosphere–ionosphere coupling models available in the literature.

We identify three possible bottom-up couplings with different mechanisms between three geo-layers. The first was about 130 days before the earthquake, with a fast (order of one day) propagation delay. The lithosphere presented a very slight increase in the stress, while the aerosol, sulfur dioxide, and carbon monoxide levels, and surface total latent energy flux were increased in the atmosphere; at the similar time, the Chengdu geomagnetic station recorded more magnetic pulses, and the electron density of the F2 ionospheric peak was higher.

The second happened about 40 days before the earthquake between the lithosphere and the atmosphere. A propagation delay of a few days suggests a slower bottom-up interaction between the two layers. A substantial stress increase occurred 47~48 days before the seismic event, followed by a rise in temperature and surface total latent energy flux after a large emission of aerosol, SO₂, and, finally, geomagnetic anomalies about 40 days before the Lushan earthquake.

The third started 2.5 weeks before, and lasted until one week before, the event. Consequently, this eventual coupling was also characterized by a longer interaction time from the bottom layers to the upper ones. In addition, all three geo-layers showed good bottom-up delay anomalies. Seismicity recorded a peak on about 3 April 2013; then the atmosphere depicted a high surface total energy flux on 4 April, followed the day after by a decrease in humidity, a high increase in aerosol from 8 to 10 April 2013, and, finally, the ionosphere TEC was high from 8 to 14 April 2013.

We can conclude that lithosphere–atmosphere–ionosphere couplings before Lushan (China) 2013 earthquake seemed to occur, but with different propagation mechanisms, locations (starting far from the involved fault and approaching it in the last few months), and delays. Further studies are necessary to confirm such possible mechanisms for other earthquakes in China and the rest of the world, considering the different tectonic and continental (as Lushan) or subduction contexts.

Our evidence suggests that the geo-layers could interact with different channels with specific propagation delays. Despite this, we cannot exclude alternative explanations of the identified anomalies, and future statistical studies applied to the lithosphere, atmosphere, and ionosphere are required to validate these results further.

We think that the “state of the art” is still insufficient to predict future earthquakes, but these studies help reduce the knowledge gap we need to implement in future prediction systems. The following step could be implementing a real-time geophysical platform monitoring system such as the one proposed in the conclusions provided in [67].