Optimization of the Vertical Wavenumber for PolInSAR Inversion Performance Based on Numerical CRLB Analysis
Abstract
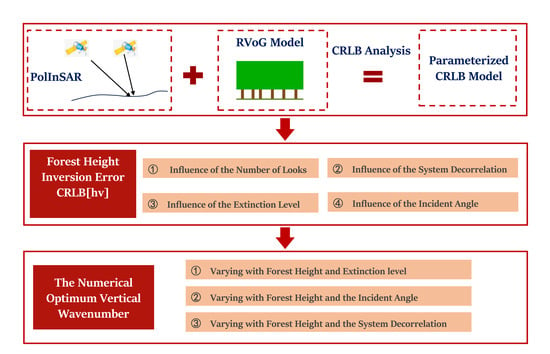
:1. Introduction
2. Materials and Methods
2.1. PolInSAR Preliminaries
2.1.1. The PolInSAR Measurements
2.1.2. Forest RVoG Scattering Model
2.1.3. Modeling of PolInSAR Coherence
2.2. CRLB for Single-Baseline PolInSAR
2.2.1. Formulation of CRLB
2.2.2. The Reduced RVoG Model
2.2.3. The Invariant Model Parameters
3. Results
3.1. Sensitivity of the Vertical Wavenumber
3.2. CRLB Analysis for Inversion Performance
3.2.1. Simulation Parameters
3.2.2. Influence of the Number of Looks
3.2.3. Influence of the System Decorrelation
3.2.4. Influence of the Extinction Level
3.2.5. Influence of the Incident Angle
3.3. The Numerical Optimum Vertical Wavenumber
3.3.1. The Optimum Varying with and
3.3.2. The Optimum Varying with and
3.3.3. The Optimum Varying with and
4. Discussion
4.1. About the Frequency
4.2. About the Temporal Decorrelation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Hajnsek, I.; Krieger, G.; Papathanassiou, K.; Eineder, M. Tandem-L: Monitoring the Earth’s Dynamics with InSAR and Pol-InSAR. In Proceedings of the 4th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry (PolInSAR 2009), Frascati, Italy, 26–30 January 2009; pp. 1–5. [Google Scholar]
- Krieger, G.; Hajnsek, I.; Papathanassiou, K.P.; Eineder, M.; Younis, M.; Zan, F.D.; Lopezdekker, P.; Huber, S.; Werner, M.; Prats, P. Tandem-L: A Mission for Monitoring Earth System Dynamics with High Resolution SAR Interferometry. In Proceedings of the European Conference on Synthetic Aperture Radar, Pasadena, CA, USA, 4–8 May 2010. [Google Scholar]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef]
- Quegan, S.; Chave, J.; Dall, J.; Toan, T.L.; Williams, M. The science and measurement concepts underlying the BIOMASS mission. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012. [Google Scholar]
- Li, C.; Zhang, H.; Deng, Y.; Wang, R.; Zhang, Y. Focusing the L-Band Spaceborne Bistatic SAR Mission Data Using a Modified RD Algorithm. IEEE Trans. Geosci. Remote Sens. 2019, 58, 294–306. [Google Scholar] [CrossRef]
- Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An Advanced Phase Synchronization Scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1735–1746. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Madsen, S.R.N.; Moghaddam, M.; Van Zyl, J.J. Vegetation characteristics and underlying topography from interferometric radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Siqueira, P.R. Vertical structure of vegetated land surfaces from interferometric and polarimetric radar. Radio Sci. 2000, 35, 141–177. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; OUP Oxford: London, UK, 2009. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Hajnsek, I.; Kugler, F.; Lee, S.K.; Papathanassiou, K.P. Tropical-Forest-Parameter Estimation by Means of Pol-InSAR: The INDREX-II Campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar] [CrossRef]
- Wang, X.; Xu, F. A PolinSAR Inversion Error Model on Polarimetric System Parameters for Forest Height Mapping. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5669–5685. [Google Scholar] [CrossRef]
- Xue, F.; Wang, X.; Xu, F.; Wang, Y. Polarimetric SAR Interferometry: A Tutorial for Analyzing System Parameters. IEEE Geosci. Remote Sens. Mag. 2020, 8, 83–107. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Zebker, H.A.; Goldstein, R. Topographic mapping from interferometric synthetic aperture radar. J. Geophys. Res. 1986, 91, 4993–4999. [Google Scholar] [CrossRef]
- Lee, S.K.; Kugler, F.; Hajnsek, I.; Papathanassiou, K. Multibaseline polarimetric SAR interferometry forest height inversion approaches. In Proceedings of the 5th ESA POLinSAR Workshop, Frascati, Italy, 24–28 January 2011; pp. 1–7. [Google Scholar]
- Garestier, F.; Le Toan, T. Estimation of the Backscatter Vertical Profile of a Pine Forest Using Single Baseline P-Band (Pol-)InSAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3340–3348. [Google Scholar] [CrossRef]
- Garestier, F.; Le Toan, T. Forest modelling for height inversion using single-baseline InSAR/Pol-InSAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1528–1539. [Google Scholar] [CrossRef]
- Kangas, A.; Maltamo, M. Forest Inventory: Methodology and Application; Springer: Berlin, Germany, 2006. [Google Scholar]
- Krieger, G.; Papathanassiou, K.P.; Cloude, S.R. Spaceborne Polarimetric SAR Interferometry: Performance Analysis and Mission Concepts. EURASIP J. Adv. Signal Process. 2005, 2005, 3272–3292. [Google Scholar] [CrossRef]
- Cloude, S.R.; Corr, D.G.; Williams, M.L. Target detection beneath foliage using polarimetric synthetic aperture radar interferometry. Waves Random Media 2004, 14, S393–S414. [Google Scholar] [CrossRef]
- Kugler, F.; Lee, S.K.; Hajnsek, I.; Papathanassiou, K.P. Forest Height Estimation by Means of Pol-InSAR Data Inversion: The Role of the Vertical Wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Roueff, A.; Arnaubec, A.; Dubois-Fernandez, P.C.; Refregier, P. Cramer-Rao Lower Bound Analysis of Vegetation Height Estimation with Random Volume Over Ground Model and Polarimetric SAR Interferometry. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1115–1119. [Google Scholar] [CrossRef]
- Réfrégier, P.; Roueff, A.; Arnaubec, A.; Dubois-Fernandez, P.C. Invariant Contrast Parameters of PolInSAR Homogenous RVoG Model. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1414–1417. [Google Scholar] [CrossRef]
- Wang, X.; Xu, F.; Jin, Y. The Optimum Baseline Analysis for Polinsar Forest Height Mapping. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Arnaubec, A.; Roueff, A.; Dubois-Fernandez, P.C.; Réfrégier, P. Vegetation Height Estimation Precision with Compact PolInSAR and Homogeneous Random Volume Over Ground Model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1879–1891. [Google Scholar] [CrossRef]
- Sportouche, H.; Roueff, A.; Dubois-Fernandez, P.C. Precision of Vegetation Height Estimation Using the Dual-Baseline PolInSAR System and RVoG Model with Temporal Decorrelation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4126–4137. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for polarimetric SAR interferometry. IEEE Proc.-Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef]
- Garthwaite, P.; Jolliffe, I.; Jones, B. Statistical Inference; Prentice-Hall: London, UK, 1995. [Google Scholar]
- Song, Q.; Albrecht, C.M.; Xiong, Z.; Zhu, X.X. Biomass Estimation and Uncertainty Quantification from Tree Height. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2023, 16, 4833–4845. [Google Scholar] [CrossRef]
- Olesk, A.; Praks, J.; Antropov, O.; Zalite, K.; Arumäe, T.; Voormansik, K. Interferometric SAR Coherence Models for Characterization of Hemiboreal Forests Using TanDEM-X Data. Remote Sens. 2016, 8, 700. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. The effect of temporal decorrelation on the inversion of forest parameters from Pol-InSAR data. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 1429–1431. [Google Scholar]
- Lavalle, M.; Simard, M.; Hensley, S. A temporal decorrelation model for polarimetric radar interferometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2880–2888. [Google Scholar] [CrossRef]













| Parameters | Values |
|---|---|
| 5 to 60 m | |
| 0.01 to 0.4 rad/m | |
| 0.2, 0.3 and 0.5 dB/m | |
| 16, 64, and 100 | |
| 0.9, 0.95, and 0.98 | |
| 1 | |
| 50 to 2000 | |
| 0 to 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, H. Optimization of the Vertical Wavenumber for PolInSAR Inversion Performance Based on Numerical CRLB Analysis. Remote Sens. 2023, 15, 5321. https://doi.org/10.3390/rs15225321
Wang X, Li H. Optimization of the Vertical Wavenumber for PolInSAR Inversion Performance Based on Numerical CRLB Analysis. Remote Sensing. 2023; 15(22):5321. https://doi.org/10.3390/rs15225321
Chicago/Turabian StyleWang, Xiao, and Hong Li. 2023. "Optimization of the Vertical Wavenumber for PolInSAR Inversion Performance Based on Numerical CRLB Analysis" Remote Sensing 15, no. 22: 5321. https://doi.org/10.3390/rs15225321