The Novel Copernicus Global Dataset of Atmospheric Total Water Vapour Content with Related Uncertainties from GNSS Observations
Abstract
:1. Introduction
- Global coverage as well as dense regional coverage;
- Sufficient time coverage;
- Being adjusted for the effect of instrumental and data processing changes.
2. Methods
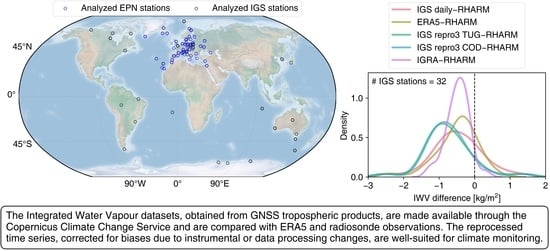
2.1. GNSS Datasets in the CDS
2.1.1. Data Source
2.1.2. Implementation
2.2. Study Setup and Analysis Method
- Having the same report timestamp;
- A distance difference of less than 30 km;
- An elevation difference within 100 m;
- Containing at least 6 months of data.
3. Results
3.1. The Impact of Estimation Approaches on IWV Value
3.2. Intercomparison of IWV and Its Trends at IGS Stations
3.3. Intercomparison of IWV and Its Trends at EPN Stations
3.4. Intercomparison of IWV at Two GRUAN Stations
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Technical Implementation of the Service
- Pre-processing of GNSS troposphere product (1–4);
- Pre-processing of ancillary data (5–7);
- Calculating IWV and its uncertainty, ingestion to the DB (8–10).

Appendix B. GNSS IWV in CDS Data Portal

Appendix C. Stations Used in the Study
| GNSS ID | Lat, ° | Lon, ° | Trend | Radiosonde ID | Distance, km | No. Night Meas. | No. Day Meas. |
|---|---|---|---|---|---|---|---|
| ALIC | − 23.67 | 133.89 | + | ASM00094326 | 13.89 | 23 | 1778 |
| BAKE | 64.32 | −96 | − | CAM00071926 | 0.17 | 1680 | 2030 |
| BOGI | 52.47 | 21.04 | − | PLM00012374 | 9.19 | 1478 | 1822 |
| CAS1 | −66.28 | 110.52 | + | AYM00089611 | 0.18 | 758 | 2705 |
| CHUR | 58.76 | −94.09 | + | CAM00071913 | 3.14 | 2545 | 2820 |
| COCO | −12.19 | 96.83 | + | CKM00096996 | 0.11 | 698 | 3572 |
| DAV1 | −68.58 | 77.97 | − | AYM00089571 | 0.39 | 610 | 1878 |
| FUNC | 32.65 | −16.91 | − | POM00008522 | 1.78 | 0 | 764 |
| GANP | 49.03 | 20.32 | − | LOM00011952 | 0.48 | 1434 | 1489 |
| HERS | 50.87 | 0.34 | + | UKM00003882 | 3.82 | 1949 | 1574 |
| HERT | 50.87 | 0.33 | − | UKM00003882 | 3.76 | 1723 | 1258 |
| HOB2 | −42.8 | 147.44 | + | ASM00094975 | 6.19 | 3117 | 3595 |
| INVK | 68.31 | −133.53 | − | CAM00071957 | 1.24 | 2109 | 2546 |
| IQAL | 63.76 | −68.51 | − | CAM00071909 | 2.05 | 1268 | 1214 |
| M0SE | 41.89 | 12.49 | − | ITM00016245 | 25.07 | 347 | 370 |
| MAC1 | −54.5 | 158.94 | + | ASM00094998 | 0.08 | 2803 | 3131 |
| MAW1 | −67.6 | 62.87 | − | AYM00089564 | 0.4 | 252 | 1314 |
| MEDI | 44.52 | 11.65 | − | ITM00016144 | 15.02 | 2021 | 1047 |
| MOBS | −37.83 | 144.98 | − | ASM00094866 | 22.15 | 2806 | 2770 |
| NYA1 | 78.93 | 11.87 | + | SVM00001004 | 1.4 | 900 | 1845 |
| NYAL | 78.93 | 11.87 | − | SVM00001004 | 1.41 | 660 | 967 |
| PARC | −53.14 | −70.88 | − | CIM00085934 | 15.05 | 189 | 950 |
| PERT | −31.8 | 115.89 | + | ASM00094610 | 16.41 | 2052 | 2762 |
| POVE | −8.71 | −63.9 | − | BRM00082824 | 6.76 | 1313 | 1818 |
| SALU | −2.59 | −44.21 | − | BRM00082281 | 2.43 | 1046 | 1586 |
| SCOR | 70.49 | −21.95 | − | GLM00004339 | 0.11 | 1568 | 1729 |
| SMST | 33.58 | 135.94 | − | JAM00047778 | 21.89 | 74 | 46 |
| STHL | −15.94 | −5.67 | − | SHM00061901 | 0.07 | 0 | 1290 |
| SUWN | 37.28 | 127.05 | + | KSM00047122 | 21.46 | 2672 | 2683 |
| TSK2 | 36.11 | 140.09 | − | JAM00047646 | 6.32 | 81 | 50 |
| TSKB | 36.11 | 140.09 | − | JAM00047646 | 6.31 | 102 | 56 |
| UFPR | −25.45 | −49.23 | − | BRM00083840 | 9.97 | 1435 | 1670 |
| UNBJ | 45.95 | −66.64 | − | CAM00071701 | 20.72 | 13 | 36 |
| WROC | 51.11 | 17.06 | + | PLM00012425 | 12.63 | 2547 | 3036 |
| GNSS ID | Lat, ° | Lon, ° | Trend | No. Night Meas. | No. Day Meas. |
|---|---|---|---|---|---|
| AJAC | 41.93 | 8.76 | − | 40,373 | 42,173 |
| BOGI | 52.47 | 21.04 | − | 28,221 | 29,710 |
| BOR1 | 52.28 | 17.07 | + | 58,791 | 59,242 |
| BRST | 48.38 | −4.5 | − | 38,761 | 38,411 |
| DYNG | 38.08 | 23.93 | − | 4310 | 4199 |
| EBRE | 40.82 | 0.49 | + | 56,467 | 56,972 |
| FUNC | 32.65 | −16.91 | − | 24,714 | 24,783 |
| GANP | 49.03 | 20.32 | − | 19,636 | 18,723 |
| GLSV | 50.36 | 30.5 | + | 41,144 | 54,539 |
| GOPE | 49.91 | 14.79 | + | 53,663 | 54,022 |
| GRAS | 43.75 | 6.92 | + | 46,226 | 45,794 |
| GRAZ | 47.07 | 15.49 | + | 55,632 | 56,074 |
| HERS | 50.87 | 0.34 | + | 54,012 | 54,629 |
| HERT | 50.87 | 0.33 | + | 46,269 | 47,458 |
| HOFN | 64.27 | −15.2 | + | 46,408 | 48,759 |
| IENG | 45.02 | 7.64 | + | 43,354 | 44,083 |
| JOZ2 | 52.1 | 21.03 | + | 37,508 | 37,952 |
| JOZE | 52.1 | 21.03 | − | 26,493 | 26,582 |
| KIR0 | 67.88 | 21.06 | + | 55,691 | 55,694 |
| KIRU | 67.86 | 20.97 | + | 50,899 | 54,973 |
| LAMA | 53.89 | 20.67 | + | 55,493 | 56,210 |
| LPAL | 28.76 | −17.89 | − | 22,355 | 23,054 |
| MAD2 | 40.43 | −4.25 | − | 21,788 | 22,363 |
| MADR | 40.43 | −4.25 | + | 48,242 | 48,914 |
| MAR6 | 60.6 | 17.26 | + | 51,396 | 52,620 |
| MARS | 43.28 | 5.35 | + | 42,741 | 42,533 |
| MAS1 | 27.76 | −15.63 | + | 51,375 | 52,402 |
| MATE | 40.65 | 16.7 | + | 47,123 | 47,870 |
| MDVJ | 56.02 | 37.21 | + | 46,461 | 46,175 |
| MEDI | 44.52 | 11.65 | + | 55,558 | 56,347 |
| METS | 60.22 | 24.4 | + | 51,327 | 51,830 |
| MORP | 55.21 | −1.69 | + | 44,164 | 44,316 |
| NICO | 35.14 | 33.4 | + | 46,182 | 46,736 |
| NOT1 | 36.88 | 14.99 | − | 38,710 | 38,998 |
| NYA1 | 78.93 | 11.87 | + | 54,319 | 51,003 |
| ONSA | 57.4 | 11.93 | + | 57,136 | 58,208 |
| PADO | 45.41 | 11.9 | + | 39,761 | 40,642 |
| PDEL | 37.75 | −25.66 | + | 55,440 | 56,583 |
| PENC | 47.79 | 19.28 | − | 38,730 | 38,895 |
| POLV | 49.6 | 34.54 | + | 49,200 | 52,509 |
| POTS | 52.38 | 13.07 | + | 50,579 | 50,554 |
| PTBB | 52.3 | 10.46 | + | 54,901 | 55,530 |
| QAQ1 | 60.72 | −46.05 | + | 47,176 | 50,235 |
| RABT | 34 | −6.85 | + | 48,511 | 49,220 |
| RAMO | 30.6 | 34.76 | + | 44,670 | 44,600 |
| REYK | 64.14 | −21.96 | + | 55,082 | 54,983 |
| SCOR | 70.49 | −21.95 | − | 37,307 | 37,212 |
| SFER | 36.46 | −6.21 | + | 54,501 | 54,740 |
| SOFI | 42.56 | 23.39 | − | 41,971 | 41,992 |
| SPT0 | 57.71 | 12.89 | − | 34,093 | 34,280 |
| TLSE | 43.56 | 1.48 | + | 44,882 | 43,903 |
| TRO1 | 69.66 | 18.94 | + | 56,951 | 53,655 |
| VILL | 40.44 | −3.95 | + | 52,293 | 52,729 |
| VIS0 | 57.65 | 18.37 | + | 50,498 | 50,907 |
| WARN | 54.17 | 12.1 | − | 31,601 | 32,042 |
| WROC | 51.11 | 17.06 | + | 52,921 | 53,479 |
| WSRT | 52.91 | 6.6 | + | 58,330 | 59,124 |
| WTZR | 49.14 | 12.88 | − | 44,088 | 42,916 |
| ZECK | 43.79 | 41.57 | − | 36,978 | 37,785 |
| ZIM2 | 46.88 | 7.47 | − | 25,959 | 26,100 |
| ZIMM | 46.88 | 7.47 | + | 57,084 | 57,931 |
References
- Karl, T.R.; Trenberth, K.E. Modern global climate change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef]
- Zhu, Y.; Newell, R.E. Atmospheric rivers and bombs. Geophys. Res. Lett. 1994, 21, 1999–2002. [Google Scholar] [CrossRef]
- Awange, J. GNSS Environmental Sensing; Springer International Publishers: Berlin/Heidelberg, Germany, 2018; Volume 10, p. 978. [Google Scholar] [CrossRef]
- Jones, J.; Guerova, G.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; Bock, O.; Pacione, R.; van Malderen, R. (Eds.) Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate; Springer: Cham, Swizerland, 2020. [Google Scholar] [CrossRef]
- WMO. The Global Observing System for Climate: Implementation Needs. 2016. Available online: https://library.wmo.int/doc_num.php?explnum_id=3417 (accessed on 11 August 2023).
- WMO. The 2022 GCOS Implementation Plan. 2022. Available online: https://library.wmo.int/doc_num.php?explnum_id=11317 (accessed on 11 August 2023).
- Randall, D.A.; Tjemkes, S. Clouds, the Earth’s radiation budget, and the hydrologic cycle. Glob. Planet. Chang. 1991, 4, 3–9. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. (1988–2005) 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A.; Hove, T.V.; Baelen, J.V. A near-global, 2-hourly data set of atmospheric precipitable water from ground-based GPS measurements. J. Geophys. Res. 2007, 112, D11107. [Google Scholar] [CrossRef]
- Guerova, G.; Brockmann, E.; Quiby, J.; Schubiger, F.; Matzler, C. Validation of NWP mesoscale models with Swiss GPS network AGNES. J. Appl. Meteorol. Climatol. 2003, 42, 141–150. [Google Scholar] [CrossRef]
- Madonna, F.; Rosoldi, M.; Güldner, J.; Haefele, A.; Kivi, R.; Cadeddu, M.; Sisterson, D.; Pappalardo, G. Quantifying the value of redundant measurements at GCOS Reference Upper-Air Network sites. Atmos. Meas. Tech. 2014, 7, 3813–3823. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Huang, J.; Zheng, F.; Cao, Y.; Liang, H.; Shi, C.; Liu, J. Multiscale variations of precipitable water over China based on 1999–2015 ground-based GPS observations and evaluations of reanalysis products. J. Clim. 2018, 31, 945–962. [Google Scholar] [CrossRef]
- Bernet, L.; Brockmann, E.; von Clarmann, T.; Kämpfer, N.; Mahieu, E.; Mätzler, C.; Stober, G.; Hocke, K. Trends of atmospheric water vapour in Switzerland from ground-based radiometry, FTIR and GNSS data. Atmos. Chem. Phys. 2020, 20, 11223–11244. [Google Scholar] [CrossRef]
- Alshawaf, F.; Balidakis, K.; Dick, G.; Heise, S.; Wickert, J. Estimating trends in atmospheric water vapor and temperature time series over Germany. Atmos. Meas. Tech. 2017, 10, 3117–3132. [Google Scholar] [CrossRef]
- Hadad, D.; Baray, J.L.; Montoux, N.; Van Baelen, J.; Fréville, P.; Pichon, J.M.; Bosser, P.; Ramonet, M.; Yver Kwok, C.; Bègue, N.; et al. Surface and Tropospheric Water Vapor Variability and Decadal Trends at Two Supersites of CO-PDD (Cézeaux and Puy de Dôme) in Central France. Atmosphere 2018, 9, 302. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, K.; Sun, T.; Yao, Y.; Li, Z. A novel regional drought monitoring method using GNSS-derived ZTD and precipitation. Remote Sens. Environ. 2023, 297, 113778. [Google Scholar] [CrossRef]
- Gradinarsky, L.; Johansson, J.; Bouma, H.; Scherneck, H.G.; Elgered, G. Climate monitoring using GPS. Phys. Chem. Earth Parts A/B/C 2002, 27, 335–340. [Google Scholar] [CrossRef]
- Vey, S.; Dietrich, R.; Rülke, A.; Fritsche, M.; Steigenberger, P.; Rothacher, M. Validation of precipitable water vapor within the NCEP/DOE reanalysis using global GPS observations from one decade. J. Clim. 2010, 23, 1675–1695. [Google Scholar] [CrossRef]
- Ning, T.; Elgered, G.; Willén, U.; Johansson, J.M. Evaluation of the atmospheric water vapor content in a regional climate model using ground-based GPS measurements. J. Geophys. Res. Atmos. 2013, 118, 329–339. [Google Scholar] [CrossRef]
- Parracho, A.B.O.; Bastin, S. Evaluation of IWV Trends and Variability in a Global Climate Mode. In Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate: COST Action ES1206 Final Action Dissemination Report; Jones, J., Guerova, G., Douša, J., Dick, G., de Haan, S., Pottiaux, E., Bock, O., Pacione, R., van Malderen, R., Eds.; Springer: Cham, Switzerland, 2020; pp. 374–381. [Google Scholar] [CrossRef]
- Parracho, A.C.; Bock, O.; Bastin, S. Global IWV trends and variability in atmospheric reanalyses and GPS observations. Atmos. Chem. Phys. 2018, 18, 16213–16237. [Google Scholar] [CrossRef]
- Prado, A.; Vieira, T.; Pires, N.; Fernandes, M.J. Wet tropospheric correction for satellite altimetry using SIRGAS-CON products. J. Geod. Sci. 2022, 12, 211–229. [Google Scholar] [CrossRef]
- Yang, L.H.C.; Jones, J. Validation and Implementation of Direct Tropospheric Delay Estimation for Precise Real-Time Positioning. In Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate: COST Action ES1206 Final Action Dissemination Report; Jones, J., Guerova, G., Douša, J., Dick, G., de Haan, S., Pottiaux, E., Bock, O., Pacione, R., van Malderen, R., Eds.; Springer: Cham, Switzerland, 2020; pp. 150–158. [Google Scholar] [CrossRef]
- Mirmohammadian, F.; Asgari, J.; Verhagen, S.; Amiri-Simkooei, A. Multi-GNSS-Weighted Interpolated Tropospheric Delay to Improve Long-Baseline RTK Positioning. Sensors 2022, 22, 5570. [Google Scholar] [CrossRef]
- Van Malderen, R.; Brenot, H.; Pottiaux, E.; Beirle, S.; Hermans, C.; De Mazière, M.; Wagner, T.; De Backer, H.; Bruyninx, C. A multi-site intercomparison of integrated water vapour observations for climate change analysis. Atmos. Meas. Tech. 2014, 7, 2487–2512. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; de Galisteo, J.P.O.; Cachorro, V.E.; Álvarez-Zapatero, P.; Román, R.; Loyola, D.; Costa, M.J.; Wang, H.; Abad, G.G.; et al. Inter-comparison of integrated water vapor from satellite instruments using reference GPS data at the Iberian Peninsula. Remote Sens. Environ. 2018, 204, 729–740. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Blewitt, G. Global comparisons of ERA5 and the operational HRES tropospheric delay and water vapor products with GPS and MODIS. Earth Space Sci. 2021, 8, e2020EA001417. [Google Scholar] [CrossRef]
- Diedrich, H.; Preusker, R.; Lindstrot, R.; Fischer, J. Retrieval of daytime total columnar water vapour from MODIS measurements over land surfaces. Atmos. Meas. Tech. 2015, 8, 823–836. [Google Scholar] [CrossRef]
- Heise, S.; Dick, G.; Gendt, G.; Schmidt, T.; Wickert, J. Integrated water vapor from IGS ground-based GPS observations: Initial results from a global 5-min data set. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2009; Volume 27, pp. 2851–2859. [Google Scholar] [CrossRef]
- Bock, O.; Bosser, P.; Pacione, R.; Nuret, M.; Fourrié, N.; Parracho, A. A high-quality reprocessed ground-based GPS dataset for atmospheric process studies, radiosonde and model evaluation, and reanalysis of HyMeX S pecial Observing Period. Q. J. R. Meteorol. Soc. 2016, 142, 56–71. [Google Scholar] [CrossRef]
- Bock, O.; Bosser, P.; Flamant, C.; Doerflinger, E.; Jansen, F.; Fages, R.; Bony, S.; Schnitt, S. IWV observations in the Caribbean Arc from a network of ground-based GNSS receivers during EUREC4A. Earth Syst. Sci. Data 2021, 13, 2407–2436. [Google Scholar] [CrossRef]
- Fersch, B.; Wagner, A.; Kamm, B.; Shehaj, E.; Schenk, A.; Yuan, P.; Geiger, A.; Moeller, G.; Heck, B.; Hinz, S.; et al. Tropospheric water vapor: A comprehensive high-resolution data collection for the transnational Upper Rhine Graben region. Earth Syst. Sci. Data 2022, 14, 5287–5307. [Google Scholar] [CrossRef]
- NGL. Troposheric Products from Nevada Geodetic Lab (NGL). Available online: http://geodesy.unr.edu/ (accessed on 25 May 2023).
- Blewitt, G.; Hammond, W.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99. [Google Scholar] [CrossRef]
- Yuan, P.; Blewitt, G.; Kreemer, C.; Hammond, W.C.; Argus, D.; Yin, X.; Van Malderen, R.; Mayer, M.; Jiang, W.; Awange, J.; et al. An enhanced integrated water vapour dataset from more than 10,000 global ground-based GPS stations in 2020. Earth Syst. Sci. Data 2023, 15, 723–743. [Google Scholar] [CrossRef]
- Yuan, P.; Blewitt, G.; Kreemer, C.; Hammond, W.C.; Argus, D.; Yin, X.; Van Malderen, R.; Mayer, M.; Jiang, W.; Awange, J.; et al. An Enhanced Integrated Water Vapour Dataset from More Than 10,000 Global Ground-Based GPS Stations in 2020; Zenodo [Data Set]; Zenodo: Geneva, Switzerland, 2022. [Google Scholar] [CrossRef]
- EUMETNET. E-GVAP Project. Available online: http://egvap.dmi.dk (accessed on 20 June 2023).
- UCAR. SUOMINET. Available online: https://data.cosmic.ucar.edu/suominet/ (accessed on 20 June 2023).
- Ware, R.; Braun, J.; Ha, S.; Hunt, D.; Kuo, Y.; Rocken, C.; Sleziak, M.; Van Hove, T.; Weber, J.; Anthes, R. Real-time water vapor sensing with suominet–today and tomorrow. In Proceedings of the International GPS Meteorology Workshop, Tsukuba, Japan, 14–17 January 2003; Citeseer: State College, PA, USA, 2003; pp. 14–17. [Google Scholar]
- WMO. The 2022 GCOS ECVs Requirements. 2022. Available online: https://library.wmo.int/doc_num.php?explnum_id=11318 (accessed on 11 August 2023).
- Su, Z.; Timmermans, W.; Zeng, Y.; Schulz, J.; John, V.; Roebeling, R.; Poli, P.; Tan, D.; Kaspar, F.; Kaiser-Weiss, A.; et al. An overview of European efforts in generating climate data records. Bull. Am. Meteorol. Soc. 2018, 99, 349–359. [Google Scholar] [CrossRef]
- Ning, T.; Elgered, G. Trends in the atmospheric water vapor content from ground-based GPS: The impact of the elevation cutoff angle. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 744–751. [Google Scholar] [CrossRef]
- Wang, J.; Dai, A.; Mears, C. Global water vapor trend from 1988 to 2011 and its diurnal asymmetry based on GPS, radiosonde, and microwave satellite measurements. J. Clim. 2016, 29, 5205–5222. [Google Scholar] [CrossRef]
- EPN. EPN-Repro2 Repository. Available online: http://www.epncb.oma.be/_productsservices/analysiscentres/repro2.php (accessed on 20 June 2023).
- Raoult, B.; Bergeron, C.; Alós, A.L.; Thépaut, J.N.; Dee, D. Climate service develops user-friendly data store. ECMWF Newsl. 2017, 151, 22–27. [Google Scholar] [CrossRef]
- IGS. IGS-Repro Repository. Available online: https://igs.org/acc/reprocessing (accessed on 20 June 2023).
- Bock, O. Global GNSS Integrated Water Vapour Data, 1994–2022 [Data Set]. Aeris: 2022. Available online: https://www.aeris-data.fr/en/landing-page/?uuid=df7cf172-31fb-4d17-8f00-1a9293eb3b95 (accessed on 24 October 2023). [CrossRef]
- Bock, O.; Parracho, A.C. Consistency and representativeness of integrated water vapour from ground-based GPS observations and ERA-Interim reanalysis. Atmos. Chem. Phys. 2019, 19, 9453–9468. [Google Scholar] [CrossRef]
- CDDIS. NASA’s Archive of Space Geodesy Data. Available online: https://cddis.nasa.gov/archive/gnss/products/troposphere/zpd/ (accessed on 20 June 2023).
- Kačmařík, M.; Douša, J.; Dick, G.; Zus, F.; Brenot, H.; Möller, G.; Pottiaux, E.; Kapłon, J.; Hordyniec, P.; Václavovic, P.; et al. Inter-technique validation of tropospheric slant total delays. Atmos. Meas. Tech. 2017, 10, 2183–2208. [Google Scholar] [CrossRef]
- Thorne, P.W.; Madonna, F.; Schulz, J.; Oakley, T.; Ingleby, B.; Rosoldi, M.; Tramutola, E.; Arola, A.; Buschmann, M.; Mikalsen, A.C.; et al. Making better sense of the mosaic of environmental measurement networks: A system-of-systems approach and quantitative assessment. Geosci. Instrum. Methods Data Syst. 2017, 6, 453–472. [Google Scholar] [CrossRef]
- IGS. IGS Formats and Standards. Available online: https://igs.org/formats-and-standards/ (accessed on 21 June 2023).
- Klein, E.; Vigny, C.; Nocquet, J.M.; Boulze, H. A 20 year-long GNSS solution across South America with focus in Chile. Bull. Soc. Géol. Fr. 2022, 193, 5. [Google Scholar] [CrossRef]
- Gazeaux, J.; Williams, S.; King, M.; Bos, M.; Dach, R.; Deo, M.; Moore, A.W.; Ostini, L.; Petrie, E.; Roggero, M.; et al. Detecting offsets in GPS time series: First results from the detection of offsets in GPS experiment. J. Geophys. Res. Solid Earth 2013, 118, 2397–2407. [Google Scholar] [CrossRef]
- Van Malderen, R.; Pottiaux, E.; Klos, A.; Domonkos, P.; Elias, M.; Ning, T.; Bock, O.; Guijarro, J.; Alshawaf, F.; Hoseini, M.; et al. Homogenizing GPS integrated water vapor time series: Benchmarking break detection methods on synthetic data sets. Earth Space Sci. 2020, 7, e2020EA001121. [Google Scholar] [CrossRef]
- Pacione, R.; Araszkiewicz, A.; Brockmann, E.; Dousa, J. EPN-Repro2: A reference GNSS tropospheric data set over Europe. Atmos. Meas. Tech. 2017, 10, 1689. [Google Scholar] [CrossRef]
- Pacione, R.; Pace, B.; Vedel, H.; De Haan, S.; Lanotte, R.; Vespe, F. Combination methods of tropospheric time series. Adv. Space Res. 2011, 47, 323–335. [Google Scholar] [CrossRef]
- Bock, O. Standardisation of ZTD screening and IPW conversion. In Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate: COST Action ES1206 Final Action Dissemination Report; Jones, J., Guerova, G., Douša, J., Dick, G., de Haan, S., Pottiaux, E., Bock, O., Pacione, R., van Malderen, R., Eds.; Springer: Cham, Switzerland, 2020; pp. 314–318. [Google Scholar] [CrossRef]
- Ning, T.; Wang, J.; Elgered, G.; Dick, G.; Wickert, J.; Bradke, M.; Sommer, M.; Querel, R.; Smale, D. The uncertainty of the atmospheric integrated water vapour estimated from GNSS observations. Atmos. Meas. Tech. 2016, 9, 79–92. [Google Scholar] [CrossRef]
- Bradke, M. SEMISYS-Sensor Meta Information System; GFZ Data Services: Potsdam, Germany, 2020. [Google Scholar] [CrossRef]
- Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A. Global estimates of water-vapor-weighted mean temperature of the atmosphere for GPS applications. J. Geophys. Res. 2005, 110, D21101. [Google Scholar] [CrossRef]
- Fionda, E.; Cadeddu, M.; Mattioli, V.; Pacione, R. Intercomparison of integrated water vapor measurements at high latitudes from co-located and near-located instruments. Remote Sens. 2019, 11, 2130. [Google Scholar] [CrossRef]
- Sapucci, L.F. Evaluation of modeling water-vapor-weighted mean tropospheric temperature for GNSS-integrated water vapor estimates in Brazil. J. Appl. Meteorol. Climatol. 2014, 53, 715–730. [Google Scholar] [CrossRef]
- Li, L.; Wu, S.Q.; Wang, X.M.; Tian, Y.; He, C.Y.; Zhang, K.F. Modelling of weighted-mean temperature using regional radiosonde observations in Hunan China. TAO Terr. Atmos. Ocean. Sci. 2018, 29, 187–199. [Google Scholar] [CrossRef]
- Glowacki, T.J.; Penna, N.T.; Bourke, W.P. Validation of GPS-based estimates of integrated water vapour for the Australian region and identification of diurnal variability. Aust. Meteorol. Mag. 2006, 55, 131–148. [Google Scholar]
- Bock, O.; Bouin, M.N.; Walpersdorf, A.; Lafore, J.P.; Janicot, S.; Guichard, F.; Agusti-Panareda, A. Comparison of ground-based GPS precipitable water vapour to independent observations and NWP model reanalyses over Africa. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2007, 133, 2011–2027. [Google Scholar] [CrossRef]
- Parracho, A.C.B. Study of Trends and Variability of Atmospheric Water Vapour with Climate Models and Observations from Global GNSS Network. Ph.D. Thesis, Université Pierre et Marie Curie-Paris VI, Paris, France, 2017. [Google Scholar]
- Graham, R.M.; Hudson, S.R.; Maturilli, M. Improved Performance of ERA5 in Arctic Gateway Relative to Four Global Atmospheric Reanalyses. Geophys. Res. Lett. 2019, 46, 6138–6147. [Google Scholar] [CrossRef]
- Madonna, F.; Tramutola, E.; SY, S.; Serva, F.; Proto, M.; Rosoldi, M.; Gagliardi, S.; Amato, F.; Marra, F.; Fassò, A.; et al. The New Radiosounding HARMonization (RHARM) Data Set of Homogenized Radiosounding Temperature, Humidity, and Wind Profiles with Uncertainties. J. Geophys. Res. Atmos. 2022, 127, e2021JD035220. [Google Scholar] [CrossRef]
- Miloshevich, L.M.; Paukkunen, A.; Vömel, H.; Oltmans, S.J. Development and Validation of a Time-Lag Correction for Vaisala Radiosonde Humidity Measurements. J. Atmos. Ocean. Technol. 2004, 21, 1305–1327. [Google Scholar] [CrossRef]
- Suncalc. Openly-Licensed, Vectorized Python Library for Calculating Sun Position and Sunlight Phases. Available online: https://pypi.org/project/suncalc/. (accessed on 24 July 2023).
- Sommer, M.; von Rohden, C.; Simeonov, T.; Oelsner, P.; Naebert, T.; Romanens, G.; Jauhiainen, H.; Survo, P.; Dirksen, R. GRUAN Technical Document 8—GRUAN Characterisation and Data Processing of the Vaisala RS41 Radiosonde. 2023. Available online: https://www.gruan.org/gruan/editor/documents/gruan/GRUAN-TD-8_RS41_v1.0.0_20230628_final.pdf (accessed on 24 October 2023).
- JCGM. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. 2008. Available online: ttps://www.bipm.org/en/publications/guides/gum. html (accessed on 24 July 2023).
- Fassò, A.; Ignaccolo, R.; Madonna, F.; Demoz, B.B.; Franco-Villoria, M. Statistical modelling of collocation uncertainty in atmospheric thermodynamic profiles. Atmos. Meas. Tech. 2014, 7, 1803–1816. [Google Scholar] [CrossRef]
- Nilsson, T.; Elgered, G. Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- SciPy. Scientific Python. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html (accessed on 24 July 2023).
- Virtanen, A.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Immler, F.; Dykema, J.; Gardiner, T.; Whiteman, D.; Thorne, P.; Vömel, H. Reference quality upper-air measurements: Guidance for developing GRUAN data products. Atmos. Meas. Tech. 2010, 3, 1217–1231. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Fan, S.; Cheng, Y. Water vapor-weighted mean temperature and its impact on the determination of precipitable water vapor and its linear trend. J. Geophys. Res. Atmos. 2016, 121, 833–852. [Google Scholar] [CrossRef]
- Bosser, P.; Bock, O.; Flamant, C.; Bony, S.; Speich, S. Integrated water vapour content retrievals from ship-borne GNSS receivers during EUREC 4 A. Earth Syst. Sci. Data 2021, 13, 1499–1517. [Google Scholar] [CrossRef]
- Ciesielski, P.E.; Yu, H.; Johnson, R.H.; Yoneyama, K.; Katsumata, M.; Long, C.N.; Wang, J.; Loehrer, S.M.; Young, K.; Williams, S.F.; et al. Quality-Controlled Upper-Air Sounding Dataset for DYNAMO/CINDY/AMIE: Development and Corrections. J. Atmos. Ocean. Technol. 2014, 31, 741–764. [Google Scholar] [CrossRef]
- Thomas, I.D.; King, M.A.; Clarke, P.J.; Penna, N.T. Precipitable water vapor estimates from homogeneously reprocessed GPS data: An intertechnique comparison in Antarctica. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Klos, A.; Hunegnaw, A.; Teferle, F.N.; Abraha, K.E.; Ahmed, F.; Bogusz, J. Statistical significance of trends in Zenith Wet Delay from re-processed GPS solutions. GPS Solut. 2018, 22, 51. [Google Scholar] [CrossRef]
- ATBD. GNSS IPW: Algorithm Theoretical Basis Description (ATBD). Available online: https://confluence.ecmwf.int/x/rZH-EQ (accessed on 21 June 2023).
- Elgered, G.; Davis, J.L.; Herring, T.A.; Shapiro, I.I. Geodesy by radio interferometry: Water vapor radiometry for estimation of the wet delay. J. Geophys. Res. Solid Earth 1991, 96, 6541–6555. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The constants in the equation for atmospheric refractive index at radio frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Boudouris, G. On the index of refraction of air, the absorption and dispersion of centimeter waves by gasses. J. Res. Natl. Bur. Stand. Sect. Phys. Chem. 1963, 67D, 631–684. [Google Scholar] [CrossRef]
- Ssenyunzi, R.C.; Oruru, B.; D’ujanga, F.M.; Realini, E.; Barindelli, S.; Tagliaferro, G.; von Engeln, A.; van de Giesen, N. Performance of ERA5 data in retrieving Precipitable Water Vapour over East African tropical region. Adv. Space Res. 2020, 65, 1877–1893. [Google Scholar] [CrossRef]
- Mateus, P.; Catalão, J.; Mendes, V.B.; Nico, G. An ERA5-based hourly global pressure and temperature (HGPT) model. Remote Sens. 2020, 12, 1098. [Google Scholar] [CrossRef]







| Consistency | ||||||
|---|---|---|---|---|---|---|
| Station | Strong | Moderate | Weak | Inconsistent | ||
| [kg/m] | [kg/m] | [%] | [%] | [%] | [%] | |
| NYA1, day | 0.4 | 0.3 | 27.9 | 46.8 | 20.7 | 4.6 |
| NYA1, night | 0.2 | 0.3 | 20.1 | 40.9 | 30.6 | 8.5 |
| TSKB, day | 1.1 | 0.4 | 47.1 | 32.6 | 14.4 | 5.8 |
| TSKB, night | 1.2 | 0.4 | 33.7 | 46.5 | 14.3 | 5.5 |
| Average | 0.7 | 0.3 | 32.2 | 41.7 | 20.0 | 6.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rannat, K.; Keernik, H.; Madonna, F. The Novel Copernicus Global Dataset of Atmospheric Total Water Vapour Content with Related Uncertainties from GNSS Observations. Remote Sens. 2023, 15, 5150. https://doi.org/10.3390/rs15215150
Rannat K, Keernik H, Madonna F. The Novel Copernicus Global Dataset of Atmospheric Total Water Vapour Content with Related Uncertainties from GNSS Observations. Remote Sensing. 2023; 15(21):5150. https://doi.org/10.3390/rs15215150
Chicago/Turabian StyleRannat, Kalev, Hannes Keernik, and Fabio Madonna. 2023. "The Novel Copernicus Global Dataset of Atmospheric Total Water Vapour Content with Related Uncertainties from GNSS Observations" Remote Sensing 15, no. 21: 5150. https://doi.org/10.3390/rs15215150