Non-Local SAR Image Despeckling Based on Sparse Representation
Abstract
:1. Introduction
2. Basic Idea
2.1. Noise Model Analysis
2.2. Sparse Representation
2.3. Motivation
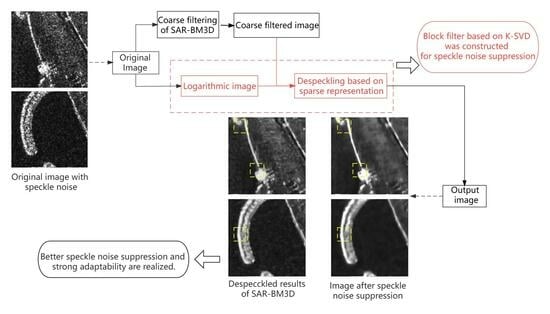
3. Proposed Algorithm
3.1. Three-Dimensional Dictionary Group
3.2. Sparse Representation Despeckling
4. Experimental Result
4.1. Parameter Setting
4.2. Evaluation Indicators and Despeckling Results
5. Discussion
6. Conclusions
- Firstly, the proposed algorithm is based on the structure of SAR-BM3D. Although it is indeed improved, and the comprehensive ability is better than the comparison methods, the upgrade of the structure needs to be further studied.
- Secondly, the sparse representation algorithms run on logarithmic domain at present, but the logarithmic domain may not be optimal. In future studies, the projection process can also be included in dictionary learning to explore the space for further improvement.
- Finally, the non-local idea of the proposed algorithm requires a large number of similarity calculations between image blocks on the whole image, so it is still a very complex and time-consuming algorithm. It may be possible to reduce the time consumption of the algorithm by improving the calculation rules of similarity accuracy between image blocks, changing the size of image blocks or the size of the selection region centered on the reference block.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SAR | SAR Synthetic Aperture Radar |
| SAR-BM3D | SAR Image Block-Matching Three-Dimensional |
| K-SVD | K-means Singular Value Decomposition |
| NLM | Non-Local Mean |
| BM3D | Block-Matching Three-Dimensional |
| PPB | Probabilistic Patch-Based |
| FT | Fourier Transform |
| DCT | Discrete Cosine Transform |
| WT | Wavelet Transform |
| MAP | Maximum A Posteriori |
| OMP | Orthogonal Matching Pursuit |
| UDWT | Undecimated Discrete Wavelet Transform |
| LLMMSE | Local Linear Minimum-Mean-Square-Error |
| PDE | Partial Differential Equation |
| ENL | Equivalent Number of Looks |
| EPI | Edge Preservation Indicator |
References
- Porcello, L.J. Speckle reduction in synthetic-aperture radars. J. Opt. Soc. Am. 1976, 66, 140–158. [Google Scholar] [CrossRef]
- Lee, J.S. Digital Image Enhancement and Noise Filtering by Use of Local Statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 2, 165–168. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S. Refined Filtering of Image Noise using Local Statistics. Comput. Graph. Image Process. 1981, 15, 380–389. [Google Scholar] [CrossRef]
- Lee, J.S. Digital Image Smoothing and the Sigma Filter. Comput. Vis. Graph. Image Process. 1983, 24, 255–269. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Lopes, A.; Nezry, E.; Touzi, R.; Laur, H. Maximum a Posteriori Speckle Filtering and First Order Texture Models in Sar Images. In Proceedings of the 10th Annual International Symposium on Geoscience and Remote Sensing, College Park, MD, USA, 20–24 May 1990; IEEE: Piscataway, NJ, USA, 1990; pp. 2409–2412. [Google Scholar]
- Donoho, D.L. De-noising by Soft-Thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Pizurica, A.; Philips, W.; Lemahieu, I.; Acheroy, M. Despeckling SAR Images Using Wavelets anda New Class of Adaptive Shrinkage Estimators. In Proceedings of the International Conference on Image Processing, Thessaloniki, Greece, 7–10 October 2001; IEEE: Piscataway, NJ, USA, 2001; Volume 2, pp. 233–236. [Google Scholar]
- Yu, Y.; Acton, S.T. Speckle reducing anisotropic diffusion. IEEE Trans. Image Process. 2002, 11, 1260–1270. [Google Scholar]
- Aja-Fernandez, S.; Alberola-Lopez, C. On the estimation of the coefficient of variation for anisotropic diffusion speckle filtering. IEEE Trans. Image Process. 2006, 15, 2694–2701. [Google Scholar] [CrossRef]
- Krissian, K.; Westin, C.F.; Kikinis, R.; Vosburgh, K.G. Oriented speckle reducing anisotropic diffusion. Image Process. IEEE Trans. 2007, 16, 1412–1424. [Google Scholar] [CrossRef]
- Brudes, A.; Coll, B.; Merel, J.M. A Review of Image Denoising Algorithms, with a New One. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar]
- Deledalle, C.A.; Denis, L.; Tupin, F. Iterative Weighted Maximum Likelihood Denoising with Probabilistic Patch-Based Weights. IEEE Trans. Image Process. 2009, 18, 2661–2672. [Google Scholar] [CrossRef] [PubMed]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef] [PubMed]
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A Nonlocal SAR Image Denoising Algorithm Based on LLMMSE Wavelet Shrinkage. IEEE Trans. Geosci. Remote Sens. 2012, 50, 606–616. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- López-Martínez, C.; Fàbregas, X. Polarimetric SAR speckle noise model. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2232–2242. [Google Scholar] [CrossRef]
- Aharon, M.; Elad, M.; Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. Signal Process. 2006, 54, 4311–4322. [Google Scholar] [CrossRef]
- He, Y.; Li, M.; Lv, D.; Huang, K. Novel Infrared Image Denoising Method Based on Curvelet Transform. Comput. Eng. Appl. 2011, 47, 191–193. [Google Scholar]
- Do, M.N.; Vetterli, M. The Contourlet Transform: An Efficient Directional Multiresolution Image Representation. IEEE Trans. Image Process. 2006, 14, 2091–2106. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993. [Google Scholar]
- Foucher, S. SAR Image Filtering Via Learned Dictionaries and Sparse Representations. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
- Zhang, J.; Chen, J.; Yu, H.; Yang, D.; Xu, X.; Xing, M. Learning an SAR image despeckling model via weighted sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7148–7158. [Google Scholar] [CrossRef]
- Liu, S.; Pu, N.; Cao, J.; Zhang, K. Synthetic Aperture Radar Image Despeckling Based on Multi-Weighted Sparse Coding. Entropy 2022, 24, 96. [Google Scholar] [CrossRef]
- Guleryuz, O.G. Nonlinear approximation based image recovery using adaptive sparse reconstructions and iterated denoising: Part I—Theory. IEEE Trans. Image Process. 2005, 15, 539–553. [Google Scholar] [CrossRef] [PubMed]
- Guleryuz, O.G. Nonlinear approximation based image recovery using adaptive sparse reconstructions and iterated denoising: Part II—Adaptive algorithms. IEEE Trans. Image Process. 2005, 15, 554–571. [Google Scholar] [CrossRef] [PubMed]












| System Parameter | Value |
|---|---|
| Pulse repetition frequency | 8300 Hz |
| Ground range resolution | 1.18 m |
| Azimuth resolution | 1.10 m |
| Signal Bandwidth | 300 MHz |
| Algorithm | ENL | EPI | Average of the Ratio of Noisy Image to Despeckled Image | Variance of the Ratio of Noisy Image to Despeckled Image |
|---|---|---|---|---|
| Noisy image | 0.99 | 1 | - | - |
| PDE | 7.9 | 0.86 | 1.05 | 0.53 |
| PPB | 10.12 | 0.76 | 0.83 | 0.57 |
| SAR-BM3D | 36.33 | 0.68 | 0.94 | 1.07 |
| Proposed algorithm | 38.61 | 0.87 | 0.92 | 0.99 |
| Algorithm | Figure | EPI | ENL |
|---|---|---|---|
| Noisy image | (c) | 1 | 0.99 |
| (d) | 1 | 0.95 | |
| SAR-BM3D | (e) | 0.30 | 3.66 |
| (f) | 0.34 | 2.64 | |
| Proposed method | (g) | 0.28 | 5.02 |
| (h) | 0.37 | 3.98 |
| Algorithm | Figure | EPI | ENL |
|---|---|---|---|
| Noisy image | (a) original | 1 | 1.38 |
| (b) SNR = 10 dB | 1 | 1.30 | |
| (c) SNR = 20 dB | 1 | 1.32 | |
| SAR-BM3D | (d) original | 0.43 | 10.13 |
| (e) SNR = 10 dB | 0.26 | 8.49 | |
| (f) SNR = 20 dB | 0.30 | 15.61 | |
| Proposed method | (g) original | 0.79 | 16.77 |
| (h) SNR = 10 dB | 0.38 | 7.52 | |
| (i) SNR = 20 dB | 0.41 | 19.35 |
| Algorithm | Refined Lee | PPB | SAR-BM3D | Ours |
|---|---|---|---|---|
| Running time (s) | 4.58 | 7.49 | 14.67 | 18.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Yu, J.; Li, Z.; Yu, Z. Non-Local SAR Image Despeckling Based on Sparse Representation. Remote Sens. 2023, 15, 4485. https://doi.org/10.3390/rs15184485
Yang H, Yu J, Li Z, Yu Z. Non-Local SAR Image Despeckling Based on Sparse Representation. Remote Sensing. 2023; 15(18):4485. https://doi.org/10.3390/rs15184485
Chicago/Turabian StyleYang, Houye, Jindong Yu, Zhuo Li, and Ze Yu. 2023. "Non-Local SAR Image Despeckling Based on Sparse Representation" Remote Sensing 15, no. 18: 4485. https://doi.org/10.3390/rs15184485
APA StyleYang, H., Yu, J., Li, Z., & Yu, Z. (2023). Non-Local SAR Image Despeckling Based on Sparse Representation. Remote Sensing, 15(18), 4485. https://doi.org/10.3390/rs15184485