A Novel Method for Monitoring Tropical Cyclones’ Movement Using GNSS Zenith Tropospheric Delay
Abstract
:1. Introduction
2. Materials and Methods
2.1. Estimation of ZTD Derived from GNSS and ERA5 Dataset
2.2. Estimation of PWV from Radiosonde Datasets
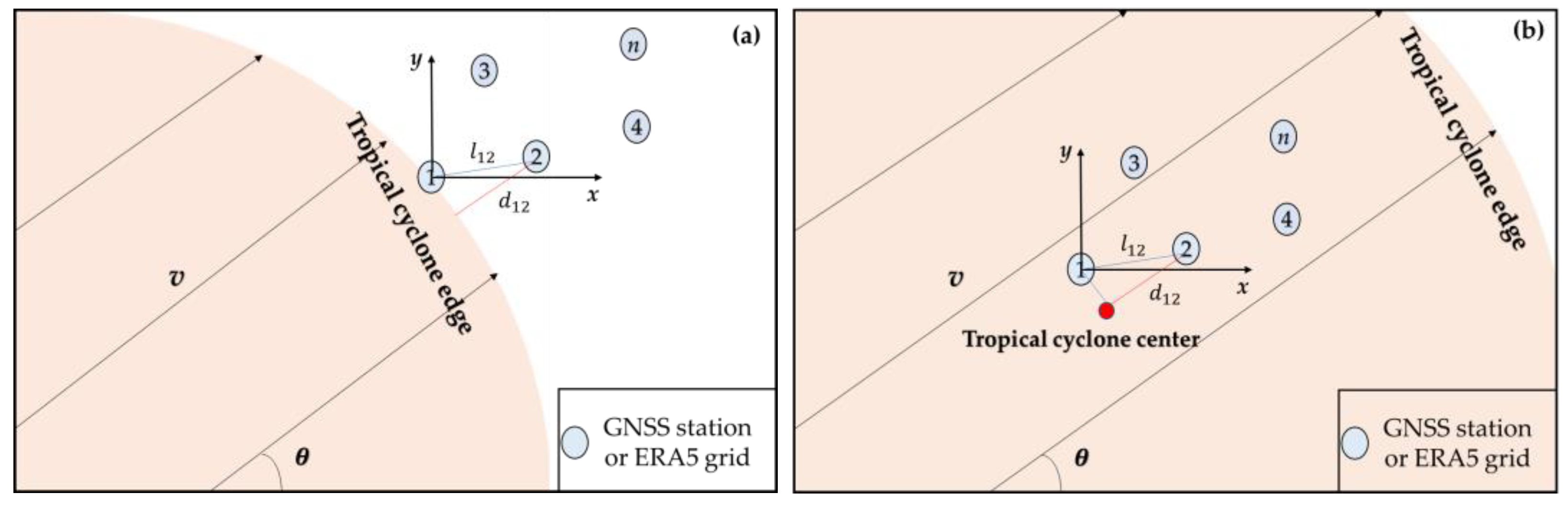
2.3. Estimation of Tropical Cyclones’ Movement Using ZTD Datasets
- (1)
- The v is constant
- (2)
- The v is changeable
2.4. Data Source and Date Processing
- (1)
- ERA5 pressure, temperature and specific humidity grids with a spatial resolution of 0.25° × 0.25° and a temporal resolution of an hour at 37 height levels in 2017 (https://cds.climate.copernicus.eu/#!/home, accessed on 22 May 2023);
- (2)
- Post-processed ZTD time series with a temporal resolution of 5 min over GNSS stations from the International GNSS Service (IGS) in 2017 (https://cddis.nasa.gov/archive/gnss/products/troposphere/zpd, accessed on 22 May 2023);
- (3)
- RS data with a time resolution of 12 h from the University of Wyoming’s department of atmospheric sciences in 2017 (http://weather.uwyo.edu/upperair/sounding.html, accessed on 22 May 2023);
- (4)
- The track and intensity analyses from the Tropical Cyclone Best Track (TCBT) dataset [47,48] provided by CMA in 2017 (http://tcdata.typhoon.org.cn, accessed on 22 May 2023);
3. Results
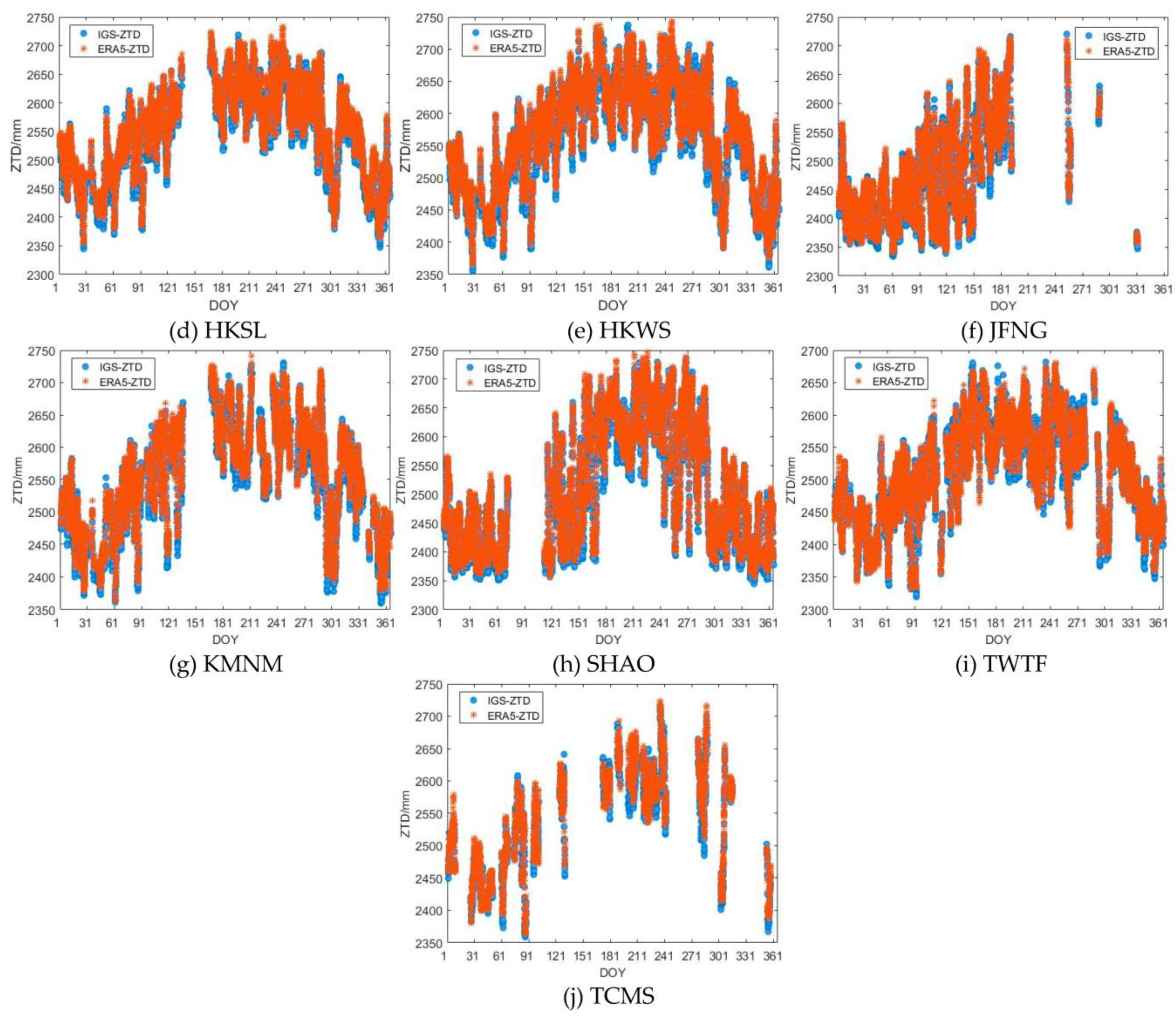
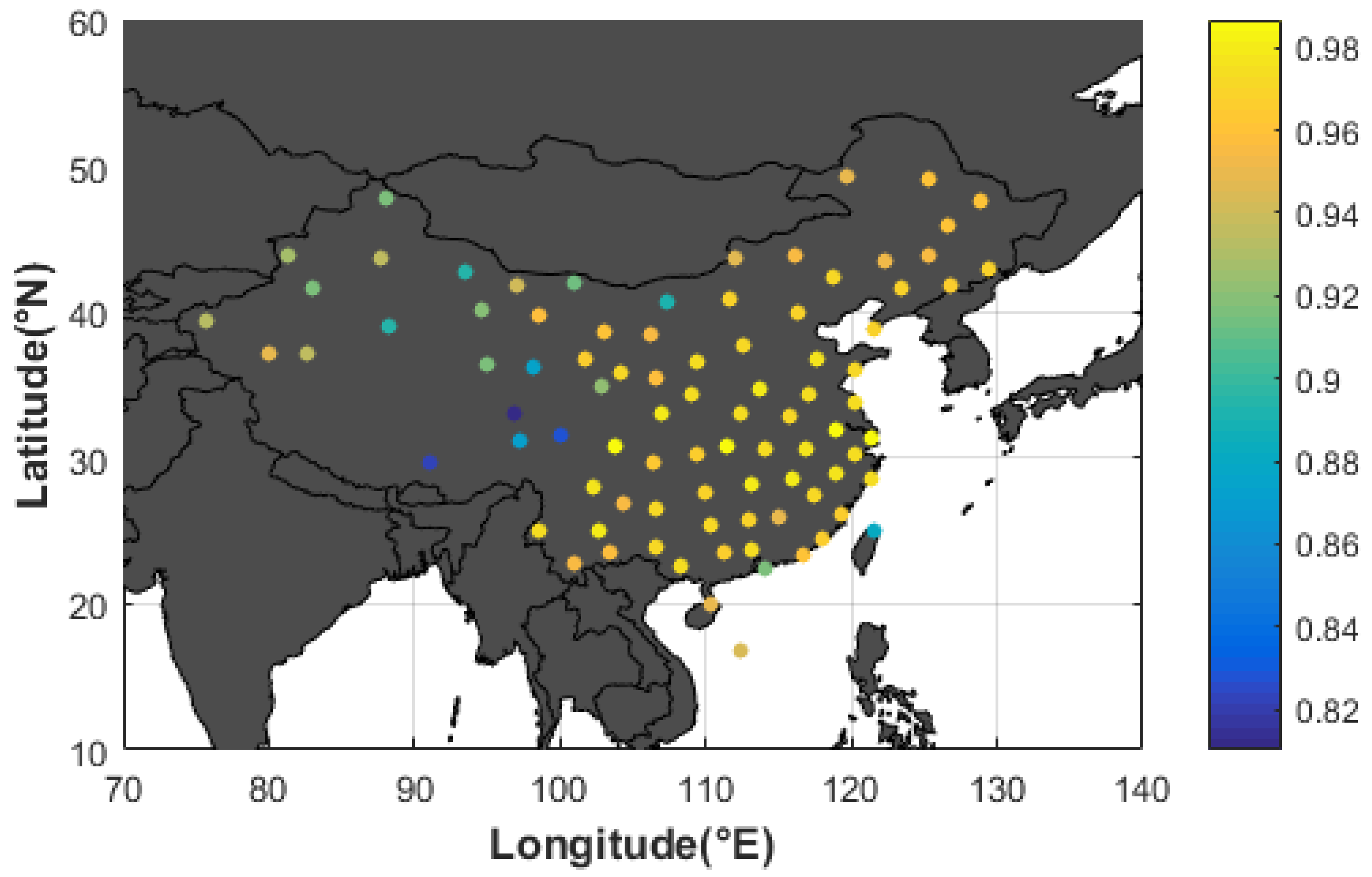
3.1. Comparison of ERA5-ZTD and IGS-ZTD Variations
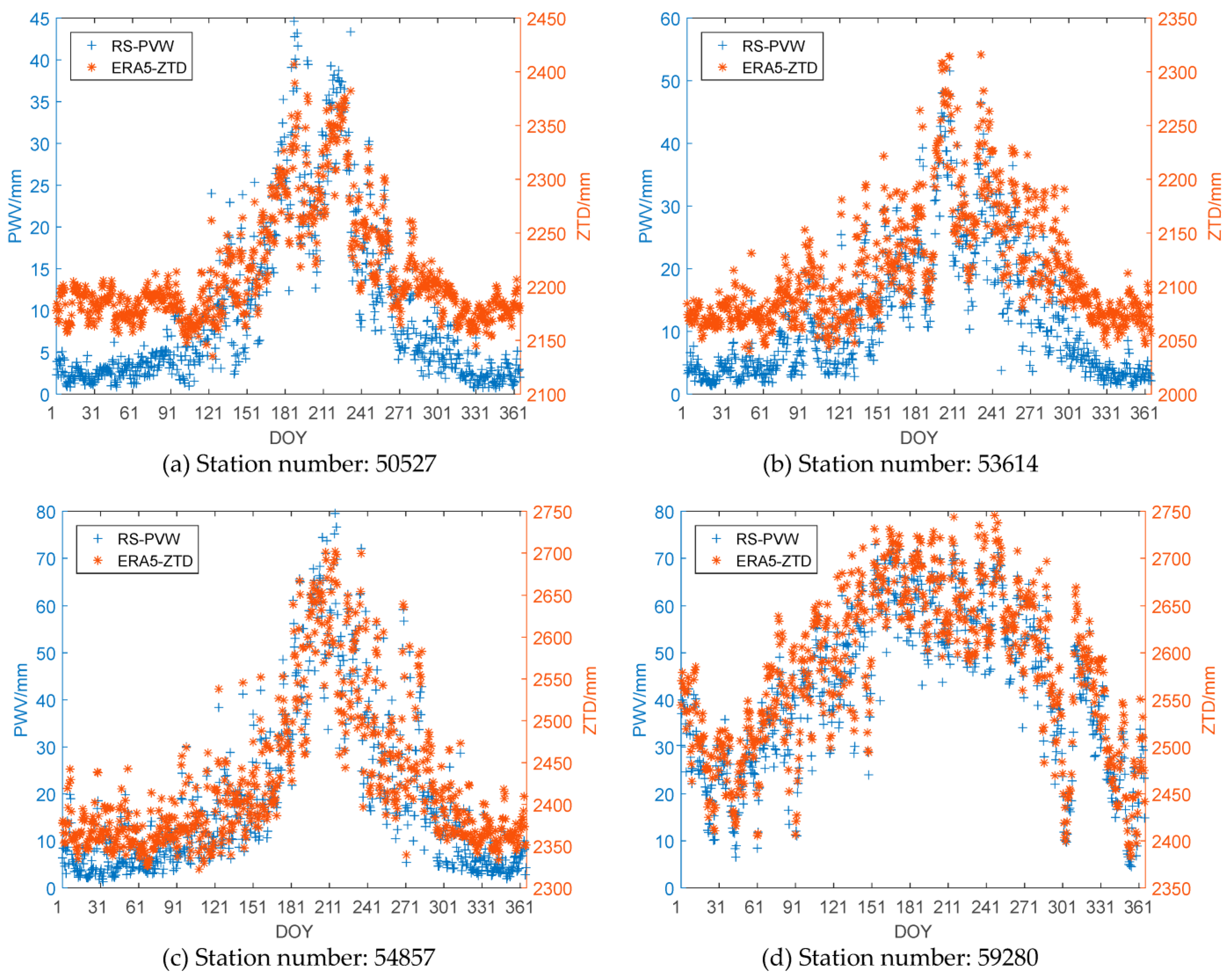
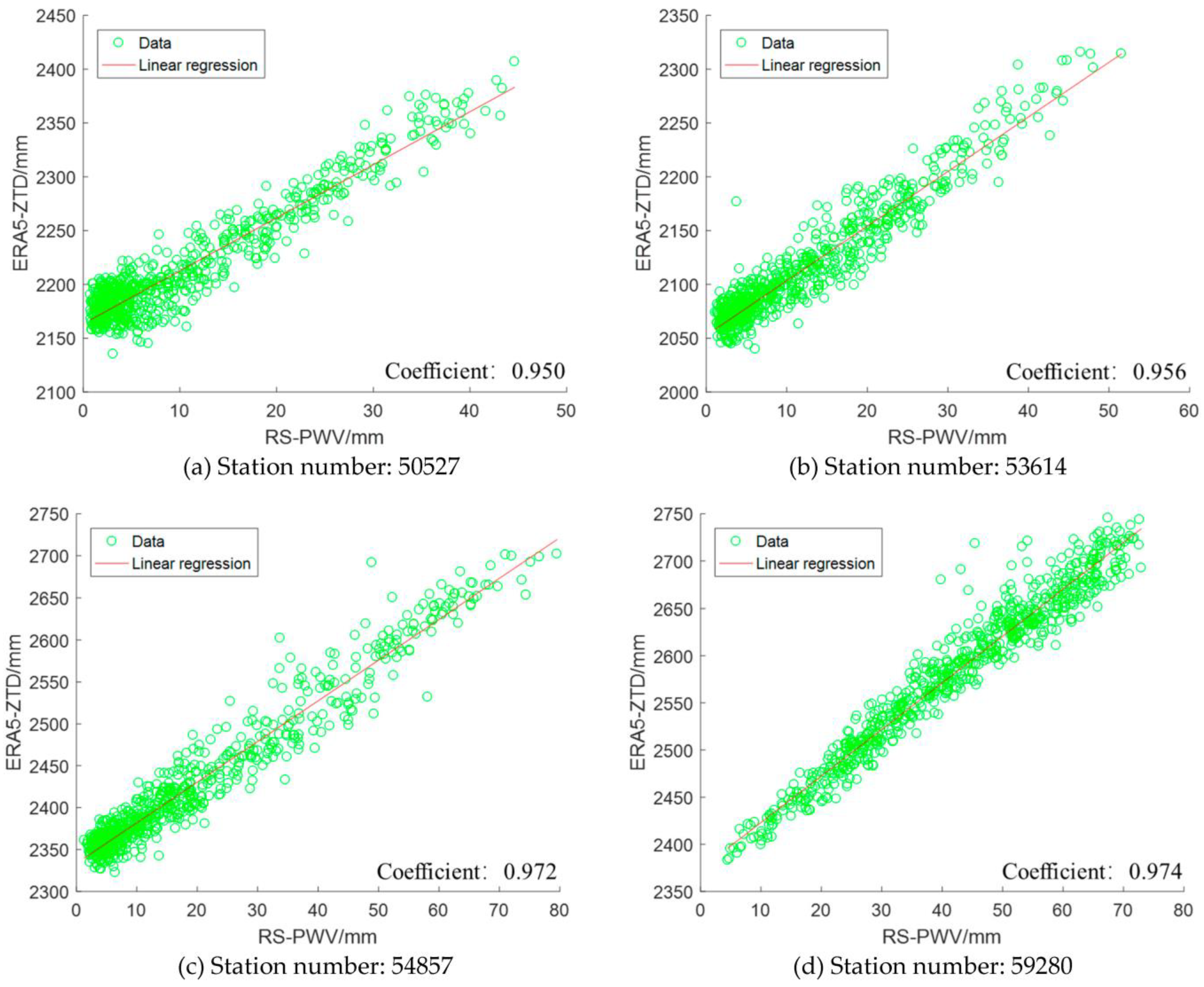
3.2. Comparison of ERA5-ZTD and RS-PWV Variations
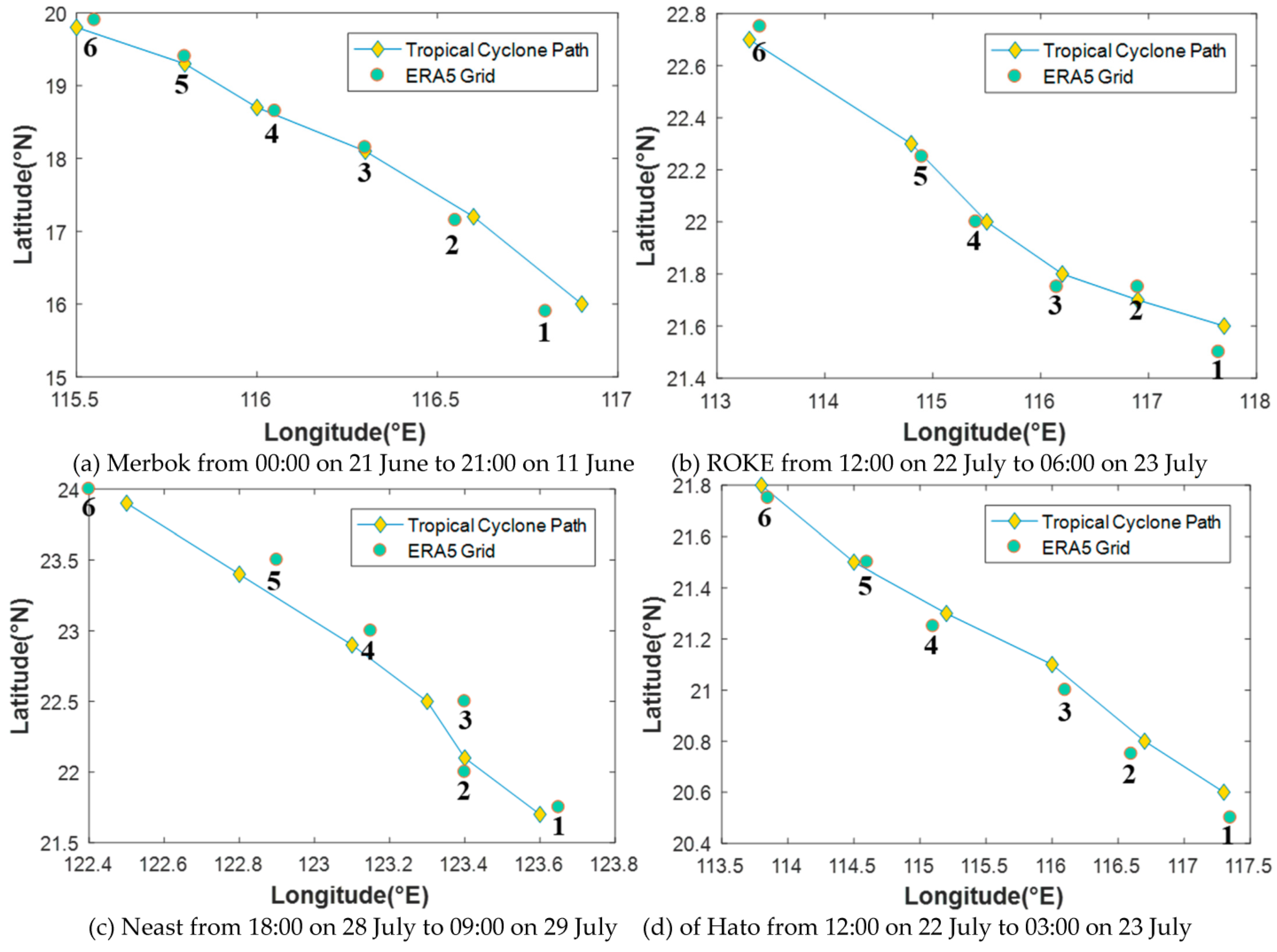
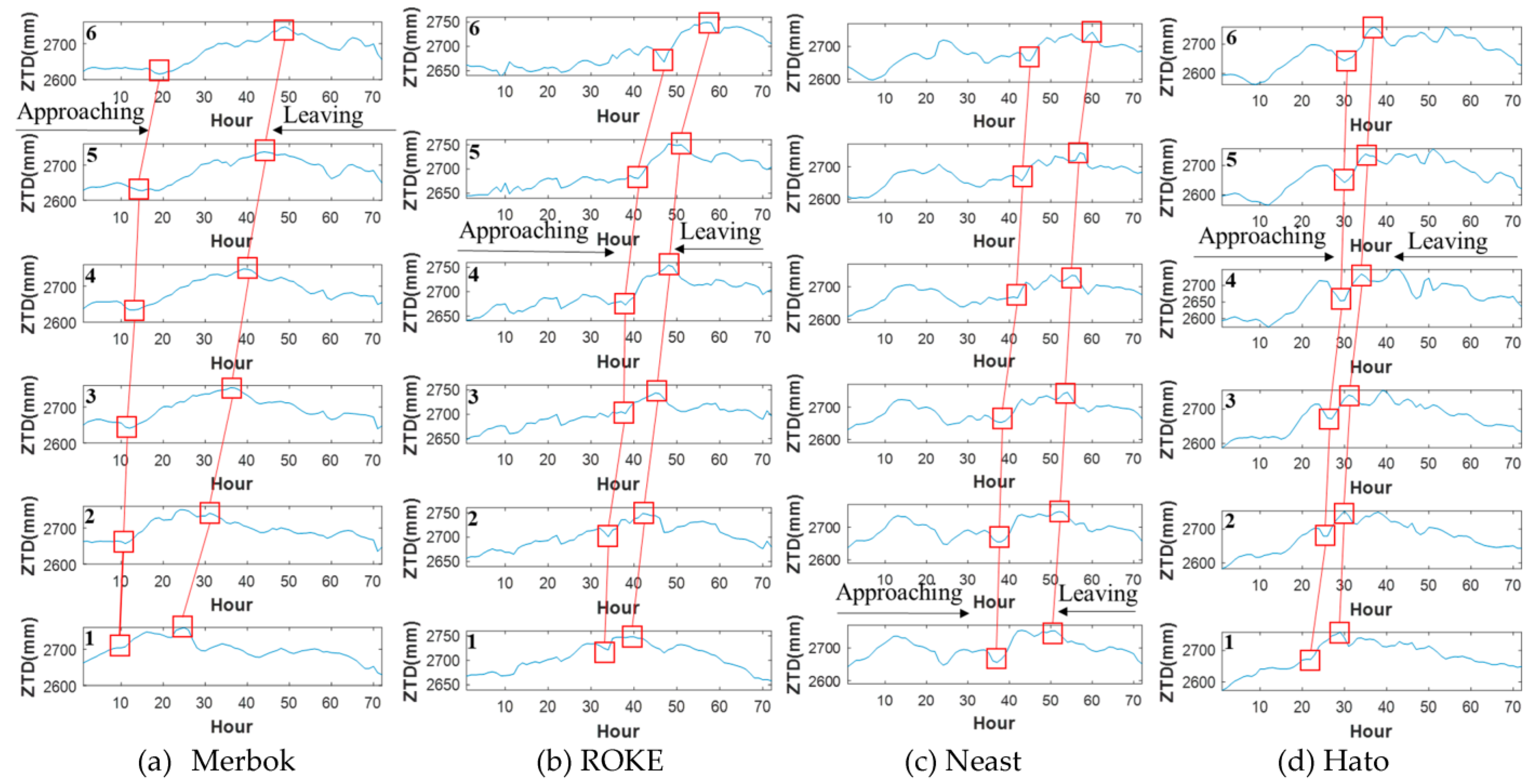
3.3. Relationship between the Spatio-Temporal Distribution of ZTD and the Movement of Tropical Cyclones
3.4. Estimation of Tropical Cyclone’s Movement Using ZTD
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sobel, A.H.; Camargo, S.J.; Hall, T.M.; Lee, C.Y.; Tippett, M.K.; Wing, A.A. Human influence on tropical cyclone intensity. Science 2016, 353, 242–246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Kepert, J.D.; Holland, G.J. The effect of sea spray evaporation on tropical cyclone boundary layer structure and intensity. Mon. Weather Rev. 2001, 129, 2481–2500. [Google Scholar] [CrossRef]
- Wu, L.; Wang, B.; Geng, S. Growing typhoon influence on East Asia. Geophys. Res. Lett. 2005, 32, L18703. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Yao, Y.; Xin, L.; Xu, X. Precipitable water vapor fusion: An approach based on spherical cap harmonic analysis and Helmert variance component estimation. J. Geod. 2019, 93, 2605–2620. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y. Precipitable water vapor fusion based on a generalized regression neural network. J. Geod. 2021, 95, 36. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmos. Sol.-Terr. Phys. 2018, 167, 124–133. [Google Scholar] [CrossRef]
- Yu, S.; Liu, Z. Temporal and spatial impact of precipitable water vapor on GPS relative positioning during the tropical cyclone Hato (2017) in Hong Kong and Taiwan. Earth Space Sci. 2021, 8, e2020EA001371. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Li, Z.; Cheng, Y.; Li, L.; Yuan, H. The correlation between GNSS-derived precipitable water vapor and sea surface temperature and its responses to El Niño–Southern Oscillation. Remote Sens. Environ. 2018, 216, 1–12. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, K.; Li, Z.; Liu, Y.; Yao, Y. A novel ENSO monitoring index and its potential for drought application. J. Atmos. Sol.-Terr. Phys. 2021, 225, 105762. [Google Scholar] [CrossRef]
- Ma, X.; Yao, Y.; Zhang, B.; Du, Z. FY-3A/MERSI precipitable water vapor reconstruction and calibration using multi-source observation data based on a generalized regression neural network. Atmos. Res. 2022, 265, 105893. [Google Scholar] [CrossRef]
- Tan, J.; Chen, B.; Wang, W.; Yu, W.; Dai, W. Evaluating Precipitable Water Vapor Products from Fengyun-4A Meteorological Satellite Using Radiosonde, GNSS, and ERA5 Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Gong, Y.; Liu, Z.; Foster, J.H. Evaluating the Accuracy of Satellite-Based Microwave Radiometer PWV Products Using Shipborne GNSS Observations Across the Pacific Ocean. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–10. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. (1988–2005) 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Zhang, B.; Yao, Y.; Fok, H.S.; Hu, Y.; Chen, Q. Potential seasonal terrestrial water storage monitoring from GPS vertical displacements: A case study in the lower three-rivers headwater region, China. Sensors 2016, 16, 1526. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Liu, Z. Improving gnss ppp accuracy through WVR PWV augmentation. J. Geod. 2019, 93, 1685–1705. [Google Scholar] [CrossRef]
- Puente, V.; Azcue, E.; Gomez-Espada, Y.; Garcia-Espada, S. Comparison of common VLBI and GNSS estimates in CONT17 campaign. J. Geod. 2021, 95, 1–20. [Google Scholar] [CrossRef]
- Nykiel, G.; Figurski, M.; Baldysz, Z. Analysis of GNSS sensed precipitable water vapour and tropospheric gradients during the derecho event in Poland of 11th August 2017. J. Atmos. Sol. Terr. Phys. 2019, 193, 105082. [Google Scholar] [CrossRef]
- Li, H.; Wang, X.; Choy, S.; Jiang, C.; Wu, S.; Zhang, J.; Qiu, C.; Zhou, K.; Li, L.; Fu, E.; et al. Detecting heavy rainfall using anomaly-based percentile thresholds of predictors derived from GNSS-PWV. Atmos. Res. 2022, 265, 105912. [Google Scholar] [CrossRef]
- He, Q.; Li, L.; Lian, D.; Yu, H.; Chen, G.; Gao, B.; Wang, R.; Song, K.; Li, L. A new method for retrieving urban heat island intensity using GNSS-derived ZTD and atmospheric empirical model. Int. J. Remote Sens. 2022, 43, 7064–7082. [Google Scholar] [CrossRef]
- Liou, Y.A.; Huang, C.Y. GPS observations of PW during the passage of a typhoon. Earth Planets Space 2000, 52, 709–712. [Google Scholar] [CrossRef] [Green Version]
- Song, D.S.; Yun, H.S.; Lee, D.H. Verification of accuracy of precipitable water vapour from GPS during typhoon RUSA. Surv. Rev. 2008, 40, 19–28. [Google Scholar] [CrossRef]
- Song, D.S.; Grejner-Brzezinska, D.A. Remote sensing of atmospheric water vapor variation from GPS measurements during a severe weather event. Earth Planets Space 2009, 61, 1117–1125. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Hancock, C.M.; Xiang, Z.; Kong, Y.; Ligt, H.D.; Shi, H.; Quaye-Ballard, J.A. Precipitable water vapour retrieval from GPS precise point positioning and NCEP CFSv2 dataset during typhoon events. Sensors 2018, 18, 3831. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, Q.; Zhang, K.; Wu, S.; Lian, D.; Li, L.; Shen, Z.; Wan, M.; Li, L.; Wang, R.; Fu, E.; et al. An investigation of atmospheric temperature and pressure using an improved spatio-temporal Kriging model for sensing GNSS-derived precipitable water vapor. Spat. Stat. 2022, 51, 100664. [Google Scholar] [CrossRef]
- Won, J.; Kim, D. Analysis of temporal and spatial variation of precipitable water vapor according to path of typhoon EWINIAR using GPS permanent stations. J. Position. Navig. Timing 2015, 4, 87–95. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Ma, X.; Yao, W.; Yao, Y. A new typhoon-monitoring method using precipitation water vapor. Remote Sens. 2019, 11, 2845. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Zhang, K.; Wu, S.; Zhao, Q.; Wang, X.; Shen, Z.; Li, L.; Wan, M.; Liu, X. Real-time GNSS-derived PWV for typhoon characterizations: A case study for super typhoon Mangkhut in Hong Kong. Remote Sens. 2019, 12, 104. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Shen, Z.; Wan, M.; Li, L. Precipitable water vapor converted from GNSS-ZTD and ERA5 datasets for the monitoring of tropical cyclones. IEEE Access 2020, 8, 87275–87290. [Google Scholar] [CrossRef]
- Kang, I.; Park, J. Use of GNSS-Derived PWV for Predicting the Path of Typhoon: Case Studies of Soulik and Kongrey in 2018. J. Surv. Eng. 2021, 147, 04021018. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Li, Z. Real-time precise point positioning-based zenith tropospheric delay for precipitation forecasting. Sci. Rep. 2018, 8, 7939. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Kuang, C.L.; Zhu, J.J.; Chen, W.; Chen, Y.Q.; Long, S.C.; Li, H.Y. Rainstorm nowcasting based on GPS real-time precise point positioning technology. Chin. J. Geophys. 2012, 55, 1129–1136. [Google Scholar]
- Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Zhang, J.; Qiu, C.; Zhang, S.; Li, L. An improved model for detecting heavy precipitation using GNSS-derived zenith total delay measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5392–5405. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, T.; Xu, G.; Lu, Z. Apparent Short-Period GNSS-ZTD Disturbance Correlated with Precipitation Events. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, Y.; Li, Z.; Yao, Y. Retrieval of a high-precision drought monitoring index by using GNSS-derived ZTD and temperature. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8730–8743. [Google Scholar] [CrossRef]
- Paziewski, J. Multi-constellation single-frequency ionospheric-free precise point positioning with low-cost receivers. GPS Solut. 2022, 26, 23. [Google Scholar] [CrossRef]
- Collins, P.; Langley, R.B. Tropospheric Delay. GPS World 1999, 53, 52–58. [Google Scholar]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The constants in the equation for atmospheric refractive index at radio frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef] [Green Version]
- Hasegawa, S.; Stokesberry, D.P. Automatic digital microwave hygrometer. Rev. Sci. Instrum. 1975, 46, 867–873. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software; Version 5.2; Astronomical Institute, University of Bern: Bern, Switzerland, 2015; p. 884. [Google Scholar]
- Herring, T.A.; Floyd, M.A.; Perry, M. Gamit/globk for gnss. GNSS Data Process. Anal. GAMIT/GLOBK Track Hotel. Soluxe Bishkek Kyrg. 2018, 2, 2–7. [Google Scholar]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geo-Phys. Res. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef] [Green Version]
- Vedel, H. Conversion of WGS84 geometric heights to NWP model HIRLAM geopotential heights, Danish Meteorological Institute. DMI Sci. Rep. 2000, 2, 1–11. [Google Scholar]
- Bonafoni, S.; Biondi, R.; Brenot, H.; Anthes, R. Radio occultation and ground-based GNSS products for observing, understanding and predicting extreme events: A review. Atmos. Res. 2019, 230, 104624. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific tropical cyclone database created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Byun, S.H.; Bar-Sever, Y.E. A new type of troposphere zenith path delay product of the international GNSS service. J. Geod. 2009, 83, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
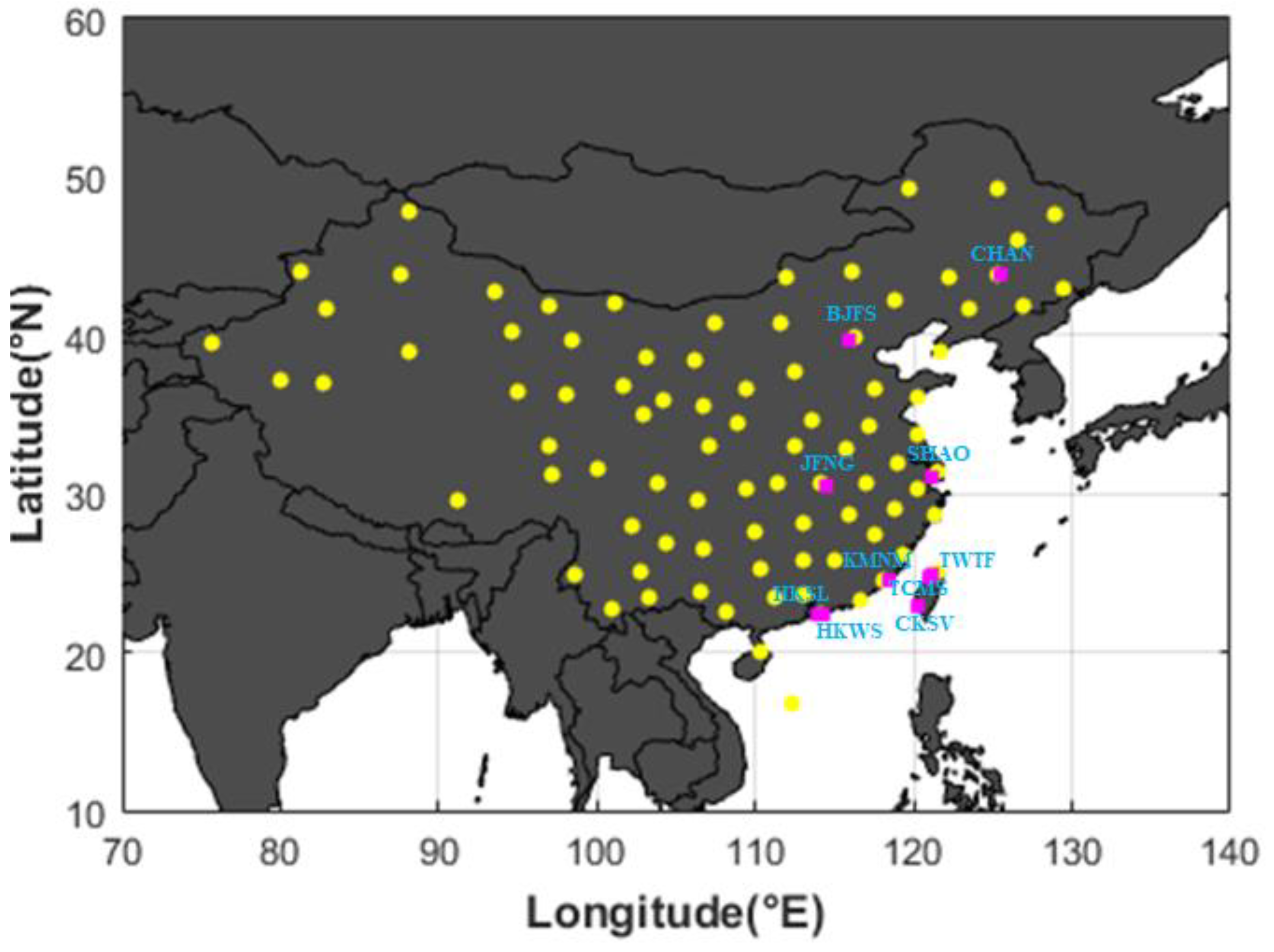

| Station | East Longitude (°) | North Latitude (°) | Elevation (m) |
|---|---|---|---|
| BJFS | 115.89 | 39.60 | 87.5 |
| CHAN | 125.44 | 43.79 | 273.2 |
| CKSV | 120.22 | 22.99 | 59.7 |
| HKSL | 113.92 | 22.37 | 95.3 |
| HKWS | 114.33 | 22.43 | 63.8 |
| JFNG | 114.49 | 30.51 | 71.3 |
| KMNM | 118.38 | 24.46 | 49.1 |
| SHAO | 121.20 | 31.09 | 22.0 |
| TWTF | 121.16 | 24.95 | 201.5 |
| TCMS | 120.98 | 24.79 | 77.2 |
| Station | Bias (mm) | RMS (mm) | STD (mm) |
|---|---|---|---|
| BJFS | 5.1 | 17.2 | 16.4 |
| CHAN | 5.4 | 13.0 | 11.9 |
| CKSV | 8.1 | 19.3 | 17.5 |
| HKSL | 7.8 | 15.7 | 13.7 |
| HKWS | 7.3 | 15.9 | 14.1 |
| JFNG | 5.7 | 17.5 | 16.5 |
| KMNM | 7.5 | 16.8 | 15.0 |
| SHAO | 8.1 | 19.2 | 17.3 |
| TWTF | 1.4 | 17.3 | 17.3 |
| TCMS | 7.2 | 19.5 | 18.1 |
| Mean | 6.4 | 17.1 | 15.78 |
| Station Number | East Longitude (°) | North Latitude (°) | Elevation (m) |
|---|---|---|---|
| 50527 | 119.70 | 49.25 | 653.3 |
| 59280 | 113.08 | 23.70 | 78.0 |
| 53614 | 106.20 | 38.46 | 1112.0 |
| 54857 | 120.33 | 36.06 | 77.0 |
| Tropical Cyclone | Approaching Velocity (km/h) | Leaving Velocity (km/h) | ||||
|---|---|---|---|---|---|---|
| Model #1 | Model #2 | Reference | Model #1 | Model #2 | Reference | |
| Merbok | 15.32 | 16.35 | 22.25 | 19.48 | 20.51 | 24.61 |
| ROKE | 19.47 | 22.06 | 24.38 | 27.38 | 26.12 | 26.47 |
| Neast | 15.31 | 15.10 | 15.22 | 36.08 | 31.58 | 33.67 |
| Hato | 27.61 | 28.71 | 31.24 | 33.79 | 29.64 | 26.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, D.; He, Q.; Li, L.; Zhang, K.; Fu, E.; Li, G.; Wang, R.; Gao, B.; Song, K. A Novel Method for Monitoring Tropical Cyclones’ Movement Using GNSS Zenith Tropospheric Delay. Remote Sens. 2023, 15, 3247. https://doi.org/10.3390/rs15133247
Lian D, He Q, Li L, Zhang K, Fu E, Li G, Wang R, Gao B, Song K. A Novel Method for Monitoring Tropical Cyclones’ Movement Using GNSS Zenith Tropospheric Delay. Remote Sensing. 2023; 15(13):3247. https://doi.org/10.3390/rs15133247
Chicago/Turabian StyleLian, Dajun, Qimin He, Li Li, Kefei Zhang, Erjiang Fu, Guangyan Li, Rui Wang, Biqing Gao, and Kangming Song. 2023. "A Novel Method for Monitoring Tropical Cyclones’ Movement Using GNSS Zenith Tropospheric Delay" Remote Sensing 15, no. 13: 3247. https://doi.org/10.3390/rs15133247
APA StyleLian, D., He, Q., Li, L., Zhang, K., Fu, E., Li, G., Wang, R., Gao, B., & Song, K. (2023). A Novel Method for Monitoring Tropical Cyclones’ Movement Using GNSS Zenith Tropospheric Delay. Remote Sensing, 15(13), 3247. https://doi.org/10.3390/rs15133247








