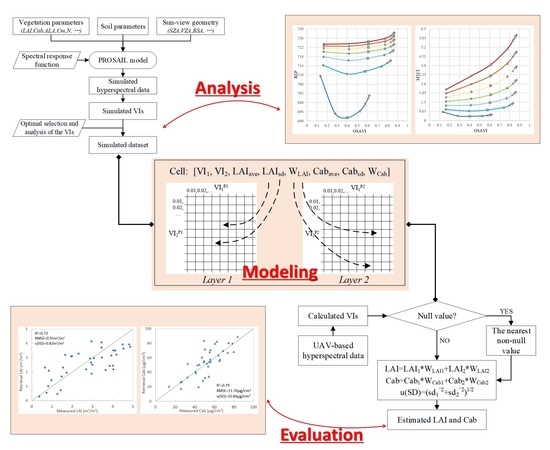
2.2.1. PROSAIL Model and Simulated Dataset
The PROSAIL model, coupling PROSPECT leaf optical properties model [
21] and SAIL canopy bidirectional reflectance model [
22], has been used for more than twenty years to study plant canopy spectral and directional reflectance in the solar domain and vegetation biophysical properties [
23,
24]. In this article, the PROSAIL model was used for the selection and evaluation of vegetation indices. The PROSPECT model simulates the leaf’s optical properties (the reflectance and transmittance) from 400 nm to 2500 nm as a function of leaf structure parameters and biochemical parameters [
24], including equivalent water thickness
Cw (g/cm
2), dry matter content
Cm (g/cm
2), leaf chlorophyll
a and
b content
Cab (μ/cm
2) and leaf structure parameter
N (unitless). The reflectance and transmittance of leaves simulated by PROSPECT are then inputted into SAIL model to simulate the canopy spectral and directional reflectance as a function of canopy structure parameters [
24], including soil reflectance
ρs (unitless), leaf area index
LAI (m
2/m
2), average leaf angle
ALA (°), hot-spot size parameter
Hot (m/m) and external parameters for view zenith angle
VZA (°), sun zenith angle
SZA (°) and relative azimuth angle
RSA (°) between the sensor and sun.
An appropriate parameterization of the PROSAIL model was required for simulating canopy reflectance. Based on the field measurements and documents [
23,
24,
25,
26,
27,
28], the ranges of input parameters are shown in
Table 2. Background reflectance can be a significant contributor to the canopy reflectance signal [
28]. In this study, a factor
f was established based on field measured soil spectrum for quantizing the variation in soil brightness.
where
and
are the minimum and maximum of field measured soil reflectance spectra.
Table 2.
The main input parameters of the PROSAIL model.
Table 2.
The main input parameters of the PROSAIL model.
| Parameters | Symbol | Unit | Expectation | Range |
|---|
| Chlorophyll a + b content | Cab | μg/cm2 | 45 | 10–90 |
| Dry matter content | Cm | g/cm2 | 0.005 | 0.001–0.01 |
| Equivalent water thickness | Cw | g/cm2 | 0.02 | 0.005–0.04 |
| Leaf area index | LAI | m2/m2 | 2.8 | 0–5 |
| Average leaf angle | ALA | ° | 15 | 10–65 |
| Leaf structure parameter | N | | 1.5 | 1.4–2.2 |
| Hot-spot size parameter | Hot | m/m | 0.2 | 0–1.4 |
| Soil factor | f | | 0.4 | 0.1–0.9 |
| View zenith angle | VZA | ° | | 5.78 |
| Sun zenith angle | SZA | ° | | 23.12 |
| Relative azimuth angle | RSA | ° | | 111.39 |
With the defined ranges, 150,000 parameter combinations were obtained using uniform random sampling to generate 150,000 canopy spectra. The simulated dataset was divided into two parts: 100,000 simulations were randomly selected and used for modeling and the other simulations were used independently for model testing.
2.2.2. Selection of the Vegetation Indices
Based on the simulated canopy spectral data, 15 typical vegetation indices were calculated and analyzed for LAI and Cab estimation, including normalized difference vegetation index (NDVI), simple ratio vegetation index (SR), etc. The 15 typical vegetation indices are listed in
Table 3. The wavelengths used were within the HSI’s band domains, in the visible and near-infrared ranges.
Table 3.
The 15 typical vegetation indices.
Table 3.
The 15 typical vegetation indices.
| Vegetation Index | Formulation | Reference |
|---|
| NDVI | | [29] |
| SR | | [30] |
| EVI | | [31] |
| MTVI1 | | [28] |
| MTVI2 | | [28] |
| OSAVI | | [32] |
| MSAVI | | [33] |
| TCARI | | [17] |
| TCARI2 | | [34] |
| MCARI | | [35] |
| MTCI | | [36] |
| CIgreen | −1 | [37] |
| CIrededge | −1 | [37] |
| REP | | [38] |
| TVI | | [39] |
To identify appropriate vegetation indices for LAI and Cab estimation, the VIs shown in
Table 2 were tested and analyzed based on the performance of different fitting models. Firstly, the VIs were taken as the independent variable, vegetation parameter (LAI or Cab) was taken as the dependent variable. Then, the optimal fitting models were constructed based on the best fit from the linear regression, power regression, logarithmic regression and exponential regression. Finally, the coefficient of determination (
R2) and root mean square error (
RMSE) of the curve fitting models were used for assessing the performance of VIs.
The inversion performance of the 15 VIs for LAI and Cab was assessed and the
RMSE/
R2 values are ranked in descending order in
Table 4 and
Table 5.
Based on the above results, NDVI (
R2 = 0.7442) and OSAVI (
R2 = 0.7325) were selected for LAI estimation, while REP (
R2 = 0.8104) and MTCI (
R2 = 0.7199) were selected for Cab estimation. The different combinations of these vegetation indices were established as shown in
Table 6.
2.2.3. Evaluation of VI Combinations
An appropriate VI combination for vegetation parameter estimation should be not only sensitive to the target parameters, but also insensitive to interference factors [
40]. To evaluate the sensitivity of the vegetation index combinations to different vegetation parameters, the PROSAIL model was used to simulate the influence of
LAI,
Cab,
Cm,
Cw,
N,
ALA and
ρs on the 15 vegetation indices described above. During the sensitivity analysis process, only the interference factor was varied according to the threshold range and the remained parameters of PROSAIL model were set to the fixed value. The VI combinations were drawn in a two-VI space, as shown in
Figure 2.
In
Figure 2, the LAI isolines (the same symbol) and the Cab isolines (the same color) had different trends. This indicates that the LAI and Cab can be well-separated by VI combinations. In general, the sensitivity of VI combinations changed with the LAI and Cab, varying in different VI spaces and positions. The VI combinations of NDVI–MTCI and OSAVI–MTCI had higher discreteness (the Cab isolines in these VI spaces were the most separated) and are better for distinguishing Cab, indicating the most sensitivity. Due to the saturation effects, the higher the LAI value, the lower the sensitivity of the VI combinations to LAI and the more dense the LAI isolines in two-VI space. When both the LAI and Cab were high, the saturation effect was most pronounced.
It was difficult to directly judge the dispersion of VI combination only from the figure. Therefore, the ability of different combinations to distinguish LAI or Cab was quantitatively described based on the distance of adjacent points in the matrix. The operations were as follows: (1) Normalize the matrix; (2) Calculate the mean value (Lave) and standard deviation (Lstd) of the distance between different Cab points on the LAI isoline to represent the dispersion of the current matrix to Cab. The larger the Lave, the better the dispersion of the matrix to Cab, and the smaller the Lstd, the better the stability of the matrix. Similarly, the distance mean and variance of LAI on Cab isolines were also calculated. The larger the Lave of LAI, the better the dispersion of the matrix for LAI, and the smaller the Lstd of LAI, the better the stability of the matrix.
As shown in
Table 7, for Cab, OSAVI–MTCI not only had the highest dispersion (
Lave of Cab was 0.0931) but also the lowest standard deviation (
Lstd of Cab was 0.0285), which was consistent with the phenomenon described above. For LAI, OSAVI–REP performed best, but at the same time, it had certain instability for Cab. It can also be seen from
Figure 2 that in the OSAVI–REP space, contour lines such as Cab = 5 μg/cm
2, 20 μg/cm
2, 35 μg/cm
2 were relatively discrete, while contour lines such as Cab = 65 μg/cm
2, 80 μg/cm
2, 90 μg/cm
2 were relatively clustered. This indicates that the degree of dispersion variability of this VI combination is relatively large (
Lstd of Cab was 0.0888). Thus, a partitioned multi-stage inversion strategy should be established for joint estimation of LAI and Cab. For example, the Cab parameter should be preferentially retrieved because its VI combinations were more sensitive to Cab.
The dispersion of OSAVI–REP to Cab under different thresholds was further analyzed to determine the combination mode of the two VI matrices. It can be seen from
Figure 3 that the dispersion degree of OSAVI–REP decreases significantly with the increase in Cab value. Therefore, it is necessary to introduce the VI matrix in stages according to the variation trend of the dispersion. That is, OSAVI–REP should be used when the Cab is low, while OSAVI–MTCI should be used when the Cab is high.
The effects of the other parameters on VI combinations are also evaluated in this paper. Taking VI combination OSAVI–MTCI as an example, its sensitivity to the parameters of
ALA,
Cm,
Cw,
N and
ρs was analyzed using the simulations of PROSAIL. The results are shown in
Figure 4. By comparing the curves in
Figure 4 with those of the curves in
Figure 2, the variation in
Cm,
Cw and
ρs had no obvious effect on the results. The changes in
ALA and
N had limited effects on OSAVI–MTCI combination, for which
N had a relatively high impact; the parameter
ALA had a great influence on LAI when LAI value was low (
Figure 4(a1)–(a4)), but it did little to change the overall properties of OSAVI–MTCI combination. Although the effect of N on Cab was minimal when the Cab value was lower than 35 μg/cm
2 (
Figure 4(d1)–(d4)), it led to a reduction in the dispersion of OSAVI–MTCI combination (the Cab curves were relatively gathered).
2.2.4. Establishment of a Two-Layer Matrix Inversion Method
As shown in
Figure 5, the VI combinations of OSAVI–REP and OSAVI–MTCI were divided into cells to establish the inversion matrix. Each matrix had 1000 × 1000 cells and each cell corresponded to a small range of vegetation index values. Based on the modeling dataset simulated from the PROSAIL model, the LAI and Cab values were assigned to a matrix cell according to the values of the two simulated VIs. Because one cell had multiple values of LAI and Cab, all the values mapped to the same cell would be calculated as average and standard deviation. Then, the average (
ave) and standard deviation (
sd) values of the LAI and Cab were mapped to each cell, constituting the average and standard deviation matrices.
The distribution of matrix dispersion was uneven due to the value change of LAI and Cab, which was described in
Section 2.2.3. The dispersion curves of OSAVI–REP matrix and OSAVI–MTCI matrix converge at Cab ≈ 50 μg/cm
2 (
Figure 3). When Cab was low, OSAVI–REP matrix had better discretization, which should be used for Cab estimation. Otherwise, OSAVI–MTCI should be used for Cab estimation. In order to reduce the error brought by the instability of the dispersion of the matrix, the range (40 μg/cm
2, 60 μg/cm
2) was determined as the intermediate choice. Then, the weight coefficient can be established to determine the participation of matrix cells in different layers. As described above, when Cab value ≤ 40 μg/cm
2, OSAVI–REP dispersion was high. Therefore, the corresponding cell in OSAVI–REP matrix should be assigned a higher weight, which was set to 1 in this paper. Similarly, when Cab value > 60 μg/cm
2, OSAVI–MTCI dispersion was high and the corresponding cell in OSAVI–MTCI should be assigned a higher weight. When 40 μg/cm
2 < Cab value ≤ 60 μg/cm
2, the corresponding cell in OSAVI–REP matrix and OSAVI–MTCI matrix were both assigned as 0.5. At last, the weight coefficient (
w) was entered in each cell to form the weight matrix.
In the retrieval process, the expected estimation value of LAI and Cab were calculated based on the average matrix and the weight matrix. Additionally, the total standard deviation represented the inversion uncertainty.
After establishing the two-layer matrix, the LAI and Cab can be easily retrieved based on the four VIs calculated from the reflectance data. If the cell value of each layer matrix was valid, its value can be calculated with the weight coefficient and set as the estimated LAI and Cab. However, in some cases, the VIs calculated from the remotely sensed data were not within the range of the matrix and LAI and Cab values of the corresponding units could not be searched. In other words, the VI combinations calculated based on simulated reflectance data still cannot cover those calculated based on the remotely sensed data. This could be due to improper parameter settings during PROSAIL model simulation or the observation deviation of remotely sensed data. If the searched LAI and Cab values in the located cell were both null in two-layer matrices, the nearest 8-connected neighborhood was averaged and used as the estimated LAI and Cab. If the values of LAI and Cab in the located cell were null only in a one-layer matrix, the non-null values of the other layer were directly set to the estimated LAI and Cab.
2.2.5. Joint Estimation of LAI and Cab
The joint estimation of LAI and Cab included two cases:
Case 1 based on simulated data: the simulated test datasets were used for retrieving LAI and Cab through VI empirical model, the single-layer VI matrix and the two-layer matrix.
As described in
Section 2.2, 50,000 canopy spectra were used as a test dataset (TD data) for joint estimation of LAI and Cab. In this case, to further consider bias in the acquisition and processing of remote sensing data, a new test dataset (NTD data) was constructed by adding 5% relative Gaussian noise to the canopy spectra as reflectance uncertainty. The new test dataset was produced, which can also be used for evaluating the influence of reflectance measurement uncertainty on the retrieval accuracy of vegetation parameters.
Therefore, in this case, the two-layer matrix was evaluated by retrieving LAI and Cab from the simulated data with and without noise.
Case 2 based on UAV hyperspectral data: the UAV hyperspectral data obtained during the field campaign were used for retrieving LAI and Cab through approaches of matrices and machine learning, including the single-layer matrix of OSAVI–REP, the single-layer matrix of OSAVI–MTCI, the two-layer matrix, partial least squares regression (PLSR) and random forest (RF).
In Case 2, to improve the model robustness when the model was used for actual observation data, the two-layer matrix was optimized by adding 5% relative Gaussian noise for comparison. Therefore, in this case, the two-layer matrix established with and without noise was evaluated by retrieving LAI and Cab from the UAV hyperspectral data.