Assessment of Three Long-Term Satellite-Based Precipitation Estimates against Ground Observations for Drought Characterization in Northwestern China
Abstract
:1. Introduction
2. Materials and Methods
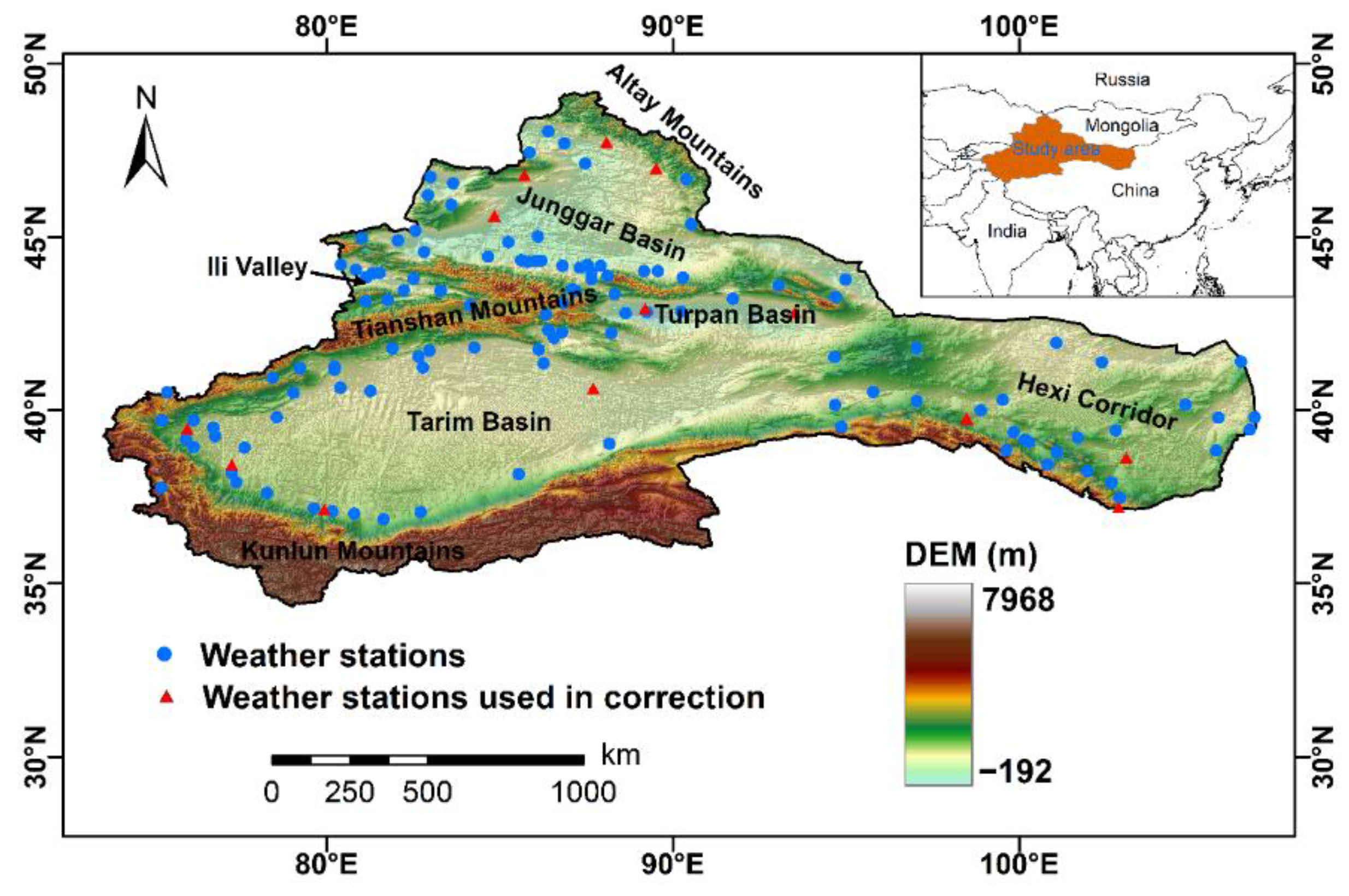
2.1. Study Area
2.2. Datasets
2.2.1. Ground-Based Observations
2.2.2. Long-Term Satellite Precipitation Datasets
2.3. Statistics Evaluation Metrics
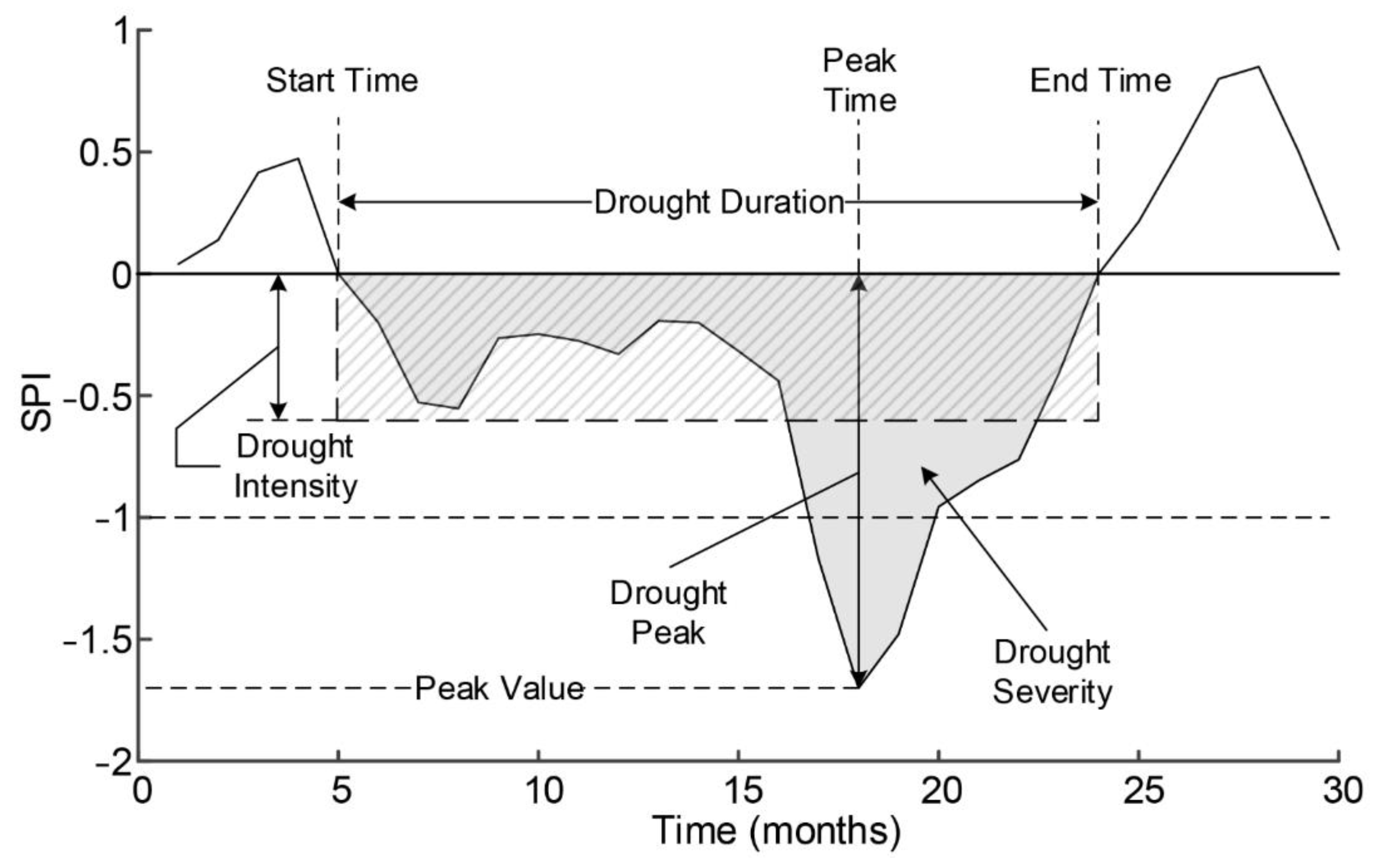
2.4. Drought Index and Drought Characteristics
2.5. Statistics for Drought Characteristic Evaluation
3. Results
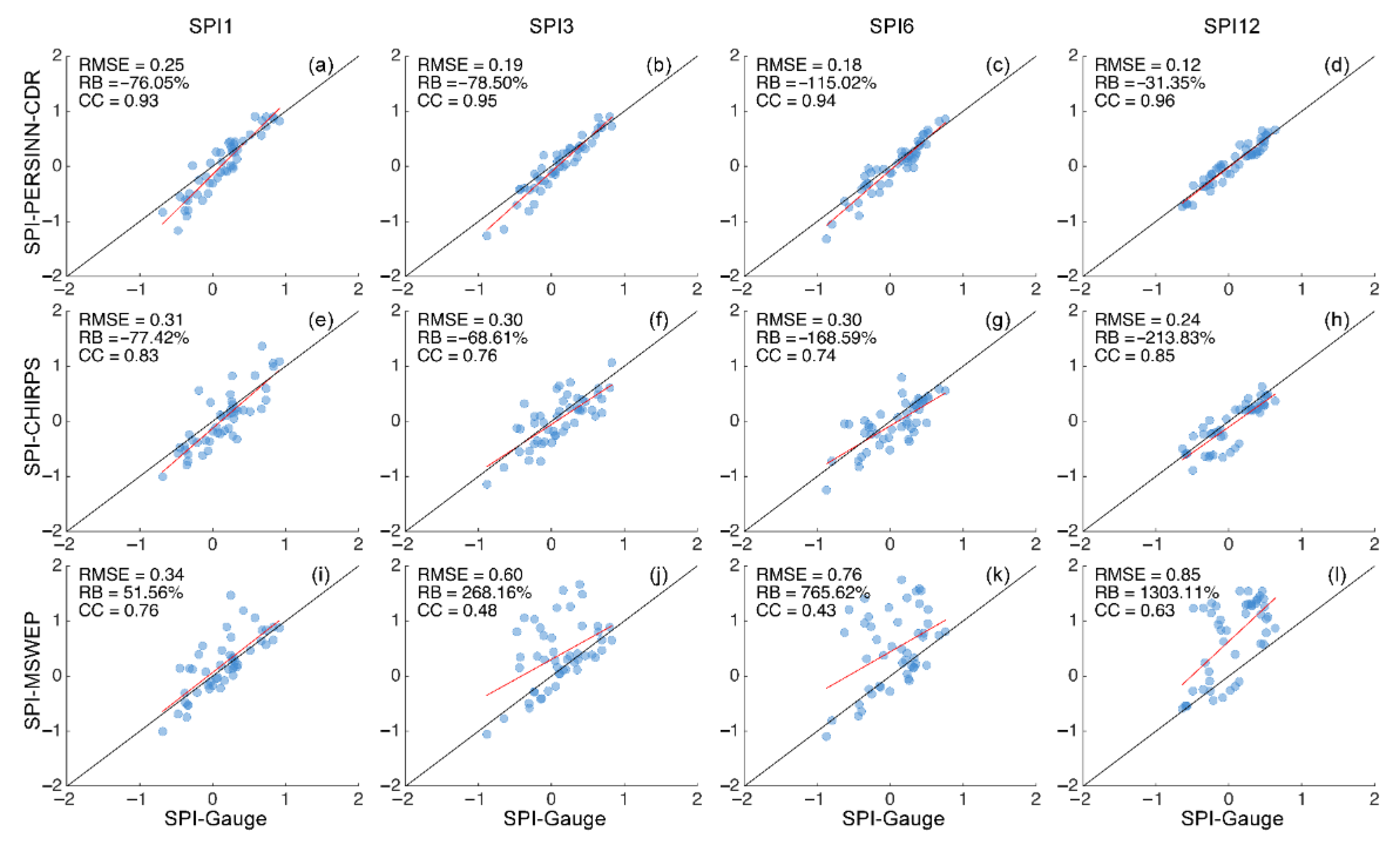
3.1. Evaluation of LSPE for Estimating Precipitation
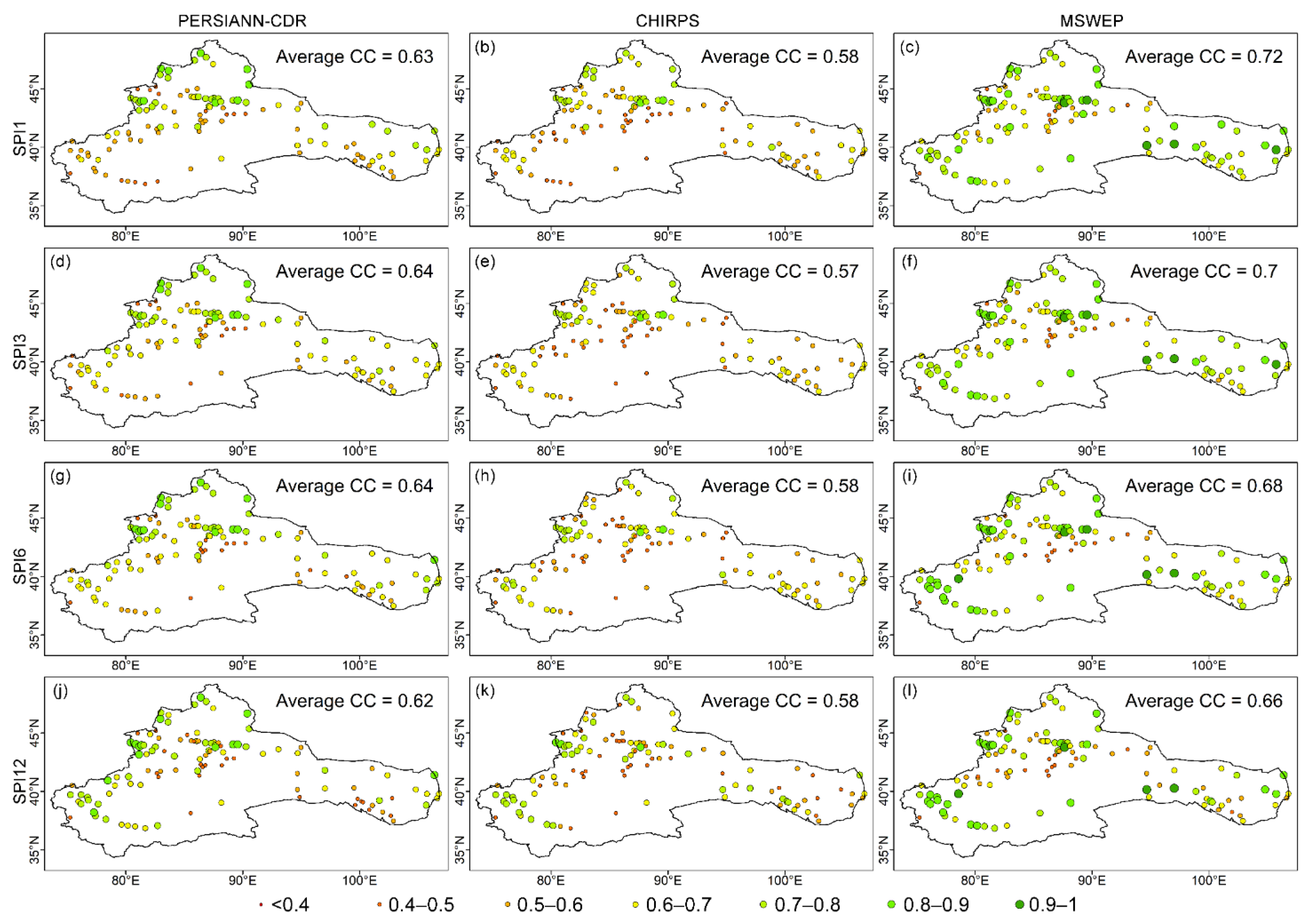
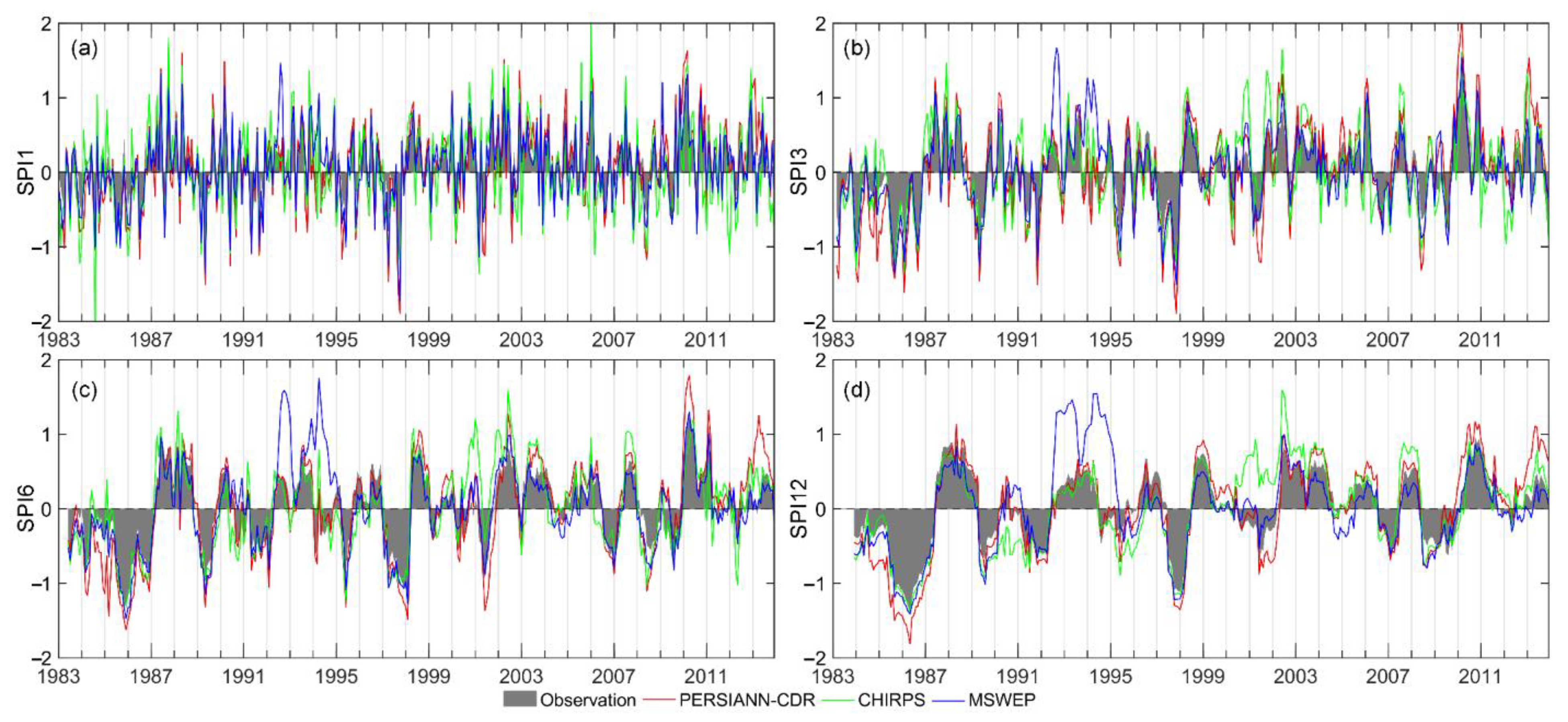
3.2. Evaluation of LSPE for Estimating SPI
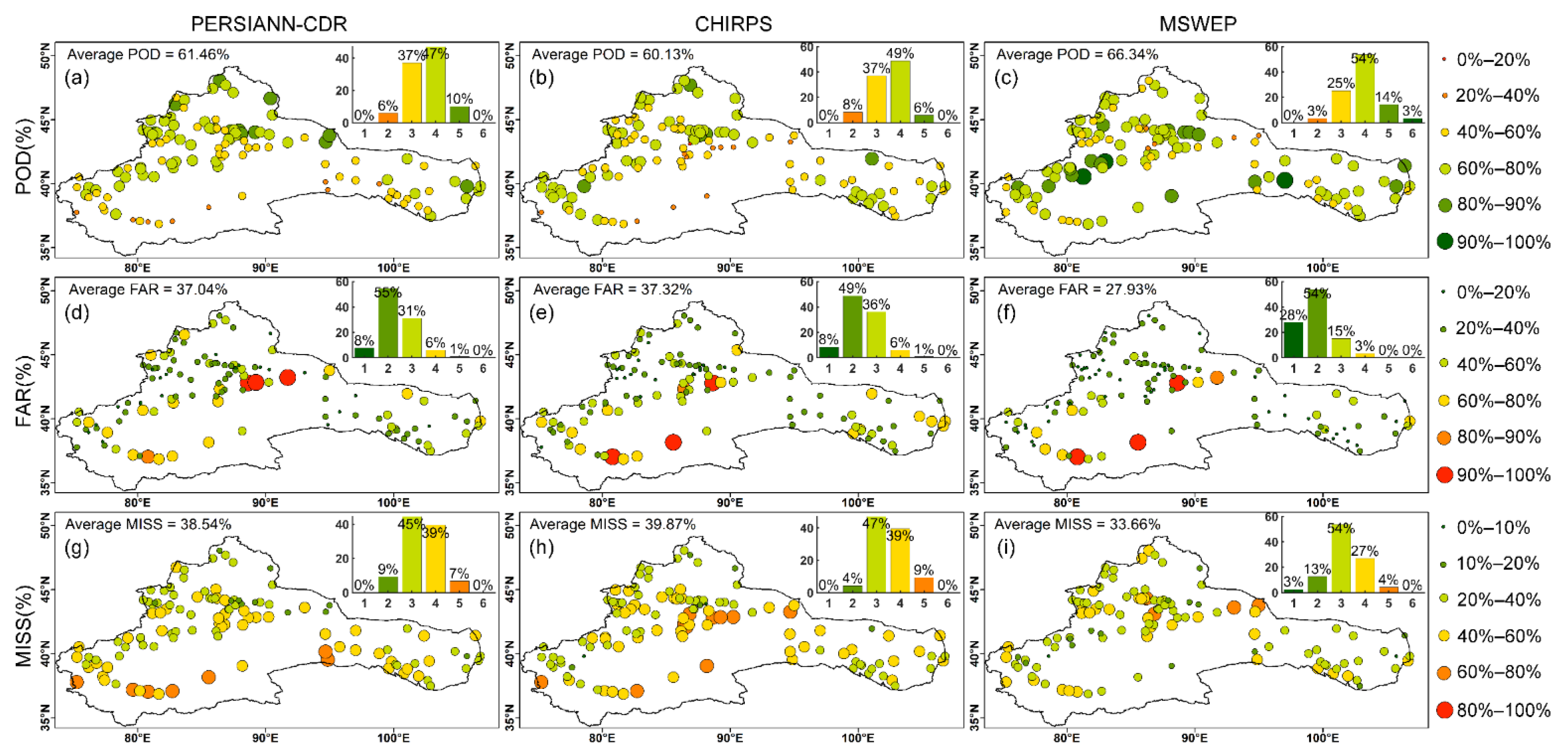
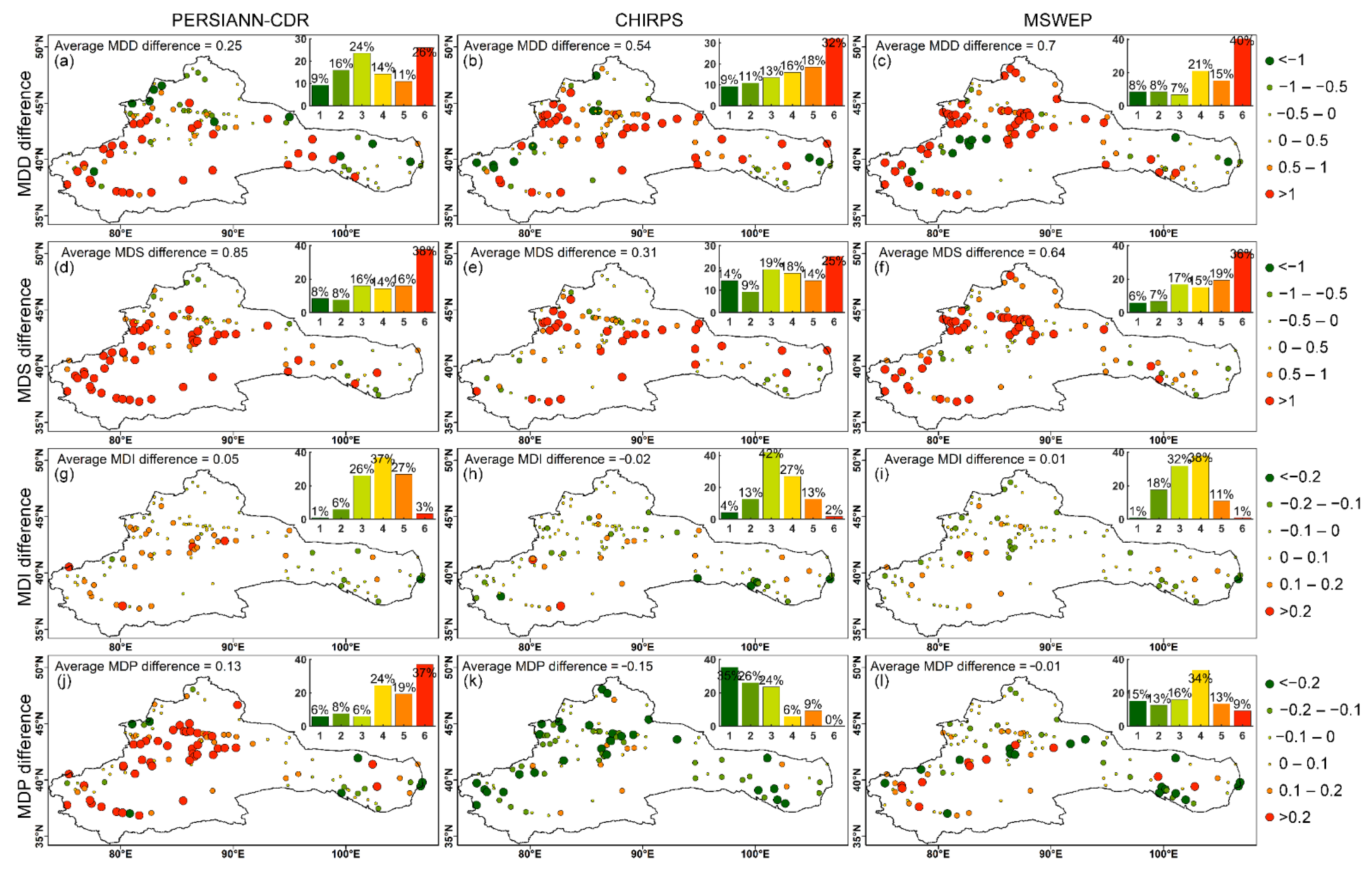
3.3. Performance of LSPE in Estimating Drought Characteristics
3.4. Performance of LSPE in Estimating Specific Drought Events
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Statistics Evaluation Metrics
Appendix B
| SPI Value | Category | Probability (%) |
|---|---|---|
| >2 | Extremely wet | 2.3 |
| 1.5~1.99 | Severe wet | 4.4 |
| 1.0~1.49 | Moderately wet | 9.2 |
| 0~0.99 | Slightly wet | 34.1 |
| −0.99~0 | Slightly dry | 34.1 |
| −1~−1.49 | Moderately dry | 9.2 |
| −1.5~−2 | Severe dry | 4.4 |
| <−2 | Extremely dry | 2.3 |
Appendix C
References
- IPCC. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Field, C.B., Barros, V., Stocker, T.F., Qin, D., Dokken, D.J., Ebi, K.L., Mastrandrea, M.D., Mach, K.J., Plattner, G.-K., Allen, S.K., et al., Eds.; Cambridge University Press: Cambridge, UK, 2012; 582p. [Google Scholar]
- Field, C.B.; Barros, V.R.; Dokken, D.J.; Mach, K.J.; Mastrandrea, M.D.; Bilir, T.E.; Chatterjee, M.; Ebi, K.L.; Estrada, Y.O.; Genova, R.C. (Eds.) Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; 1132p. [Google Scholar]
- Patrick, E. Drought Characteristics and Management in Central Asia and Turkey. In FAO Water Reports (FAO); Food and Agriculture Organization of the United Nations: Rome, Italy, 2017; 114p. [Google Scholar]
- Xu, H.J.; Wang, X.P.; Zhang, X.X. Decreased Vegetation Growth in Response to Summer Drought in Central Asia from 2000 to 2012. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 390–402. [Google Scholar] [CrossRef]
- Montaseri, M.; Amirataee, B. Comprehensive Stochastic Assessment of Meteorological Drought Indices. Int. J. Climatol. 2017, 37, 998–1013. [Google Scholar] [CrossRef]
- Kamali, B.; Abbaspour, K.C.; Lehmann, A.; Wehrli, B.; Yang, H. Identification of Spatiotemporal Patterns of Biophysical Droughts in Semi-Arid Region—A Case Study of the Karkheh River Basin in Iran. Hydrol. Earth Syst. Sci. 2015, 12, 5187–5217. [Google Scholar]
- Liu, X.; Xiufang, Z.; Yaozhong, P.; Shuangshuang, L.; Yanxu, L.; Yuqi, M. Agricultural Drought Monitoring: Progress, Challenges, and Prospects. J. Geogr. Sci. 2016, 26, 750–767. [Google Scholar] [CrossRef] [Green Version]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index User Guide. In Technical Report WMO—No. 1090; Hayes, M., Wood, D., Svoboda, M., Eds.; WMO: Geneva, Switzerland, 2012; 24p. [Google Scholar]
- Shi, L.; Feng, P.; Wang, B.; Li Liu, D.; Yu, Q. Quantifying Future Drought Change and Associated Uncertainty in Southeastern Australia with Multiple Potential Evapotranspiration Models. J. Hydrol. 2020, 590, 125394. [Google Scholar] [CrossRef]
- Kumar, K.; Krishna, K.; Kumar, R.; Rakhecha, P.R. Comparison of Penman and Thornthwaite Methods of Estimating Potential Evapotranspiration for Indian Conditions. Theor. Appl. Climatol. 1987, 38, 140–146. [Google Scholar] [CrossRef]
- Valipour, M. Temperature Analysis of Reference Evapotranspiration Models. Meteorol. Appl. 2015, 22, 385–394. [Google Scholar] [CrossRef]
- Damberg, L.; AghaKouchak, A. Global Trends and Patterns of Drought from Space. Theor. Appl. Climatol. 2014, 117, 441–448. [Google Scholar] [CrossRef]
- Thenkabail, P. Remote Sensing of Water Resources, Disasters, and Urban Studies; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Suliman, A.H.A.; Awchi, T.A.; Al-Mola, M.; Shahid, S. Evaluation of Remotely Sensed Precipitation Sources for Drought Assessment in Semi-Arid Iraq. Atmos. Res. 2020, 242, 105007. [Google Scholar] [CrossRef]
- Xu, Z.; Wu, W.; He, H.; Wu, H.; Zhou, J.; Zhang, Y.; Guo, X. Evaluating the Accuracy of Mswep V2.1 and Its Performance for Drought Monitoring over Mainland China. Atmos. Res. 2019, 226, 17–31. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.S.; Teixeira, J.; Anderson, M.C.; Wardlow, B.D.; Hain, C.R. Remote Sensing of Drought: Progress, Challenges and Opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef] [Green Version]
- Agutu, N.O.; Awange, J.L.; Zerihun, A.; Ndehedehe, C.E.; Kuhn, M.; Fukuda, Y. Assessing Multi-Satellite Remote Sensing, Reanalysis, and Land Surface Models’ Products in Characterizing Agricultural Drought in East Africa. Remote Sens. Environ. 2017, 194, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Thavorntam, W.; Tantemsapya, N.; Armstrong, L. A Combination of Meteorological and Satellite-Based Drought Indices in a Better Drought Assessment and Forecasting in Northeast Thailand. Nat. Hazards 2015, 77, 1453–1474. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nakhjiri, N. A near Real-Time Satellite-Based Global Drought Climate Data Record. Environ. Res. Lett. 2012, 7, 044037. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Gebregiorgis, A.S.; Xianwu, X.; Zhang, X. Inter-Comparison of High-Resolution Satellite Precipitation Products over Central Asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef] [Green Version]
- De Jesús, A.; Breña-Naranjo, J.A.; Pedrozo-Acuña, A.; Alcocer Yamanaka, V.H. The Use of Trmm 3b42 Product for Drought Monitoring in Mexico. Water 2016, 8, 325. [Google Scholar] [CrossRef]
- Naumann, G.; Barbosa, P.; Carrao, H.; Singleton, A.; Vogt, J. Monitoring Drought Conditions and Their Uncertainties in Africa Using Trmm Data. J. Appl. Meteorol. Climatol. 2012, 51, 1867–1874. [Google Scholar] [CrossRef] [Green Version]
- Yan, N.; Wu, B.; Chang, S.; Bao, X. Evaluation of Trmm Precipitation Product for Meteorological Drought Monitoring in Hai Basin. IOP Conf. Ser. Earth Environ. Sci. 2014, 17, 12093. [Google Scholar] [CrossRef] [Green Version]
- Zeng, H.W.; Li, L.J.; Li, J.Y. The Evaluation of Trmm Multisatellite Precipitation Analysis (Tmpa) in Drought Monitoring in the Lancang River Basin. J. Geogr. Sci. 2012, 22, 273–282. [Google Scholar] [CrossRef]
- Tan, M.; Tan, K.; Chua, V.; Chan, N. Evaluation of Trmm Product for Monitoring Drought in the Kelantan River Basin, Malaysia. Water 2017, 9, 57. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Zhang, Y.; Ren, X.; Yao, Y.; Hao, Z.; Cai, W. Evaluation of Chirps and Its Application for Drought Monitoring over the Haihe River Basin, China. Nat. Hazards 2018, 92, 155–172. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Ndayisaba, F.; He, D.; Kurban, A.; De Maeyer, P. Meteorological Drought Analysis in the Lower Mekong Basin Using Satellite-Based Long-Term Chirps Product. Sustainability 2017, 9, 901. [Google Scholar] [CrossRef] [Green Version]
- Oliveira-Júnior, J.F.; Silva Junior, C.A.; Teodoro, P.E.; Rossi, F.S.; Blanco, C.C.J.; Lima, M.; Gois, G.; Correira Filho, W.L.F.; Barros Santiago, D.; Santos Vanderley, M.H.G. Confronting Chirps Dataset and in Situ Stations in the Detection of Wet and Drought Conditions in the Brazilian Midwest. Int. J. Climatol. 2021, 41, 478–493. [Google Scholar] [CrossRef]
- Alijanian, M.; Rakhshandehroo, G.R.; Mishra, A.; Dehghani, M. Evaluation of Remotely Sensed Precipitation Estimates Using Persiann-Cdr and Mswep for Spatio-Temporal Drought Assessment over Iran. J. Hydrol. 2019, 579, 124189. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Chen, S.; Ndayisaba, F. Evaluation of Persiann-Cdr for Meteorological Drought Monitoring over China. Remote Sens. 2016, 8, 379. [Google Scholar] [CrossRef] [Green Version]
- Santos, C.A.G.; Neto, R.M.B.; do Nascimento, T.V.M.; da Silva, R.M.; Mishra, M.; Frade, T.G. Geospatial Drought Severity Analysis Based on Persiann-Cdr-Estimated Rainfall Data for Odisha State in India (1983–2018). Sci. Total Environ. 2021, 750, 141258. [Google Scholar] [CrossRef]
- Bothe, O.; Fraedrich, K.; Zhu, X. Precipitation Climate of Central Asia and the Large-Scale Atmospheric Circulation. Theor. Appl. Climatol. 2012, 108, 345–354. [Google Scholar] [CrossRef]
- Mahmood, R.; ShuangLin, L.; Babar, K. Causes of Recurring Drought Patterns in Xinjiang, China. J. Arid. Land 2010, 2, 279–285. [Google Scholar]
- Li, Y.; Yao, N.; Sahin, S.; Appels, W.M. Spatiotemporal Variability of Four Precipitation-Based Drought Indices in Xinjiang, China. Theor. Appl. Climatol. 2016, 129, 1017–1034. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Ndayisaba, F.; Liu, T.; Jiapaer, G.; El-Tantawi, A.M.; De Maeyer, P. Space-Time Characterization of Drought Events and Their Impacts on Vegetation in Central Asia. J. Hydrol. 2018, 564, 165–178. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Jiapaer, G.; Ndayisaba, F.; Jiang, L.; Kurban, A.; De Maeyer, P. Spatial and Temporal Characteristics of Droughts in Central Asia During 1966–2015. Sci. Total Environ. 2018, 624, 1523–1538. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Bake, B.; Zhang, J.; Rasulov, H. Spatio-Temporal Patterns of Drought in North Xinjiang, China, 1961–2012 Based on Meteorological Drought Index. J. Arid. Land 2015, 7, 527–543. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; van Dijk, A.I.J.M.; McVicar, T.R.; Adler, R.F. Mswep V2 Global 3-Hourly 0.1° Precipitation: Methodology and Quantitative Assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef] [Green Version]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. Persiann-Cdr Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 50066. [Google Scholar] [CrossRef] [Green Version]
- Shen, Y.; Xiong, A. Validation and Comparison of a New Gauge-Based Precipitation Analysis over Mainland China. Int. J. Climatol. 2016, 36, 252–265. [Google Scholar] [CrossRef]
- Shen, Y.; Xiong, A.Y.; Wang, Y.; Xie, P.P. Performance of High-Resolution Satellite Precipitation Products over China. J. Geophys. Res. Atmos. 2010, 115, D02114. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. Mswep: 3-Hourly 0.25 Global Gridded Precipitation (1979–2015) by Merging Gauge, Satellite, and Reanalysis Data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Chen, J.; Wang, X. Comparison of Imerg Level-3 and Tmpa 3b42v7 in Estimating Typhoon-Related Heavy Rain. Water 2017, 9, 276. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Jin, C.; Wang, A.; Guan, D.; Wu, J.; Yuan, F.; Xu, L. Comprehensive Precipitation Evaluation of Trmm 3b42 with Dense Rain Gauge Networks in a Mid-Latitude Basin, Northeast, China. Theor. Appl. Climatol. 2015, 126, 659–671. [Google Scholar] [CrossRef]
- Hofstra, N.; New, M.; McSweeney, C. The Influence of Interpolation and Station Network Density on the Distributions and Trends of Climate Variables in Gridded Daily Data. Clim. Dyn. 2012, 35, 841–858. [Google Scholar] [CrossRef]
- Mair, A.; Fares, A. Comparison of Rainfall Interpolation Methods in a Mountainous Region of a Tropical Island. J. Hydrol. Eng. 2011, 16, 371–383. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Vargas Godoy, M.R.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of Gpm Imerg Performance: A Global Perspective. Remote Sens. Environ. 2022, 268, 12754. [Google Scholar] [CrossRef]
- Edwards, D.C. Characteristics of 20th Century Drought in the United States at Multiple Time Scales; Air Force Institute of Technology: Wright-Patterson AFB, OH, USA, 1997. [Google Scholar]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and Temporal Variability of Droughts in Portugal. Water Resour. Res. 2010, 46, W03503. [Google Scholar] [CrossRef] [Green Version]
- Belayneh, A.; Adamowski, J. Standard Precipitation Index Drought Forecasting Using Neural Networks, Wavelet Neural Networks, and Support Vector Regression. Appl. Comput. Intell. Soft Comput. 2012, 2012, 1–13. [Google Scholar] [CrossRef]
- Huang, S.Z.; Li, P.; Huang, Q.; Leng, G.Y.; Hou, B.B.; Ma, L. The Propagation from Meteorological to Hydrological Drought and Its Potential Influence Factors. J. Hydrol. 2017, 547, 184–195. [Google Scholar] [CrossRef]
- Mpelasoka, F.; Hennessy, K.; Jones, R.; Bates, B. Comparison of Suitable Drought Indices for Climate Change Impacts Assessment over Australia Towards Resource Management. Int. J. Climatol. 2008, 28, 1283–1292. [Google Scholar] [CrossRef]
- Yevjevich, V.M. An Objective Approach to Definition and Investigations of Continental Hydrologic Droughts; Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1967; Volume 23, No. 23. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Guo, H.; Bao, A.; Ndayisaba, F.; Liu, T.; Kurban, A.; De Maeyer, P. Systematical Evaluation of Satellite Precipitation Estimates over Central Asia Using an Improved Error-Component Procedure. J. Geophys. Res. Atmos. 2017, 122, 10906–10927. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of Several Rainfall Products Used for Hydrological Applications over West Africa Using Two High-Resolution Gauge Networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A. Extended Contingency Table: Performance Metrics for Satellite Observations and Climate Model Simulations. Water Resour. Res. 2013, 49, 7144–7149. [Google Scholar] [CrossRef] [Green Version]
- Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. Persiann-Ccs-Cdr, a 3-Hourly 0.04° Global Precipitation Climate Data Record for Heavy Precipitation Studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef] [PubMed]
- Alijanian, M.; Rakhshandehroo, G.R.; Mishra, A.K.; Dehghani, M. Evaluation of Satellite Rainfall Climatology Using Cmorph, Persiann-Cdr, Persiann, Trmm, Mswep over Iran. Int. J. Climatol. 2017, 37, 4896–4914. [Google Scholar] [CrossRef]
- Brasil Neto, R.M.; Guimarães Santos, C.A.; da Costa Silva, J.F.C.B.; da Silva, R.M.; dos Santos, C.A.C.; Mishra, M. Evaluation of the Trmm Product for Monitoring Drought over Paraíba State, Northeastern Brazil: A Trend Analysis. Sci. Rep. 2021, 11, 1097. [Google Scholar] [CrossRef] [PubMed]
- Zhong, R.; Chen, X.; Lai, C.; Wang, Z.; Lian, Y.; Yu, H.; Wu, X. Drought Monitoring Utility of Satellite-Based Precipitation Products across Mainland China. J. Hydrol. 2019, 568, 343–359. [Google Scholar] [CrossRef]
- Yao, J.; Tuoliewubieke, D.; Chen, J.; Huo, W.; Hu, W. Identification of Drought Events and Correlations with Large-Scale Ocean-Atmospheric Patterns of Variability: A Case Study in Xinjiang, China. Atmosphere 2019, 10, 94. [Google Scholar] [CrossRef] [Green Version]
- Yu, M.; Li, Q.; Hayes, M.J.; Svoboda, M.D.; Heim, R.R. Are Droughts Becoming More Frequent or Severe in China Based on the Standardized Precipitation Evapotranspiration Index: 1951–2010? Int. J. Climatol. 2014, 34, 545–558. [Google Scholar] [CrossRef]
- Yao, J.; Zhao, Y.; Yu, X. Spatial-Temporal Variation and Impacts of Drought in Xinjiang (Northwest China) During 1961–2015. PeerJ 2018, 6, e4926. [Google Scholar] [CrossRef] [Green Version]
- Lei, T.; Wu, J.; Li, X.; Geng, G.; Shao, C.; Zhou, H.; Wang, Q.; Liu, L. A New Framework for Evaluating the Impacts of Drought on Net Primary Productivity of Grassland. Sci. Total Environ. 2015, 536, 161–172. [Google Scholar] [CrossRef]
- Ayantobo, O.O.; Li, Y.; Song, S.; Yao, N. Spatial Comparability of Drought Characteristics and Related Return Periods in Mainland China over 1961–2013. J. Hydrol. 2017, 550, 549–567. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized Precipitation Evapotranspiration Index (Spei) Revisited: Parameter Fitting, Evapotranspiration Models, Tools, Datasets and Drought Monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; Begueria, S.; Lopez-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 696–718. [Google Scholar] [CrossRef] [Green Version]
- Palmer, W.C. Meteorological Drought; U.S. Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- Svoboda, M.; Fuchs, B. Handbook of Drought Indicators and Indices; World Meteorological Organization: Geneva, Switzerland, 2016; pp. 1–44. [Google Scholar]
- Bachmair, S.; Stahl, K.; Collins, K.; Hannaford, J.; Acreman, M.; Svoboda, M.; Knutson, C.; Helm Smith, K.; Wall, N.; Fuchs, B.; et al. Drought Indicators Revisited: The Need for a Wider Consideration of Environment and Society. Wiley Interdiscip. Rev. Water 2016, 3, 516–536. [Google Scholar] [CrossRef] [Green Version]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A Review of Water Scarcity and Drought Indexes in Water Resources Planning and Management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef] [Green Version]
- Hao, Z.C.; Singh, V.P. Drought Characterization from a Multivariate Perspective: A Review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Ashraf, M.; Routray, J.K. Spatio-Temporal Characteristics of Precipitation and Drought in Balochistan Province, Pakistan. Nat. Hazards 2015, 77, 229–254. [Google Scholar] [CrossRef]
- Ukkola, A.; De Kauwe, M.G.; Roderick, M.L.; Abramowitz, G.; Pitman, A.J. Robust Future Changes in Meteorological Drought in Cmip6 Projections Despite Uncertainty in Precipitation. Geophys. Res. Lett. 2020, 47, e2020GL087820. [Google Scholar] [CrossRef]




| Dataset | Data Range | Highest Resolution | Coverage | Reference |
|---|---|---|---|---|
| PERSIANN-CDR V1R1 | 1983–current | 0.25°-monthly | 60° S–60° N | [40] |
| CHIRPS2.0 | 1983–current | 0.05°-daily | 60° S–60° N | [41] |
| MSWEP2.8 | 1979–current | 0.1°-3 hourly | 90° S–90° N | [39] |
| Scale | Name | Wet Months (SPI > 0) | Dry Months (SPI < 0) | ||||
|---|---|---|---|---|---|---|---|
| RB (%) | CC | RMSE | RB (%) | CC | RMSE | ||
| SPI1 | PERSIANN-CDR | 16.72 | 0.86 | 0.20 | 66.34 | 0.81 | 0.31 |
| CHIRPS | 12.05 | 0.70 | 0.29 | 62.96 | 0.63 | 0.34 | |
| MSWEP | −3.14 | 0.81 | 0.20 | 37.31 | 0.89 | 0.20 | |
| SPI3 | PERSIANN-CDR | 23.87 | 0.85 | 0.22 | 42.21 | 0.84 | 0.29 |
| CHIRPS | 17.98 | 0.49 | 0.34 | 21.07 | 0.74 | 0.24 | |
| MSWEP | −0.10 | 0.66 | 0.26 | 17.93 | 0.89 | 0.16 | |
| SPI6 | PERSIANN-CDR | 24.27 | 0.82 | 0.22 | 33.99 | 0.84 | 0.27 |
| CHIRPS | 16.15 | 0.54 | 0.31 | 12.66 | 0.67 | 0.25 | |
| MSWEP | 0.63 | 0.51 | 0.31 | 12.97 | 0.88 | 0.16 | |
| SPI12 | PERSIANN-CDR | 21.41 | 0.75 | 0.20 | 27.78 | 0.89 | 0.24 |
| CHIRPS | 2.55 | 0.64 | 0.23 | 19.78 | 0.86 | 0.20 | |
| MSWEP | −1.49 | 0.30 | 0.38 | 11.69 | 0.89 | 0.17 | |
| Event Index | Product | Start Time–End Time (yyyymm–yyyymm) | Peak Time (yyyymm) | DD (Months) | DS | DI | DP |
|---|---|---|---|---|---|---|---|
| DE1 | Gauge | 198412–198611 | 198509 | 24 | 11.88 | 0.61 | 1.28 |
| PERSIANN-CDR | 198407–198611 | 198602 | 29 | 21.94 | 0.76 | 1.61 | |
| CHIRPS | 198408–198611 | 198602 | 28 | 13.79 | 0.54 | 1.35 | |
| MSWEP | 198412–198611 | 198509 | 24 | 14.36 | 0.60 | 1.35 | |
| DE2 | Gauge | 199105–199107 | 199107 | 3 | 1.83 | 0.61 | 0.66 |
| PERSIANN-CDR | 199104–199107 | 199105 | 4 | 2.49 | 0.62 | 0.94 | |
| CHIRPS | 199105–199107 | 199106 | 3 | 2.19 | 0.73 | 0.88 | |
| MSWEP | 199104–199107 | 199106 | 4 | 1.99 | 0.50 | 0.67 | |
| DE3 | Gauge | 199701–199712 | 199711 | 12 | 8.03 | 0.67 | 1.24 |
| PERSIANN-CDR | 199701–199802 | 199711 | 14 | 10.84 | 0.77 | 1.90 | |
| CHIRPS | 199701–199712 | 199711 | 12 | 9.22 | 0.77 | 1.21 | |
| MSWEP | 199701–199712 | 199711 | 12 | 9.71 | 0.81 | 1.50 | |
| DE4 | Gauge | 200606–200703 | 200610 | 10 | 3.43 | 0.34 | 0.86 |
| PERSIANN-CDR | 200605–200702 | 200610 | 10 | 3.25 | 0.33 | 0.77 | |
| CHIRPS | 200604–200704 | 200702 | 13 | 5.33 | 0.41 | 0.80 | |
| MSWEP | 200605–200703 | 200610 | 11 | 3.61 | 0.32 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, H.; Li, M.; Nzabarinda, V.; Bao, A.; Meng, X.; Zhu, L.; De Maeyer, P. Assessment of Three Long-Term Satellite-Based Precipitation Estimates against Ground Observations for Drought Characterization in Northwestern China. Remote Sens. 2022, 14, 828. https://doi.org/10.3390/rs14040828
Guo H, Li M, Nzabarinda V, Bao A, Meng X, Zhu L, De Maeyer P. Assessment of Three Long-Term Satellite-Based Precipitation Estimates against Ground Observations for Drought Characterization in Northwestern China. Remote Sensing. 2022; 14(4):828. https://doi.org/10.3390/rs14040828
Chicago/Turabian StyleGuo, Hao, Min Li, Vincent Nzabarinda, Anming Bao, Xiangchen Meng, Li Zhu, and Philippe De Maeyer. 2022. "Assessment of Three Long-Term Satellite-Based Precipitation Estimates against Ground Observations for Drought Characterization in Northwestern China" Remote Sensing 14, no. 4: 828. https://doi.org/10.3390/rs14040828








