A New Exospheric Temperature Model Based on CHAMP and GRACE Measurements
Abstract
1. Introduction
2. Data and Methods
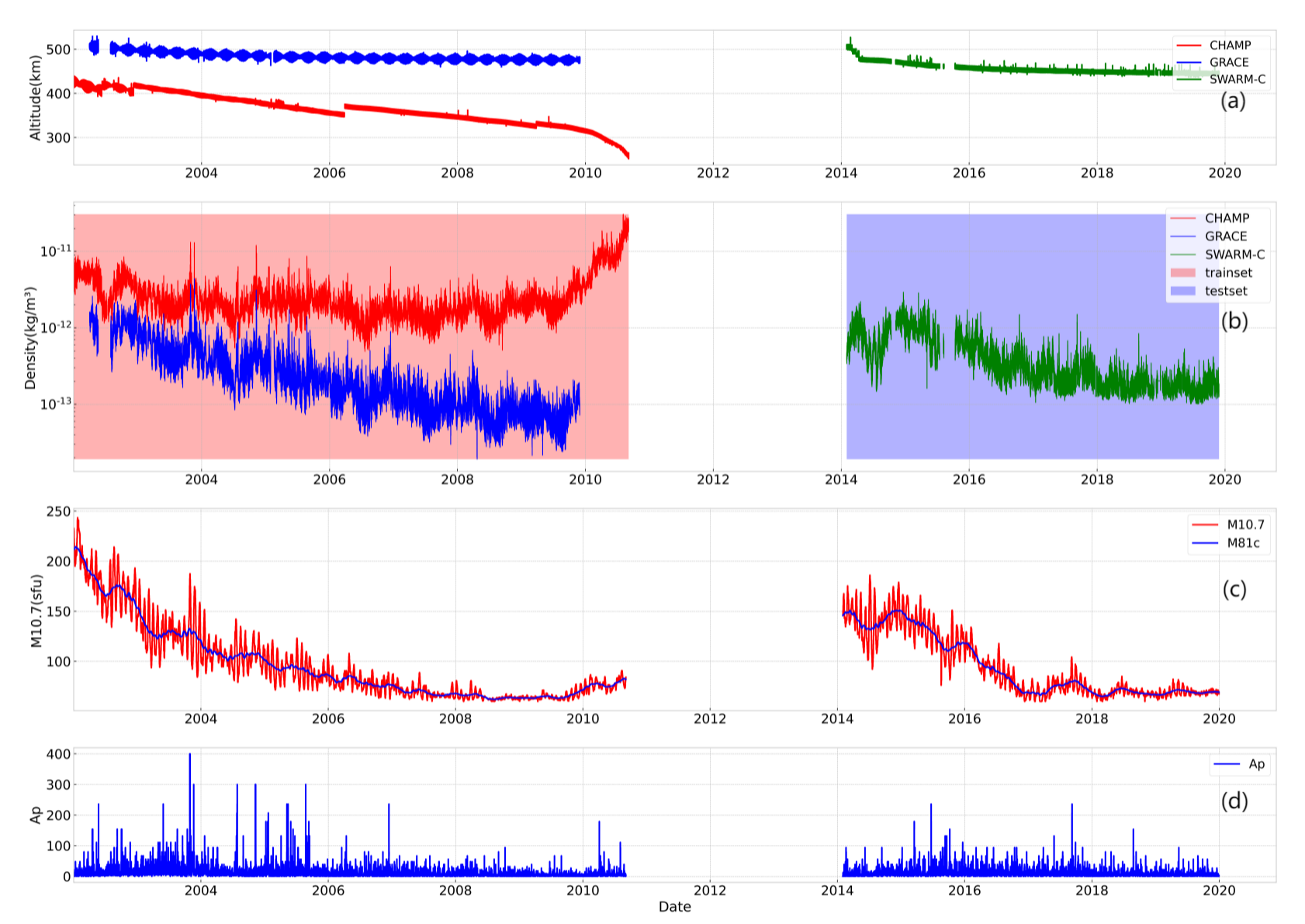
2.1. Observations
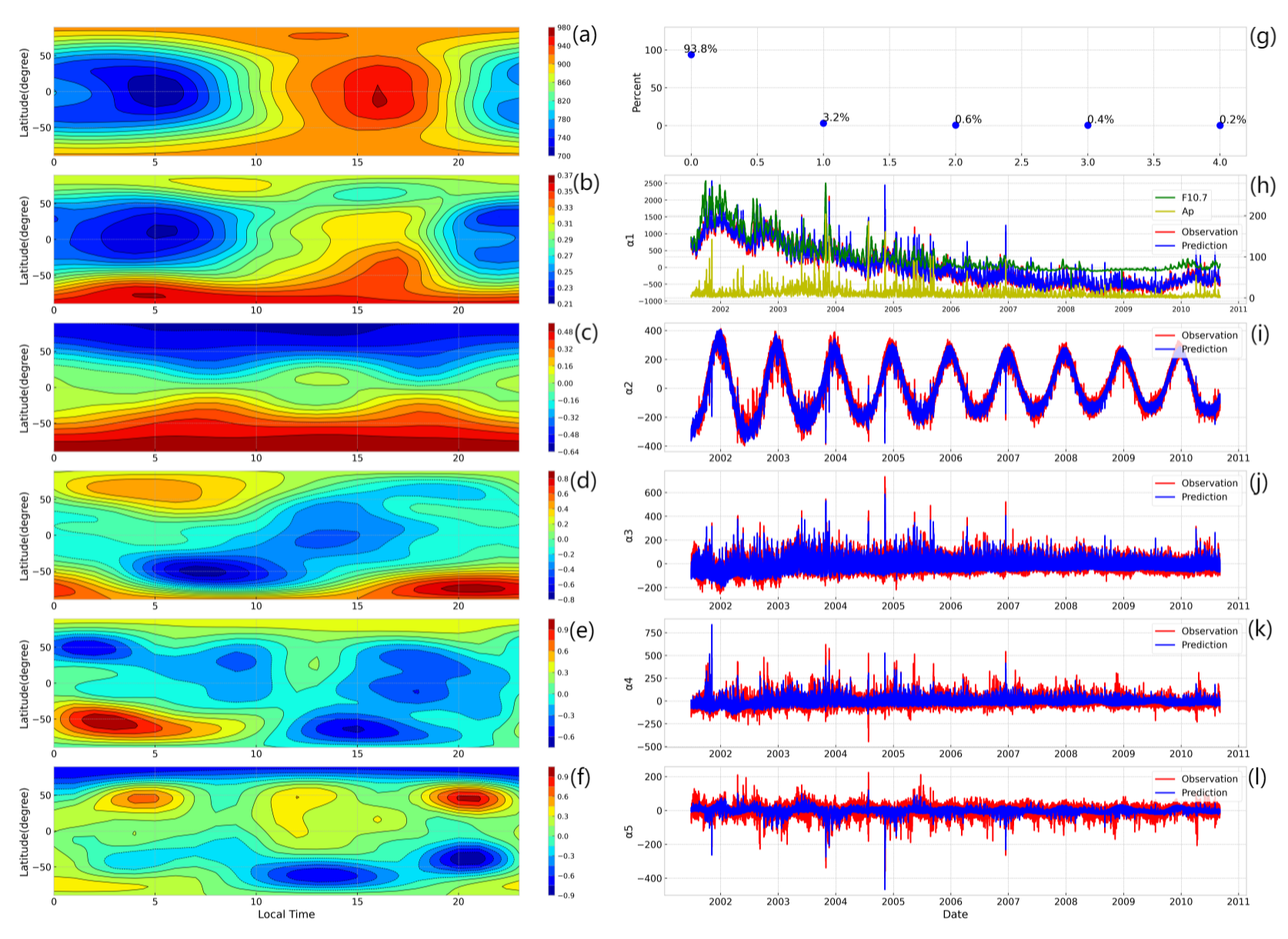
2.2. Method Formulation
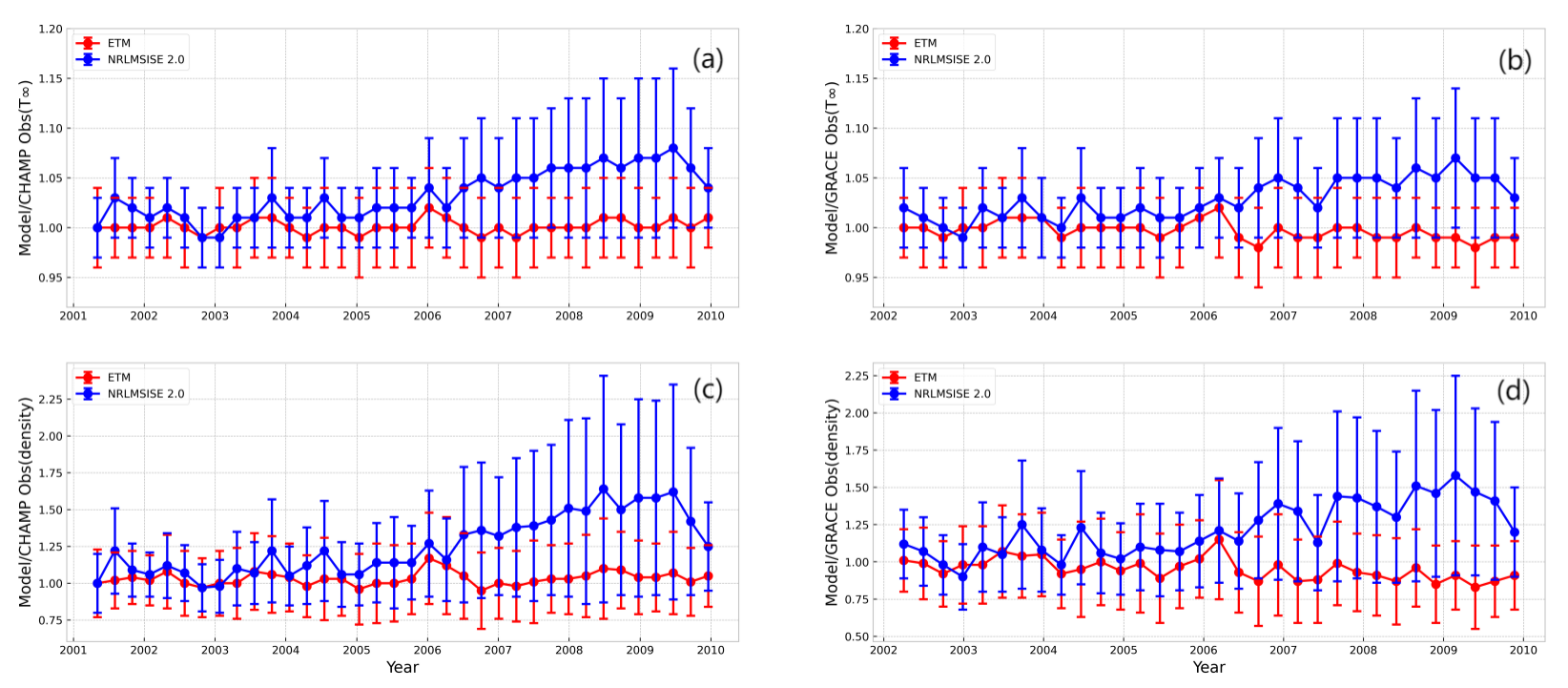
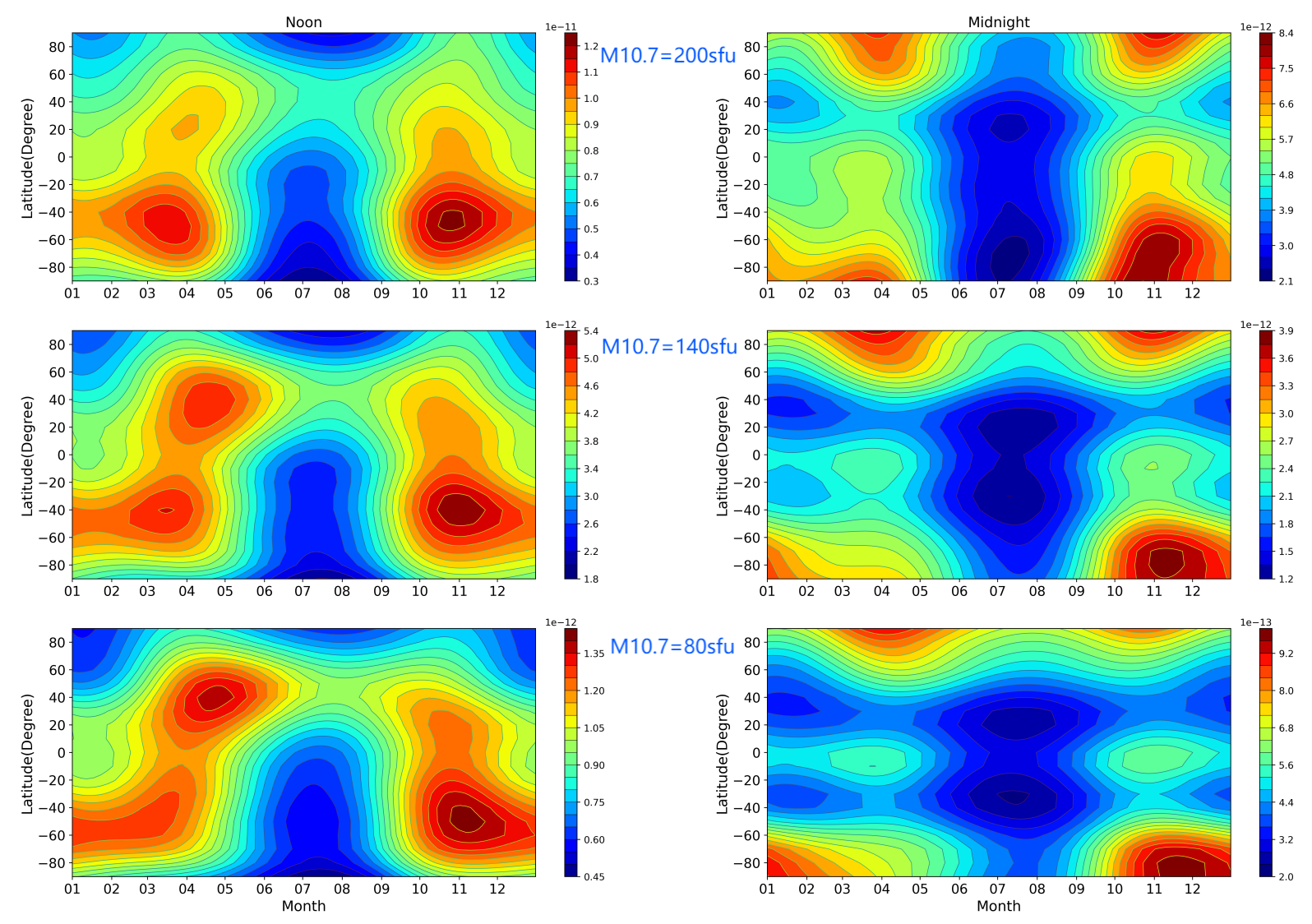
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bowman, B.R.; Tobiska, W.K.; Marcos, F.A.; Huang, C.Y.; Lin, C.S.; Burke, W.J. A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Bruinsma, S. The DTM-2013 thermosphere model. J. Space Weather Space Clim. 2015, 5, A1. [Google Scholar] [CrossRef]
- Hedin, A.E. Extension of the MSIS Thermosphere Model into the middle and lower atmosphere. J. Geophys. Res. Space Phys. 1991, 96, 1159–1172. [Google Scholar] [CrossRef]
- Kong, Q.; Chen, Y.; Fang, W.; Wang, G.; Li, C.; Wang, T.; Bai, Q.; Han, J. Analysis of Space-Borne GPS Data Quality and Evaluation of Precise Orbit Determination for COSMIC-2 Mission Based on Reduced Dynamic Method. Remote Sens. 2022, 14, 3544. [Google Scholar] [CrossRef]
- March, G.; Doornbos, E.N.; Visser, P.N.A.M. High-fidelity geometry models for improving the consistency of CHAMP, GRACE, GOCE and Swarm thermospheric density data sets. Adv. Space Res. 2019, 63, 213–238. [Google Scholar] [CrossRef]
- Mehta, P.M.; Linares, R. A methodology for reduced order modeling and calibration of the upper atmosphere. Space Weather 2017, 15, 1270–1287. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, SIA 15-11–SIA 15-16. [Google Scholar] [CrossRef]
- Jacchia, L.G. New Static Models of the Thermosphere and Exosphere with Empirical Temperature Profiles. SAO Special Report 313; Smithsonian Astrophysical Observator: Cambridge, MA, USA, 1970. [Google Scholar]
- Doornbos, E.; van den Ijssel, J.; Luhr, H.; Forster, M.; Koppenwallner, G. Neutral Density and Crosswind Determination from Arbitrarily Oriented Multiaxis Accelerometers on Satellites. J. Spacecr. Rocket. 2010, 47, 580–589. [Google Scholar] [CrossRef]
- Emmert, J.T. Thermospheric mass density: A review. Adv. Space Res. 2015, 56, 773–824. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, B.; Meng, X.; Tang, X.; Yan, F.; Zhang, X.; Bai, W.; Du, Q.; Wang, X.; Cai, Y.; et al. Analysis of Orbital Atmospheric Density from QQ-Satellite Precision Orbits Based on GNSS Observations. Remote Sens. 2022, 14, 3873. [Google Scholar] [CrossRef]
- Wise, J.O.; Burke, W.J.; Sutton, E.K. Globally averaged exospheric temperatures derived from CHAMP and GRACE accelerometer measurements. J. Geophys. Res. Space Phys. 2012, 117, A04312. [Google Scholar] [CrossRef]
- Ruan, H.; Lei, J.; Dou, X.; Liu, S.; Aa, E. An Exospheric Temperature Model Based On CHAMP Observations and TIEGCM Simulations. Space Weather 2018, 16, 147–156. [Google Scholar] [CrossRef]
- Weimer, D.R.; Sutton, E.K.; Mlynczak, M.G.; Hunt, L.A. Intercalibration of neutral density measurements for mapping the thermosphere. J. Geophys. Res. Space Phys. 2016, 121, 5975–5990. [Google Scholar] [CrossRef]
- Weng, L.; Lei, J.; Sutton, E.; Dou, X.; Fang, H. An exospheric temperature model from CHAMP thermospheric density. Space Weather 2017, 15, 343–351. [Google Scholar] [CrossRef]
- Weimer, D.R.; Mehta, P.M.; Tobiska, W.K.; Doornbos, E.; Mlynczak, M.G.; Drob, D.P.; Emmert, J.T. Improving Neutral Density Predictions Using Exospheric Temperatures Calculated on a Geodesic, Polyhedral Grid. Space Weather 2020, 18, e2019SW002355. [Google Scholar] [CrossRef]
- Weimer, D.R.; Tobiska, W.K.; Mehta, P.M.; Licata, R.J.; Drob, D.P.; Yoshii, J. Comparison of a Neutral Density Model With the SET HASDM Density Database. Space Weather 2021, 19, e2021sw002888. [Google Scholar] [CrossRef]
- Licata, R.J.; Mehta, P.M.; Weimer, D.R.; Tobiska, W.K. Improved Neutral Density Predictions Through Machine Learning Enabled Exospheric Temperature Model. Space Weather 2021, 19, e2021sw002918. [Google Scholar] [CrossRef]
- Siemes, C.; de Teixeira da Encarnação, J.; Doornbos, E.; van den Ijssel, J.; Kraus, J.; Pereštý, R.; Grunwaldt, L.; Apelbaum, G.; Flury, J.; Holmdahl Olsen, P.E. Swarm accelerometer data processing from raw accelerations to thermospheric neutral densities. Earth Planets Space 2016, 68, 92. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef]
- Othman, A.; Abdelrady, A.; Mohamed, A. Monitoring Mass Variations in Iraq Using Time-Variable Gravity Data. Remote Sens. 2022, 14, 3346. [Google Scholar] [CrossRef]
- Weng, L.; Lei, J.; Zhong, J.; Dou, X.; Fang, H. A Machine-Learning Approach to Derive Long-Term Trends of Thermospheric Density. Geophys. Res. Lett. 2020, 47, e2020GL087140. [Google Scholar] [CrossRef]
- Emmert, J.T.; Drob, D.P.; Picone, J.M.; Siskind, D.E.; Jones, M.; Mlynczak, M.G.; Bernath, P.F.; Chu, X.; Doornbos, E.; Funke, B.; et al. NRLMSIS 2.0: A Whole-Atmosphere Empirical Model of Temperature and Neutral Species Densities. Earth Space Sci. 2020, 7, e2020EA001321. [Google Scholar] [CrossRef]
- Lei, J.; Matsuo, T.; Dou, X.; Sutton, E.; Luan, X. Annual and semiannual variations of thermospheric density: EOF analysis of CHAMP and GRACE data. J. Geophys. Res. Space Phys. 2012, 117, A01310. [Google Scholar] [CrossRef]
- Calabia, A.; Jin, S. New modes and mechanisms of thermospheric mass density variations from GRACE accelerometers. J. Geophys. Res. Space Phys. 2016, 121, 11191–111212. [Google Scholar] [CrossRef]
- Delforge, D.; de Viron, O.; Durand, F.; Dehant, V. The Global Patterns of Interannual and Intraseasonal Mass Variations in the Oceans from GRACE and GRACE Follow-On Records. Remote Sens. 2022, 14, 1861. [Google Scholar] [CrossRef]
- Matsuo, T.; Forbes, J.M. Principal modes of thermospheric density variability: Empirical orthogonal function analysis of CHAMP 2001-2008 data. J. Geophys. Res. Space Phys. 2010, 115, A07309. [Google Scholar] [CrossRef]
- Sutton, E.K.; Cable, S.B.; Lin, C.S.; Qian, L.; Weimer, D.R. Thermospheric basis functions for improved dynamic calibration of semi-empirical models. Space Weather 2012, 10, S10001. [Google Scholar] [CrossRef]
- Matsuo, T.; Fedrizzi, M.; Fuller-Rowell, T.J.; Codrescu, M.V. Data assimilation of thermospheric mass density. Space Weather 2012, 10, S05002. [Google Scholar] [CrossRef]
- Liu, Z.; Fang, H.; Hoque, M.M.; Weng, L.; Yang, S.; Gao, Z. A New Empirical Model of NmF2 Based on CHAMP, GRACE, and COSMIC Radio Occultation. Remote Sensing 2019, 11, 1386. [Google Scholar] [CrossRef]
- Weng, L.; Lei, J.; Doornbos, E.; Fang, H.; Dou, X. Seasonal variations of thermospheric mass density at dawn/dusk from GOCE observations. Ann. Geophys. 2018, 36, 489–496. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Zhu, X.; Weng, L.; Yang, S. A New Exospheric Temperature Model Based on CHAMP and GRACE Measurements. Remote Sens. 2022, 14, 5198. https://doi.org/10.3390/rs14205198
Yang X, Zhu X, Weng L, Yang S. A New Exospheric Temperature Model Based on CHAMP and GRACE Measurements. Remote Sensing. 2022; 14(20):5198. https://doi.org/10.3390/rs14205198
Chicago/Turabian StyleYang, Xu, Xiaoqian Zhu, Libin Weng, and Shenggao Yang. 2022. "A New Exospheric Temperature Model Based on CHAMP and GRACE Measurements" Remote Sensing 14, no. 20: 5198. https://doi.org/10.3390/rs14205198
APA StyleYang, X., Zhu, X., Weng, L., & Yang, S. (2022). A New Exospheric Temperature Model Based on CHAMP and GRACE Measurements. Remote Sensing, 14(20), 5198. https://doi.org/10.3390/rs14205198




