GPS, BDS-3, and Galileo Inter-Frequency Clock Bias Deviation Time-Varying Characteristics and Positioning Performance Analysis
Abstract
:1. Introduction
2. Methods
2.1. Triple-Frequency Uncombined PPP Model with IFCB
2.2. IFCB Estimation Method
3. Experiment and Analysis
3.1. Data Introduction and Processing Strategy
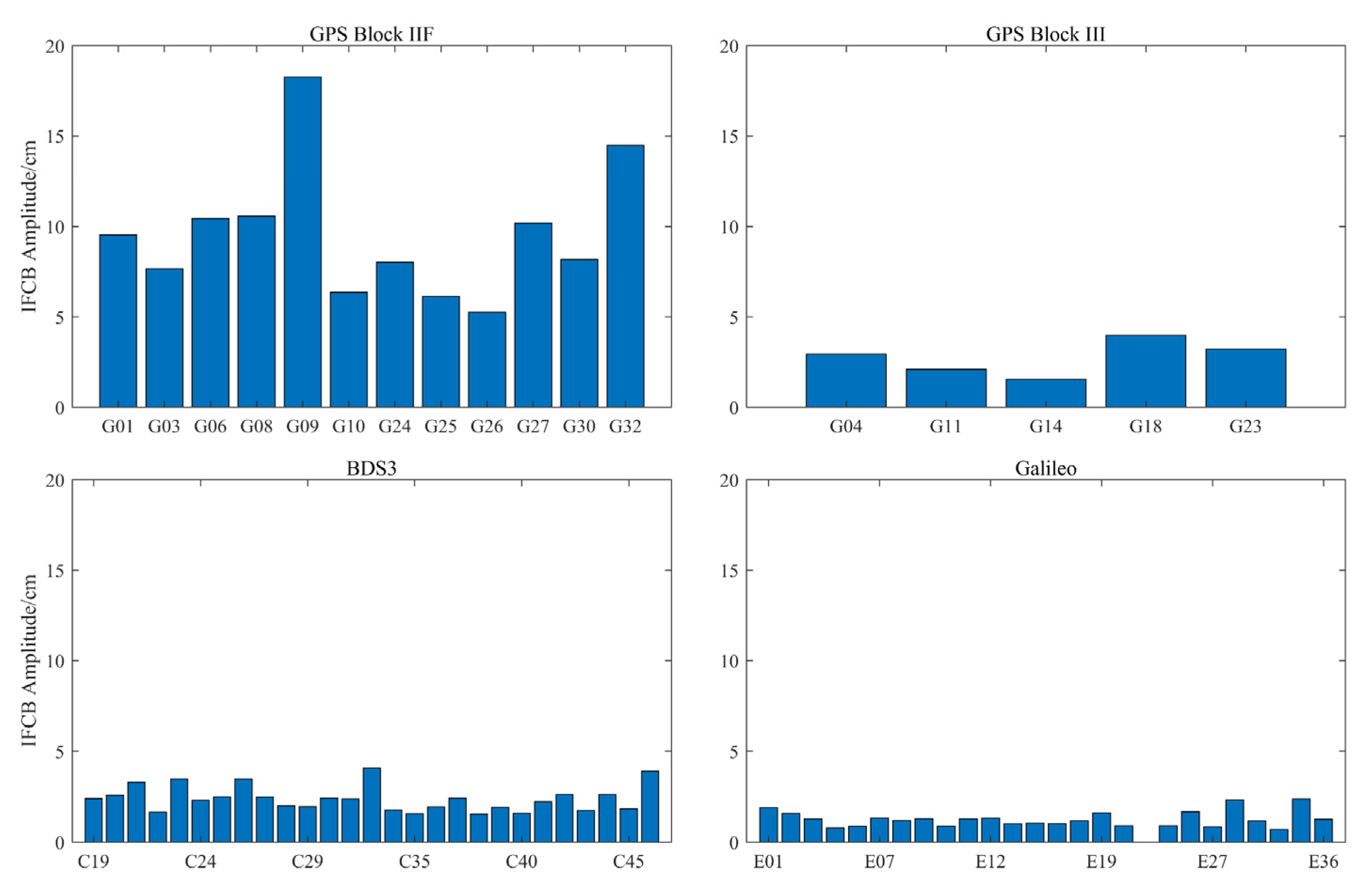
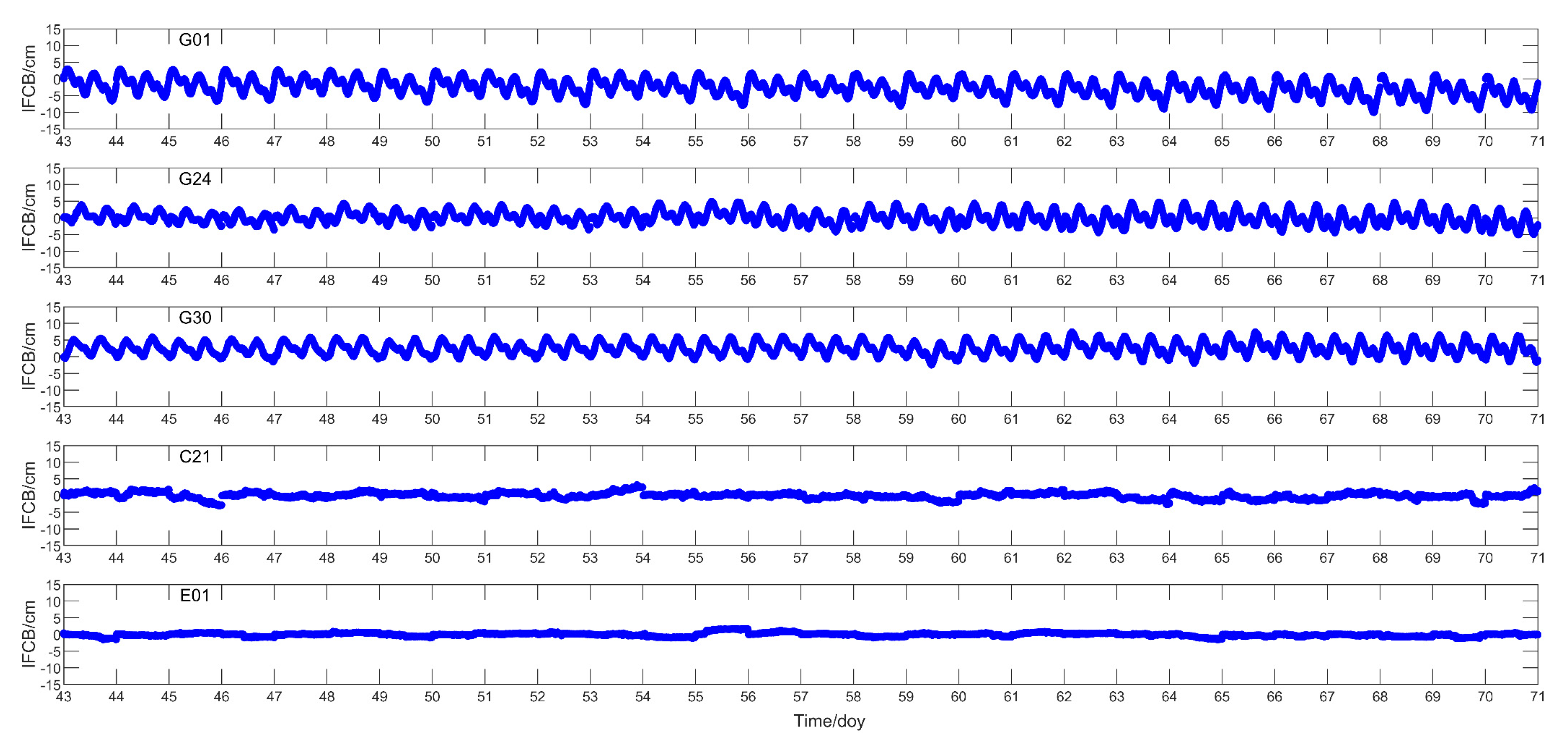
3.2. Time-Varying Feature Analysis of IFCB
3.2.1. Intraday Time-Varying Characteristics Analysis of IFCB
3.2.2. Inter-Day Variation Characteristics of IFCB
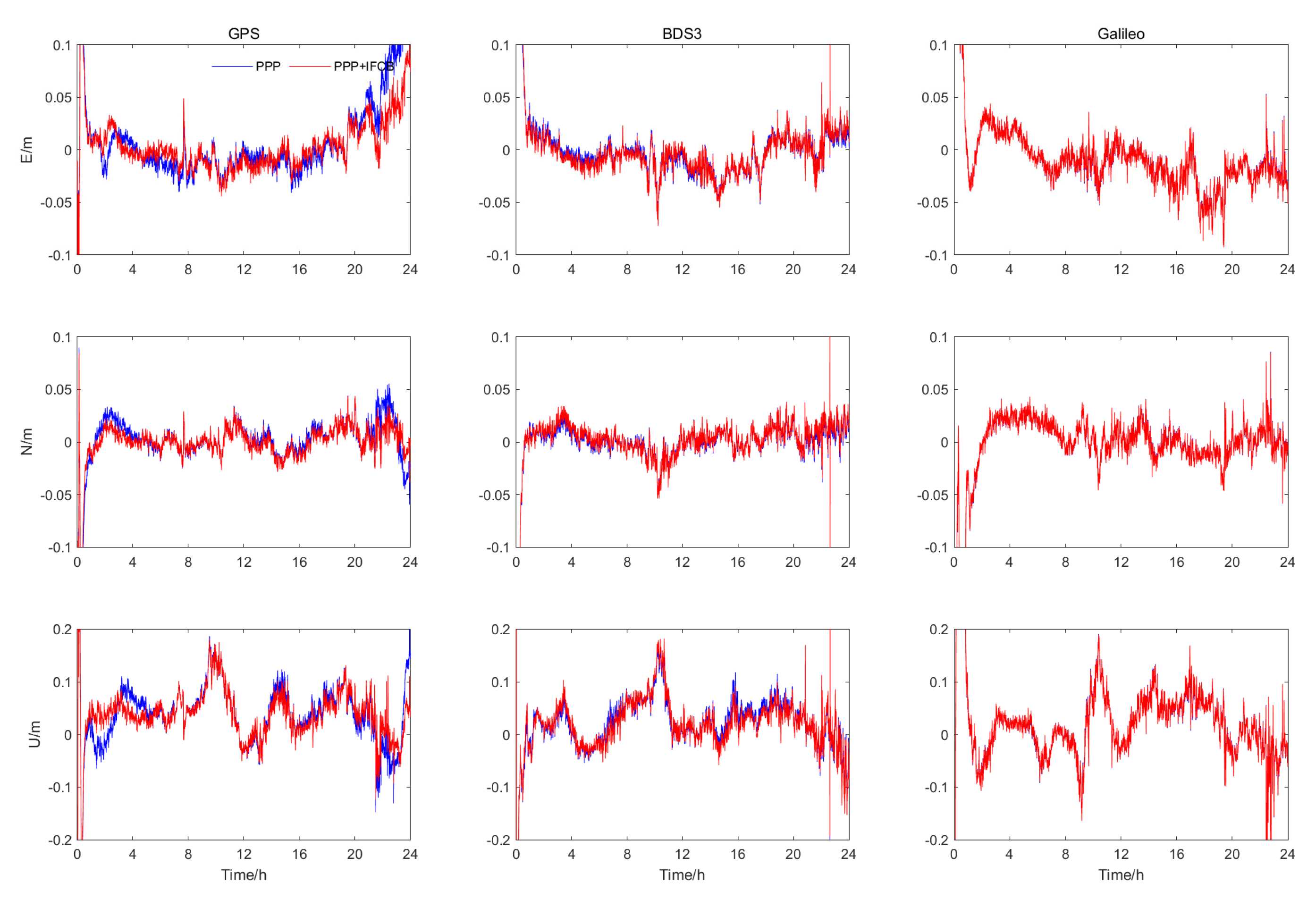
3.3. Triple-Frequency PPP Positioning Performance Analysis
3.3.1. Static Mode
3.3.2. Imitation Kinetic Mode
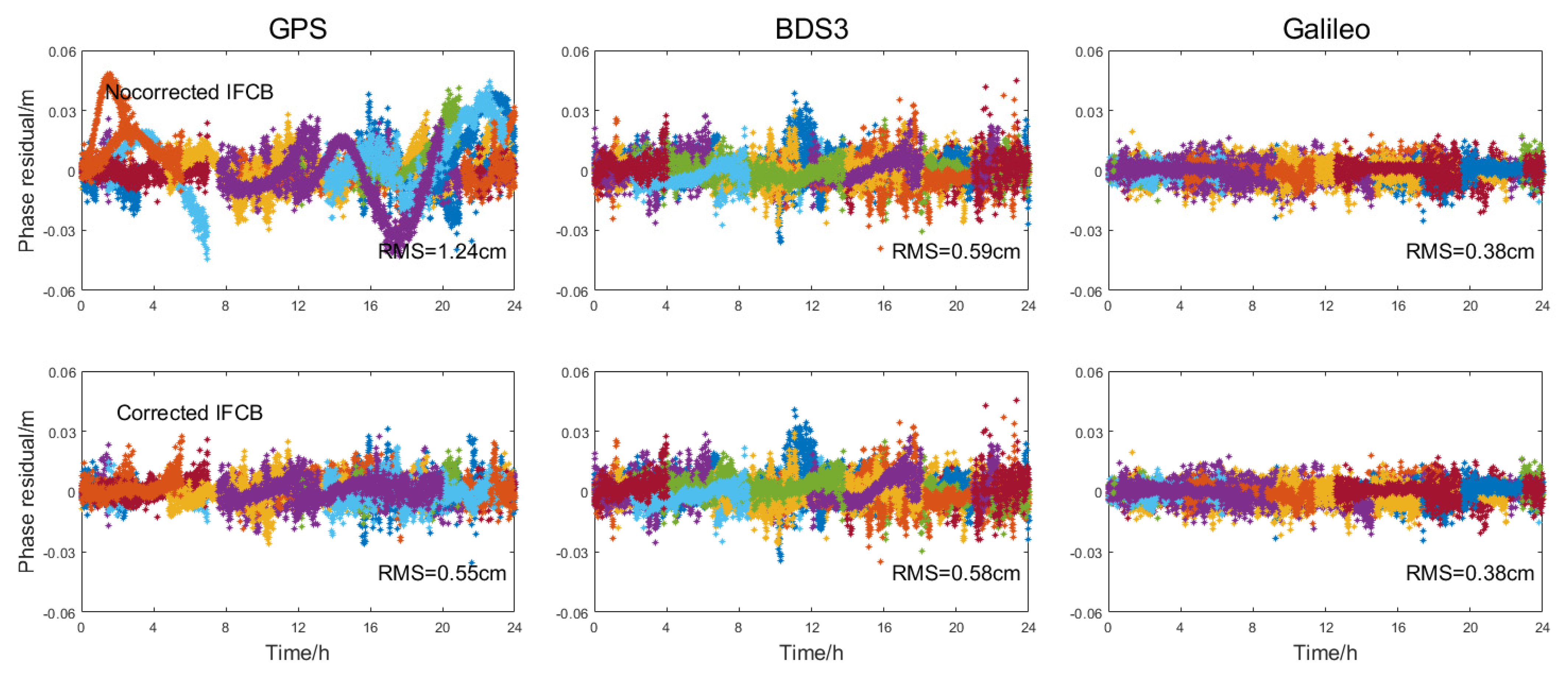
3.4. Model Deviation and Residual Analysis
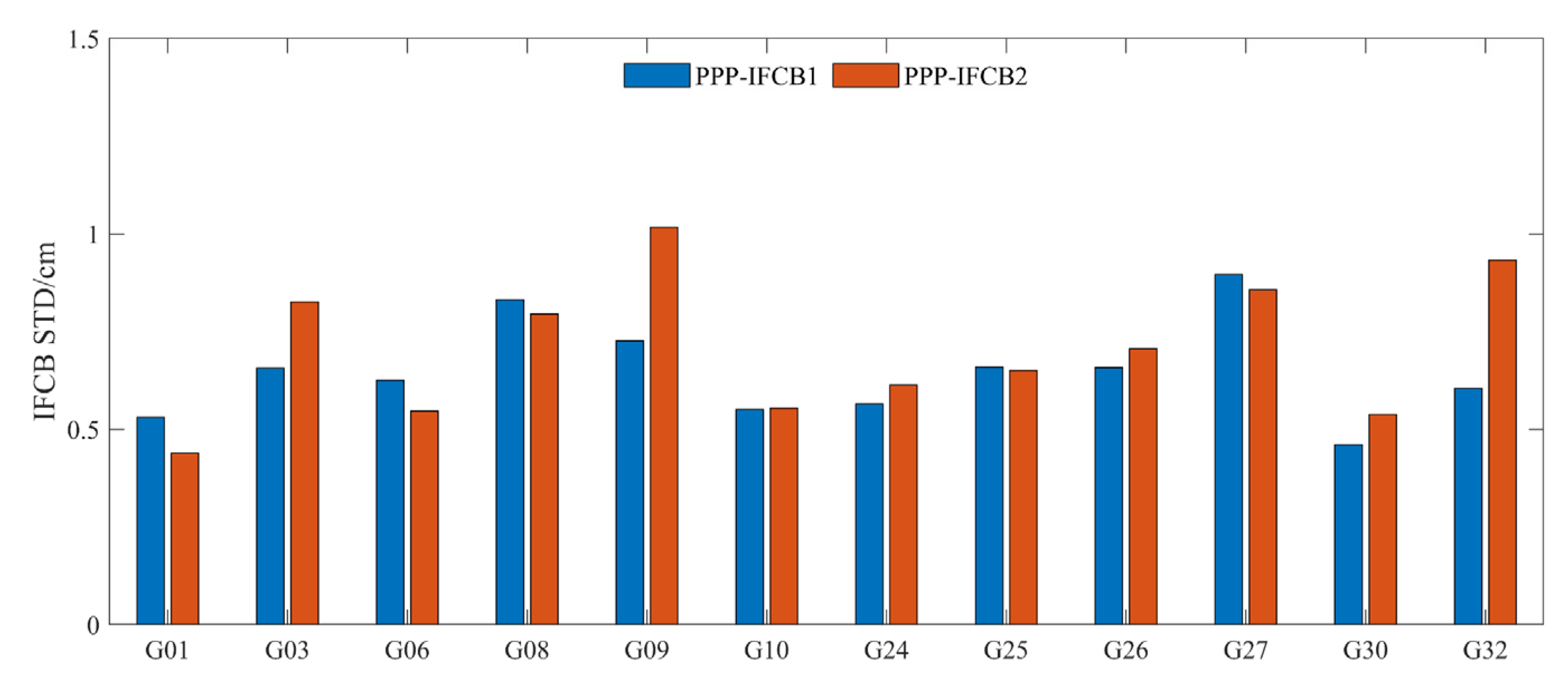
3.5. Short-Term Stability of IFCB
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Guo, J.; Geng, J. GPS satellite clock determination in case of inter-frequency clock biases for triple-frequency precise point posi-tioning. J. Geod. 2017, 92, 1133–1142. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, X.; Li, P. Improving the Performance of Galileo Uncombined Precise Point Positioning Ambiguity Resolution Using Triple-Frequency Observations. Remote Sens. 2019, 11, 341. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, J.; Ren, X. New progress of PPP/PPP-RTK and positioning performance comparison of BDS/GNSS PPP. Acta Geod. Cartogr. Sin. 2020, 49, 1084–1100. [Google Scholar]
- Su, K.; Jin, S. Analytical performance and validations of the Galileo five-frequency precise point positioning models. Measurement 2021, 172, 108890. [Google Scholar] [CrossRef]
- Cai, H.; Meng, Y.; Geng, C.; Weiguang, G.; Tianqiao, Z.; Gang, L.; Bo, S.; Jie, X.; Hongyang, L.; Yue, M.; et al. BDS-3 performan ceassessment: PNT, SBAS, PPP, SMC and SAR. Acta Geod. Cartogr. Sin. 2021, 50, 427–435. [Google Scholar]
- Zhou, F.; Xu, T. Modeling and assessment of GPS/BDS/Galileo treple-frequency precise point positioning. Acta Geod. Cartogr. Sin. 2021, 50, 61–70. [Google Scholar]
- Zhou, W.; Cai, H.; Chen, G.; Jiao, W.; He, Q.; Yang, Y. Multi-GNSS Combined Orbit and Clock Solutions at iGMAS. Sensors 2022, 22, 457. [Google Scholar] [CrossRef]
- Yang, X.; Gu, S.; Gong, X.; Song, W.; Lou, Y.; Liu, J. Regional BDS satellite clock estimation with triple-frequency ambiguity resolution based on un-differenced observation. GPS Solut. 2019, 23, 33. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romerof, I.; Nollg, C.; Stürzeh, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Zhang, X. Three frequency GNSS navigation prospect demonstrated with semi-simulated data. Adv. Space Res. 2013, 51, 1175–1185. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Langley, R. Three’s the Challenge: A Close Look at GPS SVN62 Triple-frequency Signal Combinations Finds Carrier-phase Variations on the New L5. GPS World 2010, 21, 8–19. [Google Scholar]
- Montenbruck, O.; Hugentobler, U.; Dach, R.; Steigenberger, P.; Hauschild, A. Apparent clock variations of the Block IIF-1 (SVN62) GPS satellite. GPS Solut. 2012, 16, 303–313. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.; Li, X.; Liu, J.; Li, X. Characteristics of inter-frequency clock bias for Block IIF satellites and its effect on triple-frequency GPS precise point positioning. GPS Solut. 2017, 21, 811–822. [Google Scholar] [CrossRef]
- Li, P.; Jiang, X.; Zhang, X.; Ge, M.; Schuh, H. GPS + Galileo + BeiDou precise point positioning with triple-frequency ambiguity resolution. GPS Solut. 2020, 24, 78. [Google Scholar] [CrossRef]
- Fan, L.; Shi, C.; Li, M.; Wang, C.; Zheng, F.; Jing, G.; Zhang, J. GPS satellite inter-frequency clock bias estimation using triple-frequency raw observations. J. Geod. 2019, 93, 2465–2479. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, G.; Liu, Z.; Hu, Z.; Dai, Z.; Liu, J. Analysis of BeiDou Satellite Measurements with Code Multipath and Geometry-Free Iono-sphere-Free Combinations. Sensors 2016, 16, 123. [Google Scholar] [CrossRef] [PubMed]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Steigenberger, P.; Hauschild, A.; Montenbruck, O.; Rodriguez-Solano, C.; Hugentobler, U. Orbit and Clock Determination of QZS-1 Based on the CONGO Network. Navig. J. Inst. Navig. 2013, 60, 31–40. [Google Scholar] [CrossRef]
- Zhao, L.; Ye, S.; Song, J. Handling the satellite inter-frequency biases in triple-frequency observations. Adv. Space Res. 2017, 59, 2048–2057. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Jiao, G. GNSS carrier phase time-variant observable-specific signal bias (OSB) handling: An absolute bias perspective in multi-frequency PPP. GPS Solut. 2022, 26, 71. [Google Scholar] [CrossRef]
- Gong, X.; Gu, S.; Lou, Y.; Zheng, F.; Yang, X.; Wang, Z.; Liu, J. Research on empirical correction models of GPS Block IIF and BDS satellite inter-frequency clock bias. J. Geod. 2020, 94, 36. [Google Scholar] [CrossRef]
- Li, H.; Li, B.; Xiao, G.; Wang, J.; Xu, T. Improved method for estimating the inter-frequency satellite clock bias of triple-frequency GPS. GPS Solut. 2016, 20, 751–760. [Google Scholar] [CrossRef]
- Zhang, F.; Chai, H.; Li, L.; Xiao, G.; Du, Z. Estimation and analysis of GPS inter-fequency clock biases from long-term triple-frequency ob-servations. GPS Solut. 2021, 25, 126. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Ge, M.; Schuh, H. Three-frequency BDS precise point positioning ambiguity resolution based on raw observables. J. Geod. 2018, 92, 1357–1369. [Google Scholar] [CrossRef]
- Li, H.; Zhou, X.; Wu, B. Fast estimation and analysis of the inter-frequency clock bias for Block IIF satellites. GPS Solut. 2013, 17, 347–355. [Google Scholar] [CrossRef]



| System | Remark | PRN |
|---|---|---|
| GPS | Block IIF (12) | G01, G03, G06, G08, G09, G10, G24, G25, G26, G27, G30, G32 |
| Block III (5) | G04, G11, G14, G18, G23 | |
| BDS-3 | MEO (24) | C19~C30, C32~C37, C41~C46 |
| IGSO (3) | C38, C39, C40 | |
| Galileo | (26) | E1~E5, E7~E15, E18, E19, E21, E24~E27, E30, E31, E33, E34, E36 |
| Type | Processing Strategies |
|---|---|
| Observation data | GPS: L1, L2, L5 BDS-3: B1I, B3I, B2a Galileo: E1, E5a, E5b |
| Sampling interval | 30s |
| Cutoff elevation | 10° |
| Clock and orbital products | CODE |
| Satellite antenna correction | igs14.atx |
| Receiver antenna correction | igs14.atx |
| Weight for observations | Elevation-dependent weight |
| Receiver coordinates | Static mode: estimated as constant Kinematic mode: estimated as white noise |
| Receiver clock | Estimated as white noise |
| Inter-frequency bias | Estimated as white noise |
| Ionospheric delay | Estimated as white noise |
| Tropospheric delay | Dry component corrected by Saastamoinen mode; wet component estimated as a random walk |
| Phase ambiguity | Float |
| Static | E | N | U | 3D | Convergence Time |
|---|---|---|---|---|---|
| PPP | 1.56 | 0.60 | 1.69 | 2.38 | 24.19 |
| PPP + IFCB | 0.99 | 0.48 | 1.34 | 1.73 | 21.64 |
| Improvement | 36.89% | 19.18% | 21.16% | 27.39% | 10.55% |
| Kinematic | E | N | U | 3D | Convergence Time |
|---|---|---|---|---|---|
| PPP | 2.59 | 1.77 | 4.81 | 5.74 | 46.72 |
| PPP + IFCB | 2.00 | 1.43 | 4.06 | 4.75 | 39.61 |
| Promote | 22.86% | 19.45% | 15.53% | 17.34% | 15.22% |
| Stations | PPP | PPP + IFCB | Promote | Stations | PPP | PPP + IFCB | Promote |
|---|---|---|---|---|---|---|---|
| ABPO | 1.09 | 0.43 | 60.05% | BRUX | 1.33 | 0.23 | 82.74% |
| ALIC | 1.20 | 0.35 | 70.97% | BSHM | 1.37 | 0.30 | 78.46% |
| ASCG | 1.14 | 0.55 | 52.07% | DAV1 | 0.82 | 0.36 | 56.46% |
| CRO1 | 1.29 | 0.46 | 64.79% | DGAR | 1.12 | 0.48 | 57.16% |
| CUSV | 1.05 | 0.35 | 66.12% | MBAR | 1.34 | 0.44 | 66.81% |
| FAA1 | 1.35 | 0.55 | 59.49% | MDO1 | 1.18 | 0.33 | 71.57% |
| FFMJ | 1.34 | 0.22 | 83.88% | MET3 | 1.26 | 0.30 | 76.27% |
| KRGG | 1.03 | 0.43 | 58.59% | QAQ1 | 1.13 | 0.38 | 66.67% |
| MAYG | 1.19 | 0.55 | 53.61% | QUIN | 1.25 | 0.35 | 71.56% |
| TOW2 | 1.17 | 0.42 | 63.82% | SUTM | 1.19 | 0.51 | 57.28% |
| ULAB | 0.98 | 0.53 | 45.84% |
| Mode | E | N | U | 3D | Convergence Time | |
|---|---|---|---|---|---|---|
| Static | PPP + IFCB | 0.99 | 0.48 | 1.34 | 1.73 | 21.64 |
| PPP + IFCB1 | 0.98 | 0.48 | 1.34 | 1.73 | 22.16 | |
| PPP + IFCB2 | 0.99 | 0.49 | 1.36 | 1.76 | 21.96 | |
| Kinematic | PPP + IFCB | 2.00 | 1.43 | 4.06 | 4.75 | 39.61 |
| PPP + IFCB1 | 2.01 | 1.44 | 4.06 | 4.76 | 39.66 | |
| PPP + IFCB2 | 2.04 | 1.46 | 4.09 | 4.79 | 39.70 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Mi, J.; Gu, S.; Li, B.; Li, H.; Yang, L.; Pang, Y. GPS, BDS-3, and Galileo Inter-Frequency Clock Bias Deviation Time-Varying Characteristics and Positioning Performance Analysis. Remote Sens. 2022, 14, 3991. https://doi.org/10.3390/rs14163991
Chen Y, Mi J, Gu S, Li B, Li H, Yang L, Pang Y. GPS, BDS-3, and Galileo Inter-Frequency Clock Bias Deviation Time-Varying Characteristics and Positioning Performance Analysis. Remote Sensing. 2022; 14(16):3991. https://doi.org/10.3390/rs14163991
Chicago/Turabian StyleChen, Yibiao, Jinzhong Mi, Shouzhou Gu, Bo Li, Hongchao Li, Lijun Yang, and Yuqi Pang. 2022. "GPS, BDS-3, and Galileo Inter-Frequency Clock Bias Deviation Time-Varying Characteristics and Positioning Performance Analysis" Remote Sensing 14, no. 16: 3991. https://doi.org/10.3390/rs14163991





