On-Orbit Characterization of TanSat Instrument Line Shape Using Observed Solar Spectra
Abstract
:1. Introduction
2. Data and Method
2.1. TanSat Instrument and Data
2.2. ILS Functions and Fitting Algorithm
3. ILS Calibration
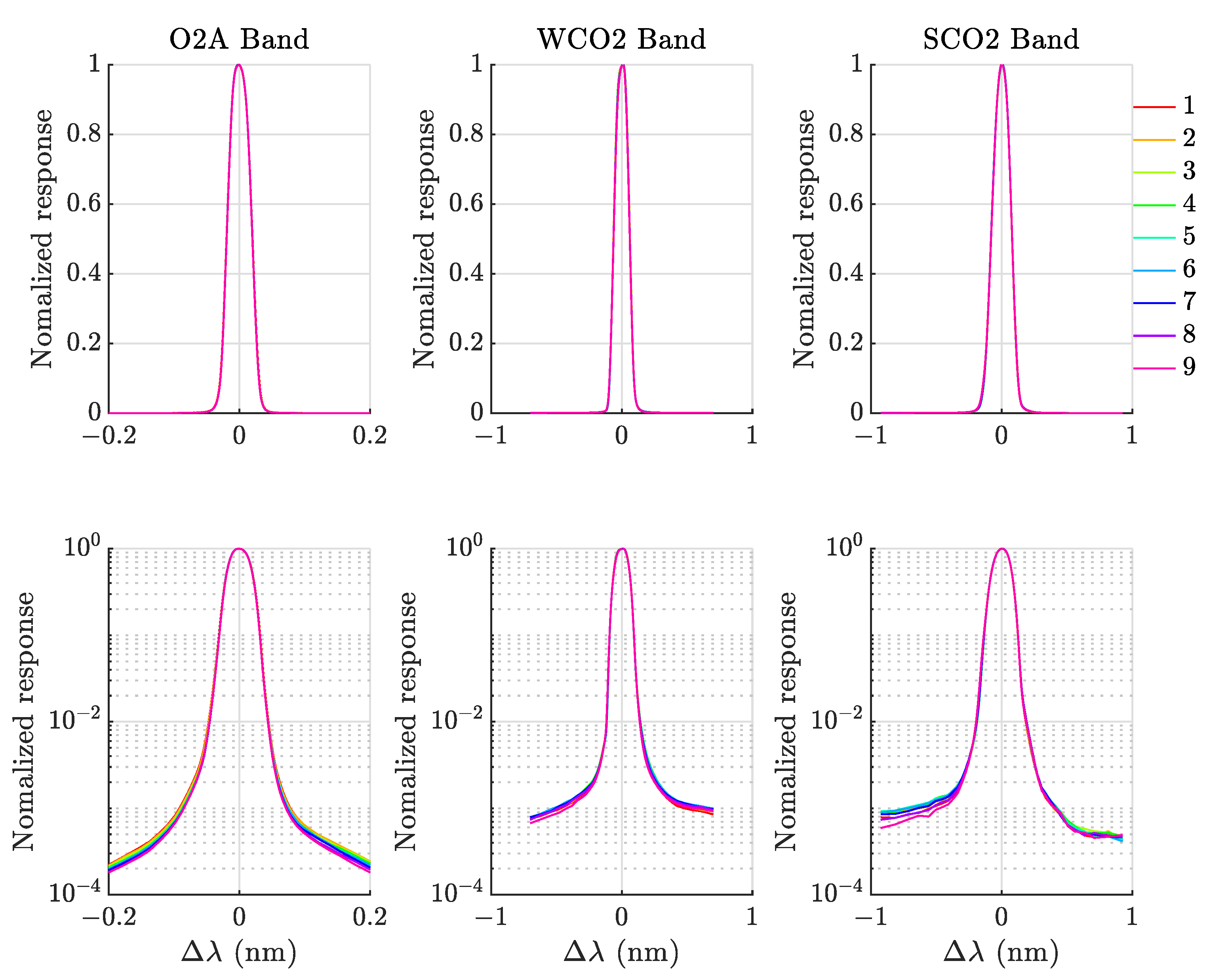
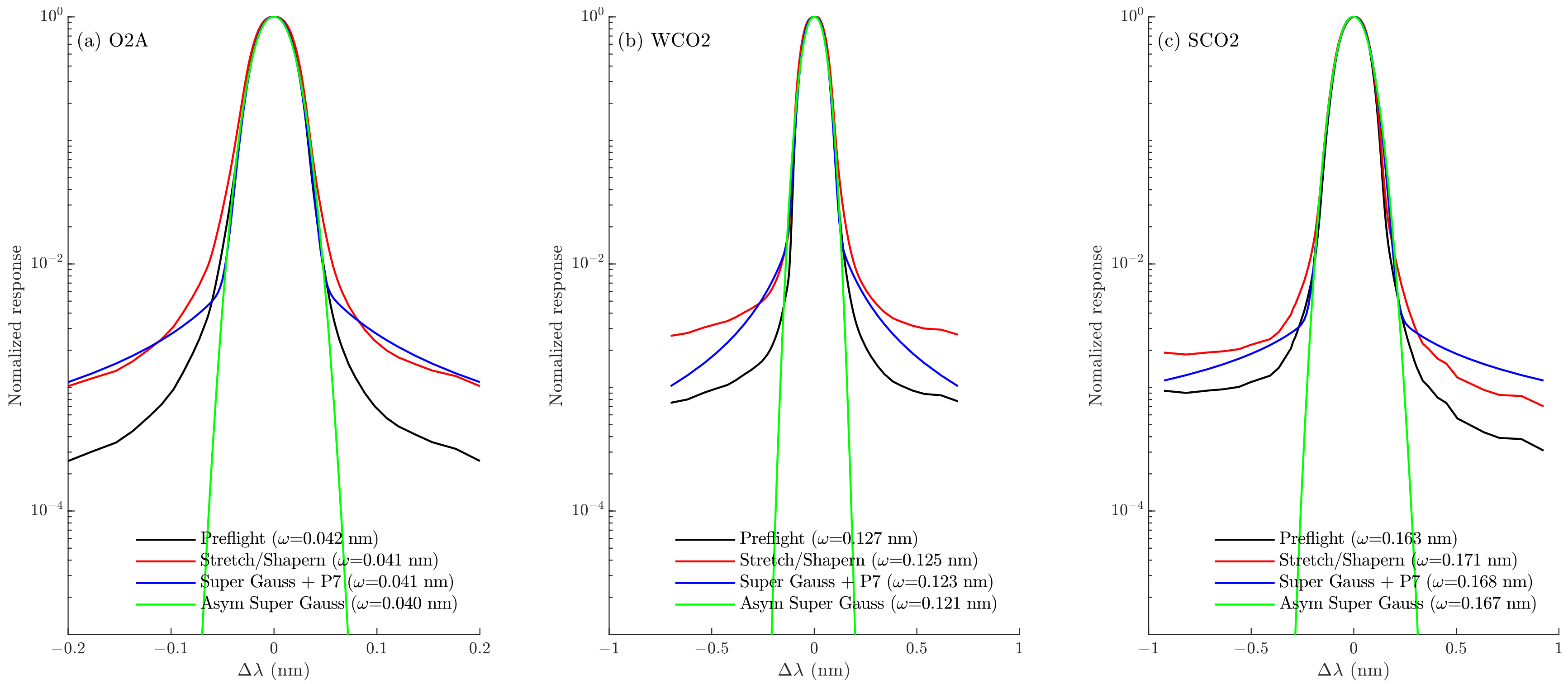
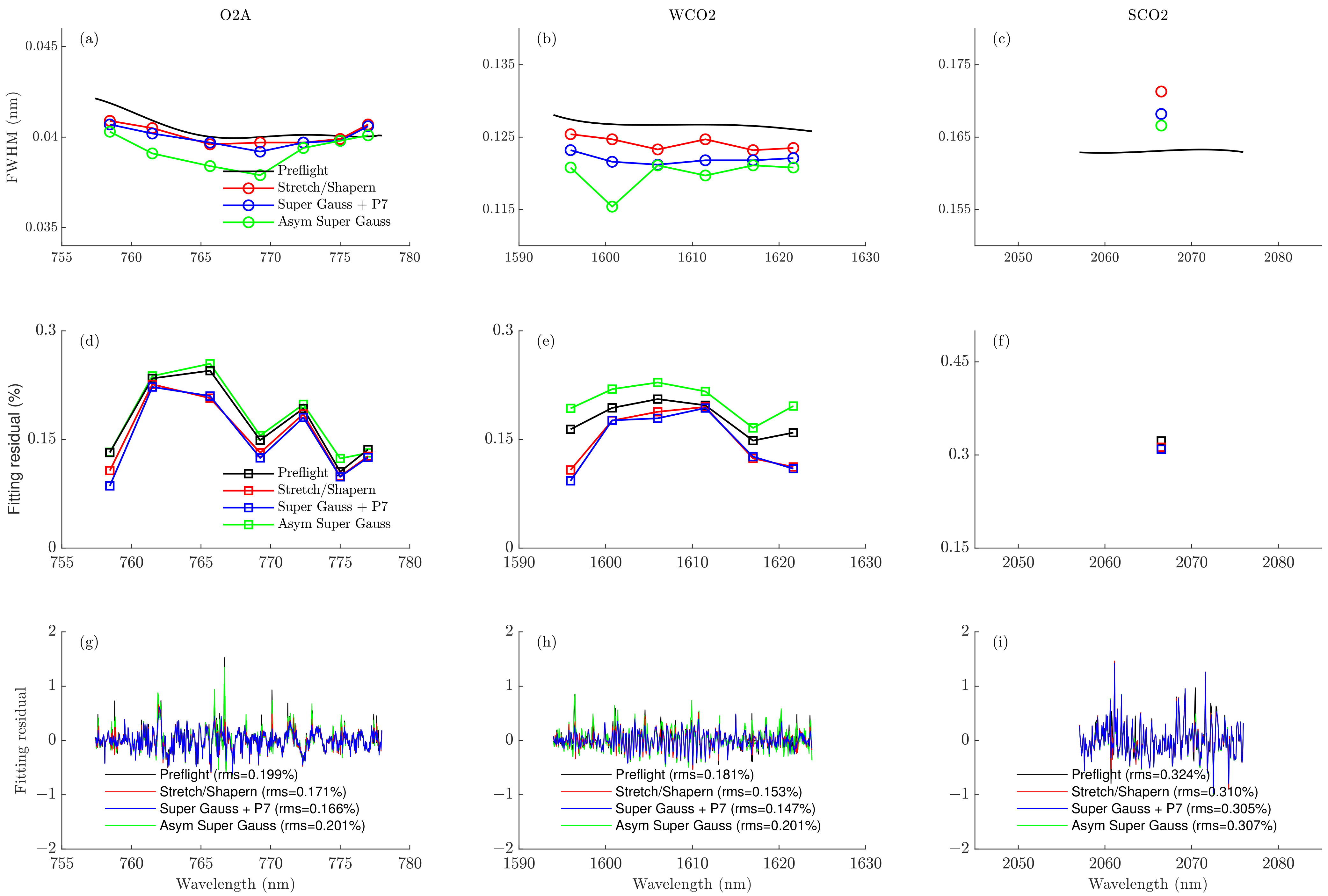
3.1. Spectral Variation in ILS
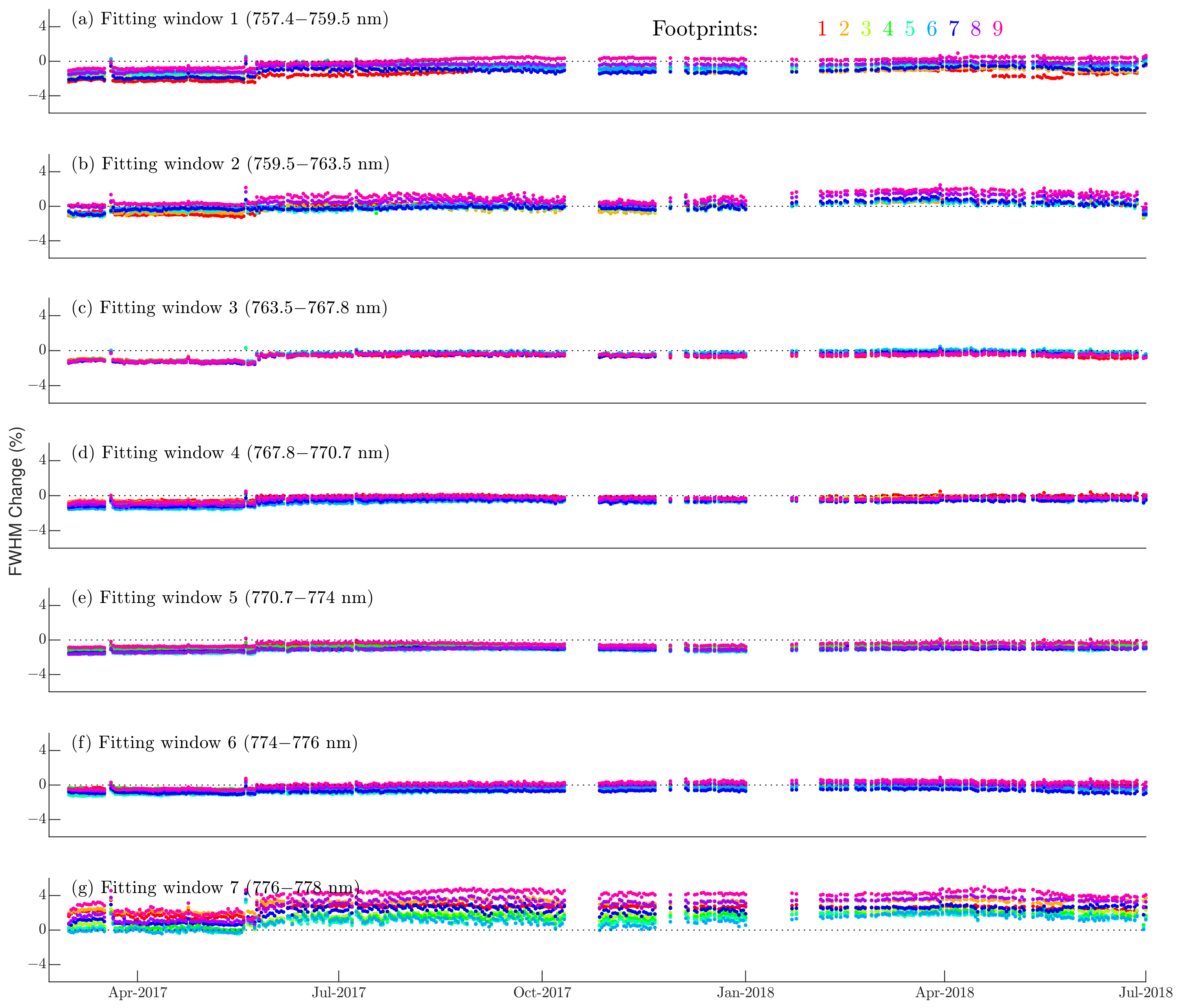
3.2. Temporal Variation in On-Orbit TanSat ILS
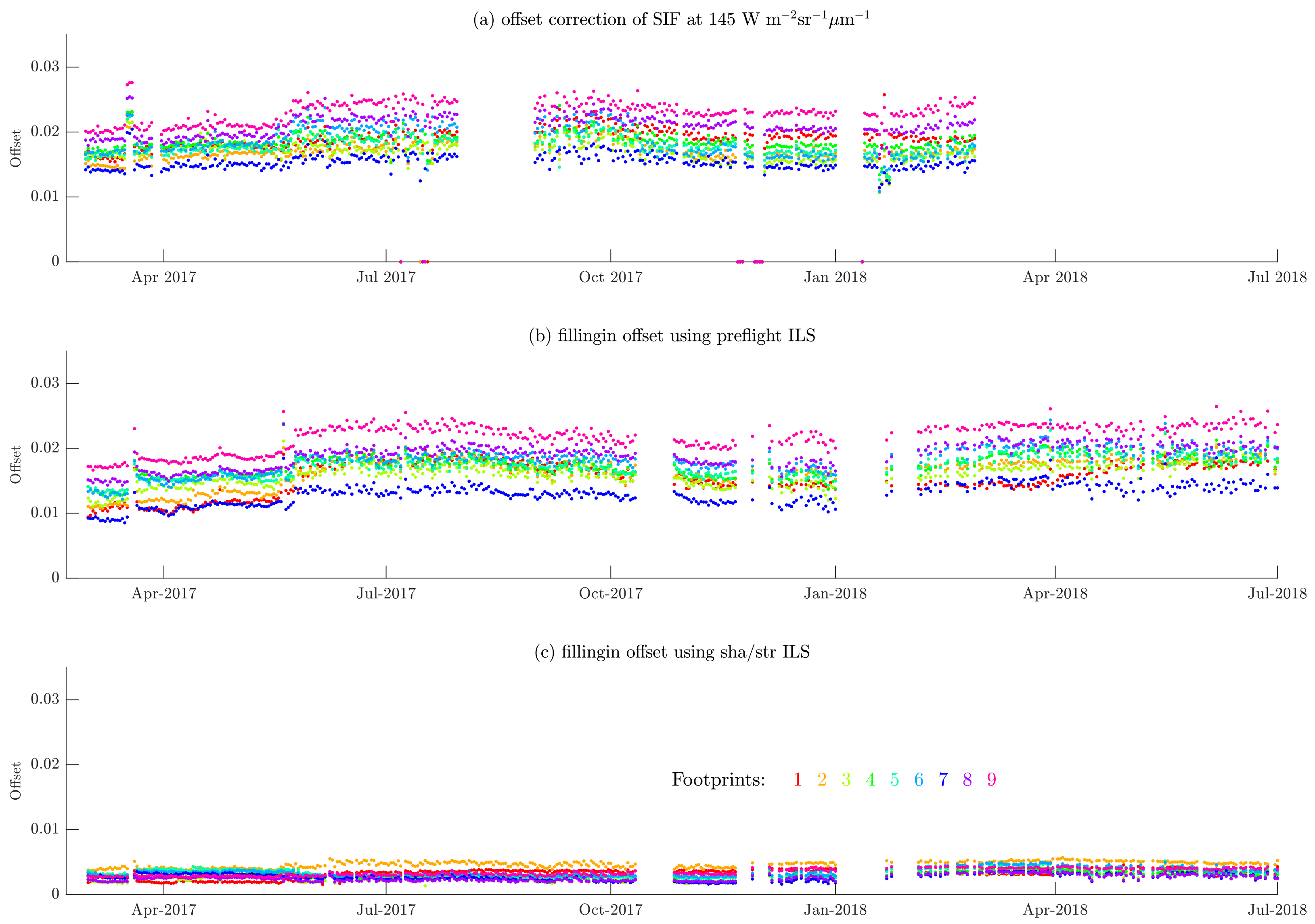
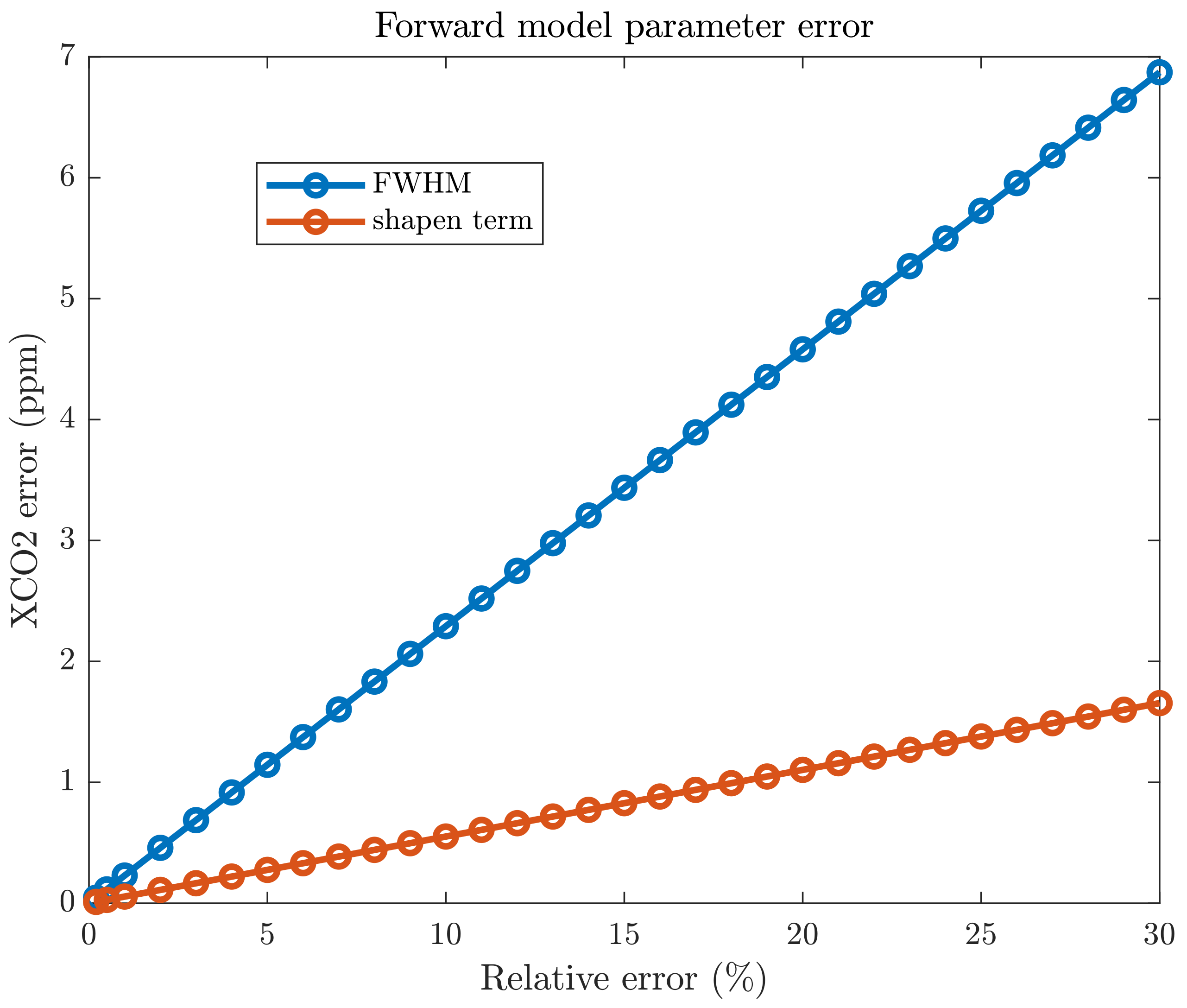
4. Effects of ILS on SIF and XCO2 Retrieval
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Y.; Wang, J.; Yao, L.; Chen, X.; Cai, Z.; Yang, D.; Yin, Z.; Gu, S.; Tian, L.; Lu, N.; et al. The TanSat mission: Preliminary global observations. Sci. Bull. 2018, 63, 1200–1207. [Google Scholar] [CrossRef] [Green Version]
- Crisp, D.; Pollock, H.R.; Rosenberg, R.; Chapsky, L.; Lee, R.A.M.; Oyafuso, F.A.; Frankenberg, C.; O’Dell, C.W.; Bruegge, C.J.; Doran, G.B.; et al. The on-orbit performance of the Orbiting Carbon Observatory-2 (OCO-2) instrument and its radiometrically calibrated products. Atmos. Meas. Tech. 2017, 10, 59–81. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Liu, Y.; Yang, D. Analysis of XCO2 retrieval sensitivity using simulated Chinese Carbon Satellite (TanSat) measurements. Sci. China Earth Sci. 2014, 57, 1919–1928. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Liu, Y.; Xu, X.; Cai, Z.; Yang, D.; Yan, C.X.; Feng, L. Angular dependence of aerosol information content in CAPI/TanSat observation over land: Effect of polarization and synergy with A-train satellites. Remote Sens. Environ. 2017, 196, 163–177. [Google Scholar] [CrossRef]
- Yang, Z.; Zhen, Y.; Yin, Z.; Lin, C.; Bi, Y.; Liu, W.; Wang, Q.; Wang, L.; Gu, S.; Tian, L. Prelaunch radiometric calibration of the tan sat atmospheric carbon dioxide grating spectrometer. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4225–4233. [Google Scholar] [CrossRef]
- Li, Z.; Lin, C.; Li, C.; Wang, L.; Ji, Z.; Xue, H.; Wei, Y.; Gong, C.; Gao, M.; Liu, L.; et al. Prelaunch spectral calibration of a carbon dioxide spectrometer. Meas. Sci. Technol. 2017, 28, 065801. [Google Scholar] [CrossRef]
- Hu, H.; Hasekamp, O.; Butz, A.; Galli, A.; Landgraf, J.; de Brugh, J.A.; Borsdorff, T.; Scheepmaker, R.; Aben, I. The operational methane retrieval algorithm for TROPOMI. Atmos. Meas. Tech. 2016, 9, 5423–5440. [Google Scholar] [CrossRef] [Green Version]
- Day, J.O.; O’Dell, C.W.; Pollock, R.; Bruegge, C.J.; Rider, D.; Crisp, D.; Miller, C.E. Preflight Spectral Calibration of the Orbiting Carbon Observatory. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2793–2801. [Google Scholar] [CrossRef]
- van Hees, R.M.; Tol, P.J.J.; Cadot, S.; Krijger, M.; Persijn, S.T.; van Kempen, T.A.; Snel, R.; Aben, I.; Hoogeveen, R.W. Determination of the TROPOMI-SWIR instrument spectral response function. Atmos. Meas. Tech. 2018, 11, 3917–3933. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Boesch, H.; Liu, Y.; Somkuti, P.; Cai, Z.; Chen, X.; Di Noia, A.; Lin, C.; Lu, N.; Lyu, D.; et al. Toward High Precision XCO2 Retrievals From TanSat Observations: Retrieval Improvement and Validation Against TCCON Measurements. J. Geophys. Res. Atmos. 2020, 125, e2020JD032794. [Google Scholar] [CrossRef]
- Wang, S.; van der A, R.J.; Piet, S.; Weihe, W.; Peng, Z.; Naimeng, L.; Fang, L. Carbon Dioxide Retrieval from TanSat Observations and Validation with TCCON Measurements. Remote Sens. 2020, 12, 2204. [Google Scholar] [CrossRef]
- Hong, X.; Zhang, P.; Bi, Y.; Liu, C.; Sun, Y.; Wang, W.; Chen, Z.; Hao, Y.; Zhang, C.; Tian, Y.; et al. Retrieval of Global Carbon Dioxide From TanSat Satellite and Comprehensive Validation With TCCON Measurements and Satellite Observations. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Sun, K.; Liu, X.; Nowlan, C.; Cai, Z.; Chance, K.; Frankenberg, C.; Lee, R.; Pollock, R.; Rosenberg, R.; Crisp, D. Characterization of the OCO-2 instrument line shape functions using on-orbit solar measurements. Atmos. Meas. Tech. 2017, 10, 939–953. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Chance, K.; Kurosu, T.P. Improved ozone profile retrievals from GOME data with degradation correction in reflectance. Atmos. Chem. Phys. 2007, 7, 1575–1583. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Liu, Y.; Liu, X.; Chance, K.; Nowlan, C.; Lang, R.; Munro, R.; Suleiman, R. Characterization and correction of global ozone monitoring experiment 2 ultraviolet measurements and application to ozone profile retrievals. J. Geophys. Res. Atmos. 2012, 117, D07305. [Google Scholar] [CrossRef]
- Yao, L.; Yang, D.; Liu, Y.; Wang, J.; Liu, L.; Du, S.; Cai, Z.; Lu, N.; Lu, D.; Wang, M.; et al. A New Global Solar-induced Chlorophyll Fluorescence (SIF) Data Product from TanSat Measurements. Adv. Atmos. Sci. 2021, 38, 341–345. [Google Scholar] [CrossRef]
- Frankenberg, C.; Pollock, R.; Lee, R.A.M.; Rosenberg, R.; Blavier, J.F.; Crisp, D.; O’Dell, C.W.; Osterman, G.B.; Roehl, C.; Wennberg, P.O.; et al. The Orbiting Carbon Observatory (OCO-2): Spectrometer performance evaluation using pre-launch direct sun measurements. Atmos. Meas. Tech. 2015, 8, 301–313. [Google Scholar] [CrossRef] [Green Version]
- Toon, G.C. Solar line list for GGG2014, hosted by the carbon dioxide information analysis center. Inf. Anal. Cent. 2014. [Google Scholar] [CrossRef]
- Boesch, H.; Brown, L.; Castano, R.; Christi, M.; Crisp, D.; Eldering, A.; Fisher, B.; Frankenberg, C.; Gunson, M.; Granat, R.; et al. Orbiting Carbon Observatory (OCO)-2 Level 2 Full Physics Algorithm Theoretical Basis Document 2015. Available online: https://disc.gsfc.nasa.gov/OCO-2/documentation/oco-2-v6/OCO2_L2_ATBD.V6.pdf (accessed on 3 December 2015).
- Coddington, O.M.; Richard, E.C.; Harber, D.; Pilewskie, P.; Woods, T.N.; Chance, K.; Liu, X.; Sun, K. The TSIS-1 Hybrid Solar Reference Spectrum. Geophys. Res. Lett. 2021, 48, e2020GL091709. [Google Scholar] [CrossRef]
- Chance, K.; Kurosu, T.P.; Sioris, C.E. Undersampling correction for array detector-based satellite spectrometers. Appl. Opt. 2005, 44, 1296–1304. [Google Scholar] [CrossRef] [Green Version]
- Frankenberg, C.; Butz, A.; Toon, G. Disentangling chlorophyll fluorescence from atmospheric scattering effects in O2 A-band spectra of reflected sun-light. Geophys. Res. Lett. 2011, 38, L03801. [Google Scholar] [CrossRef]
- Spurr, R.J. VLIDORT: A linearized pseudo-spherical vector discrete ordinate radiative transfer code for forward model and retrieval studies in multilayer multiple scattering media. J. Quant. Spectrosc. Radiat. Transf. 2006, 102, 316–342. [Google Scholar] [CrossRef]
- Bak, J.; Liu, X.; Sun, K.; Chance, K.; Kim, J.H. Linearization of the effect of slit function changes for improving Ozone Monitoring Instrument ozone profile retrievals. Atmos. Meas. Tech. 2019, 12, 3777–3788. [Google Scholar] [CrossRef] [Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Z.; Sun, K.; Yang, D.; Liu, Y.; Yao, L.; Lin, C.; Liu, X. On-Orbit Characterization of TanSat Instrument Line Shape Using Observed Solar Spectra. Remote Sens. 2022, 14, 3334. https://doi.org/10.3390/rs14143334
Cai Z, Sun K, Yang D, Liu Y, Yao L, Lin C, Liu X. On-Orbit Characterization of TanSat Instrument Line Shape Using Observed Solar Spectra. Remote Sensing. 2022; 14(14):3334. https://doi.org/10.3390/rs14143334
Chicago/Turabian StyleCai, Zhaonan, Kang Sun, Dongxu Yang, Yi Liu, Lu Yao, Chao Lin, and Xiong Liu. 2022. "On-Orbit Characterization of TanSat Instrument Line Shape Using Observed Solar Spectra" Remote Sensing 14, no. 14: 3334. https://doi.org/10.3390/rs14143334





