Modeling Mean Radiant Temperature Distribution in Urban Landscapes Using DART

Abstract

The microclimatic conditions of the urban environment influence significantly the thermal comfort of human beings. One of the main human biometeorology parameters of thermal comfort is the Mean Radiant Temperature (Tmrt), which quantifies effective radiative flux reaching a human body. Simulation tools have proven useful to analyze the radiative behavior of an urban space and its impact on the inhabitants. We present a new method to produce detailed modeling of Tmrt spatial distribution using the 3-D Discrete Anisotropic Radiation Transfer model (DART). Our approach is capable to simulate Tmrt at different scales and under a range of parameters including the urban pattern, surface material of ground, walls, roofs, and properties of the vegetation (coverage, shape, spectral signature, Leaf Area Index and Leaf Area Density). The main advantages of our method are found in (1) the fine treatment of radiation in both short-wave and long-wave domains, (2) detailed specification of optical properties of urban surface materials and of vegetation, (3) precise representation of the vegetation component, and (4) capability to assimilate 3-D inputs derived from multisource remote sensing data. We illustrate and provide a first evaluation of the method in Singapore, a tropical city experiencing strong Urban Heat Island effect (UHI) and seeking to enhance the outdoor thermal comfort. The comparison between DART modelled and field estimated Tmrt shows good agreement in our study site under clear-sky condition over a time period from 10:00 to 19:00 (R² = 0.9697, RMSE = 3.3249). The use of a 3-D radiative transfer model shows promising capability to study urban microclimate and outdoor thermal comfort with increasing landscape details, and to build linkage to remote sensing data. Our methodology has the potential to contribute towards optimizing climate-sensitive urban design when combined with the appropriate tools.

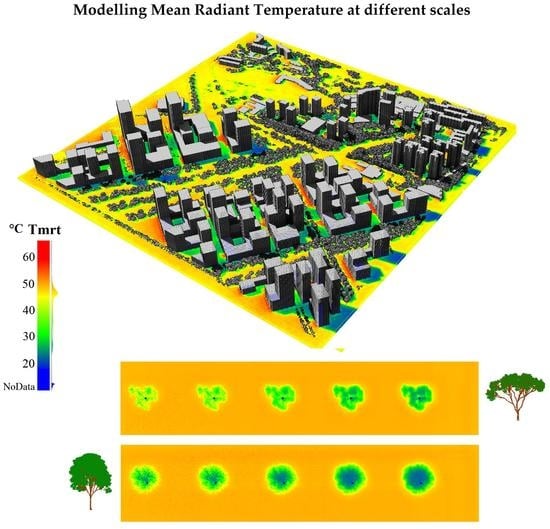
1. Introduction

The increased number of heat waves due to global climate change experienced in growing urban areas across the world directly and indirectly affects thermal comfort and health of urban residents, particularly in the tropics. The environmental factors controlling outdoor thermal comfort are the Mean Radiant Temperature (Tmrt), wind speed, air temperature, and humidity [1]. Outdoor thermal comfort and heat related mortality are more influenced by the Tmrt and less by the other three factors [2]. Tmrt is considered an essential bio-meteorological variable having a strong influence on thermal comfort indices such as the Physiological Equivalent Temperature (PET) [3], Predicted Mean Vote (PMV) [1], Universal Thermal Climate Index (UTCI) [4], the Perceived Temperature (PT) [5], and Global Outdoor Comfort Index (GOCI) [6]. A comprehensive review of thermal comfort studies in urban spaces can be found in Lai et al. 2020 [7].

In solar exposure conditions, the energy loss or gain by radiation is the most important heat flux in the energy balance; followed by convective fluxes of sensible and latent heat and at last, the conductive heat flux [8]. The concept of Tmrt is based on the fact that the net exchange of radiant energy between two objects is approximately proportional to their temperature difference multiplied by their ability to emit and absorb heat [1]. This is valid as long as the absolute temperatures of objects in question are large compared to the temperature differences, allowing linearization of the Stefan–Boltzmann Law in the relevant temperature range [9,10]. Different city structures in the same thermal region differ mainly in their radiation temperatures [11]. This is due to the geometrical complexity of buildings, their surface radiative properties and their wavelength dependency. These properties play an important role in the radiation exchange and therefore, on its modelling. Numerical tools such as Rayman [9], ENVI-met [12], SOLWEIG [13], TUF-3D [14], CityComfort+ [15], and VTUF 3D [16] are increasingly being used by planners and architects to assess the bio-meteorological performance of urban scenarios. Such tools vary in terms of dimensionality, i.e., 1-D/3-D, accuracy in predicting the radiation fluxes, consideration of surface material properties, distribution of surface temperatures, physical representation of the vegetation, scale of analysis, speed of computation, and capability to assimilate remote sensing data as input for simulations.

Remote sensing technologies have great potential to study the thermal behavior of cities in space and time [17], particularly when combining information of urban surfaces and their spectral characteristics using physically-based radiative transfer models (RTMs). Recent studies have successfully combined a variety of remotely acquired data with RTMs to derive urban surface properties (albedo and temperature), energy fluxes, and Tmrt [18,19,20,21,22,23]. These studies highlight an increasing demand for advanced tools capable of 3-D analysis of detailed urban data including the vegetation. RTMs used in the field of remote sensing were developed to compute accurate canopy spectral radiance, to invert and evaluate existing data, and for the configuration of future satellite missions [24]. Only a few RTMs simultaneously simulate the canopy spectral radiance and the canopy 3-D radiative budget (RB). To our knowledge, advanced physically-based RTM models have not been fully employed for modelling Tmrt. Therefore, this study seeks to (1) exploit the advanced capabilities of a physically-based 3-D RTM for the estimation of Tmrt of complex urban scenes, and (2) introduce its use for a broader application by planners and urban climate scientists.

In this study we propose a new method for detailed 3-D modelling of Tmrt in complex urban scenes by improving the radiative budget module of the Discrete Anisotropic Radiation Transfer model DART [25]. The characteristics that make DART a powerful tool to model radiation are summarized hereafter. (1) DART considers the full spectral domain from ultraviolet to thermal infrared in solar/atmosphere radiation and optical properties. Therefore, it provides more accurate results than models that consider that radiation only belongs to two spectral domains (i.e., short and long wave domains) and/or that the canopy optical property is only defined by its albedo and emissivity. (2) DART considers all types of surface optical properties, including spectral reflectance, transmittance, and absorbance; spectral emissivity of opaque material is equal to one minus spectral reflectance of this material. Surface reflectance can be isotropic (Lambertian) or anisotropic using Fresnel equations or predefined bidirectional reflectance distribution function, which allows DART to consider any material. (3) DART can simulate vegetation either as a set of facet-like leaves with specific locations, orientations, and optical properties, or as a 3-D distribution of turbid medium (i.e., infinite number of infinitely small plane elements) defined by specific clumping, leaf angle distribution, Leaf Area Index (LAI)/Leaf Area Density (LAD), and optical properties. Therefore, DART simulates light propagation below trees conversely to models that represent trees as opaque volumes. The turbid representation of vegetation is adopted in this work. (4) DART simulates 3-D multiple scattering within vegetation and between vegetation and other materials (e.g., walls). This is very important in presence of high reflectance scene elements (e.g., green vegetation in the near infrared domain), and also to simulate the grey body (emissivity less than one) in long wave domain. (5) In addition to the radiative budget of canopies, DART simulates their remote sensing signal [21,24,26]. DART is considered one of the most advanced 3-D RTMS and that it has been positively evaluated in the framework of the Radiative transfer inter-comparison project (RAMI) [27,28].

Our methodology for modelling Tmrt can be applied at different scales and under a range of parameters including the urban pattern, surface material of ground, walls, roofs, and vegetation properties (coverage, shape, spectral properties, Leaf Area Index, and Leaf Area Density). Three dimensional scenes can be generated from multi-source remote sensing data as shown on our previous study on 3-D Reconstruction of urban landscapes from satellite data, where a detailed workflow for the derivation of 3-D urban scenes was presented, together with an evaluation of 3-D radiative budget over different urban typologies found in Singapore [21]; additionally, scenes can be generated from Aerial LiDAR Scanning (ALS) point cloud data [29] or using 3-D modelling software. Depending on the desired scale of analysis, vegetation turbid plots (i.e., volume of turbid material) can be generated from satellite data [21], from ALS point clouds [29] or using realistic 3-D models. Moreover, vegetation properties (e.g., LAI/LAD) can be retrieved from terrestrial laser scanning data (TLS) at plant scale [30,31], from ALS [32,33] at neighborhood scale or from other remote sensing systems. Finally, the spatial distribution of vegetation can be modelled from hybrid point cloud data [29]. Information on suggested data sources for scene creation can be found in

Table A1. Remote Sensing Inputs, Level of Detail and Recommeded Scene Settings for Simulation.

Data Source	Scale of Study	LOD Buildings	LOD Vegetation	Scene Dimensions	Cell Size (x,y)	Cell Size (z)	Reference
VHR satellite imagery	Town	1.1–1.2	location, approx. height and volume (cube)	1000 m * 1000 m	2 m–5 m	1 m or 2 m	i.e. Dissegna et al. 2019
(WorldView2)	Neighbourhood	1.1–1.2		500 m * 500 m	1 m–2 m	1 m
Aerial LiDAR Scanning	Town	2	location, accurate height and volume (rounded)	1000 m * 1000 m	2 m–5 m	1 m or 2 m	i.e. Urech et al. 2020
	Neighbourhood	2.1		500 m * 500 m	1 m–2 m	1 m
	Building	2.1		<100 m * 100 m	0.5 m–1 m	0.5 m–1 m
3-D Objects of architectural designs	Neighbourhood	2	location, accurate height and volume (rounded)	500 m * 500 m	1 m–2 m	1 m	Created with any 3-D modelling software
	Building	3.1	n/a	<100 m * 100 m	0.5 m–1 m	0.5 m–1 m
	Tree	n/a	Explicit shape	50 m * 50 m	0.25 m–0.5 m	0.25 m–0.5 m	Laubwerk
Hybrid ALS/3-D designs	Town	1.1–1.2	location, accurate height and volume (rounded)	1000 m * 1000 m	2 m–5 m	1 m or 2 m	i.e. Urech et al. 2020
	Neighbourhood	up to 1.3		500 m * 500 m	1 m–2 m	1 m
	Building	up to 3.2		<100 m * 100 m	0.5 m–1 m	0.5 m–1 m

Remarks: regardless on the source, the different surface materials have to be grouped in order to be linked to their respective spectral properties found within the DART database. For more information on LOD visit: https://osmbuildings.org/blog/2018-02-28_level_of_detail/ accessed on 31 January 2021.

and

Table A3. Characteristics of Remote Sensing Inputs.

Remote Sensing Products	Provider	Characteristics	Reference
WorldView2 imagery	Digital Globe	Ten high-resolution WorldView2 images (8-band, 2 m pixel size). Used to derive land cover map.	Dissegna et al. 2019
Building footprint data	Openstreetmap
Digital surface model (DSM)	AW3D	Derived from photogrammetric reconstruction of Digital Globe stereo satellite images. Nominal resolution of the DSM dataset is 1m for the urban areas and 5m for the densely vegetated area. Used to derive a digital terrain model (DTM), buildings and vegetation heights.
2014 Aerial LiDAR of Singapore	Singapore Land Authority	Obtained using the Optech Pegasus HA500 sensor with a planar density of 30 points/m².	Urech et al. 2020
Terrestrial LiDAR Scanning (TLS)	SEC/SMART field campaign	Field measurements of leaf area density derived from TLS pointcloud collected using Leica P40 sensor.	Wei et al. 2020

.

We illustrate our approach in Singapore, a city experiencing strong UHI and seeking to enhance outdoor thermal comfort. We present a field comparison and perform a sensitivity analysis to examine how building materials and vegetation properties influence Tmrt. Then, we discuss limitations of our approach, possible areas of improvement and future research directions.

2. Materials and Methods

2.1. Scene Generation and Parameter Setting

A 3-D model of the Tanjong Pagar District, Singapore, was reconstructed. The building height, vegetation shape, and distribution was obtained from the Aerial LiDAR Scanning dataset of Singapore [34]. This dataset was acquired by the Optech Pegasus HA500 sensor with a planar density of about 30 points/m² which proved to be well adapted to map vegetation. The buildings were reconstructed using 3DsMax software, obtaining a Level of Detail (LOD) of 1.2. The north part of the scene corresponds to the existing urban setting, whereas its southern part (former Tanjong Pagar Port) corresponds to a design proposal with a high-density urban form [29]. The scene elements were grouped by surface material, allowing them to be linked to their respective surface temperatures and optical spectral properties in the DART database. All trees were assumed to have the same LAI value of 1.5 (single-side leaf area divided by the tree projection area). This value falls within the range of measured LAI of urban trees found in Singapore [35]. Surface temperature is an essential term for simulations in the longwave domain. It can be derived from field observations of a calibrated thermal camera [36] or from an energy balance model, i.e., DART EB. It is provided as an input to DART either as thermal functions (i.e., mean and standard deviation of hourly modelled temperatures) or as a 3-D temperature distribution. DART uses these thermal functions to distribute the temperature values over the scene using a virtual sun illumination of the scene: the most irradiated surfaces are given the highest temperature values. In our study, the mean and standard deviation of hourly surface temperatures were estimated using the Urban Eco-hydrological model UT&C [37]. UT&C is a fully coupled energy and water balance model which accounts for the biophysical and eco-physiological characteristics of urban trees. UT&C is a 1D model, providing as output the mean and standard deviations of surface temperatures of impervious roof, impervious ground, ground covered with grass, tree, sunlit wall, and shaded wall for each of the parametrized areas of interest. Our study area was classified in urban “typologies” to extract the neighborhood parameters such as building height, height to width ratio and fraction of vegetation. The model requires meteorological data of incoming shortwave and longwave radiation, rainfall, pressure, wind speed, air temperature, and humidity at forcing height above the urban canyon. The model was run over the time period from 1 May 2013 to 30 April 2014. The mean and standard deviation of the temperatures were obtained considering all the hours with a cloudiness of less than 50% with the aim to approximate the average conditions on rather sunny days in Singapore. Information on the values such as volumetric heat capacity and thermal conductivity are reported in the supplementary information on the UT&C model development document [37].

2.2. Mean Radiant Temperature Computation

To compute the Tmrt of Tanjong Pagar District, we carried out two sets of DART radiative budget simulations, one in the shortwave domain (0.3–2.5 μm) and one in the longwave domain (3–50 μm). Simulations were run at a resolution of 2 m horizontally and 1 m vertically. The use of “repetitive scene mode” in the longwave domain reduces the computation time without producing substantial differences on the resulting radiative budget. However, in the shortwave domain, the use of repetitive scene mode would cause the emergence of shadows which do not correspond to the reality. Therefore, we used “isolated scene mode” when running simulations in the shortwave domain. During the simulation process, DART converts the scene into voxels at a defined dimension. These voxels contain information on the material reflectance, surface temperature, and additional properties such as LAI/LAD for the case of turbid vegetation plots. DART stores the resulting radiation that has entered each voxel. The previous versions of DART did not compute the radiative budget on empty cells; therefore, it was not suitable for estimating and mapping Tmrt. The recently improved releases of DART’s radiative budget 3-D allow one to store separately the direct, diffuse, and emitted irradiance reaching each and every voxel of the scene from six directions (N-S, E-W, and Upwelling–Downwelling). This allows to virtually transform the voxels into equivalent cylinders [38] on which the absorption coefficient of the human surface to solar radiation (1 − α) and emissivity of clothed body (ε) can be considered and be varied at the Tmrt computation stage. In the short waves (i.e., solar radiation), the absorption coefficient of the skin (1 − α) ranges between 0.55 and 0.85 depending on the skin color [39]. In the long waves (i.e., terrestrial radiation), the emissivity of the human skin is assumed to be 0.99 and 0.95 for normal clothing surfaces [40]. The complete list of the simulation parameters can be found in

Table A4. DART Parameters for Longwave Simulations.

Flux-tracking
		Radiation-Radiative method	Flux Tracking
		Atmosphere radiative transfer TOA<->BOA	Radiative transfer simulation
Flux tracking parameters			Sparse voxel acceleration: NO
Products			Radiation budget products only
Spectral interval	Spectral band	Longwave	Central Wavelength 25, Bandwidth 50
Products
	Radiative	…	3D INTR, ABS, SCAR
	Budget	Radiative budget unit	W/m2
		Radiative budget components	Irradiance—Six directions
		Scene element components
Direction input parameters
		Sun angles or date	Exact date
		Year	20xx
		Month	xx
		Day	xx
		Hours	* To be set in sequence launcher tool
		Local time	yes
		Time Zone (UTC)	8 (For Singapore)
Optical and temperatures properties
Lambertian	Building walls	Property name	Building walls
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	Sand white
Lambertian	Glass	Property name	Glass
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	glass_window
Lambertian	Aluminium Roof	Property name	Aluminium roof
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	aluminium_window
Lambertian	Badminton Court	Property name	Badminton Court
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	concrete_brown
Lambertian	Stem	Property name	Stem
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	Bark_deciduous
Lambertian	Grass	Property name	Grass
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	Grass_rye
Vegetation	Tree leaf	Vegetation property name	Tree leaf
		3D vegetation database	Lambertian_Vegetation.bd
		3D vegetation model	leaf_deciduous
Temperature	Thermal function	Temperature (Mean and Delta)	Hourly mean and deltas obtained from energy balance model for each scene component (Table A6).
Atmosphere
		Gas optical properties	Tropical
		Gas temperature profile	Tropical
		Gas O3 and other gases vertical profile	Tropical
		Redefine temperature profile	✓
		Altitude	1.5 m
		Temperature [K]	Specific temperature at each time step (Table A6)
Aerosol	Aerosol properties	Aerosol optical properties	Tropical_urbav5
		Aerosol vertical profile	Urbanv5
		Aerosol Henyey Greenstein parameters	Urbanv5

and

Table A5. DART Parameters for Shortwave Simulations.

Flux-Tracking
		Radiation-Radiative method	Flux Tracking
		Atmosphere radiative transfer TOA<->BOA	Analytic model
Flux-tracking parameters			Sparse voxel acceleration: NO
Products			Radiation budget products only
Spectral interval	Spectral band	Shortwave	Central Wavelength 1.4, Bandwidth 2.2
Products
	Radiative Budget	…	3D INTR, ABS, SCAR
		Radiative budget unit	W/m2
		Radiative budget components	Irradiance—Six directions
		Scene element components
Direction input parameters
		Sun angles or date	Exact date
		Year	20xx
		Month	xx
		Day	xx
		Hours	* To be set in sequence launcher tool
		Local time	yes
		Time Zone (UTC)	8 (For Singapore)
Optical and temperatures properties
Lambertian	Building walls	Property name	Building walls
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	Sand white
Lambertian	Glass	Property name	Glass
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	glass_window
Lambertian	Aluminium Roof	Property name	Aluminium roof
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	aluminium_window
Lambertian	Badminton Court	Property name	Badminton Court
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	concrete_brown
Lambertian	Stem	Property name	Stem
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	Bark_deciduous
Lambertian	Grass	Property name	Grass
		2D lambertian database	Lambertian_mineral.db
		2D lambertian model	Grass_rye
Vegetation	Tree leaf	Vegetation property name	Tree leaf
		3D vegetation database	Lambertian_Vegetation.bd
		3D vegetation model	leaf_deciduous
Temperature	Thermal function	Mean temperature	Hourly mean and deltas obtained from energy balance model for each scene component (Table A6).
		Delta temperature
Atmosphere
		Gas optical properties	Tropical
		Gas temperature profile	Tropical
		Gas O3 and other gases vertical profile	Tropical
Aerosol	Aerosol properties
		Aerosol optical properties	Tropical_urbav5
		Aerosol vertical profile	Urbanv5
		Aerosol Henyey Greenstein parameters	Urbanv5
		AOD multiplicative factor	Retrieved from Aeronet for each time step of the simulation date (Table A7).

. The surface temperatures used for each time step are reported in

Table A6. DART Parameters for Longwave Simulations.

	Longwave Sequence Parameters
	Sequence name	seq_0	seq_1	seq_2	seq_3	seq_4	seq_5	seq_6	seq_7	seq_8	seq_9	seq_10	seq_11	seq_12
	Time	7:00	8:00	9:00	10:00	11:00	12:00	13:00	14:00	15:00	16:00	17:00	18:00	19:00
Surface temperatures (K)	Badminton court	299.15	300.65	304.65	309.15	314.15	314.15	315.15	318.15	316.65	313.15	312.15	310.65	307.65
	Delta	0	1	7	14	20	20	22	26	25	18	16	15	11
	Glass windows	299.15	301.15	303.65	306.15	309.15	307.65	307.15	308.15	308.65	309.65	308.65	306.15	303.15
	Delta	0	2	5	8	12	7	4	6	9	11	9	6	0
	Walls	299.15	300.65	302.15	308.15	313.15	312.65	311.15	316.15	316.65	312.65	311.65	310.15	307.65
	Delta	0	1	2	12	18	17	14	22	25	17	15	14	11
	Aluminum roof	299.15	300.65	302.15	303.65	306.15	308.65	311.65	312.15	311.15	310.15	308.15	305.65	302.65
	Delta	0	1	2	3	6	9	13	14	14	12	8	5	1
	Grass	299.15	301.15	304.15	305.15	306.15	307.15	308.15	307.15	307.15	306.15	305.15	304.15	302.15
	Delta	0	2	6	6	6	6	6	6	6	6	4	2	0
	Leaves	299.15	301.15	304.15	305.15	306.15	307.15	308.15	307.15	307.15	306.15	305.15	304.15	302.15
	Delta	0	2	6	6	6	6	6	6	6	6	4	2	0
	Trunk	299.15	301.15	303.15	304.15	306.15	305.15	304.15	304.15	305.15	306.15	305.15	304.15	302.15
	Delta	0	2	4	4	6	4	2	2	4	6	4	2	0
	Air temperature * (K)	299.51	300.06	301.01	301.48	303.5	303.75	304.55	306.28	305.31	305.08	304.58	304.25	303.15

* Measured from a Vaisala weather station mounted next to radiometers.

and

Table A7. DART Parameters for Shortwave Simulations.

Shortwave Sequence Parameters
	Sequence name	seq_0	seq_1	seq_2	seq_3	seq_4	seq_5	seq_6	seq_7	seq_8	seq_9	seq_10	seq_11	seq_12
	Time	7:00	8:00	9:00	10:00	11:00	12:00	13:00	14:00	15:00	16:00	17:00	18:00	19:00
AOD multiplicative factor *		0.171	0.172	0.185	0.192	0.361	0.422	0.337	0.340	0.297	0.211	0.214	0.158	0.185

* Obtained from NASA AERONET for Singapore for simulation date 29 February 2020.

.

The computation of Tmrt is done according to the method proposed by Peter Höppe [41], with further considerations [38]. These include (1) the representation of the human body as a cylinder as opposed to a box, (2) separated treatment of direct and diffuse short-wave radiation as well as for long-wave radiation, (3) consideration of solar elevation and azimuth for every time step. We used a cylinder with the measurements reported in

Table 1. Characteristics of the cylindrical representation of the human body.

Cylinder Dimensions
Diameter:	0.28 m
Height:	1 m
Total area:	1 m2
roof area:	0.06 m2
wall area:	0.88 m2
Area of frontal view:	0.28 m × 1 m = 0.28 m2
Surface fraction wi Cylroof:	0.0616 m2/1 m2 = 0.0616
Surface fraction wi Cylwall:	0.28 m2/1 m2 = 0.28

to derive the surface fractions w_{i Cylroof} = 0.0616 and w_iCylwall = 0.28, respectively. The cylindrical representation of the human body is centered at a height of 1.5 m from the ground.

The mean radiant flux (Sstr) reaching a rotationally symmetrical (cylindrical) representation of the human body is computed at a specified layer height using Equation (1).

$$\mathrm{Sstr},\mathrm{cyl}=\left(1-\mathsf{\alpha }\right)·\left[w_{\mathrm{Cylwall}}·{\displaystyle \sum }_{1-4}{\mathrm{K}}_{\mathrm{dir},\mathrm{hor}}+w_{\mathrm{Cylroof}}·\left({\mathrm{K}}_{\uparrow \mathrm{dir}}+{\mathrm{K}}_{\downarrow \mathrm{dir}}+{\mathrm{K}}_{\uparrow \mathrm{diff}}+{\mathrm{K}}_{\downarrow \mathrm{diff}}\right)+{\displaystyle \sum }_{1-4}{\mathrm{K}}_{\mathrm{diff},\mathrm{hor}}·w_{\mathrm{Cylwall}}\right]+ \mathsf{\epsilon }·{\displaystyle \sum }_{1-6 }{w}_{\mathrm{i}}·L_{\mathrm{i}}$$

(1)

where

• α is Albedo of clothed human body (0.37)
• K_dir, _hor is Horizontal direct shortwave radiation (KE, KS, KW, KN)
• K_↑dir, K_↓dir is Vertical direct shortwave radiation
• K_↑diff, K_↓diff is Vertical diffuse shortwave radiation
• K_diff,hor is Horizontal diffuse shortwave radiation (KE, KS, KW, KN)
• ε is Emissivity of clothed human body (0.97)
• w_i is Surface fractions of the standing “cylinder man” (w_Cylwall = 0.28 and w_Cylroof = 0.0616)
• L_i is Longwave radiation

The mean radiation temperature Tmrt [°C] results from the Stefan–Boltzmann law using Equation (2).

$$\mathrm{Tmrt}=\sqrt[4]{\frac{{\mathrm{S}}_{\mathrm{str},\mathrm{cyl}}}{\mathsf{\epsilon }·\mathsf{\sigma }}}-273.15$$

(2)

where

• Ss_{tr, cyl} is the mean radiant flux
• ε is Emissivity of clothed human body
• σ is Stefan–Boltzmann constant 5.670374419 × 10⁻⁸ W·m⁻²·K⁻⁴

2.3. Study Area and Data Collection

Our study area is located in Tanjong Pagar district, Singapore (Figure 1a). Singapore has a tropical humid climate with no distinctive seasons. Near-surface air temperature usually ranges from 23 °C to 32 °C. The “Cantonment Towers” site, a modern social housing compound with a playground surrounded by high-density housing blocks was selected to carry out the field evaluation (Figure 1b). Three net radiometers Kipp and Zonen CNR4 [42] were mounted on a mobile platform at 1.5 m from the ground. The minimum height suggested by manufacturer to avoid interference from the mounting structure to the readings is 1.5 m. Additionally, a Vaisala WXT536 weather station [43] and a Campbell Scientific 152 mm black globe thermometer [44] were mounted on the platform to record wind speed, precipitation, air temperature, and globe temperature, respectively (Figure 1c). Special care was made to keep the tower leveled and oriented with the geodetic north [38]. Figure 1b shows the location of the measurement station in the study site.

A time series composite was generated by collecting observations of the maximum incoming radiation from 20 February 2020 to 2 March 2020 between 9:30 and 19:00 with a time step of one minute. This was done with the aim to approximate the maximum attainable Tmrt values for the site over a day with clear sky Tmrt was estimated using the integral radiation measurement technique [10,41]. Calculations of Sstr,cyl were based on angular factors for a rotationally symmetric standing person using Equation (3).

$$\mathrm{Sstr},\mathrm{cyl}=\left(1-\mathsf{\alpha }\right)·\left[ w_{\mathrm{Cylwall}}·{\displaystyle \sum }{\mathrm{K}}_{\mathrm{dir},\mathrm{tot}}+w_{\mathrm{Cylroof}}·\left({\mathrm{K}}_{\uparrow }+{\mathrm{K}}_{\downarrow }\right)+0.88·{\mathrm{K}}_{\mathrm{diff}}\right]+\mathsf{\epsilon }·{\displaystyle \sum }{w}_{\mathrm{i}}·L_{\mathrm{i}}$$

(3)

where

• K_dir, _tot is Direct and reflected horizontal shortwave radiation (KE, KS, KW, KN)
• K_↑, K_↓ is Vertical shortwave radiation
• K_diff is Diffuse radiation = min (KE, KS, KW, KN)
• ε is Emissivity of clothed human body
• w_i is Surface fractions of the standing cylinder man (w_iCylwall = 0.28 and w_{i Cylroof} = 0.0616)
• L_i is Longwave radiation

Then, the Tmrt is determined using Equation (2).

3. Results

3.1. Modelled Tmrt over Tanjong Pagar, Singapore

The Figure 2 shows the results of Tmrt simulation over the Tanjong Pagar district, Singapore, at 15:00 on 29 February 2020. In sunlit areas, the Tmrt at pedestrian level reaches 68 °C. The highest Tmrt values are observed near the sunlit walls of buildings. Tmrt decreases as the distance to the sun-exposed surfaces increases. Under trees, Tmrt varies between 40 °C and 28 °C. The combined effect of building shade and tree shade results in Tmrt values that are below 28 °C. This suggests a slight underestimation of Tmrt in areas without direct solar radiation.

3.2. Field Evaluation

A smaller subset corresponding to the Cantonment towers was generated for the purpose of field evaluation. Simulations were carried out assuming absence of clouds over the scene and using hourly values of Aerosol Optical Depth (AOD) reported by NASA-AERONET Singapore. They were run at 1m resolution. Then, the values of DART cells with the center 1.5 m above the ground were extracted to compute Tmrt maps at different times of the day (Figure 3). The highest Tmrt values are mostly observed close to the walls that receive direct solar radiation, prominently at 10:00 on the east facing walls and at 16:00 on the west facing walls. Generally, higher Tmrt occurs at 16:00.

The Figure 4 shows the comparison of modelled and field estimated Tmrt. The green line shows the field estimated Tmrt during the sunniest day of the study period, 29 February 2020. The downward peaks indicate reduction of Tmrt due to the passage of clouds over the site. The blue line presents the maximum Tmrt value of each time step obtained from the net radiometers during the entire study period (20 February 2020 to 2 March 2020). The black asterisks indicate the DART-modelled Tmrt for 29 February 2020 assuming clear sky conditions. The results show good agreement between 10:00 and 19:00 h (R² = 0.9697, RMSE = 3.3249) when comparing DART-modelled Tmrt with the maximum Tmrt values reported over the entire study period (blue line). In the morning at 9:00, the modelled Tmrt was overestimated in 19.54 °C. This explained by the fact that the DART simulation for Cantonment towers was run on a small subset of the scene, therefore neglecting the shadows that are casted by buildings outside the scene, particularly at low solar angles. Around 13:00, we observe a slight overestimation of 2.16 °C in the modelled Tmrt. From 17:15 onwards, our measuring site is affected by the shadow cast by buildings within the scene. Tmrt decreases considerably until the sunset just after 19:00. Then, Tmrt is only determined by the longwave radiation fluxes and remains relatively constant throughout the night. From 18:00 to 19:00, in absence of direct solar radiation, we observe an underestimation of 5.55 °C and 6.395 °C respectively on our modelled Tmrt.

3.3. Radiation Fluxes Recorded at the Study Site

The diurnal longwave and shortwave radiation fluxes received from each of the six directions (i.e., North ↔ South, East ↔ West, Up ↔ Down) on 29 February 2020 are illustrated in Figure 5 and Figure 6. In terms of longwave radiation, we observe a steady behavior from the six directions throughout the day ranging between 450 and 600 W/m². The maximum values are observed around 14:00. Before midday, the upwelling and West directions have the strongest signal. After midday, the downwelling direction becomes more prominent.

The downwelling shortwave radiation is the predominant flux with a maximum around 13:00 with 980W/m² and changes considerably during the day. This flux is primarily determined by the sun’s position and sky view factor of the site. The upwelling shortwave is due to the reflection of solar radiation by the ground. It peaks around 13:00 with 120 W/m² with a slight variation during the day. The radiation from the South direction is greater than that from the North, hovering around 250 W/m² at 1:00 p.m. and varying gently throughout the day. This is because Singapore geographically located at 1° North. The downward peaks correspond to the effect of passing clouds over the study site.

3.4. Sensitivity Analysis

A sensitivity analysis was performed to demonstrate (1) how much the variation of a biophysical vegetation property (LAI) impacts on Tmrt, (2) how much does ground surface temperature impacts Tmrt, (3) how do spectral properties of wall material impacts spatially the Tmrt at pedestrian level.

3.4.1. Effect of Variying LAI on Tmrt under the Tree Canopy

Urban trees are an important component that contributes to the urban microclimate because of their potential to attenuate solar radiation, evapotranspiration, and control the wind speed. In tropical humid regions, the cooling effect by trees is caused mainly by the reduction of Tmrt due to shading. The benefits provided by trees are constrained by several factors such as spatial arrangement, type, age, height, phenology, crown shape, characteristics of trunk and twigs, leaf size, LAI, and leaf reflectance. Strategic placement and optimal selection of vegetation are essential to obtain the desired Tmrt attenuation. Biophysical properties of vegetation such as LAI/LAD are required to obtain realistic Tmrt simulations and to assess the differences between species and planting regimes. The effect of varying LAI on the Tmrt under the tree canopy of three common tree species of Singapore namely Albizia Saman, Khaya Senegalensis and Tabebuia Rosea was explored and reported in Appendix E. A scene was created using 3-D models of the tree species, assuming the ground material to be grass. Simulations were run at 13:00 and 16:00 using the respective surface temperatures reported in Table A6. The results show that for the three species, the impact on Tmrt due to increasing LAI is large if LAI is low. The impact decreases when LAI increases, and becomes minimal when LAI is larger than 5.5. Khaya Senegalensis has the highest potential for reducing Tmrt. For instance, with small LAI values (LAI = 0.1), we observed a difference in Tmrt up to 16.19 °C when comparing Khaya Senegalensis against Tabebuia Rosea. This is primarily due to the amount of twigs and branches and their homogeneous distribution throughout the canopy; this implies a reduction of Tmrt even when LAI = 0.

3.4.2. Effect of Surface Temperature on Tmrt for Different Ground Materials

To provide an idea of the effect of surface temperature of different ground materials on Tmrt, we simulated a small scene where the surface temperatures of grass, concrete and three types of asphalt varied between 20 °C and 60 °C. In the case of grass, the range was assumed to be 20 °C to 40 °C This is because a surface temperature of grass higher than 40 °C is unrealistic. The overall response in terms of Tmrt of the studied materials is almost linear to the change in surface temperature. It was observed that light materials tend to give higher Tmrt, due to their higher reflectance. The results of the sensitivity analysis and additional details are reported in Appendix F.

3.4.3. Effect of Spectral Properties of Wall Material on Tmrt

The radiative response of the urban surface materials plays an important role in the radiative budget and thus, on Tmrt and in the overall urban microclimatic conditions. To assess the influence of different wall materials on Tmrt, we recreated a small scene with three buildings of dimensions (L:10 m, W:24 m, H:18 m). The first building has 100% white walls, the second has 66.6% white walls, and 33.3% glass and the third is 100% glass walls. The simulation was run at 16:00 with a cell size (x, y, z) of 1 m. The results indicate values of 79.39 °C, 68.59 °C, and 64.47 °C Tmrt in the first cell adjacent to the respective building. A detailed representation of results together with the surface temperatures assumed for this exercise is reported in Appendix G.

4. Discussion

This work introduced a new method, which uses for the first time the DART model to estimate and map Tmrt at different scales. Our motivation to use the DART model to estimate Tmrt stems from its capability to assimilate a large variety of 3-D data derived from state-of-the-art remote sensing techniques; providing the possibility to better analyze how Tmrt is influenced by vegetation and its biophysical properties, by the optical properties of surface materials, by surface temperature, and also by local atmospheric conditions. The field evaluation indicated good agreement between DART-simulated Tmrt and field estimated Tmrt at the Cantonment towers measurement site. However, a substantial underestimation is observed in areas with absence of solar radiation and in the late afternoon. This might be explained by a number of considerations in which our method is based. Firstly, we assumed clear sky conditions throughout the day. This is valid as long as one seeks to map temperature extremes. However, in a tropical city such as Singapore, the presence of clouds and episodes of rain have a major impact in the actual mean radiant temperature. To give an idea of this, we plotted the field observed Tmrt under different meteorological conditions over the study period in Figure 7. The inclusion of clouds on DART simulations has been recently explored [45]. However, this has not been implemented in our study. Atmospheric conditions such as water content and aerosols are highly variable over the course of a day. They influence the amount of radiation reaching the ground and consequently, Tmrt. However, in the case of Singapore there is not much variation in terms of water content. The annual average of relative humidity is 84.0%. Therefore, we only included real time (local) AOD observations obtained from the NASA AERONET website for each time step simulated.

Secondly, the designation of optical properties was merely based on site inspection and matching with the closest material existing within the DART database, this, however, is a source of uncertainty since the spectral library of DART might not well represent the actual characteristics of the surfaces of our study area. An overview of the spectral signatures of construction materials and vegetation used on our simulations can be found in Appendix D. The correct consideration of optical properties of surface materials play an important role in the radiative budget and thus, on Tmrt. To obtain a more accurate representation of optical properties, spectral signatures could be collected using a spectroradiometer and measuring the emissivity of the surfaces in the actual site. Unfortunately, we did not have access to such equipment. A detailed methodology on the derivation spectral signatures of urban materials through emittance and reflectance spectroscopy can be found in Kotthaus et al. 2014 [46].

Thirdly, the variation of surface temperatures impacts pedestrian Tmrt, particularly in sunny conditions. This is expected since in sun hours the intensity of Tmrt is primarily driven by shortwave radiation. The influence of longwave emission tends to decrease with the distance between the emitting surface and the absorbing human body. The sensitivity analysis to changing the surface material of ground showed that the ground material greatly influences Tmrt. For instance, the maximum difference of Tmrt observed between the five materials was 7.5 °C when surface temperature = 20 °C. This difference decreases to 5 °C if surface temperature equals 60 °C. A possible reason of underestimation in the areas with no direct shortwave radiation is that the surface temperatures obtained from UT&C energy balance model were obtained considering all the hours with a cloudiness of less than 50% over the time period from 1 May 2013 to 30 April 2014. This resulted in relatively lower surface temperatures compared to the actual surface temperatures occurring on a day with no cloud cover.

Fourthly, the accuracy of LAI retrievals from indirect methods relies on the integrity of the data used and on the retrieval technique. The retrieval of biophysical properties of vegetation has received particular attention in recent years, nevertheless, important gaps still exist for example in the estimation of LAI of heterogeneous tropical vegetation and for individual urban trees [35]. Further field investigations on the relationship between LAI and under canopy Tmrt would help to validate and improve the predictions of our proposed method. In our study over Tanjong Pagar, Singapore, a uniform LAI value was assumed for all the trees in the site. If local LAI/LAD data becomes available, for instance retrieved from ALS [32], this information could be assimilated. Additionally, more evaluation sites are required to further assess the robustness of our method under different vegetation and urban settings, and in different climatic zones.

Finally, our method currently provides Tmrt at pedestrian level (1.5 m above the ground). Mapping 3-D Tmrt for instance on facades, balconies and elevated terraces could be possible since Tmrt is computed per vertical column of voxels of the scene. This would require to select the voxels in proximity to walls and roofs and to ignore the empty spaces where a person could not stand. Despite the advantages of using DART to perform analysis at different scales, a high level of detail over large scenes will result in long computation times. Therefore, it is crucial for the user to balance the trade-offs between scene size, level of detail and computation time. A table with examples of computation times is provided in

Table A2. Estimated Computation Times for One Time-Step Simulations.

Scale	Scene Dimensions (m)	Cell Size (m)	Shortwave (DART)	Longwave (DART)	Tmrt Calculation (Python Code)	Total
Tree	30 × 30 × 20	0.5 (x,y,z)	9′	100′	2′	111′
Building	100 × 100 × 20	1 (x,y,z)	12′	138′	3′	153′
Neighbourhood	1000 × 1000 × 30	2 (x,y) 1 (z)	450′	5175′	112′	5737′

* PC characteristics: 128 GB RAM, CPU Intel® Xeon® E5-1650 v3 @ 3.50GHz. 6 Cores, 12 Logical processors.

. With the continuous increase in computing power, this technical limitation will continue to decrease in the coming years.

5. Conclusions

The increasing availability of data of urban areas opens up new possibilities for detailed analysis in terms of urban microclimate and thermal comfort. Affordable laser scanners are being developed, opening opportunities for wide range of research on the processing and data retrieval for urban 3-D mapping. This unprecedented increase of data and computation capacity highlights the need for more detailed simulation tools and methods for planners and designers to evaluate the performance of existing areas and to assess future designs under different climatic scenarios. This study explored the potential of using the 3-D physically based RTM DART to model Tmrt. We presented a new method for the estimation and mapping Tmrt at different scales with a detailed consideration of surface materials and vegetation. The field evaluation showed good agreement between modelled and field estimated Tmrt. The impact of LAI on pedestrian Tmrt was explored as part of the sensitivity analysis. The results indicate a reduction of up to 38.2 °C Tmrt under canopy when LAI = 5.5 compared to an “exposed” setting. This highlights the importance of using accurate vegetation properties for simulations. The sensitivity analysis showed consistency across different resolutions and changing simulation parameters. We demonstrated a potential first application of our proposed method. Our approach can be used to visualize locations in need of interventions, to help to optimize climate sensitive urban design, and to support urban microclimate and outdoor thermal comfort studies when combined with adequate simulation tools for wind analysis and energy balance models.

A correct designation of surface temperatures is crucial to avoid erroneous simulations and wrong conclusions of the study. In future work, we will explore coupling our method with 3-D energy balance model such as DART EB [47] for a more precise designation of surface temperatures and a detailed calibration of input parameters. Additional validation exercises in different urban settings and other climatic regions would contribute to improve the robustness and applicability of this newly proposed method.

Quantifying the influence of urban design, construction materials, and vegetation on Tmrt can be very helpful in order to evaluate urban planning scenarios to reduce heat stress in existing urban areas, to promote enhanced thermal comfort in future developments and to contribute in reducing the energy consumption for cooling systems. Future research could, for instance, explore the effect of building morphology and urban patterns; which species to plant and their optimal spatial arrangement such as in street-tree scenarios; as well as the effect of construction materials on Tmrt by using the existing DART spectral database or by adding the actual spectral information of the materials found on the site of interest.