Complex Principal Component Analysis of Antarctic Ice Sheet Mass Balance
Abstract
1. Introduction
2. Materials and Methods
2.1. GRACE Data
2.2. Glacial Isostatic Adjustment
2.3. Data Processing and Equivalent Water Height
2.4. Complex Principal Component Analysis
2.5. WAPS
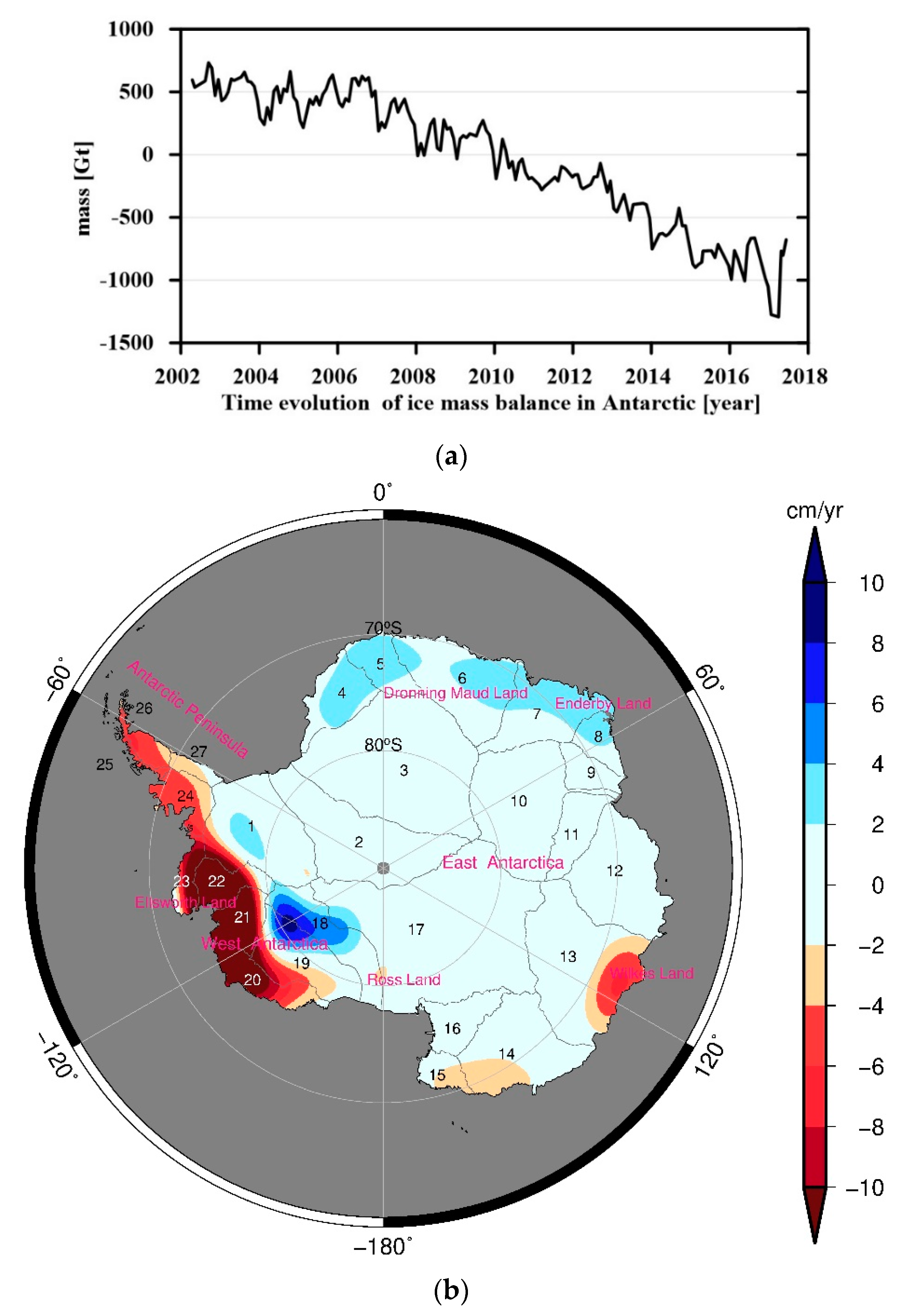
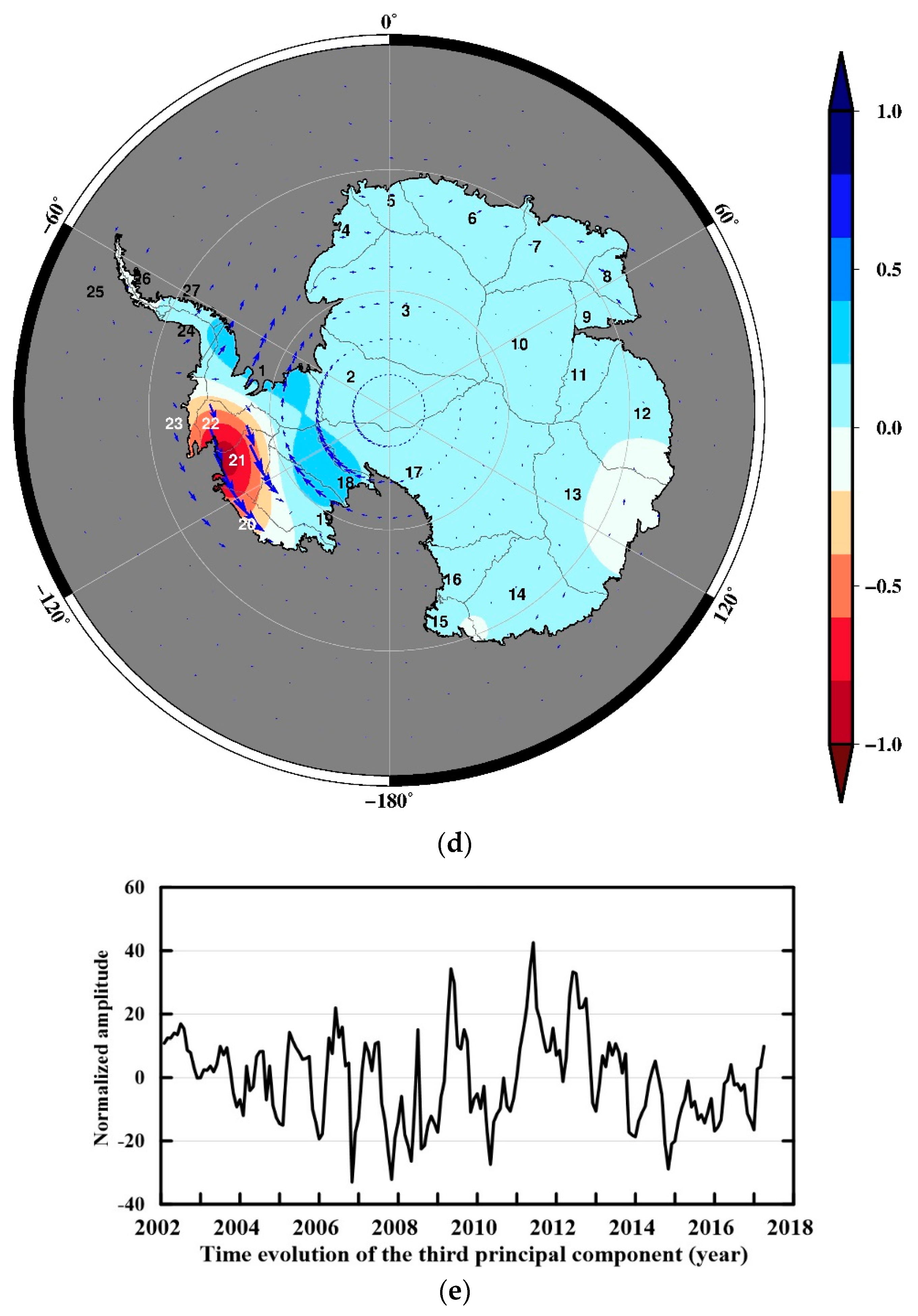
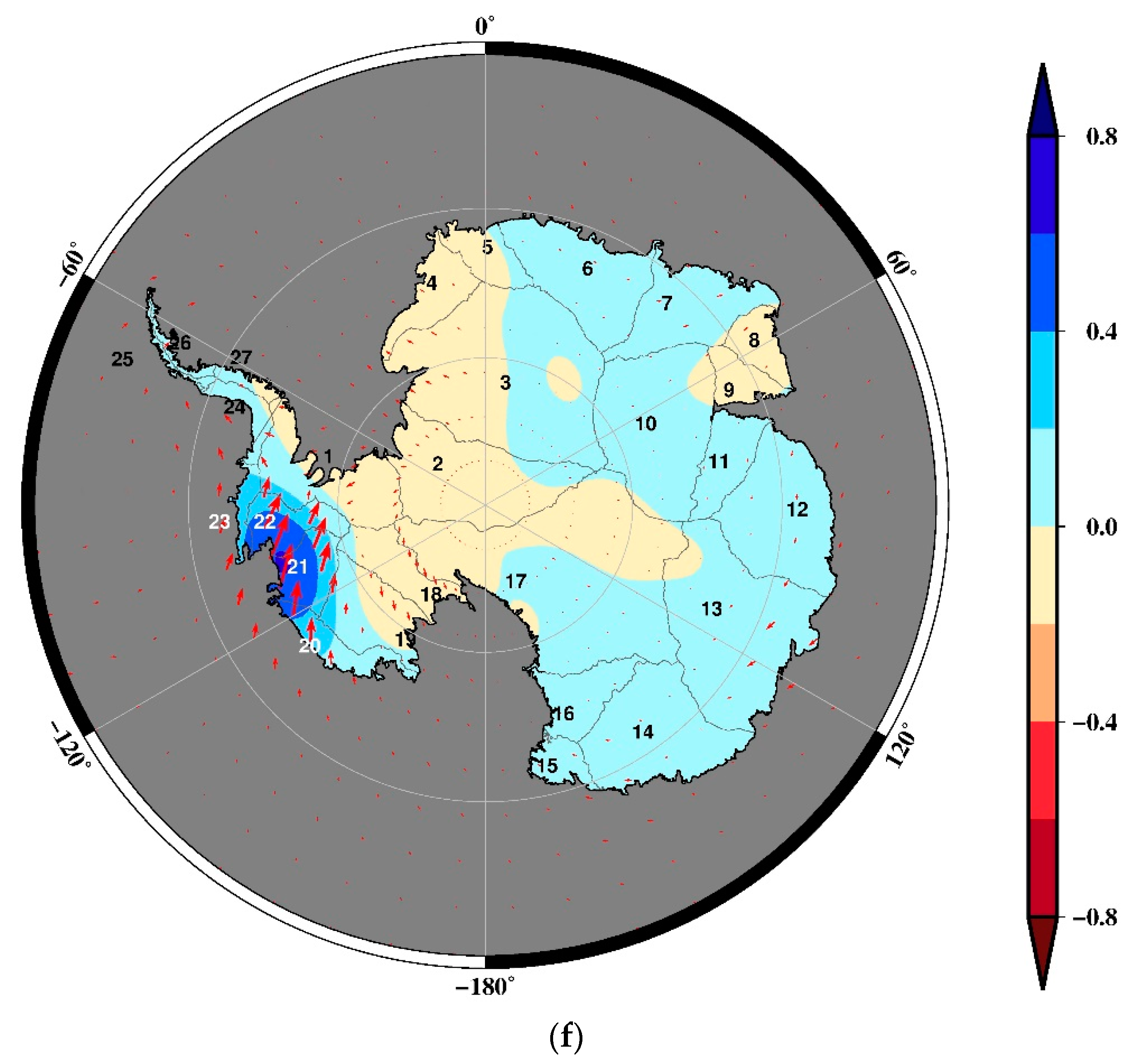
3. Results
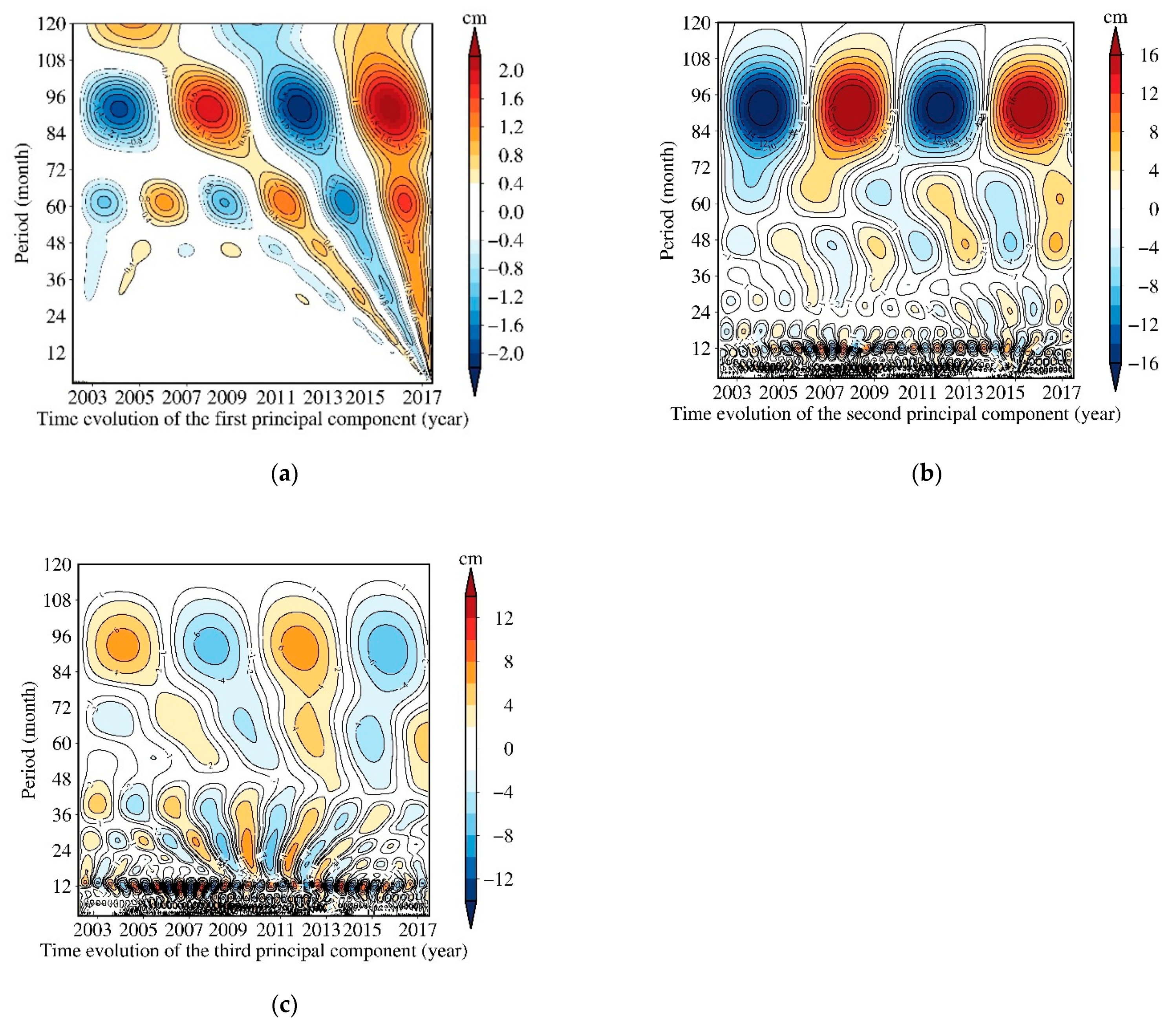
4. Discussion
4.1. The First Three Principal Components
4.2. The Low-Frequency Signals with 5-Year and Longer Periodicity in the First Principal Component
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chapman, W.L.; Walsh, J.E. Simulations of Arctic Temperature and Pressure by Global Coupled Models. J. Clim. 2007, 20, 609–632. [Google Scholar] [CrossRef]
- Vaughan, D.G.; Marshall, G.J.; Connolley, W.M.; Parkinson, C.; Mulvaney, R.; Hodgson, D.A.; King, J.C.; Pudsey, C.J.; Turner, J. Recent rapid regional climate warming on the Antarctic Peninsula. Clim. Chang. 2003, 60, 243–274. [Google Scholar] [CrossRef]
- Turner, J.; Colwell, S.R.; Marshall, G.J.; Lachlan-Cope, T.A.; Carleton, A.M.; Jones, P.D.; Lagun, V.; Reid, P.A.; Iagovkina, S. Antarctic climate change during the last 50 years. Int. J. Climatol. 2005, 25, 279–294. [Google Scholar] [CrossRef]
- Turner, J.; Bindschadler, R.; Convey, P.; Di Prisco, G.; Fahrbach, E.; Gutt, J.; Hodgson, D.; Mayewski, P.; Summerhayes, C. Antarctic Climate Change and the Environment; Scientific Commitee on Antarctic Research: Cambridge, UK, 2009. [Google Scholar]
- Steig, E.J.; Schneider, D.P.; Rutherford, S.D.; Mann, M.E.; Comiso, J.C.; Shindell, D.T. Warming of the Antarctic ice-sheet surface since the 1957 International Geophysical Year (vol 457, pg 459, 2009). Nature 2009, 460, 766. [Google Scholar] [CrossRef][Green Version]
- Ding, Q.; Steig, E.J.; Battisti, D.S.; Küttel, M. Winter warming in West Antarctica caused by central tropical Pacific warming. Nat. Geosci. 2011, 4, 398–403. [Google Scholar] [CrossRef]
- Turner, J.; Lu, H.; White, I.; King, J.C.; Phillips, T.; Hosking, J.S.; Bracegirdle, T.J.; Marshall, G.J.; Mulvaney, R.; Deb, P. Absence of 21st century warming on Antarctic Peninsula consistent with natural variability. Nature 2016, 535, 411–415. [Google Scholar] [CrossRef]
- Oliva, M.; Navarro, F.; Hrbáek, F.; Hernández, A.; Nyvlt, D.; Pereira, P.; Ruiz-Fernández, J.; Trigo, R. Recent regional climate cooling on the Antarctic Peninsula and associated impacts on the cryosphere. Sci. Total Environ. 2017, 580, 210–223. [Google Scholar] [CrossRef]
- Clem, K.R.; Fogt, R.L. Varying roles of ENSO and SAM on the Antarctic Peninsula climate in austral spring. J. Geophys. Res. Atmos. 2013, 118, 11481–11492. [Google Scholar] [CrossRef]
- Paolo, F.S.; Padman, L.; Fricker, H.A.; Adusumilli, S.; Howard, S.; Siegfried, M.R. Response of Pacific-sector Antarctic ice shelves to the El Nio/Southern Oscillation. Nat. Geosci. 2018, 11, 121–126. [Google Scholar] [CrossRef]
- Scambos, T.A.; Bohlander, J.A.; Shuman, C.A.; Skvarca, P. Glacier acceleration and thinning after ice shelf collapse in the Larsen B embayment, Antarctica. Geophys. Res. Lett. 2004, 31, L18402. [Google Scholar] [CrossRef]
- Rignot, E.; Casassa, G.; Gogineni, S.; Kanagaratnam, P.; Krabill, W.; Pritchard, H.; Rivera, A.; Thomas, R.; Turner, J.; Vaughan, D. Recent ice loss from the Fleming and other glaciers, Wordie Bay, West Antarctic Peninsula. Geophys. Res. Lett. 2005, 32, 4. [Google Scholar] [CrossRef]
- Jacobs, S.S.; Jenkins, A.; Giulivi, C.F.; Dutrieux, P. Stronger ocean circulation and increased melting under Pine Island Glacier ice shelf. Nat. Geosci. 2011, 4, 519–523. [Google Scholar] [CrossRef]
- MacAyeal, D.; Scambos, T.; Hulbe, C.; Fahnestock, M. Catastrophic ice-shelf break-up by an ice-shelf-fragment-capsize mechanism. J. Glaciol. 2003, 49, 22–36. [Google Scholar] [CrossRef]
- Schmidtko, S.; Heywood, K.J.; Thompson, A.F.; Aoki, S. Multidecadal warming of Antarctic waters. Science 2014, 346, 1227–1231. [Google Scholar] [CrossRef]
- Turner, J. The El Niño–southern oscillation and Antarctica. Int. J. Climatol. 2004, 24, 1–31. [Google Scholar] [CrossRef]
- Sasgen, I.; Dobslaw, H.; Martinec, Z.; Thomas, M. Satellite gravimetry observation of Antarctic snow accumulation related to ENSO. Earth Planet. Sci. Lett. 2010, 299, 352–358. [Google Scholar] [CrossRef]
- Mémin, A.; Flament, T.; Alizier, B.; Watson, C.; Rémy, F. Interannual variation of the Antarctic Ice Sheet from a combined analysis of satellite gravimetry and altimetry data. Earth Planet. Sci. Lett. 2015, 422, 150–156. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Xiang, L.W.; Wang, H.S.; Steffen, H.; Wu, P.; Jia, L.L.; Jiang, L.M.; Shen, Q. Groundwater storage changes in the Tibetan Plateau and adjacent areas revealed from GRACE satellite gravity data. Earth Planet. Sci. Lett. 2016, 449, 228–239. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Blankenship, D.; Tapley, B.D. Accelerated Antarctic ice loss from satellite gravity measurements. Nat. Geosci. 2009, 2, 859–862. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Interannual variability of Greenland ice losses from satellite gravimetry. J. Geophys. Res. Solid Earth 2011, 116. [Google Scholar] [CrossRef]
- Zwally, H.J.; Mario, B.; Matthew, G.; Beckley, A.; Saba, J.L. Antarctic and Greenland Drainage Systems. Available online: http://icesat4.gsfc.nasa.gov/cryo_data/ant_grn_drainage_systems.php (accessed on 5 September 2020).
- Bettadpur, S.; Kang, Z.; Peter, N.; Rick, P.; Steve, P.; John, R.; Save, H. Status and Assessments of CSR GRACE Level-2 Data Products. In Proceedings of the EGU General Assembly Conference, Vienna, Austria, 12–17 April 2015; p. 4142. [Google Scholar]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 22. [Google Scholar] [CrossRef]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, L19503. [Google Scholar] [CrossRef]
- Rignot, E.; Velicogna, I.; Broeke, M.R.V.D.; Monaghan, A.; Lenaerts, J.T.M. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Grand, S. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Blankenship, D.; Young, D. Antarctic regional ice loss rates from GRACE. Earth Planet. Sci. Lett. 2008, 266, 140–148. [Google Scholar] [CrossRef]
- Tarvainen, M.P.; Ranta-aho, P.O.; Karjalainen, P.A. An advanced detrending method with application to HRV analysis. IEEE Trans. Biomed. Eng. 2002, 49, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Ramillien, G.; Lombard, A.; Cazenave, A.; Ivins, E.R.; Llubes, M.; Remy, F.; Biancale, R. Interannual variations of the mass balance of the Antarctica and Greenland ice sheets from GRACE. Glob. Planet. Chang. 2006, 53, 198–208. [Google Scholar] [CrossRef]
- Zhan, J.G.; Wang, Y.; Shi, H.L.; Chai, H.; Zhu, C.D. Removing correlative errors in GRACE data by the smoothness priors method. Chin. J. Geophys. Chin. Ed. 2015, 58, 1135–1144. [Google Scholar] [CrossRef]
- Whitehouse, P.L.; Bentley, M.J.; Milne, G.A.; King, M.A.; Thomas, I.D. A new glacial isostatic adjustment model for Antarctica: Calibrated and tested using observations of relative sea-level change and present-day uplift rates. Geophys. J. Int. 2012, 190, 1464–1482. [Google Scholar] [CrossRef]
- Ivins, E.R.; James, T.S.; Wahr, J.; Schrama, E.J.O.; Landerer, F.W.; Simon, K.M. Antarctic contribution to sea level rise observed by GRACE with improved GIA correction. J. Geophys. Res. Solid Earth 2013, 118, 3126–3141. [Google Scholar] [CrossRef]
- Peltier, W.R.; Argus, D.F.; Drummond, R. Space geodesy constrains ice age terminal deglaciation: The global ICE-6G_C (VM5a) model. J. Geophys. Res. Solid Earth 2015, 120, 450–487. [Google Scholar] [CrossRef]
- Caron, L.; Ivins, E.R.; Larour, E.; Adhikari, S.; Nilsson, J.; Blewitt, G. GIA Model Statistics for GRACE Hydrology, Cryosphere, and Ocean Science. Geophys. Res. Lett. 2018, 45, 2203–2212. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, 12. [Google Scholar] [CrossRef]
- Horel, J.D. Complex Principal Component Analysis: Theory and Examples. J. Appl. Meteorol. 1984, 23, 1660–1673. [Google Scholar] [CrossRef]
- Harlander, U.; Larcher, T.; Wright, G.B.; Hoff, M.; Alexandrov, K.; Egbers, C. Orthogonal Decomposition Methods to Analyze PIV, LDV, and Thermography Data of Thermally Driven Rotating Annulus Laboratory Experiments. In Modeling Atmospheric and Oceanic Flows; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014; pp. 315–336. [Google Scholar] [CrossRef]
- Von Larcher, T.; Viazzo, S.; Harlander, U.; Vincze, M.; Randriamampianina, A. Instabilities and small-scale waves within the Stewartson layers of a thermally driven rotating annulus. J. Fluid Mech. 2018, 841, 380–407. [Google Scholar] [CrossRef]
- Walcker, R.; Anthony, E.J.; Cassou, C.; Aller, R.C.; Gardel, A.; Proisy, C.; Martinez, J.M.; Fromard, F. Fluctuations in the extent of mangroves driven by multi-decadal changes in North Atlantic waves. J. Biogeogr. 2015, 42, 2209–2219. [Google Scholar] [CrossRef]
- Hoff, M.; Harlander, U.; Egbers, C. Experimental survey of linear and nonlinear inertial waves and wave instabilities in a spherical shell. J. Fluid Mech. 2016, 789, 589–616. [Google Scholar] [CrossRef]
- Liu, L. Basic Wavelet Theory and Its Applications in Geosciences. Ph.D. Thesis, Institute of Geodesy and Geophysics, CAS, Wuhan, China, 1999. [Google Scholar]
- Zhan, J.G.; Wang, Y.; Liu, L.T. Time-frequency analysis of the inter-seasonal variations of China-neighboring seas level. Chin. J. Geophys. Chin. Ed. 2003, 46, 36–41. [Google Scholar] [CrossRef]
- Zhan, J.G.; Shi, H.L.; Wang, Y.; Yao, Y.X. Complex principal component analysis of mass balance changes on the Qinghai-Tibetan Plateau. Cryosphere 2017, 11, 1487–1499. [Google Scholar] [CrossRef]
- Liu, L.; Hsu, H. Inversion and normalization of time-frequency transform. In Proceedings of the 2011 International Conference on Multimedia Technology, Hangzhou, China, 26–28 July 2011; pp. 2164–2168. [Google Scholar]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar] [CrossRef]
- Nagler, T.; Floricioiu, D.; Groh, A.; Horwath, M.; Kusk, A.; Muir, A.; Wuite, J. Algorithm Theoretical Basis Document (ATBD) for the Antarctic_Ice_Sheet_cci project of ESA’s Climate Change Initiative, Version 2.1. 2017. Available online: https://data1.geo.tu-dresden.de/ais_gmb/source/ST-UL-ESA-AISCCI-ATBD-Draft_GMB.pdf (accessed on 29 January 2021).
- Gao, C.; Lu, Y.; Shi, H.; Zhang, Z.; Xu, C.; Tan, B. Detection and analysis of ice sheet mass changes over 27 Antarctic drainage systems from GRACE RL06 data. Chin. J. Geophys. 2019, 62, 864–882. (In Chinese) [Google Scholar] [CrossRef]
- Wouters, B.; Martin-Espanol, A.; Helm, V.; Flament, T.; van Wessem, J.M.; Ligtenberg, S.R.M.; van den Broeke, M.R.; Bamber, J.L. Dynamic thinning of glaciers on the Southern Antarctic Peninsula. Science 2015, 348, 899–903. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E.; Scheuchl, B. Sustained increase in ice discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013. Geophys. Res. Lett. 2014, 41, 1576–1584. [Google Scholar] [CrossRef]
- Dutrieux, P.; De Rydt, J.; Jenkins, A.; Holland, P.R.; Ha, H.K.; Lee, S.H.; Steig, E.J.; Ding, Q.; Abrahamsen, E.P.; Schröder, M. Strong Sensitivity of Pine Island Ice-Shelf Melting to Climatic Variability. Science 2014, 343, 174–178. [Google Scholar] [CrossRef]
- Boening, C.; Lebsock, M.; Landerer, F.; Stephens, G. Snowfall-driven mass change on the East Antarctic ice sheet. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Raphael, M.N.; Marshall, G.J.; Turner, J.; Fogt, R.L.; Schneider, D.; Dixon, D.A.; Hosking, J.S.; Jones, J.M.; Hobbs, W.R. The Amundsen Sea Low: Variability, Change and Impact on Antarctic Climate. Bull. Am. Meteorol. Soc. 2016, 97, 197–210. [Google Scholar] [CrossRef]
- Schneider, D.P.; Deser, C.; Okumura, Y. An assessment and interpretation of the observed warming of West Antarctica in the austral spring. Clim. Dyn. 2012, 38, 323–347. [Google Scholar] [CrossRef]
- Li, X.; Holland, D.M.; Gerber, E.P.; Yoo, C. Impacts of the north and tropical Atlantic Ocean on the Antarctic Peninsula and sea ice. Nature 2014, 505, 538–542. [Google Scholar] [CrossRef]
- Fogt, R.L.; Bromwich, D.H.; Hines, K.M. Understanding the SAM influence on the South Pacific ENSO teleconnection. Clim. Dyn. 2011, 36, 1555–1576. [Google Scholar] [CrossRef]
- Lachlan-Cope, T.; Connolley, W. Teleconnections between the tropical Pacific and the Amundsen-Bellinghausens Sea: Role of the El Niño/Southern Oscillation. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Hosking, J.S.; Orr, A.; Bracegirdle, T.J.; Turner, J. Future circulation changes off West Antarctica: Sensitivity of the Amundsen Sea Low to projected anthropogenic forcing. Geophys. Res. Lett. 2016, 43, 367–376. [Google Scholar] [CrossRef]


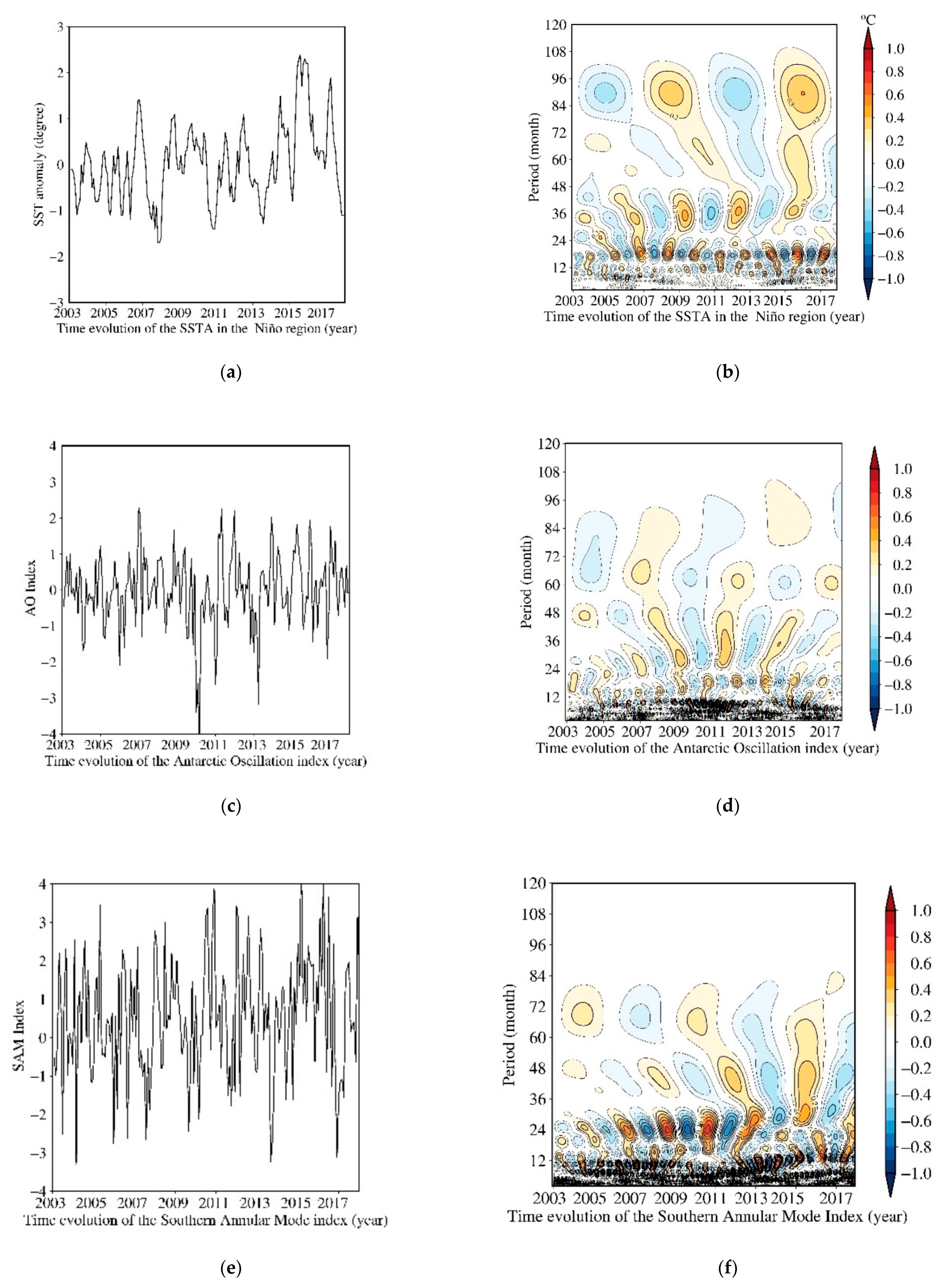

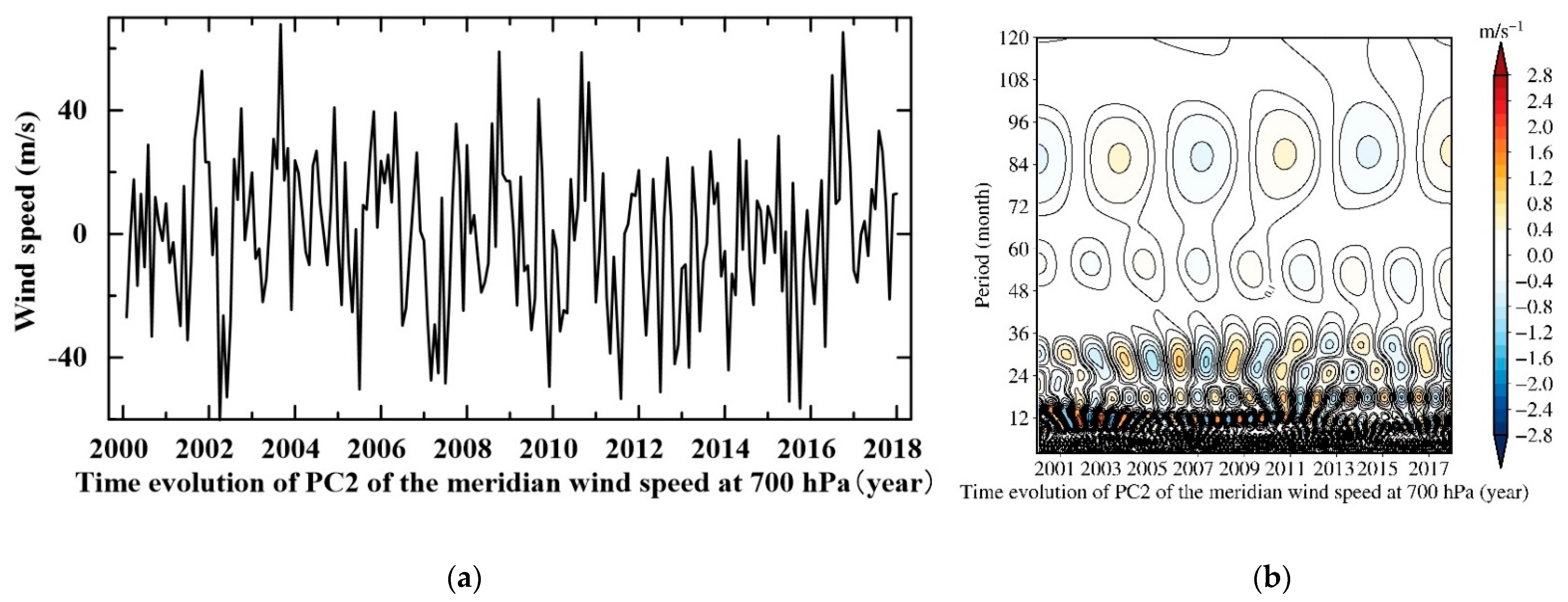
| Number | Eigenvalues | As Percentages | Cumul. Percentages |
|---|---|---|---|
| 1 | 9703.61 | 83.73 | 83.73 |
| 2 | 297.32 | 2.57 | 86.29 |
| 3 | 216.33 | 1.87 | 88.16 |
| Time Lag (month) | First Principal Component | Low Frequency Signal of Meridional Wind | 95% Confidence Level | |
|---|---|---|---|---|
| El Niño | −9 | 0.24 | - | 0.17 |
| Low Frequency Signal of El Niño | 1 | 0.73 | 0.77 | 0.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, J.; Shi, H.; Wang, Y.; Yao, Y. Complex Principal Component Analysis of Antarctic Ice Sheet Mass Balance. Remote Sens. 2021, 13, 480. https://doi.org/10.3390/rs13030480
Zhan J, Shi H, Wang Y, Yao Y. Complex Principal Component Analysis of Antarctic Ice Sheet Mass Balance. Remote Sensing. 2021; 13(3):480. https://doi.org/10.3390/rs13030480
Chicago/Turabian StyleZhan, Jingang, Hongling Shi, Yong Wang, and Yixin Yao. 2021. "Complex Principal Component Analysis of Antarctic Ice Sheet Mass Balance" Remote Sensing 13, no. 3: 480. https://doi.org/10.3390/rs13030480
APA StyleZhan, J., Shi, H., Wang, Y., & Yao, Y. (2021). Complex Principal Component Analysis of Antarctic Ice Sheet Mass Balance. Remote Sensing, 13(3), 480. https://doi.org/10.3390/rs13030480







