A Novel Deeplabv3+ Network for SAR Imagery Semantic Segmentation Based on the Potential Energy Loss Function of Gibbs Distribution
Abstract
1. Introduction
2. Materials and Methods
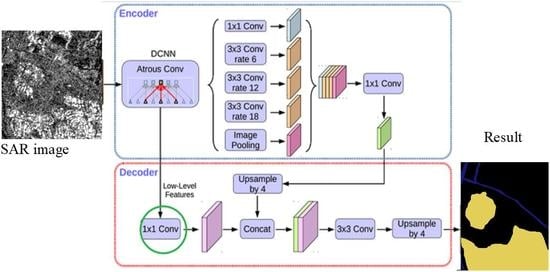
2.1. The Structure of Deeplabv3+ Network
2.2. Potential Energy Loss Function Based on the Gibbs Distribution
2.3. Improved Channel Spatial Attention Module (CBAM)
3. Results and Analysis
3.1. Dataset
3.2. Implement Details
3.3. Ablation Study
3.3.1. Designing the Network for SAR Imagery Semantic Segmentation
| Network | Time | |||||||
|---|---|---|---|---|---|---|---|---|
| PSPNet [11] | 60.93% | 90.22% | 83.14% | 47.02% | 53.76% | 40.75% | 54.98% | 3.13s |
| FCN [9] | 68.99% | 90.10% | 87.39% | 59.83% | 63.33% | 17.10% | 63.55% | 3.03s |
| Deeplabv3+ –Resnet [15] | 72.83% | 92.14% | 87.34% | 85.98% | 73.20% | 0 | 67.73% | 4.52s |
| Deeplabv3+ –drn [22] | 70.77% | 91.95% | 89.04% | 84.51% | 70.99% | 0 | 66.94% | 3.65s |
| Deeplabv3+ –Mobilenetv2 [16] | 73.37% | 92.51% | 87.38% | 88.36% | 73.18% | 0 | 68.28% | 2.94s |
3.3.2. The Potential Energy Loss Function Based on the Gibbs Distribution
3.3.3. Influence of Weighting Coefficient Compared with RMI Loss Function
3.3.4. The Influence of Improved CBAM
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, W.; Zhang, X.; Chen, L.; Hong, S. Semantic Segmentation of Polarimetric SAR Imagery Using Conditional Random Fields. In Proceedings of the 2010 IEEE Geoscience & Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.Q. Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2017, 13, 1935–1939. [Google Scholar] [CrossRef]
- Lee, J.S.; Jurkevich, I. Segmentation of SAR images. IEEE Trans. Geosci. Remote Sens. 1989, 27, 674–680. [Google Scholar] [CrossRef]
- Ji, J.; Wang, K.L. A robust nonlocal fuzzy clustering algorithm with between-cluster separation measure for SAR image segmentation. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 4929–4936. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, X.; Wang, S.; Hou, B. Context-based hierarchical unequal merging for SAR image segmentation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 995–1009. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet Classification with Deep Convolutional Neural Networks. In Proceedings of the NIPS’12: 25th International Conference on Neural Information Processing Systems, Lake Tahoe, 3–6 December 2012; Curran Associates, Inc.: Red Hook, NY, USA, 2012; Volume 60. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Farabet, C.; Couprie, C.; Najman, L.; LeCun, Y. Learning Hierarchical Features for Scene Labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 39, 640–651. [Google Scholar] [CrossRef]
- Liang, X.; Liu, S.; Shen, X.; Yang, J.; Liu, L.; Dong, J.; Lin, L.; Yan, S. Deep Human Parsing with Active Template Regression. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2402–2414. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Duan, Y.; Tao, X.; Han, C.; Qin, X.; Lu, J. Multi-scale Convolutional Neural Network for SAR Image Semantic Segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Abu Dhabi, UAE, 9–13 December 2018; Volume 2, pp. 941–947. [Google Scholar]
- Zhang, Z.; Guo, W.; Yu, W.; Yu, W. Multi-task fully convolutional networks for building segmentation on SAR image. In Proceedings of the IET International Radar Conference (IRC 2018), Nanjing City, China, 17–19 October 2018; Volume 2019, pp. 7074–7077. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; So Kweon, I. In So Kweon. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; Springer Healthcare: New York, NY, USA, 2018. [Google Scholar]
- Zhao, S.; Wang, Y.; Yang, Z.; Cai, D. Region Mutual Information Loss for Semantic Segmentation. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, UK, 2019. [Google Scholar]
- Cover, M.T.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Koller, D.; Friedman, N. Probabilistic Graphical Models: Principles and Techniques; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization; ICLR: New Orleans, LA, USA, 2015. [Google Scholar]
- Yu, F.; Koltun, V.; Funkhouser, T. Dilated Residual Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]







| 90.90% | 90.27% | 97.20% | 96.63% | 95.92% | 88.80% | 46.84% | 85.08% |
| Network | Time | |||||||
|---|---|---|---|---|---|---|---|---|
| Deeplabv3+–Resnet | 86.46% | 96.45% | 95.35% | 95.02% | 85.52% | 36.84% | 81.84% | 4.45 s |
| Deeplabv3+–drn | 90.80% | 97.19% | 96.69% | 95.46% | 88.99% | 50.32% | 85.73% | 3.82 s |
| Deeplabv3+–Mobilenetv2 | 90.27% | 97.18% | 96.85% | 95.64% | 88.60% | 46.69% | 84.99% | 2.83 s |
| Method | Time | |||||||
|---|---|---|---|---|---|---|---|---|
| 89.62% | 97.15% | 96.69% | 95.69% | 88.57% | 45.15% | 84.65% | 2.84 s | |
| 90.27% | 97.18% | 96.85% | 95.64% | 88.60% | 46.69% | 84.99% | 2.83 s | |
| 89.15% | 97.17% | 96.92% | 95.79% | 88.37% | 42.66% | 84.19% | 2.86 s | |
| RMI loss | 88.05% | 96.63% | 96.30% | 95.09% | 86.26% | 37.08% | 82.27% | 2.93 s |
| Method | Time | |||||||
|---|---|---|---|---|---|---|---|---|
| No-CBAM | 90.27% | 97.18% | 96.85% | 95.64% | 88.60% | 46.69% | 84.99% | 2.83 s |
| Origin CBAM | 89.24% | 97.09% | 96.90% | 95.38% | 88.06% | 44.64% | 84.41% | 2.86 s |
| Improved CBAM | 90.57% | 97.20% | 96.63% | 95.92% | 88.80% | 46.84% | 85.08% | 2.94 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, Y.; Liu, Y.; Yan, B.; Leung, H.; Peng, X. A Novel Deeplabv3+ Network for SAR Imagery Semantic Segmentation Based on the Potential Energy Loss Function of Gibbs Distribution. Remote Sens. 2021, 13, 454. https://doi.org/10.3390/rs13030454
Kong Y, Liu Y, Yan B, Leung H, Peng X. A Novel Deeplabv3+ Network for SAR Imagery Semantic Segmentation Based on the Potential Energy Loss Function of Gibbs Distribution. Remote Sensing. 2021; 13(3):454. https://doi.org/10.3390/rs13030454
Chicago/Turabian StyleKong, Yingying, Yanjuan Liu, Biyuan Yan, Henry Leung, and Xiangyang Peng. 2021. "A Novel Deeplabv3+ Network for SAR Imagery Semantic Segmentation Based on the Potential Energy Loss Function of Gibbs Distribution" Remote Sensing 13, no. 3: 454. https://doi.org/10.3390/rs13030454
APA StyleKong, Y., Liu, Y., Yan, B., Leung, H., & Peng, X. (2021). A Novel Deeplabv3+ Network for SAR Imagery Semantic Segmentation Based on the Potential Energy Loss Function of Gibbs Distribution. Remote Sensing, 13(3), 454. https://doi.org/10.3390/rs13030454