Vector Current Measurement Using Doppler Scatterometry with Optimally Selected Observation Azimuths
Abstract
:1. Introduction
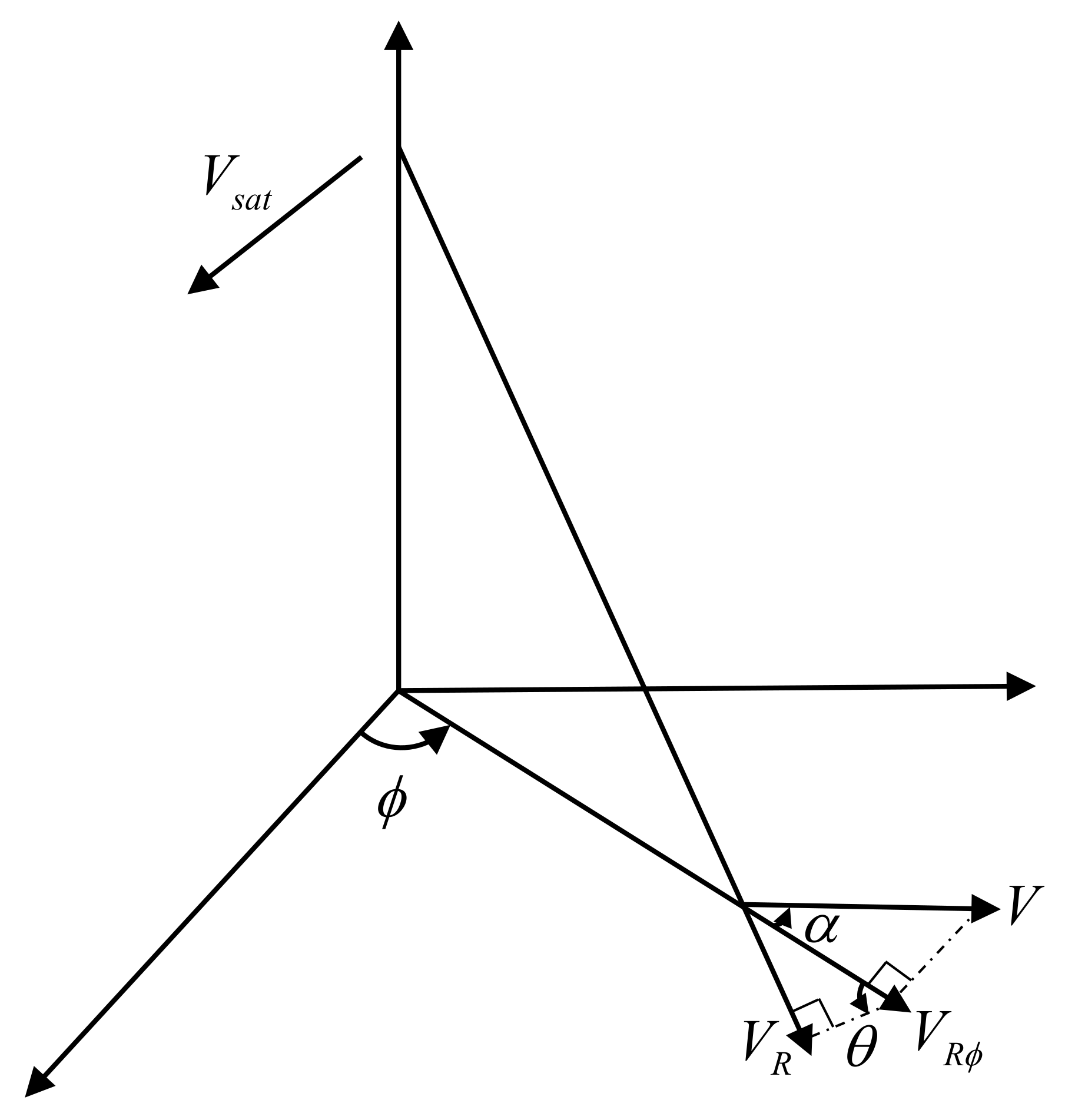
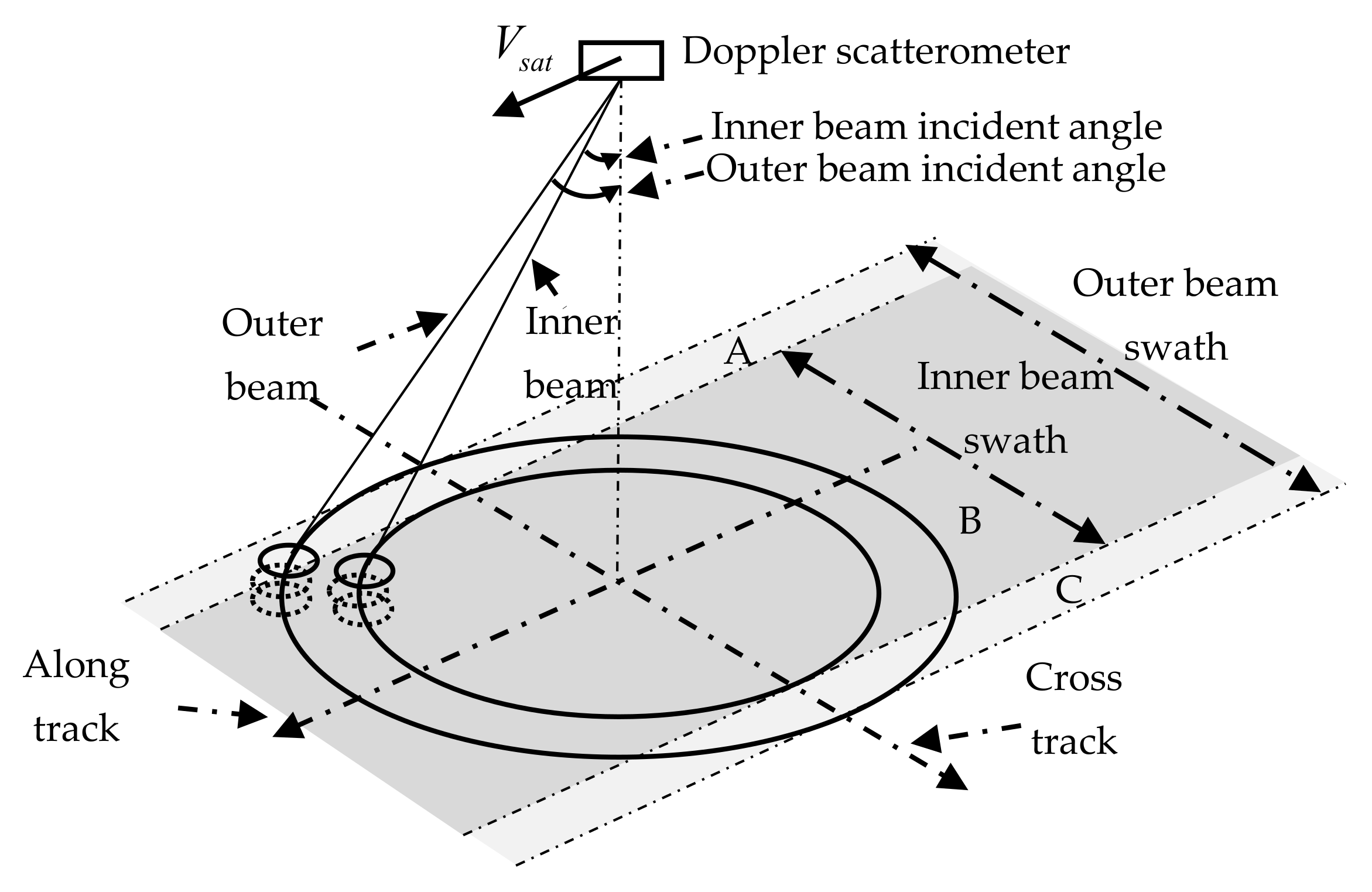
2. The Principle of Ocean Current Velocity Measurement Using Doppler Scatterometry
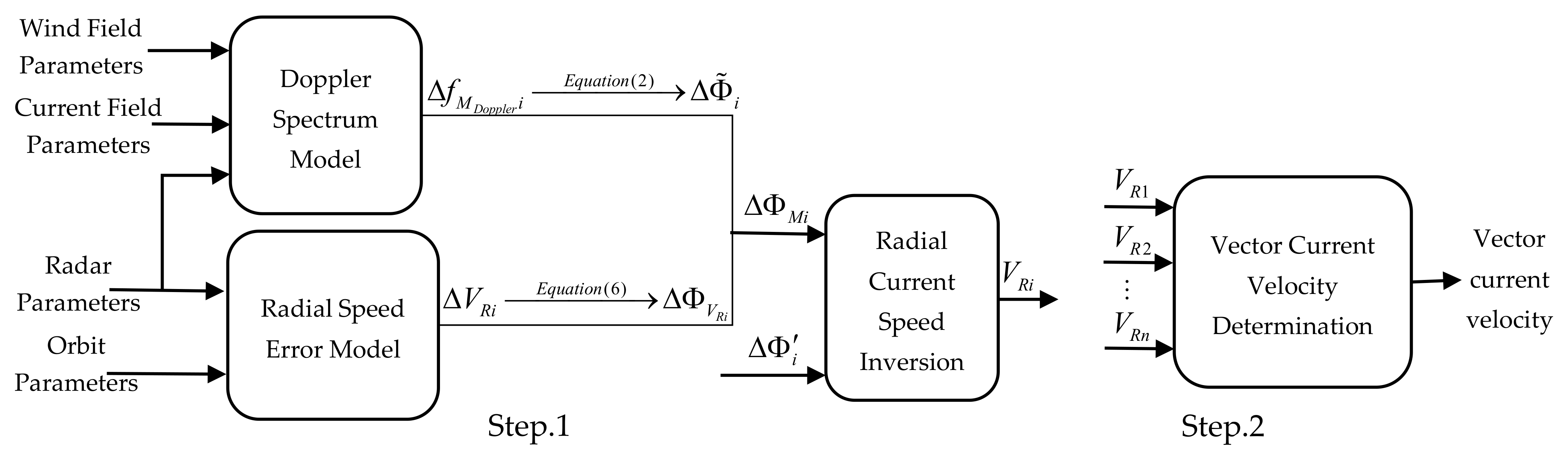
3. The Proposed Ocean Current Velocity Determination Method
3.1. Data Simulation Module
| Algorithm 1 Data simulation for Doppler scatterometer. |
| 1: Input: The local incident angles and , the observation azimuths , , |
| 2: and , polarization mode and , wind field parameters and , the |
| 3: current field parameters and . |
| 4: Output: The simulated interference phase difference measurements , |
| 5: , and . |
| 6: ① For an observation position on the sea surface, radial current speeds , , |
| 7: and in three different observation azimuths , and are calculated |
| 8: using Equation (1) according to the given ocean current velocity. |
| 9: ② The echo-Doppler spectra along three observation azimuths are calculated using |
| 10: the Doppler spectrum model [24] with , , , , , |
| 11: , , and as input parameters. The corresponding Doppler spectra for |
| 12: and can also be obtained. |
| 13: ③ Based on the obtained Doppler spectra, the Doppler center frequencies can be |
| 14: calculated using Equation (3). Then the Doppler frequency shifts , |
| 15: and can be obtained based on Equation (4). |
| 16: ④ The ideal echo interference phase differences for obser- |
| 17: vation azimuths and can be respectively calculated using Equation (2) |
| 18: with the obtained , and . |
| 19: ⑤ The radial current speed error model is used to generate the radial current speed |
| 20: error and in observation azimuths and . Then |
| 21: Equation (6) is applied to obtain the interference phase difference |
| 22: and caused by and . |
| 23: ⑥ The simulated interference phase difference measurements and |
| 24: are calculated using Equation (7) with the obtained and |
| 25: and and . |
3.2. Radial Current Speed Inversion Module
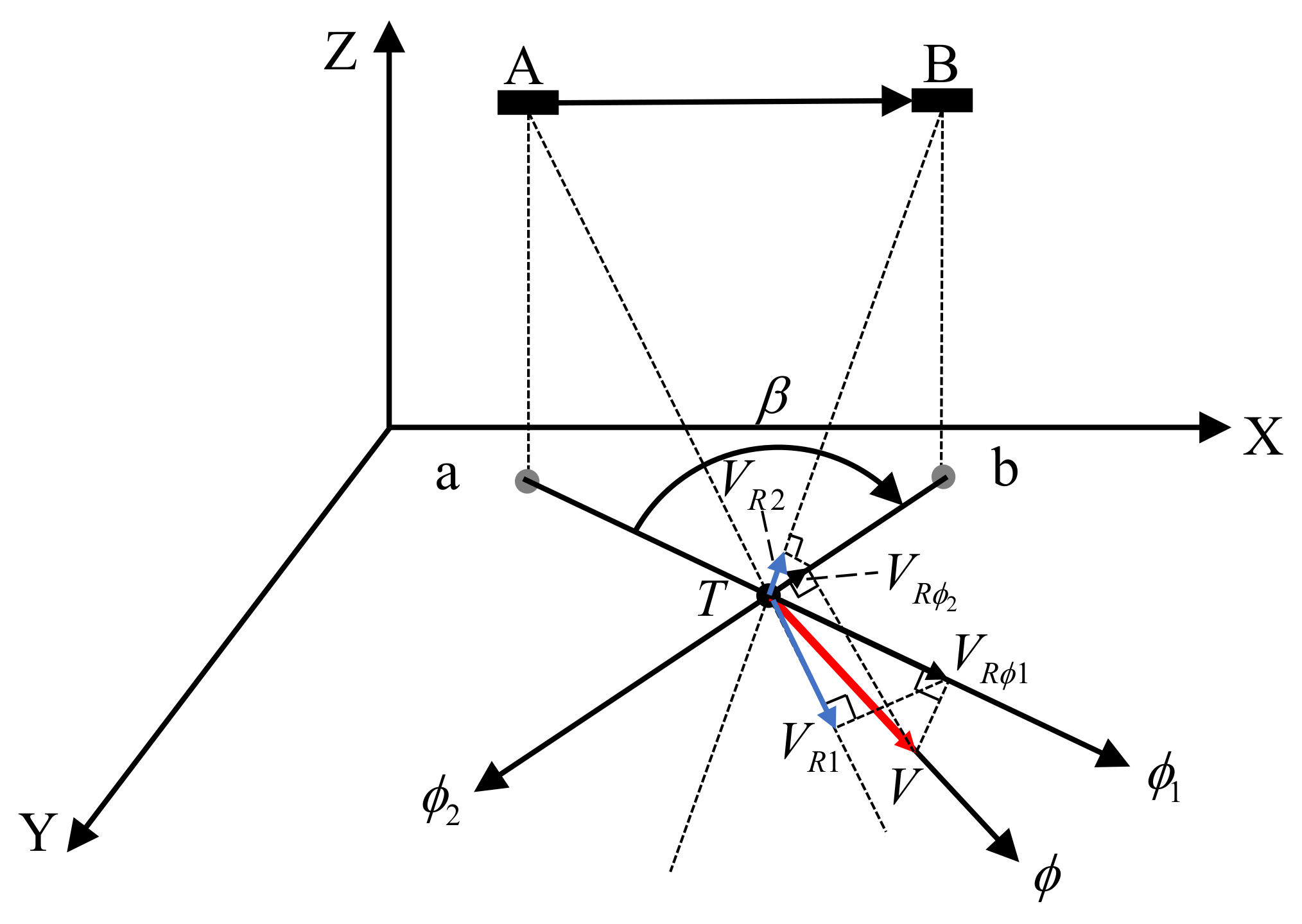
3.3. Vector Current Velocity Determination Module
3.3.1. Proposed Vector Current Velocity Determination Method
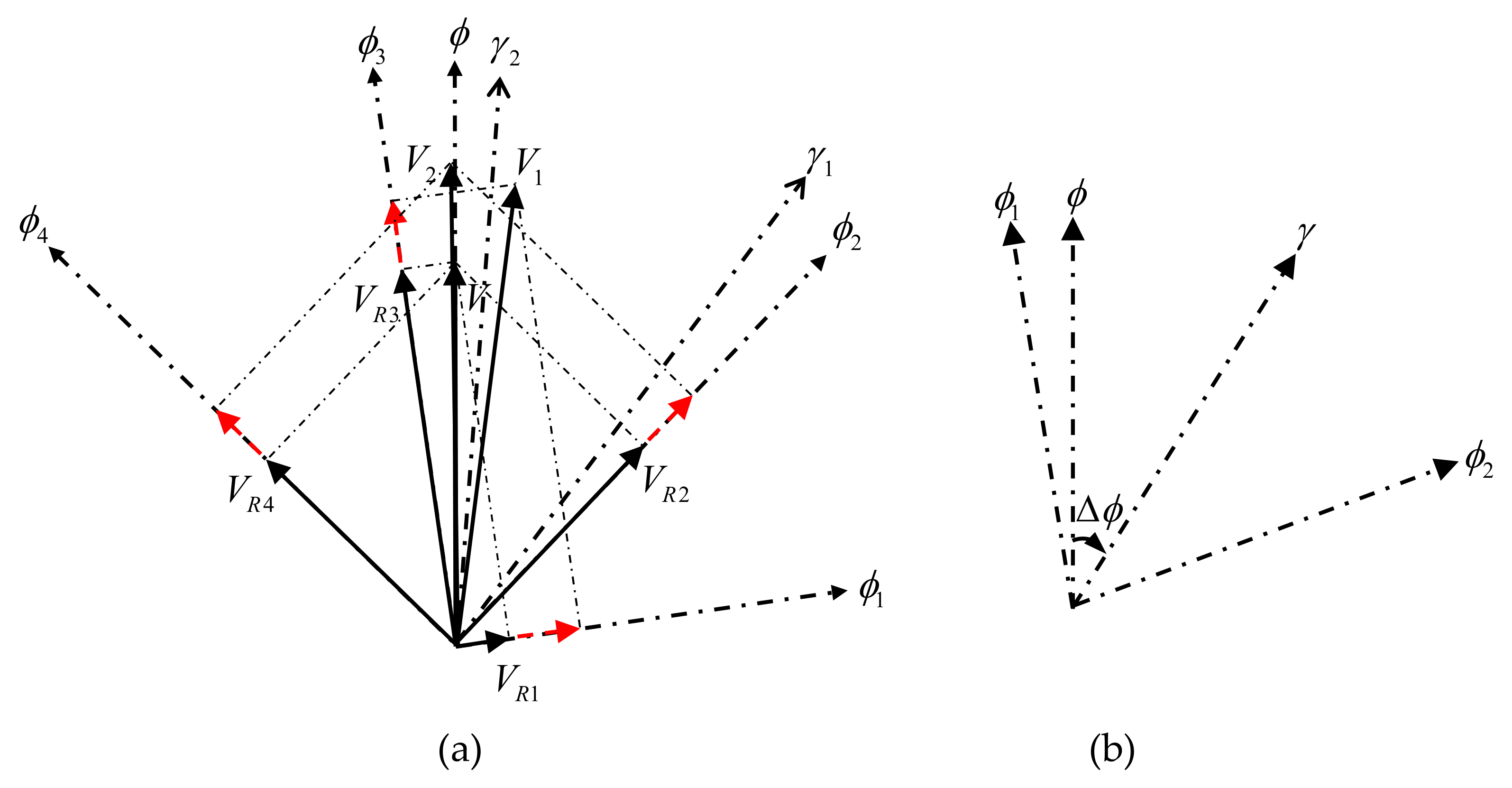
3.3.2. A Method for Optimal Observation Azimuth Selection
| Algorithm 2 Vector current velocity estimation based on optimally selected observation azimuths. |
| 1: Input: The observation azimuths , and , the measured interference phase |
| 2: difference , and . |
| 3: Output: The vector current velocity at an observation position. |
| 4: ① According to , and , the radial current speeds , and |
| 5: in , and are estimated using the interference phase difference |
| 6: matching method (see Equation (8)). |
| 7: ② Any two radial current speeds from two different observation azimuths are se- |
| 8: lected to determine a vector current velocity using Equations (13) and (14). The |
| 9: obtained current direction is used as a preliminary estimation of the current |
| 10: direction. |
| 11: ③ The optimal observation azimuths and are determined using |
| 12: Equations (15) and (16) with , and as input. |
| 13: ④ The final vector current velocity is obtained using Equations (13) and (14) with |
| 14: radial current speeds obtained from observation azimuths and . |
4. Experimental Results
4.1. Data Simulation Results and Analysis
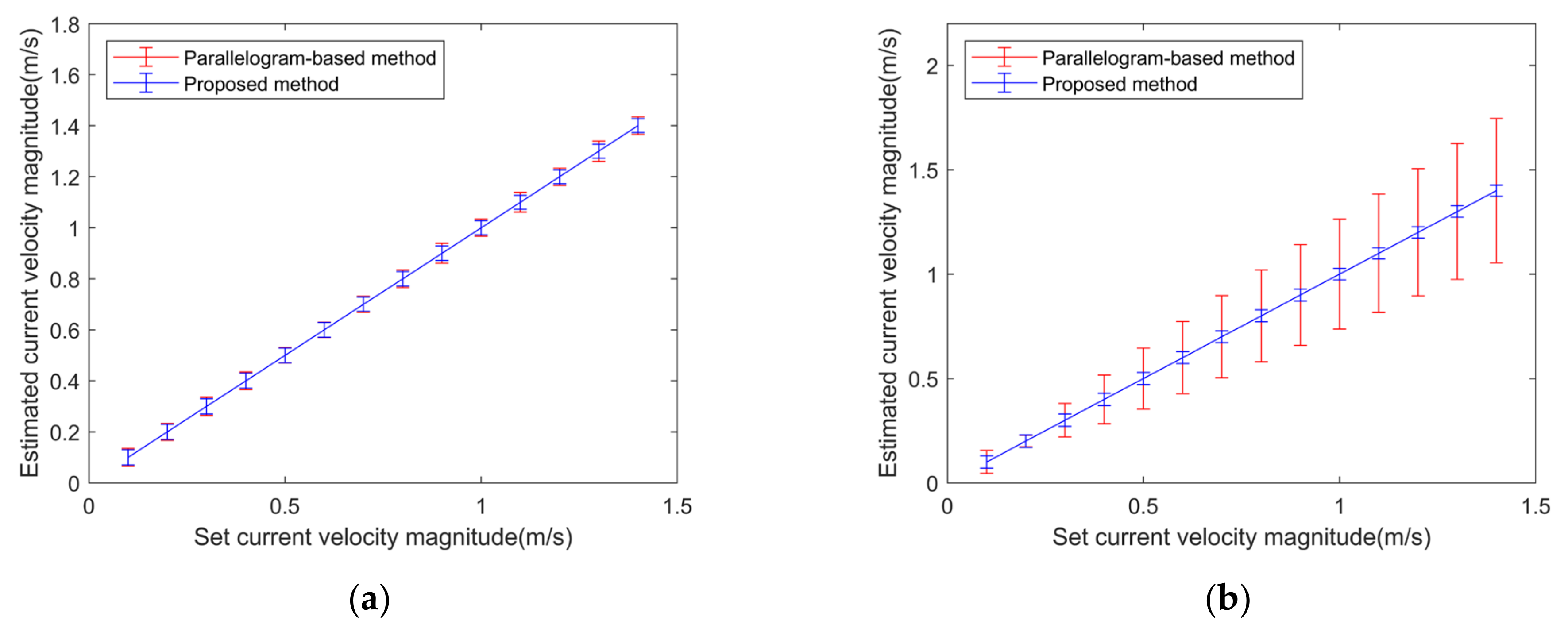
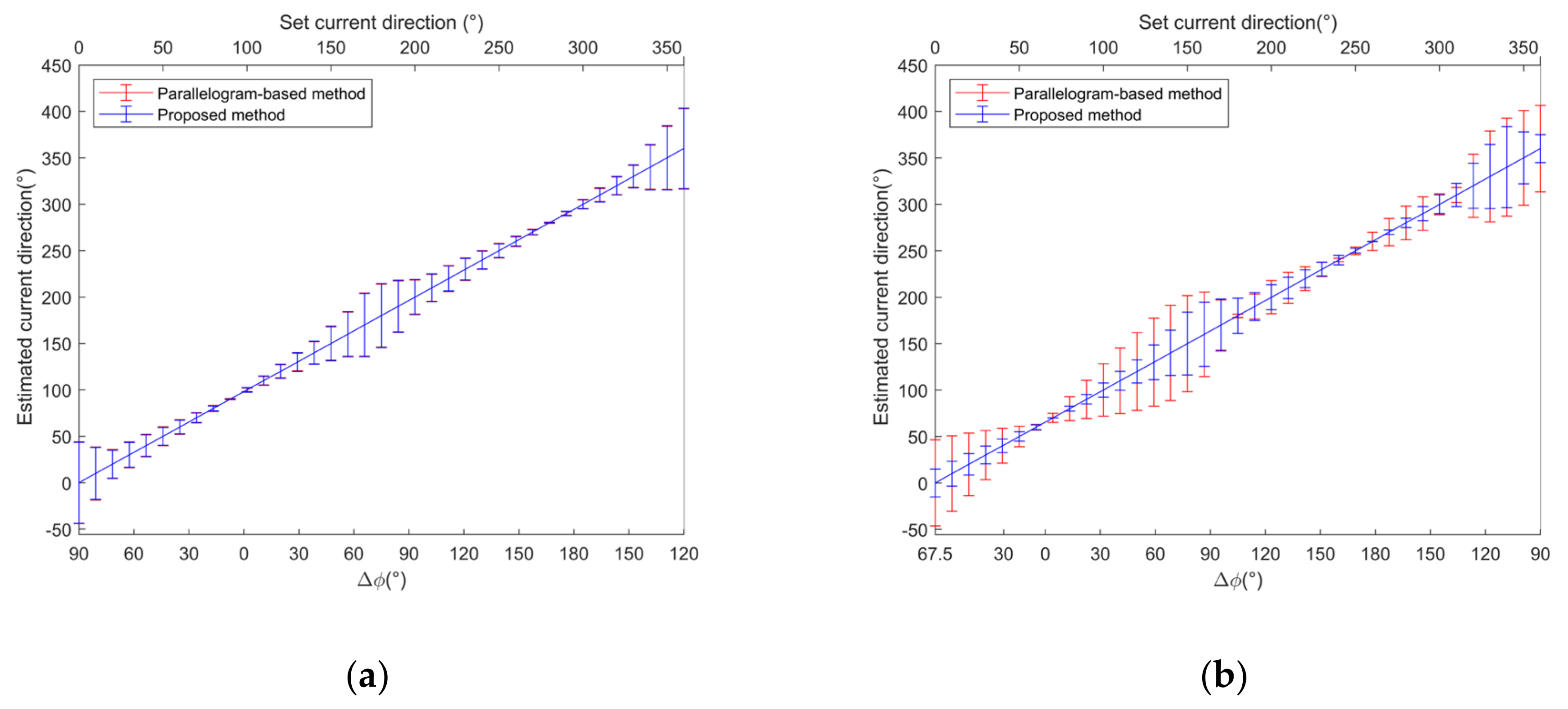
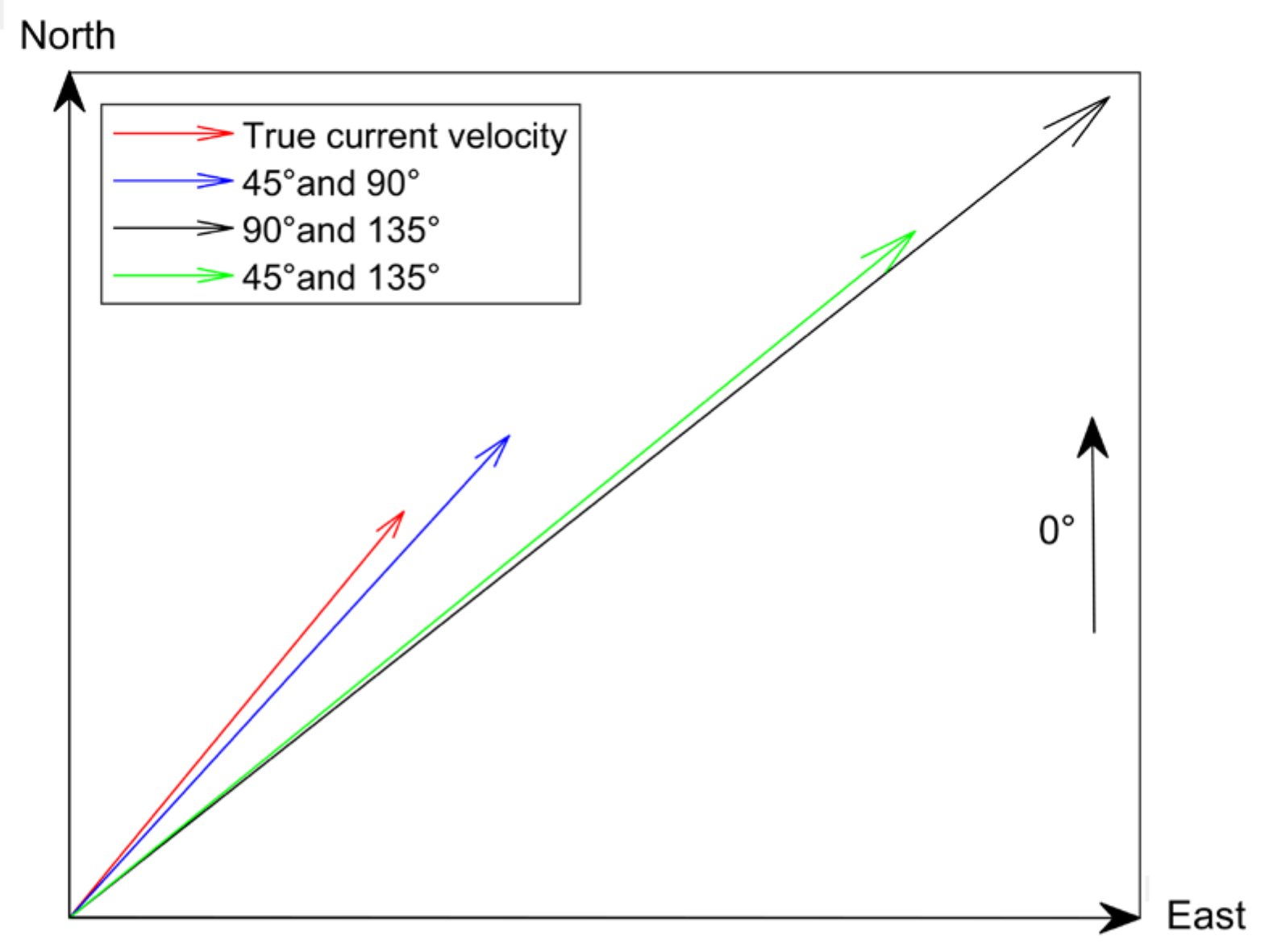
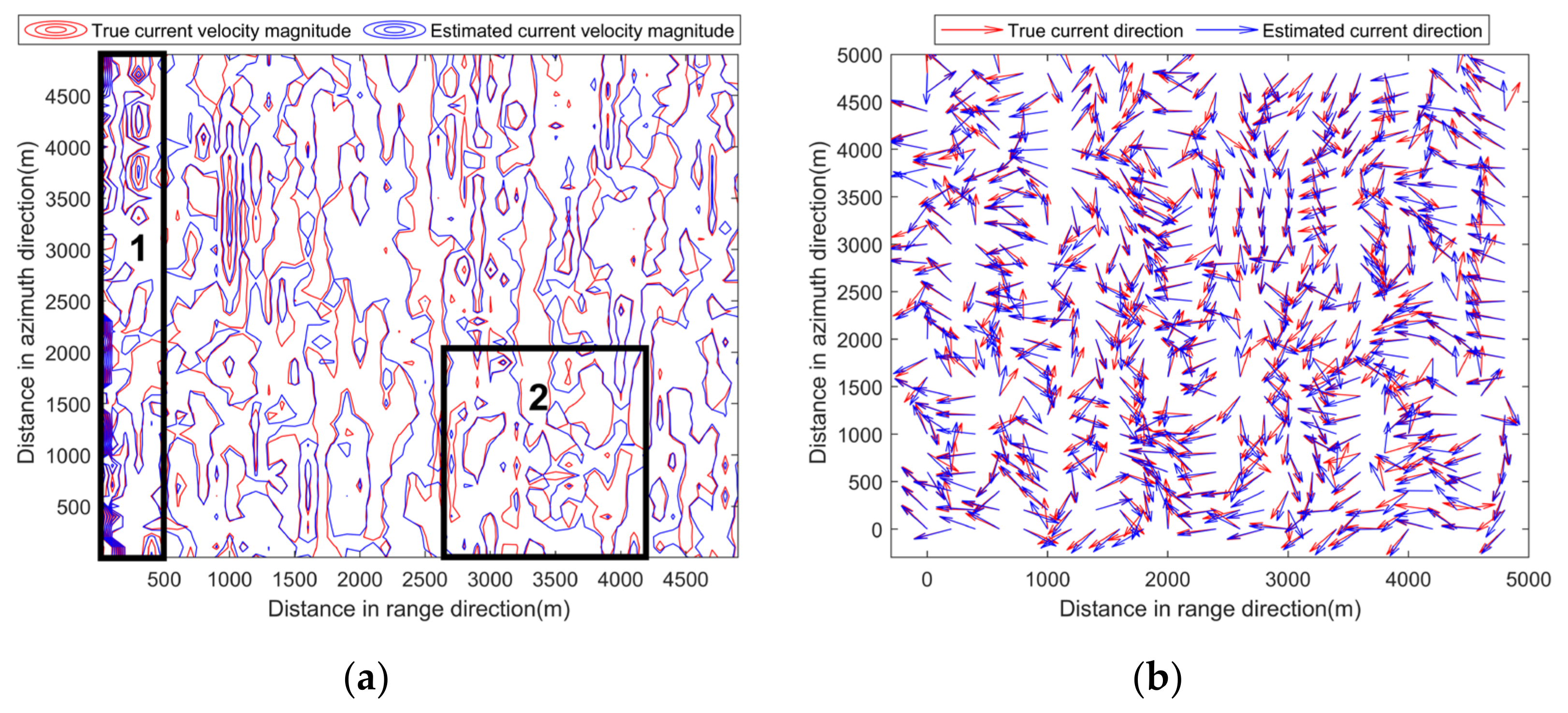
4.2. Verification of the Proposed Vector Current Velocity Determination Method
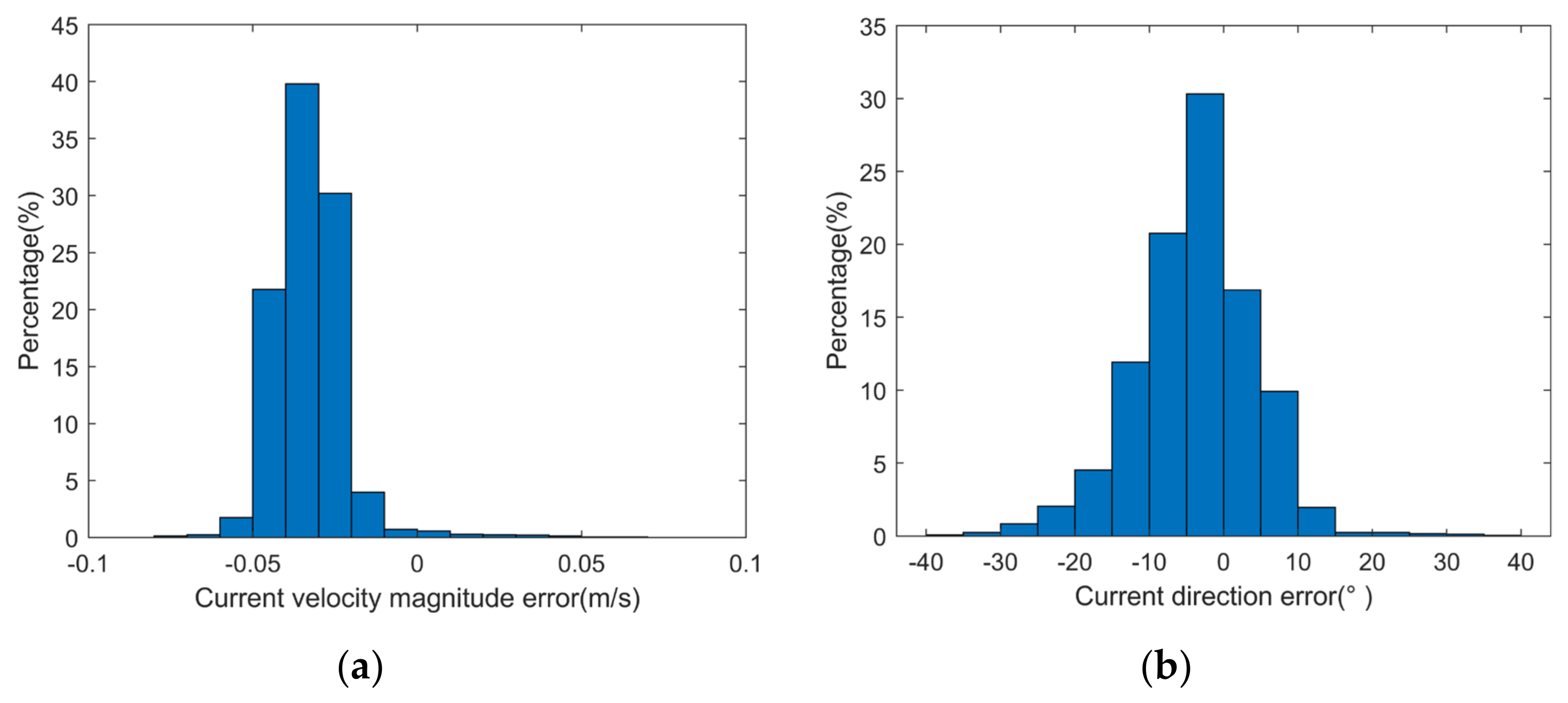
4.3. Current Velocity Inversion Results and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fois, F.; Hoogeboom, P.; Chevalier, F.L.; Stoffelen, A.; Mouche, A. DopSCAT: A mission concept for simultaneous measurements of marine winds and surface currents. J. Geophys. Res. Ocean. 2015, 120, 7857–7879. [Google Scholar] [CrossRef] [Green Version]
- Brumley, B.H.; Cabrera, R.G.; Deines, K.L.; Terray, E.A. Performance of a broad-band acoustic Doppler current profiler. IEEE J. Ocean. Eng. 1991, 16, 402–407. [Google Scholar] [CrossRef]
- Drever, R.G.; Sanford, T.B. A free-fall electromagnetic current meter-instrumentation. In Proceedings of the Conference on Electronic Engineering in Ocean Technology, Swansea, UK, 21–24 September 1970; pp. 353–370. [Google Scholar]
- Carter, R.W.; Anderson, I.E. Accuracy of current meter measurements. J. Hydraul. Div. 1963, 4, 105–115. [Google Scholar] [CrossRef]
- Georges, T.M.; Harlan, J.A.; Lematta, R.A. Large-scale mapping of ocean-surface currents with dual over-the-horizon radars. Lett. Nat. 1996, 379, 434–436. [Google Scholar] [CrossRef]
- Barrick, D. History, present status, and future directions of HF surface-wave radars in the US. In Proceedings of the International Conference on Radar, Adelaide, SA, Australia, 3–5 September 2003; pp. 652–655. [Google Scholar]
- Emery, W.J.; Baldwin, D.G.; Matthews, D.K. Sampling the Mesoscale Ocean Surface Currents with Various Satellite Altimeter Configurations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 795–803. [Google Scholar] [CrossRef]
- Romeiser, R.; Johannessen, J.; Collard, F.; Kudryavtsev, V.; Suchandt, S. Direct surface current field imaging from space by along-track InSAR and conventional SAR. In Oceanography from Space; Springer: New York, NY, USA, 2010; pp. 73–91. [Google Scholar]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. Oceans. 2005, 110, C07008. [Google Scholar] [CrossRef]
- Kim, D.; Moon, W.M.; Moller, D.; Imel, D.A. Measurements of ocean surface waves and currents using L-and C-Band along-track interferometric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2821–2832. [Google Scholar]
- Martin, A.; Gommenginger, C.P.; Yves, Q. Simultaneous ocean surface current and wind vectors retrieval with squinted SAR interferometry: Geophysical inversion and performance assessment. Remote Sens. Environ. 2018, 216, 798–808. [Google Scholar] [CrossRef] [Green Version]
- Ali, M.M.; Bhat, G.S.; Long, D.G.; Bharadwaj, S.; Bourassa, M.A. Estimating Wind Stress at the Ocean Surface from Scatterometer Observations. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1129–1132. [Google Scholar] [CrossRef] [Green Version]
- Spencer, M.W.; Wu, C.; Long, D. Improved resolution backscatter measurements with the SeaWinds Pencil-beam scatterometer. IEEE Trans. Geosci. Remote Sens. 2000, 38, 89–104. [Google Scholar] [CrossRef] [Green Version]
- Spencer, M.W. A Methodology for the Design of Spaceborne Pencil-Beam Scatterometer Systems. Ph.D. Thesis, Brigham Young University, Provo, UT, USA, 2001. [Google Scholar]
- Fabry, P.; Recchia, A.; de Kloe, J.; Stoffelen, A.; Husson, R.; Collard, F.; Chapron, B.; Mouche, A.; Enjolras, V.; Johannessen, J.; et al. Feasibility Study of Sea Surface Currents Measurements with Doppler Scatterometers. In Proceedings of the Esa Living Planet Symposium, Edinburgh, UK, 9–13 September 2013. [Google Scholar]
- Bao, Q.; Dong, X.; Zhu, D.; Lang, S.; Xu, X. The feasibility of ocean surface current measurement using pencil-beam rotating scatterometer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3441–3451. [Google Scholar] [CrossRef]
- Bao, Q.; Dong, X.; Zhu, D.; Xu, X. Ocean Surface Current Measurement Using Rotating Pencil-Beam Scatterometer. Acta Electron. Sin. 2015, 43, 1200–1204. [Google Scholar] [CrossRef]
- Fois, F.; Hoogeboom, P.; Chevalier, F.L.; Stoffelen, A. DOPSCAT: A mission concept for a Doppler wind-scatterometer. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2572–2575. [Google Scholar]
- Bao, Q. System Design and Simulation of Doppler Scatterometer—Wide Swath Ocean Surface Current Measurement. Ph.D. Thesis, Department of Electromagnetic Field and Microwave Technology, University of Chinese Academy of Sciences, Beijing, China, 2015. [Google Scholar]
- Bao, Q.; Lin, M.; Zhang, Y.; Dong, X.; Lang, S.; Gong, P. Ocean Surface Current Inversion Method for a Doppler Scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6505–6516. [Google Scholar] [CrossRef]
- Rodríguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Stiles, B.W.; Niamsuwan, N.; Monje, R.R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sens. 2018, 10, 576. [Google Scholar] [CrossRef] [Green Version]
- Wineteer, A.; Torres, H.S.; Rodríguez, E. On the Surface Current Measurement Capabilities of Spaceborne Doppler Scatterometry. Geophys Res. Lett. 2020, 47, e2020GL090116. [Google Scholar] [CrossRef]
- Romeiser, R.; Thompson, D.R. Numerical study on the along-track interferometric radar imaging mechanism of oceanic surface currents. IEEE Trans. Geosci. Remote Sens. 2000, 38, 446–458. [Google Scholar] [CrossRef] [Green Version]
- Thompson, D.R. Calculation of Microwave Doppler Spectra from the Ocean Surface with a Time-Dependent Composite Model. In Radar Scattering from Modulated Wind Waves; Komen, G.J., Oost, W.A., Eds.; Kluwer: Dordrecht, The Netherlands, 1989; pp. 27–40. [Google Scholar]
- Thompson, D.R.; Gotwols, B.L.; Keller, W.C. A comparison of Ku-band Doppler measurements at 20° incidence with predictions from a time-dependent scattering model. J. Geophys. Res. 1991, 96, 4947–4955. [Google Scholar] [CrossRef]
- Bao, Q. A Method of Measuring Ocean Surface Current Velocity Using Real Aperture Radar. Patent CN201510542007.0, 28 August 2015. Available online: http://d.wanfangdata.com.cn/patent/CN201510542007.0 (accessed on 10 May 2021).

| Application | Coverage | Measurement Accuracy (m/s) | Time Resolution (h) | Spatial Resolution (km) |
|---|---|---|---|---|
| Weather Service | Global | 0.1 | 6 | 12.5 |
| Ocean Service | Global | 0.1 | 1 | 12.5 |
| Ship Routing | Global | 0.05 | 1 | 1 |
| Pollution | Local | 0.1 | 1 | 0.1 |
| Fisheries Management | Local | 0.1 | 6 | 1 |
| Parameters | Specification |
|---|---|
| Satellite Velocity | 7373 m/s |
| Orbit Altitude | 963 km |
| Observation Azimuth | 10°, 30°, and 170° |
| Local Incident Angle | |
| Antenna Incident Angle | |
| Antenna Gain | 48 dB |
| Rotation Rate | 18 rpm |
| Carrier Frequency | 13.5 GHz |
| PRF | 12 kHz |
| Pulse Bandwidth | 5 MHz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Wang, Q.; Huang, W.; Fan, C.; Dai, Y. Vector Current Measurement Using Doppler Scatterometry with Optimally Selected Observation Azimuths. Remote Sens. 2021, 13, 4263. https://doi.org/10.3390/rs13214263
Sun W, Wang Q, Huang W, Fan C, Dai Y. Vector Current Measurement Using Doppler Scatterometry with Optimally Selected Observation Azimuths. Remote Sensing. 2021; 13(21):4263. https://doi.org/10.3390/rs13214263
Chicago/Turabian StyleSun, Weifeng, Qing Wang, Weimin Huang, Chenqing Fan, and Yongshou Dai. 2021. "Vector Current Measurement Using Doppler Scatterometry with Optimally Selected Observation Azimuths" Remote Sensing 13, no. 21: 4263. https://doi.org/10.3390/rs13214263
APA StyleSun, W., Wang, Q., Huang, W., Fan, C., & Dai, Y. (2021). Vector Current Measurement Using Doppler Scatterometry with Optimally Selected Observation Azimuths. Remote Sensing, 13(21), 4263. https://doi.org/10.3390/rs13214263








