BDS-3/Galileo Time and Frequency Transfer with Quad-Frequency Precise Point Positioning
Abstract
:1. Introduction
2. Methods
2.1. General Observations
2.2. Dual-Frequency IF PPP Model
2.3. Quad-Frequency IF PPP Models
2.4. Quad-Frequency Uncombined PPP Model
2.5. Characteristic of Quad-Frequency GNSS PPP Time Transfer Models
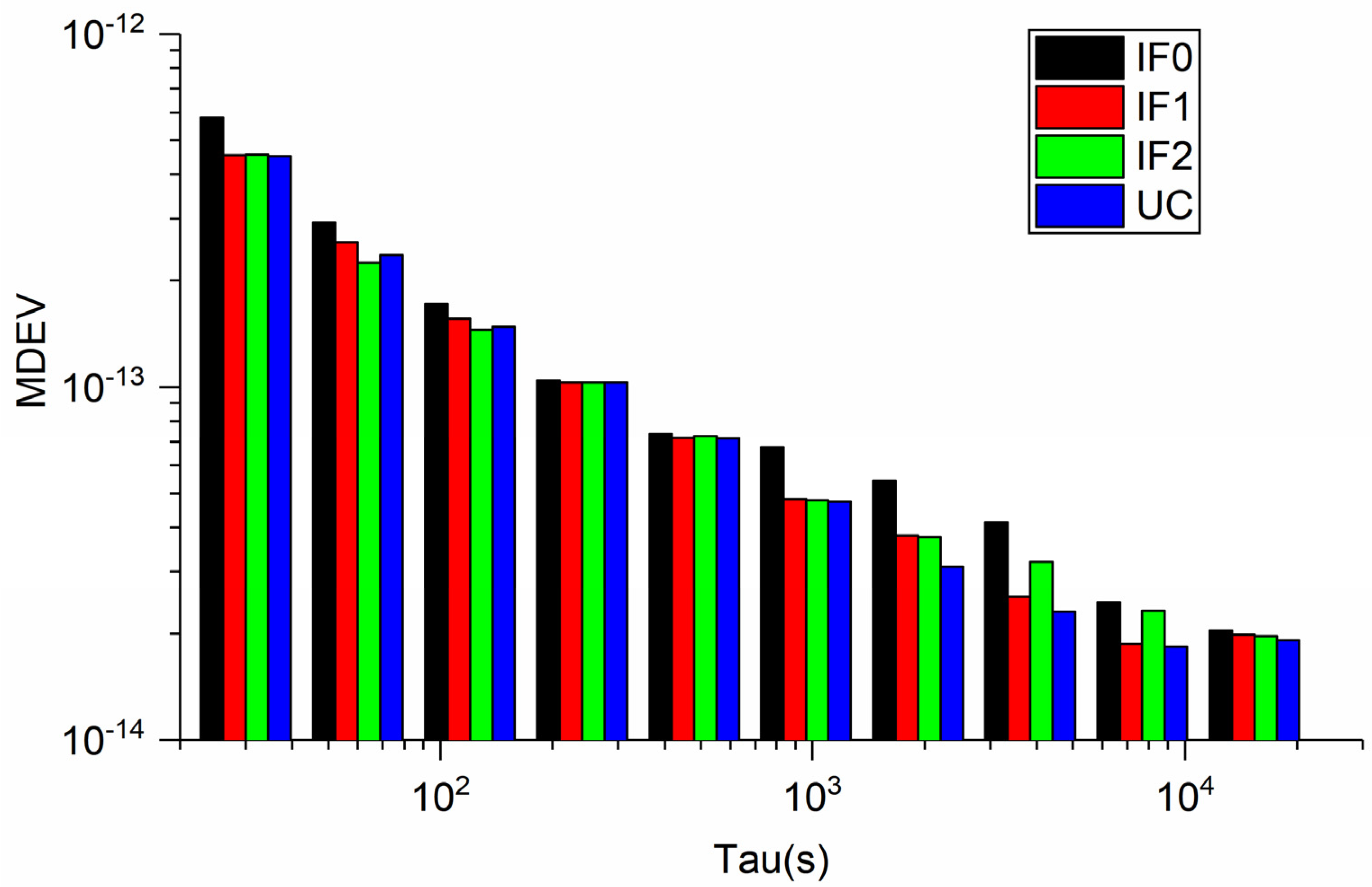
3. Results and Discussion
3.1. Data Acquisition and Processing Strategies
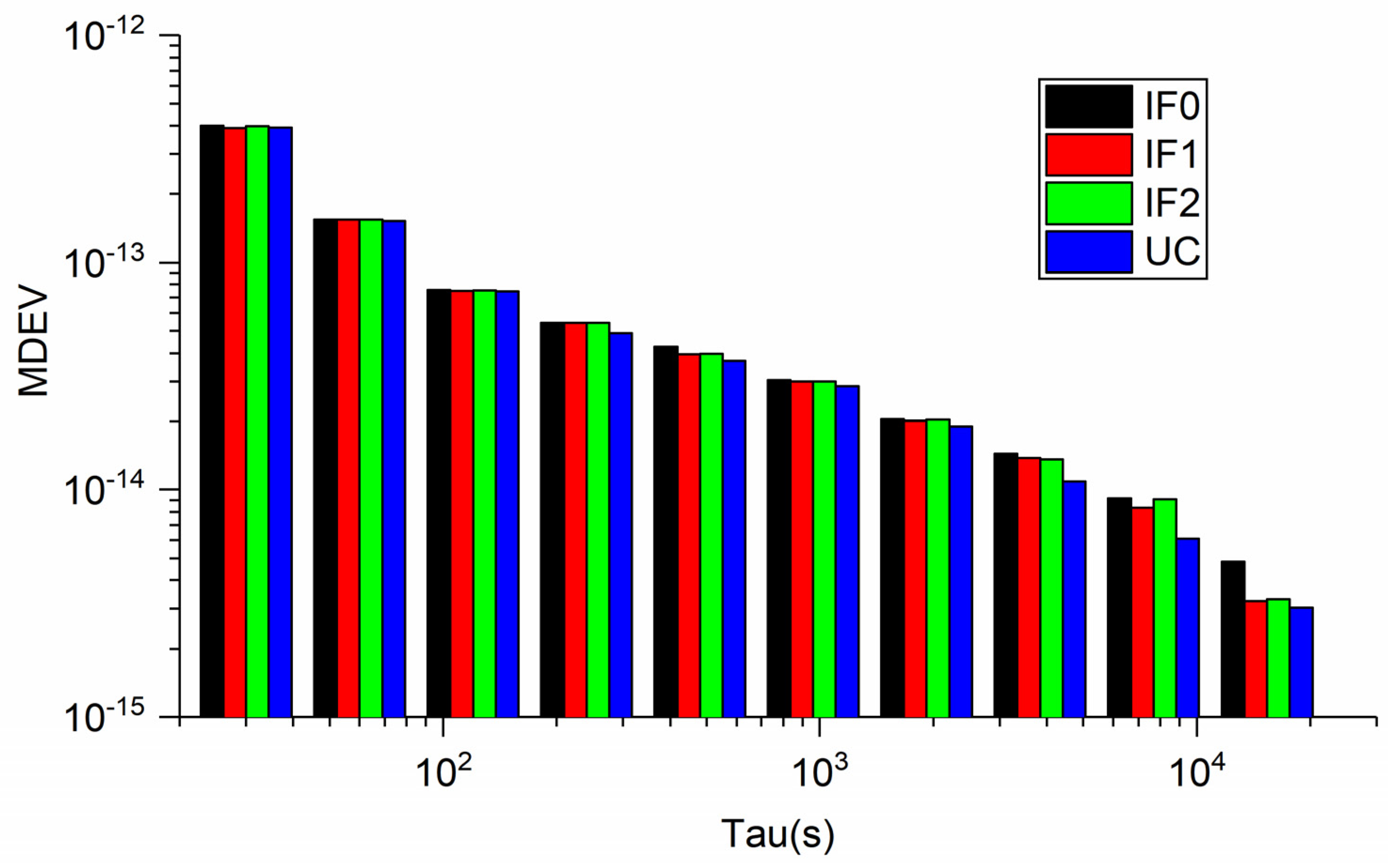
3.2. Quad-Frequency BDS-3 PPP Time Transfer Solutions
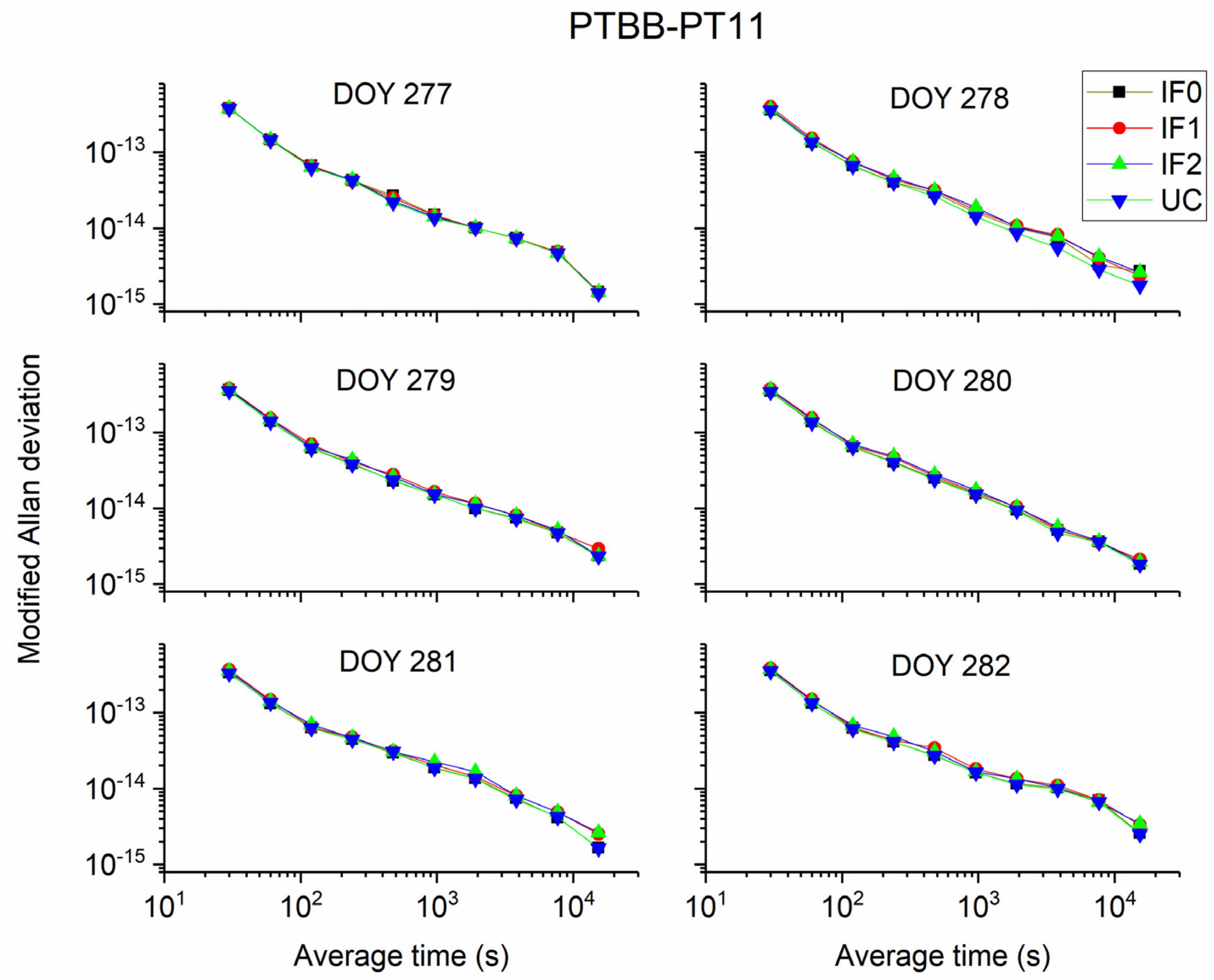
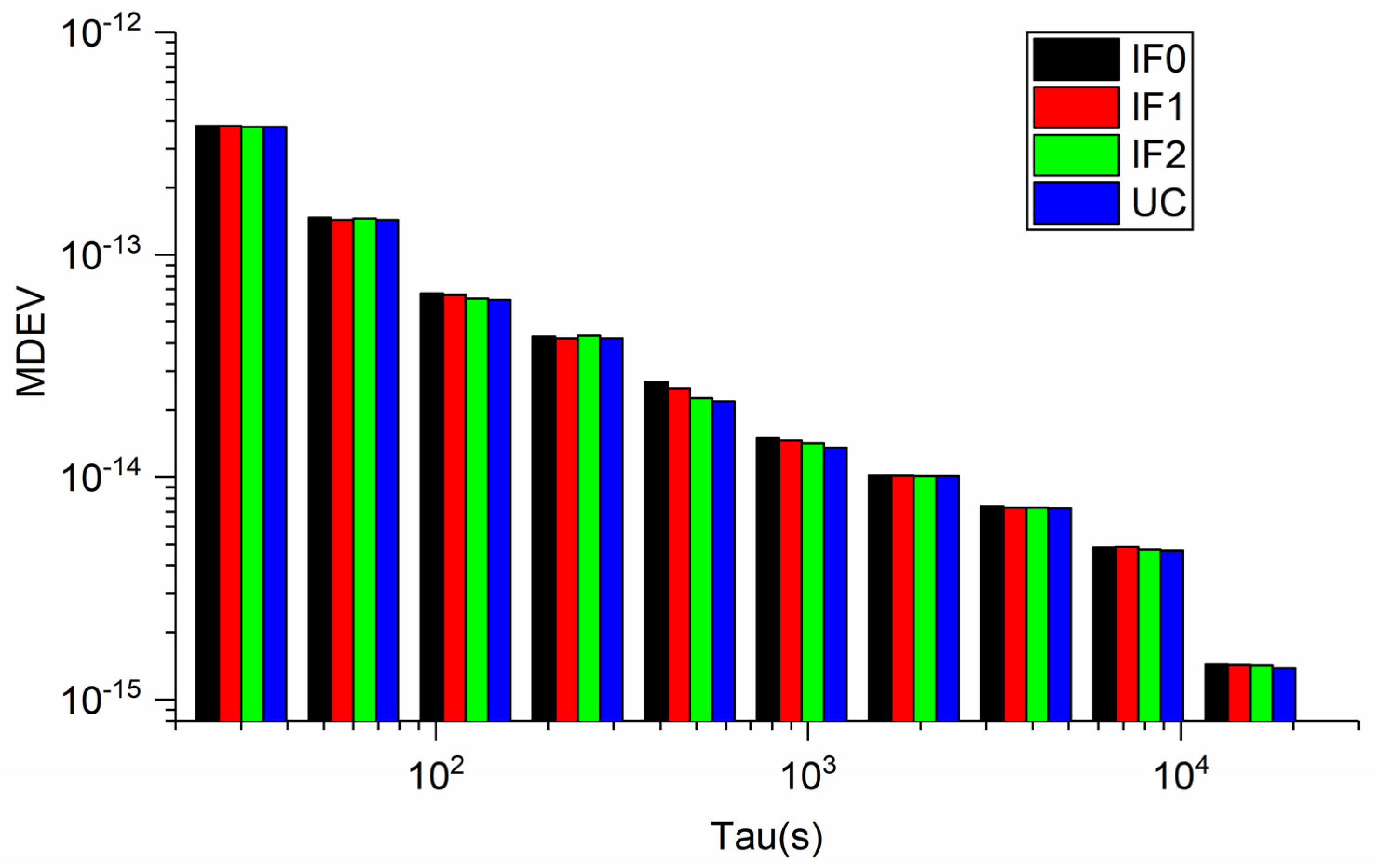
3.3. Quad-Frequency Galileo PPP Time Transfer Solutions
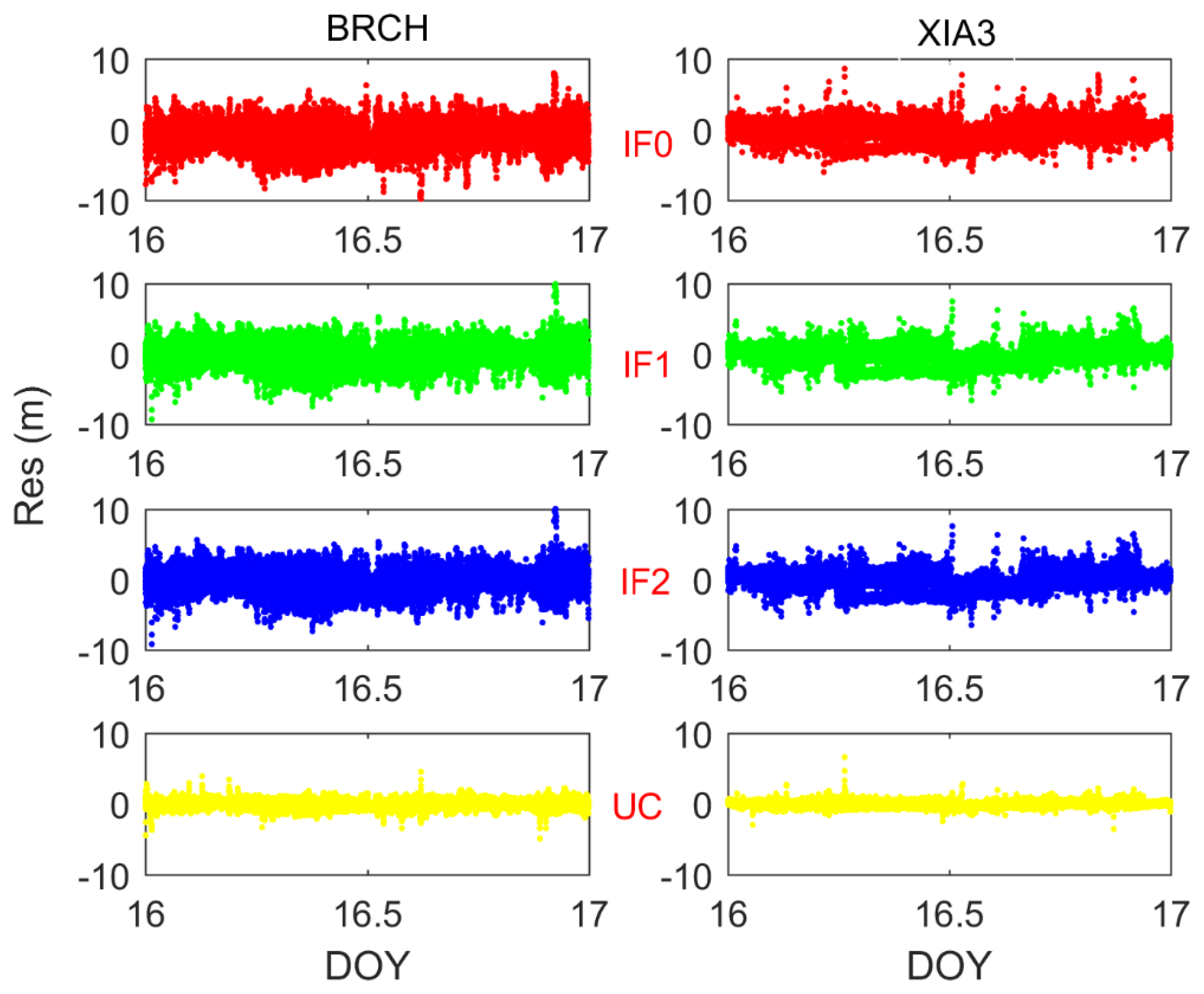
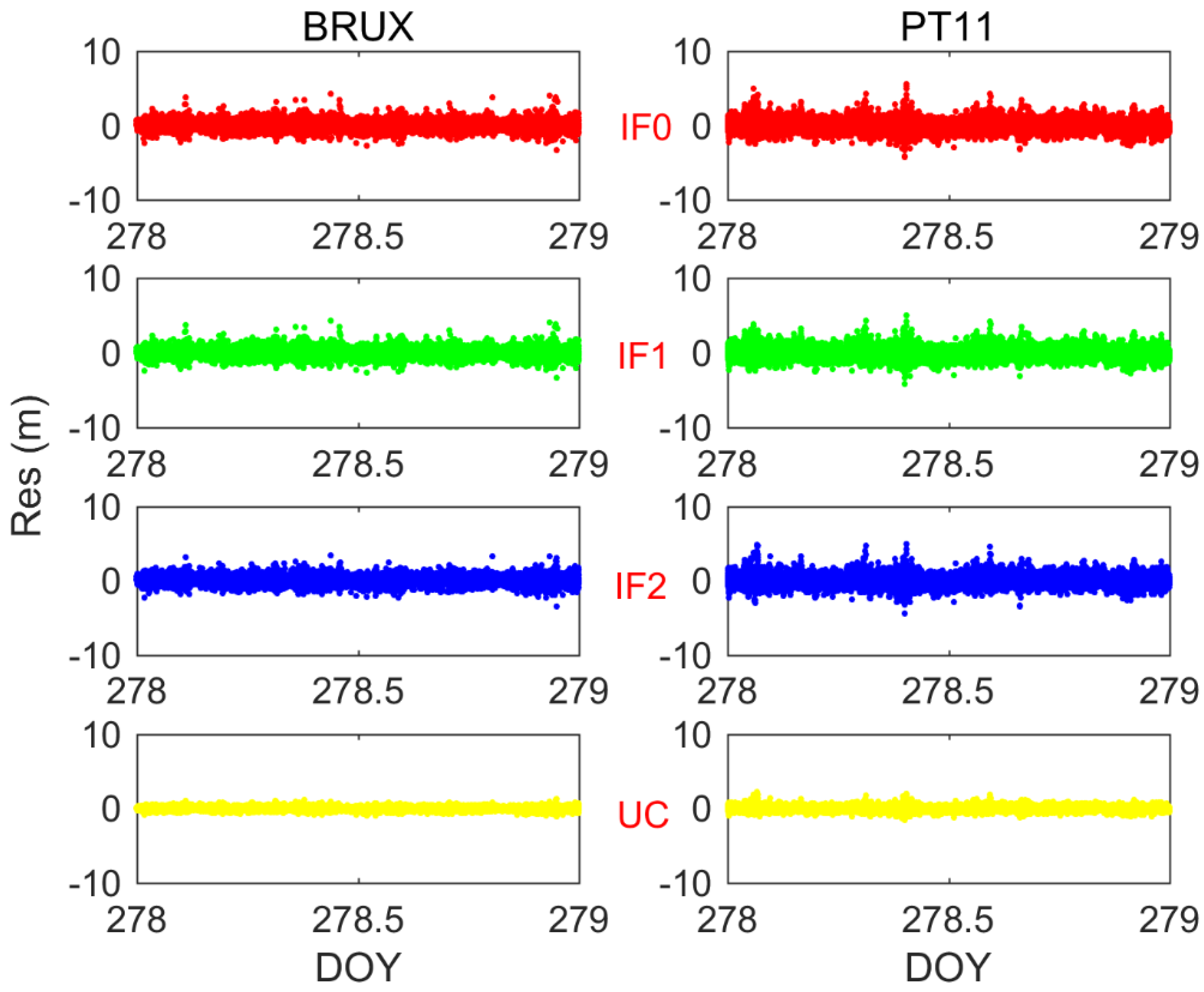
3.4. Observation Residuals
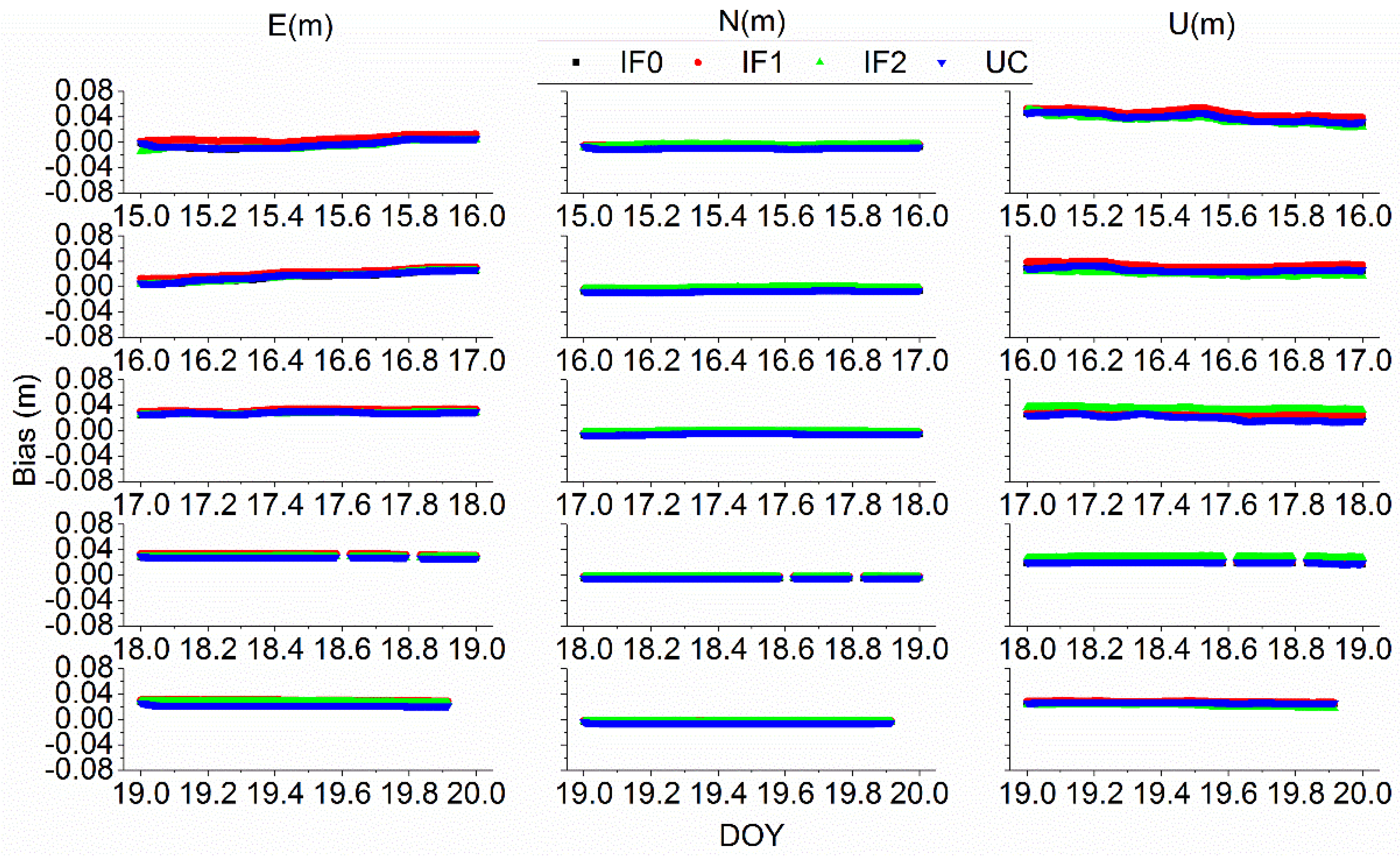
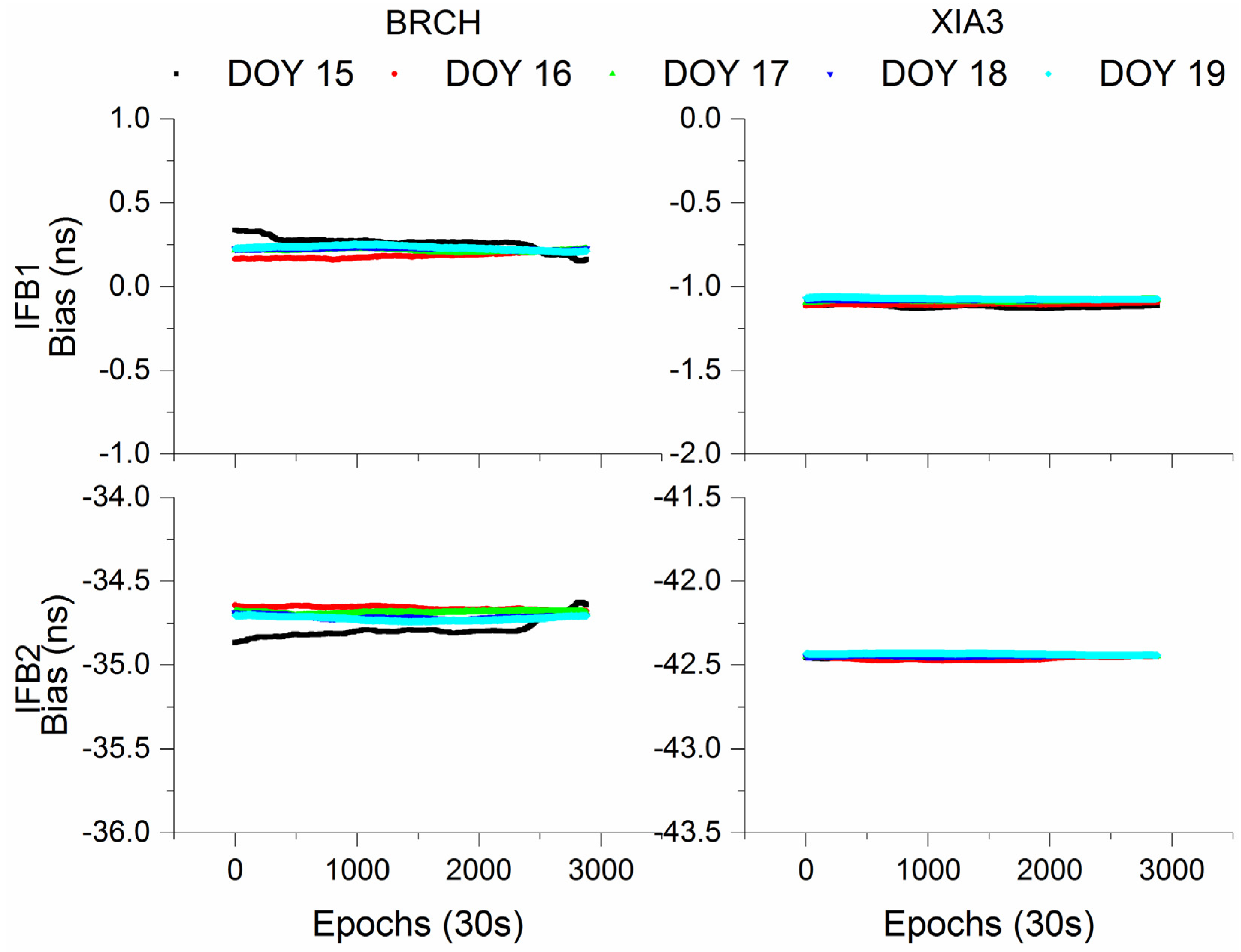
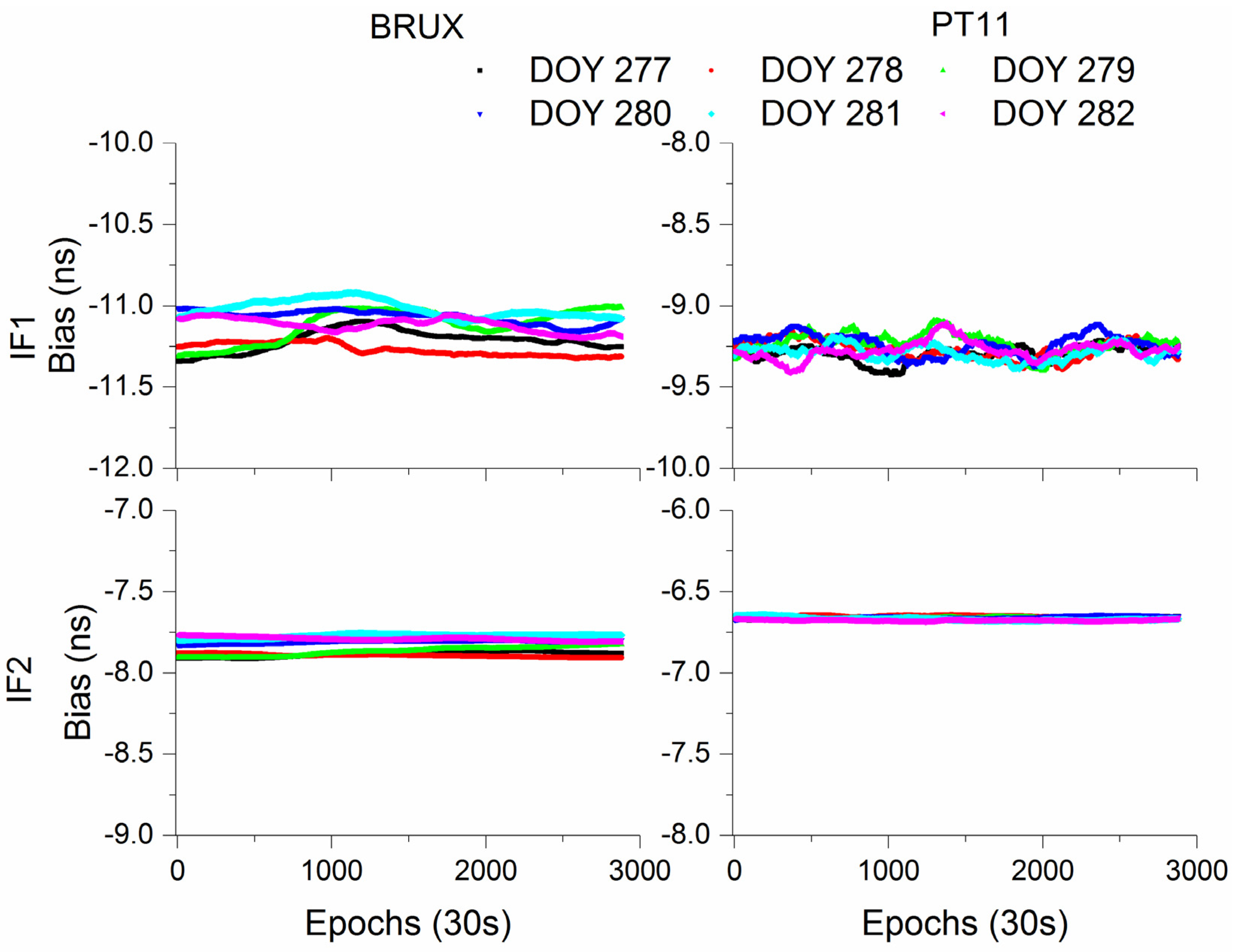
3.5. Positioning, Tropospheric Delay, and IFB Estimates
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y. GLONASS fractional-cycle bias estimation across inhomogeneous receivers for PPP ambiguity resolution. J. Geod. 2015, 90, 379–396. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, X.; Li, M. A modified carrier-to-code leveling method for retrieving ionospheric observables and detecting short-term temporal variability of receiver differential code biases. J. Geod. 2018, 93, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Li, X.; Ge, M.; Heinkelmann, R.; Nilsson, T.; Soja, B.; Dick, G.; Schuh, H. Estimation and evaluation of real-time precipitable water vapor from GLONASS and GPS. GPS Solut. 2016, 20, 703–713. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Zhou, F.; Liu, T.; Qin, W.; Wang, S.; Yang, X. Enhancing real-time precise point positioning time and frequency transfer with receiver clock modeling. GPS Solut. 2018, 23, 1–14. [Google Scholar] [CrossRef]
- Petit, G.; Jiang, Z. Precise Point Positioning for TAI Computation. Int. J. Navig. Obs. 2008, 2008, 1–8. [Google Scholar] [CrossRef]
- Steigenberger, P.; Fritsche, M.; Dach, R.; Schmid, R.; Montenbruck, O.; Uhlemann, M.; Prange, L. Estimation of satellite antenna phase center offsets for Galileo. J. Geod. 2016, 90, 773–785. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2013, 57, 144–152. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Hadas, T.; Kazmierski, K.; Sośnica, K. Performance of Galileo-only dual-frequency absolute positioning using the fully serviceable Galileo constellation. GPS Solut. 2019, 23, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Kubo, N.; Chen, J.; Wang, J.; Wang, H. Initial Positioning Assessment of BDS New Satellites and New Signals. Remote Sens. 2019, 11, 1320. [Google Scholar] [CrossRef] [Green Version]
- Dai, P.; Ge, Y.; Qin, W.; Yang, X. BDS-3 Time Group Delay and Its Effect on Standard Point Positioning. Remote Sens. 2019, 11, 1819. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Lv, H.; Shu, Y.; Zheng, J.; Zhang, K.; Liu, J. Improved performance of GNSS precise point positioning for high-rate seismogeodesy with recent BDS-3 and Galileo. Adv. Space Res. 2021. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Nie, L.; Wei, C.; Jia, S.; Jiang, S. Initial assessment of BeiDou-3 global navigation satellite system: Signal quality, RTK and PPP. GPS Solut. 2019, 23, 1–12. [Google Scholar] [CrossRef]
- Shi, C.; Wu, X.; Zheng, F.; Wang, X.; Wang, J. Modeling of BDS-2/BDS-3 single-frequency PPP with B1I and B1C signals and positioning performance analysis. Measurement 2021, 178, 109355. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Li, X.; Zhou, F.; Feng, G.; Yuan, Y.; Zhang, K. Galileo PPP rapid ambiguity resolution with five-frequency observations. GPS Solut. 2019, 24, 1–13. [Google Scholar] [CrossRef]
- Fidalgo, J.; Píriz, R.; Cezón, A.; Fernández, A.; Callewaert, K.; Bolchi, M.; Defraigne, P.; Bauch, A.; Danesi, A.; Jeannot, M.; et al. Proposal for the Definition of a Galileo Timing Service. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 827–839. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.; Liu, J. A comparison of three widely used GPS triple-frequency precise point positioning models. GPS Solut. 2019, 23, 1–3. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Modeling and Performance Analysis of GPS/GLONASS/BDS Precise Point Positioning. In Lecture Notes in Electrical Engineering, Proceeding of the China Satellite Navigation Conference (CSNC) 2014 Proceedings, Nanjing, China, 21–23 May 2014; Springer: Berlin/Heidelberg, Germany, 2014; Volume III, pp. 251–263. [Google Scholar] [CrossRef]
- Geng, J.; Bock, Y. Triple-frequency GPS precise point positioning with rapid ambiguity resolution. J. Geod. 2013, 87, 449–460. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and performance analysis of precise time transfer based on BDS triple-frequency un-combined observations. J. Geod. 2018, 93, 837–847. [Google Scholar] [CrossRef]
- Li, B.; Shen, Y.; Zhang, X. Three frequency GNSS navigation prospect demonstrated with semi-simulated data. Adv. Space Res. 2013, 51, 1175–1185. [Google Scholar] [CrossRef]
- Tu, R.; Liu, J.; Zhang, R.; Zhang, P.; Huang, X.; Lu, X. RTK model and positioning performance analysis using Galileo four-frequency observations. Adv. Space Res. 2019, 63, 913–926. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, Q.; Fu, W.; Guo, H. GPS/GLONASS time offset monitoring based on combined Precise Point Positioning (PPP) approach. Adv. Space Res. 2015, 55, 2950–2960. [Google Scholar] [CrossRef]
- Ge, Y.; Qin, W.; Cao, X.; Zhou, F.; Wang, S.; Yang, X. Consideration of GLONASS Inter-Frequency Code Biases in Precise Point Positioning (PPP) International Time Transfer. Appl. Sci. 2018, 8, 1254. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Dai, P.; Qin, W.; Yang, X.; Zhou, F.; Wang, S.; Zhao, X. Performance of Multi-GNSS Precise Point Positioning Time and Frequency Transfer with Clock Modeling. Remote Sens. 2019, 11, 347. [Google Scholar] [CrossRef] [Green Version]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Xiang, Y.; Gao, Y.; Shi, J.; Xu, C. Carrier phase-based ionospheric observables using PPP models. Geod. Geodyn. 2017, 8, 17–23. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Ge, M.; Li, P.; Wickert, J.; Schuh, H. Simultaneous estimation of GLONASS pseudorange inter-frequency biases in precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 19. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, Y.; Yuan, Y. PPP-RTK based on undifferenced and uncombined observations: Theoretical and practical aspects. J. Geod. 2018, 93, 1011–1024. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satellite System Signal In Space Interface Control Document; Open Service Signal China Satellite Navigation Office: Beijing, China, February 2018.
- Su, K.; Jin, S. Triple-frequency carrier phase precise time and frequency transfer models for BDS-3. GPS Solut. 2019, 23, 1–12. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Gao, Y.; Zhang, R.; Han, J. Performance of Galileo precise time and frequency transfer models using quad-frequency carrier phase observations. GPS Solut. 2020, 24, 1–18. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 1–10. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); Bureau International des Poids et Mesures: Sevres, France, 2010; No. IERS-TN-36. [Google Scholar]
- Wu, J.T.; Wu, S.C.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orienation on GPS carrier phase. Astrodynamics 1992, 18, 91–98. [Google Scholar]
- Kouba, J. Testing of global pressure/temperature (GPT) model and global mapping function (GMF) in GPS analyses. J. Geod. 2009, 83, 199–208. [Google Scholar] [CrossRef]






| e1 | e2 | e3 | e4 | Noise Amplification | ||
|---|---|---|---|---|---|---|
| IF0 | B1I-B3I | 2.9437 | −1.9437 | 0 | 0 | 3.5275 |
| IF1 | B1I-B3I | 2.9437 | −1.9437 | 0 | 0 | 3.5275 |
| B1C-B2a | 0 | 0 | 2.2606 | −1.2606 | 2.5883 | |
| IF2 | B1I-B3I-B1C | 1.3877 | −1.8908 | 1.5031 | 0 | 2.7857 |
| B1I-B3I-B2a | 2.3433 | −0.0893 | 0 | −1.2543 | 2.6594 | |
| UC | B1I | 1 | 0 | 0 | 0 | 1 |
| B3I | 0 | 1 | 0 | 0 | 1 | |
| B1C | 0 | 0 | 1 | 0 | 1 | |
| B2a | 0 | 0 | 0 | 1 | 1 |
| e1 | e2 | e3 | e4 | Noise Amplification | ||
|---|---|---|---|---|---|---|
| IF0 | E1-E5a | 2.2606 | −1.2606 | 0 | 0 | 2.5883 |
| IF1 | E1-E5a | 2.2606 | −1.2606 | 0 | 0 | 2.5883 |
| E1-E5b | 2.4220 | −1.4220 | 0 | 0 | 2.8086 | |
| E1-E5 | 2.3380 | −1.3380 | 0 | 0 | 2.6938 | |
| IF2 | E1-E5a-E5b | 2.3149 | −0.8363 | −0.4787 | 0 | 2.5075 |
| E1-E5a-E5 | 2.2929 | −0.7340 | 0 | −0.5589 | 2.4715 | |
| UC | E1 | 1 | 0 | 0 | 0 | 1 |
| E5a | 0 | 1 | 0 | 0 | 1 | |
| E5b | 0 | 0 | 1 | 0 | 1 | |
| E5 | 0 | 0 | 0 | 1 | 1 |
| Station Name | Timing Lab | Receiver | Antenna | External Clock | |
|---|---|---|---|---|---|
| BDS-3 | BRCH | PTB | CETC-54-GMR-4016 | GNSS-750 | UTC(PTB) |
| XIA3 | NTSC | CETC-54-GMR-4016 | NOV750.R4 | UTC(NTSC) | |
| Galileo | PTBB | PTB | SEPT POLARX4TR | LEIAR25.R4—LEIT | UTC(PTB) |
| PT11 | PTB | SEPT POLARX5TR | LEIAR25.R4—LEIT | UTC(PTB) | |
| BRUX | ROB | SEPT POLARX4TR | JAVRINGANT_DM—NONE | UTC(ROB) |
| Item | Strategy |
|---|---|
| Observations | BDS-3: undifferenced and uncombined observations in B1I, B3I, B1C, and B2a frequency Galileo: undifferenced and uncombined observations in E1, E5a, E5b, and E5 frequency |
| Weight of observation | Elevation-dependent |
| Cutoff angle | 10° |
| Sampling rate | 30 s |
| PCO and PCV | Corrected |
| Station displacement | Corrected [35] |
| Wind up | Corrected [36] |
| Relativistic effect | Corrected |
| Estimator | Kalman filter |
| Phase ambiguity | Estimated as constants at each arc (float values) |
| IFB | Estimated as random walk (RW) noise [18] |
| Receiver position | Estimated as constants in static model |
| Receiver clock offset | Estimated as white noise |
| Ionospheric delay | IF0, IF1, IF2 models: first-order effects removed with IF combination UC model: estimated as white noise |
| Tropospheric delay | Wet delay: estimated as random walk noise Dry delay: corrected by Saastamoinen model Mapping function: GMF [37] |
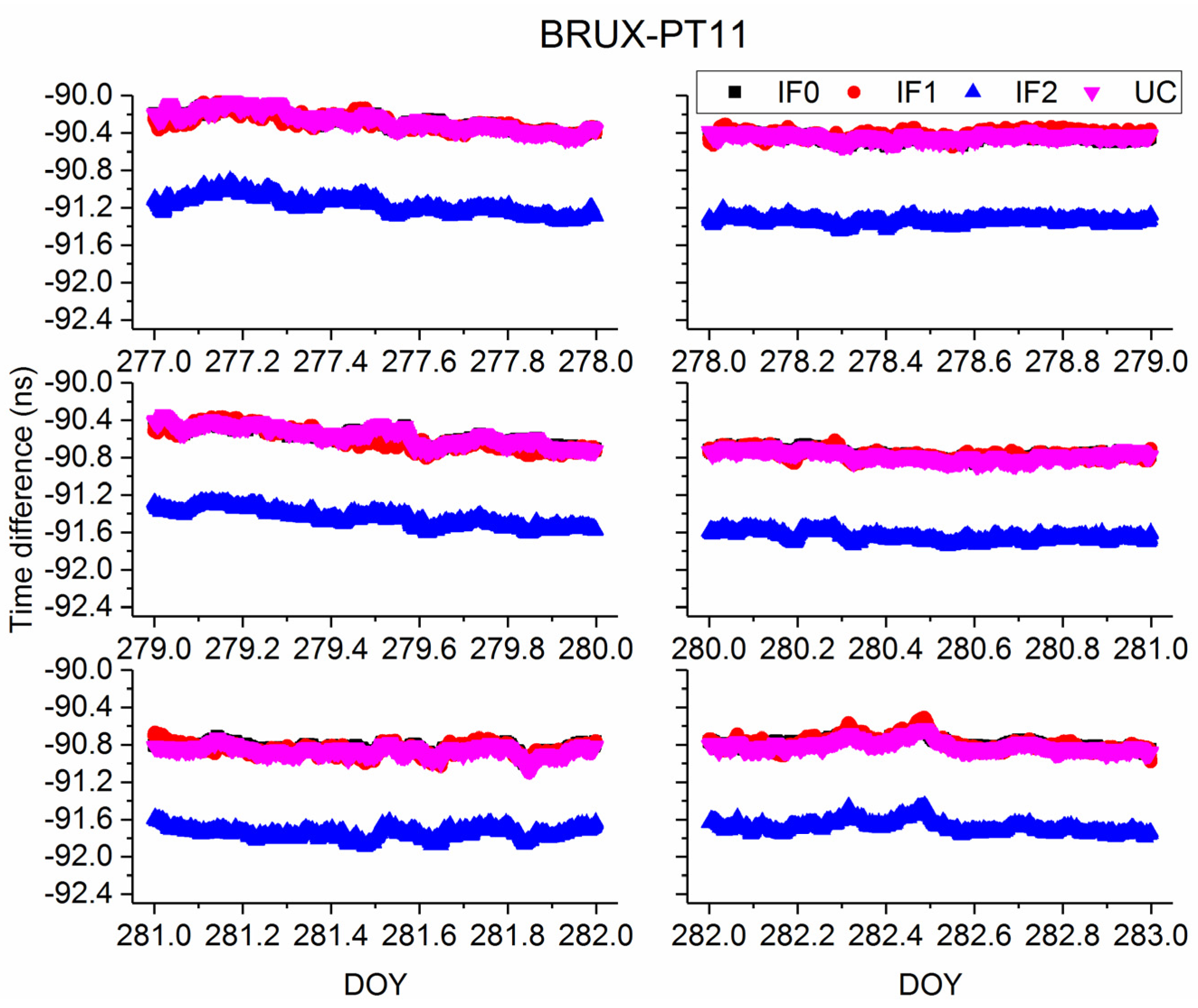
| DOY | IF0 | IF1 | IF2 | UC | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
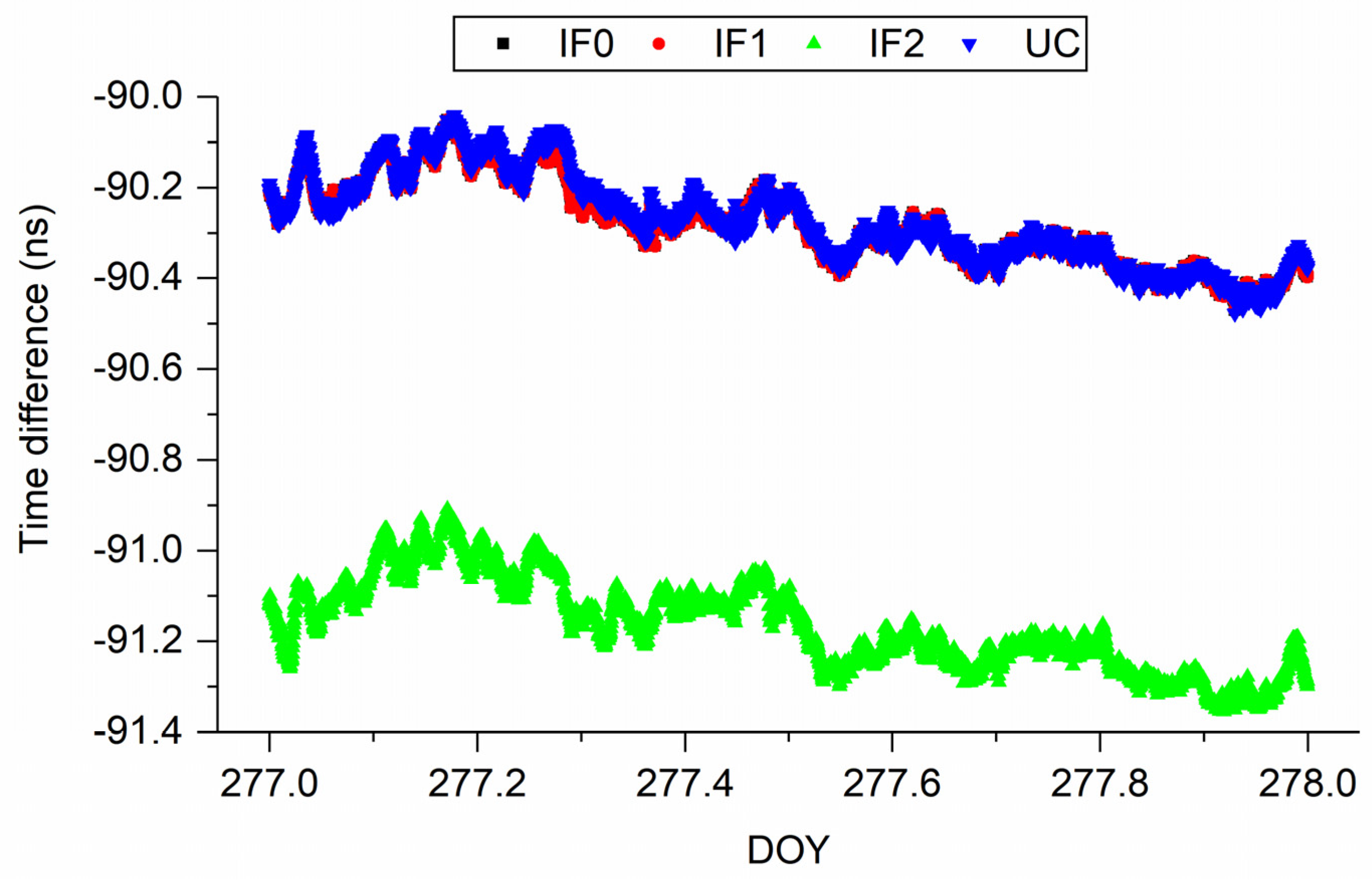
| 277 | −90.28 | 0.10 | −90.29 | 0.09 | −91.17 | 0.10 | −90.27 | 0.10 |
| 278 | −90.46 | 0.03 | −90.42 | 0.04 | −91.34 | 0.03 | −90.44 | 0.03 |
| 279 | −90.57 | 0.09 | −90.60 | 0.11 | −91.44 | 0.09 | −90.57 | 0.09 |
| 280 | −90.77 | 0.05 | −90.77 | 0.05 | −91.65 | 0.05 | −90.78 | 0.05 |
| 281 | −90.85 | 0.05 | −90.86 | 0.06 | −91.74 | 0.06 | −90.87 | 0.05 |
| 282 | −90.79 | 0.06 | −90.79 | 0.08 | −91.68 | 0.07 | −90.81 | 0.06 |
| DOY | IF0 | IF1 | IF2 | UC | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | |
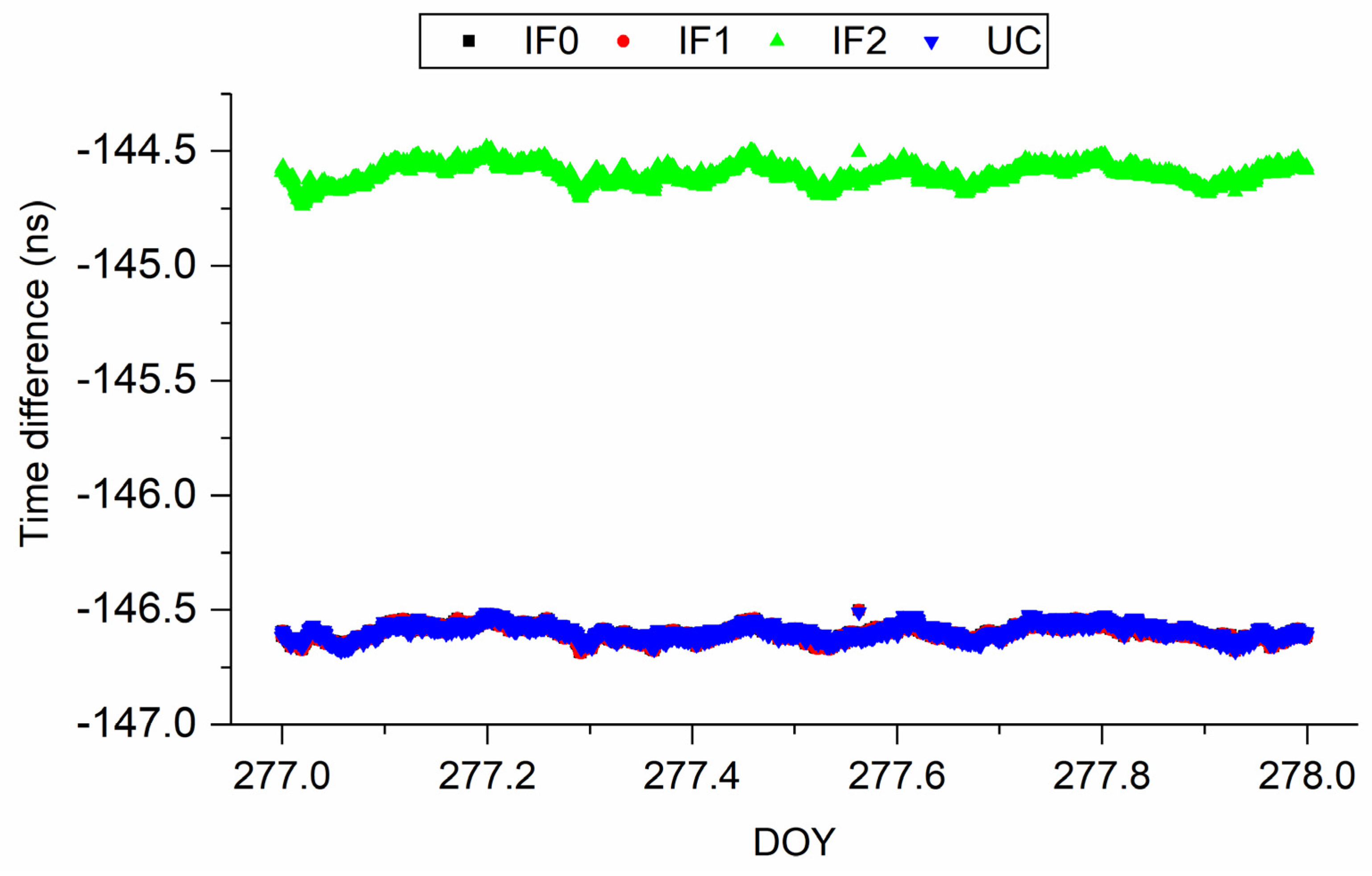
| 277 | −146.60 | 0.03 | −146.67 | 0.05 | −144.60 | 0.04 | −146.60 | 0.03 |
| 278 | −146.61 | 0.03 | −146.66 | 0.04 | −144.62 | 0.04 | −146.61 | 0.03 |
| 279 | −146.60 | 0.03 | −146.65 | 0.06 | −144.59 | 0.05 | −146.59 | 0.04 |
| 280 | −146.66 | 0.03 | −146.69 | 0.04 | −144.63 | 0.04 | −146.65 | 0.03 |
| 281 | −146.66 | 0.03 | −146.72 | 0.05 | −144.70 | 0.05 | −146.64 | 0.03 |
| 282 | −146.63 | 0.04 | −146.68 | 0.06 | −144.65 | 0.05 | −146.61 | 0.04 |
| DOY | E (cm) | N (cm) | U (cm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IF0 | IF1 | IF2 | UC | IF0 | IF1 | IF2 | UC | IF0 | IF1 | IF2 | UC | ||
| BRCH | 15 | 2.03 | 0.71 | 0.65 | 1.03 | 0.51 | 0.29 | 0.59 | 0.59 | 2.76 | 2.25 | 2.72 | 2.13 |
| 16 | 1.84 | 0.56 | 0.41 | 0.56 | 0.77 | 0.31 | 0.69 | 0.48 | 2.87 | 2.46 | 2.67 | 2.79 | |
| 17 | 1.67 | 0.41 | 0.70 | 0.82 | 0.92 | 0.43 | 0.77 | 0.75 | 2.10 | 2.67 | 2.14 | 2.05 | |
| 18 | 1.64 | 0.30 | 0.64 | 0.90 | 0.84 | 0.31 | 0.61 | 0.67 | 2.54 | 2.52 | 2.34 | 2.50 | |
| 19 | 0.85 | 0.30 | 0.22 | 0.55 | 0.85 | 0.35 | 0.51 | 0.84 | 2.42 | 2.38 | 2.15 | 2.41 | |
| XIA3 | 15 | 0.75 | 0.67 | 0.90 | 0.59 | 0.93 | 0.50 | 0.52 | 0.84 | 3.91 | 3.68 | 3.48 | 3.70 |
| 16 | 1.59 | 2.25 | 1.61 | 1.91 | 0.71 | 0.38 | 0.27 | 0.62 | 2.53 | 3.39 | 2.91 | 2.49 | |
| 17 | 2.79 | 2.75 | 2.62 | 2.03 | 0.45 | 0.19 | 0.22 | 0.41 | 3.35 | 3.53 | 3.00 | 3.20 | |
| 18 | 2.86 | 2.81 | 2.84 | 2.86 | 0.52 | 0.19 | 0.33 | 0.43 | 3.85 | 3.10 | 3.79 | 3.57 | |
| 19 | 2.63 | 2.60 | 2.75 | 2.25 | 0.45 | 0.18 | 0.35 | 0.43 | 3.61 | 3.60 | 3.57 | 3.57 | |
| DOY | E(cm) | N(cm) | U(cm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IF0 | IF1 | IF2 | UC | IF0 | IF1 | IF2 | UC | IF0 | IF1 | IF2 | UC | ||
| BRUX | 277 | 0.42 | 0.14 | 0.15 | 0.36 | 0.15 | 0.17 | 0.12 | 0.08 | 0.96 | 1.17 | 1.51 | 0.95 |
| 278 | 0.35 | 0.09 | 0.11 | 0.35 | 0.19 | 0.20 | 0.15 | 0.08 | 0.99 | 1.16 | 1.18 | 0.91 | |
| 279 | 0.46 | 0.21 | 0.23 | 0.40 | 0.20 | 0.20 | 0.15 | 0.09 | 0.94 | 0.88 | 0.88 | 0.90 | |
| 280 | 0.39 | 0.16 | 0.17 | 0.35 | 0.23 | 0.22 | 0.18 | 0.13 | 0.86 | 0.86 | 0.87 | 0.81 | |
| 281 | 0.34 | 0.14 | 0.15 | 0.32 | 0.24 | 0.24 | 0.20 | 0.14 | 0.89 | 0.83 | 0.84 | 0.85 | |
| 282 | 0.35 | 0.16 | 0.18 | 0.31 | 0.24 | 0.25 | 0.20 | 0.14 | 0.88 | 0.85 | 0.87 | 0.85 | |
| PT11 | 277 | 0.45 | 0.46 | 0.13 | 0.45 | 0.13 | 0.12 | 0.13 | 0.13 | 1.10 | 1.09 | 1.21 | 1.06 |
| 278 | 0.41 | 0.42 | 0.11 | 0.40 | 0.11 | 0.08 | 0.11 | 0.11 | 0.90 | 0.88 | 1.00 | 0.77 | |
| 279 | 0.39 | 0.39 | 0.10 | 0.33 | 0.10 | 0.07 | 0.10 | 0.10 | 0.78 | 0.76 | 0.81 | 0.79 | |
| 280 | 0.34 | 0.34 | 0.08 | 0.37 | 0.08 | 0.06 | 0.08 | 0.08 | 0.80 | 0.80 | 0.82 | 0.75 | |
| 281 | 0.34 | 0.33 | 0.08 | 0.31 | 0.08 | 0.06 | 0.08 | 0.08 | 0.77 | 0.79 | 0.77 | 0.77 | |
| 282 | 0.35 | 0.34 | 0.12 | 0.31 | 0.12 | 0.06 | 0.12 | 0.12 | 0.80 | 0.83 | 0.83 | 0.73 | |
| PTBB | 277 | 0.10 | 0.39 | 0.11 | 0.10 | 0.31 | 0.58 | 0.47 | 0.49 | 0.85 | 0.80 | 0.90 | 0.51 |
| 278 | 0.36 | 0.80 | 0.34 | 0.26 | 0.13 | 0.21 | 0.12 | 0.11 | 1.12 | 0.82 | 0.92 | 0.73 | |
| 279 | 0.63 | 0.63 | 0.19 | 0.07 | 0.11 | 0.19 | 0.13 | 0.12 | 1.43 | 0.75 | 0.98 | 0.98 | |
| 280 | 0.20 | 0.52 | 0.20 | 0.18 | 0.15 | 0.18 | 0.13 | 0.09 | 1.28 | 0.99 | 0.89 | 0.82 | |
| 281 | 0.15 | 0.27 | 0.07 | 0.14 | 0.18 | 0.12 | 0.08 | 0.12 | 1.31 | 0.99 | 0.80 | 0.83 | |
| 282 | 0.10 | 0.08 | 0.11 | 0.07 | 0.19 | 0.09 | 0.08 | 0.09 | 1.33 | 0.89 | 0.78 | 0.82 | |
| DOY | IF0 | IF1 | IF2 | UC | |
|---|---|---|---|---|---|
| BRCH | 15 | 1.3 | 1.32 | 1.32 | 1.31 |
| 16 | 0.80 | 0.80 | 0.83 | 0.84 | |
| 17 | 1.20 | 1.40 | 1.40 | 1.21 | |
| 18 | 1.20 | 1.02 | 1.02 | 0.64 | |
| 19 | 1.00 | 0.88 | 0.88 | 0.74 | |
| XIA3 | 15 | 1.76 | 1.82 | 1.82 | 1.81 |
| 16 | 2.06 | 2.11 | 2.11 | 2.01 | |
| 17 | 2.17 | 2.20 | 2.19 | 2.01 | |
| 18 | 1.66 | 1.93 | 1.94 | 1.95 | |
| 19 | 1.72 | 1.78 | 1.78 | 1.78 |
| DOY | IF0 | IF1 | IF2 | UC | |
|---|---|---|---|---|---|
| BRUX | 277 | 0.98 | 1.00 | 1.04 | 0.88 |
| 278 | 0.61 | 0.76 | 0.70 | 0.57 | |
| 279 | 0.60 | 0.92 | 0.76 | 0.64 | |
| 280 | 0.52 | 0.63 | 0.63 | 0.52 | |
| 281 | 0.83 | 1.04 | 0.96 | 0.81 | |
| 282 | 0.77 | 0.80 | 0.86 | 0.71 | |
| PT11 | 277 | 0.97 | 0.96 | 0.98 | 0.84 |
| 278 | 0.60 | 0.81 | 0.73 | 0.58 | |
| 279 | 0.59 | 0.72 | 0.58 | 0.54 | |
| 280 | 0.40 | 0.48 | 0.47 | 0.39 | |
| 281 | 0.65 | 0.74 | 0.69 | 0.64 | |
| 282 | 0.79 | 0.80 | 0.84 | 0.78 | |
| PTBB | 277 | 0.86 | 0.90 | 0.91 | 0.72 |
| 278 | 0.53 | 0.63 | 0.62 | 0.50 | |
| 279 | 0.75 | 0.88 | 0.90 | 0.70 | |
| 280 | 0.53 | 0.68 | 0.57 | 0.51 | |
| 281 | 0.8 | 0.91 | 1.05 | 0.83 | |
| 282 | 0.60 | 0.90 | 0.87 | 0.56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; Cao, X.; Shen, F.; Yang, X.; Wang, S. BDS-3/Galileo Time and Frequency Transfer with Quad-Frequency Precise Point Positioning. Remote Sens. 2021, 13, 2704. https://doi.org/10.3390/rs13142704
Ge Y, Cao X, Shen F, Yang X, Wang S. BDS-3/Galileo Time and Frequency Transfer with Quad-Frequency Precise Point Positioning. Remote Sensing. 2021; 13(14):2704. https://doi.org/10.3390/rs13142704
Chicago/Turabian StyleGe, Yulong, Xinyun Cao, Fei Shen, Xuhai Yang, and Shengli Wang. 2021. "BDS-3/Galileo Time and Frequency Transfer with Quad-Frequency Precise Point Positioning" Remote Sensing 13, no. 14: 2704. https://doi.org/10.3390/rs13142704
APA StyleGe, Y., Cao, X., Shen, F., Yang, X., & Wang, S. (2021). BDS-3/Galileo Time and Frequency Transfer with Quad-Frequency Precise Point Positioning. Remote Sensing, 13(14), 2704. https://doi.org/10.3390/rs13142704






