Focus Improvement of Airborne High-Squint Bistatic SAR Data Using Modified Azimuth NLCS Algorithm Based on Lagrange Inversion Theorem
Abstract
:1. Introduction
2. BiSAR Signal Model and Modified LIT Spectrum for High-Squint BiSAR
2.1. BiSAR Signal Model and LIT Spectrum
2.2. Modified LIT Spectrum for High-Squint BiSAR
3. A Modified Bistatic Azimuth NLCS Algorithm for the High-Squint BiSAR Imaging
3.1. Range Focusing via the Bulk Secondary Range Compression Operation
3.2. Azimuth Focusing via the Modified Bistatic Azimuth NLCS Operation
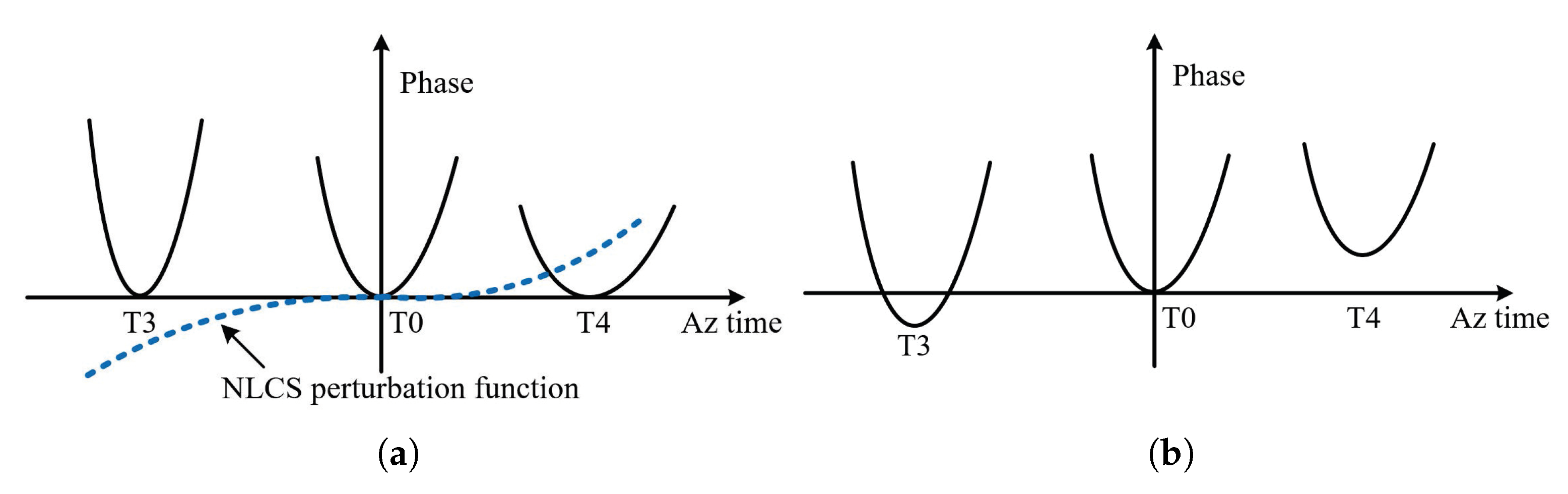
3.2.1. Azimuth-Dependent Characteristic Evaluation
3.2.2. Derivation of the Modified Bistatic Azimuth NLCS Coeffcients
4. Simulation Experiments and Discussion
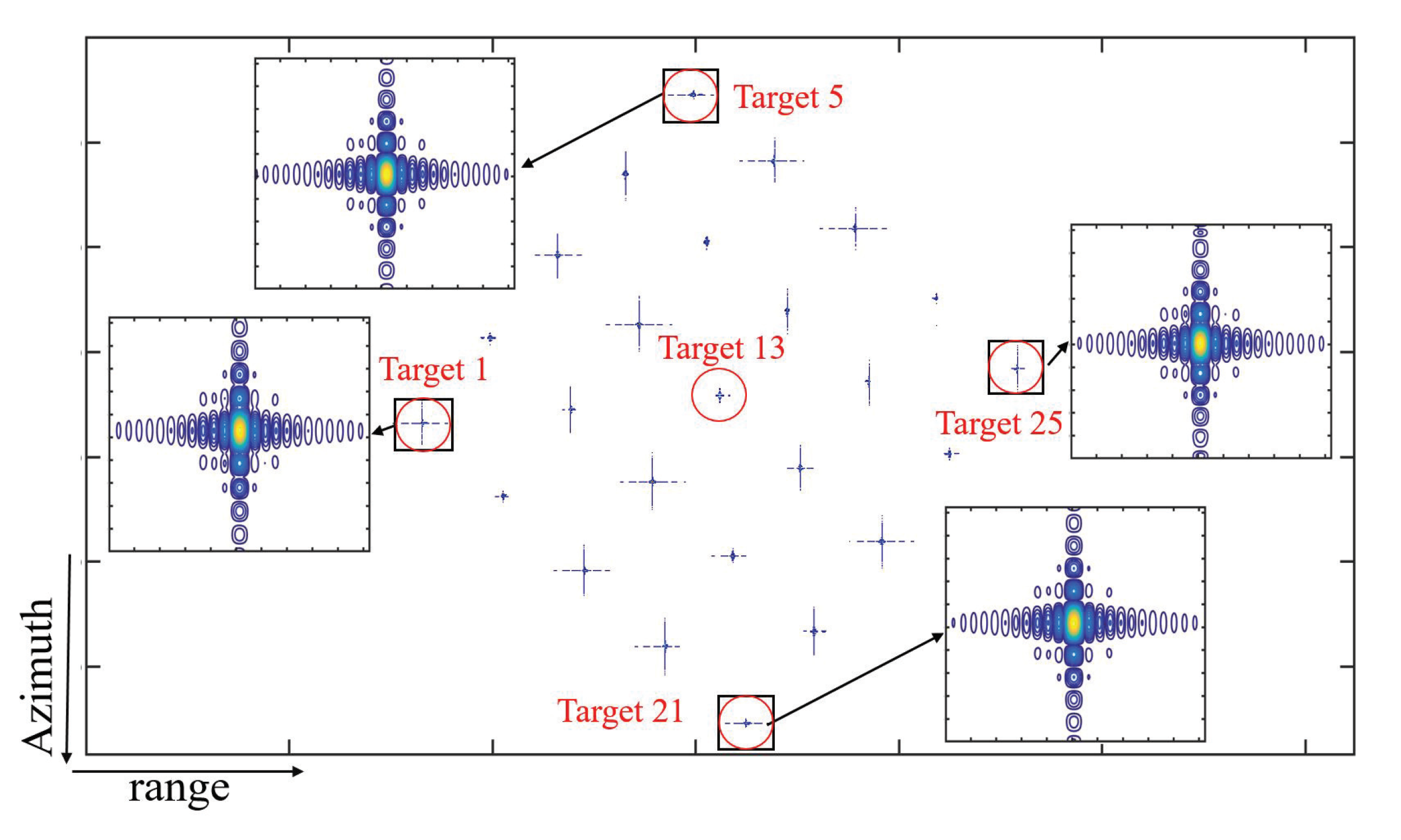
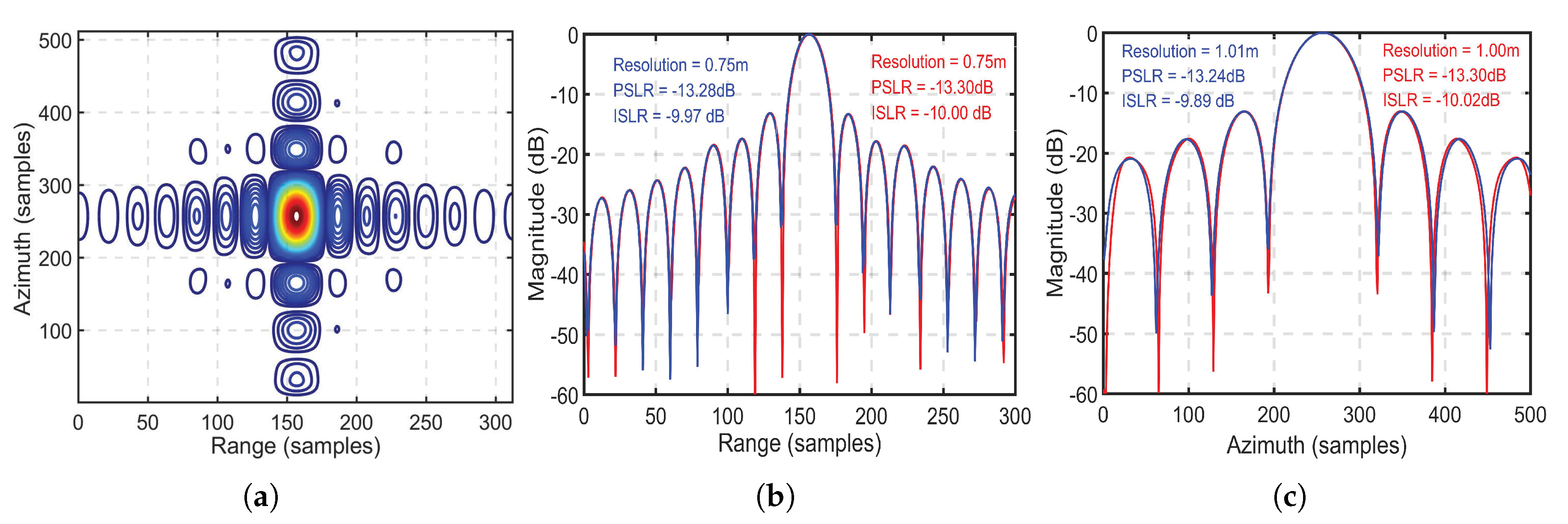
4.1. Simulation Results by the Modified Bistatic ANLCS Algorithm
4.2. Comparison Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Loffeld, O.; Nies, H.; Peters, V.; Knedlik, S. Models and useful relations for bistatic SAR processing. IEEE Trans. Geosci. Remote Sens. 2004, 10, 2031–2038. [Google Scholar] [CrossRef]
- Wang, R.; Deng, Y.; Loffeld, O.; Nies, H.; Walterscheid, I.; Espeter, T.; Klare, J.; Ender, J. Processing the Azimuth-Variant Bistatic SAR Data by Using Monostatic Imaging Algorithms Based on Two-Dimensional Principle of Stationary Phase. IEEE Trans. Geosci. Remote Sens. 2011, 10, 3504–3520. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Y.; Wang, R.; Ning, L.; Loffeld, O. Spaceborne/stationary bistatic sar imaging with terrasarx as an illuminator in staring-spotlight mode. IEEE Trans. Geosci. Remote Sens. 2016, 9, 5203–5216. [Google Scholar] [CrossRef]
- Li, C.; Zhang, H.; Deng, Y.; Wang, R.; Liu, K.; Liu, D.; Jin, G.; Zhang, Y. Focusing the L-Band Spaceborne Bistatic SAR Mission Data Using a Modified RD Algorithm. IEEE Trans. Geosci. Remote Sens. 2020, 1, 294–306. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A. Spaceborne bi- and multistatic SAR: Potential and challenges. Proc. Inst. Elect. Eng. Radar Sonar Navig. 2006, 3, 184–198. [Google Scholar] [CrossRef] [Green Version]
- Duque, S.; Lopez-Dekker, P.; Mallorqui, J.J. Single-Pass Bistatic SAR Interferometry Using Fixed-Receiver Configurations: Theory and Experimental Validation. IEEE Trans. Geosci. Remote Sens. 2010, 6, 2740–2749. [Google Scholar] [CrossRef]
- Maslikowski, L.; Samczynski, P.; Baczyk, M.; Krysik, P.; Kulpa, K. Passive bistatic SAR imaging—Challenges and limitations. IEEE Aerosp. Electron. Syst. Mag. 2014, 7, 23–29. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, J.; Wang, R.; Deng, Y.; Wang, W.; Li, N. An Accelerated Backprojection Algorithm for Monostatic and Bistatic SAR Processing. Remote Sens. 2018, 10, 140. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Loffeld, O.; Ul-Ann, Q.; Nies, H.; Ortiz, A.M.; Samarah, A. A Bistatic Point Target Reference Spectrum for General Bistatic SAR Processing. IEEE Geosci. Remote Sens. Lett. 2008, 3, 517–521. [Google Scholar] [CrossRef]
- Wu, J.; Yang, J.; Huang, Y.; Yang, H.; Liu, Z. A point target reference spectrum for general bistatic SAR processing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 1393–1396. [Google Scholar]
- Vu, V.T.; Sjögren, T.K.; Pettersson, M.I. Two-Dimensional Spectrum for BiSAR Derivation Based on Lagrange Inversion Theorem. IEEE Geosci. Remote Sens. Lett. 2014, 7, 1210–1214. [Google Scholar] [CrossRef] [Green Version]
- Natroshvili, K.; Loffeld, O.; Nies, H.; Ortiz, A.M.; Knedlik, S. Focusing of General Bistatic SAR Configuration Data With 2-D Inverse Scaled FFT. IEEE Trans. Geosci. Remote Sens. 2006, 10, 2718–2727. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Nies, H.; Knedlik, S.; Ender, J.H.G. Chirp-scaling algorithm for bistatic SAR data in the constant-offset configuration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 952–964. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.; Cumming, I.G. A Two-Dimensional Spectrum for Bistatic SAR Processing Using Series Reversion. IEEE Geosci. Remote Sens. Lett. 2007, 1, 93–96. [Google Scholar] [CrossRef]
- Neo, Y.L.; Wong, F.H.; Cumming, I.G. Processing of Azimuth-Invariant Bistatic SAR Data Using the Range Doppler Algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 1, 14–21. [Google Scholar] [CrossRef] [Green Version]
- Wong, F.H.; Cumming, I.G.; Neo, Y.L. Focusing bistatic SAR data using the nonlinear chirp scaling algorithm. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2493–2505. [Google Scholar] [CrossRef] [Green Version]
- Qiu, X.; Hu, D.; Ding, C. An improved NLCS algorithm with capability analysis for one-stationary BiSAR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3179–3186. [Google Scholar] [CrossRef]
- Zeng, T.; Hu, C.; Wu, L.; Liu, L.; Tian, W.; Zhu, M.; Long, T. Extended NLCS algorithm of BiSAR systems with a squinted transmitter and a fixed receiver: Theory and experimental confirmation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5019–5030. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Nies, H.; Ender, J.H.G. Focusing spaceborne/airborne hybrid bistatic SAR data using wavenumber-domain algorithm. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2275–2283. [Google Scholar] [CrossRef]
- Liu, B.; Wang, T.; Wu, Q.; Bao, Z. Bistatic SAR Data Focusing Using an Omega-K Algorithm Based on Method of Series Reversion. IEEE Trans. Geosci. Remote Sens. 2009, 8, 2899–2912. [Google Scholar]
- Zhang, X.; Huang, H.; Ying, W.; Wang, H.; Xiao, J. An Indirect Range-Doppler Algorithm for Multireceiver Synthetic Aperture Sonar Based on Lagrange Inversion Theorem. IEEE Trans. Geosci. Remote Sens. 2017, 6, 3572–3587. [Google Scholar] [CrossRef]
- Cumming, I.; Wong, F. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Boston, MA, USA, 2005; pp. 113–168. [Google Scholar]
- Sun, G.; Jiang, X.; Xing, M.; Qiao, Z.; Wu, Y.; Bao, Z. Focus Improvement of Highly Squinted Data Based on Azimuth Nonlinear Scaling. IEEE Trans. Geosci. Remote Sens. 2011, 6, 2308–2322. [Google Scholar] [CrossRef]
- An, D.; Huang, X.; Jin, T.; Zhou, Z. Extended Nonlinear Chirp Scaling Algorithm for High-Resolution Highly Squint SAR Data Focusing. IEEE Trans. Geosci. Remote Sens. 2012, 9, 3595–3609. [Google Scholar] [CrossRef]
- Wang, W.; Liao, G.; Li, D.; Xu, Q. Focus Improvement of Squint Bistatic SAR Data Using Azimuth Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2014, 1, 229–233. [Google Scholar] [CrossRef]
- Li, D.; Liao, G.; Wang, W.; Xu, Q. Extended Azimuth Nonlinear Chirp Scaling Algorithm for Bistatic SAR Processing in High-Resolution Highly Squinted Mode. IEEE Geosci. Remote Sens. Lett. 2014, 6, 1134–1138. [Google Scholar] [CrossRef]
- Li, D.; Lin, H.; Liu, H.; Liao, G.; Tan, X. Focus Improvement for High-Resolution Highly Squinted SAR Imaging Based on 2-D Spatial-Variant Linear and Quadratic RCMs Correction and Azimuth-Dependent Doppler Equalization. IEEE Trans. Geosci. Remote Sens. 2017, 1, 168–183. [Google Scholar] [CrossRef]
- Li, Z.; Liang, Y.; Xing, M.; Huai, Y.; Zeng, L.; Bao, Z. Focusing of Highly Squinted SAR Data With Frequency Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2016, 1, 23–27. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, Y.; Chang, Y.; Liu, E.; Tang, X.; Zhang, J. Focus High-Resolution Highly Squint SAR Data Using Azimuth-Variant Residual RCMC and Extended Nonlinear Chirp Scaling Based on a New Circle Model. IEEE Geosci. Remote Sens. Lett. 2018, 4, 547–551. [Google Scholar] [CrossRef]
- Sun, Z.; Wu, J.; Li, Z.; Huang, Y.; Yang, J. Highly Squint SAR Data Focusing Based on Keystone Transform and Azimuth Extended Nonlinear Chirp Scaling. IEEE Geosci. Remote Sens. Lett. 2015, 1, 145–149. [Google Scholar]
- Zhao, S.; Deng, Y.; Wang, R. Attitude-steering strategy for squint spaceborne synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2016, 8, 1163–1167. [Google Scholar] [CrossRef]
- Davidson, G.W.; Cumming, I. Signal properties of spaceborne squintmode SAR. IEEE Trans. Geosci. Remote Sens. 1997, 3, 611–617. [Google Scholar] [CrossRef] [Green Version]
- Bamler, R.; Meyer, F.; Liebhart, W. Processing of bistatic sar data from quasi-stationary configurations. IEEE Trans. Geosci. Remote Sens. 2007, 11, 3350–3358. [Google Scholar] [CrossRef]
- Yeo, T.S.; Tan, N.L.; Zhang, C.B.; Lu, Y.H. A new subaperture approach to high squint SAR processing. IEEE Trans. Geosci. Remote Sens. 2001, 5, 954–968. [Google Scholar]
- Jin, M.Y.; Wu, C. A SAR correlation algorithm which accommodates large-range migration. IEEE Trans. Geosci. Remote Sens. 1984, 6, 592–597. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M.; Xia, X.; Zhang, L.; Guo, R.; Bao, Z. Focus Improvement of High-Squint SAR Based on Azimuth Dependence of Quadratic Range Cell Migration Correction. IEEE Geosci. Remote Sens. Lett. 2013, 1, 150–154. [Google Scholar] [CrossRef]
- An, D.; Li, Y.; Huang, X.; Li, X.; Zhou, Z. Performance evaluation of frequency-domain algorithms for chirped low frequency uwb sar data processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 2, 678–690. [Google Scholar] [CrossRef]
- Davidson, G.W.; Cumming, I.G. A chirp scaling approach for processing squint mode SAR data. Aerosp. Electron. Syst. IEEE Trans. 1996, 32, 121–133. [Google Scholar] [CrossRef]
- Krieger, G.; Fiedler, H.; Houman, D.; Moreira, A. Analysis of system concepts for bi-and multi-static sar missions. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 2, pp. 770–772. [Google Scholar]
- Walterscheid, I.; Brenner, A.; Ender, J. Results on bistatic synthetic aperture radar. Electron. Lett. 2004, 19, 1224–1225. [Google Scholar] [CrossRef] [Green Version]




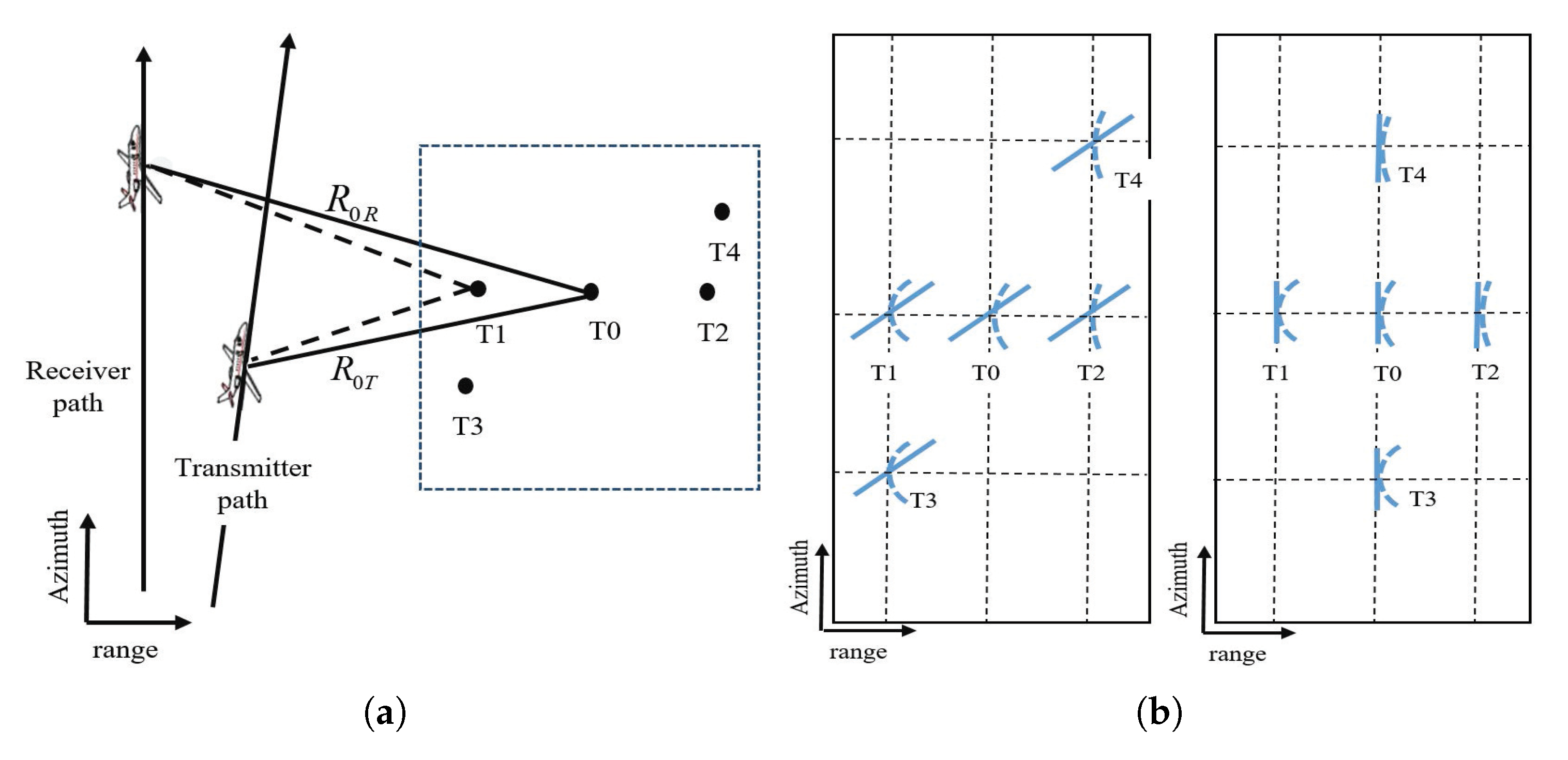
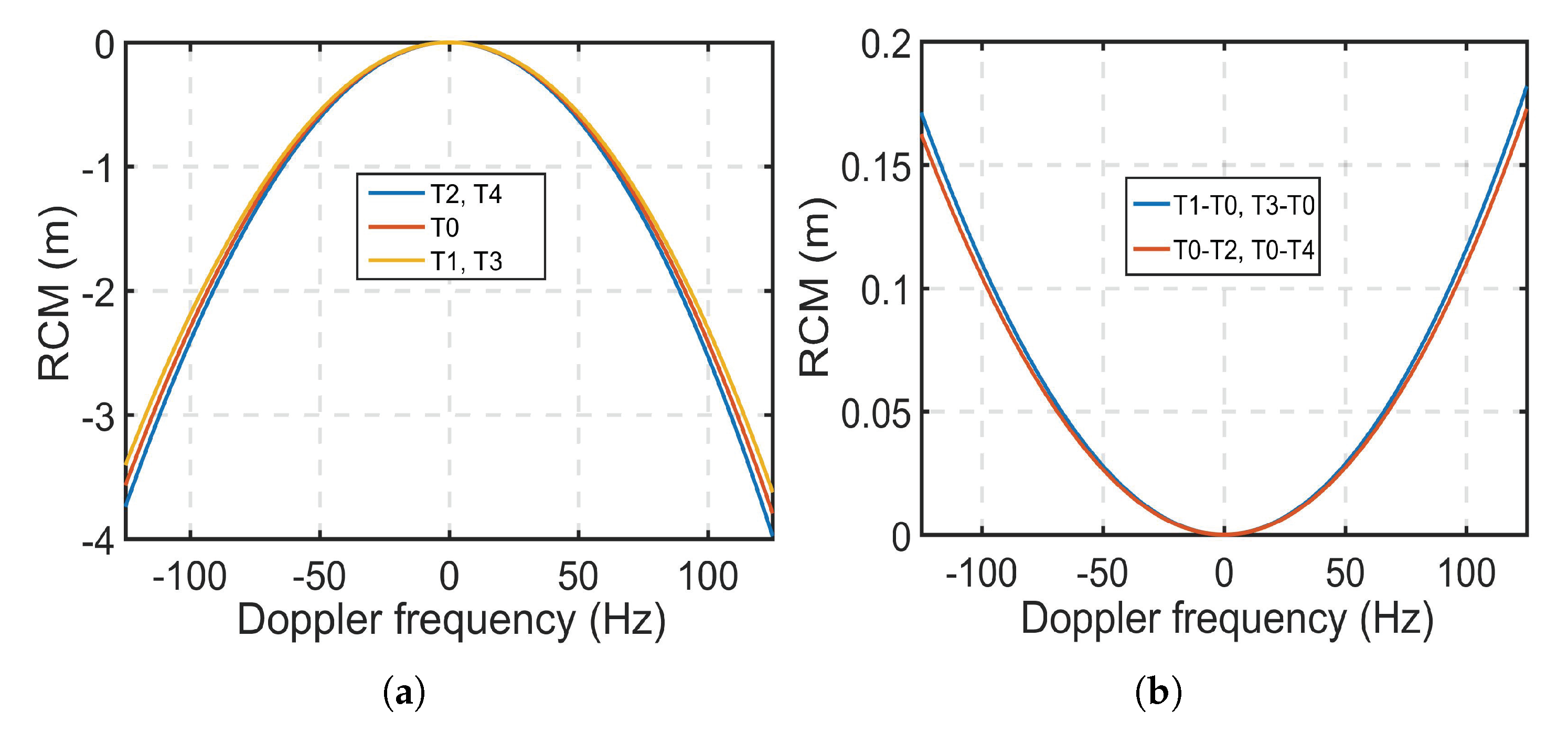
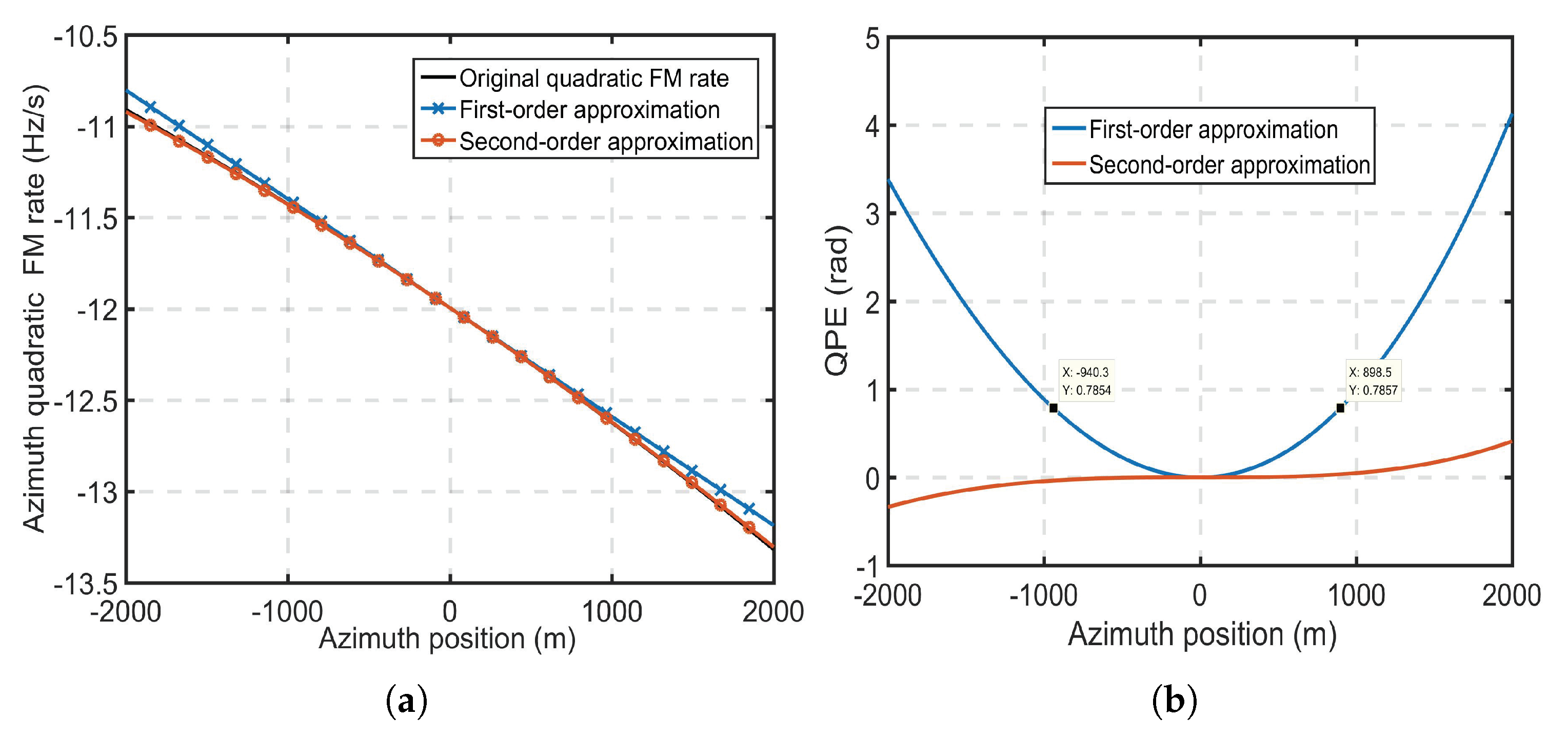
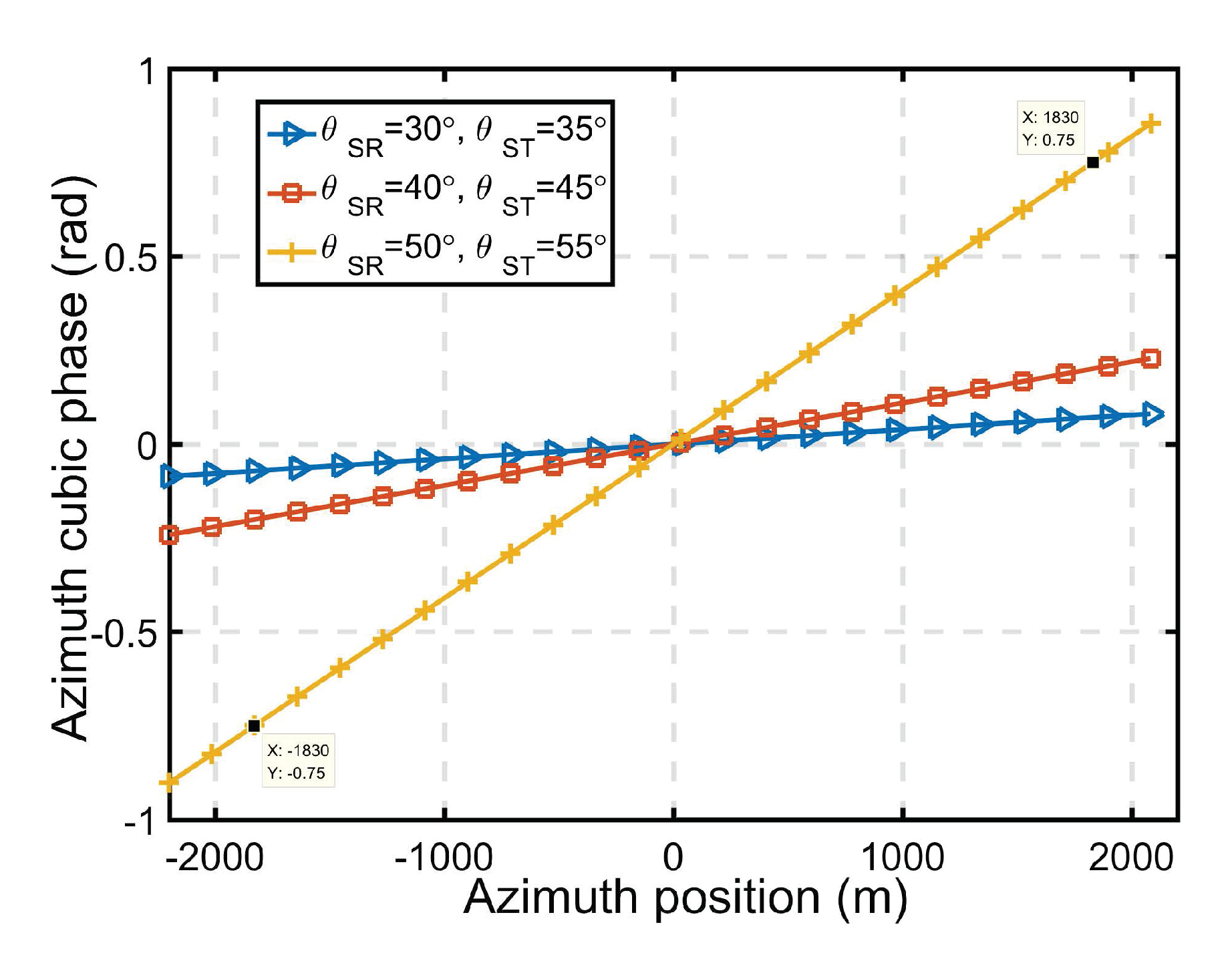
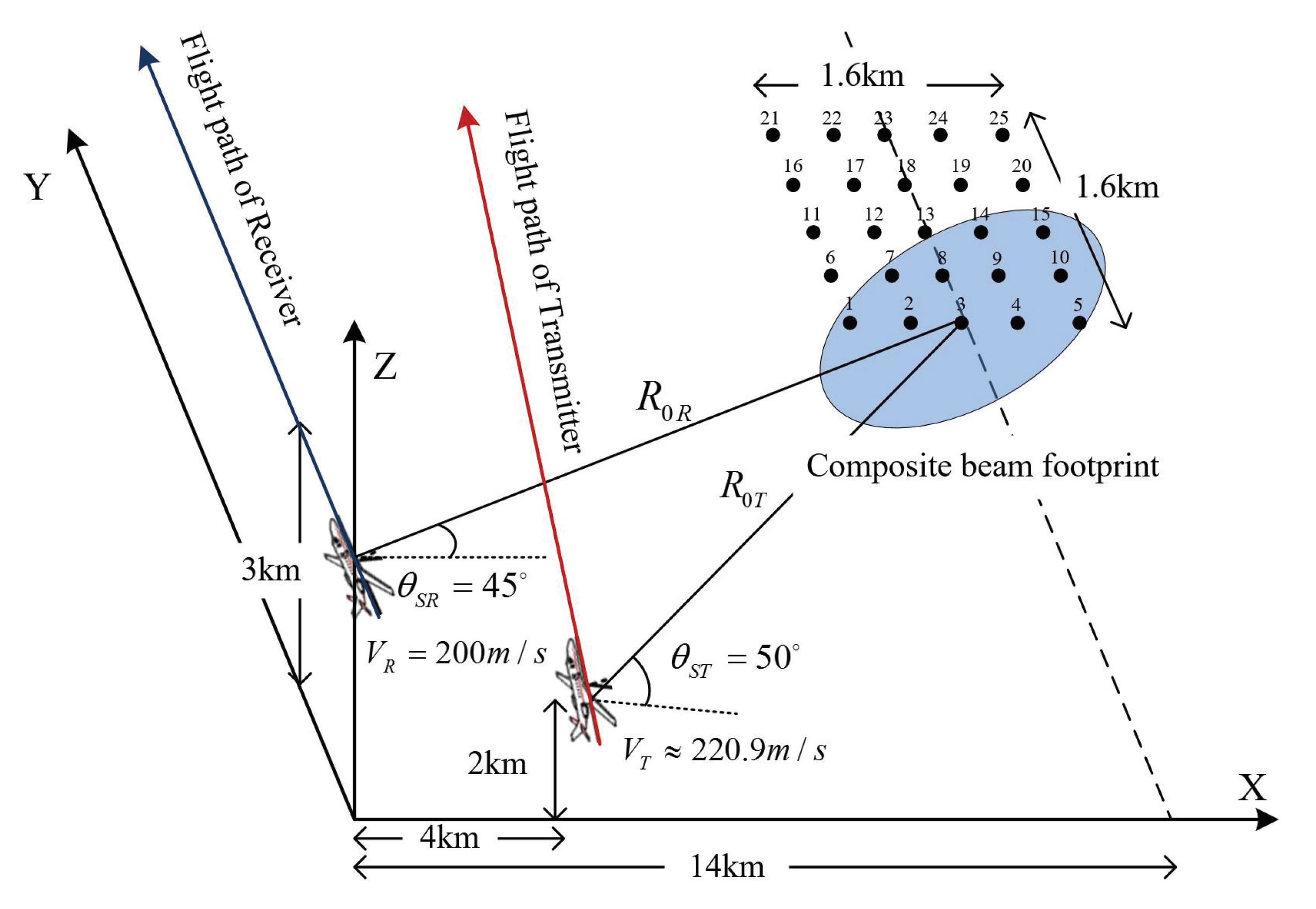

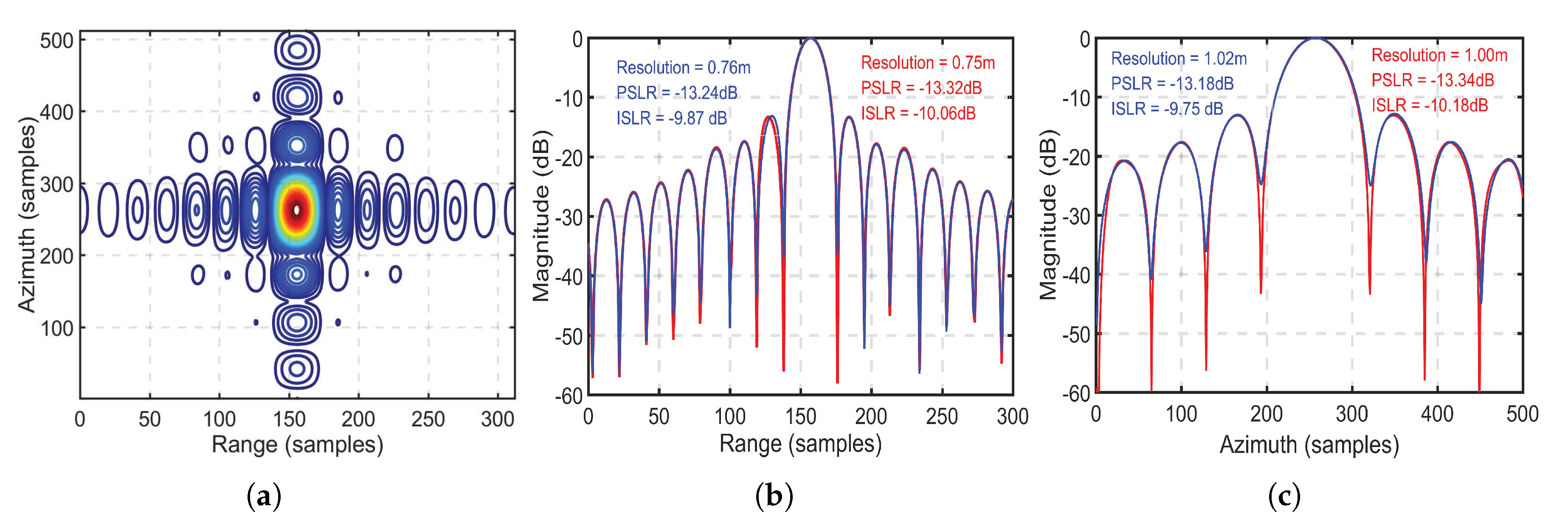
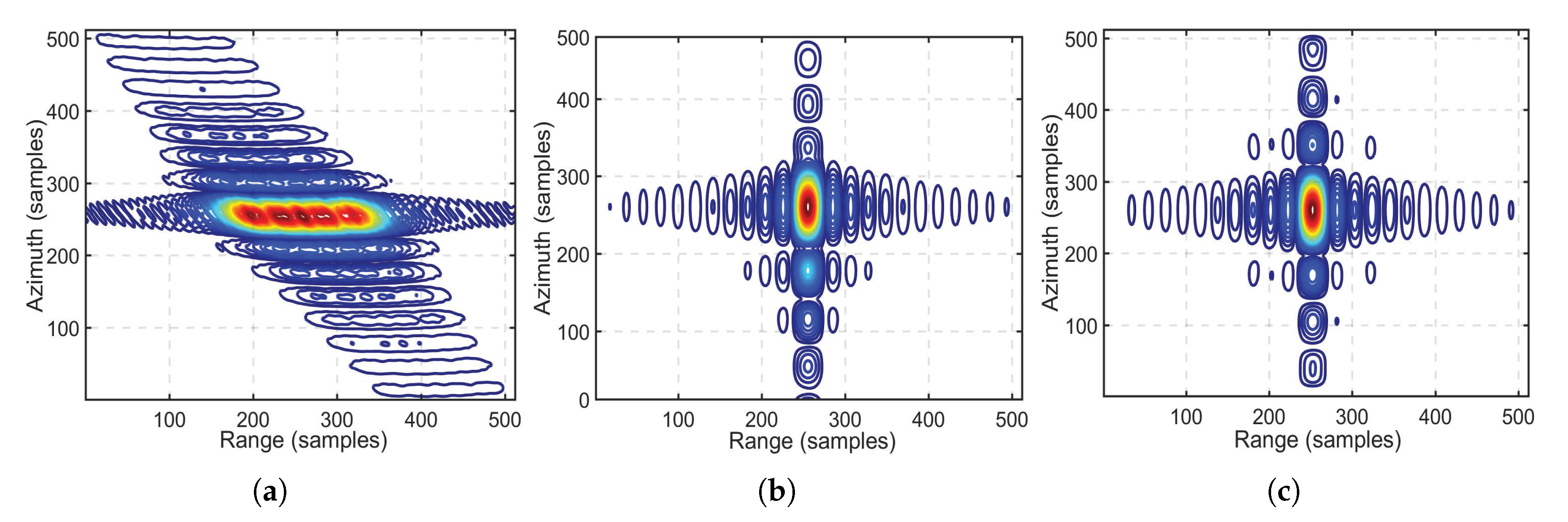
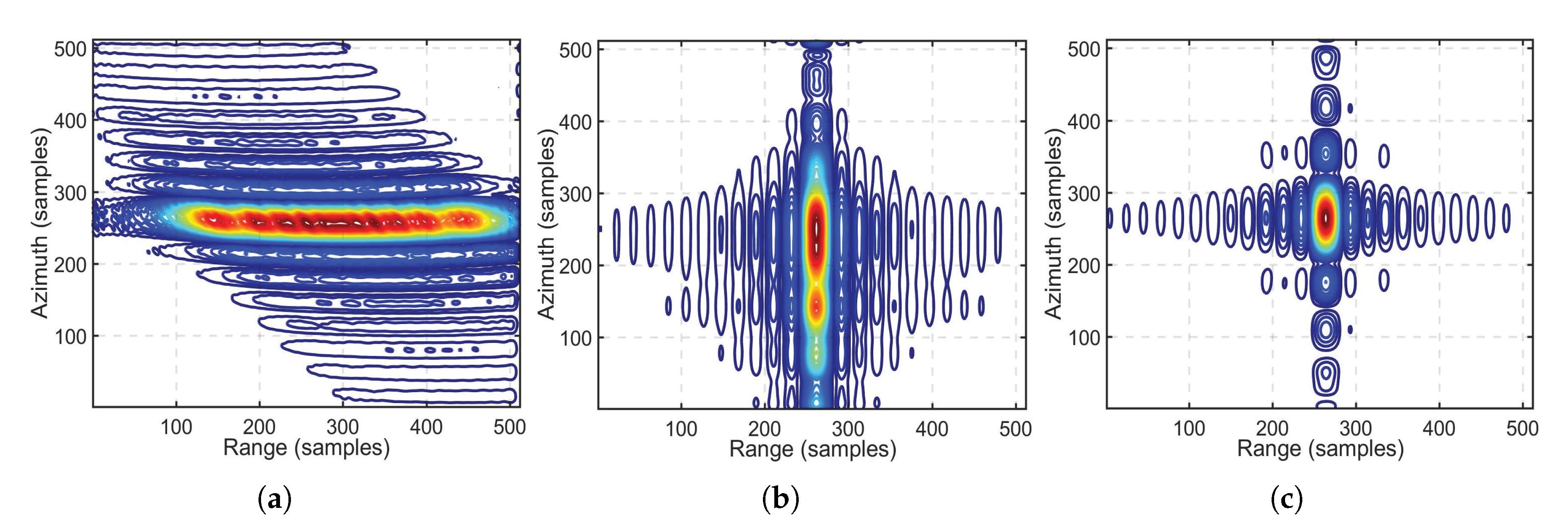
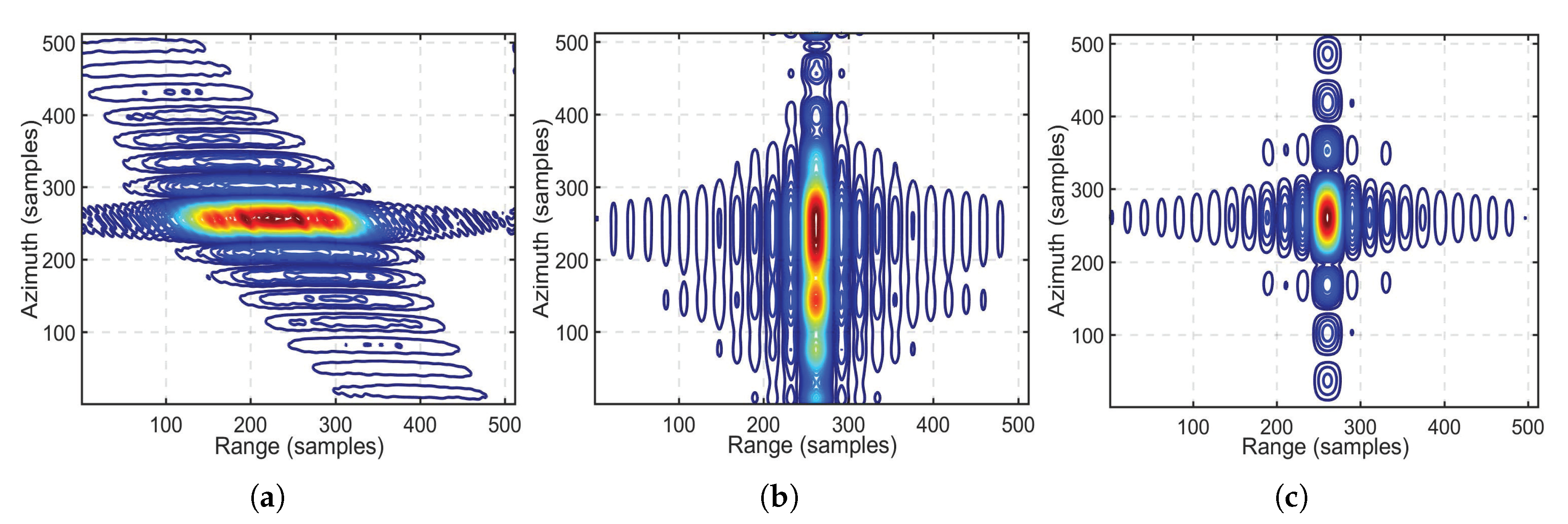


| Simulation Parameters | Receiver | Transmitter |
|---|---|---|
| Velocity in y-direction | 200 m/s | 200 m/s |
| Velocity in x-direction | 0 m/s | 20 m/s |
| Altitude | 3000 m | 2000 m |
| Squint angle | 45 | 50 |
| Center frequency | 9.6 GHz | |
| Range bandwidth | 200 MHz | |
| Transmitted pulse duration | 20 s | |
| PRF | 500 | |
| Antenna length | 2 m | |
| Range | Azimuth | ||||||
|---|---|---|---|---|---|---|---|
| Target | Resolution (m) | PSLR (dB) | ISLR (dB) | Resolution (m) | PSLR (dB) | ISLR (dB) | |
| Zhang’s RDA | 14 | 0.885 | −17.33 | −3.58 | 1.94 | −7.30 | −3.08 |
| 15 | 0.815 | −15.68 | −4.66 | 2.11 | −6.54 | −1.19 | |
| 18 | 0.796 | −14.21 | −8.92 | 1.53 | −10.89 | −8.18 | |
| 23 | 0.782 | −14.93 | −7.04 | 1.66 | −9.33 | −6.73 | |
| Wong’s NLCSA | 14 | 0.759 | −12.87 | −10.80 | 1.12 | −12.01 | −8.23 |
| 15 | 0.754 | −12.05 | −9.13 | 1.24 | −10.41 | −5.31 | |
| 18 | 0.760 | −12.58 | −9.76 | 1.47 | −12.86 | −5.37 | |
| 23 | 0.754 | −11.33 | −9.09 | 1.53 | −9.91 | −4.56 | |
| Proposed method | 14 | 0.757 | −13.39 | −10.30 | 1.01 | −13.26 | −10.13 |
| 15 | 0.752 | −13.48 | −10.44 | 1.02 | −13.18 | −10.25 | |
| 18 | 0.751 | −13.21 | −9.81 | 1.01 | −13.23 | −10.30 | |
| 23 | 0.758 | −13.01 | −9.64 | 1.02 | −13.11 | −10.33 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhang, H.; Deng, Y. Focus Improvement of Airborne High-Squint Bistatic SAR Data Using Modified Azimuth NLCS Algorithm Based on Lagrange Inversion Theorem. Remote Sens. 2021, 13, 1916. https://doi.org/10.3390/rs13101916
Li C, Zhang H, Deng Y. Focus Improvement of Airborne High-Squint Bistatic SAR Data Using Modified Azimuth NLCS Algorithm Based on Lagrange Inversion Theorem. Remote Sensing. 2021; 13(10):1916. https://doi.org/10.3390/rs13101916
Chicago/Turabian StyleLi, Chuang, Heng Zhang, and Yunkai Deng. 2021. "Focus Improvement of Airborne High-Squint Bistatic SAR Data Using Modified Azimuth NLCS Algorithm Based on Lagrange Inversion Theorem" Remote Sensing 13, no. 10: 1916. https://doi.org/10.3390/rs13101916







