Geometric Quality Assessment of Chang’E-2 Global DEM Product
Abstract
:1. Introduction
2. Data
3. Method
3.1. DEM Matching Based on Simulated Images
3.2. DEM Geometric Quality Assessment
3.2.1. Displacement Statistics
3.2.2. Gross Error Detection
3.2.3. Periodic Systematic Error Detection
4. Results and Discussion
4.1. DEM Matching Results
4.2. Geometric Quality Assessment of CE2TMap2015
4.2.1. Gross Error Detection Results
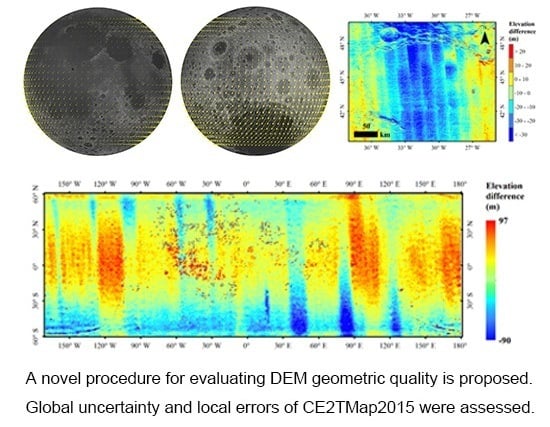
4.2.2. Global Geometric Quality of CE2TMap2015
4.2.3. Finding of Periodic Systematic Error
4.3. Local Assessment of CE2TMap2015 in the CE-4 Landing Area
5. Conclusions
- Widespread geometric inconsistencies existed between CE2TMap2015 and SLDEM2015 based on the automatically matched tie points. The average planimetric displacement and elevation difference were 183.1 m and 2.3 m, respectively, with standard deviations of 101.2 m and 15.4 m.
- The displacement between CE2TMap2015 and SLDEM2015 was smaller in lunar maria than that in high lands and was smaller on the near side than on the far side. These findings are consistent with the distribution of the five high accuracy control points (i.e., the LRRRs), which were used in CE2TMap2015 production.
- Gross errors were detected using the LOF algorithm based on the displacement vector field. It was found through manual checking that the actual gross errors may have been in CE2TMap2015 or SLDEM2015. The positions of the gross error areas are provided for users to use with caution.
- Systematic errors in the periodic pattern were found for both the CE-3 and CE-4 landing site regions of CE2TMap2015. These periodic errors were mainly in the across-track direction and in the along-track direction after a frequency domain analysis. The issue of periodic error deserves more in-depth investigation in more areas, even globally.
- Local details of CE2TMap2015 and SLDEM2015 for the CE-4 landing site were compared using a recently available LROC NAC DEM as the reference. The two DEMs were generally consistent after co-registration but provided different details in different areas.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jin, S.; Arivazhagan, S.; Araki, H. New results and questions of lunar exploration from SELENE, Chang’E-1, Chandrayaan-1 and LRO/LCROSS. Adv. Space Res. 2013, 52, 285–305. [Google Scholar] [CrossRef]
- Rosenburg, M.A.; Aharonson, O.; Head, J.W.; Kreslavsky, M.A.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Torrence, M.H.; Zuber, M.T. Global surface slopes and roughness of the Moon from the Lunar Orbiter Laser Altimeter. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Yue, Z.; Di, K.; Liu, Z.; Michael, G.; Jia, M.; Xin, X.; Liu, B.; Peng, M.; Liu, J. Lunar regolith thickness deduced from concentric craters in the CE-5 landing area. Icarus 2019, 329, 46–54. [Google Scholar] [CrossRef]
- Wang, J.; Cheng, W.; Luo, W.; Zheng, X.; Zhou, C. An Iterative Black Top Hat Transform Algorithm for the Volume Estimation of Lunar Impact Craters. Remote Sens. 2017, 9, 952. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Di, K.; Wang, B.; Tang, G.; Xu, B.; Zhang, L.; Liu, Z. Positioning and precision validation of Chang’E-3 Lander based on multiple LRO NAC images. China Sci. Bull. 2015, 60, 2750–2757. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Di, K.; Peng, M.; Wan, W.; Liu, B.; Li, L.; Yu, T.; Wang, B.; Zhou, J.; Chen, H. High precision landing site mapping and rover localization for Chang’e-3 mission. Sci. China Phys. Mech. Astron. 2014, 58, 1–11. [Google Scholar] [CrossRef]
- Kirk, R.L.; Archinal, B.A.; Gaddis, L.R.; Rosiek, M.R. Lunar cartography: Progress in the 2000s and prospects for the 2010s. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B4, 489–494. [Google Scholar] [CrossRef] [Green Version]
- Smith, D.E.; Zuber, M.T.; Neumann, G.A.; Lemoine, F.G.; Mazarico, E.; Torrence, M.H.; McGarry, J.F.; Rowlands, D.D.; Head, J.W.; Duxbury, T.H.; et al. Initial observations from the Lunar Orbiter Laser Altimeter (LOLA). Geophys. Res. Lett. 2010, 37, L18204. [Google Scholar] [CrossRef]
- Barker, M.K.; Mazarico, E.; Neumann, G.A.; Zuber, M.T.; Haruyama, J.; Smith, D.E. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Liu, J.; Ren, X.; Yan, W.; Zuo, W.; Mou, L.; Zhang, H.; Su, Y.; Wen, W.; Tan, X.; et al. Lunar Global High-precision Terrain Reconstruction Based on Chang’e-2 Stereo Images. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 485–495. [Google Scholar]
- Liu, J.; Ren, X.; Yan, W.; Li, C.; Zhang, H.; Jia, Y.; Zeng, X.; Chen, W.; Gao, X.; Liu, D.; et al. Descent trajectory reconstruction and landing site positioning of Chang’E-4 on the lunar farside. Nat. Commun 2019, 10, 4229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, B.; Niu, S.; Xin, X.; Jia, M.; Di, K.; Liu, Z.; Peng, M.; Yue, Z. High precision DTM and DOM generating using multi-source orbital data on Chang’E-4 landing site. In Proceedings of the ISPRS Geospatial Week 2019-GSW2019, “International workshop on Planetary Remote Sensing and Mapping”, Enschede, The Netherlands, 10–14 June 2019; pp. 1413–1417. [Google Scholar]
- Adkins, K.F.; Merry, C.J. Accuracy assessment of elevation data sets using the Global Positioning System. Photogramm. Eng. Remote Sens. 1994, 60, 195–202. [Google Scholar]
- Day, T.; Muller, J.P. Quality assessment of digital elevation models produced by automatic stereomatchers from SPOT image pairs. Photogramm. Rec. 1988, 12, 797–808. [Google Scholar] [CrossRef]
- Archinal, B.A.; Rosiek, M.R.; Kirk, R.L.; Redding, B.L.; The Unified Lunar Control Network 2005. Open-File Rep. 2006. Available online: https://pdfs.semanticscholar.org/2458/f764f87b91fa677c87a2e2d31b39406597de.pdf (accessed on 2 December 2019).
- Archinal, B.A.; Rosiek, M.R.; Kirk, R.L.; Hare, T.L.; Redding, B.L. Final completion of the unified lunar control network 2005 and lunar topographic model. In Proceedings of the 38th Lunar and Planetary Science Conference, League City, TX, USA, 12–16 March 2007; p. 1904. [Google Scholar]
- Di, K.; Liu, B.; Peng, M.; Xin, X.; Jia, M.; Zuo, W.; Ping, J.; Wu, B.; Oberst, J. An Initiative for Construction of New-Generation Lunar Global Control Network Using Multi-Mission Data. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-3/W1, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.C.; Zheng, C.M.; Tang, Z.S.; Qi, D.X. Lunar digital elevation model and elevation distribution model based on Chang’E-1 LAM data. Sci. China Tech. Sci. 2010, 40, 2558–2568. [Google Scholar] [CrossRef]
- Lee, H.; Hahn, M. KOMPSAT-3 Digital Elevation Model Correction Based on Point-to-Surface Matching. Remote Sens. 2019, 11, 2340. [Google Scholar] [CrossRef] [Green Version]
- Gruen, A.; Akca, D. Least squares 3D surface and curve matching. ISPRS J. Photogramm. Remote Sens. 2005, 59, 151–174. [Google Scholar] [CrossRef] [Green Version]
- Besl, P.; McKay, N. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Rosenholm, D.; Torlegard, K. Three-dimensional absolute orientation of stereo models using digital elevation models. Photogramm. Eng. Remote Sens. 1988, 54, 1385–1389. [Google Scholar]
- Guo, J.; Wu, B. Comparison of lunar topographic models derived from multiple sources based on least squares matching. Int. Arch. of the Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B4, 313–319. [Google Scholar]
- Kim, J.R.; Muller, J.P.; Morley, J. Automated MOLA track registration in MOC and Viking images and it’s application for the establishment of new 3-D control points on Mars. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2000, XXXⅢ, 469–475. [Google Scholar]
- Wu, B.; Guo, J.; Hu, H.; Li, Z.; Chen, Y. Co-registration of lunar topographic models derived from Chang’E-1, SELENE, and LRO laser altimeter data based on a novel surface matchingmethod. Earth Planet. Sci. Lett. 2013, 364, 68–84. [Google Scholar] [CrossRef]
- Michael, G.G. Coordinate registration by automated crater recognition. Planet. Space Sci. 2003, 51, 563–568. [Google Scholar] [CrossRef]
- Oksanen, J. Tracing the gross errors of DEM-visiualization techniques for preliminary quality analysis. In Proceedings of the 21st International Cartographic Conference, Durban, South Africa, 10–16 August 2003; pp. 2410–2416. [Google Scholar]
- Hunter, G.J.; Goodchild, M.F. A new model for handling vector data uncertainty in geographic information systems. In Proceedings of the URISA ‘95, San Antonio, TX, USA, 16–20 July 1995; pp. 410–419. [Google Scholar]
- Hobbs, K.F. An investigation of RGB multi-band shading for relief visualisation. Int. J. Appl. Earth Obs. Geoinf. 1999, 1-3/4, 181–186. [Google Scholar] [CrossRef]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Karkee, M.; Steward, B.L.; Aziz, S.A. Improving quality of public domain digital elevation models through data fusion. Biosyst. Eng. 2008, 101, 293–305. [Google Scholar] [CrossRef]
- Morel, J.-M.; Yu, G. ASIFT: A New Framework for Fully Affine Invariant Image Comparison. Siam J. Imaging Sci. 2009, 2, 438–469. [Google Scholar] [CrossRef]
- Li, C.L.; Ren, X.; Liu, J.J.; Wang, F.F.; Wang, W.R.; Yan, W.; Zhang, G.H. A new global and high resolution topographic map product of the moon from Chang’E-2 image data. In Proceedings of the 46th Lunar and Planetary Science Conference, The Woodlands, TX, USA, 16–20 March 2015; p. 1638. [Google Scholar]
- Ren, X.; Liu, J.; Li, C.; Li, H.; Yan, W.; Wang, F.; Wang, W.; Zhang, X.; Gao, X.; Chen, W. A global adjustment method for photogrammetric processing of Chang’E-2 stereo images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6832–6843. [Google Scholar] [CrossRef]
- Goossens, S.; Mazarico, E.; Lemoine, F.G.; Rowlands, D.D.; Neumann, G.A.; Torrence, M.H.; Smith, D.E.; Zuber, M.T. Improved precision orbit determination of lunar orbiters from the GRAIL-derived lunar gravity models. Proceedings of 23rd AAS/AIAA Space Flight Mechanics Meeting, Kauai, HI, USA, 10–14 February 2013; pp. 13–274. [Google Scholar]
- Haruyama, J.; Hara, S.; Hioki, K.; Iwasaki, A.; Morota, T.; Ohtake, M.; Matsunaga, T.; Araki, H.; Matsumoto, K.; Ishihara, Y.; et al. Lunar global digital terrain model dataset produced from SELENE (KAGUYA) terrain camera stereo observations. In Proceedings of the 43rd Lunar and Planetary Science Conference, The Woodlands, TX, USA, 19–23 March 2012; p. 1200. [Google Scholar]
- Horn, B.K.P.; Bachman, B.L. Using synthetic images to register real images with surface models. Graph. Image Process. 1978, 21, 914–924. [Google Scholar] [CrossRef] [Green Version]
- Horn, B.K.P. Hill shading and the reflectance map. Proc. IEEE 1981, 69, 14–47. [Google Scholar] [CrossRef] [Green Version]
- McKay, D.S.; Heiken, G.; Basu, A.; Blanford, G.; Simon, S.; Reedy, R.; French, B.M.; Papike, J. The lunar regolith. In Lunar Sourcebook; Heiken, G., Vaniman, D., French, B.M., Eds.; Cambridge University Press: Cambridge, UK, 1991; pp. 285–356. [Google Scholar]
- Yu, G.; Morel, J.-M. ASIFT: An Algorithm for Fully Affine Invariant Comparison. Image Process. Line 2011, 1, 11–38. [Google Scholar] [CrossRef] [Green Version]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Read. Comput. Vis. 1987, 726–740. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000; pp. 93–104. [Google Scholar]
- Bracewell, R.N. The Fourier Transform and Its Application, 3rd ed.; McGrawHill: New York, NY, USA, 2000. [Google Scholar]
- Mather, P.M. Computer Processing of Remotely-Sensed Images: An Introduction, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
















| Longitude of Lower-Left Corner | Latitude of Lower-Left Corner | DEM That the Low-Quality or Gross Error Was Located In |
|---|---|---|
| 58°W | 0° | CE2TMap2015 |
| 58°W | 1°N | CE2TMap2015 |
| 58°W | 2°N | CE2TMap2015 |
| 57°W | 0° | CE2TMap2015 |
| 57°W | 1°N | CE2TMap2015 |
| 57°W | 4°N | CE2TMap2015 |
| 48°W | 7°N | CE2TMap2015 |
| 48°W | 8°N | CE2TMap2015 |
| 48°W | 9°N | CE2TMap2015 |
| 48°W | 10°N | CE2TMap2015 |
| 48°W | 11°N | CE2TMap2015 |
| 48°W | 13°N | CE2TMap2015 |
| 9°W | 2°N | CE2TMap2015 |
| 13°E | 28°N | CE2TMap2015 |
| 168°W | 58°S | SLDEM2015 |
| 127°W | 29°S | SLDEM2015 |
| 108°W | 28°S | SLDEM2015 |
| 105°W | 32°S | SLDEM2015 |
| 105°W | 31°S | SLDEM2015 |
| 105°W | 18°S | SLDEM2015 |
| 104°W | 48°S | SLDEM2015 |
| 18°W | 48°N | SLDEM2015 |
| 149°E | 50°S | SLDEM2015 |
| 151°E | 60°S | SLDEM2015 |
| 154°E | 49°S | SLDEM2015 |
| 160°E | 51°S | SLDEM2015 |
| 170°E | 58°S | SLDEM2015 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, X.; Liu, B.; Di, K.; Yue, Z.; Gou, S. Geometric Quality Assessment of Chang’E-2 Global DEM Product. Remote Sens. 2020, 12, 526. https://doi.org/10.3390/rs12030526
Xin X, Liu B, Di K, Yue Z, Gou S. Geometric Quality Assessment of Chang’E-2 Global DEM Product. Remote Sensing. 2020; 12(3):526. https://doi.org/10.3390/rs12030526
Chicago/Turabian StyleXin, Xin, Bin Liu, Kaichang Di, Zongyu Yue, and Sheng Gou. 2020. "Geometric Quality Assessment of Chang’E-2 Global DEM Product" Remote Sensing 12, no. 3: 526. https://doi.org/10.3390/rs12030526