Missing Pixel Reconstruction on Landsat 8 Analysis Ready Data Land Surface Temperature Image Patches Using Source-Augmented Partial Convolution
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Architecture
2.1.1. Overview
2.1.2. Encoder
2.1.3. Decoder
2.1.4. Partial Convolution Layer
2.1.5. Partial Merge Layer and Merge Layer
2.1.6. Linear Convolution Layer and Final Mean and Standard Deviation Adjustment Layer
2.2. Baseline Models
2.2.1. SAPC1
- (a)
- the initial skip connection for the last decoder is the source image instead of PMerge of the source and target;
- (b)
- the first encoder does not have batch normalization after PConv;
- (c)
- the first four encoders’ PConv s use ReLU as activations;
- (d)
- the last (5th) encoder is implemented as PConv on the previous encoder’s target output image and there is no batch normalization or activation before passing its output to the first decoder;
- (e)
- the first four decoders’ (i.e., Decoders 4, 3, 2, and 1 in Figure 1) activations are LeakyReLU;
- (f)
- the last decoder does not have batch normalization nor activation; and
- (g)
- no unmasked mean square error (MSE) losses imposed between the encoder and decoder pairs (e.g., encoder 1′s target input vs. decoder 1′s output) to encourage the matching levels have similar abstract features.
2.2.2. SAPC2-Original Partial Convolution (SAPC2-OPC)
2.2.3. SAPC2-Standard Convolution (SAPC2-SC)
2.2.4. STS-CNN
- (a)
- There is almost no change in number of features (i.e., 60) across the STS-CNN framework except in the first and last convolution steps. The spatial size is constant for the entire network. In contrast, SAPC2 is based on U-Net framework with intended feature and spatial size variations.
- (b)
- STS-CNN utilizes multiscale convolution to extract more features for the multi-context information and dilated convolution to enlarge the receptive field while maintaining the minimal kernel size.
- (c)
- STS-CNN uses standard convolution instead of partial convolution in the framework.
- (d)
- STS-CNN uses ReLU for all activations.
- (e)
- STS-CNN takes the satellite images as inputs but does not utilize date related inputs as in SAPC2 (i.e., day of year and date difference from the target acquisition date). To take into account the seasonal LST variations, each sample’s source and target images are independently scaled to the same range [0,1].
- (f)
- STS-CNN aims to have fast convergence and chooses to optimize the MSE of the residual map, which is close to (but not the same as) the masked MSE used in SAPC2. As a result, many metric/loss functions for SAPC2 that are dependent on the unmasked part or on the feature domains are not provided.
2.3. Training Procedure
2.3.1. Number of Trainable Variables
2.3.2. Loss Functions
2.3.3. Learning Rate Scheduling
2.4. Implementation
2.4.1. Software and Hardware
2.4.2. Hyperparameter Tuning
2.5. Dataset
3. Results
3.1. Training Process
3.2. Validation Statistics
- MSEmasked: The Mean Square Error (MSE) between the model prediction and ground truth in the masked part
- Lsobel,masked: The source-target-correlation-coefficient-weighted MSE between the Sobel-edge transformed model prediction and the corresponding transformed ground truth in the masked part
- MSEunmasked: The MSE between the model prediction and ground truth in the unmasked part
- MSEsobel,unmasked: The MSE between the Sobel-edge transformed model prediction and the corresponding transformed ground truth in the unmasked part
- MSEweighted: The weighted sum of MSEmasked, Lsobel,masked, MSEunmasked, and MSEsobel,unmasked, with the weights given in Equation (13)
- MSEmosaic: The MSE between the mosaicked model prediction and ground truth
- CCmosaic: The Correlation Coefficient between the mosaicked model prediction and ground truth
- PSNRmosaic: The Peak Signal-To-Noise ratio of the mosaicked model prediction
- SSIMmosaic: The Structural Similarity Index of the mosaicked model prediction
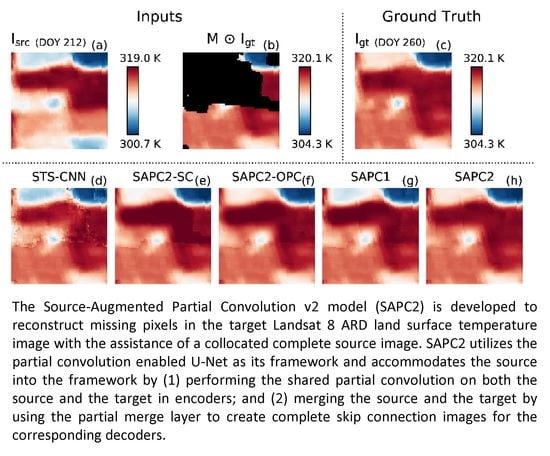
3.3. Case Study
4. Discussion
4.1. SAPC2 Versus STS-CNN
4.2. SAPC2 Versus SAPC2-OPC and SAPC2-SC
4.3. SAPC2 Versus SAPC1
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- King, M.D.; Ackerman, S.; Hubanks, P.A.; Platnick, S.; Menzel, W.P. Spatial and Temporal Distribution of Clouds Observed by MODIS Onboard the Terra and Aqua Satellites. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3826–3852. [Google Scholar] [CrossRef]
- Ottle, C.; Vidal-Madjar, D. Estimation of Land Surface Temperature with NOAA9 data. Remote Sens. Environ. 1992, 40, 27–41. [Google Scholar] [CrossRef]
- Quattrochi, D.; Luvall, J.C. Thermal Infrared Remote Sensing for Analysis of Landscape Ecological Processes: Methods and Applications. Landsc. Ecol. 1999, 14, 577–598. [Google Scholar] [CrossRef]
- Cook, M.; Schott, J.R.; Mandel, J.; Raqueno, N. Development of an Operational Calibration Methodology for the Landsat Thermal Data Archive and Initial Testing of the Atmospheric Compensation Component of a Land Surface Temperature (LST) Product from the Archive. Remote Sens. 2014, 6, 11244–11266. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Li, W.; Travis, D. Gaps-fill of SLC-off Landsat ETM+ Satellite Image Using a Geostatistical Approach. Int. J. Remote Sens. 2007, 28, 5103–5122. [Google Scholar] [CrossRef]
- Caselles, V. Variational models for image inpainting. In Proceedings of the European Congress of Mathematics, Kraków, Poland, 2–7 July 2012; European Mathematical Society Publishing House: Berlin, Germany, 2013; pp. 227–242. [Google Scholar]
- Shen, H.; Zhang, L. A MAP-Based Algorithm for Destriping and Inpainting of Remotely Sensed Images. IEEE Trans. Geosci. Remote Sens. 2008, 47, 1492–1502. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Restoration of Aqua MODIS Band 6 Using Histogram Matching and Local Least Squares Fitting. IEEE Trans. Geosci. Remote Sens. 2008, 47, 613–627. [Google Scholar] [CrossRef]
- Criminisi, A.; Perez, P.; Toyama, K. Region Filling and Object Removal by Exemplar-Based Image Inpainting. IEEE Trans. Image Process. 2004, 13, 1200–1212. [Google Scholar] [CrossRef]
- Holben, B.N. Characteristics of Maximum-Value Composite Images from Temporal AVHRR Data. Int. J. Remote Sens. 1986, 7, 1417–1434. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved Monitoring of Vegetation Dynamics at Very High Latitudes: A New Method Using MODIS NDVI. Remote Sens. Environ. 2006, 100, 321–334. [Google Scholar] [CrossRef]
- Abdellatif, B.; Lecerf, R.; Mercier, G.; Hubert-Moy, L. Preprocessing of Low-Resolution Time Series Contaminated by Clouds and Shadows. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2083–2096. [Google Scholar] [CrossRef]
- Cheng, Q.; Shen, H.; Zhang, L.; Yuan, Q.; Zeng, C. Cloud Removal for Remotely Sensed Images by Similar Pixel Replacement Guided with a Spatio-Temporal MRF Model. ISPRS J. Photogramm. Remote Sens. 2014, 92, 54–68. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.; Zhang, L.; Li, H. Sparse-Based Reconstruction of Missing Information in Remote Sensing Images from Spectral/Temporal Complementary Information. ISPRS J. Photogramm. Remote Sens. 2015, 106, 1–15. [Google Scholar] [CrossRef]
- Sun, Q.; Yan, M.; Donoho, D.; Boyd, S. Convolutional Imputation of Matrix Networks. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Jennifer, D., Andreas, K., Eds.; Stockholmsmässan: Stockholm, Sweden, 2018; Volume 80, pp. 4818–4827. [Google Scholar]
- Quan, J.; Zhan, W.; Chen, Y.; Wang, M. Time Series Decomposition of Remotely Sensed Land Surface Temperature and Investigation of Trends and Seasonal Variations in Surface Urban Heat Islands. J. Geophys. Res. Atmos. 2016, 121, 2638–2657. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.S.; Howard, R.E.; Habbard, W.; Jackel, L.D.; Henderson, D. Handwritten Digit Recognition with a Back-Propagation Network. In Advances in Neural Information Processing Systems; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1990; pp. 396–404. ISBN 1558601007. [Google Scholar]
- Shao, Z.; Pan, Y.; Diao, C.; Cai, J. Cloud Detection in Remote Sensing Images Based on Multiscale Features-Convolutional Neural Network. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 40624076. [Google Scholar] [CrossRef]
- Lei, S.; Shi, Z.; Zou, Z. Super-Resolution for Remote Sensing Images via Local–Global Combined Network. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 1243–1247. [Google Scholar] [CrossRef]
- Gu, J.; Sun, X.; Zhang, Y.; Fu, K.; Wang, L. Deep Residual Squeeze and Excitation Network for Remote Sensing Image Super-Resolution. Remote. Sens. 2019, 11, 1817. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Shao, J.; Li, X.; Shen, H.T. Remote Sensing Image Super-Resolution via Mixed High-Order Attention Network. IEEE Trans. Geosci. Remote. Sens. 2020, 1–14. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y. Hyperspectral Imagery Denoising by Deep Learning with Trainable Nonlinearity Function. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 1963–1967. [Google Scholar] [CrossRef]
- Liu, W.; Lee, J. A 3-D Atrous Convolution Neural Network for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 5701–5715. [Google Scholar] [CrossRef]
- Wei, K.; Fu, Y.; Huang, H. 3-D Quasi-Recurrent Neural Network for Hyperspectral Image Denoising. IEEE Trans. Neural Networks Learn. Syst. 2020, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liu, S.; Yang, J.; Yang, M.-H. Generative Face Completion. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5892–5900. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Yan, Z.; Li, X.; Li, M.; Zuo, W.; Shan, S. Shift-Net: Image Inpainting via Deep Feature Rearrangement. In Proceedings of the Computer Vision; Springer Science and Business Media LLC: Munich, Germany, October 2018; pp. 3–19. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2017; pp. 105–114. [Google Scholar]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning Spectral-Spatial-Temporal Features via a Recurrent Convolutional Neural Network for Change Detection in Multispectral Imagery. IEEE Trans. Geosci. Remote. Sens. 2018, 57, 924–935. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Q.; Yuan, Q.; Zeng, C.; Li, X.; Wei, Y. Missing Data Reconstruction in Remote Sensing Image with a Unified Spatial-Temporal-Spectral Deep Convolutional Neural Network. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.-C.; Tao, A.; Catanzaro, B. Image Inpainting for Irregular Holes Using Partial Convolutions. In Proceedings of the Haptics: Science, Technology, Applications, Munich, Germany, 8–14 September 2018; Springer Science and Business Media LLC: Cham, Switzerland, 2018; pp. 89–105. [Google Scholar]
- Chen, M.; Newell, B.H.; Sun, Z.; Corr, C.A.; Gao, W. Reconstruct Missing Pixels of Landsat Land Surface Temperature Product Using a CNN with Partial Convolution. Appl. Mach. Learn. 2019, 11139, 111390E. [Google Scholar] [CrossRef]
- Smith, L.N. Cyclical Learning Rates for Training Neural Networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–26 March 2017; pp. 464–472. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. Tensorflow: Large-scale Machine Learning on Heterogeneous Systems. arXiv 2016, arXiv:1603.044672015. [Google Scholar]














| Metric | SAPC2 | SAPC1 | SAPC2-OPC | SAPC2-SC | STS-CNN |
|---|---|---|---|---|---|
| MSEmasked ↓(↓) | 0.00317 (0.00645) | 0.00341 (0.00699) | 0.00398 (0.00700) | 0.00566 (0.00832) | 0.00769 (0.01198) |
| Lsobel,masked ↓(↓) | 0.01156 (0.01430) | 0.01203 (0.01531) | 0.01608 (0.01641) | 0.01600 (0.01734) | N/A (N/A) |
| MSEunmasked ↓(↓) | 0.00025 (0.00023) | 0.00033 (0.00030) | 0.00072 (0.00050) | 0.00063 (0.00050) | N/A (N/A) |
| MSEsobel,unmasked ↓(↓) | 0.00221 (0.00188) | 0.00273 (0.00221) | 0.00803 (0.00565) | 0.00482 (0.00342) | N/A (N/A) |
| MSEweighted ↓(↓) | 0.01793 (0.02576) | 0.01913 (0.02786) | 0.02635 (0.02950) | 0.02852 (0.03249) | N/A (N/A) |
| MSEmosaic ↓(↓) | 0.00098 (0.00232) | 0.00105 (0.00250) | 0.00121 (0.00251) | 0.00168 (0.00290) | 0.00228 (0.00444) |
| CCmosaic ↑(↓) | 0.986 (0.019) | 0.985 (0.019) | 0.981 (0.022) | 0.973 (0.034) | 0.955 (0.074) |
| PSNRmosaic ↑(↓) | 47.55 (5.34) | 47.33 (5.42) | 46.12 (4.92) | 44.21 (4.59) | 42.85 (4.33) |
| SSIMmosaic ↑(↓) | 0.989 (0.020) | 0.989 (0.021) | 0.986 (0.022) | 0.983 (0.025) | 0.971 (0.031) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Sun, Z.; Newell, B.H.; Corr, C.A.; Gao, W. Missing Pixel Reconstruction on Landsat 8 Analysis Ready Data Land Surface Temperature Image Patches Using Source-Augmented Partial Convolution. Remote Sens. 2020, 12, 3143. https://doi.org/10.3390/rs12193143
Chen M, Sun Z, Newell BH, Corr CA, Gao W. Missing Pixel Reconstruction on Landsat 8 Analysis Ready Data Land Surface Temperature Image Patches Using Source-Augmented Partial Convolution. Remote Sensing. 2020; 12(19):3143. https://doi.org/10.3390/rs12193143
Chicago/Turabian StyleChen, Maosi, Zhibin Sun, Benjamin H. Newell, Chelsea A. Corr, and Wei Gao. 2020. "Missing Pixel Reconstruction on Landsat 8 Analysis Ready Data Land Surface Temperature Image Patches Using Source-Augmented Partial Convolution" Remote Sensing 12, no. 19: 3143. https://doi.org/10.3390/rs12193143