Multiparameter Elastic Full Waveform Inversion of Ocean Bottom Seismic Four-Component Data Based on A Modified Acoustic-Elastic Coupled Equation
Abstract
1. Introduction
2. Methods
2.1. General FWI Formulation
2.2. Acoustic-Elastic Coupled EFWI Method
2.3. Preconditioned Truncated Gauss–Newton Algorithm
| Algorithm 1 Preconditioned Truncated Gauss–Newton algorithm |
|
3. Sensitivity Analysis
4. Results
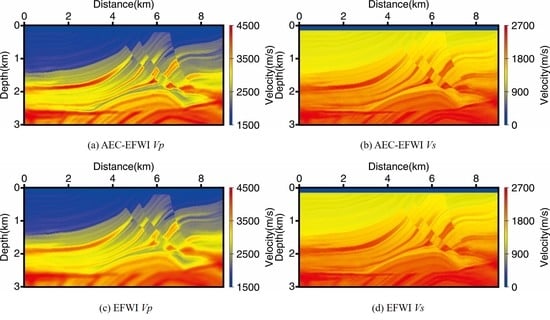
4.1. Overthrust Model Test
4.2. Marmousi Model Test
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Modified Acoustic-Elastic Coupled Equation
Appendix B. Derivation of Gradient Computation for Aec-Efwi Method
References
- Gaiser, J.E.; Moldoveanu, N.; Macbeth, C.; Michelena, R.J.; Spitz, S. Multicomponent technology: The players, problems, applications, and trends: Summary of the workshop sessions. Geophysics 2001, 20, 974–977. [Google Scholar] [CrossRef]
- Tatham, R.H.; Stoffa, P.L. Vp/Vs—A potential hydrocarbon indicator. Geophysics 1976, 41, 837–849. [Google Scholar] [CrossRef]
- Mora, P. Nonlinear two-dimensional elastic inversion of multioffset seismic data. Geophysics 1987, 52, 1211–1228. [Google Scholar] [CrossRef]
- Tarantola, A. Inversion of seismic reflection data in the acoustic approximation. Geophysics 1984, 49, 1259–1266. [Google Scholar] [CrossRef]
- Sears, T.J.; Barton, P.J.; Singh, S.C. Elastic full waveform inversion of multicomponent ocean-bottom cable seismic data: Application to Alba Field, UK North Sea. Geophysics 2010, 75, R109–R119. [Google Scholar] [CrossRef]
- Crase, E.; Pica, A.; Noble, M.; Mcdonald, J.; Tarantola, A. Robust elastic nonlinear waveform inversion; application to real data. Geophysics 1990, 55, 527–538. [Google Scholar] [CrossRef]
- Crase, E.; Wideman, C.; Noble, M.; Tarantola, A. Nonlinear elastic waveform inversion of land seismic reflection data. J. Geophys. Res. 1992, 97, 4685–4703. [Google Scholar] [CrossRef]
- Sears, T.J.; Singh, S.C.; Barton, P.J. Elastic full waveform inversion of multi-component OBC seismic data. Geophys. Prospect. 2008, 56, 843–862. [Google Scholar] [CrossRef]
- Vigh, D.; Jiao, K.; Watts, D.; Sun, D. Elastic full-waveform inversion application using multicomponent measurements of seismic data collection. Geophysics 2014, 79, R63–R77. [Google Scholar] [CrossRef]
- Oh, J.; Kalita, M.; Alkhalifah, T. 3D elastic full waveform inversion using P-wave excitation amplitude: Application to OBC field data. Geophysics 2018, 83, R129–R140. [Google Scholar] [CrossRef]
- Choi, Y.; Min, D.; Shin, C. Two-dimensional waveform inversion of multicomponent data in acoustic-elastic coupled media. Geophys. Prospect. 2008, 56, 863–881. [Google Scholar] [CrossRef]
- Singh, H.; Shragge, J.; Tsvankin, I. Coupled-domain acoustic-elastic solver for anisotropic media: A mimetic finite difference approach. Seg Tech. Program Expand. Abstr. 2019, 2019, 3755–3759. [Google Scholar]
- Qu, Y.; Liu, Y.; Li, J.; Li, Z. Fluid-solid coupled full-waveform inversion in the curvilinear coordinates for ocean-bottom cable data. Geophysics 2020, 85, R113–R133. [Google Scholar] [CrossRef]
- De Basabe, J.D.; Sen, M.K. A comparison of monolithic methods for elastic wave propagation in media with a fluid–solid interface. Seg Tech. Program Expand. Abstr. 2014, 2014, 3323–3328. [Google Scholar]
- Yu, P.; Geng, J.; Li, X.; Wang, C. Acoustic-elastic coupled equation for ocean bottom seismic data elastic reverse time migration. Geophysics 2016, 81, S333–S345. [Google Scholar] [CrossRef]
- Yu, P.; Geng, J.; Ma, J. Vector-wave-based elastic reverse time migration of ocean-bottom 4C seismic data. Geophysics 2018, 83, S333–S343. [Google Scholar] [CrossRef]
- Yu, P.; Geng, J. Acoustic-elastic coupled equations in vertical transverse isotropic media for pseudo acoustic-wave reverse time migration of ocean-bottom 4C seismic data. Geophysics 2019, 84, 1–48. [Google Scholar] [CrossRef]
- Operto, S.; Gholami, Y.; Prieux, V.; Ribodetti, A.; Brossier, R.; Metivier, L.; Virieux, J. A guided tour of multiparameter full-waveform inversion with multicomponent data: From theory to practice. Geophysics 2013, 32, 1040–1054. [Google Scholar] [CrossRef]
- Metivier, L.; Brossier, R.; Virieux, J.; Operto, S. Full Waveform Inversion and the Truncated Newton Method. SIAM J. Sci. Comput. 2013, 35, B401–B437. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, J.; Chi, B.; Dong, L. An improved scattering-integral approach for frequency-domain full waveform inversion. Geophys. J. Int. 2015, 202, 1827–1842. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Y.; Dong, L. Simultaneous estimation of velocity and density in acoustic multiparameter full-waveform inversion using an improved scattering-integral approach. Geophysics 2016, 81, R399–R415. [Google Scholar] [CrossRef]
- Pan, W.; Innanen, K.A.; Margrave, G.F.; Fehler, M.; Fang, X.; Li, J. Estimation of elastic constants for HTI media using Gauss-Newton and full-Newton multiparameter full-waveform inversion. Geophysics 2016, 81, R275–R291. [Google Scholar] [CrossRef]
- Sun, M.; Yang, J.; Dong, L.; Liu, Y.; Huang, C. Density reconstruction in multiparameter elastic full-waveform inversion. J. Geophys. Eng. 2017, 14, 1445–1462. [Google Scholar] [CrossRef]
- Ren, Z.; Liu, Y.; Sen, M.K. Least-squares reverse time migration in elastic media. Geophys. J. Int. 2017, 208, 1103–1125. [Google Scholar] [CrossRef]
- Sun, M.; Dong, L.; Yang, J.; Huang, C.; Liu, Y. Elastic least-squares reverse time migration with density variations. Geophysics 2018, 83, S533–S547. [Google Scholar] [CrossRef]
- Operto, S.; Virieux, J.; Dessa, J.; Pascal, G. Crustal seismic imaging from multifold ocean bottom seismometer data by frequency domain full waveform tomography: Application to the eastern Nankai trough. J. Geophys. Res. 2006, 111, B09306. [Google Scholar] [CrossRef]
- Shin, C.; Jang, S.; Min, D.J. Improved amplitude preservation for prestack depth migration by inverse scattering theory. Geophys. Prospect. 2001, 49, 592–606. [Google Scholar] [CrossRef]
- Plessix, R.E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications. Geophys. J. Int. 2006, 167, 495–503. [Google Scholar] [CrossRef]
- Gholami, Y.; Brossier, R.; Operto, S.; Ribodetti, A.; Virieux, J. Which parameterization is suitable for acoustic vertical transverse isotropic full waveform inversion? Part 1: Sensitivity and trade-off analysis. Geophysics 2013, 78, R81–R105. [Google Scholar] [CrossRef]
- Gholami, Y.; Brossier, R.; Operto, S.; Prieux, V.; Ribodetti, A.; Virieux, J. Which parameterization is suitable for acoustic vertical transverse isotropic full waveform inversion? Part 2: Synthetic and real data case studies from Valhall. Geophysics 2013, 78, R107–R124. [Google Scholar] [CrossRef]
- Prieux, V.; Brossier, R.; Operto, S.; Virieux, J. Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field. Part 1: Imaging compressional wave speed, density and attenuation. Geophys. J. Int. 2013, 194, 1640–1664. [Google Scholar] [CrossRef]
- Prieux, V.; Brossier, R.; Operto, S.; Virieux, J. Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field. Part 2: Imaging compressive-wave and shear-wave velocities. Geophys. J. Int. 2013, 194, 1665–1681. [Google Scholar] [CrossRef]
- Woodward, M.J. Wave-equation tomography. Geophysics 1992, 57, 15–26. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, L.; Wang, Y.; Zhu, J.; Ma, Z. Sensitivity kernels for seismic Fresnel volume tomography. Geophysics 2009, 74, U35–U46. [Google Scholar] [CrossRef]
- Gelis, C.; Virieux, J.; Grandjean, G. Two-dimensional elastic full waveform inversion using Born and Rytov formulations in the frequency domain. Geophys. J. Int. 2007, 168, 605–633. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Q.; Wang, Z.; Liu, T. Computation of lightning horizontal field over the two-dimensional rough ground by using the three-dimensional FDTD. IEEE Trans. Electromagn. Compat. 2013, 56, 143–148. [Google Scholar]
- Komatitsch, D.; Martin, R. An unsplit convolutional Perfectly Matched Layer improved at grazing incidence for the seismic wave equation. Geophysics 2007, 72, SM155–SM167. [Google Scholar] [CrossRef]
- Martin, R.; Komatitsch, D. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation. Geophys. J. Int. 2009, 179, 333–344. [Google Scholar] [CrossRef]
- Ma, Y.; Hale, D. Wave-equation reflection traveltime inversion with dynamic warping and full-waveform inversion. Geophysics 2013, 78, R223–R233. [Google Scholar] [CrossRef]
- Brossier, R.; Operto, S.; Virieux, J. Velocity model building from seismic reflection data by full-waveform inversion. Geophys. Prospect. 2015, 63, 354–367. [Google Scholar] [CrossRef]
- Chi, B.; Dong, L.; Liu, Y. Correlation-based reflection full-waveform inversion. Geophysics 2015, 80, R189–R202. [Google Scholar] [CrossRef]
- Guo, Q.; Alkhalifah, T. Elastic reflection-based waveform inversion with a nonlinear approach. Geophysics 2017, 82, R309–R321. [Google Scholar] [CrossRef]
- Wang, T.; Cheng, J.; Guo, Q.; Wang, C. Elastic wave-equation-based reflection kernel analysis and traveltime inversion using wave mode decomposition. Geophys. J. Int. 2018, 215, 450–470. [Google Scholar] [CrossRef]
- Biondi, B.; Symes, W.W. Angle-domain common-image gathers for migration velocity analysis by wavefield- continuation imaging. Geophysics 2004, 69, 1283–1298. [Google Scholar] [CrossRef]
- Symes, W.W. Migration velocity analysis and waveform inversion. Geophys. Prospect. 2008, 56, 765–790. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, J.; Weibull, W.W.; Arntsen, B. Elastic wave-equation migration velocity analysis preconditioned through mode decoupling. Geophysics 2019, 84, R341–R353. [Google Scholar] [CrossRef]
- Virieux, J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1986, 51, 889–901. [Google Scholar] [CrossRef]





















| RMS Errors (%) | ||
|---|---|---|
| PTGN | 3.08 | 2.86 |
| PCG | 3.22 | 4.20 |
| RMS Errors (%) | ||
|---|---|---|
| EFWI | 5.29 | 3.93 |
| AEC-EFWI | 4.25 | 3.43 |
| RATIO | −24.5 | −14.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, M.; Jin, S. Multiparameter Elastic Full Waveform Inversion of Ocean Bottom Seismic Four-Component Data Based on A Modified Acoustic-Elastic Coupled Equation. Remote Sens. 2020, 12, 2816. https://doi.org/10.3390/rs12172816
Sun M, Jin S. Multiparameter Elastic Full Waveform Inversion of Ocean Bottom Seismic Four-Component Data Based on A Modified Acoustic-Elastic Coupled Equation. Remote Sensing. 2020; 12(17):2816. https://doi.org/10.3390/rs12172816
Chicago/Turabian StyleSun, Minao, and Shuanggen Jin. 2020. "Multiparameter Elastic Full Waveform Inversion of Ocean Bottom Seismic Four-Component Data Based on A Modified Acoustic-Elastic Coupled Equation" Remote Sensing 12, no. 17: 2816. https://doi.org/10.3390/rs12172816
APA StyleSun, M., & Jin, S. (2020). Multiparameter Elastic Full Waveform Inversion of Ocean Bottom Seismic Four-Component Data Based on A Modified Acoustic-Elastic Coupled Equation. Remote Sensing, 12(17), 2816. https://doi.org/10.3390/rs12172816