Predicting Channel Conveyance and Characterizing Planform Using River Bathymetry via Satellite Image Compilation (RiBaSIC) Algorithm for DEM-Based Hydrodynamic Modeling
Abstract
1. Introduction
- to develop an algorithm for predicting channel conveyance and characterizing planform via satellite images and observed (in situ) WSE as input;
- to estimate river discharge using the predicted conveyance via an HD model after applying the algorithm.
2. Materials and Method
2.1. Developing a River Conveyance Prediction and Planform Characterization Algorithm via Satellite Image and Observed WSE
- the WSE of the study area is not affected by the tide;
- the seasonal variation of WSE within the study area is uniform;
- the river reach maintains flow continuity meaning no major lateral inflow or outflow;
- the reach for which the channel profile is determined does not have any abrupt changes in elevation such as a cascade or rapid;
- the river reach is free from any natural and/or artificial storage areas such as lakes;
- no significant natural and/or artificial changes happened in the river planform or conveyance within the study period;
- the width of the actively flowing channel increases with increasing WSE;
- the satellite image has sufficient bands to cover the visible and Infra-Red (IR) spectrum;
- the river bankfull width is at least three times the spatial resolution of the satellite image for identifying the channel and side slopes;
- there are a sufficient number of satellite images available to capture a minimum of one hydrologic cycle.
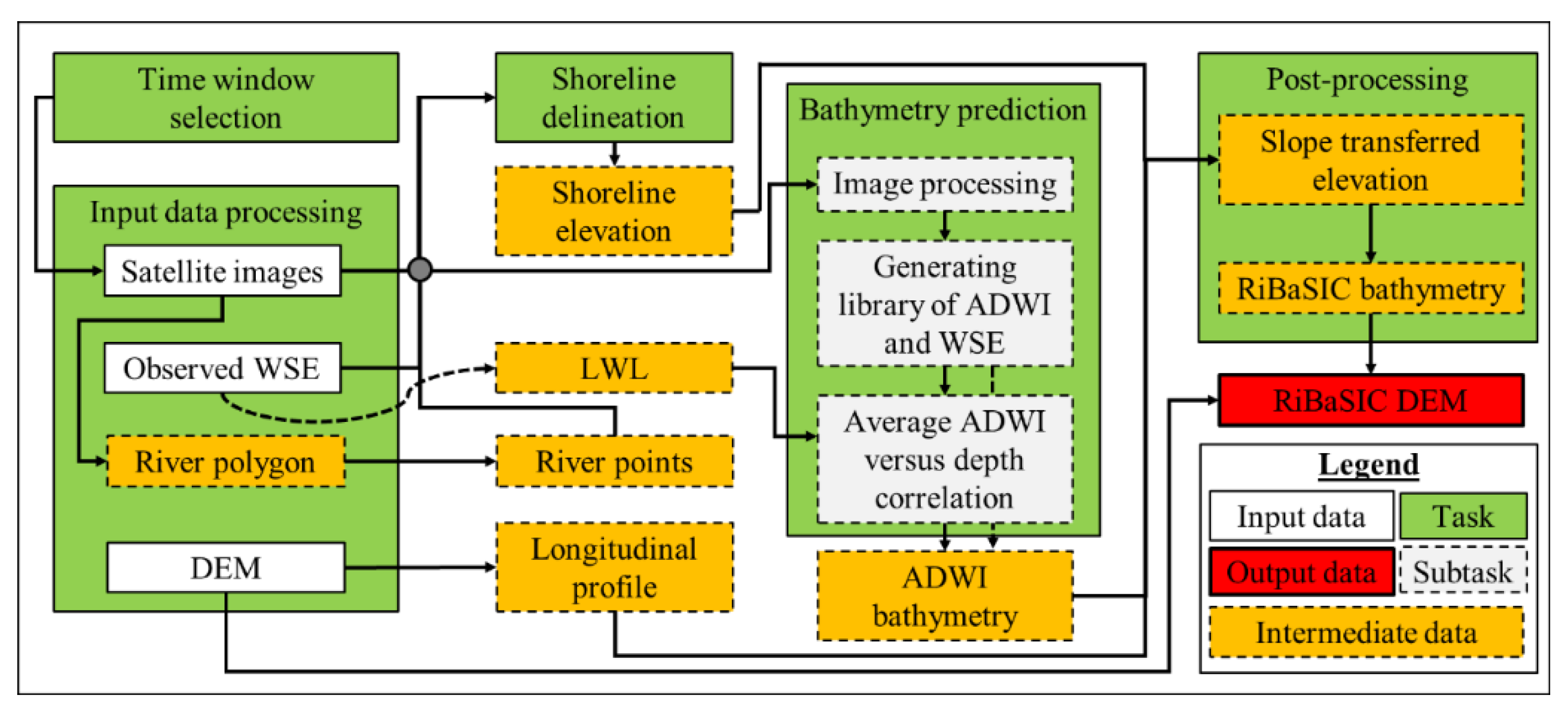
2.1.1. Time Window Selection
2.1.2. Input Data Processing
2.1.3. Shoreline Delineation
2.1.4. Bathymetry Prediction
- Image Processing: typically, water reflects 10% of the incoming radiation that is limited to visible to NIR spectrum but soil reflects throughout the IR bands [44,45]. The highest reflectance is provided by turbid water [45] which is commonly found in river channels. Additionally, pixels in a river channel are mainly covered by soil that is periodically inundated. Therefore, short wavelength infra-red (SWIR) bands are useful for separating inundated and non-inundated river pixels in an image. So, the ratio of visible and IR (NIR and SWIR) bands are used in this step for predicting bathymetry. Similar to Section 2.1.3, cloud-covered pixels are removed first via the “Fmask” tool. Once the cloudy pixels are removed, Equation (4) is used to calculate a novel index called Average Difference Water Index (ADWI) for each cell. The ADWI values are stored as integers where a positive index value indicates a channel cell (inundated) and a negative indicates non-channel (non-inundated) cell. The selected channel cells in each image are assigned WSE of the image acquisition date.
- Generating Library of ADWI and WSE: a library of ADWI and corresponding WSE for each cell within the RiBaSIC extent (also referred to as river points) is generated. The library is used to determine the lowest and highest WSE at which a cell is found to be within a channel (LWSE and HWSE, respectively) along with the highest WSE at which a cell is found to be dry or non-channel (DWSE). If any cell is found to be in the channel at only one instance, then that WSE would be categorized as LWSE for that cell. The ADWI value corresponding to a cell’s LWSE is stored as that cell’s “Low Water Index” (LWI).
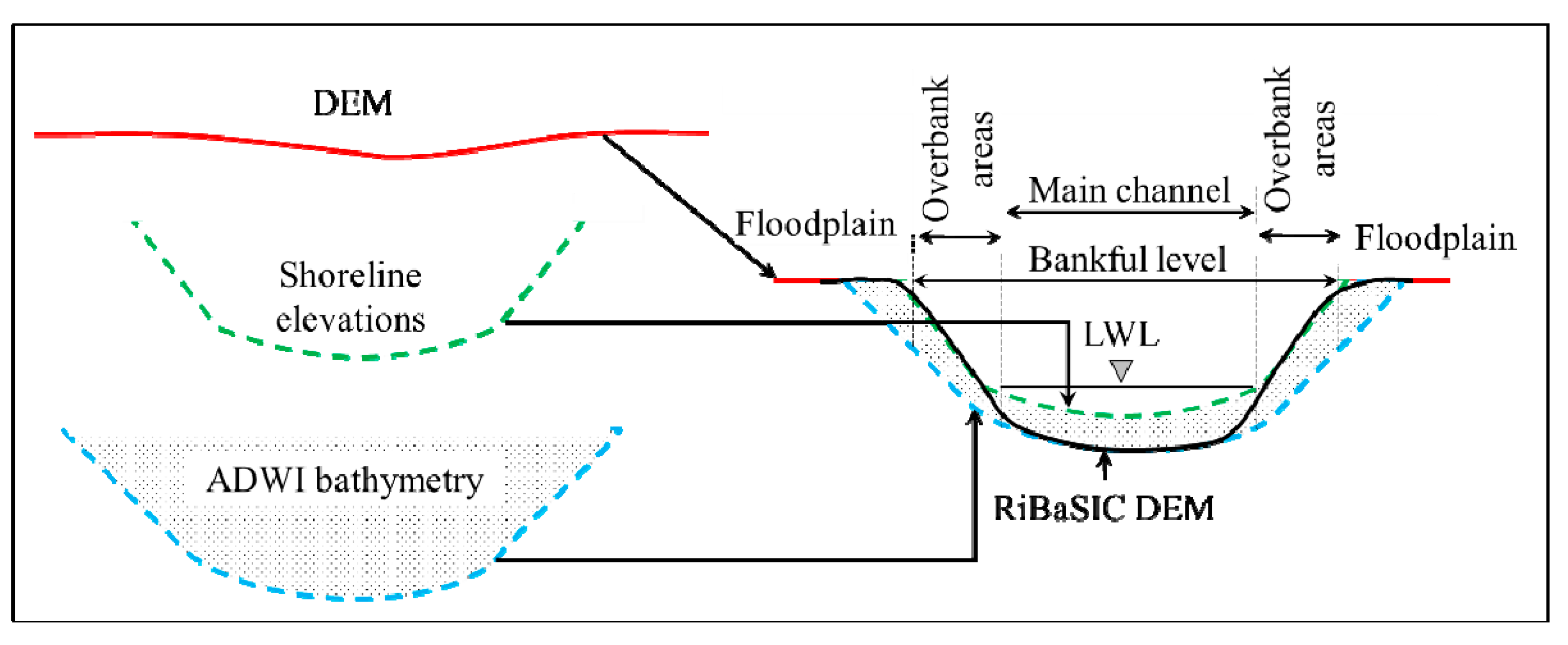
- ADWI versus Depth Correlation: the historic LWL of the nearby streamflow gauge is required to establish the ADWI versus depth correlation. If the riverbed is static (i.e., no significant bed level aggradation-degradation), then the thalweg elevation (lowest elevation of the riverbed) should be less than the LWL. Riverbed elevation for each cell or river point is approximated by two trials using the equations provided below.
1st Trial
2nd Trial
2.1.5. Post-Processing
- Slope Transferred Elevation: the shoreline elevations and ADWI bathymetry elevations for the cells obtained in Section 2.1.3 and Section 2.1.4 are transferred to their geographic locations using the channel profile [refer to Equation (1)] and distance.
- RiBaSIC Bathymetry: the shoreline delineation method using NDWI (please refer to Section 2.1.3) cannot predict the bathymetry in the main channel that is under water during the dry season. Therefore, the shorelines delineated from a dry season cloud-free image is assumed as the main channel. The cells inside the main channel are assigned ADWI bathymetry estimated in Section 2.1.4. The cells outside of the main channel but found wet in at least one image in Section 2.1.3 are considered as overbank areas. The shoreline elevations are assigned for cells in overbank areas. This merged dataset is, hereafter, called “RiBaSIC bathymetry”.
- RiBaSIC DEM: the cells that are neither in the main channel nor in overbank areas are considered as floodplain areas. The elevations of the floodplain cells are obtained from a DEM. Finally, RiBaSIC bathymetry and the DEM are merged to create a raster surface that is, hereafter, called “RiBaSIC DEM”.
2.2. Discharge Estimation from HD Model Using a Moderate Quality Global DEM
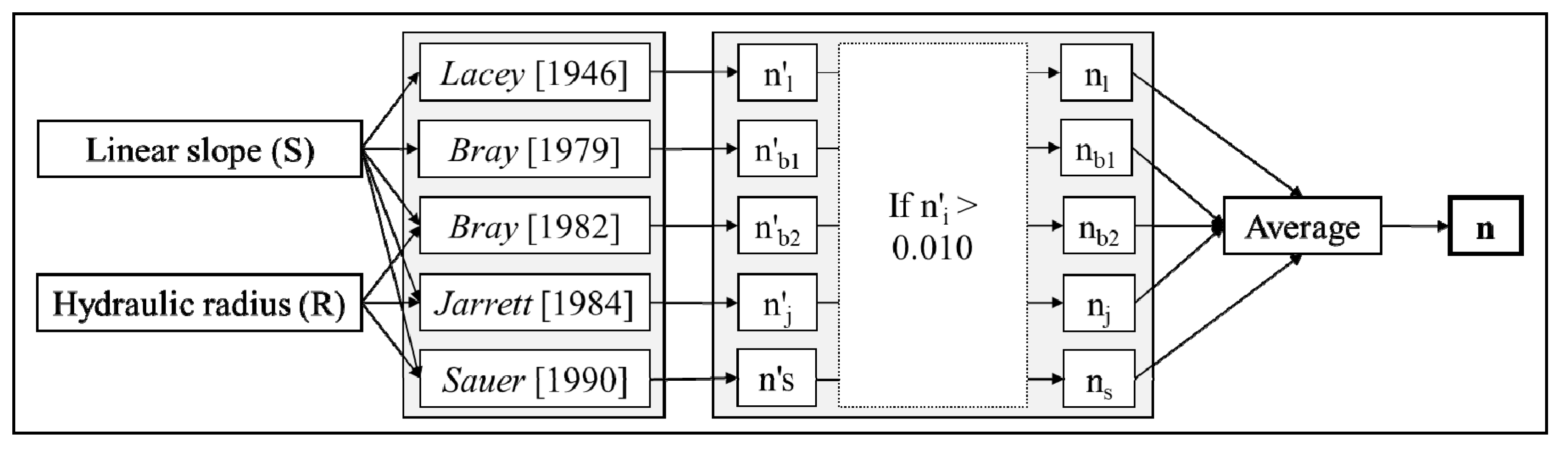
2.2.1. Manning’s Roughness Factor Approximation
- Step 1:
- hydraulic radius of the cross-sections at upstream of the model extent is calculated.
- Step 2:
- linear slope at the upstream location is estimated. For more details on estimating linear slopes at upstream and downstream locations, the readers are referred to Section 2.1.2 and Appendix A.
- Step 3:
- Manning’s n values for the upstream location is calculated using the equations listed in Table 1.
- Step 4:
- any Manning’s n value less than 0.010 is considered as “unreasonable” for natural rivers (for the flow within the main channel) and hence discarded. This filtering is important because Manning’s n values can be as small as 0.025 for minor streams (width at flood stage < 30 m) although for major streams, the value can be smaller than that of a minor stream of similar characteristics [51]. Moreover, alluvial sand bed rivers could have Manning’s n value ranging from 0.018 to 0.035 [52]. The smallest prescribed Manning’s n value is 0.016, which is applicable for straight and uniform earthen channels [51]. Therefore, Manning’s n value as small as 0.010 is likely to be an erroneous one and needs to be excluded.
- Step 5:
- the average of Manning’s n estimates (from step 4) is calculated.
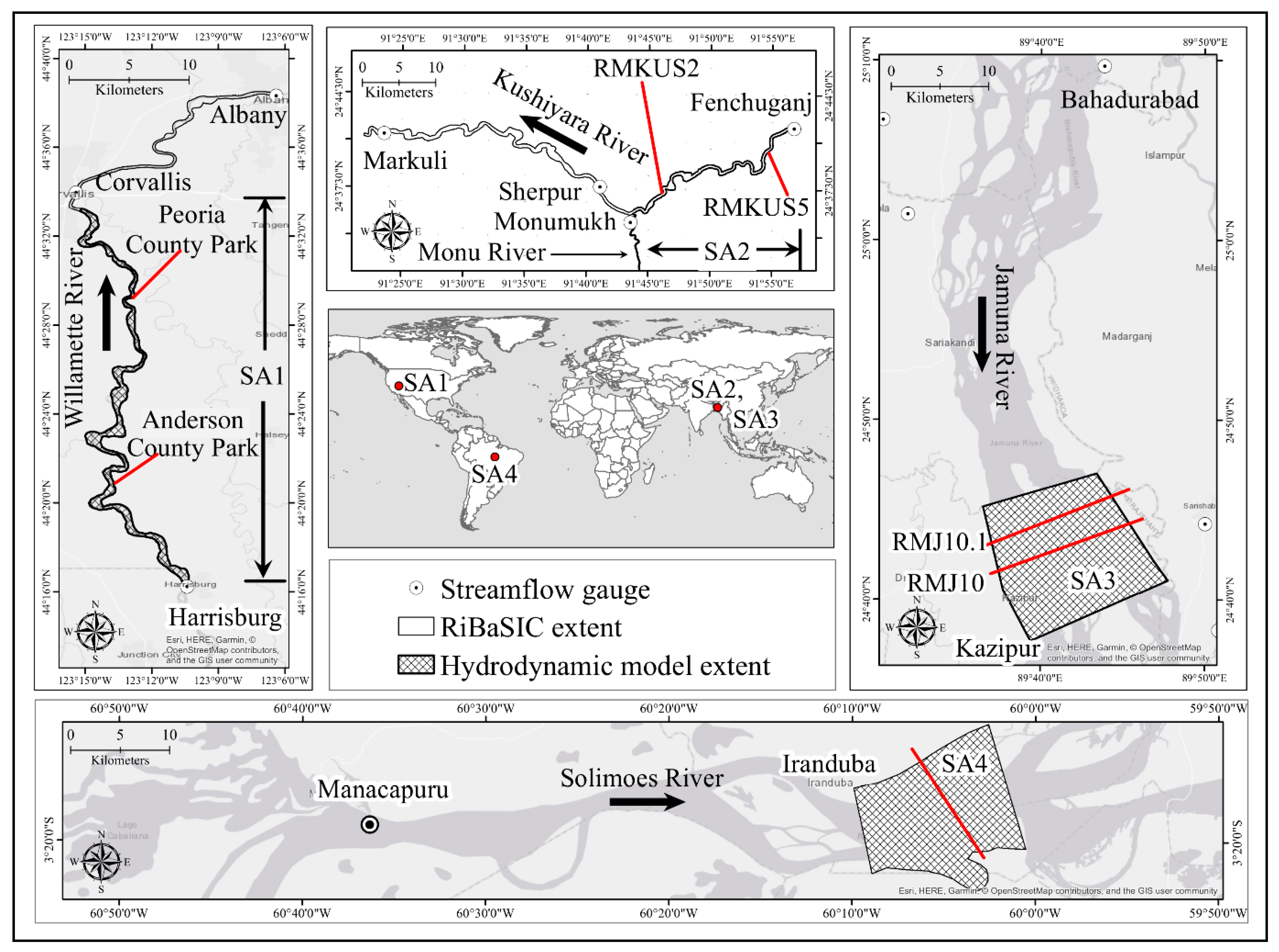
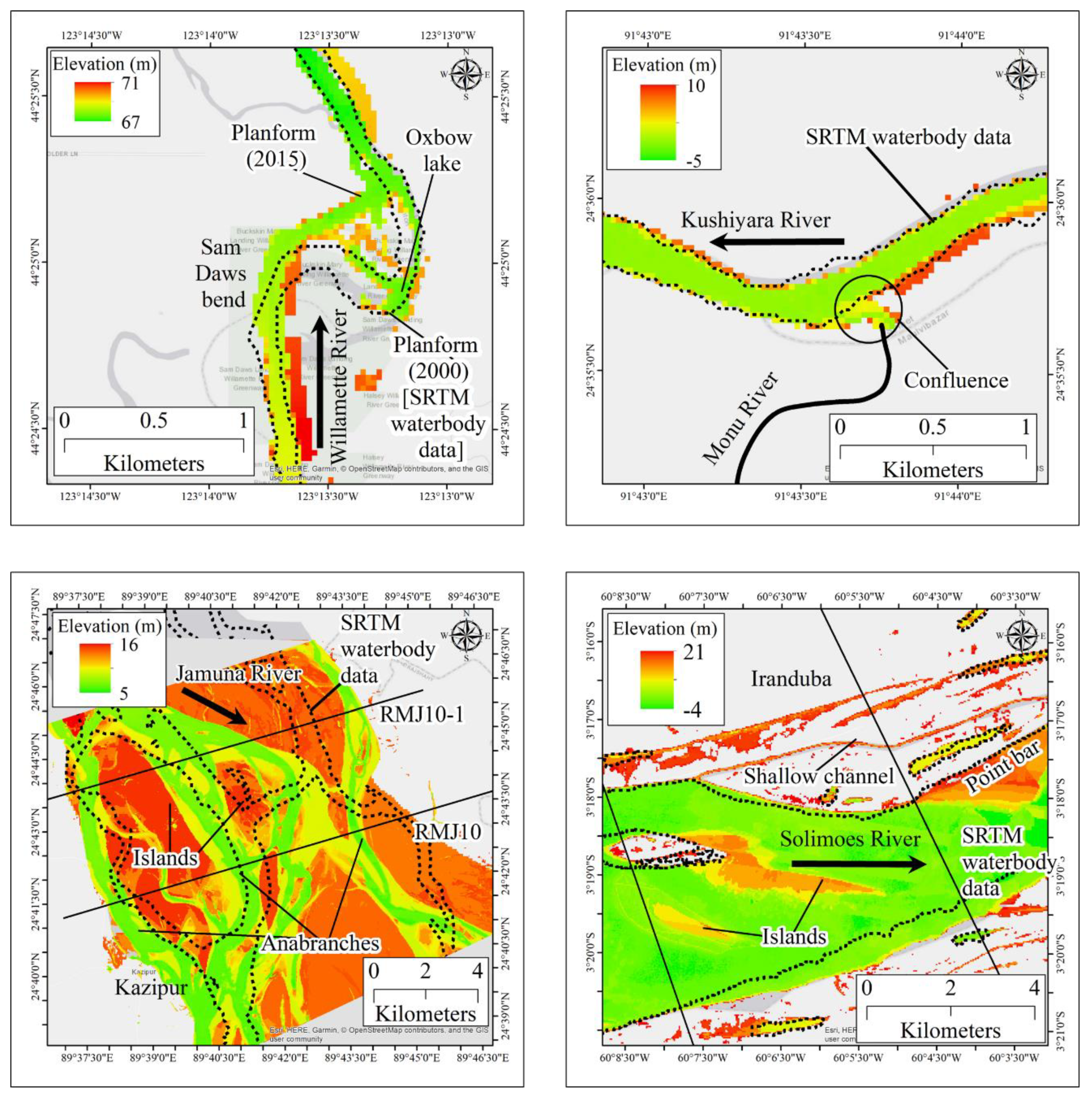
2.2.2. Study Areas
2.2.3. Data
3. Results
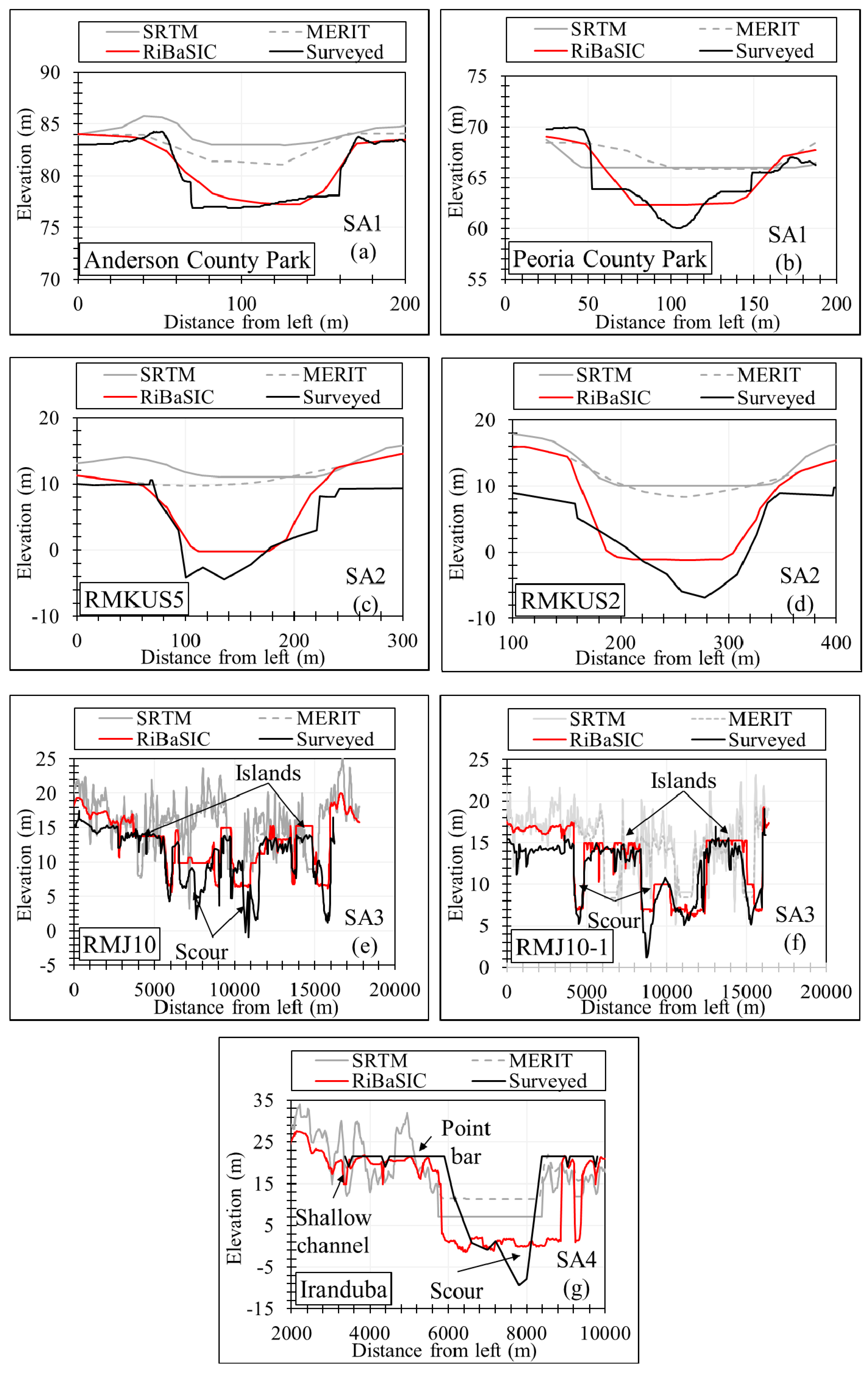
3.1. Validation of the RiBaSIC Algorithm
3.2. Discharge Estimation by a Moderate Resolution Global DEM-Based HD Modeling
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
Abbreviatons
| 2D | Two-dimensional |
| ADWI | Average Difference Water Index |
| ALOS | Advanced Land Observing Satellite |
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer |
| AW3D30 | Advanced Land Observing Satellite Global Digital Surface Model |
| AW3DDEM | Advanced Land Observing Satellite World 3D-DEM |
| BWDB | Bangladesh Water Development Board |
| DEM | Digital Elevation Model |
| DOGAMI | Department of Geology and Mineral Industries |
| DWSE | Highest WSE at which a cell is found to be dry |
| EGM96 | Earth Gravitational Model 1996 |
| ESRI | Environmental Systems Research Institute |
| FREEBIRD | Flow Resistance Equation-Based Imaging of River Depths |
| HAB | Hydraulically Assisted Bathymetry |
| HD | Hydrodynamic |
| HEC-RAS | Hydrologic Engineering Center’s River Analysis System |
| HWSE | Highest WSE at which a cell is found to be within a channel |
| HydroSHEDS | Hydrological data and maps based on Shuttle Elevation Derivatives at multiple Scales |
| ICESat-2 | Ice, Cloud and land Elevation Satellite - 2 |
| IDQT | Image-to-Depth Quantile Transformation |
| IR | Infra-Red |
| LWI | Low Water Index |
| LWL | Lowest Water level |
| LWSE | Lowest WSE at which a cell is found to be within a channel |
| MERIT | Multi-Error-Removed Improved-Terrain |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NASA | National Aeronautics and Space Administration |
| NDWI | Normalized Difference Water Index |
| NIR | Near Infra-Red |
| NSE | Nash–Sutcliffe model efficiency |
| RiBaSIC | River Bathymetry via Satellite Image Compilation |
| RRMSE | Relative Root Mean Squared Error |
| SARAL | Satellite with ARgos and ALtiKa |
| SRTM | Shuttle Radar Topography Mission |
| SWIR | Short Wavelength Infra-Red |
| SWOT | Surface Water and Ocean Topography |
| TanDEM-X | TerraSAR-X add-on for Digital Elevation Measurement |
| USGS | United States Geologic Survey |
| WSE | Water Surface Elevation |
Appendix A
Appendix A.1. Time Window Selection
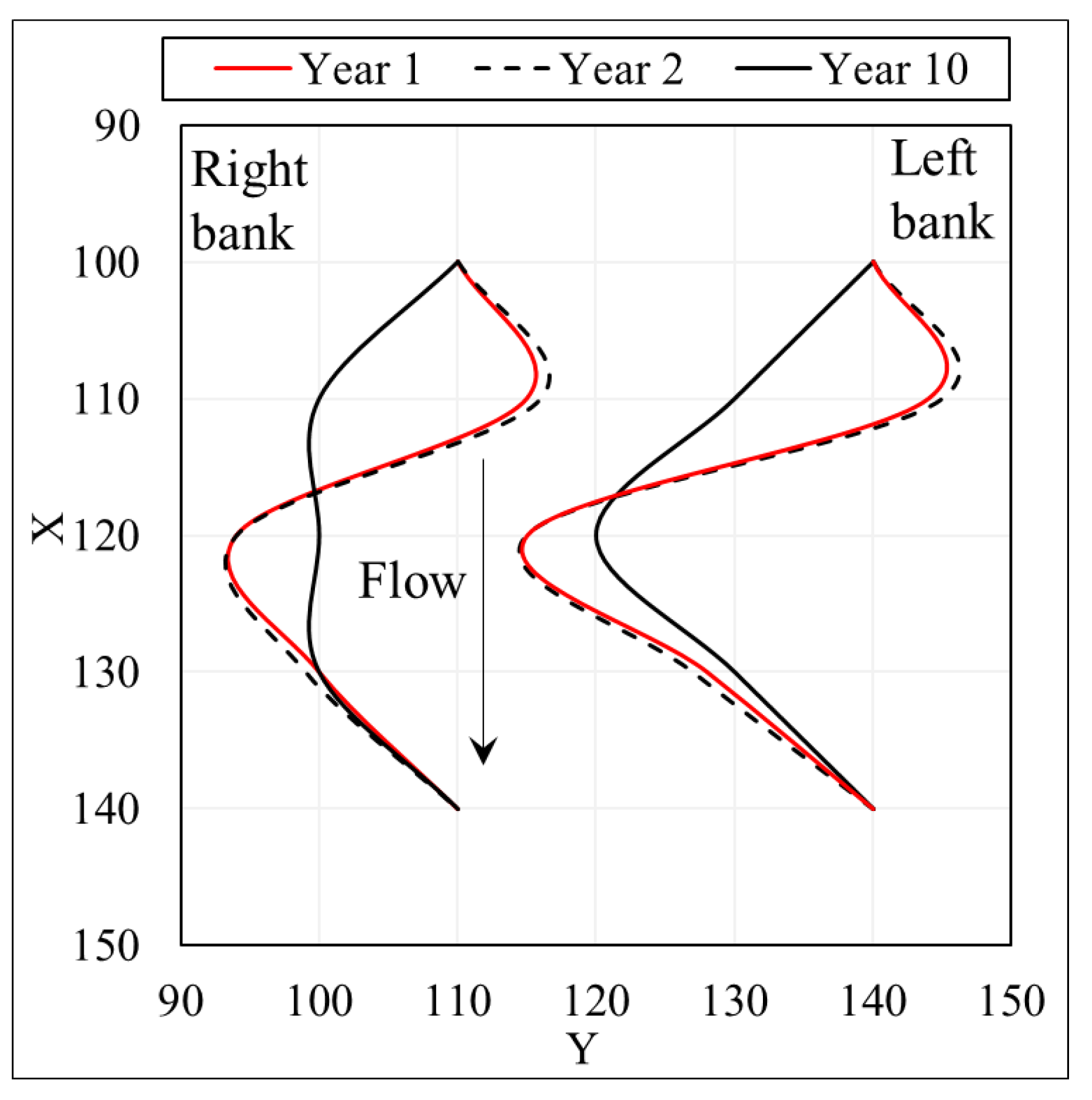
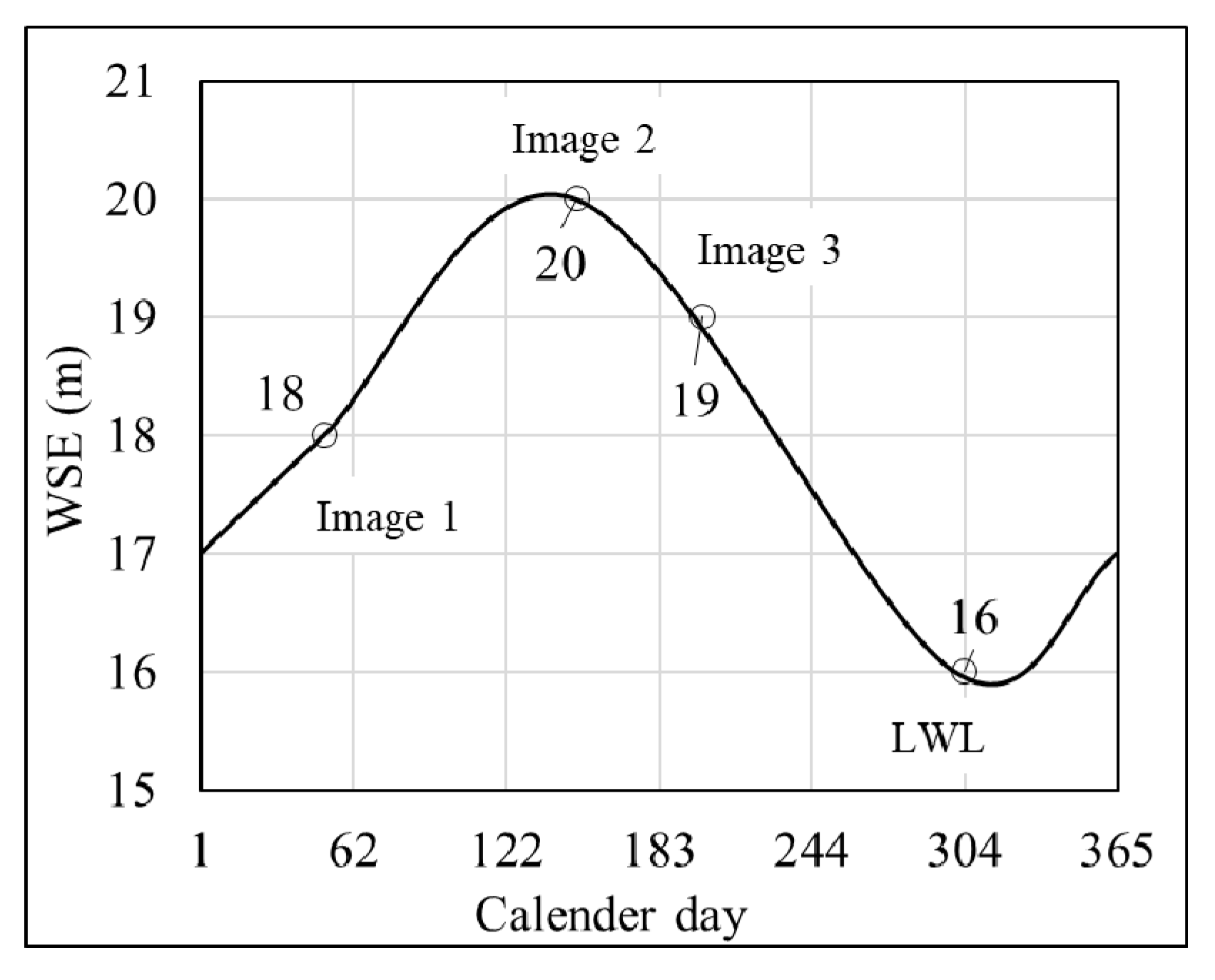
Appendix A.2. Input Data Processing
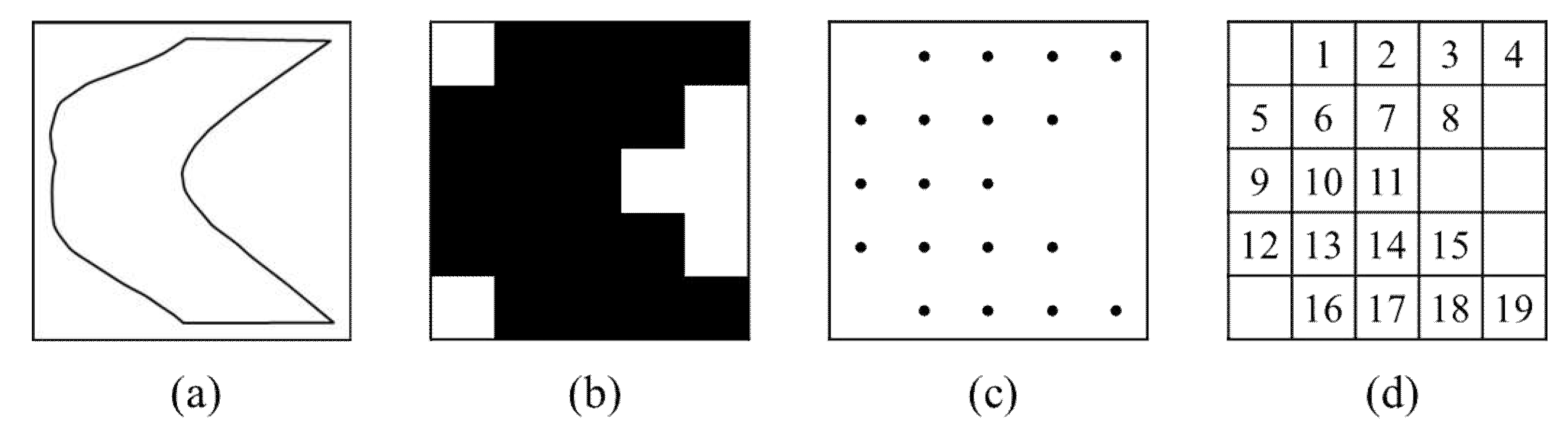
Appendix A.3. Shoreline Delineation

Appendix A.4. Bathymetry Prediction
- Image Processing: the ADWI values for channel cells in three images are shown in Figure A6.
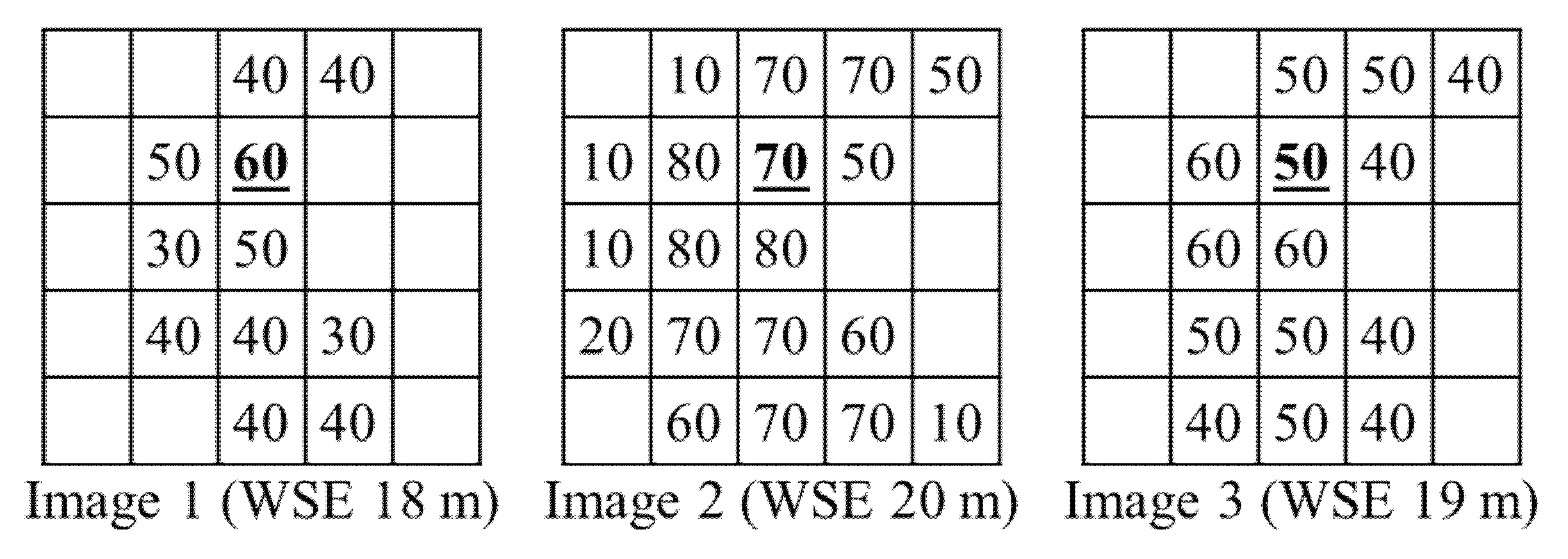
- b.
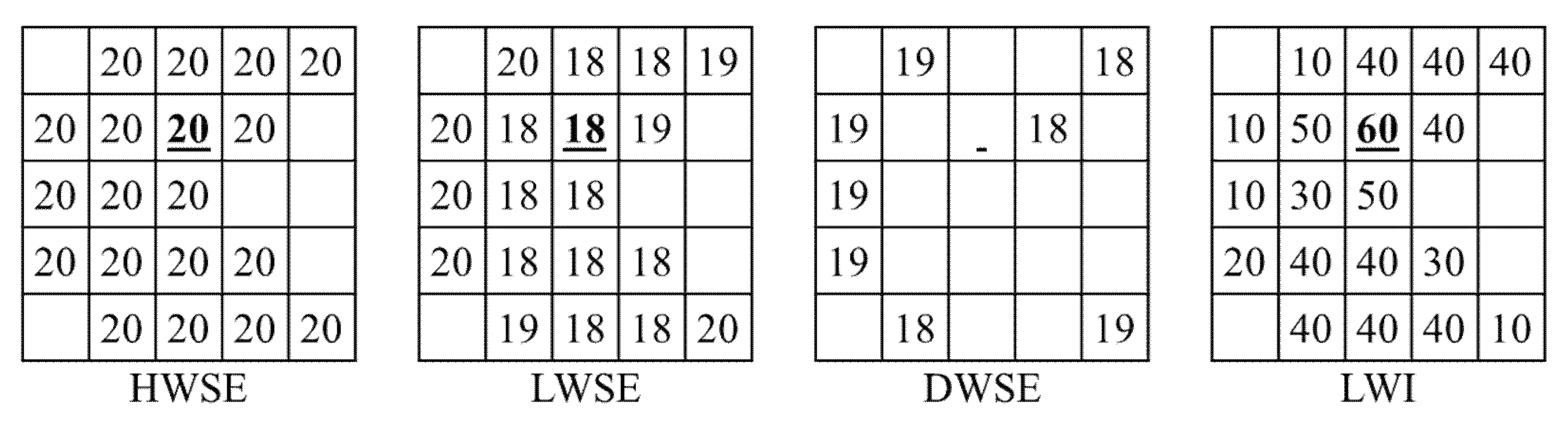
- Generating Library of ADWI and WSE: the HWSE, LWSE, DWSE, and LWI is calculated in this step are presented in Figure A7.For cell ID number 7, from image processing:
- −
- the highest WSE at which it is in the channel is 20 m, therefore, HWSE = 20 m;
- −
- the lowest WSE at which it is in the channel is 18 m, therefore, LWSE = 18 m;
- −
- the cell is not found dry in any image, therefore, DWSE = null;
- −
- ADWI at 18 m WSE is 60, therefore, LWI = 60.
- c.
- ADWI versus Depth Correlation:
- Zt = LWL = 16 (see Figure A1)
- Therefore, depth factor, f = = 2
- For cell ID 7,
- HWSE − LWSE = 2
- Factored depth, df = f × (HWSE − LWSE) = 2 × 2 = 4 m
- Approximate bed elevation = 20 − 4 = 16 m
- Hence, depth in Image 1 = 18 − 16 = 2 m
- Depth in Image 2 = 20 − 16 = 4 m
- Depth in Image 3 = 19 − 16 = 3 m


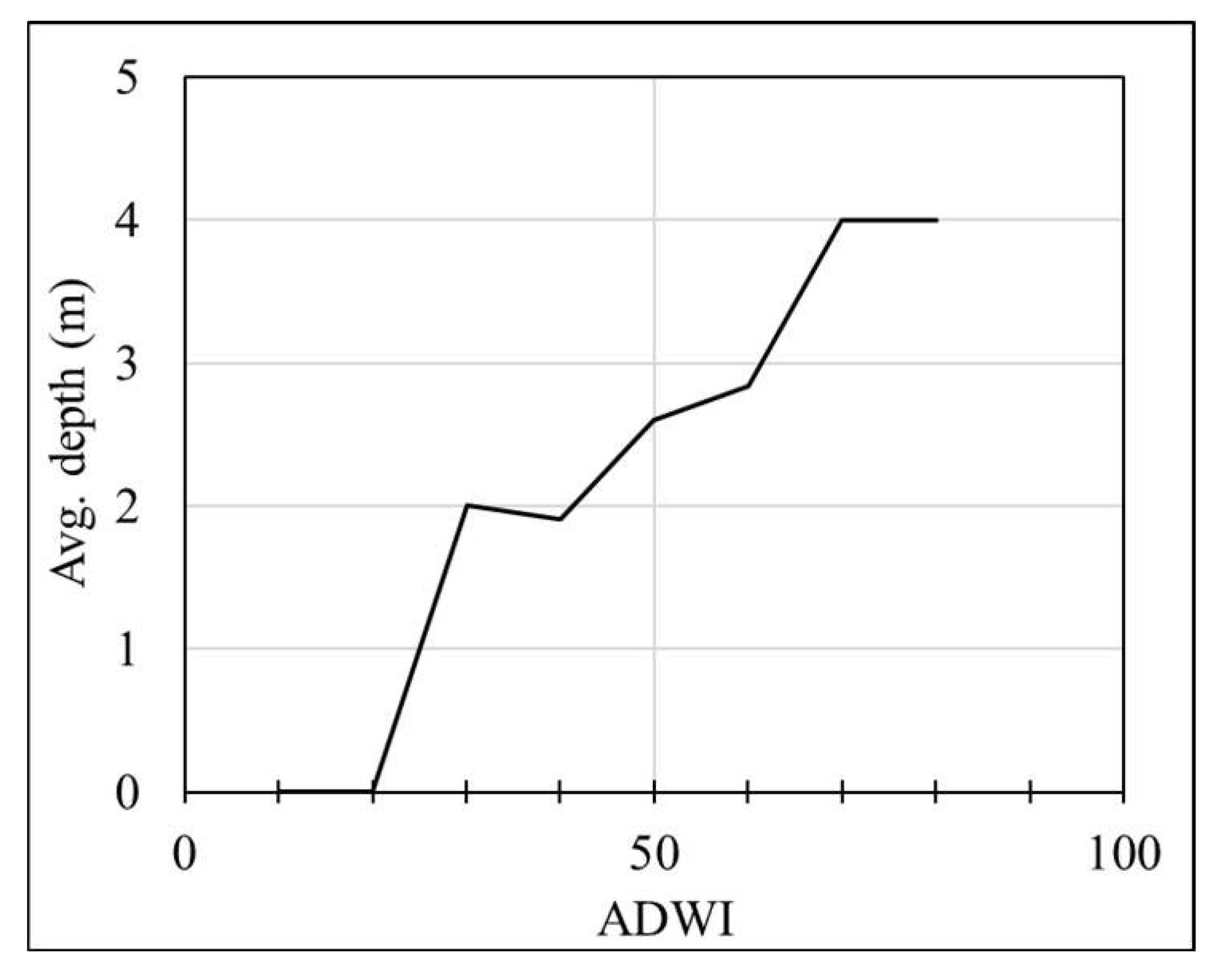
- 1 percentile of the average depth values ≈ 0 m
- Thalweg elevation, Zt = 16 − 0 ≈ 16 m
- Since Zt remains the same as the 1st trial, the same ADWI versus depth correlation is found after the 2nd trial.
- d.
- ADWI Bathymetry:
- For cell ID 7,
- LWSE = 18 m
- LWI = 60
- Average depth from ADWI versus depth correlation = 2.8 m
- ADWI bathymetry = 18 − 2.8 = 15.2 m
Appendix A.5. Post-Processing
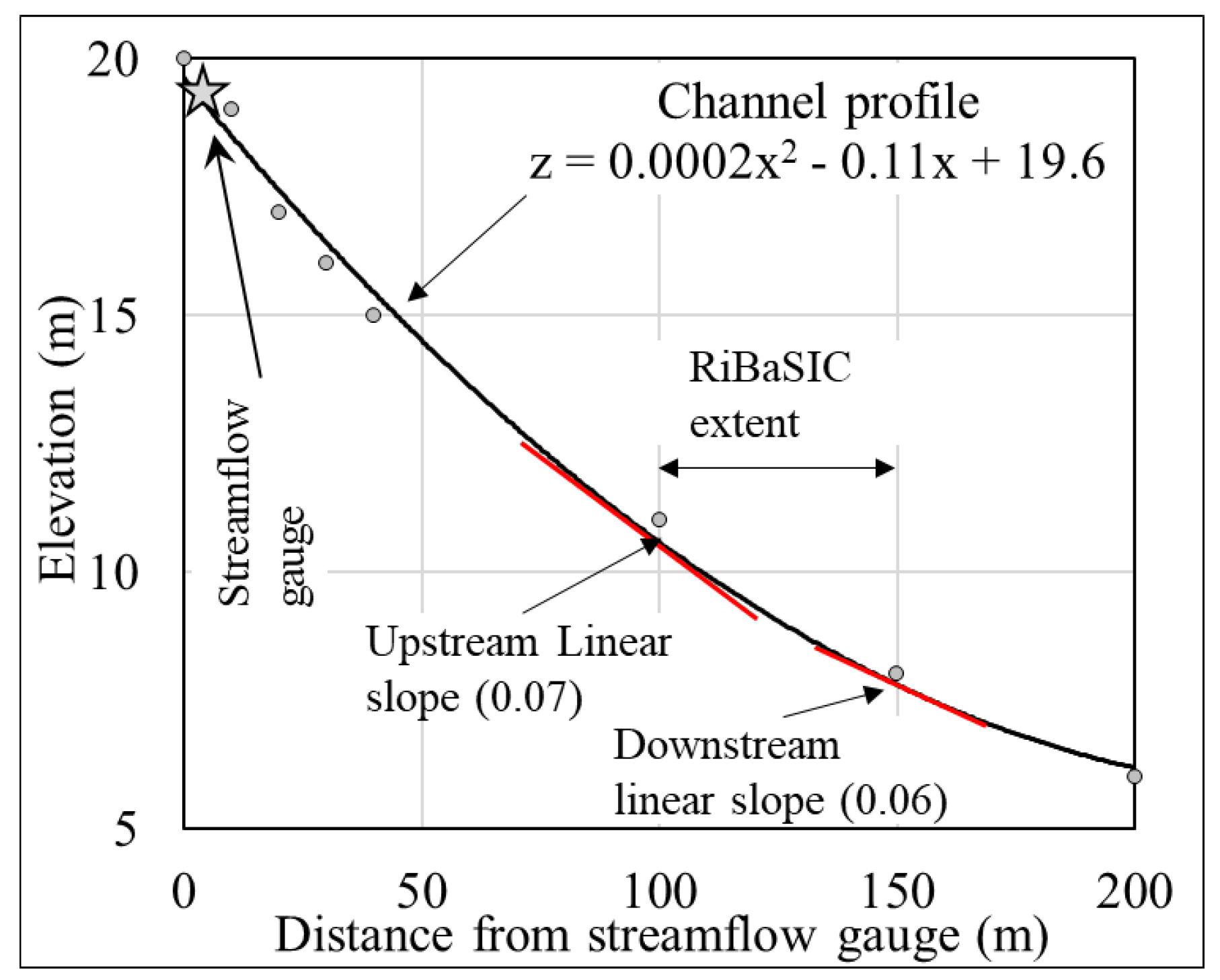
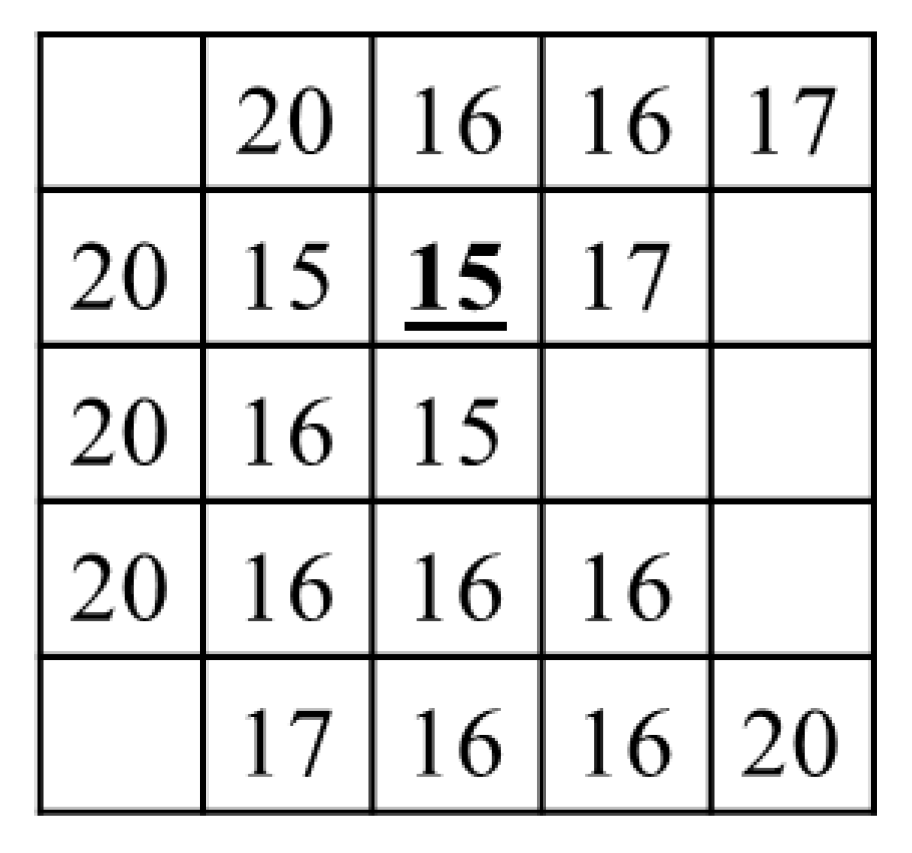
- Slope Transferred Elevation: the shoreline elevations and ADWI bathymetry for the cells are transferred to their corresponding geographic location using the channel profile shown in Figure A4.
- For cell ID 7,
- Distance, x = distance of RiBaSIC upstream from streamflow gauge + distance of cell center from RiBaSIC upstream = 100 + 15 = 115
- Therefore, using the channel profile from Figure A4
- Slope transferred shoreline elevation = 0.002 × 1152 − 0.11 × 115 + 18 = 8 m
- Slope transferred ADWI bathymetry = 0.002 × 1152 − 0.11 × 115 + 15.2 = 5.2 m
- The slope transferred cell values are presented in Figure A12.
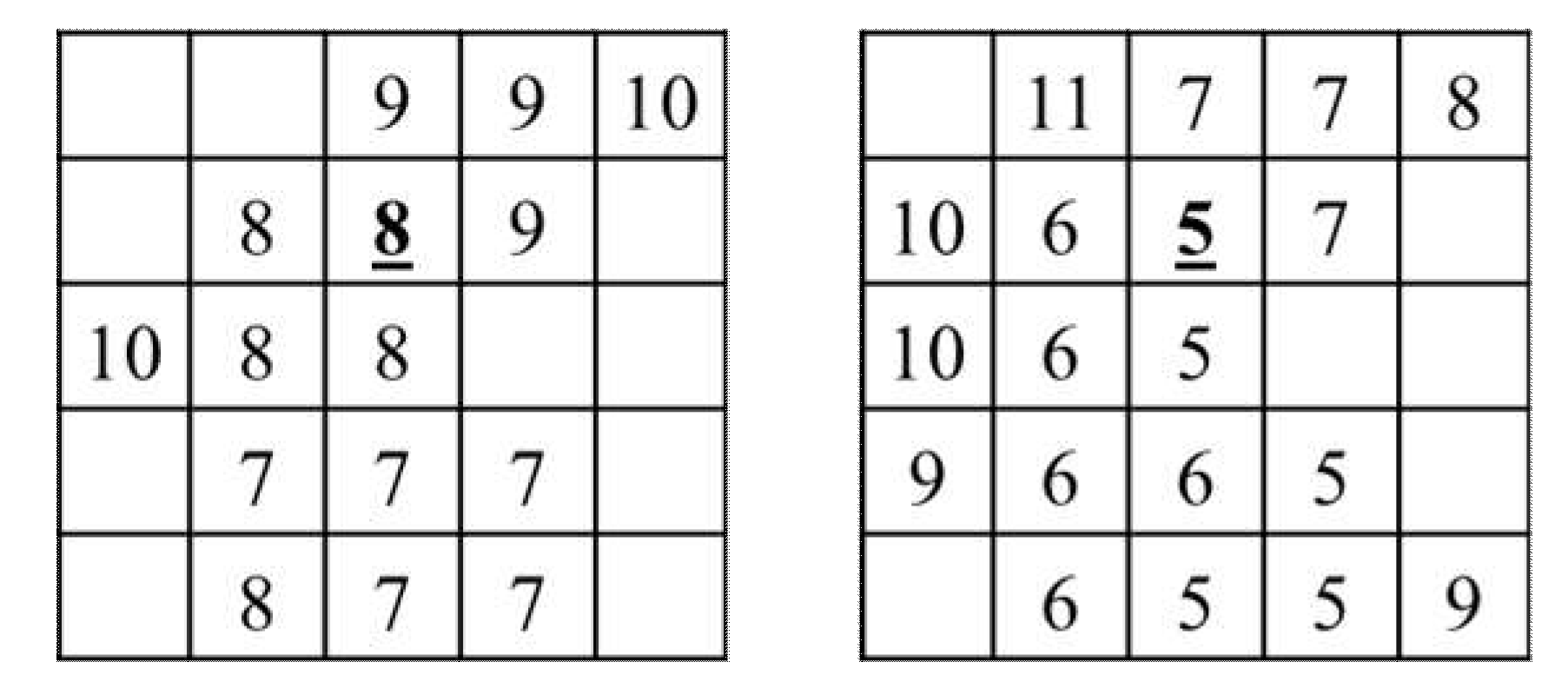
- b.
- RiBaSIC Bathymetry: the main channel of the Fusion River is obtained from a dry season satellite image as shown in Figure A13. The cells inside the main channel are assigned. Slope transferred ADWI bathymetry and shoreline elevations are assigned for the cell outside of the main channel to get the RiBaSIC bathymetry as shown in Figure A13.Cell ID 7 falls inside the main channel; therefore, ADWI bathymetry has the same elevation as slope transferred ADWI bathymetry (5 m).
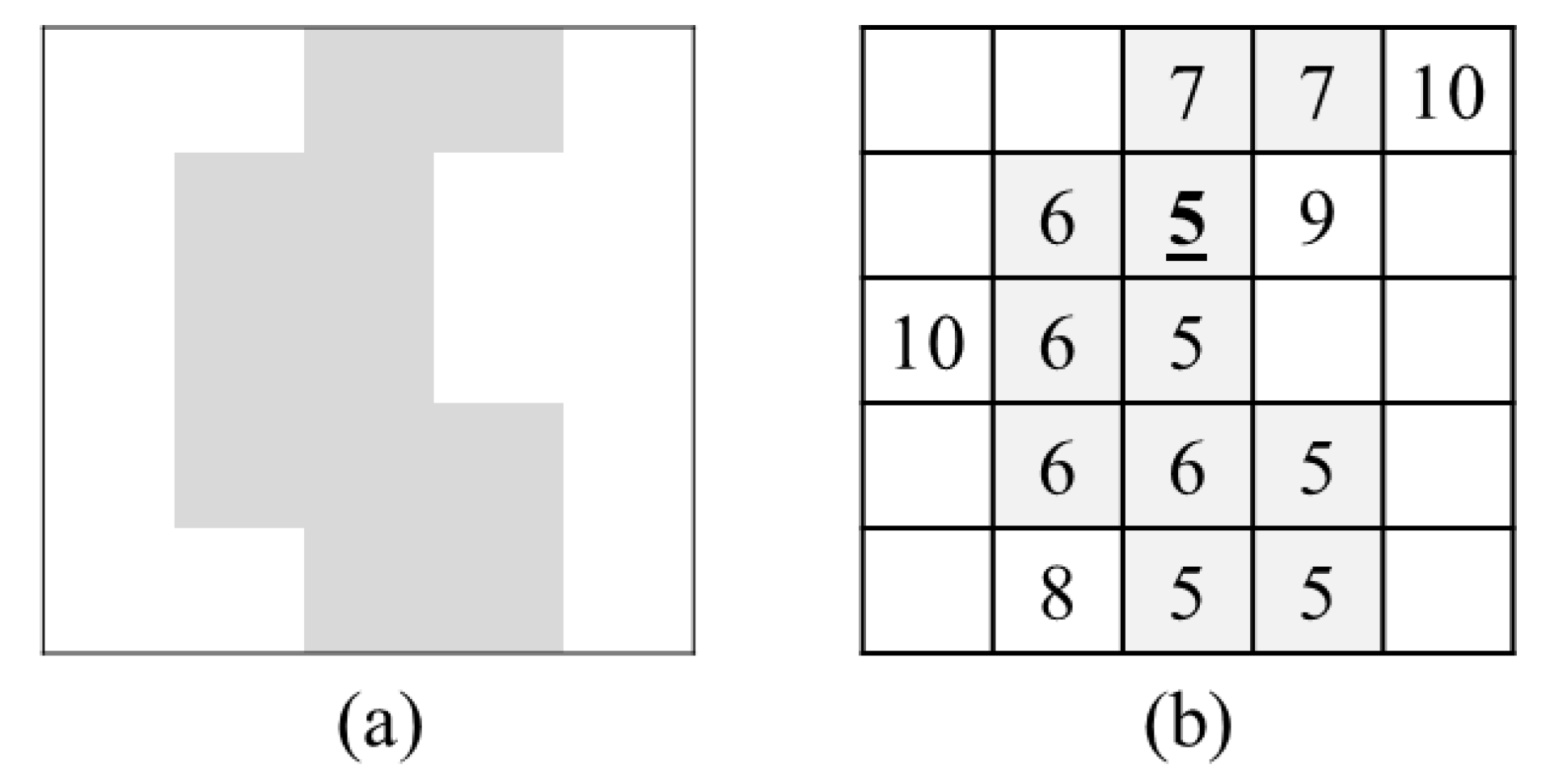
- c.
- RiBaSIC DEM: the empty cells in RiBaSIC bathymetry are filled by elevations extracted from the DEM to produce RiBaSIC DEM as shown in Figure A14. It can be seen that for cell ID 7, the DEM elevation is 9m but that has been modified to 5 m in RiBaSIC DEM.
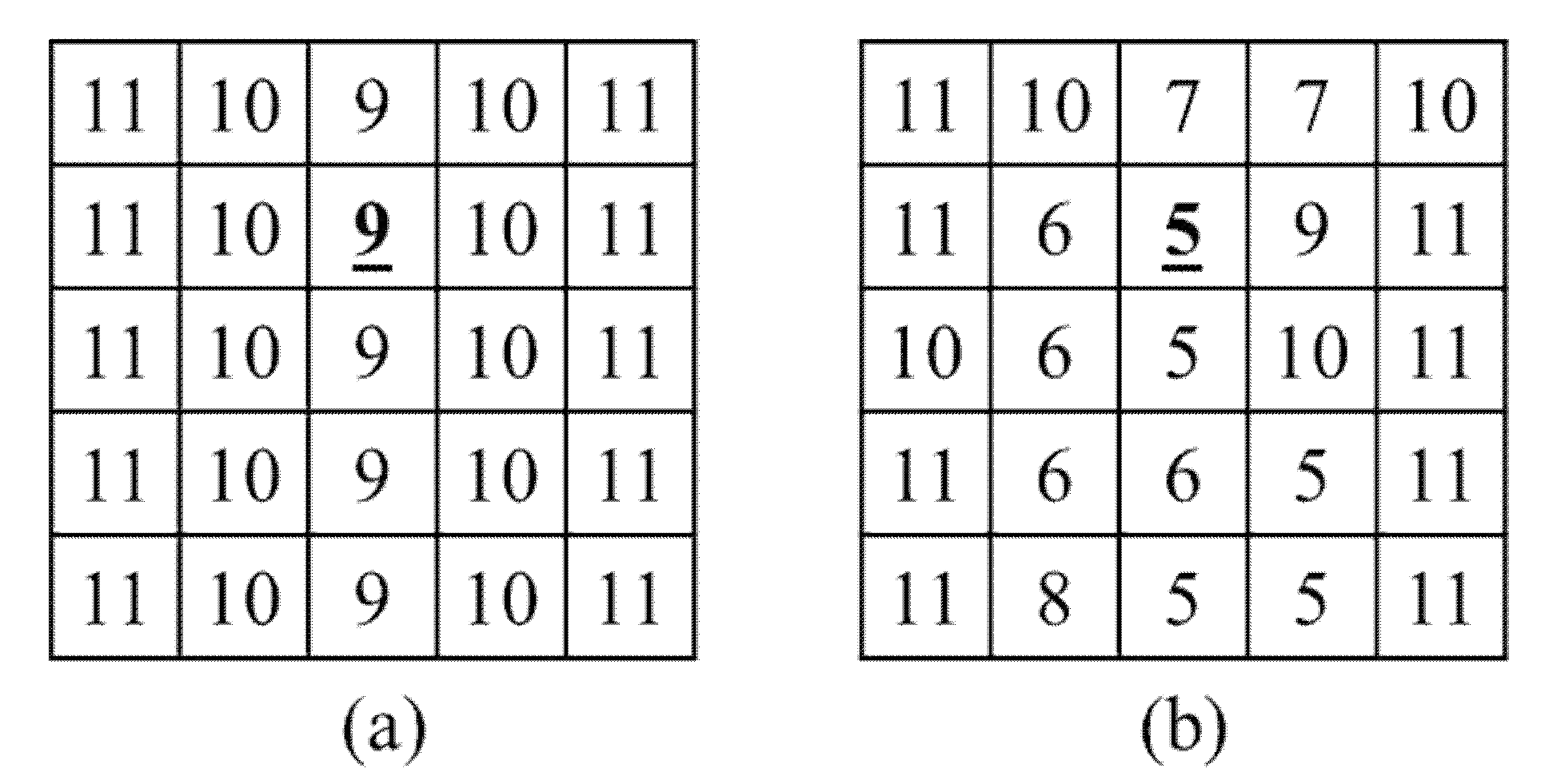
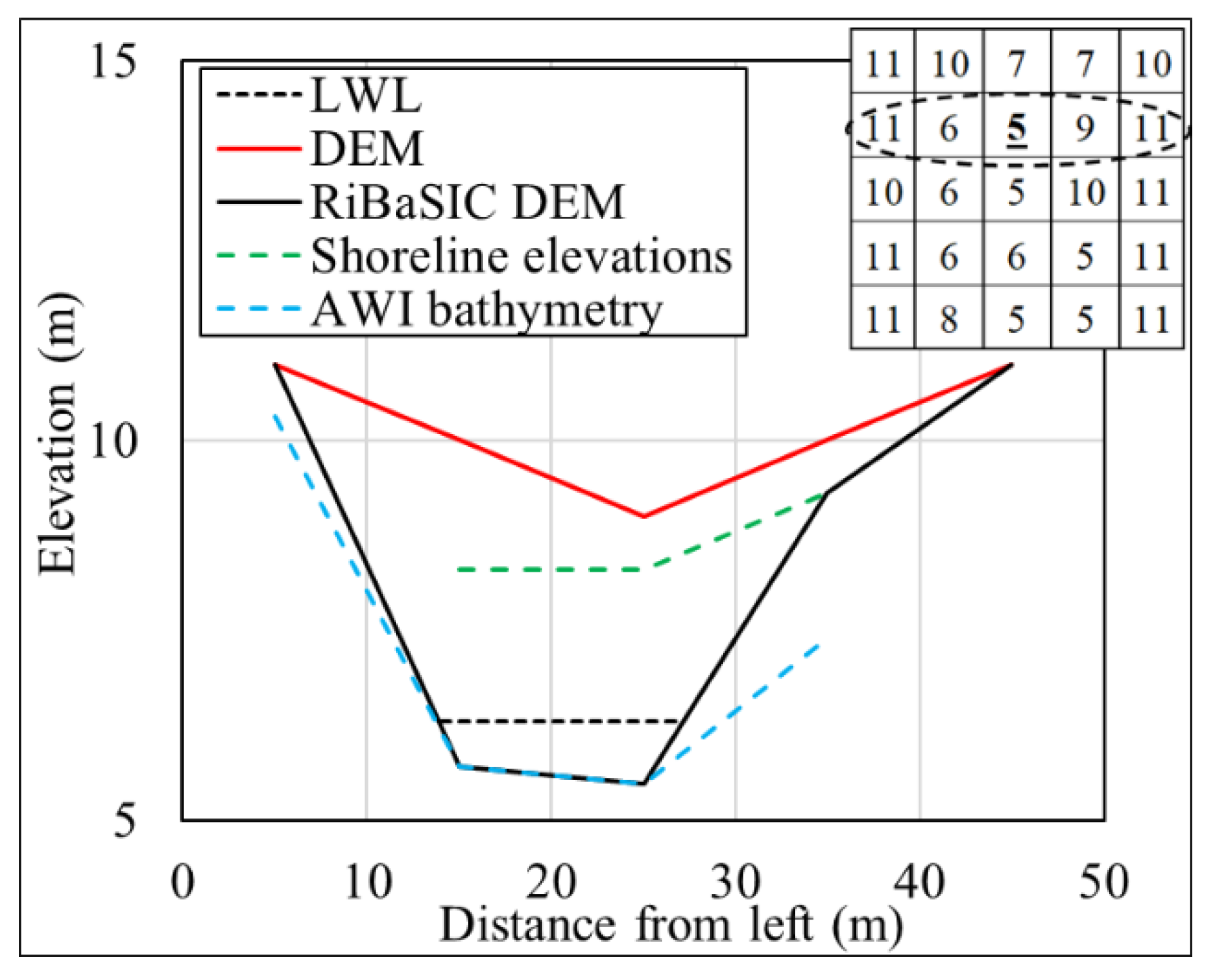
References
- Wilson, M.; Bates, P.; Alsdorf, D.; Forsberg, B.; Horritt, M.; Melack, J.; Frappart, F.; Famiglietti, J. Modeling large-scale inundation of Amazonian seasonally flooded wetlands. Geophys. Res. Lett. 2007, 34, 15. [Google Scholar] [CrossRef]
- Bhuyian, M.; Kalyanapu, A.; Nardi, F. Approach to Digital Elevation Model Correction by Improving Channel Conveyance. J. Hydrol. Eng. 2014, 20, 04014062. [Google Scholar] [CrossRef]
- Kalyanapu, A.J.; Judi, D.R.; McPherson, T.N.; Burian, S.J. Annualised risk analysis approach to recommend appropriate level of flood control: Application to Swannanoa river watershed. J. Flood Risk Manag. 2015, 8, 368–385. [Google Scholar] [CrossRef]
- Burnham, M.; Davis, D. Effects of Data Errors on Computed Steadyâ Flow Profiles. J. Hydraul. Eng. 1990, 116, 914–929. [Google Scholar] [CrossRef]
- Wechsler, S.P.; Kroll, C.N. Quantifying DEM Uncertainty and its Effect on Topographic Parameters. Photogramm. Eng. Remote Sens. 2006, 72, 1081–1090. [Google Scholar] [CrossRef]
- Yamazaki, D.; Baugh, C.A.; Bates, P.D.; Kanae, S.; Alsdorf, D.E.; Oki, T. Adjustment of a spaceborne DEM for use in floodplain hydrodynamic modeling. J. Hydrol. 2012, 436, 81–91. [Google Scholar] [CrossRef]
- Brandt, S.A.; Lim, N.J. Importance of river bank and floodplain slopes on the accuracy of flood inundation mapping. In Proceedings of the International Conference on Fluvial Hydraulics (River Flow 2012), San Jose, Costa Rica, 5–7 September 2012; CRC Press/Balkema: Leiden, The Netherlands, 2012; pp. 1015–1020. [Google Scholar]
- Fisher, G.B.; Bookhagen, B.; Amos, C.B. Channel planform geometry and slopes from freely available high-spatial resolution imagery and DEM fusion: Implications for channel width scalings, erosion proxies, and fluvial signatures in tectonically active landscapes. Geomorphology 2013, 194, 46–56. [Google Scholar] [CrossRef]
- Jung, H.C.; Jasinski, M.F. Sensitivity of a floodplain hydrodynamic model to satellite-based DEM scale and accuracy: Case study—The Atchafalaya Basin. Remote Sens. 2015, 7, 7938. [Google Scholar] [CrossRef]
- Casas, A.; Benito, G.; Thorndycraft, V.R.; Rico, M. The topographic data source of digital terrain models as a key element in the accuracy of hydraulic flood modelling. Earth Surf Process Landf. 2006, 31, 444–456. [Google Scholar] [CrossRef]
- Ettritch, G.; Hardy, A.; Bojang, L.; Cross, D.; Bunting, P.; Brewer, P. Enhancing digital elevation models for hydraulic modelling using flood frequency detection. Remote Sens. Environ. 2018, 217, 506–522. [Google Scholar] [CrossRef]
- Mason, D.C.; Trigg, M.; Garcia-Pintado, J.; Cloke, H.L.; Neal, J.C.; Bates, P.D. Improving the TanDEM-X Digital Elevation Model for flood modelling using flood extents from Synthetic Aperture Radar images. Remote Sens. Environ. 2016, 173, 15–28. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Bogoni, M.; Putti, M.; Lanzoni, S. Modeling meander morphodynamics over self-formed heterogeneous floodplains. Water Resour. Res. 2017, 53, 5137–5157. [Google Scholar] [CrossRef]
- Downward, S.; Gurnell, A.; Brookes, A. A methodology for quantifying river channel planform change using GIS. IAHS Publ. Ser. Proc. Rep. Intern Assoc. Hydrol. Sci. 1994, 224, 449–456. [Google Scholar]
- Maswood, M.; Hossain, F. Advancing river modelling in ungauged basins using satellite remote sensing: The case of the Ganges-Brahmaputra-Meghna basin. Int. J. River Basin Manag. 2016, 14, 103–117. [Google Scholar] [CrossRef]
- Schaperow, J.R.; Li, D.; Margulis, S.A.; Lettenmaier, D.P. A curve-fitting method for estimating bathymetry from water surface height and width. Water Resour. Res. 2019, 55, 4288–4303. [Google Scholar] [CrossRef]
- Gichamo, T.Z.; Popescu, I.; Jonoski, A.; Solomatine, D. River cross-section extraction from the ASTER global DEM for flood modeling. Environ. Model. Softw. 2012, 31, 37. [Google Scholar] [CrossRef]
- Merwade, V.; Maidment, D.R. A GIS Framework for Describing River Channel Bathymetry; University of Texas at Austin, Center for Research in Water Resources, JJ Pickle Research Campus: Austin, TX, USA, 2004. [Google Scholar]
- Wood, M.; Hostache, R.; Neal, J.; Wagener, T.; Giustarini, L.; Chini, M.; Corato, G.; Matgen, P.; Bates, P. Calibration of channel depth and friction parameters in the LISFLOOD-FP hydraulic model using medium-resolution SAR data and identifiability techniques. Hydrol. Earth Syst. Sci. 2016, 20, 4983–4997. [Google Scholar] [CrossRef]
- Neal, J.C.; Odoni, N.A.; Trigg, M.A.; Freer, J.E.; Garcia-Pintado, J.; Mason, D.C.; Wood, M.; Bates, P.D. Efficient incorporation of channel cross-section geometry uncertainty into regional and global scale flood inundation models. J. Hydrol. 2015, 529, 169–183. [Google Scholar] [CrossRef]
- Lim, N.J.; Brandt, S.A. Flood map boundary sensitivity due to combined effects of DEM resolution and roughness in relation to model performance. Geomat. Nat. Hazards Risk 2019, 10, 1613–1647. [Google Scholar] [CrossRef]
- Bizzi, S.; Demarchi, L.; Grabowski, R.C.; Weissteiner, C.J.; van de Bund, W. The use of remote sensing to characterise hydromorphological properties of European rivers. Aquat. Sci. 2016, 78, 57–70. [Google Scholar] [CrossRef]
- Legleiter, C.J. Calibrating remotely sensed river bathymetry in the absence of field measurements: Flow REsistance Equation-Based Imaging of River Depths (FREEBIRD). Water Resour. Res. 2015, 51, 2865–2884. [Google Scholar] [CrossRef]
- Legleiter, C. Mapping river depth from publicly available aerial images. River Res. Appl. 2013, 29, 760–780. [Google Scholar] [CrossRef]
- Legleiter, C.J. Remote measurement of river morphology via fusion of LiDAR topography and spectrally based bathymetry. Earth Surf Process Landf. 2012, 37, 499–518. [Google Scholar] [CrossRef]
- Marcus, W.A.; Fonstad, M.A. Remote sensing of rivers: The emergence of a subdiscipline in the river sciences. Earth Surf Process Landf. 2010, 35, 1867–1872. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, D.A.; Lawrence, R.L. Spectrally based remote sensing of river bathymetry. Earth Surf Process Landf. 2009, 34, 1039–1059. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Marcus, W.A. Remote sensing of stream depths with hydraulically assisted bathymetry (HAB) models. Geomorphology 2005, 72, 320–339. [Google Scholar] [CrossRef]
- Legleiter, C.J. Inferring river bathymetry via image-to-depth quantile transformation (IDQT). Water Resour. Res. 2016, 52, 3722–3741. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Bjerklie, D.M.; Fulton, J.W.; Tarpanelli, A. River Bathymetry Estimate and Discharge Assessment from Remote Sensing. Water Resour. Res. 2019, 55, 6692–6711. [Google Scholar] [CrossRef]
- Dey, S.; Saksena, S.; Merwade, V. Assessing the effect of different bathymetric models on hydraulic simulation of rivers in data sparse regions. J. Hydrol. 2019, 575, 838–851. [Google Scholar] [CrossRef]
- McCabe, M.F.; Rodell, M.; Alsdorf, D.E.; Miralles, D.G.; Uijlenhoet, R.; Wagner, W.; Lucieer, A.; Houborg, R.; Verhoest, N.E.; Franz, T.E. The future of Earth observation in hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3879. [Google Scholar] [CrossRef] [PubMed]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT mission and its capabilities for land hydrology. In Remote Sensing and Water Resources; Springer: Berlin/Heidelberg, Germany, 2016; pp. 117–147. [Google Scholar]
- Bhuyian, M.N.; Kalyanapu, A. Predicting Channel Conveyance in the Obion River Watershed Using SAMBLE Method. J. Hydrol. Eng. 2020, 25, 05019033. [Google Scholar] [CrossRef]
- Khan, M.J.U.; Ansary, M.; Durand, F.; Testut, L.; Ishaque, M.; Calmant, S.; Krien, Y.; Islam, A.; Papa, F. High-Resolution Intertidal Topography from Sentinel-2 Multi-Spectral Imagery: Synergy between Remote Sensing and Numerical Modeling. Remote Sens. 2019, 11, 2888. [Google Scholar] [CrossRef]
- Bergmann, M.; Durand, F.; Krien, Y.; Khan, M.J.U.; Ishaque, M.; Testut, L.; Calmant, S.; Maisongrande, P.; Islam, A.S.; Papa, F. Topography of the intertidal zone along the shoreline of Chittagong (Bangladesh) using PROBA-V imagery. Int. J. Remote Sens. 2018, 39, 9004–9024. [Google Scholar] [CrossRef]
- Mason, D.; Davenport, I.; Flather, R. Interpolation of an intertidal digital elevation model from heighted shorelines: A case study in the western Wash. Oceanogr. Lit. Rev. 1998, 7, 1102–1103. [Google Scholar] [CrossRef]
- Wang, Y.; Koopmans, B. Mapping and monitoring the tidal flats of coastal areas on basis of sequential ERS SAR. In Proceedings of the Second ERS Applications Workshop, London, UK, 6–8 December 1996; pp. 343–347. [Google Scholar]
- Mason, D.; Davenport, I.; Robinson, G.; Flather, R.; McCartney, B. Construction of an inter-tidal digital elevation model by the ‘Water-Line’Method. Geophys. Res. Lett. 1995, 22, 3187–3190. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, S.; Woodcock, C.E. Improvement and expansion of the Fmask algorithm: Cloud, cloud shadow, and snow detection for Landsats 4–7, 8, and Sentinel 2 images. Remote Sens. Environ. 2015, 159, 269–277. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Polidorio, A.M.; Flores, F.C.; Franco, C.; Imai, N.N.; Tommaselli, A.M. Enhancement of terrestrial surface features on high spatial resolution multispectral aerial images. In Proceedings of the IEEE 23rd SIBGRAPI Conference on Graphics, Patterns and Images, Gramado, Brazil, 30 August–3 September 2010; pp. 295–300. [Google Scholar]
- Woldai, T. Electromagnetic energy and remote sensing. In Principles of Remote Sensing: An Introductory Textbook; International Institute for Geo-Information Science and Earth Observation: Enschede, The Netherlands, 2004; pp. 29–38. [Google Scholar]
- Lacey, G. A general theory of flow in alluvium. J. Inst. Civ. Eng. 1946, 27, 16–47. [Google Scholar] [CrossRef]
- Bray, D.I. Estimating average velocity in gravel-bed rivers. J. Hydraul. Div. 1979, 105, 1103–1122. [Google Scholar]
- Coon, W.F. Estimation of Roughness Coefficients for Natural Stream Channels with Vegetated Banks; US Geological Survey: Reston, VA, USA, 1998.
- Lang, S.; Ladson, T.; Anderson, B. A review of empirical equations for estimating stream roughness and their application to four streams in Victoria. Australas. J. Water Resour. 2004, 8, 69–82. [Google Scholar] [CrossRef]
- Jarrett, R.D. Hydraulics of high-gradient streams. J. Hydraul. Eng. 1984, 110, 1519–1539. [Google Scholar] [CrossRef]
- Te Chow, V. Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- LeFavour, G.; Alsdorf, D. Water slope and discharge in the Amazon River estimated using the shuttle radar topography mission digital elevation model. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Hall, A.C.; Schumann, G.J.; Bamber, J.L.; Bates, P.D.; Trigg, M.A. Geodetic corrections to Amazon River water level gauges using ICESat altimetry. Water Resour. Res. 2012, 48, 6. [Google Scholar] [CrossRef]
- FAP24. River Survey Project Annex 3: Hydrology; Final Report; Water Resources Planning Organization: Dhaka, Bangladesh, 1996.
- Lind, G.D.; Wellman, R.E.; Mangano, J.F. Boat-Based River Bathymetry and Stream Velocity on the Upper Willamette River, Oregon, Spring 2015; U.S. Geological Survey: Reston, VA, USA, 2017. [CrossRef]
- Bjerklie, D.M.; Moller, D.; Smith, L.C.; Dingman, S.L. Estimating discharge in rivers using remotely sensed hydraulic information. J. Hydrol. 2005, 309, 191–209. [Google Scholar] [CrossRef]
- Brombacher, J.; Reiche, J.; Dijksma, R.; Teuling, A.J. Near-daily discharge estimation in high latitudes from Sentinel-1 and 2: A case study for the Icelandic Þjórsá river. Remote Sens. Environ. 2020, 241, 111684. [Google Scholar] [CrossRef]
- Feng, D.; Gleason, C.J.; Yang, X.; Pavelsky, T.M. Comparing discharge estimates made via the BAM algorithm in high-order Arctic rivers derived solely from optical CubeSat, Landsat, and Sentinel-2 data. Water Resour. Res. 2019, 55, 7753–7771. [Google Scholar] [CrossRef]
- Kim, D.; Yu, H.; Lee, H.; Beighley, E.; Durand, M.; Alsdorf, D.E.; Hwang, E. Ensemble learning regression for estimating river discharges using satellite altimetry data: Central Congo River as a Test-bed. Remote Sens. Environ. 2019, 221, 741–755. [Google Scholar] [CrossRef]
- Bogning, S.; Frappart, F.; Blarel, F.; Niño, F.; Mahé, G.; Seyler, F.; Braun, J.; Onguéné, R.; Etamé, J. Estimating River Discharges in the Ogooue River Basin Using Satellite Altimetry Data. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2018), Valencia, Spain, 22–27 July 2018; pp. 9304–9307. [Google Scholar]
- Sichangi, A.; Wang, L.; Hu, Z. Estimation of River Discharge Solely from Remote-Sensing Derived Data: An Initial Study Over the Yangtze River. Remote Sens. 2018, 10, 1385. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Santi, E.; Tourian, M.J.; Filippucci, P.; Amarnath, G.; Brocca, L. Daily river discharge estimates by merging satellite optical sensors and radar altimetry through artificial neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 329–341. [Google Scholar] [CrossRef]
- Oubanas, H.; Gejadze, I.; Malaterre, P.; Durand, M.; Wei, R.; Frasson, R.P.; Domeneghetti, A. Discharge estimation in ungauged basins through variational data assimilation: The potential of the SWOT mission. Water Resour. Res. 2018, 54, 2405–2423. [Google Scholar] [CrossRef]
- Durand, M.; Gleason, C.; Garambois, P.; Bjerklie, D.; Smith, L.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J. An intercomparison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Tourian, M.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal densification of river water level time series by multimission satellite altimetry. Water Resour. Res. 2016, 52, 1140–1159. [Google Scholar] [CrossRef]
- Bhuyian, M.N.; Kalyanapu, A. Accounting digital elevation uncertainty for flood consequence assessment. J. Flood Risk Manag. 2018, 11, S1051–S1062. [Google Scholar] [CrossRef]
- Andreadis, K.M.; Clark, E.A.; Lettenmaier, D.P.; Alsdorf, D.E. Prospects for river discharge and depth estimation through assimilation of swath-altimetry into a raster-based hydrodynamics model. Geophys. Res. Lett. 2007, 34, 10. [Google Scholar] [CrossRef]

| Equation | Method | Formula | Source | Remarks |
|---|---|---|---|---|
| 9 | Lacey (1946) | [46] | R = Hydraulic radius (ft) S = Channel slope Sw = Slope of water surface Sf = Energy gradient | |
| 10 | Bray (1979) | [47,48] | ||
| 11 | Bray (1982) | [49] | ||
| 12 | Jarrett (1984) | [50] | ||
| 13 | Sauer (1990) | [48,49] |
| Study Area | SA1 | SA2 | SA3 | SA4 | |
|---|---|---|---|---|---|
| River | Willamette | Kushiyara | Jamuna | Solimoes | |
| Basin | Columbia | Meghna | Brahmaputra | Amazon | |
| Country | USA | Bangladesh | Bangladesh | Brazil | |
| River characteristics | Planform | Meandering | Meandering | Braided | Wandering |
| Top width (m) | 120 | 200 | 12,000 | 7000 | |
| Tidal effect | No | No | No | No | |
| Season | Dry | Jul–Nov | Jan–May | Jan–May | Aug–Dec |
| Wet | Dec–Jun | Jun–Dec | Jun–Dec | Jan–Jul | |
| Extent | RiBaSIC | Harrisburg to Albany (67 km) | Fenchuganj to Markuli (80 km) | Kazipur (25 km) | Iranduba (15 km) |
| HD model | Harrisburg to Corvallis (47 km) | Fenchuganj to Monu confluence (32 km) | |||
| Period | RiBaSIC | 2013–2015 | 2000–2002 | 2010 | 2010 |
| HD model | 2009–2013 | 2001–2005 | 2009–2013 | 2009–2013 | |
| HD model | Grid size (m) | 30 × 30 | 30 × 30 | 100 × 100 | 100 × 100 |
| Time step (s) | 300 | 300 | 300 | 300 | |
| Satellite Image | Landsat | 7, 8 | 5, 7 | 5, 7 | 5, 7 |
| Count | 129 | 67 | 29 | 30 | |
| DEM | Slope estimation | SRTM | SRTM | SRTM | 1 [52] |
| Floodplain | MERIT | MERIT | MERIT | MERIT | |
| WSE | Location | Harrisburg | Fenchuganj | Bahadurabad | 2 Manacapuru |
| Source | USGS | BWDB | BWDB | 2 SO-HYBAM | |
| Discharge | Location | Harrisburg | Sherpur | Bahadurabad | Manacapuru |
| Source | USGS | BWDB | 3FAP24 | HYBAM | |
| Bathymetric survey | Period | 2015 | 2004 | 2011 | 4 N/A |
| Source | 5 USGS | BWDB | BWDB | 4 Brazil Navy | |
| Slope (upstream–downstream) | RiBaSIC | 0.0009–0.0002 | 0.00006–0.000005 | 0.00008 | 0.000019 |
| ID | SA1 | SA2 | SA3 | SA4 | |
|---|---|---|---|---|---|
| River | Willamette | Kushiyara | Jamuna | Solimoes | |
| Location | Harrisburg | Monu confluence | Kazipur | Iranduba | |
| Streamflow gauge | Harrisburg | Sherpur | Bahadurabad | Manacapuru | |
| Slope | Upstream | 0.0009 | 0.000059 | 0.00008 | 0.000019 |
| Downstream | 0.0004 | 0.000056 | 0.00008 | 0.000019 | |
| Hydraulic Radius (m) | Upstream | 3.75 | 7.47 | 4.04 | 17.33 |
| Downstream | 3.29 | 7.39 | 4.04 | 17.33 | |
| Manning’s n (upstream) | Lacey (1946) | 0.029 | 0.018 | 0.019 | 0.015 |
| Bray (1979) | 0.030 | 0.019 | 0.020 | 0.015 | |
| Bray (1982) | 0.034 | 0.020 | 0.020 | 0.017 | |
| Jarrett (1984) | 0.018 | 0.006 | 0.007 | 0.003 | |
| Sauer (1990) | 0.038 | 0.025 | 0.025 | 0.021 | |
| Average | 0.030 | 0.020 | 0.021 | 0.017 | |
| Manning’s n (downstream) | Lacey (1946) | 0.025 | 0.018 | 0.019 | 0.015 |
| Bray (1979) | 0.026 | 0.018 | 0.020 | 0.015 | |
| Bray (1982) | 0.028 | 0.020 | 0.020 | 0.017 | |
| Jarrett (1984) | 0.013 | 0.006 | 0.007 | 0.003 | |
| Sauer (1990) | 0.032 | 0.024 | 0.025 | 0.021 | |
| Average | 0.025 | 0.020 | 0.021 | 0.017 | |
| RRMSE | Dry | 11% | 19% | 25% | 21% |
| Wet | 17% | 17% | 16% | 10% | |
| Annual | 17% | 19% | 19% | 14% | |
| NSE | 0.97 | 0.95 | 0.98 | 0.93 | |
| Correlation coefficient | 0.98 | 0.99 | 0.98 | 0.98 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhuyian, M.N.M.; Kalyanapu, A. Predicting Channel Conveyance and Characterizing Planform Using River Bathymetry via Satellite Image Compilation (RiBaSIC) Algorithm for DEM-Based Hydrodynamic Modeling. Remote Sens. 2020, 12, 2799. https://doi.org/10.3390/rs12172799
Bhuyian MNM, Kalyanapu A. Predicting Channel Conveyance and Characterizing Planform Using River Bathymetry via Satellite Image Compilation (RiBaSIC) Algorithm for DEM-Based Hydrodynamic Modeling. Remote Sensing. 2020; 12(17):2799. https://doi.org/10.3390/rs12172799
Chicago/Turabian StyleBhuyian, Md N M, and Alfred Kalyanapu. 2020. "Predicting Channel Conveyance and Characterizing Planform Using River Bathymetry via Satellite Image Compilation (RiBaSIC) Algorithm for DEM-Based Hydrodynamic Modeling" Remote Sensing 12, no. 17: 2799. https://doi.org/10.3390/rs12172799
APA StyleBhuyian, M. N. M., & Kalyanapu, A. (2020). Predicting Channel Conveyance and Characterizing Planform Using River Bathymetry via Satellite Image Compilation (RiBaSIC) Algorithm for DEM-Based Hydrodynamic Modeling. Remote Sensing, 12(17), 2799. https://doi.org/10.3390/rs12172799






