Increasing Historical Tropical Cyclone-Induced Extreme Wave Heights in the Northern East China Sea during 1979 to 2018
Abstract
:1. Introduction
2. Methods
2.1. Parametric TC Wind Simulation
2.2. Coupled Wave-Circulation Simulation
3. Results
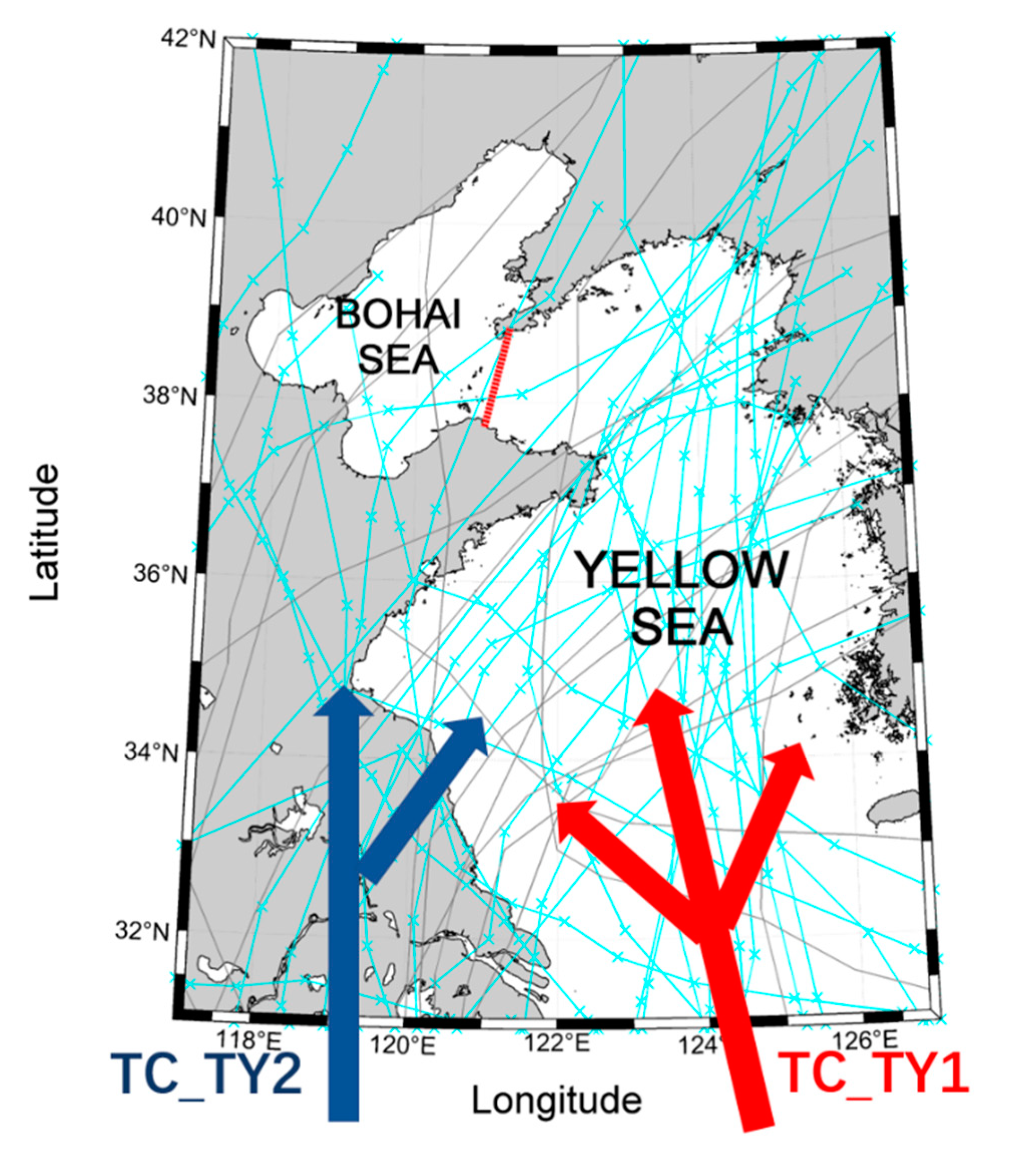
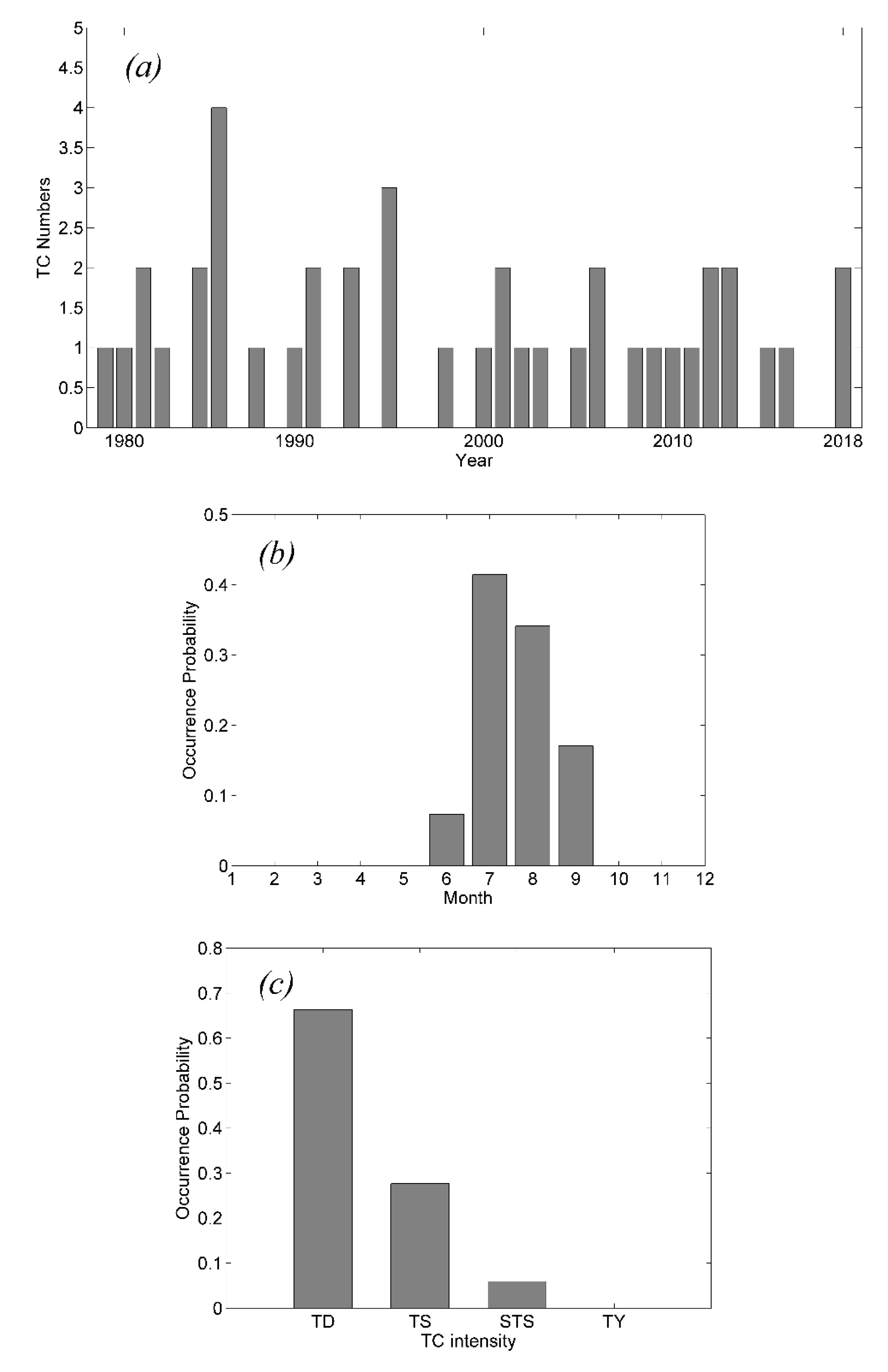
3.1. Distribution of Extreme Wave Height and Wind Speed
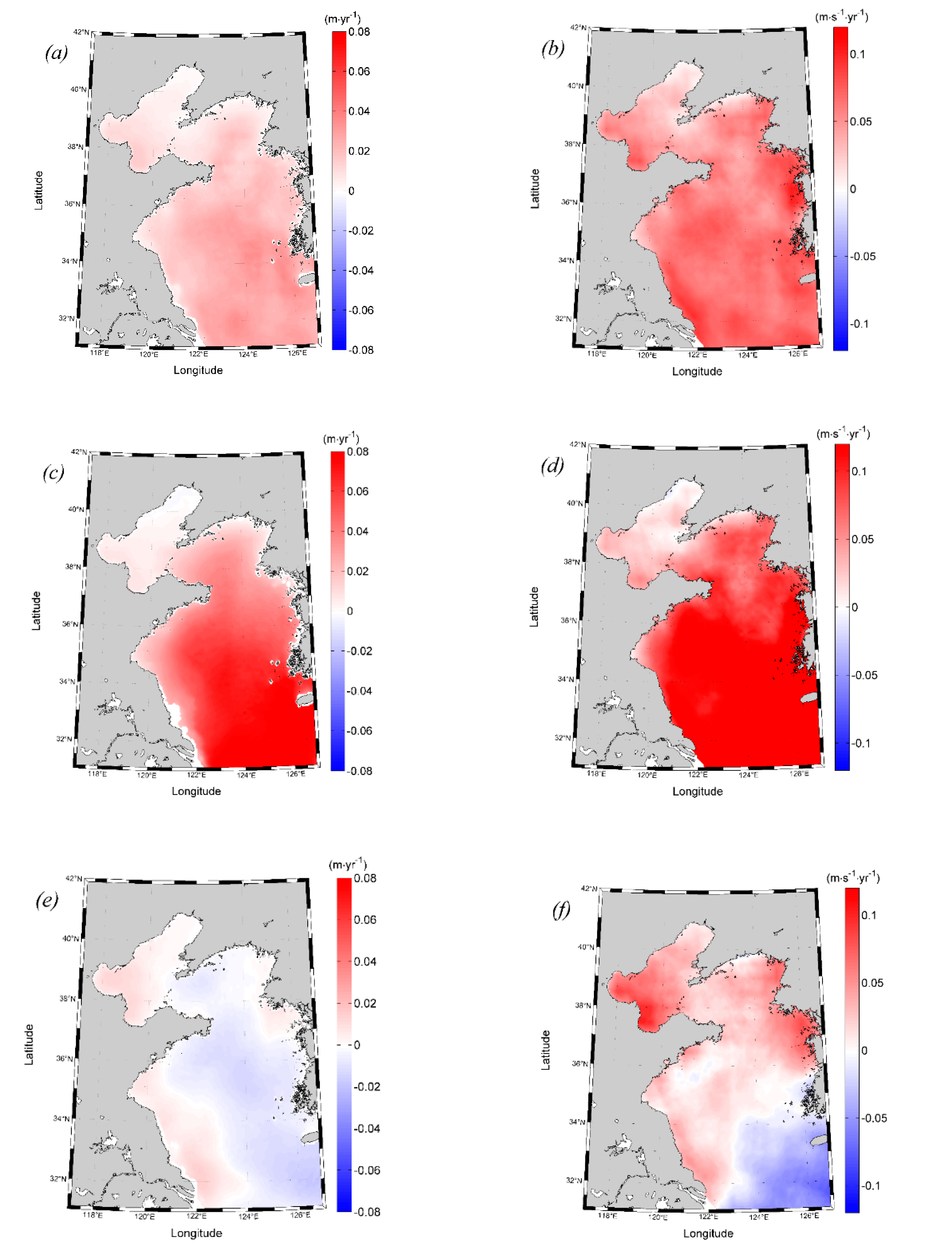
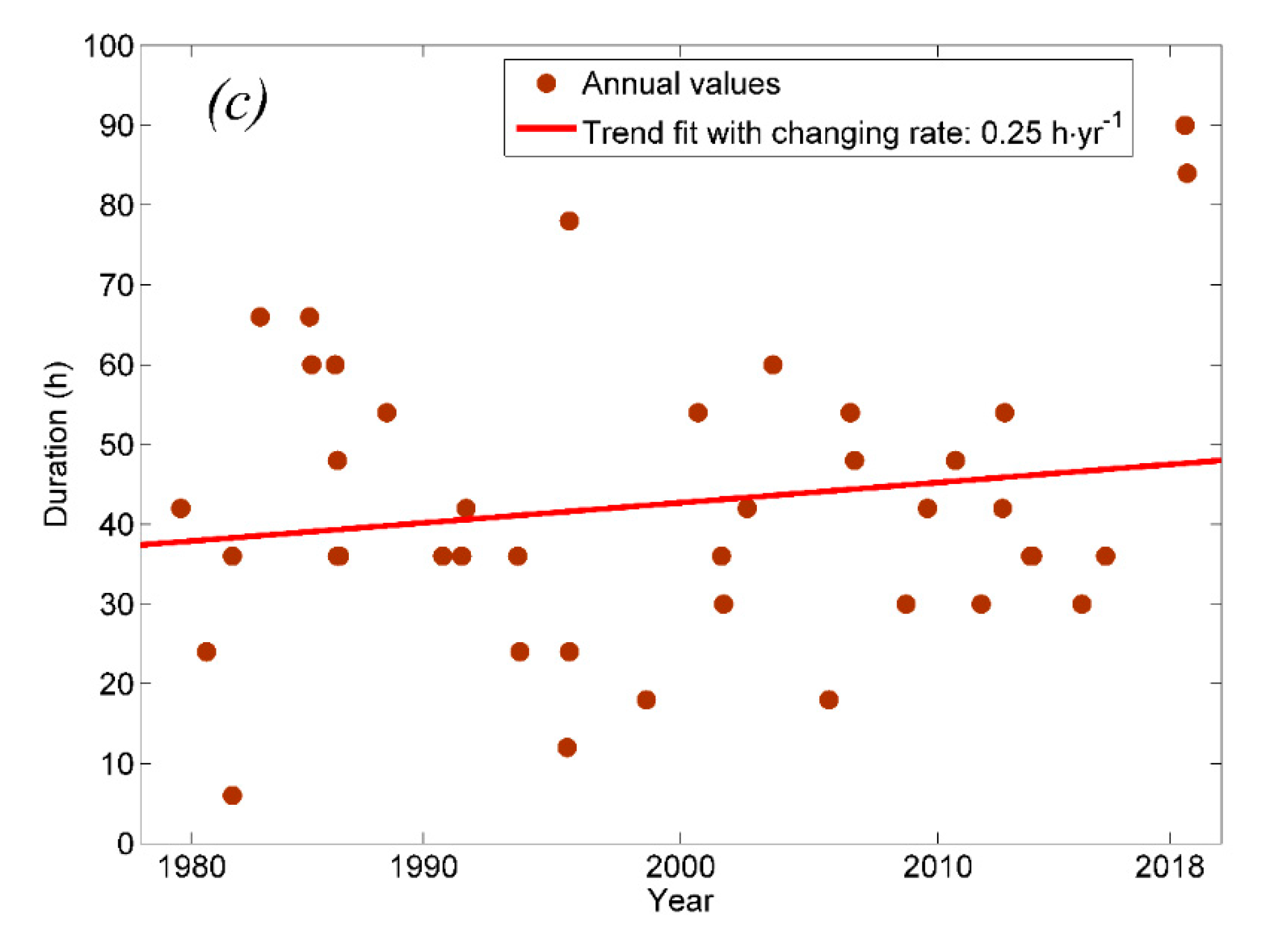
3.2. Trends of Extreme Wave Height and Wind Speed
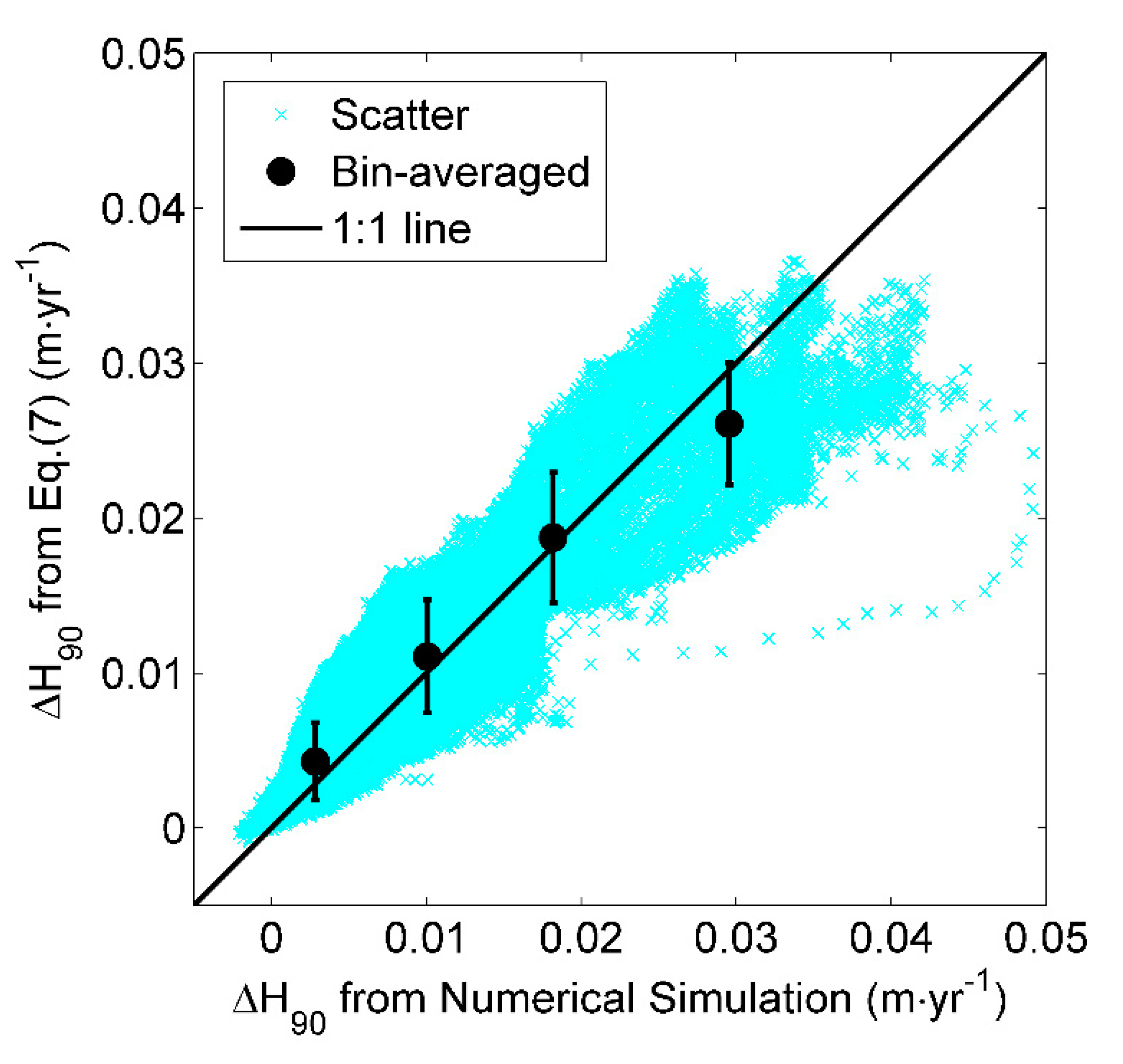
3.3. Relation Between the Extreme Wind Speed and Wave Height Trends
4. Discussions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Peduzzi, P.; Chatenoux, B.; Dao, H.; De Bono, A.; Herold, C.; Kossin, J.P.; Mouton, F.; Nordbeck, O. Global trends in tropical cyclone risk. Nat. Clim. Chang. 2012, 2, 289–294. [Google Scholar] [CrossRef]
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.-R. Changes in tropical cyclone number, duration, and intensity in a warming environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emanuel, K. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
- Mei, W.; Xie, S.-P.; Primeau, F.; McWilliams, J.C.; Pasquero, C. Northwestern Pacific typhoon intensity controlled by changes in ocean temperatures. Sci. Adv. 2015, 1, e1500014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guan, S.; Li, S.; Hou, Y.; Hu, P.; Liu, Z.; Feng, J. Increasing threat of landfalling typhoons in the western North Pacific between 1974 and 2013. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 279–286. [Google Scholar] [CrossRef]
- Li, S.; Guan, S.; Hou, Y.; Liu, Y.; Bi, F. Evaluation and adjustment of altimeter measurement and numerical hindcast in wave height trend estimation in China’s coastal seas. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 161–172. [Google Scholar] [CrossRef]
- Feng, X.; Li, M.; Yin, B.; Yang, D.; Yang, H. Study of storm surge trends in typhoon-prone coastal areas based on observations and surge-wave coupled simulations. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 272–278. [Google Scholar] [CrossRef]
- Izaguirre, C.; Mendez, F.J.; Menéndez, M.; Luceño, A.; Losada, I.J. Extreme wave climate variability in southern Europe using satellite data. J. Geophys. Res. Space Phys. 2010, 115, 04009. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A. Global Trends in Wind Speed and Wave Height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef]
- Zhang, C.K. Estimation of long-term wave statistics in the East China Sea. J. Coast. Res. 2013, 65, 177–182. [Google Scholar]
- Stephens, S.A.; Gorman, R. Extreme wave predictions around New Zealand from hindcast data. N. Z. J. Mar. Freshw. Res. 2006, 40, 399–411. [Google Scholar] [CrossRef]
- Xu, F.; Perrie, W.; Toulany, B.; Smith, P.C. Wind-generated waves in Hurricane Juan. Ocean Model. 2007, 16, 188–205. [Google Scholar] [CrossRef]
- Liu, H.; Xie, L.; Pietrafesa, L.J.; Bao, S. Sensitivity of wind waves to hurricane wind characteristics. Ocean Model. 2007, 18, 37–52. [Google Scholar] [CrossRef]
- Wang, N.; Hou, Y.; Li, S.; Li, R. Numerical simulation and preliminary analysis of typhoon waves during three typhoons in the Yellow Sea and East China Sea. J. Oceanol. Limnol. 2019, 37, 1805–1816. [Google Scholar] [CrossRef]
- Holland, G.J. An Analytic Model of the Wind and Pressure Profiles in Hurricanes. Mon. Weather. Rev. 1980, 108, 1212–1218. [Google Scholar] [CrossRef]
- Feng, X.; Yin, B.; Yang, D. Development of an unstructured-grid wave-current coupled model and its application. Ocean Model. 2016, 104, 213–225. [Google Scholar] [CrossRef]
- Wang, K.; Hou, Y.; Li, S.; Du, M.; Chen, J.; Lu, J. A comparative study of storm surge and wave setup in the East China Sea between two severe weather events. Estuar. Coast. Shelf Sci. 2020, 235, 106583. [Google Scholar] [CrossRef]
- Jelesnianski, C.P.; Taylor, A.D. A Preliminary View of Storm Surges before and after Storm Modifications NOAA, Technical Memorandum, ERL WMPO-3; Environmental Research Laboratories, Weather Modification Program Office: Boulder, CO, USA, 1973; Volume 3, p. 33. [Google Scholar]
- Willoughby, H.E.; Darling, R.W.R.; Rahn, M.E. Parametric representation of the primary hurricane vortex. part II: A new family of sectionally continuous profiles. Mon. Weather. Rev. 2006, 134, 1102–1120. [Google Scholar] [CrossRef] [Green Version]
- Emanuel, K.; Rotunno, R. Self-stratification of tropical cyclone outflow. Part I: Implications for storm structure. J. Atmos. Sci. 2011, 68, 2236–2249. [Google Scholar] [CrossRef]
- Krien, Y.; Arnaud, G.; Cécé, R.; Ruf, C.; Belmadani, A.; Khan, J.U.; Bernard, D.C.; Islam, A.; Durand, F.; Testut, L.; et al. Can We Improve Parametric Cyclonic Wind Fields Using Recent Satellite Remote Sensing Data? Remote Sens. 2018, 10, 1963. [Google Scholar] [CrossRef] [Green Version]
- Vickery, P.J.; Masters, F.J.; Powell, M.; Wadhera, D. Hurricane hazard modeling: The past, present, and future. J. Wind Eng. Ind. Aerodyn. 2009, 97, 392–405. [Google Scholar] [CrossRef]
- Powell, M.; Soukup, G.; Cocke, S.; Gulati, S.; Morisseau-Leroy, N.; Hamid, S.; Dorst, N.; Axe, L. State of Florida hurricane loss projection model: Atmospheric science component. J. Wind Eng. Ind. Aerodyn. 2005, 93, 651–674. [Google Scholar] [CrossRef] [Green Version]
- Graham, H.E. Meteorological Considerations Pertinent to Standard Project Hurricane, Atlantic and Gulf Coasts of the United States; U.S. Department of Commerce, Weather Bureau: Washington, DC, USA, 1959.
- Jiang, Z.H.; Hua, F.; Qu, P. A new scheme for adjusting the tropical cyclone parameters. Adv. Mar. Sci. 2008, 26, 1–7, (in Chinese with English abstract). [Google Scholar]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Sheng, J. A comparative study of wave-current interactions over the eastern Canadian shelf under severe weather conditions using a coupled wave-circulation model. J. Geophys. Res. Oceans 2016, 121, 5252–5281. [Google Scholar] [CrossRef]
- Mao, M.; Xia, M. Dynamics of wave–current–surge interactions in Lake Michigan: A model comparison. Ocean Model. 2017, 110, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, J.C.; Zijlema, M.; Westerink, J.; Holthuijsen, L.; Dawson, C.N.; Luettich, R.A.; Jensen, R.E.; Smith, J.M.; Stelling, G.; Stone, G.W. Modeling hurricane waves and storm surge using integrally-coupled, scalable computations. Coast. Eng. 2011, 58, 45–65. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, K. On the existence of a fully developed wind-sea spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewign, J.A.; Gienapp, H.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Dtsch. Hydrogr. Z. 1973, 12, 1–95. [Google Scholar]
- Bilskie, M.V.; Hagen, S.C.; Medeiros, S.C.; Cox, A.T.; Salisbury, M.; Coggin, D. Data and numerical analysis of astronomic tides, wind-waves, and hurricane storm surge along the northern Gulf of Mexico. J. Geophys. Res. Oceans 2016, 121, 3625–3658. [Google Scholar] [CrossRef]
- Garratt, J.R. Review of drag coefficients over oceans and continents. Mon. Weather Rev. 1977, 105, 915–929. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Hou, Y.; Li, S.; Mo, D.; Li, J. Numerical simulation of the hazard distribution of typhoon waves in 1979—2018. J. Oceanol. Limnol. 2020, 51, 525–532, (in Chinese with English abstract). [Google Scholar]
- Young, I.R. Directional spectra of hurricane wind waves. J. Geophys. Res. Space Phys. 2006, 111, C8. [Google Scholar] [CrossRef]
- Xu, Y.; He, H.; Song, J.; Hou, Y.; Li, F. Observations and Modeling of Typhoon Waves in the South China Sea. J. Phys. Oceanogr. 2017, 47, 1307–1324. [Google Scholar] [CrossRef]
- The WAMDI Group. The WAM model: A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef] [Green Version]
- Emanuel, K. Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century. Proc. Natl. Acad. Sci. USA 2013, 110, 12219–12224. [Google Scholar] [CrossRef] [PubMed] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Jiang, H.; Hou, Y.; Wang, N.; Lu, J. Increasing Historical Tropical Cyclone-Induced Extreme Wave Heights in the Northern East China Sea during 1979 to 2018. Remote Sens. 2020, 12, 2464. https://doi.org/10.3390/rs12152464
Li S, Jiang H, Hou Y, Wang N, Lu J. Increasing Historical Tropical Cyclone-Induced Extreme Wave Heights in the Northern East China Sea during 1979 to 2018. Remote Sensing. 2020; 12(15):2464. https://doi.org/10.3390/rs12152464
Chicago/Turabian StyleLi, Shuiqing, Haoyu Jiang, Yijun Hou, Ning Wang, and Jiuyou Lu. 2020. "Increasing Historical Tropical Cyclone-Induced Extreme Wave Heights in the Northern East China Sea during 1979 to 2018" Remote Sensing 12, no. 15: 2464. https://doi.org/10.3390/rs12152464




