A Temporal Disaggregation Approach for TRMM Monthly Precipitation Products Using AMSR2 Soil Moisture Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Resources
2.3. The Relationship between Precipitation and Soil Moisture
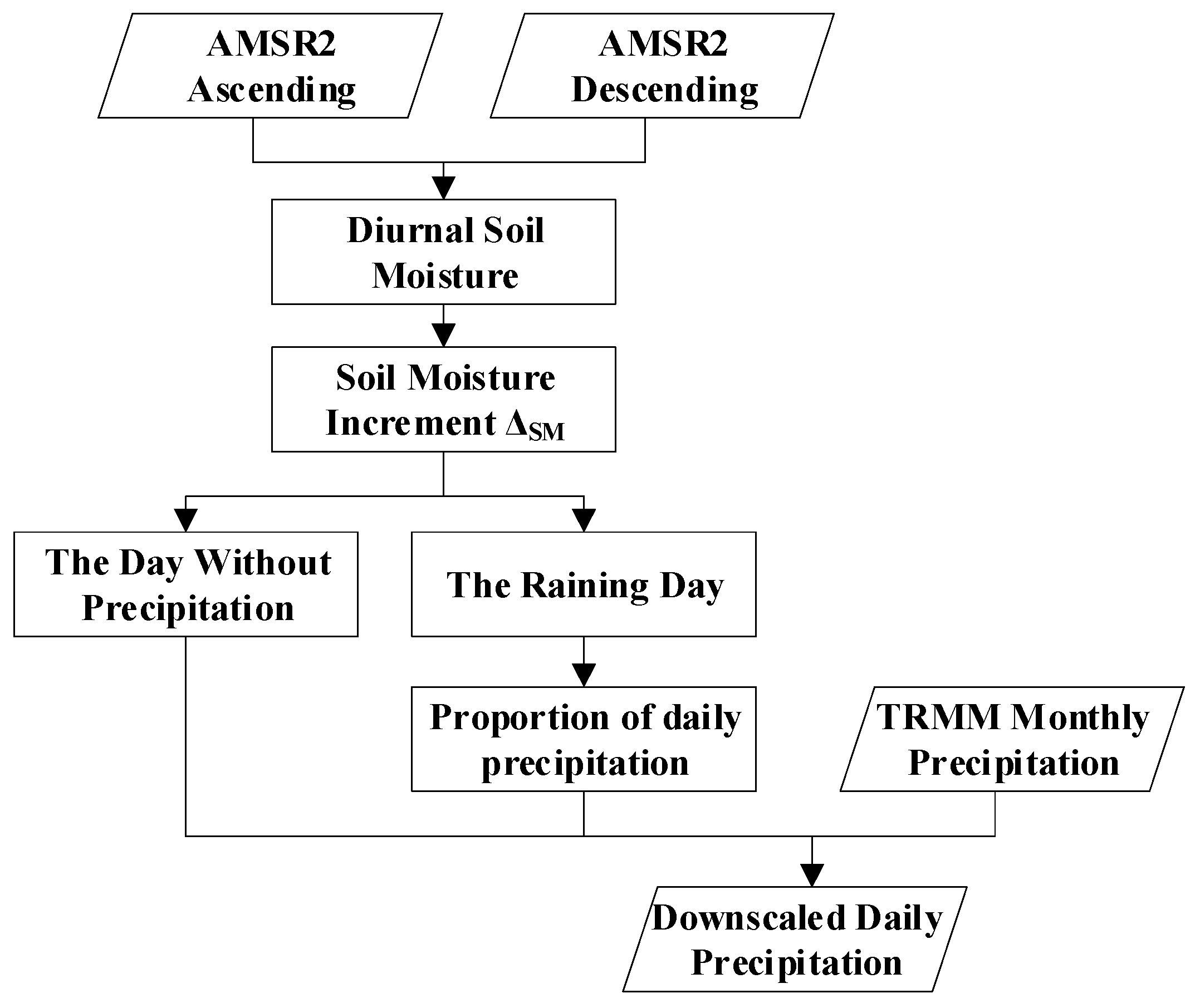
2.4. Temporal Downscaling Method
3. Results
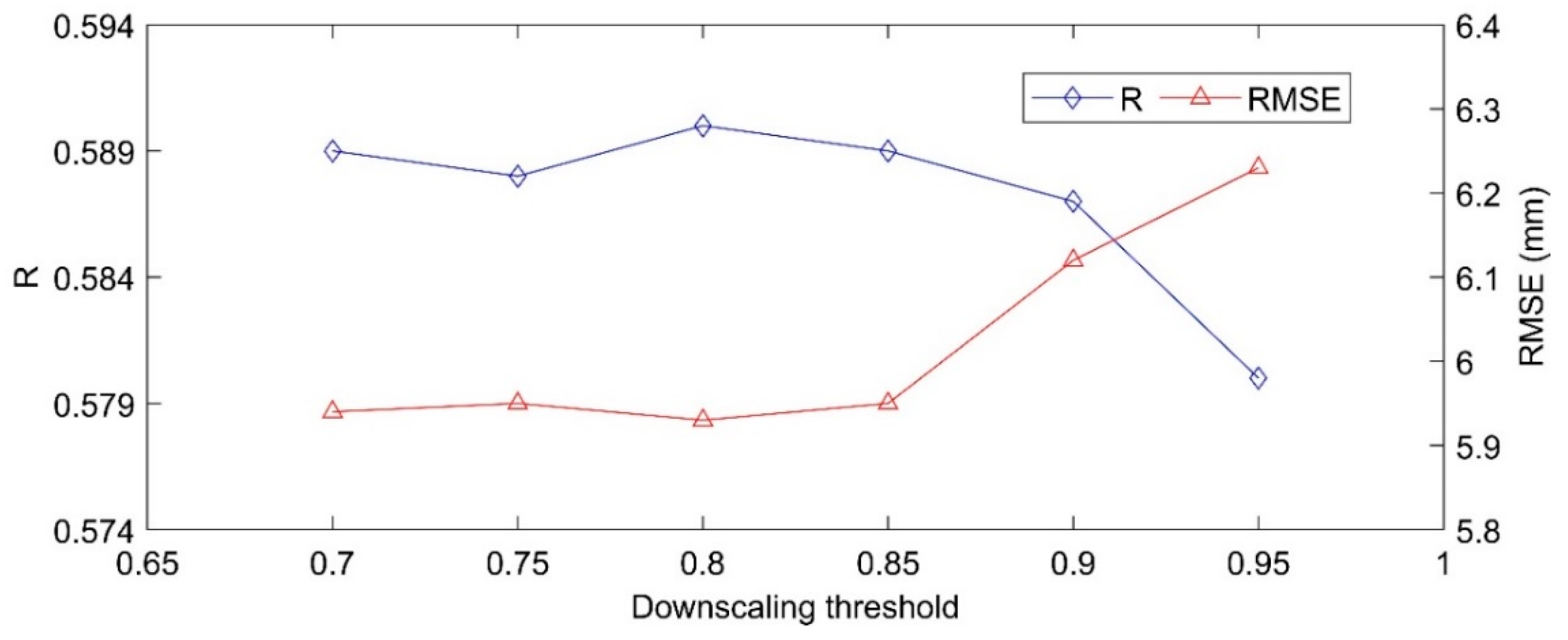
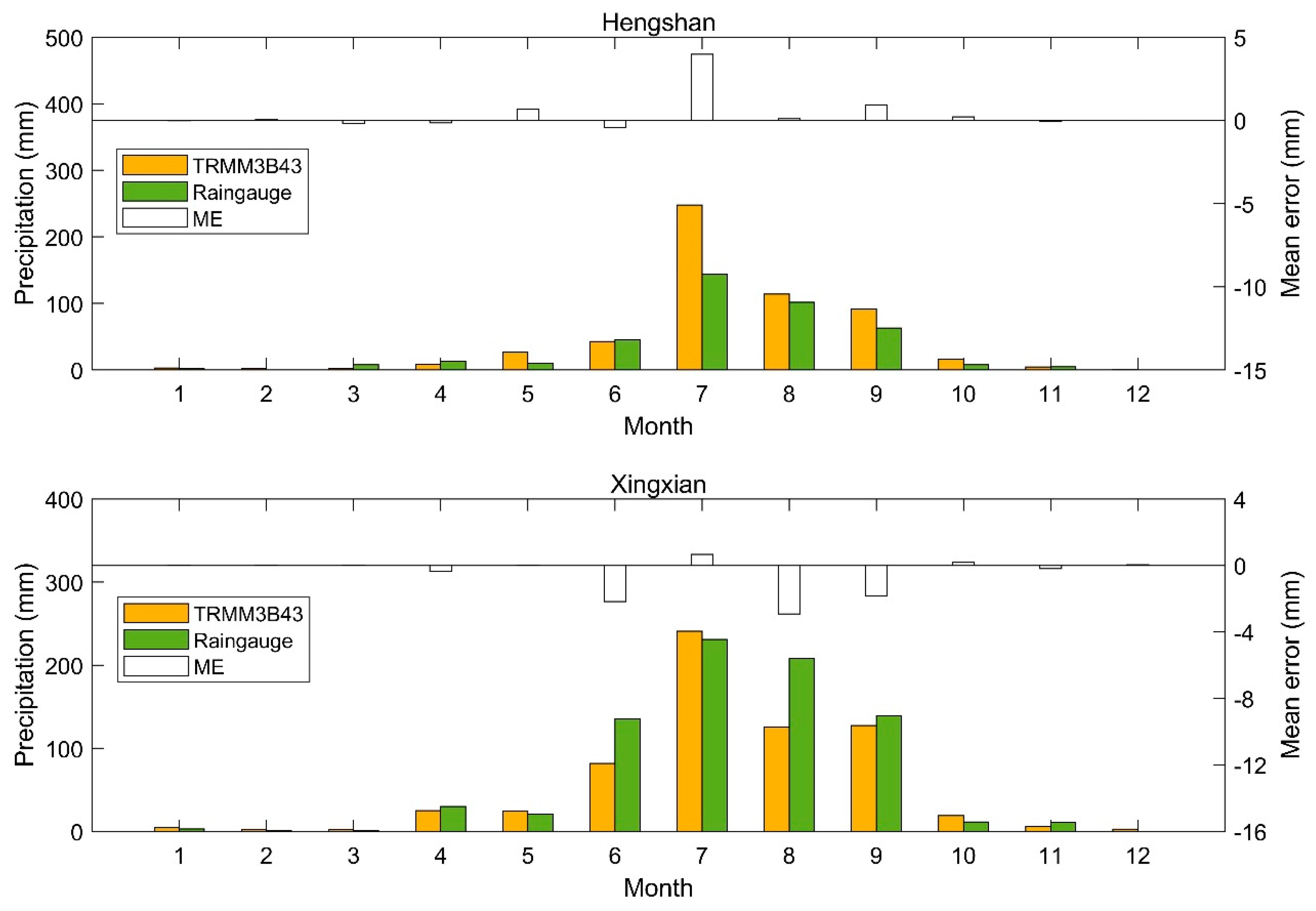
3.1. Spatial Estimation of Daily Precipitation
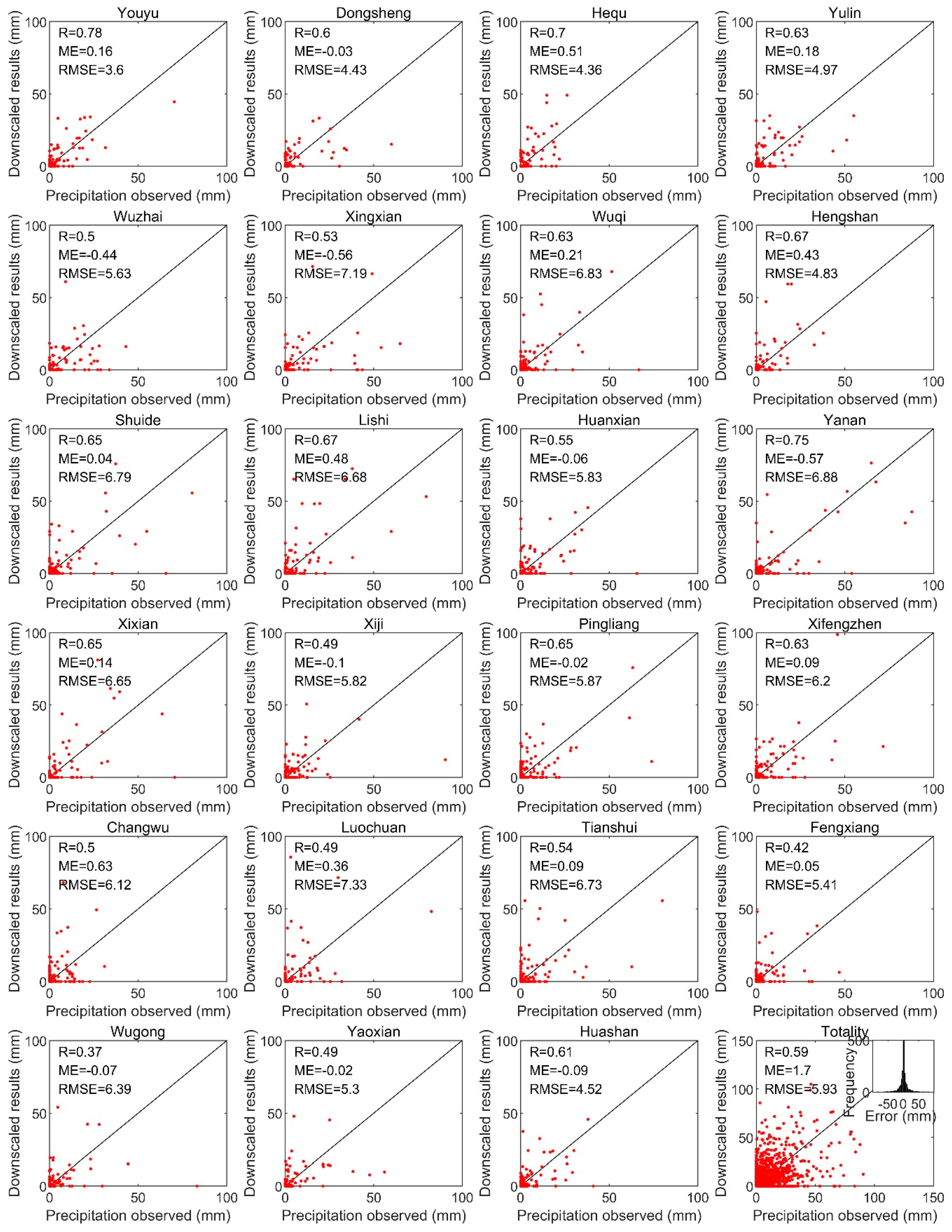
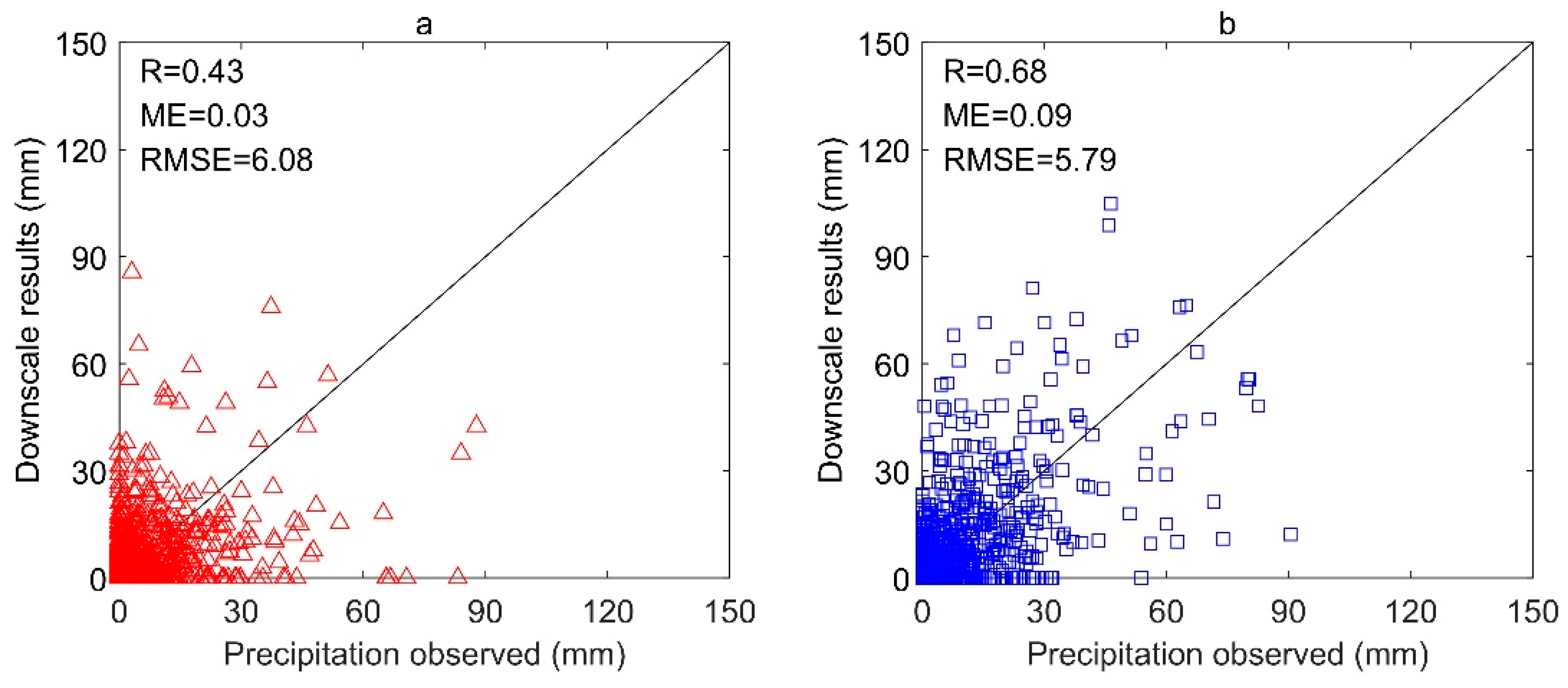
3.2. Comparison between Downscaling Results and Ground Observations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Environ. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Rutten, M.M.; Droogers, P. Spatial downscaling of TRMM precipitation using vegetative response on the Iberian Peninsula. Remote Sens. Environ. 2009, 113, 362–370. [Google Scholar] [CrossRef]
- Sun, R.; Yuan, H.; Liu, X.; Jiang, X. Evaluation of the latest satellite-gauge precipitation products and their hydrologic applications over the Huaihe River basin. J. Hydrol. 2016, 536, 302–319. [Google Scholar] [CrossRef]
- Mahmud, M.R.; Numata, S.; Matsuyama, H.; Hosaka, T.; Hashim, M. Assessment of Effective Seasonal Downscaling of TRMM Precipitation Data in Peninsular Malaysia. Remote Sens. 2015, 7, 4092–4111. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myneni, R.B.; Choi, S.; Wang, L.; Ni, X.; Lao, C.; Yang, F. Mapping Annual Precipitation across Mainland China in the Period 2001–2010 from TRMM3B43 Product Using Spatial Downscaling Approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Huang, J.; Sheng, S.; Mansaray, L.R.; Liu, Z.; Wu, H.; Wang, X. A new downscaling-integration framework for high-resolution monthly precipitation estimates: Combining rain gauge observations, satellite-derived precipitation data and geographical ancillary data. Remote Sens. Environ. 2018, 214, 154–172. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, H.; He, D.; Chen, J. Integrating precipitation zoning with random forest regression for the spatial downscaling of satellite-based precipitation: A case study of the Lancang-Mekong River basin. Int. J. Climatol. 2019, 39, 3947–3961. [Google Scholar] [CrossRef]
- Zhang, T.; Li, B.; Yuan, Y.; Gao, X.; Sun, Q.; Xu, L.; Jiang, Y. Spatial downscaling of TRMM precipitation data considering the impacts of macro-geographical factors and local elevation in the Three-River Check for updates Headwaters Region. Remote Sens. Environ. 2018, 215, 109–127. [Google Scholar] [CrossRef]
- Wang, L.; Chen, R.; Han, C.; Yang, Y.; Liu, J.; Liu, Z.; Wang, X.; Liu, G.; Guo, S. An Improved Spatial-Temporal Downscaling Method for TRMM Precipitation Datasets in Alpine Regions: A Case Study in Northwestern China’s Qilian Mountains. Remote Sens. 2019, 11, 870. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, C.D. Assessing the effect of integrating elevation data into the estimation of monthly precipitation in Great Britain. J. Hydrol. 2005, 308, 128–150. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling-calibration procedure. Remote Sens. Environ. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Park, N.; Kyriakidis, P.; Hong, S. Geostatistical Integration of Coarse Resolution Satellite Precipitation Products and Rain Gauge Data to Map Precipitation at Fine Spatial Resolutions. Remote Sens. 2017, 9, 255. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Du, J.; Xu, W.; Shi, P.; Li, M.; Ming, X. Spatial downscaling of TRMM precipitation data based on the orographical effect and meteorological conditions in a mountainous area. Adv. Water Resour. 2013, 61, 42–50. [Google Scholar] [CrossRef]
- He, K.; Ma, Z.; Zhao, R.; Biswas, A.; Teng, H.; Xu, J.; Yu, W.; Shi, Z. A Methodological Framework to Retrospectively Obtain Downscaled Precipitation Estimates over the Tibetan Plateau. Remote Sens. 2018, 10, 1974. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Xu, X.; Liu, M.; Sun, A.; Wang, K. Spatial downscaling of TRMM precipitation product using a combined multifractal and regression approach: Demonstration for south China. Water 2015, 7, 3083–3102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Yan, X. A new statistical precipitation downscaling method with Bayesian model averaging: A case study in China. Clim. Dyn. 2015, 45, 2541–2555. [Google Scholar] [CrossRef]
- Park, N. Spatial Downscaling of TRMM Precipitation Using Geostatistics and Fine Scale Environmental Variables. Adv. Meteorol. 2013, 2013, 187–190. [Google Scholar] [CrossRef]
- Ceccherini, G.; Ameztoy, I.; Hernández, C.; Moreno, C. High-Resolution Precipitation Datasets in South America and West Africa based on Satellite-Derived Rainfall, Enhanced Vegetation Index and Digital Elevation Model. Remote Sens. 2015, 7, 6454–6488. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Atkinson, P.M.; Zhang, J. Downscaling remotely sensed imagery using area-to-point cokriging and multiple-point geostatistical simulation. ISPRS J. Photogramm. Remote Sens. 2015, 101, 174–185. [Google Scholar] [CrossRef]
- Teng, H.; Shi, Z.; Ma, Z.; Li, Y. Estimating spatially downscaled rainfall by regression kriging using TRMM precipitation and elevation in Zhejiang Province, southeast China. Int. J. Remote Sens. 2014, 35, 7775–7794. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Ji, X.; Luo, X.; Li, X. Fine-Resolution Precipitation Mapping in a Mountainous Watershed: Geostatistical Downscaling of TRMM Products Based on Environmental Variables. Remote Sens. 2018, 10, 119. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.; Wu, C.; Wang, L.; Gonsamo, A.; Shen, Y.; Niu, Z. A new satellite-based monthly precipitation downscaling algorithm with non-stationary relationship between precipitation and land surface characteristics. Remote Sens. Environ. 2015, 162, 119–140. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Li, X. Spatial downscaling of TRMM 3B43 precipitation considering spatial heterogeneity. Int. J. Remote Sens. 2014, 35, 3074–3093. [Google Scholar] [CrossRef]
- Zhao, N.; Yue, T.; Zhou, X.; Zhao, M.; Liu, Y.; Du, Z.; Zhang, L. Statistical downscaling of precipitation using local regression and high accuracy surface modeling method. Theor. Appl. Climatol. 2016, 129, 281–292. [Google Scholar] [CrossRef]
- Lv, A.; Zhou, L. A rainfall model based on a geographically weighted regression algorithm for rainfall estimations over the arid Qaidam basin in China. Remote Sens. 2016, 8, 310–323. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Zhao, S.; Duan, Z.; Qin, Z. An Improved Spatial Downscaling Procedure for TRMM 3B43 Precipitation Product Using Geographically Weighted Regression. IEEE J.-Stars. 2015, 8, 4592–4604. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A Spatial Downscaling Algorithm for Satellite-Based Precipitation over the Tibetan Plateau Based on NDVI, DEM, and Land Surface Temperature. Remote Sens. 2016, 8, 655. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; He, K.; Tan, X.; Xu, J.; Fang, W.; He, Y.; Hong, Y. Comparisons of Spatially Downscaling TMPA and IMERG over the Tibetan Plateau. Remote Sens. 2018, 10, 1883. [Google Scholar] [CrossRef] [Green Version]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A Comparison of Different Regression Algorithms for Downscaling Monthly Satellite-Based Precipitation over North China. Remote Sens. 2016, 8, 835. [Google Scholar] [CrossRef] [Green Version]
- Alexakis, D.D.; Tsanis, I.K. Comparison of multiple linear regression and artificial neural network models for downscaling TRMM precipitation products using MODIS data. Environ. Earth Sci. 2016, 75, 1077. [Google Scholar] [CrossRef]
- Chaudhuri, C.; Srivastava, R. A novel approach for statistical downscaling of future precipitation over the Indo-Gangetic Basin. J. Hydrol. 2017, 547, 21–38. [Google Scholar] [CrossRef]
- Zheng, X.; Zhu, J.J. A methodological approach for spatial downscaling of TRMM precipitation data in North China. Int. J. Remote Sens. 2015, 36, 144–169. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling Satellite Precipitation Estimates with Multiple Linear Regression, Artificial Neural Networks, and Spline Interpolation Techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef] [Green Version]
- Ulloa, J.; Ballari, D.; Campozano, L.; Samaniego, E. Two-Step Downscaling of Trmm 3b43 V7 Precipitation in Contrasting Climatic Regions with Sparse Monitoring: The Case of Ecuador in Tropical South America. Remote Sens. 2017, 9, 758. [Google Scholar] [CrossRef] [Green Version]
- Fang, B.; Lakshmi, V.; Bindlish, R.; Jackson, T.J. AMSR2 Soil Moisture Downscaling Using Temperature and Vegetation Data. Remote Sens. 2018, 10, 1575. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Yang, S.; Liu, X.; Liu, C.; Song, W.; Dong, G.; Zhao, H.; Lou, H. Land use change in the reach from Hekouzhen to Tongguan of the Yellow River during 1998–2010. Acta Geogr. Sin. 2014, 69, 42–53. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multi-satellite precipitation analysis: Quasi-global, multi-year, combined-sensor precipitation estimates at fine scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Cho, E.; Su, C.H.; Ryu, D.; Kim, H.; Choi, M. Does AMSR2 produce better soil moisture retrievals than AMSR-E over Australia? Remote Sens. Environ. 2017, 188, 95–105. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, H.; Wang, L.; Deng, C. Evaluation of AMSR2 soil moisture products over the contiguous United States using in situ data from the International Soil Moisture Network. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 187–199. [Google Scholar] [CrossRef]
- Walters, R.D.; Watson, K.A.; Marshall, H.; McNamara, J.P.; Flores, A.N. A physiographic approach to downscaling fractional snow cover data in mountainous regions. Remote Sens. Environ. 2014, 152, 413–425. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP soil moisture estimation with gradient boosting decision tree regression over the Tibetan Plateau. Remote Sens. Environ. 2019, 225, 30–44. [Google Scholar] [CrossRef]
- Jin, Y.; Ge, Y.; Wang, J.; Chen, Y.; Heuvelink, G.B.M.; Atkinson, P.M. Downscaling AMSR-2 Soil Moisture Data with Geographically Weighted Area-to-Area Regression Kriging. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2362–2376. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Sun, H.; Cai, C.; Liu, H.; Yang, B. Microwave and Meteorological Fusion: A method of Spatial Downscaling of Remotely Sensed Soil Moisture. IEEE J.-Stars. 2019, 12, 1107–1119. [Google Scholar] [CrossRef]
- Li, W.; Ni, L.; Li, Z.; Duan, S.; Wu, H. Evaluation of Machine Learning Algorithms in Spatial Downscaling of MODIS Land Surface Temperature. IEEE J.-Stars. 2019, 12, 1107–1119. [Google Scholar] [CrossRef]
- Gao, L.; Zhan, W.; Huang, F.; Zhu, X.; Zhou, J.; Quan, J.; Du, P.; Li, M. Disaggregation of remotely sensed land surface temperature: A simple yet flexible index (SIFI) to assess method performances. Remote Sens. Environ. 2017, 200, 206–219. [Google Scholar] [CrossRef]
- Hutengs, C.; Vohland, M. Downscaling land surface temperatures at regional scales with random forest regression. Remote Sens. Environ. 2016, 178, 127–141. [Google Scholar] [CrossRef]
- Duan, S.B.; Li, Z.L. Spatial downscaling of MODIS land surface temperatures using geographically weighted regression: Case study in northern China. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6458–6469. [Google Scholar] [CrossRef]
- Chen, F.; Gao, Y.; Wang, Y.; Qin, F.; Li, X. Downscaling satellite-derived daily precipitation products with an integrated framework. Int. J. Climatol. 2019, 39, 1287–1304. [Google Scholar] [CrossRef]
- Shi, Z.H.; Yue, B.J.; Wang, L.; Fang, N.F.; Wang, D.; Wu, F.Z. Effects of Mulch Cover Rate on Interrill Erosion Processes and the Size Selectivity of Eroded Sediment on Steep Slopes. Soil Sci. Soc. Am. J. 2013, 77, 257–267. [Google Scholar] [CrossRef] [Green Version]
- Feng, H.H.; Liu, Y.B. Combined effects of precipitation and air temperature on soil moisture in different land covers in a humid basin. J. Hydrol. 2015, 531, 1129–1140. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Q.; Zheng, D.; Zhang, J.; Mo, K.; Li, Z.; Tang, G. Multiscale Comparative Evaluation of the GPM IMERG v5 and TRMM 3B42 v7 Precipitation Products from 2015 to 2017 over a Climate Transition Area of China. Remote Sens. 2018, 10, 944. [Google Scholar] [CrossRef] [Green Version]
- Sawada, Y.; Tsutsui, H.; Koike, T.; Rasmy, M.; Fujii, H. A Field Verification of an Algorithm for Retrieving Vegetation Water Content from Passive Microwave Observations. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2082–2095. [Google Scholar] [CrossRef]
- Wang, Z.W.; Wu, X.D.; Yue, G.Y.; Zhao, L.; Wang, Q.; Nan, Z.T.; Qin, Y.; Wu, T.H.; Shi, J.Z.; Zou, D.F. Spatial and Temporal Variations in Spectrum-Derived Vegetation Growth Trend in Qinghai-Tibetan Plateau from 1982 to 2014. Spectrosc. Spect. Anal. 2016, 36, 471–477. [Google Scholar]

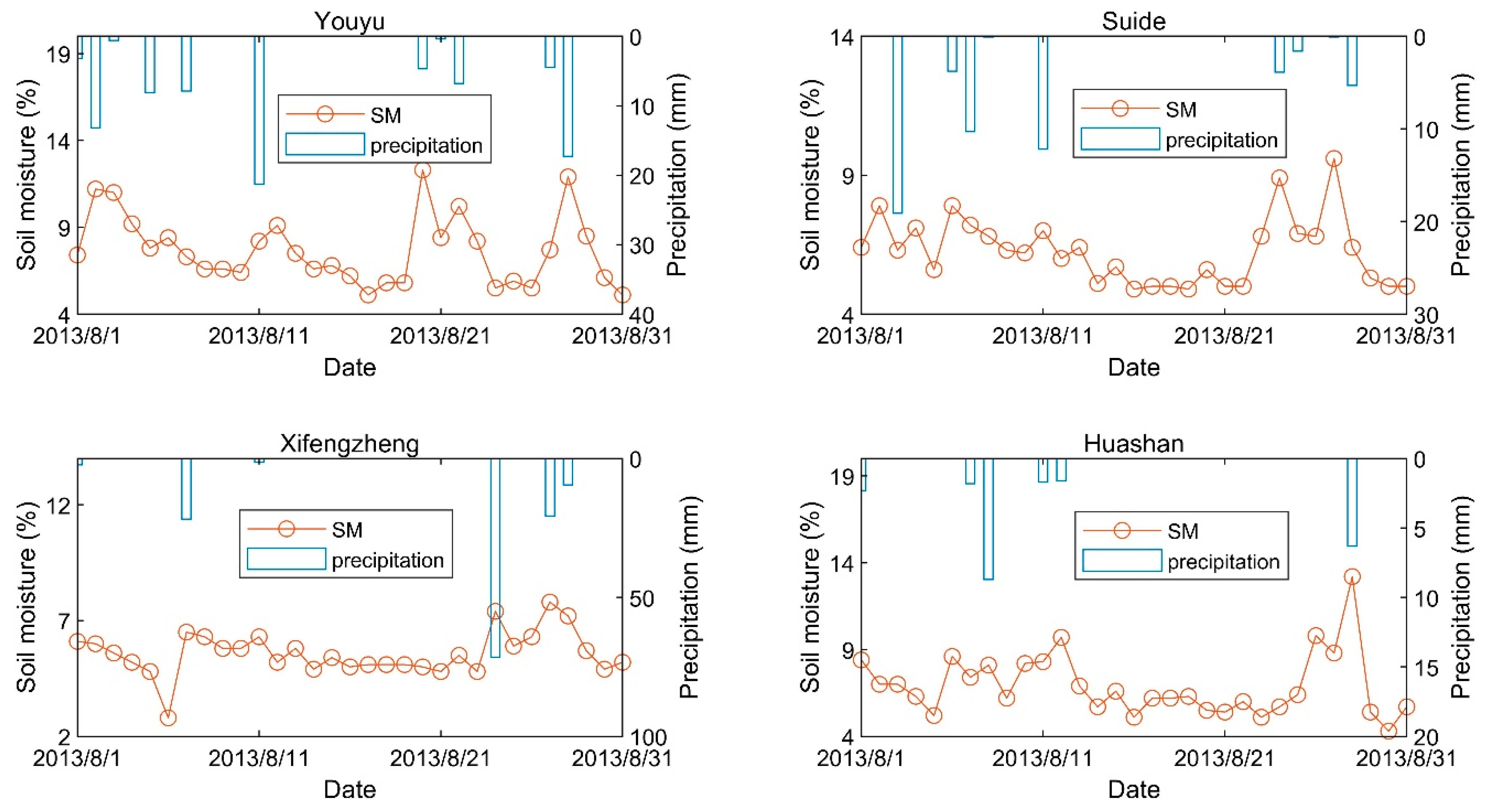
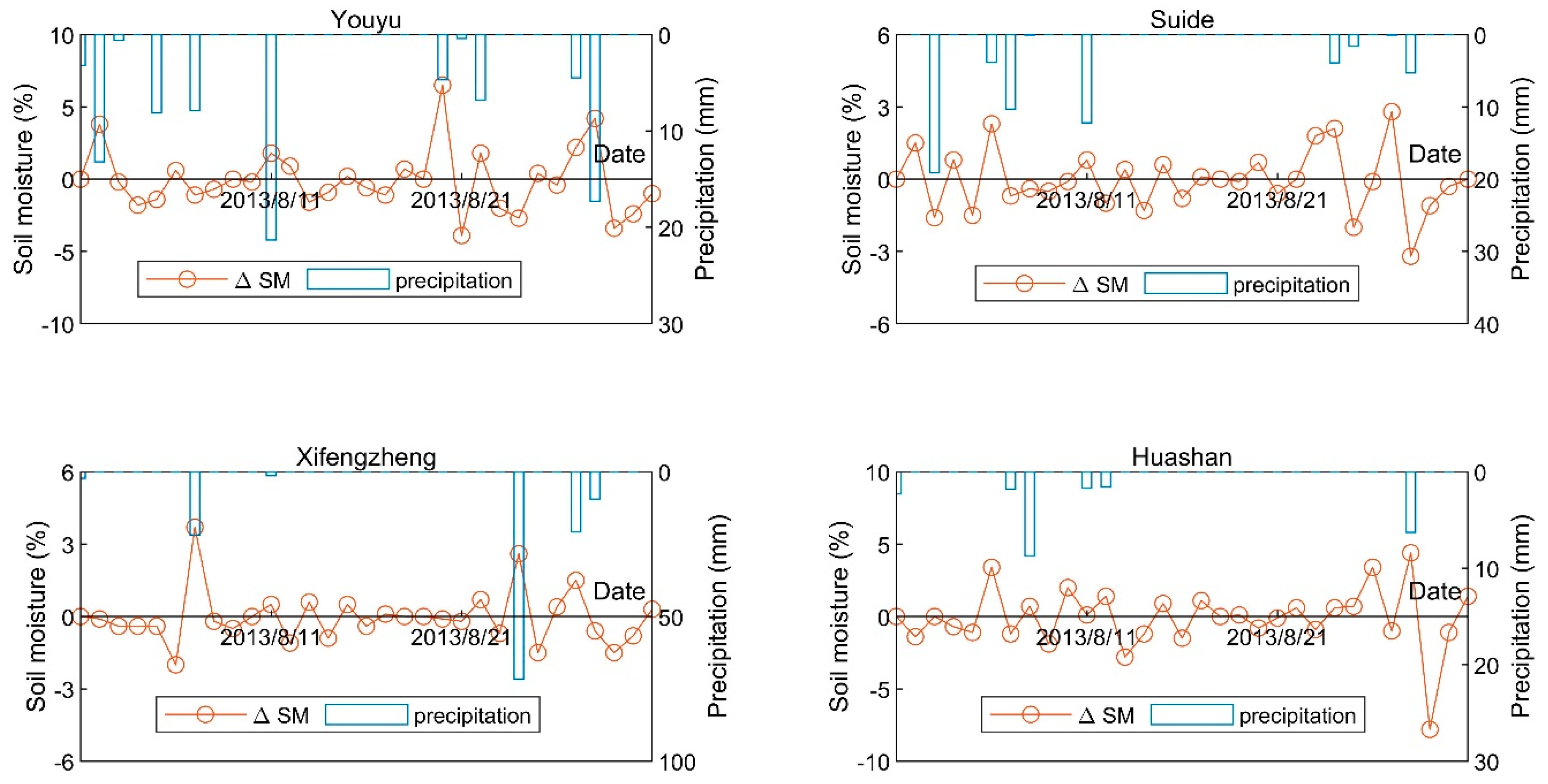
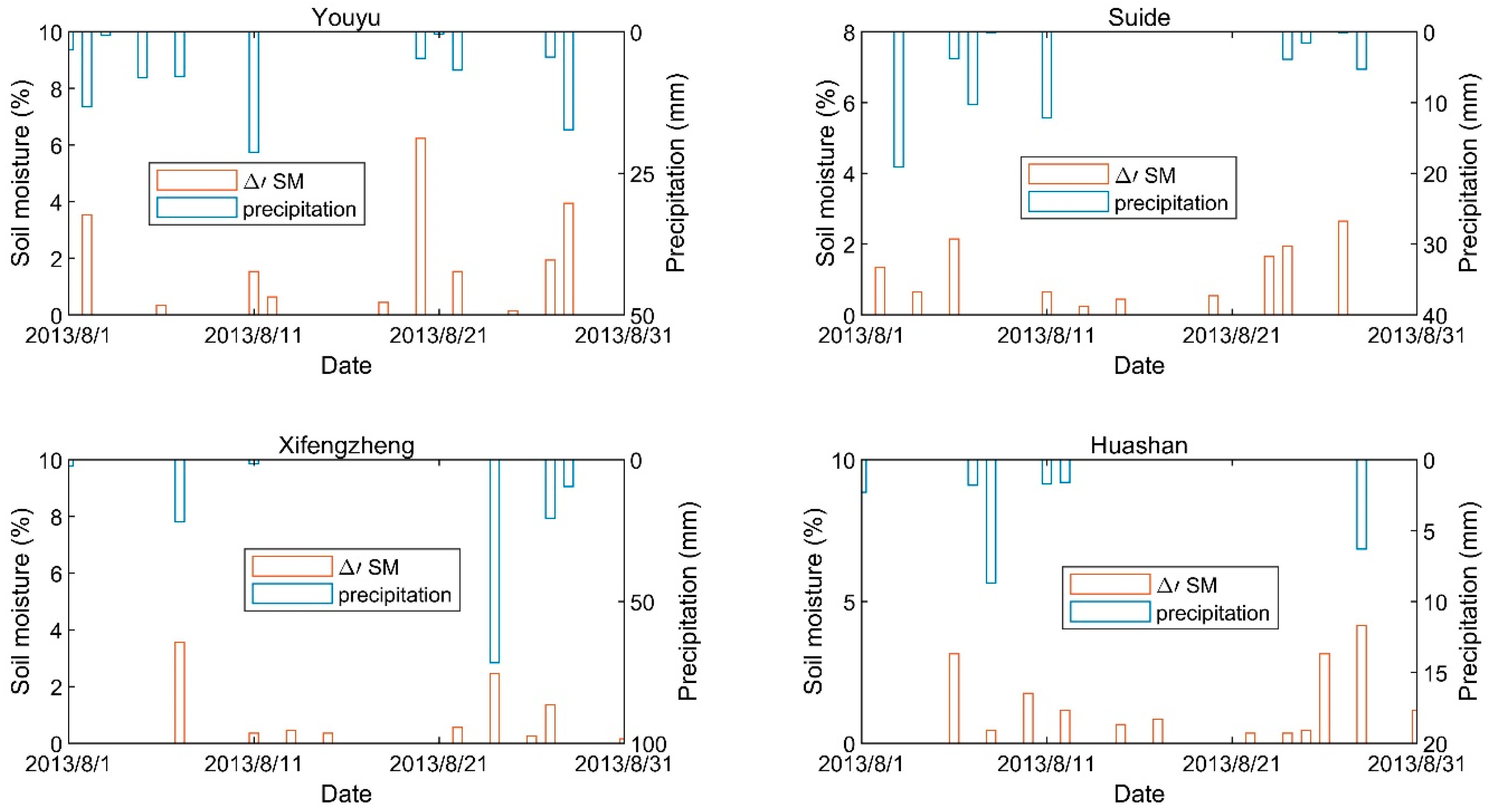



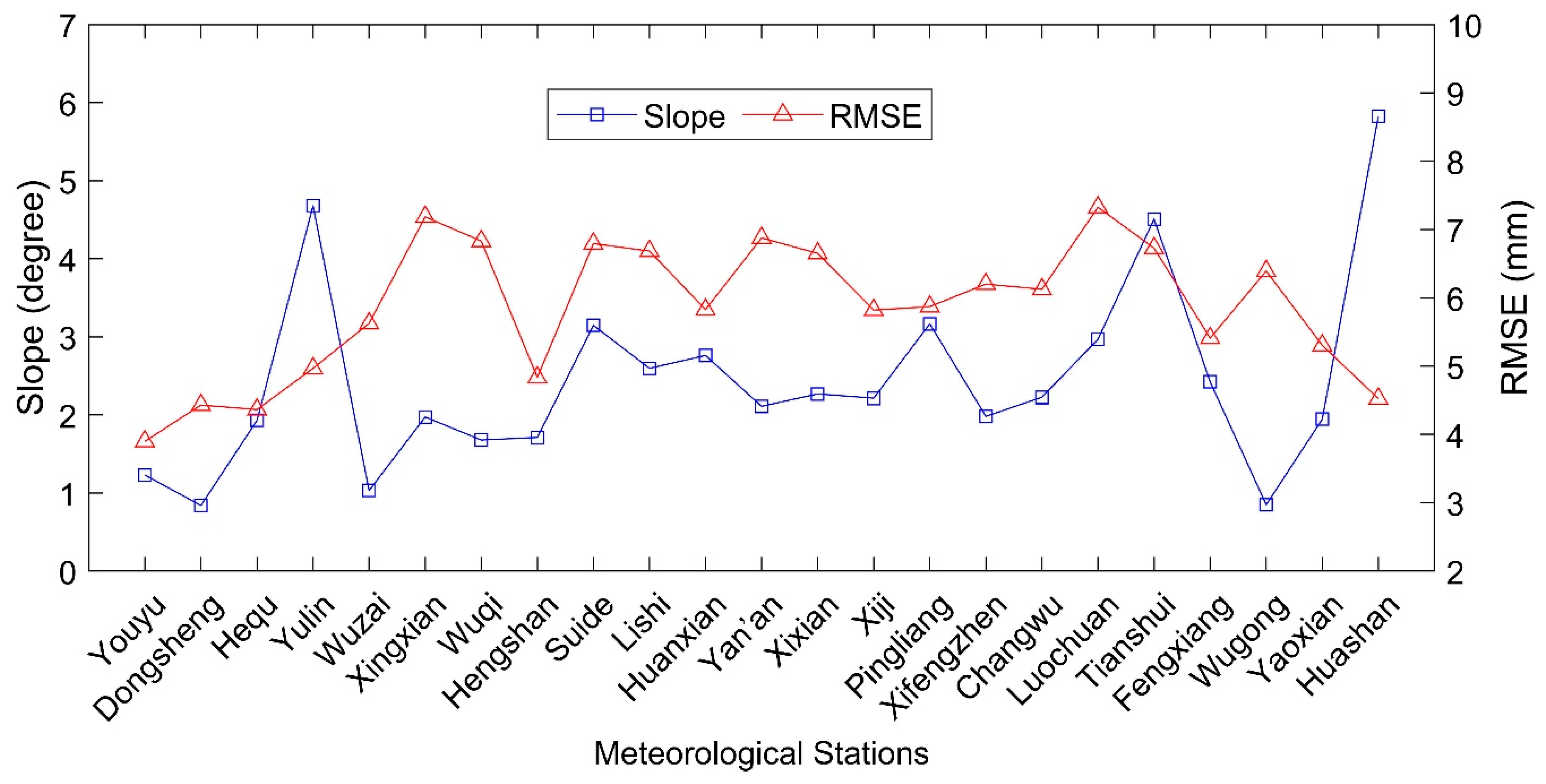
| ID | Name | Longitude (°) | Latitude (°) | Altitude (m) | Land Use and Land Cover (IGBP) |
|---|---|---|---|---|---|
| 53478 | Youyu | 112.445 | 39.997 | 1348 | grasslands |
| 53543 | Dongsheng | 109.985 | 39.827 | 1462 | grasslands |
| 53564 | Hequ | 111.147 | 39.383 | 862 | grasslands |
| 53646 | Yulin | 109.779 | 38.272 | 1156 | grasslands |
| 53663 | Wuzai | 111.818 | 38.921 | 1401 | croplands |
| 53664 | Xingxian | 111.132 | 38.463 | 1012 | grasslands |
| 53738 | Wuqi | 108.169 | 36.924 | 1332 | grasslands |
| 53740 | Hengshan | 109.237 | 37.920 | 1110 | grasslands |
| 53754 | Suide | 110.215 | 37.501 | 929 | grasslands |
| 53764 | Lishi | 111.098 | 37.507 | 951 | grasslands |
| 53821 | Huanxian | 107.295 | 36.580 | 1256 | grasslands |
| 53845 | Yan’an | 109.500 | 36.600 | 959 | grasslands |
| 53853 | Xixian | 110.951 | 36.694 | 1053 | grasslands |
| 53903 | Xiji | 105.718 | 35.964 | 1917 | grasslands |
| 53915 | Pingliang | 106.667 | 35.548 | 1365 | croplands |
| 53923 | Xifengzhen | 107.631 | 35.734 | 1420 | urban and built-up lands |
| 53929 | Changwu | 107.793 | 35.199 | 1196 | croplands |
| 53942 | Luochuan | 109.506 | 35.811 | 1159 | croplands |
| 57014 | Tianshui | 105.868 | 34.567 | 1085 | urban and built-up lands |
| 57025 | Fengxiang | 107.384 | 34.514 | 782 | urban and built-up lands |
| 57034 | Wugong | 108.214 | 34.258 | 448 | urban and built-up lands |
| 57037 | Yaoxian | 108.977 | 34.932 | 710 | croplands |
| 57046 | Huashan | 110.083 | 34.468 | 1830 | grasslands |
| ID | Name | TRMM 3B42 | Downscaled Precipitation | ||||
|---|---|---|---|---|---|---|---|
| R | ME (mm) | RMSE (mm) | R | ME (mm) | RMSE (mm) | ||
| 53478 | Youyu | 0.81 | 0.13 | 3.24 | 0.78 | 0.16 | 3.60 |
| 53543 | Dongsheng | 0.82 | −0.05 | 3.31 | 0.60 | −0.03 | 4.43 |
| 53564 | Hequ | 0.63 | 0.55 | 4.24 | 0.70 | 0.51 | 4.36 |
| 53646 | Yulin | 0.64 | 0.17 | 5.07 | 0.63 | 0.18 | 4.97 |
| 53663 | Wuzhai | 0.77 | −0.27 | 3.80 | 0.50 | −0.44 | 5.63 |
| 53664 | Xingxian | 0.76 | −0.38 | 5.23 | 0.53 | −0.56 | 7.19 |
| 53738 | Wuqi | 0.74 | 0.17 | 4.72 | 0.63 | 0.21 | 6.83 |
| 53740 | Hengshan | 0.64 | 0.33 | 3.96 | 0.67 | 0.43 | 4.83 |
| 53754 | Shuide | 0.60 | −0.06 | 6.85 | 0.65 | 0.04 | 6.79 |
| 53764 | Lishi | 0.60 | 0.26 | 6.36 | 0.67 | 0.48 | 6.68 |
| 53821 | Huanxian | 0.62 | −0.28 | 5.08 | 0.55 | −0.06 | 5.83 |
| 53845 | Yanan | 0.85 | −0.44 | 5.50 | 0.75 | −0.57 | 6.88 |
| 53853 | Xixian | 0.75 | 0.26 | 5.72 | 0.65 | 0.14 | 6.65 |
| 53903 | Xiji | 0.24 | −0.04 | 7.32 | 0.49 | −0.10 | 5.82 |
| 53915 | Pingliang | 0.59 | −0.11 | 6.45 | 0.65 | −0.02 | 5.87 |
| 53923 | Xifengzhen | 0.48 | 0.00 | 6.98 | 0.63 | 0.09 | 6.20 |
| 53929 | Changwu | 0.78 | 0.18 | 5.34 | 0.50 | 0.63 | 6.12 |
| 53942 | Luochuan | 0.56 | 0.17 | 7.34 | 0.49 | 0.36 | 7.33 |
| 57014 | Tianshui | 0.81 | −0.35 | 6.01 | 0.54 | 0.09 | 6.73 |
| 57025 | Fengxiang | 0.74 | 0.15 | 3.72 | 0.42 | 0.05 | 5.41 |
| 57034 | Wugong | 0.55 | 0.04 | 5.54 | 0.37 | −0.07 | 6.39 |
| 57037 | Yaoxian | 0.54 | −0.01 | 4.97 | 0.49 | −0.02 | 5.30 |
| 57046 | Huashan | 0.50 | −0.12 | 4.88 | 0.61 | −0.09 | 4.52 |
| ID | Name | TRMM 3B43 Downscaling | Rain Gauge Data Downscaling | ||||
|---|---|---|---|---|---|---|---|
| R | ME (mm) | RMSE (mm) | R | ME (mm) | RMSE (mm) | ||
| 53478 | Youyu | 0.78 | 0.16 | 3.60 | 0.81 | −0.04 | 3.25 |
| 53543 | Dongsheng | 0.60 | −0.03 | 4.43 | 0.62 | −0.03 | 4.34 |
| 53564 | Hequ | 0.70 | 0.51 | 4.36 | 0.70 | −0.09 | 2.92 |
| 53646 | Yulin | 0.63 | 0.18 | 4.97 | 0.63 | −0.08 | 4.67 |
| 53663 | Wuzhai | 0.50 | −0.44 | 5.63 | 0.53 | −0.31 | 5.61 |
| 53664 | Xingxian | 0.53 | −0.56 | 7.19 | 0.58 | −0.32 | 6.9 |
| 53738 | Wuqi | 0.63 | 0.21 | 6.83 | 0.62 | −0.04 | 6.43 |
| 53740 | Hengshan | 0.67 | 0.43 | 4.83 | 0.71 | −0.04 | 3.21 |
| 53754 | Shuide | 0.65 | 0.04 | 6.79 | 0.66 | 0.06 | 6.88 |
| 53764 | Lishi | 0.67 | 0.48 | 6.68 | 0.68 | 0.13 | 5.91 |
| 53821 | Huanxian | 0.55 | −0.06 | 5.83 | 0.55 | 0.06 | 6.11 |
| 53845 | Yanan | 0.75 | −0.57 | 6.88 | 0.76 | −0.24 | 7.1 |
| 53853 | Xixian | 0.65 | 0.14 | 6.65 | 0.65 | −0.21 | 6.3 |
| 53903 | Xiji | 0.49 | −0.10 | 5.82 | 0.56 | −0.1 | 5.41 |
| 53915 | Pingliang | 0.65 | −0.02 | 5.87 | 0.68 | −0.08 | 5.68 |
| 53923 | Xifengzhen | 0.63 | 0.09 | 6.20 | 0.69 | −0.02 | 5.68 |
| 53929 | Changwu | 0.50 | 0.63 | 6.12 | 0.49 | 0.31 | 5.86 |
| 53942 | Luochuan | 0.49 | 0.36 | 7.33 | 0.49 | 0.14 | 6.58 |
| 57014 | Tianshui | 0.54 | 0.09 | 6.73 | 0.54 | 0.29 | 7.16 |
| 57025 | Fengxiang | 0.42 | 0.05 | 5.41 | 0.41 | −0.20 | 5.00 |
| 57034 | Wugong | 0.37 | −0.07 | 6.39 | 0.34 | −0.16 | 7.08 |
| 57037 | Yaoxian | 0.49 | −0.02 | 5.30 | 0.52 | −0.09 | 5.05 |
| 57046 | Huashan | 0.61 | −0.09 | 4.52 | 0.63 | −0.08 | 4.39 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, D.; Wu, H.; Dong, G.; Jiang, X.; Xue, H. A Temporal Disaggregation Approach for TRMM Monthly Precipitation Products Using AMSR2 Soil Moisture Data. Remote Sens. 2019, 11, 2962. https://doi.org/10.3390/rs11242962
Fan D, Wu H, Dong G, Jiang X, Xue H. A Temporal Disaggregation Approach for TRMM Monthly Precipitation Products Using AMSR2 Soil Moisture Data. Remote Sensing. 2019; 11(24):2962. https://doi.org/10.3390/rs11242962
Chicago/Turabian StyleFan, Dong, Hua Wu, Guotao Dong, Xiaoguang Jiang, and Huazhu Xue. 2019. "A Temporal Disaggregation Approach for TRMM Monthly Precipitation Products Using AMSR2 Soil Moisture Data" Remote Sensing 11, no. 24: 2962. https://doi.org/10.3390/rs11242962






