Effect of Inspection Policies and Residual Value of Collected Used Products: A Mathematical Model and Genetic Algorithm for a Closed-Loop Green Manufacturing System
Abstract
:1. Introduction
1.1. Background
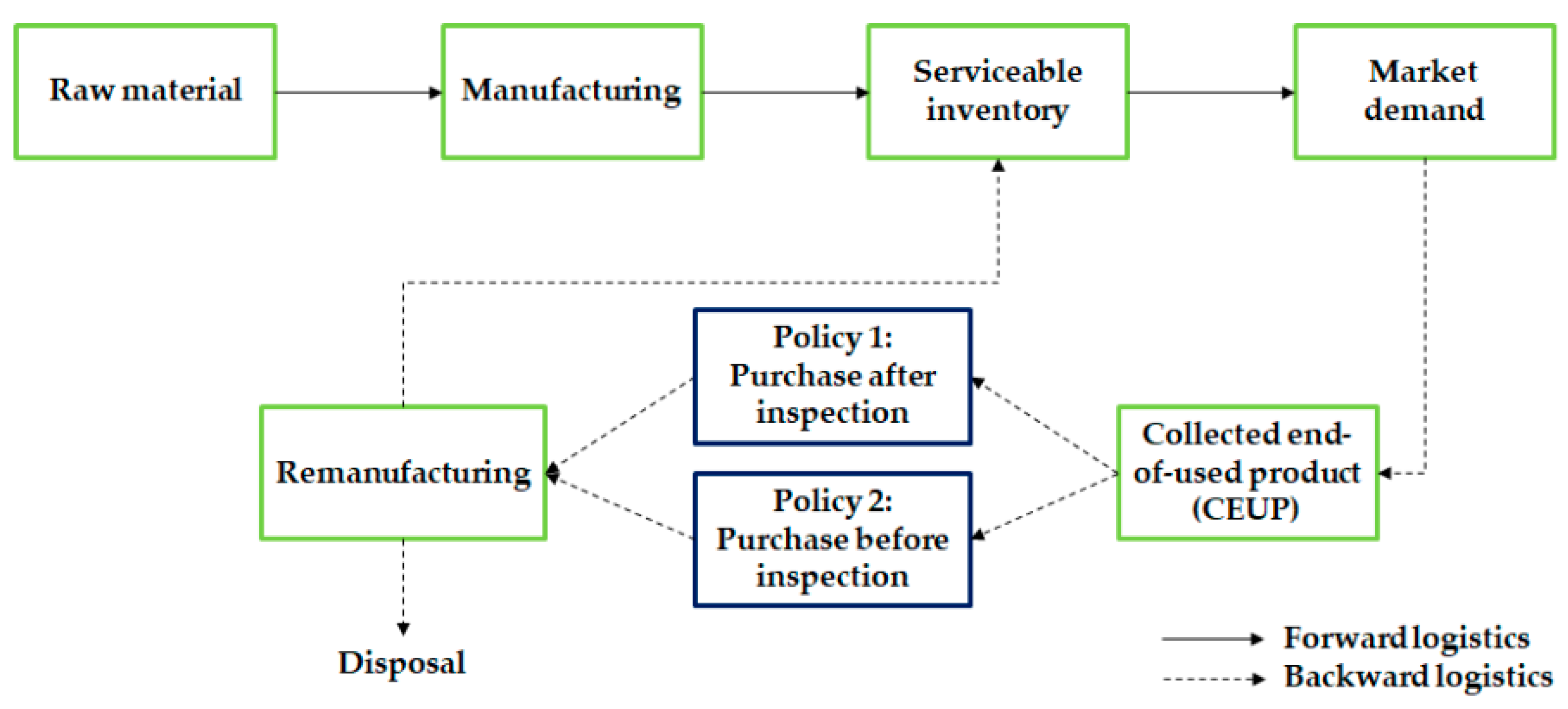
1.2. Problem Description
2. Literature Review
3. Mathematical Model
3.1. Notations
| Cins_before | Unit inspection cost before collection |
| Cins_after | Unit inspection cost after collection |
| Cmanuf | Unit manufacturing cost |
| Cdisposal | Unit disposal cost |
| Craw | Unit raw material cost for manufacturing |
| Cpenalty | Fine for violating obligatory take-back quota |
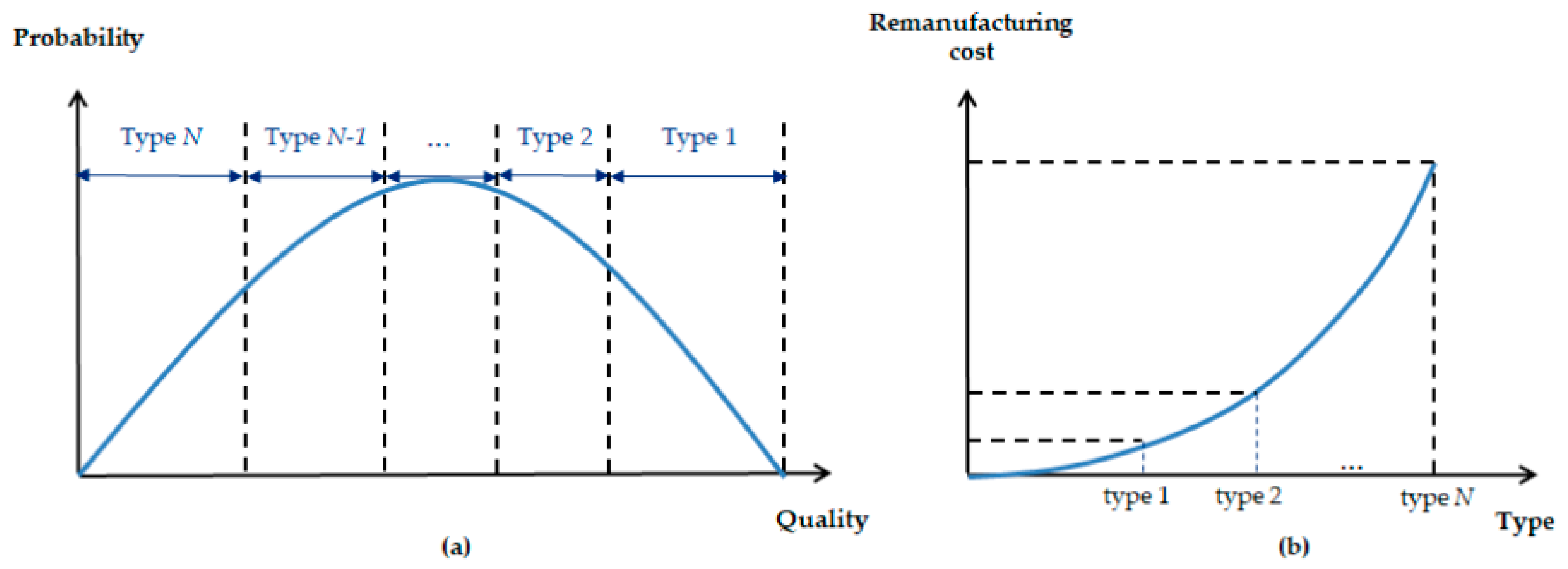
| N | Remanufacturing types |
| Ctype_n | Unit remanufacturing cost for type n, n = 1 ,…, N |
| Qmin,type_n | Minimum quality level for type n remanufacturing |
| Q | Quality level of used products, 0 ≤ q ≤ 1 |
| P | Unit sale price for new (or remanufactured) products |
| πi | Revenue of green manufacturing company of model i |
| D | Demand for new (or remanufactured) products |
| R | Amount of CUPs |
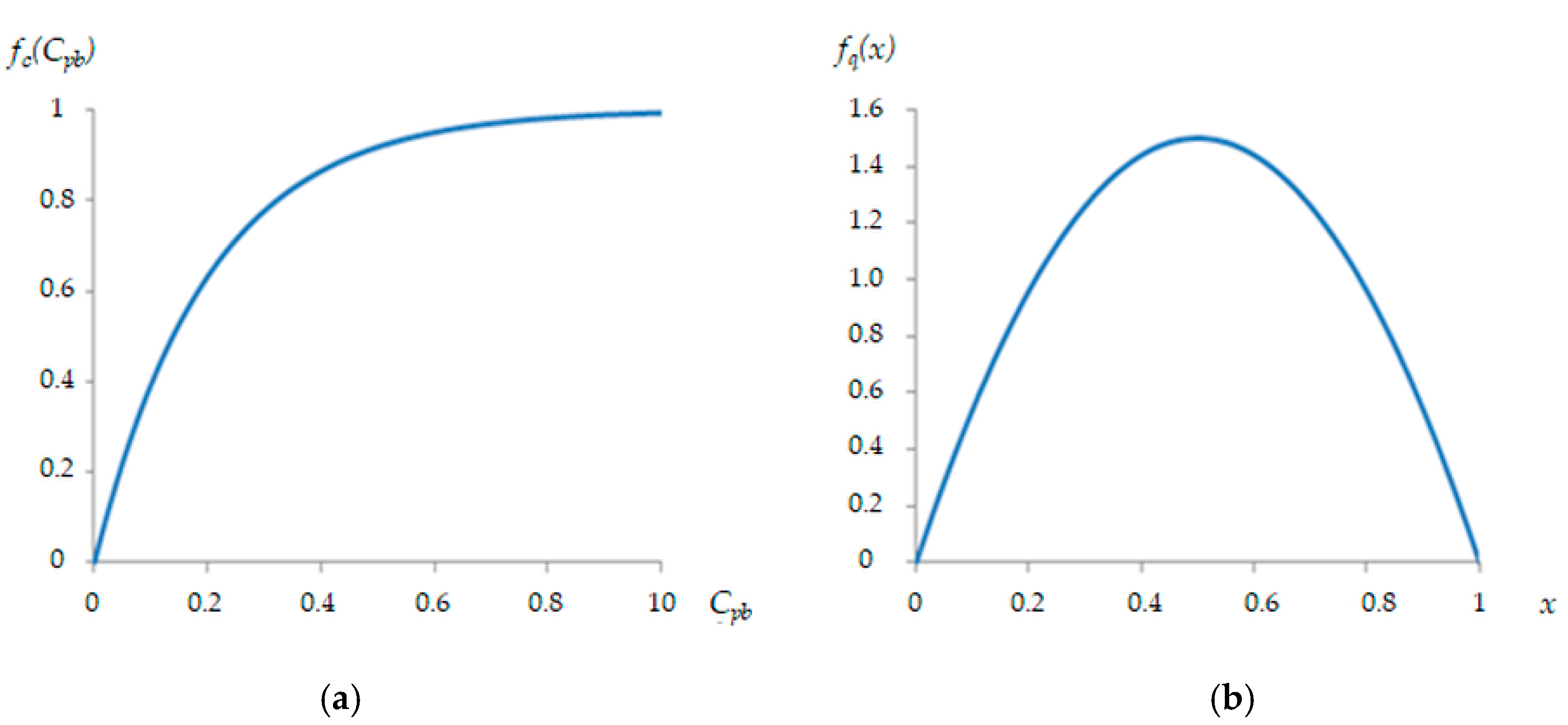
| fc(Cpb) | Collection rate function |
| fq(x) | Quality distribution of used products |
| βi | Disposal rate for CUPs for model i |
| ai, bi | Systemic parameters for disposal rate function for model i |
| δ | Obligatory take-back quota |
| dn | An amount of CUP of type n remanufacturing |
| Qmin,i | Decision variable and minimum quality level of CUPs for model i |
| Cpb,i | Decision variable and unit buy-back cost for model i |
3.2. Assumptions
3.3. Collection Rate and Quality Distribuion of Collected Used Products
3.4. Objective Functions
3.4.1. Profit Functions of Model 1: Inspection Policy 1
3.4.2. Profit Functions of Model 2: Inspection Policy 2
3.5. Constraints
4. Solution Procedure
| STEP 1: | Set generation index i = 0 and current best fitness value = −∞. |
| STEP 2: | Generate initial population (Nc chromosomes) of ith generation. |
| STEP 3: | For each chromosome, calculate its fitness value according to Equations (3) and (4) for model 1 and 2, respectively. If the fitness value of a chromosome in ith generation is greater than the current best fitness value, update the current best fitness value and save the corresponding chromosome. |
| STEP 4: | If i < Ng, create next population for (i + 1)th generation by selection, crossover and mutation in Section 4.3. Otherwise, go to STEP 6 |
| STEP 5: | i← i + 1 and go to STEP 3. |
| STEP 6: | Finish genetic algorithm. |
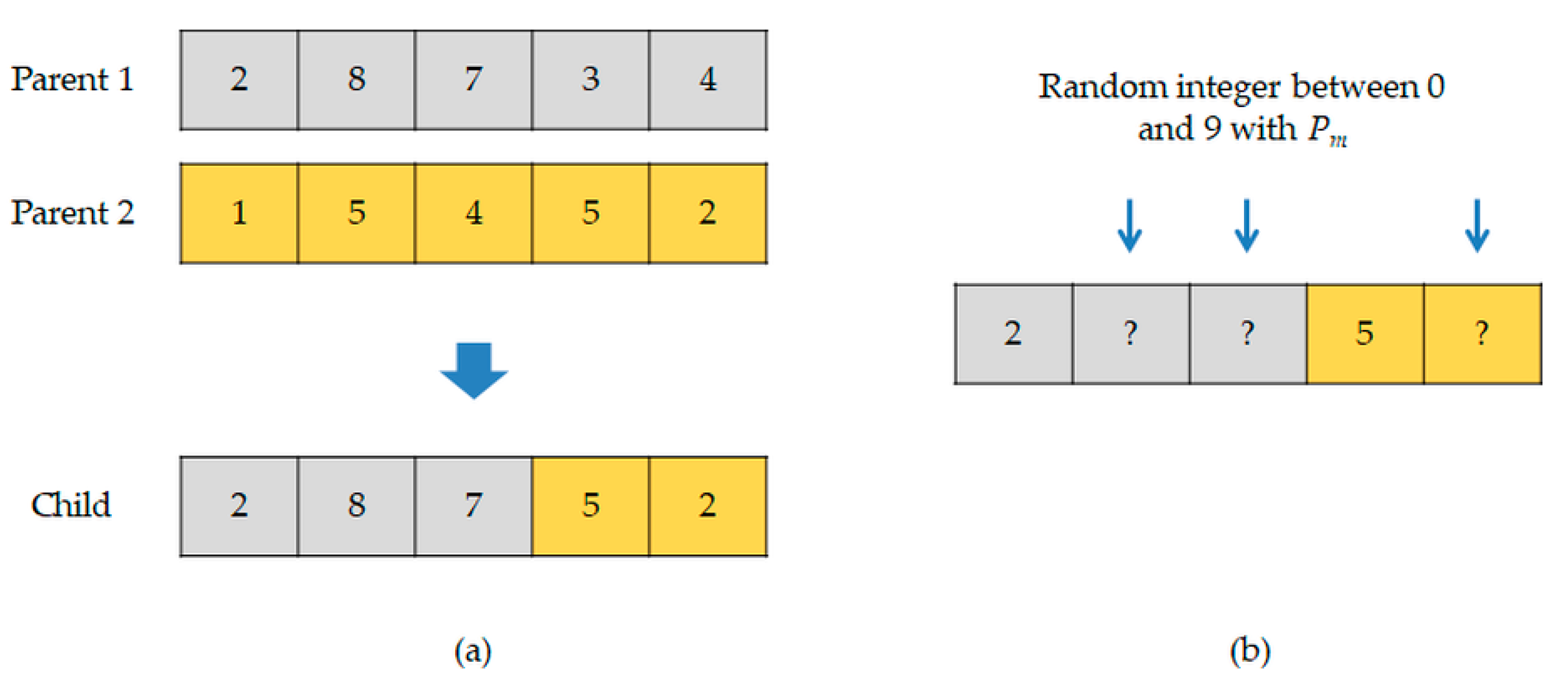
4.1. Chromosome Structure
4.2. Fitness Function
4.3. Selection, Crossover, and Mutation
| STEP 1: | Let Pi be the population of ith generation. Let Cm be the mth chromosome of population Pi,m∈{1,…, Nc}. Let FF(Cm) be the fitness value of chromosome Cm. |
| STEP 2: | Calculate |
| STEP 3: | Select chromosome c as Parent 1 with the probability of |
| STEP 4: | Repeat STEP 3 to obtain Parent 2 |
5. Numerical Experiments
5.1. Validity Analysis of Proposed Models
5.1.1. Systemic Parameters
5.1.2. Computational Results
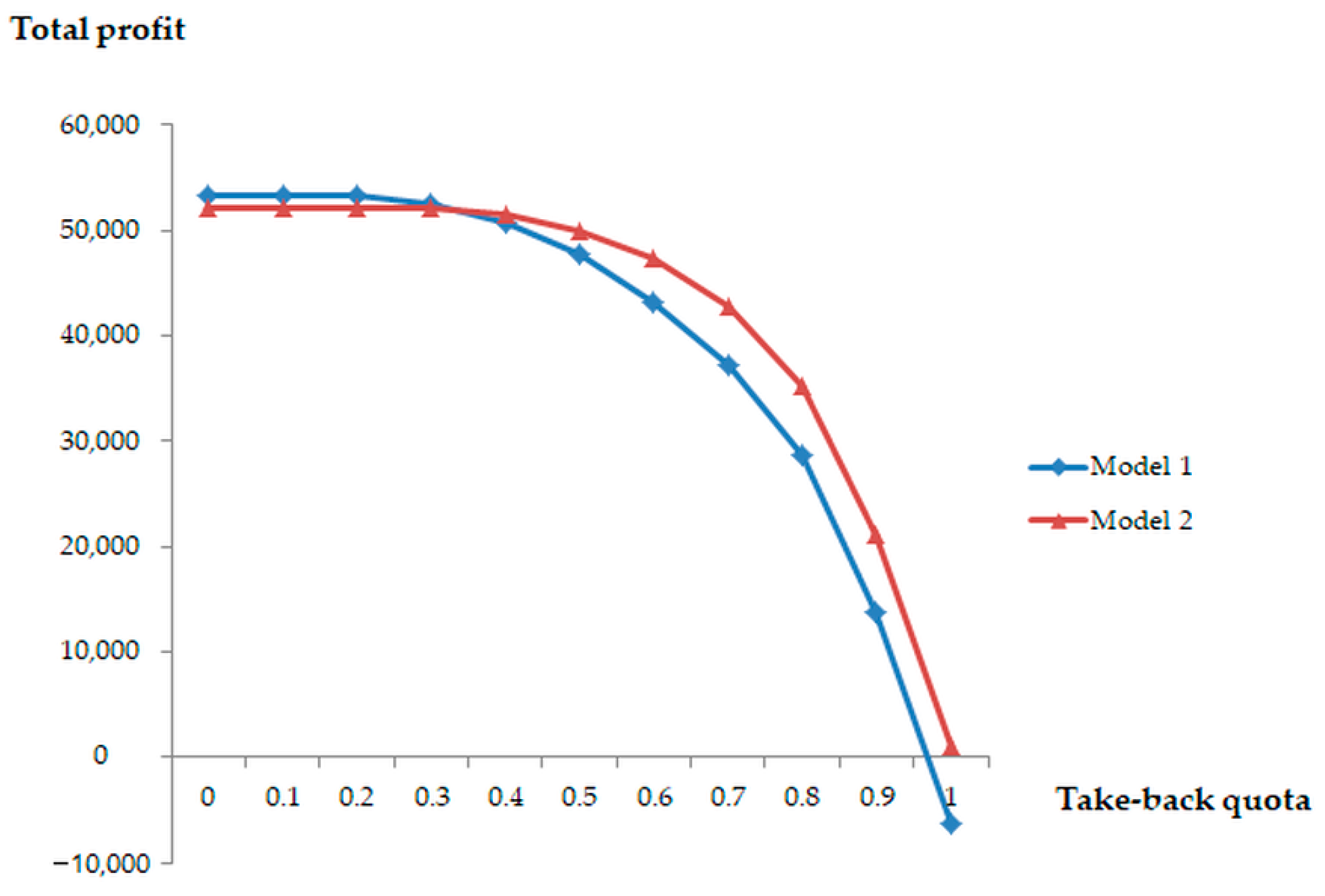
5.2. Sensitivity Test on the Obligatory Take-Back Quota
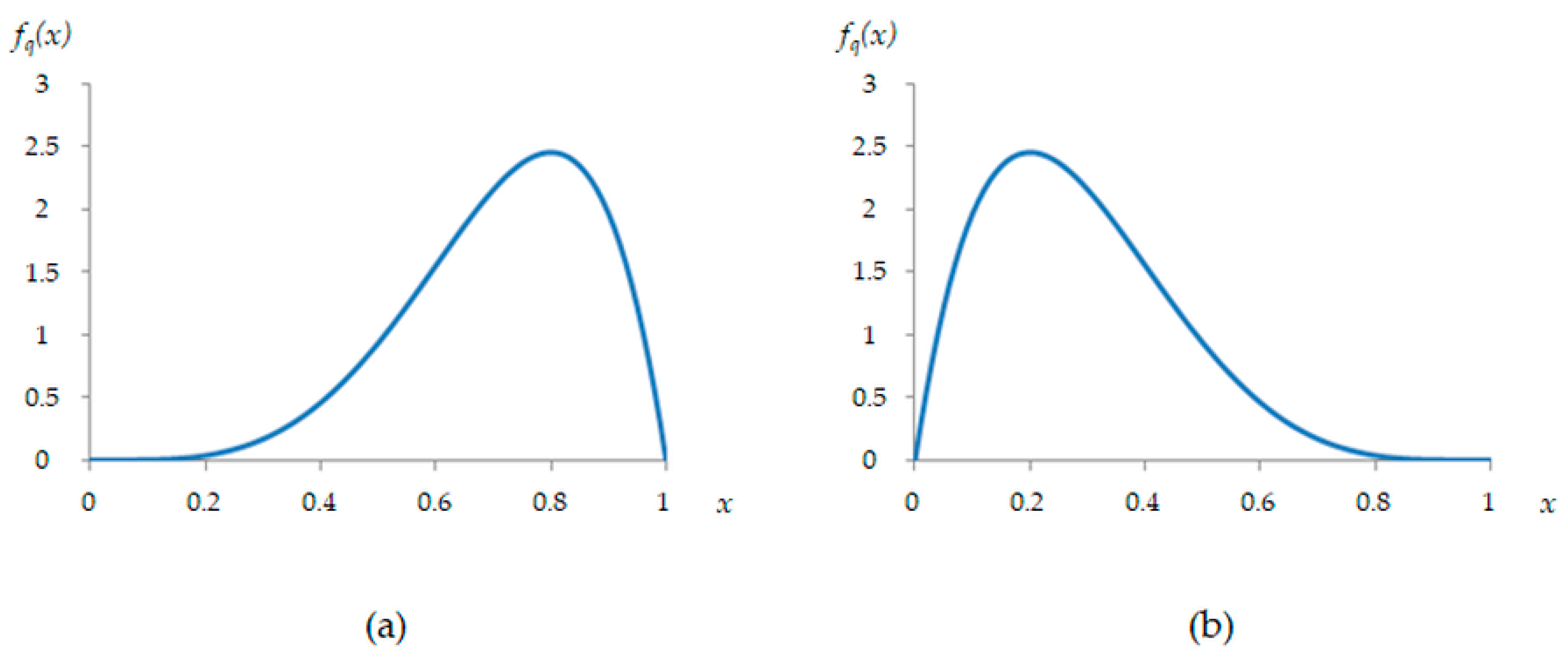
5.3. Sensitivity Test on Quality Distribution
6. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Allne, D.; Bauer, D.; Bras, B.; Gutowski, T.; Murphy, C.; Piwonka, T.; Sheng, P.; Suthernald, J.; Thurston, D.; Wolff, E. Environmentally Benign Manufacturing: Trends in Europe, Japan, and the USA. J. Manuf. Sci. Eng. 2002, 124, 908–920. [Google Scholar] [CrossRef]
- Deng, Q.; Liu, X.; Liao, H. Identifying Critical Factors in the Eco-Efficiency of Remanufacturing Based on the Fuzzy DEMATEL Method. Sustainability 2015, 7, 15527–15547. [Google Scholar] [CrossRef]
- Schrady, D.A. A Deterministic Inventory Model for Reparable Items. Nav. Res. Log. 1967, 14, 391–398. [Google Scholar] [CrossRef]
- Mabini, M.C.; Pintelon, L.M.; Gelders, L.F. EOQ Type Formulation for Controlling Repairable Inventories. Int. J. Prod. Econ. 1992, 28, 21–33. [Google Scholar] [CrossRef]
- Nahmias, S.; Rivera, H. A Deterministic Model for a Repairable Item Inventory System with a Finite Repair Rate. Int. J. Prod. Res. 1979, 17, 215–221. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, D.; Park, M. Pricing and Return Policy under Various Supply Contracts in a Closed-Loop Supply Chain. Int. J. Prod. Res. 2015, 53, 106–126. [Google Scholar] [CrossRef]
- Wei, J.; Zhao, J. Pricing and Remanufacturing Decisions in Two Competing Supply Chains. Int. J. Prod. Res. 2015, 53, 258–278. [Google Scholar] [CrossRef]
- Teunter, R.H. Economic Order Quantities for Recoverable Item Inventory System. Nav. Res. Log. 2011, 48, 484–495. [Google Scholar] [CrossRef]
- Richter, K.; Dobos, I. Analysis of the EOQ Repair and Waste Disposal Model with Integer Setup Numbers. Int. J. Prod. Econ. 1999, 59, 463–467. [Google Scholar] [CrossRef]
- Dobos, I.; Richter, K. The Integer EOQ Repair and Waste Disposal Model-Further Analysis. Cent. Eur. J. Oper. Res. 2000, 8, 173–194. [Google Scholar]
- Dobos, I.; Richter, K. A Production/Recycling Model with Stationary Demand and Return Rates. Cent. Eur. J. Oper. Res. 2003, 11, 35–46. [Google Scholar] [CrossRef]
- Zaarour, N.; Melachrinoudis, E.; Solomon, M.M.; Min, H. The optimal determination of the collection period for returned products in the sustainable supply chain. Int. J. Logist. Res. Appl. 2014, 17, 35–45. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, S.; Dai, Y.; Ye, Y.S. Pay-as-you-throw versus recycling fund system in closed-loop supply chains with alliance recycling. Int. Trans. Oper. Res. 2016. [Google Scholar] [CrossRef]
- Salameh, M.K.; Jaber, M.Y. Economic Production Quantity Model for Items with Imperfect Quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Rahim, M.A.; Ben-Daya, M. Joint determination of production quantity, inspection schedule, and quality control for an imperfect process with deteriorating products. J. Oper. Res. Soc. 2001, 52, 1370–1378. [Google Scholar] [CrossRef]
- Chang, H.C. An Application of Fuzzy Sets to EOQ Model with Imperfect Quality Items. Comput. Oper. Res. 2004, 31, 2079–2092. [Google Scholar] [CrossRef]
- Hwang, H.; Ko, Y.D.; Yoon, S.H.; Ko, C.S. A Closed-Loop Recycling System with Minimum Allowed Quality Level on Returned Products. Int. J. Serv. Oper. Manag. 2008, 5, 758–773. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Ji, P. Optimal Acquisition Policy in Remanufacturing under General Core Quality Distributions. Int. J. Prod. Res. 2015, 53, 1425–1438. [Google Scholar] [CrossRef]
- Gu, Q.; Tagaras, G. Optimal Collection and Remanufacturing Decisions in Reverse Supply Chains with Collector’s Imperfect Sorting. Int. J. Prod. Res. 2014, 52, 5155–5170. [Google Scholar] [CrossRef]
- Ko, Y.D.; Noh, I.J.; Hwang, H. Cost Benefits from Standardization of the Packaging Glass Bottles. Comput. Ind. Eng. 2012, 62, 693–702. [Google Scholar] [CrossRef]
- Gu, W.; Chhajed, D.; Petruzzi, N.C.; Yalabik, B. Quality Design and Environmental Implications of Green Consumerism in Remanufacturing. Int. J. Prod. Econ. 2015, 162, 55–69. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Fan, Z.; Sutherland, J.W.; Zhang, H.; Zhang, X. Development of an Optimal Method for Remanufacturing Process Plan Selection. Int. J. Adv. Manuf. Technol. 2014, 72, 1511–1558. [Google Scholar] [CrossRef]
- Fleischmann, M.; Bloemhof-Ruwaard, J.M.; Dekker, R.; Van der Laan, E.; van Nunen, J.A.E.E.; Van Wassenhove, L.N. Quantitative Models for Reverse Logistics: A Review. Eur. J. Oper. Res. 1997, 103, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Guide, D.; Jayraman, V.; Srivastava, R.; Benton, W.C. Supply Chain Management for Recoverable Manufacturing Systems. Interfaces 2000, 30, 125–142. [Google Scholar] [CrossRef]
- Krill, M.; Thurston, D.L. Remanufacturing: Impacts of Sacrificial Cylinder Liners. J. Manuf. Sci. Eng. 2005, 127, 687–697. [Google Scholar] [CrossRef]
- Ko, Y.D.; Hwang, H. Efficient Operation Policy in a Closed-loop Tire Manufacturing System with ERP. Ind. Eng. Manag. Syst. 2009, 8, 162–170. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial System: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Kesen, S.E.; Güngör, Z. Job scheduling in virtual manufacturing cells with lot-streaming strategy: A new mathematical model formulation and a genetic algorithm approach. J. Oper. Res. Soc. 2012, 63, 683–695. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, X.; Yu, Y.L. A Capacitated Production Planning Problem for Closed-Loop Supply Chain with Remanufacturing. Int. J. Adv. Manuf. Technol. 2011, 54, 757–766. [Google Scholar] [CrossRef]
- Yildirim, M.B.; Mouzon, G. Single-Machine Sustainable Production Planning to Minimize Total Energy Consumption and Total Completion Time Using a Multi Objective Genetic Algorithm. IEEE Trans. Eng. Manag. 2012, 59, 585–597. [Google Scholar] [CrossRef]
- Yan, H.S.; Wa, X.Q.; Xiong, F.L. Integrated production planning and scheduling for a mixed batch job-shop based on alternant iterative genetic algorithm. J. Oper. Res. Soc. 2015, 66, 1250–1258. [Google Scholar] [CrossRef]
- Liu, P.; Yi, S. New algorithm for Evaluating the Green Supply Chain Performance in an Uncertain Environment. Sustainability 2016, 8, 960. [Google Scholar] [CrossRef]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| P | $10.00/unit | Ctype_3 | 1.60 |
| D | 10,000 unit | Qmin, type_4 | 0.60 |
| Cins_before | $0.05/unit | Ctype_4 | 2.50 |
| Cins_after | $0.03/unit | Qmin, type_5 | 0.50 |
| Cmanuf | $3.00/unit | Ctype_5 | 3.50 |
| Cdisposal | $0.10/unit | Qmin, type_6 | 0.40 |
| Cpenalty | $20.00/unit | Ctype_6 | 4.60 |
| Craw | $2.00/unit | Qmin, type_7 | 0.30 |
| (a1, a2, b1, b2) | (0.07, 0.07, 0.03, 0.03) | Ctype_7 | 5.90 |
| δ | 0.70 | Qmin, type_8 | 0.20 |
| Qmin, type_1 | 0.90 | Ctype_8 | 7.20 |
| Ctype_1 | 0.30 | Qmin, type_9 | 0.10 |
| Qmin, type_2 | 0.80 | Cype_9 | 8.60 |
| Ctype_2 | 0.90 | Qmin, type_10 | 0.00 |
| Qqmin, type_3 | 0.70 | Ctype_10 | 10.00 |
| Cpb,i ($) | Qmin,i | Amount of Remanufactured Products Per Type (Unit) | Total Profit ($) | CPU Time (s) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| Model 1 | 2.52 | 0.09 | 188 | 510 | 752 | 913 | 995 | 995 | 913 | 752 | 510 | 94 | 37,230.1 | 0.235 |
| Model 2 | 2.41 | 0.40 | 192 | 521 | 767 | 932 | 1014 | 1014 | 0 | 0 | 0 | 0 | 42,810.4 | 0.192 |
| Take-Back Quota | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| Return Rate | M1 | 0.42 | 0.42 | 0.42 | 0.48 | 0.59 | 0.63 | 0.67 | 0.72 | 0.80 | 0.89 | 0.89 |
| M2 | 0.27 | 0.27 | 0.27 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.80 | 0.89 | 0.89 | |
| Buy-Back Cost | M1 | 1.12 | 1.12 | 1.12 | 1.33 | 1.79 | 2.03 | 2.22 | 2.58 | 3.22 | 4.41 | 4.41 |
| M2 | 0.64 | 0.64 | 0.64 | 0.72 | 1.03 | 1.39 | 1.84 | 2.41 | 3.22 | 4.40 | 4.40 | |
| Min. Quality Level | M1 | 0.50 | 0.50 | 0.50 | 0.42 | 0.38 | 0.30 | 0.20 | 0.11 | 0.01 | 0.00 | 0.00 |
| M2 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | |
| Case1) Beta (5, 2) | Cpb,i ($) | Qmin,i | Amount of Remanufactured Products Per Type (Unit) | Total Profit ($) | CPU Time (s) | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| Model 1 | 2.44 | 0.27 | 785 | 1579 | 1612 | 1281 | 849 | 469 | 205 | 29 | 0 | 0 | 52,518.5 | 0.198 |
| Model 2 | 2.41 | 0.40 | 783 | 1580 | 1613 | 1282 | 849 | 436 | 0 | 0 | 0 | 0 | 53,202.0 | 0.190 |
| Case2) Beta (2, 5) | Cpb,i ($) | Qmin,i | Amount of Remanufactured Products Per Type (Unit) | Total Profit ($) | CPU Time (s) | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| Model 1 | 2.41 | 0.00 | 0 | 10 | 60 | 195 | 445 | 806 | 1217 | 1531 | 1500 | 744 | 20,865.4 | 0.191 |
| Model 2 | 2.41 | 0.40 | 0 | 10 | 64 | 206 | 469 | 849 | 0 | 0 | 0 | 0 | 34,729.7 | 0.194 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, B.D.; Ko, Y.D. Effect of Inspection Policies and Residual Value of Collected Used Products: A Mathematical Model and Genetic Algorithm for a Closed-Loop Green Manufacturing System. Sustainability 2017, 9, 1589. https://doi.org/10.3390/su9091589
Song BD, Ko YD. Effect of Inspection Policies and Residual Value of Collected Used Products: A Mathematical Model and Genetic Algorithm for a Closed-Loop Green Manufacturing System. Sustainability. 2017; 9(9):1589. https://doi.org/10.3390/su9091589
Chicago/Turabian StyleSong, Byung Duk, and Young Dae Ko. 2017. "Effect of Inspection Policies and Residual Value of Collected Used Products: A Mathematical Model and Genetic Algorithm for a Closed-Loop Green Manufacturing System" Sustainability 9, no. 9: 1589. https://doi.org/10.3390/su9091589





