Situational Assessments Based on Uncertainty-Risk Awareness in Complex Traffic Scenarios
Abstract
:1. Introduction
2. Related Work
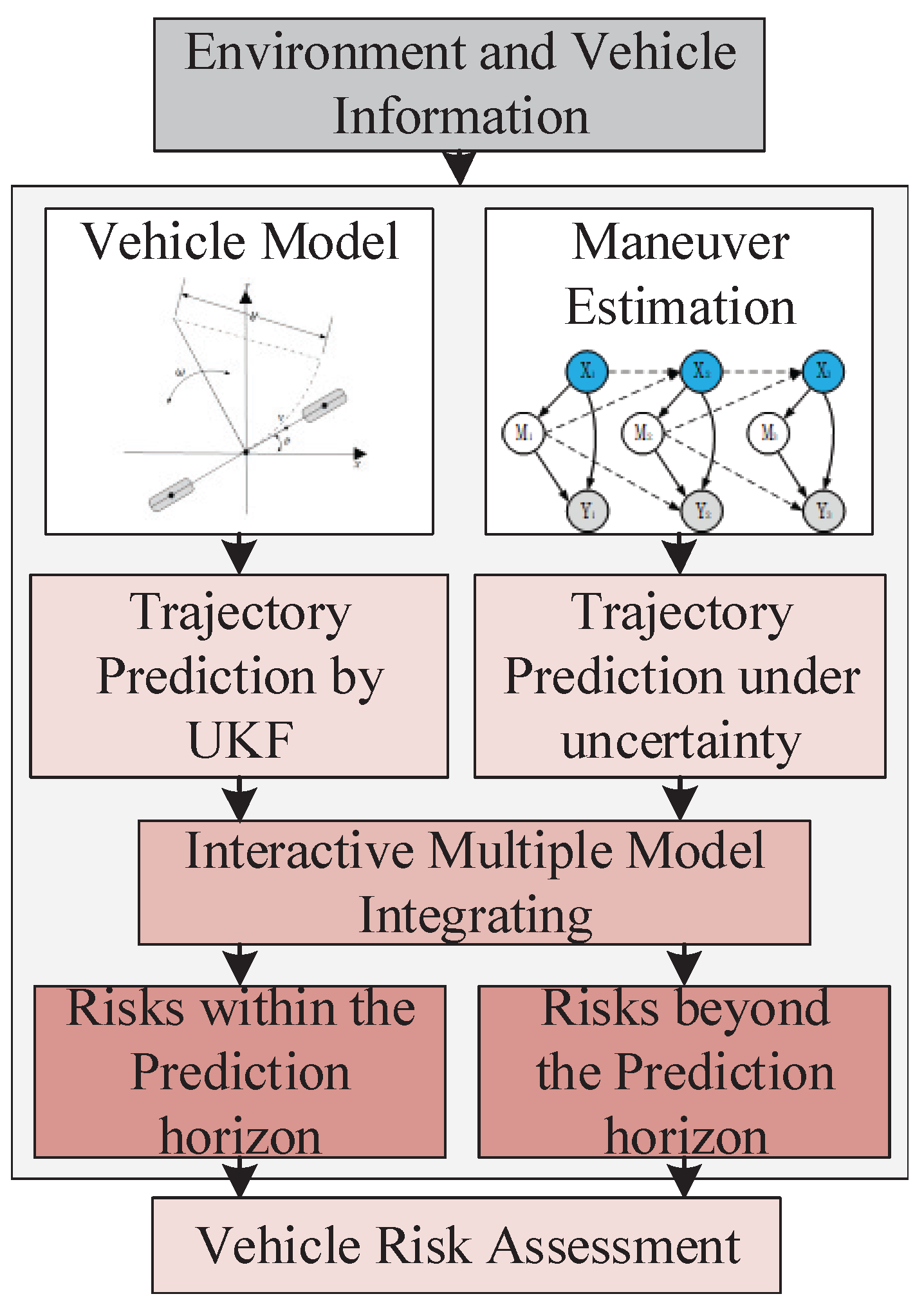
3. Collision Assessments under Prediction and Uncertainty
3.1. Environment Models
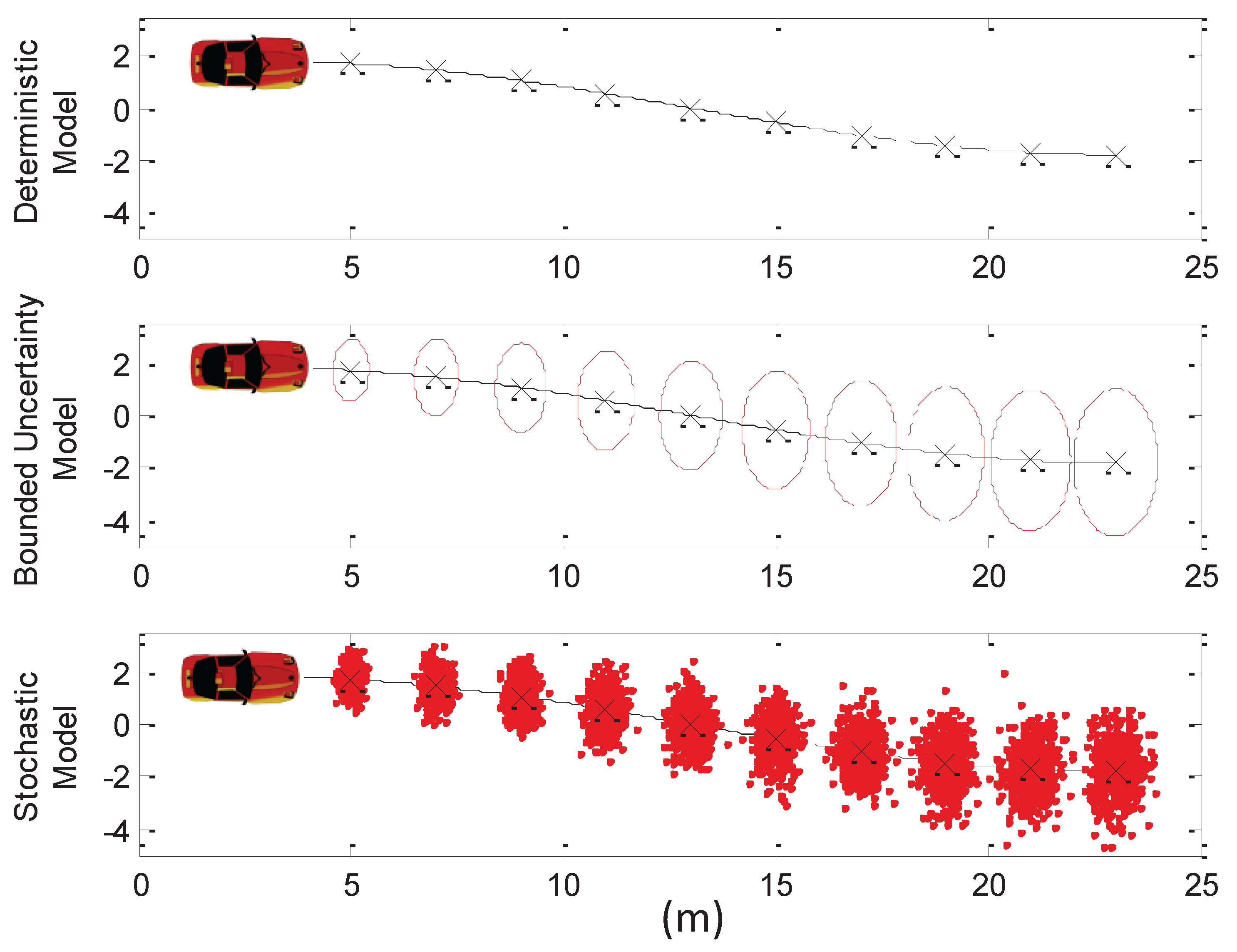
3.2. Collision Probability Based on Trajectory Prediction
3.3. Collision Probability for Planned Maneuvers and Trajectories
4. Risk Assessments
4.1. Risk Assessments within the Prediction Horizon
4.2. Risk Assessments beyond the Prediction Horizon
4.3. Integrated Risk Assessments Using Gaussian Distributions
5. Uncertainty Analysis in Application Scenarios
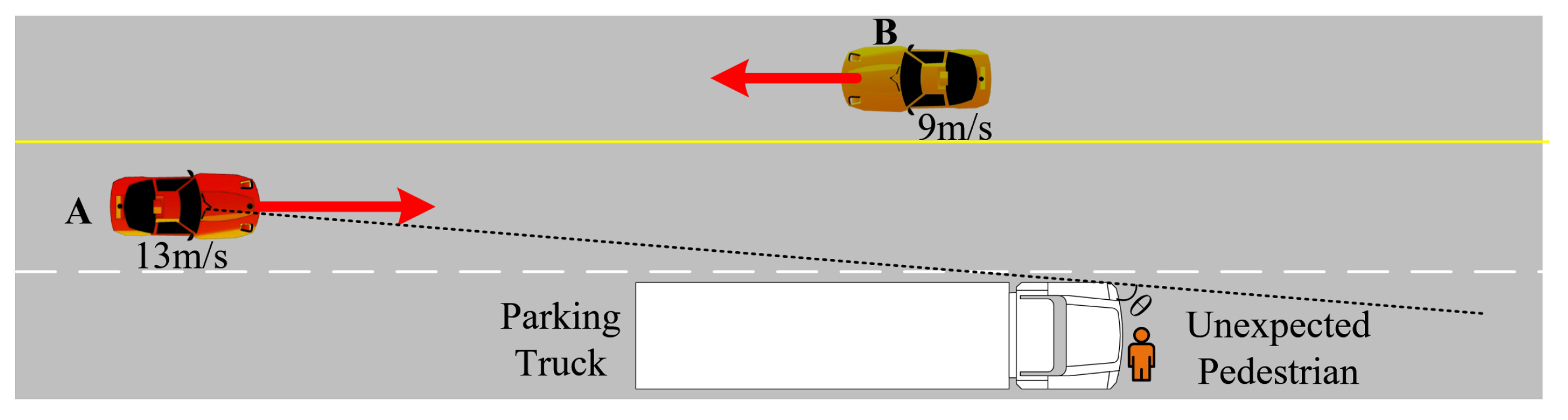
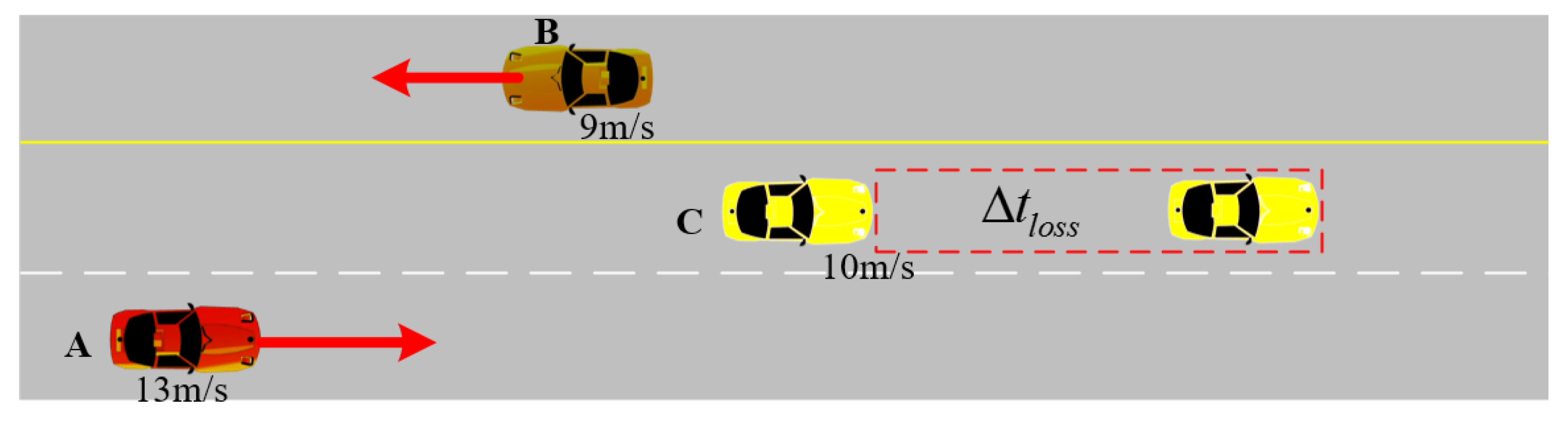
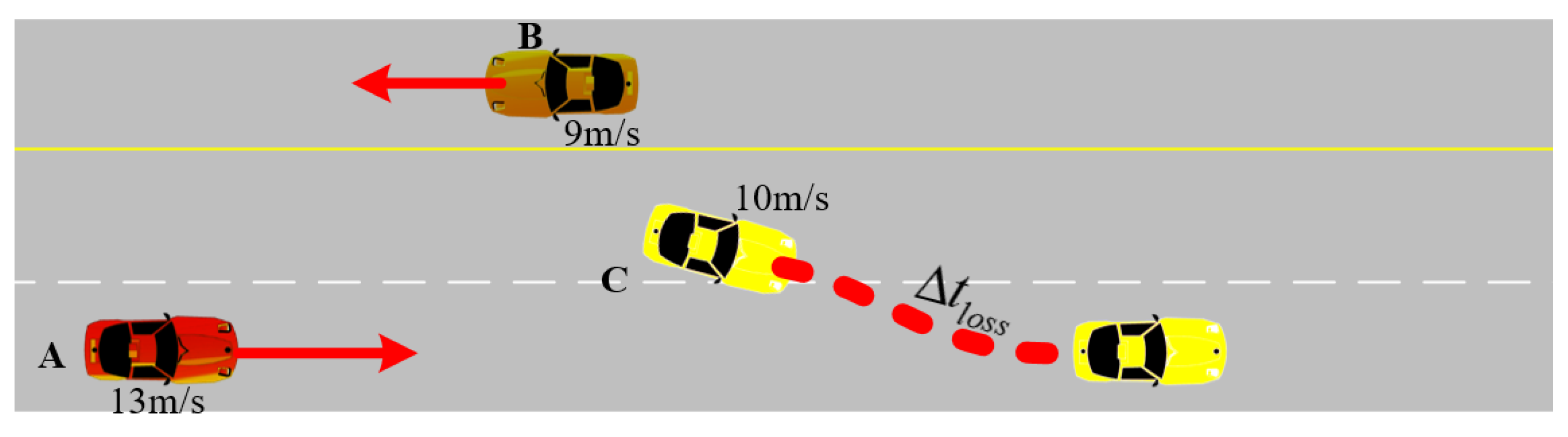
5.1. Situational Assessments Regarding Unexpected Objects
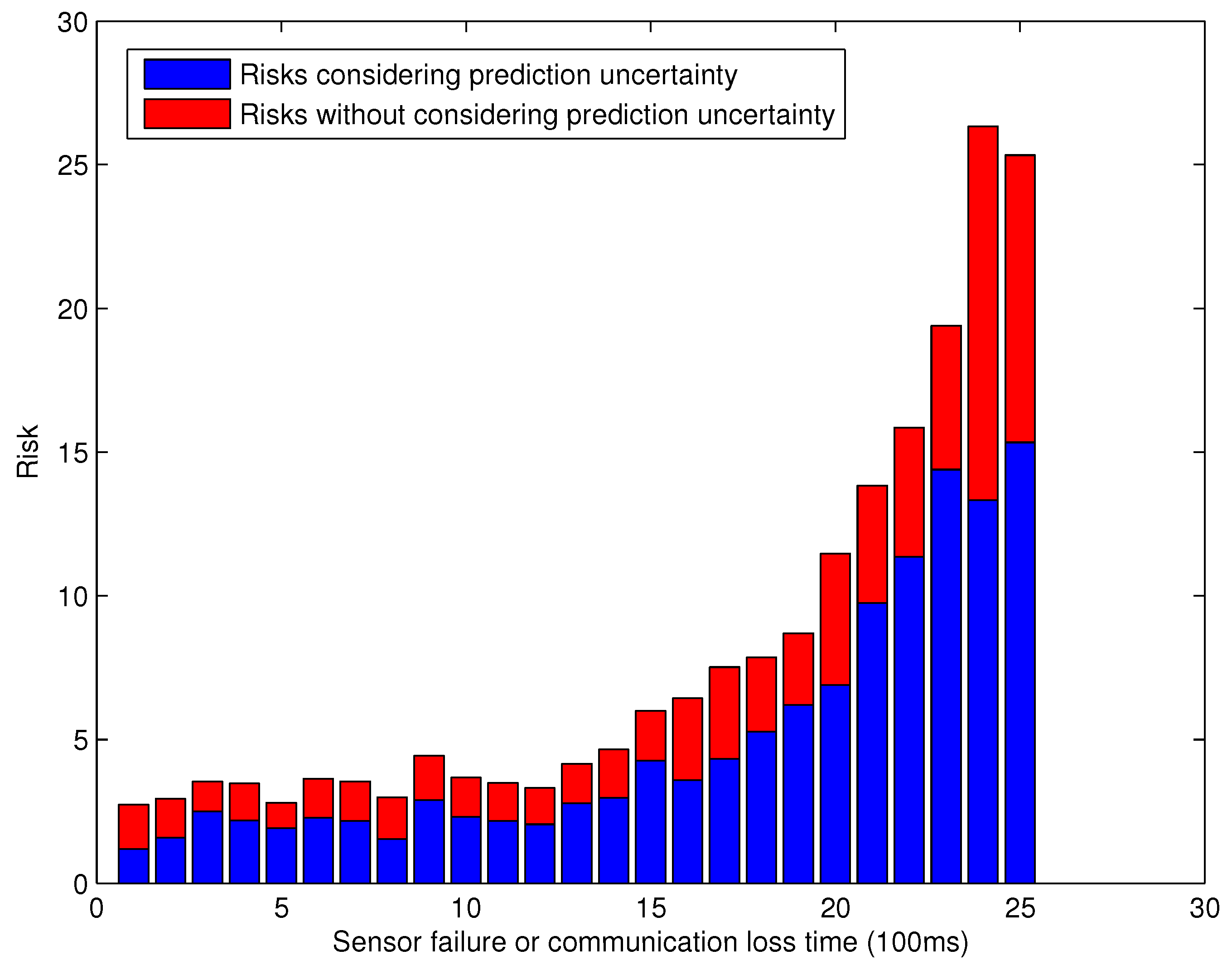
5.2. Situational Assessments Regarding Sensor Failure or Communication Loss
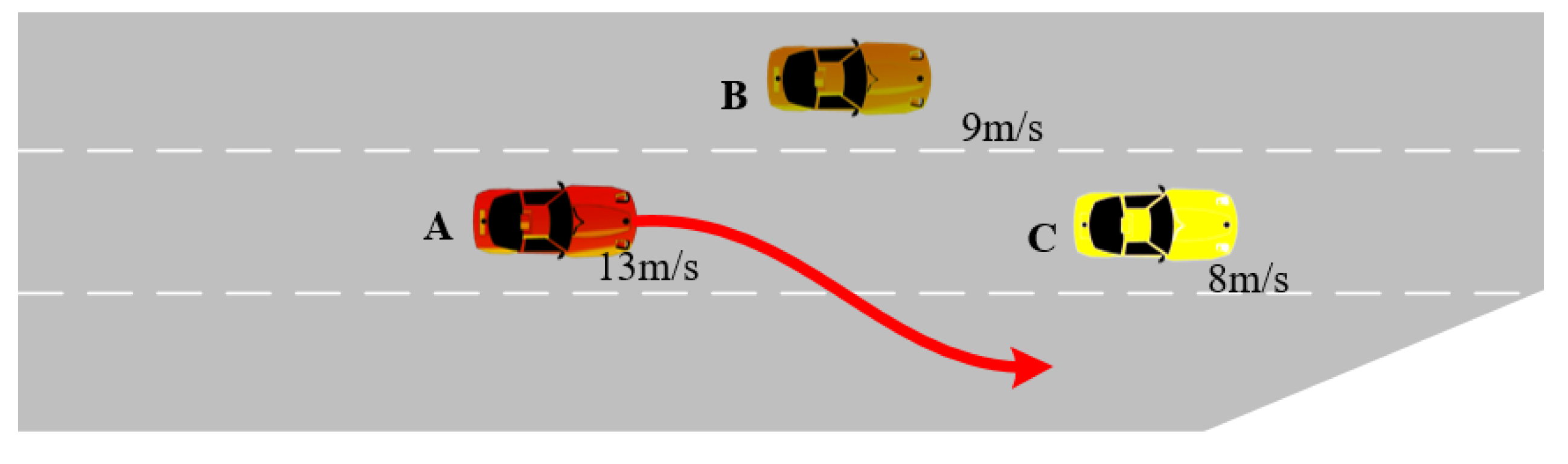
5.3. Situational Assessments Regarding Imperfect Sensing with Different Accuracies
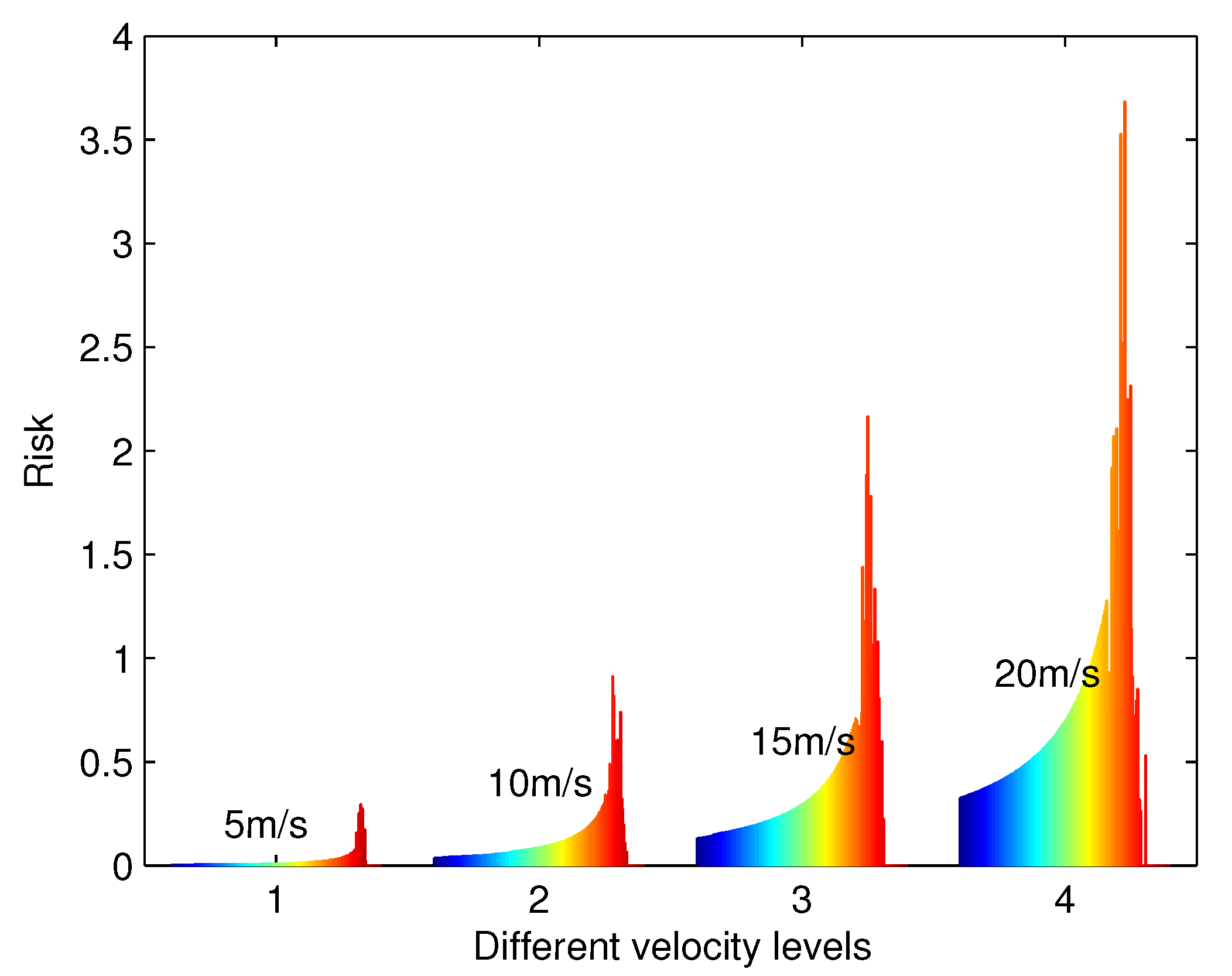
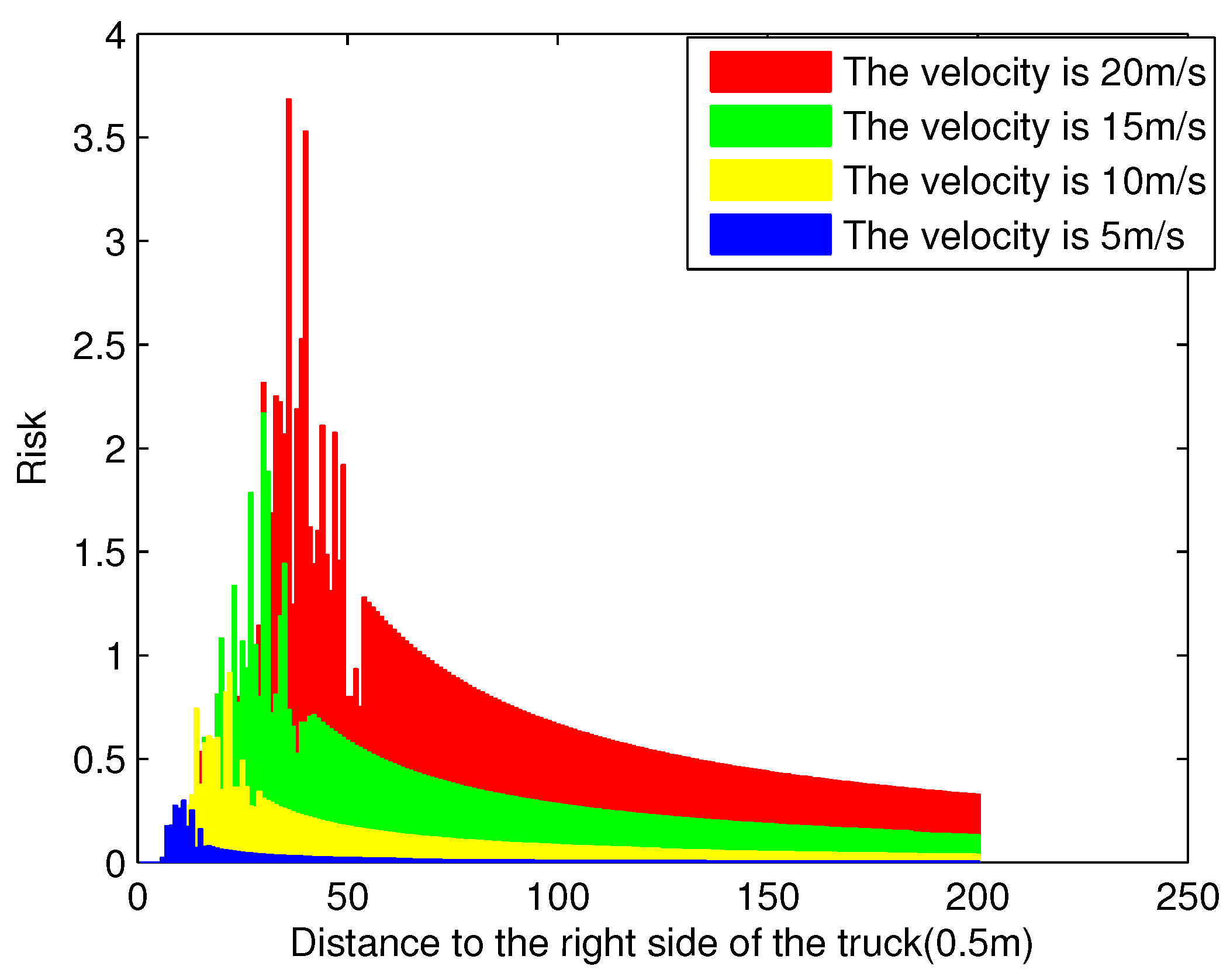
5.4. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Arem, B. A Strategic Approach to Intelligent Functions in Vehicles. In Handbook of Intelligent Vehicles; Springer: London, UK, 2012; pp. 17–29. ISBN 978-0-85729-085-4. [Google Scholar]
- Qi, X.; Barth, M.J.; Wu, G.; Boriboonsomsin, K.; Wang, P. Energy Impact of Connected Eco-driving on Electric Vehicles. In Road Vehicle Automation 4. Lecture Notes in Mobility; Springer: London, UK, 2018; pp. 97–111. ISBN 978-3-319-60934-8. [Google Scholar]
- Baines, V.; Padget, J. A situational awareness approach to intelligent vehicle agents. In Modeling Mobility with Open Data; Springer: London, UK, 2015; pp. 77–103. ISBN 978-3-319-15024-6. [Google Scholar]
- Endsley, M.R. Toward a theory of situation awareness in dynamic systems. Hum. Factors 1995, 37, 32–64. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, J.; Li, Y.; Lv, C. Regenerative Brake-by-Wire System Development and Hardware-In-Loop Test for Autonomous Electrified Vehicle. SAE Tech. Pap. 2017. [Google Scholar] [CrossRef]
- Lv, C.; Zhang, J.; Li, Y.; Yuan, Y. Mechanism analysis and evaluation methodology of regenerative braking contribution to energy efficiency improvement of electrified vehicles. Energy Convers. Manag. 2015, 92, 469–482. [Google Scholar] [CrossRef]
- Kang, W.M.; Lee, J.D.; Jeong, Y.S.; Park, J.H. Vcc-ssf: Service-oriented security framework for vehicular cloud computing. Sustainability 2015, 7, 2028–2044. [Google Scholar] [CrossRef]
- Lambert, F. Understanding the Fatal Tesla Accident on Autopilot and the NHTSA Probe. Available online: https://electrek.co/2016/07/01/understanding-fatal-tesla-accident-autopilot-nhtsa-probe/ (accessed on 10 August 2017).
- Wang, H.; Huang, Y.; Lv, C.; Khajepour, A. A Global Optimal Energy Management System for Hybrid Electric off-road Vehicles. SAE Int. J. Commer. Veh. 2017, 10, 2. [Google Scholar] [CrossRef]
- Lv, C.; Wang, H.; Cao, D. High-Precision Hydraulic Pressure Control Based on Linear Pressure-Drop Modulation in Valve Critical Equilibrium State. IEEE Trans. Ind. Electron. 2017, 1. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Flohr, F.; Wang, J.; Xiong, H.; Bernhard, M.; Pan, S.; Gavrila, D.M.; Li, K. A unified framework for concurrent pedestrian and cyclist detection. IEEE Trans. Intell. Transp. Syst. 2017, 18, 269–281. [Google Scholar] [CrossRef]
- Chen, Y.L.; Shen, K.Y.; Wang, S.C. Forward collision warning system considering both time-to-collision and safety braking distance. Int. J. Veh. Saf. 2013, 6, 347–360. [Google Scholar] [CrossRef]
- Hou, Y.; Edara, P.; Sun, C. Modeling mandatory lane changing using Bayes classifier and decision trees. IEEE Trans. Intell. Transp. Syst. 2014, 15, 647–655. [Google Scholar] [CrossRef]
- González, D.S.; Dibangoye, J.S.; Laugier, C. High-speed highway scene prediction based on driver models learned from demonstrations. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 149–155. [Google Scholar]
- Laugier, C.; Paromtchik, I.E.; Perrollaz, M.; Yong, M.; Yoder, J.D.; Tay, C.; Mekhnacha, K.; Nègre, A. Probabilistic analysis of dynamic scenes and collision risks assessment to improve driving safety. IEEE Trans. Intell. Transp. Syst. Mag. 2011, 3, 4–19. [Google Scholar] [CrossRef]
- Annell, S.; Gratner, A.; Svensson, L. Probabilistic collision estimation system for autonomous vehicles. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 473–478. [Google Scholar]
- Barrios, C.; Motai, Y.; Huston, D. Intelligent forecasting using dead reckoning with dynamic errors. IEEE Trans. Ind. Inform. 2016, 12, 2217–2227. [Google Scholar] [CrossRef]
- Liu, M.; Chen, Y.; Lu, G.; Wang, Y. Modeling crossing behavior of drivers at unsignalized intersections with consideration of risk perception. Transp. Res. Part F 2017, 45, 14–26. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Zheng, X.; Ni, D.; Li, K. Driving safety field theory modeling and its application in pre-collision warning system. Transp. Res. Part C 2016, 72, 306–324. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Li, Y. The Driving Safety Field Based on Driver–Vehicle–Road Interactions. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2203–2214. [Google Scholar] [CrossRef]
- Kim, K.; Kim, B.; Lee, K.; Ko, B.; Yi, K. Design of Integrated Risk Management-Based Dynamic Driving Control of Automated Vehicles. IEEE Trans. Intell. Transp. Syst. Mag. 2017, 9, 57–73. [Google Scholar] [CrossRef]
- Ward, J.R.; Agamennoni, G.; Worrall, S.; Bender, A.; Nebot, E. Extending time to collision for probabilistic reasoning in general traffic scenarios. Transp. Res. Part C 2015, 51, 66–82. [Google Scholar] [CrossRef]
- Rummelhard, L.; Nègre, A.; Perrollaz, M.; Laugier, C. Probabilistic grid-based collision risk prediction for driving application. In Experimental Robotics; Springer: London, UK, 2016; pp. 821–834. ISBN 978-3-319-23778-7. [Google Scholar]
- Wu, C.; Peng, L.; Huang, Z.; Zhong, M.; Chu, D. A method of vehicle motion prediction and collision risk assessment with a simulated vehicular cyber physical system. Transp. Res. Part C 2014, 47, 179–191. [Google Scholar] [CrossRef]
- Lefèvre, S.; Vasquez, D.; Laugier, C. A survey on motion prediction and risk assessment for intelligent vehicles. Robomech J. 2014, 1, 1. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.Y.; Cho, H.J.; Ryu, K.Y. A probabilistic approach for collision avoidance of uncertain moving objects within black zones. Ad Hoc Netw. 2016, 52, 50–62. [Google Scholar] [CrossRef]
- Choi, M.; Rubenecia, A.; Shon, T.; Choi, H.H. Velocity Obstacle Based 3D Collision Avoidance Scheme for Low-Cost Micro UAVs. Sustainability 2017, 9, 1174. [Google Scholar] [CrossRef]
- Xie, G.; Gao, H.; Qian, L.; Huang, B.; Li, K.; Wang, J. Vehicle trajectory prediction by integrating physics- and maneuver-based approaches using interactive multiple models. IEEE Trans. Ind. Electron. 2017. under review. [Google Scholar]
- Lv, C.; Zhang, J.; Li, Y. Extended-Kalman-filter-based regenerative and friction blended braking control for electric vehicle equipped with axle motor considering damping and elastic properties of electric powertrain. Veh. Syst. Dyn. 2014, 52, 1372–1388. [Google Scholar] [CrossRef]
- Althoff, D. Safety Assessment for Motion Planning in Uncertain and Dynamic Environments. Ph.D. Thesis, Universitätsbibliothek der TU München, Deutschland, Germany, 24 September 2014. [Google Scholar]
- Schlechtriemen, J.; Wabersich, K.P.; Kuhnert, K.D. Wiggling through complex traffic: Planning trajectories constrained by predictions. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 1293–1300. [Google Scholar]
- Tay, M.K.C.; Laugier, C. Modelling smooth paths using gaussian processes. In Field and Service Robotics; Springer: London, UK, 2008; pp. 381–390. ISBN 978-3-540-75404-6. [Google Scholar]
- Fulgenzi, C.; Spalanzani, A.; Laugier, C.; Tay, C. Risk based motion planning and navigation in uncertain dynamic environment. INRIA, Research Report. 2010, p. 14. Available online: http://hal.inria.fr/inria-00526601/en/ (accessed on 1 August 2017).
- Xie, G.; Gao, H.; Huang, B.; Qian, L.; Wang, J. A Driving Behavior Awareness Model based on Dynamic Bayesian Network and Distributed Genetic Algorithm. Int. J. Comput. Int. Syst. 2017. under review. [Google Scholar]
- Hollnagel, E. Anticipating Failures: What Should Predictions Be About? Linkoeping Univ (Sweden) Graduate School for Human-Machine Interaction, Technical Report. 2001. Available online: http://www.dtic.mil/get-tr-doc/pdf?AD=ADP010439 (accessed on 29 August 2017).
- Useche, S.A.; Alonso, F. The Importance of Fatigue-Monitoring as a Tool for the Intelligent Transport Systems (ITS). EC Neurol. 2017, 5, 71–73. [Google Scholar]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, G.; Zhang, X.; Gao, H.; Qian, L.; Wang, J.; Ozguner, U. Situational Assessments Based on Uncertainty-Risk Awareness in Complex Traffic Scenarios. Sustainability 2017, 9, 1582. https://doi.org/10.3390/su9091582
Xie G, Zhang X, Gao H, Qian L, Wang J, Ozguner U. Situational Assessments Based on Uncertainty-Risk Awareness in Complex Traffic Scenarios. Sustainability. 2017; 9(9):1582. https://doi.org/10.3390/su9091582
Chicago/Turabian StyleXie, Guotao, Xinyu Zhang, Hongbo Gao, Lijun Qian, Jianqiang Wang, and Umit Ozguner. 2017. "Situational Assessments Based on Uncertainty-Risk Awareness in Complex Traffic Scenarios" Sustainability 9, no. 9: 1582. https://doi.org/10.3390/su9091582





