Break-Even Point Analysis of Sodium-Cooled Fast Reactor Capital Investment Cost Comparing the Direct Disposal Option and Pyro-Sodium-Cooled Fast Reactor Nuclear Fuel Cycle Option in Korea
Abstract
:1. Introduction
2. Methods
2.1. Capital Investment Cost Expensing Method Based on Engineering Cost Estimation
2.2. SFR Capital Investment Cost Expensing
SFR Capital Investment Cost Calculation
3. Electricity Generation Cost and Pyro-SFR Nuclear-Fuel-Cycle Cost Calculation
3.1. Reactor Cost Calculation
3.2. Nuclear Fuel Cycle Cost Calculation
3.3. Electricity Generation Cost Calculation
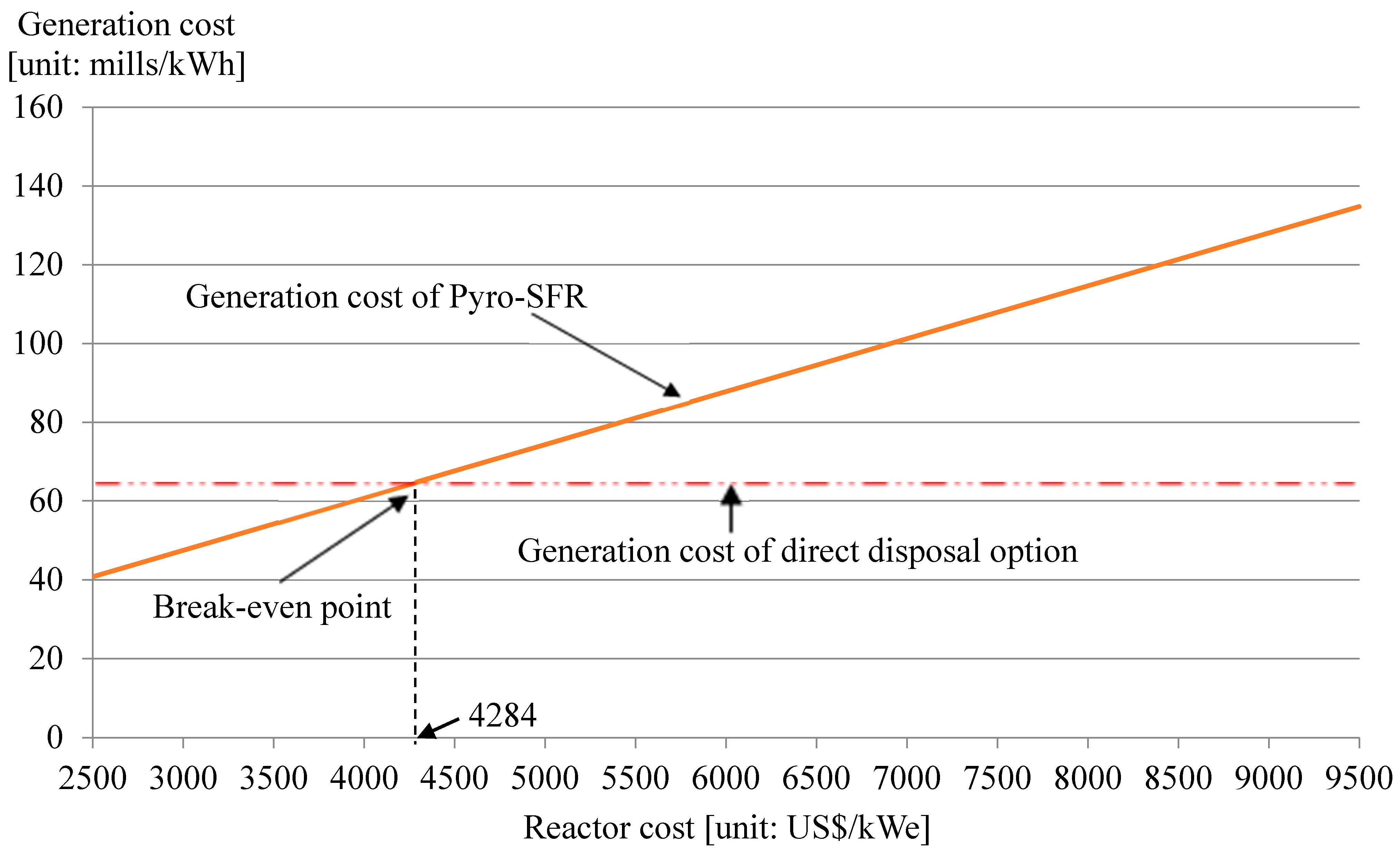
3.4. Break-Even Point Calculation
3.5. Cost Calculation Results
4. Break-Even Point Analysis of the SFR Capital Investment Cost for the Pyro-SFR Nuclear Fuel Cycle Option and the Direct Disposal Option
5. Conclusions and Implication
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cerullo, N.; Lomonaco, G. Generation IV reactor designs, operation and fuel cycle. In Nuclear Fuel Cycle Science and Engineering; Woodhead Publishing: Cambridge, UK, 2012; pp. 333–395. [Google Scholar]
- Kim, S.K.; Ko, W.I.; Youn, S.R.; Gao, R.; Bang, S.S. Advanced fuel cycle cost estimation model and its cost estimation results for three nuclear fuel cycles using a dynamic model in Korea. Nucl. Eng. Des. 2015, 293, 159–165. [Google Scholar] [CrossRef]
- Organization for Economic Cooperation and Development/Nuclear Energy Agency (OECD/NEA). Advanced Nuclear Fuel Cycles and Radioactive Waste Management; OECD Publishing: Paris, France, 2006; pp. 243–244.
- Kang, S.J. The Theory of Cost Estimation; Dunam Press: Seoul, Korea, 2010; pp. 25–33, 341–345. [Google Scholar]
- Korea Atomic Energy Research Institute (KAERI). Development of System Engineering Technology for Nuclear Fuel Cycle; KAERI/RR-3426: Daejeon, Korea, 2011; p. 186. [Google Scholar]
- Weygandt, J.J.; Kieso, D.E.; Kimmel, P.D. Accounting Principles; Wiley: Danvers, MA, USA, 2008; pp. 422–441. [Google Scholar]
- Amos, S.J. Skills & Knowledge of Cost Engineering; AACE International Press: Morgantown, WV, USA, 2004; p. 96. [Google Scholar]
- Organization for Economic Cooperation and Development/Nuclear Energy Agency (OECD/NEA). The Economics of the Back-End of the Nuclear Fuel Cycle; OECD Publishing: Paris, France, 2013; p. 65.
- Korea Atomic Energy Research Institute (KAERI). Preliminary Conceptual Design and Cost Estimation for Korea Advanced Pyroprocess Facility Plus (KAPF+); KAERI/CM-1382: Daejeon, Korea, 2010; pp. 103–104. [Google Scholar]
- Bang, S.; Chung, Y.; Chun, D.; Kwon, C.; Hong, S. Cost estimation and efficiency analysis of Korean CANDU spent fuel disposal alternatives in consideration of future price volatility. Sci. Technol. Nucl. Install. 2016, 2016. [Google Scholar] [CrossRef]
- Shropshire, D.E.; Williams, K.A.; Boore, W.B.; Smith, J.D.; Dixon, B.W.; Dunzik-Gougar, M.; Adams, R.D.; Gombert, D. Advanced Fuel Cycle Cost Basis; Idaho National Laboratory (INL): Idaho Falls, ID, USA, 2009; pp. 21–23.
- Yang, Y.J.; Park, G.J.; Jo, S.H.; Kim, S.C.; Kim, M.C.; Jong, Y.H.; Park, S.E. An Economic Feasibility Study on the Introduction Scenarios of Sodium-Cooled Fast Reactor; KAERI/CM-2007; KAERI: Daejeon, Korea, 2014; pp. 44–45. [Google Scholar]
- Bunn, M.; Fetter, S.; Holdren, J.P.; Van Der Zwaan, B. The Economics of Reprocessing vs. Direct Disposal of Spent Nuclear Fuel; Harvard University: Cambridge, MA, USA, 2003; pp. 13–17. [Google Scholar]
- Korea Atomic Energy Research Institute (KAERI). Geological Disposal System Development; KAERI/RR-2336; KAERI: Daejeon, Korea, 2002; pp. 660–663. [Google Scholar]
- Organization for Economic Cooperation and Development/Nuclear Energy Agency (OECD/NEA). The Economics of the Nuclear Fuel Cycle; OECD Publishing: Paris, France, 1993; pp. 95–97.
- Massachusetts Institute of Technology (MIT). The Future of the Nuclear Fuel Cycle; MIT: Cambridge, MA, USA, 2011; p. 72. [Google Scholar]
- Shimazu, Y. Fuel Cycle Cost Analysis on Molten-Salt Reactors. J. Nucl. Sci. Technol. 1976, 13, 190–198. [Google Scholar] [CrossRef]
- Kim, S.K.; Ko, W.I.; Lee, Y.H. Economic Viability of Metallic Sodium-Cooled Fast Reactor Fuel in Korea. Sci. Technol. Nucl. Install. 2013, 2013. [Google Scholar] [CrossRef]
- Hyundai Engineering Co., Ltd. The Development of Cost Estimation System for Nuclear Liability; Hyundai Engineering Co., Ltd.: Seoul, Korea, 2009; pp. 63–75. [Google Scholar]
- Korea Atomic Energy Research Institute (KAERI). Development of Head-End Pyrochemical Reduction Process for Advanced Oxide Fuels; KAERI/RR-2939; KAERI: Daejeon, Korea, 2007; p. 35. [Google Scholar]
- Xia, L.; Luo, D. A method for calculating economic critical depth of shale gas resources in China via break-even analysis. J. Nat. Gas Sci. Eng. 2014, 21, 1091–1098. [Google Scholar] [CrossRef]
- Keast, S.L.; Jacobs, E.; Harrison, D.; Farmer, K.; Thompson, D. Future economic outlook of Nebraska rural community pharmacies based on break-even analysis of community operational costs and county population. Res. Soc. Adm. Pharm. 2010, 6, 209–220. [Google Scholar] [CrossRef] [PubMed]
- Potkany, M.; Krajcirova, L. Quantification of the volume of products to achieve the break-even point and desired profit in non-homogeneous production. Procedia Econ. Financ. 2015, 26, 194–201. [Google Scholar] [CrossRef]
- Morano, P.; Tajani, F. The break-even analysis applied to urban renewal investments: A model to evaluate the share of social housing financially sustainable for private investors. Habitat Int. 2017, 59, 10–20. [Google Scholar] [CrossRef]
- Hatch, M.D.; Daniels, S.D.; Glerum, K.M.; Higgins, L.D. The cost effectiveness of vancomycin for preventing infections after shoulder arthroplasty: A break-even analysis. J. Shoulder Elbow Surg. 2017, 26, 472–477. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.K.; Ko, W.I.; Kim, H.D.; Revankar, S.T.; Zhou, W.; Jo, D. Cost–benefit analysis of BeO–UO2 nuclear fuel. Prog. Nucl. Energy 2010, 52, 813–821. [Google Scholar] [CrossRef]
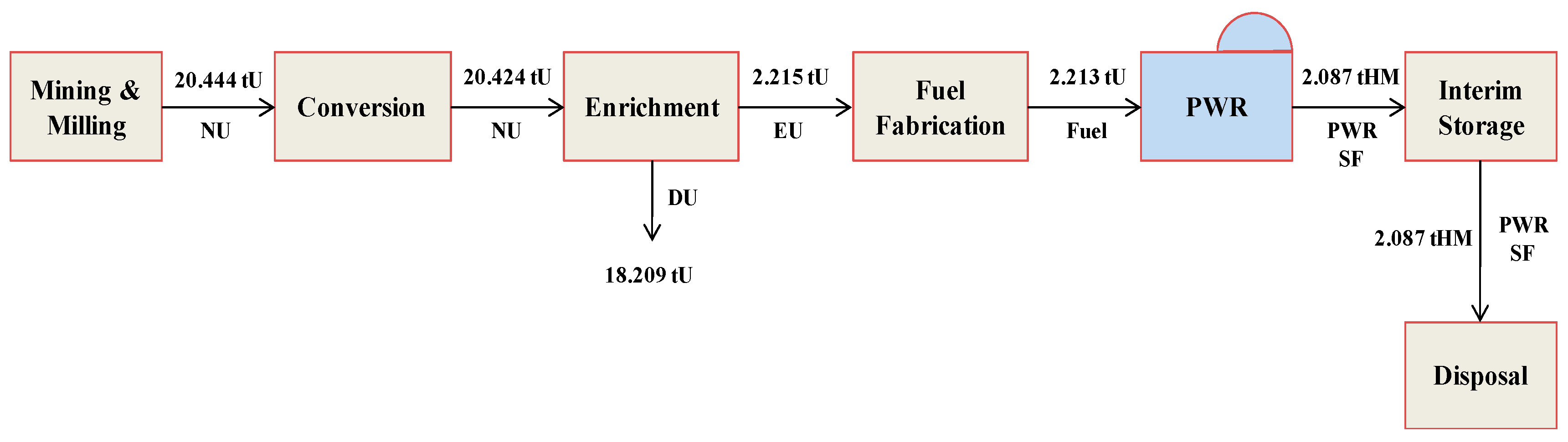
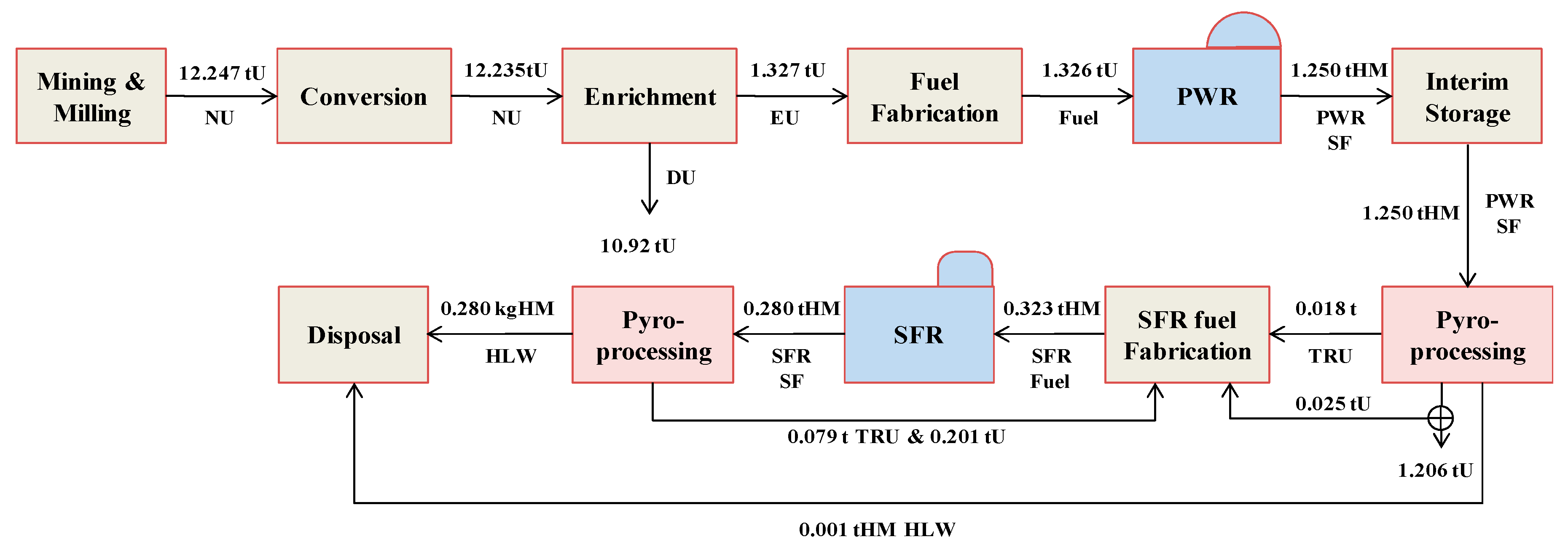
| Category | KAPF+ |
|---|---|
| Site area | 272,000 m2 (680 m × 400 m) |
| Capacity | Front-end: 400 tHM/year, Temporary storage: 400 tHM/year, Pyroprocess: 200 tHM/year/module × 2 module |
| Capacity factor | 55% (200 day/year) |
| Life time | 60 year |
| Raw material | PWR spent fuel |
| Products | U, U/TRU metal ingot Waste (ceramic, metal, etc.) |
| Category | 5% Discounted Amount (Unit: kUS$) | Ratio (%) |
|---|---|---|
| Capital Cost | 261,180 | 33.5 |
| O & M (Operation and Maintenance) Cost | 496,219 | 63.7 |
| D & D (Decommission and Disposal) Cost | 21,988 | 2.8 |
| Total | 779,386 | 100 |
| Category | SFR1200 FOAK * × 2 Unit | SFR800 FOAK × 2 Unit |
|---|---|---|
| NSSS | 1702.2 | 1389.9 |
| Category | SFR1200 FOAK × 2 Units | SFR800 FOAK × 2 Units |
|---|---|---|
| SFR turbine-generator | 386.9 | 300.9 |
| Cost Items | Value | Units | Remarks | |||
|---|---|---|---|---|---|---|
| Uranium | 50 | US$/kgU | Spot market price as of September in 2015 | |||
| Conversion | 10 | US$/kgU | Spot market price as of September in 2015 | |||
| Enrichment | 120 | US$/SWU | Spot market price as of September in 2015 | |||
| Pyro-process for PWR S/F | UO2 Pyro (reduction/refining) | 850 | US$/kgHM | KAERI 2010, Ko et al., 2014 conceptual KAPF | ||
| Fuel fabrication | UO2 Fuel | 270 | US$/kgHM | Advanced Fuel Cycle Cost Basis, INL (2009) | ||
| Pyro-process for SFR S/F | Pyro-process for SFR S/F | 1860 | US$/kgHM | Advanced Fuel Cycle Cost Basis, INL (2009) | ||
| TRU Metal Fabrication | 4070 | US$/kgHM | Advanced Fuel Cycle Cost Basis, INL (2009) | |||
| Transport/Storage | UO2 S/F Dry Storage | 495 | US$/kgHM | Ministry of Knowledge Economy 2012 | ||
| Decay storage (Cs/Sr) | 131 | US$/kgHM | Advanced Fuel Cycle Cost Basis, INL (2009) | |||
| Disposal | Packing Cost | Spent Fuel_UO2 | 718 | US$/kgHM | Ministry of Knowledge Economy 2012 | |
| HLW | 230,730 | US$/m3 | OECD/NEA (2006) | |||
| Geological disposal cost (Excavation) | 1384 | US$/m3 | OECD/NEA (2006) | |||
| PWR SF Transport | 76 | US$/kgHM | Hyundai Engineering Co. (2009), PWR SF Transport, Seoul, Korea | |||
| Waste Data | Unit volume for SF | 1.5 | m3/tHM | 1994 OECD-NEA | ||
| Unit volume of HLW from UOX Pyro | 0.115 | m3/tHM | Same as UOX PUREX | |||
| Unit volume of HLW from SFR Pyro | 0.033 | m3/tHM | no voloxidation/reduction process | |||
| Category | Unit Cost (US$/kWe, 2015 USD) | Remarks | |
|---|---|---|---|
| PWR | Capital cost | 4266 | Advanced Fuel Cycle Cost Basis, INL (2009) |
| O&M cost, D&D cost | 72 | ||
| Total | 4338 | ||
| SFR | Capita cost | 5032 | Advanced Fuel Cycle Cost Basis, INL (2009) |
| O&M cost, D&D cost | 77 | ||
| Total | 5109 | ||
| Category | Direct Disposal Cycle | Pyro-SFR Recycle |
|---|---|---|
| Reactor cost (mills/kWh) | 58.26 | 68.61 |
| Nuclear fuel cycle cost (mills/kWh) | 6.44 | 6.14 |
| Electricity generation cost (mills/kWh) | 64.70 | 74.75 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Jang, H.; Gao, R.; Kim, C.; Chung, Y.; Bang, S. Break-Even Point Analysis of Sodium-Cooled Fast Reactor Capital Investment Cost Comparing the Direct Disposal Option and Pyro-Sodium-Cooled Fast Reactor Nuclear Fuel Cycle Option in Korea. Sustainability 2017, 9, 1518. https://doi.org/10.3390/su9091518
Kim S, Jang H, Gao R, Kim C, Chung Y, Bang S. Break-Even Point Analysis of Sodium-Cooled Fast Reactor Capital Investment Cost Comparing the Direct Disposal Option and Pyro-Sodium-Cooled Fast Reactor Nuclear Fuel Cycle Option in Korea. Sustainability. 2017; 9(9):1518. https://doi.org/10.3390/su9091518
Chicago/Turabian StyleKim, Sungki, Hong Jang, Ruxing Gao, Chulmin Kim, Yanghon Chung, and Sungsig Bang. 2017. "Break-Even Point Analysis of Sodium-Cooled Fast Reactor Capital Investment Cost Comparing the Direct Disposal Option and Pyro-Sodium-Cooled Fast Reactor Nuclear Fuel Cycle Option in Korea" Sustainability 9, no. 9: 1518. https://doi.org/10.3390/su9091518





