A Combined Voltage Control Strategy for Fuel Cell
Abstract
:1. Introduction
2. Problem Formulation
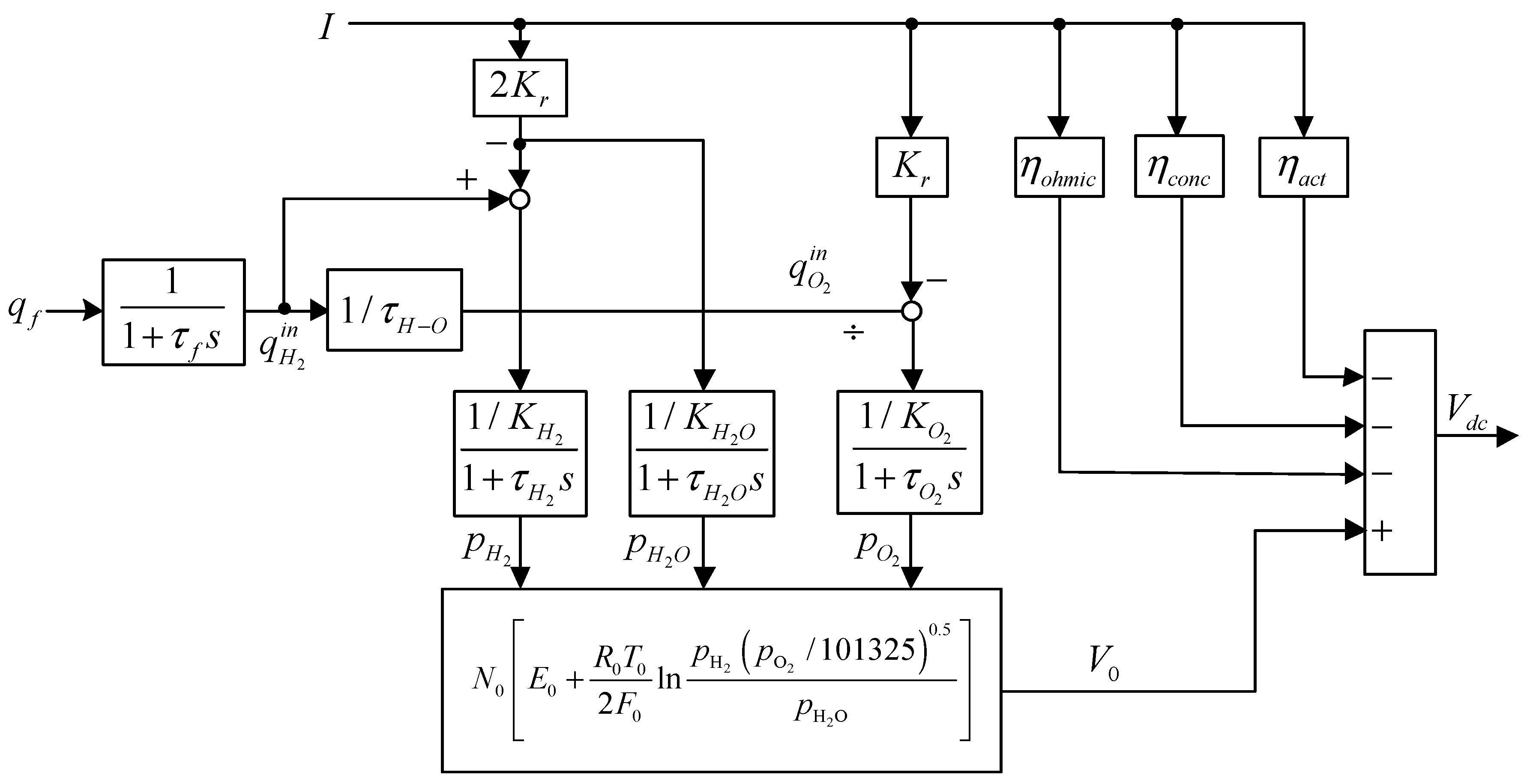
2.1. System Description
2.2. Control Difficulties
2.3. An Offset-Free MPC Solution
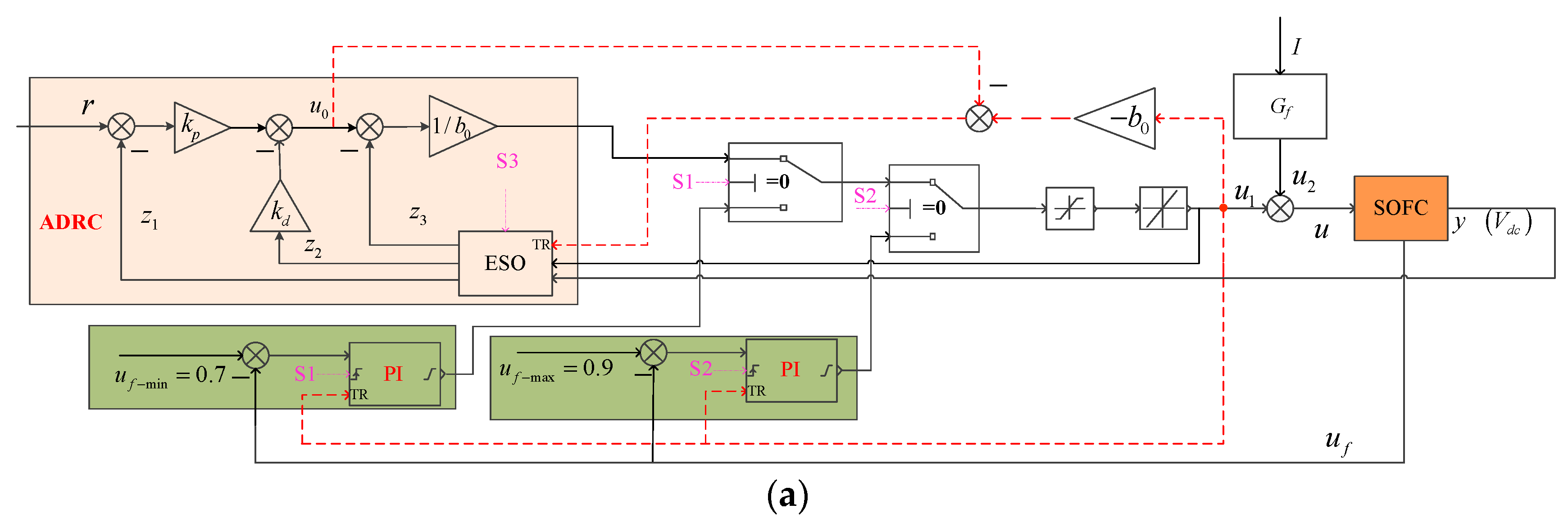
3. Combined Control Design
3.1. Fundamentals of ADRC
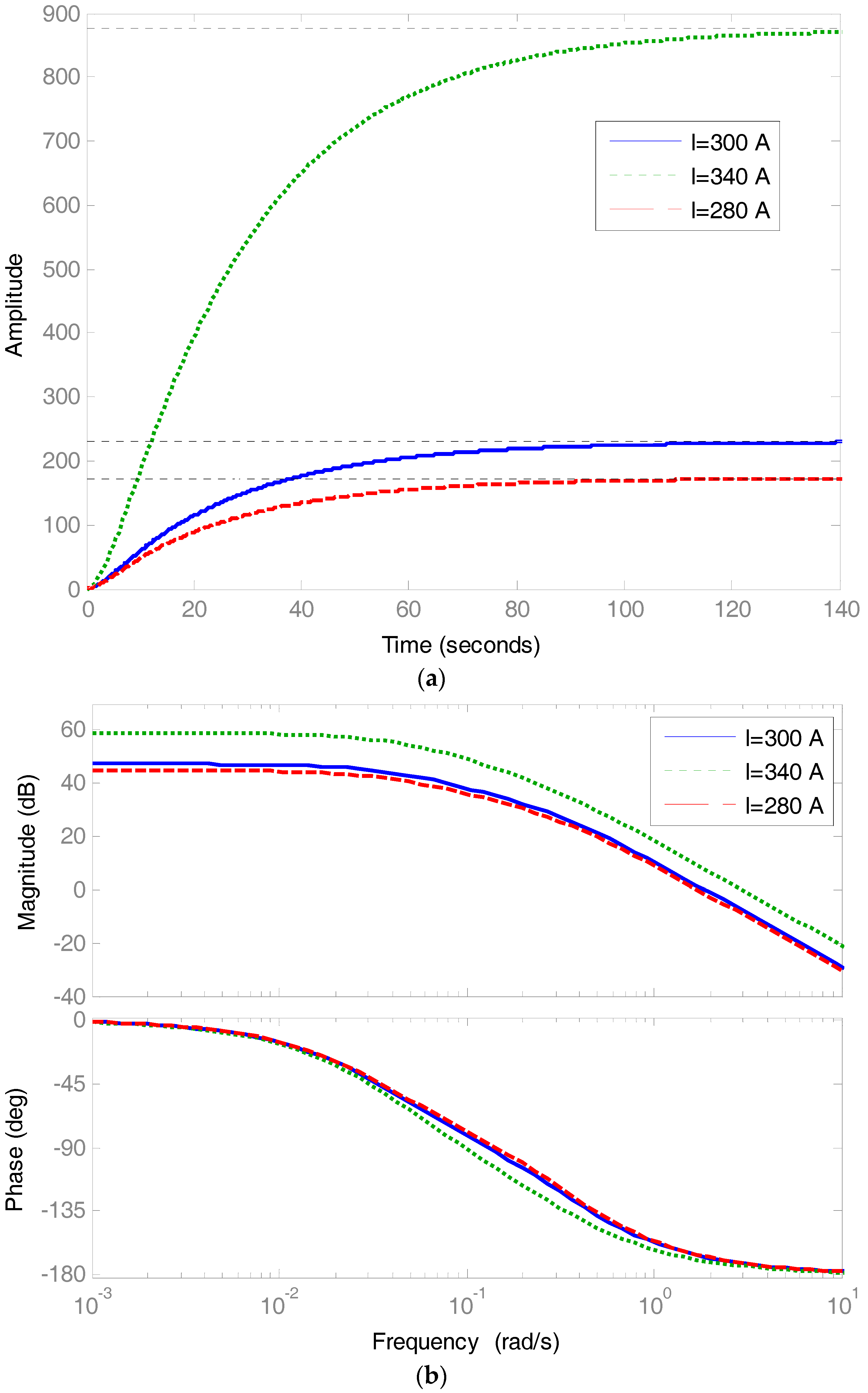
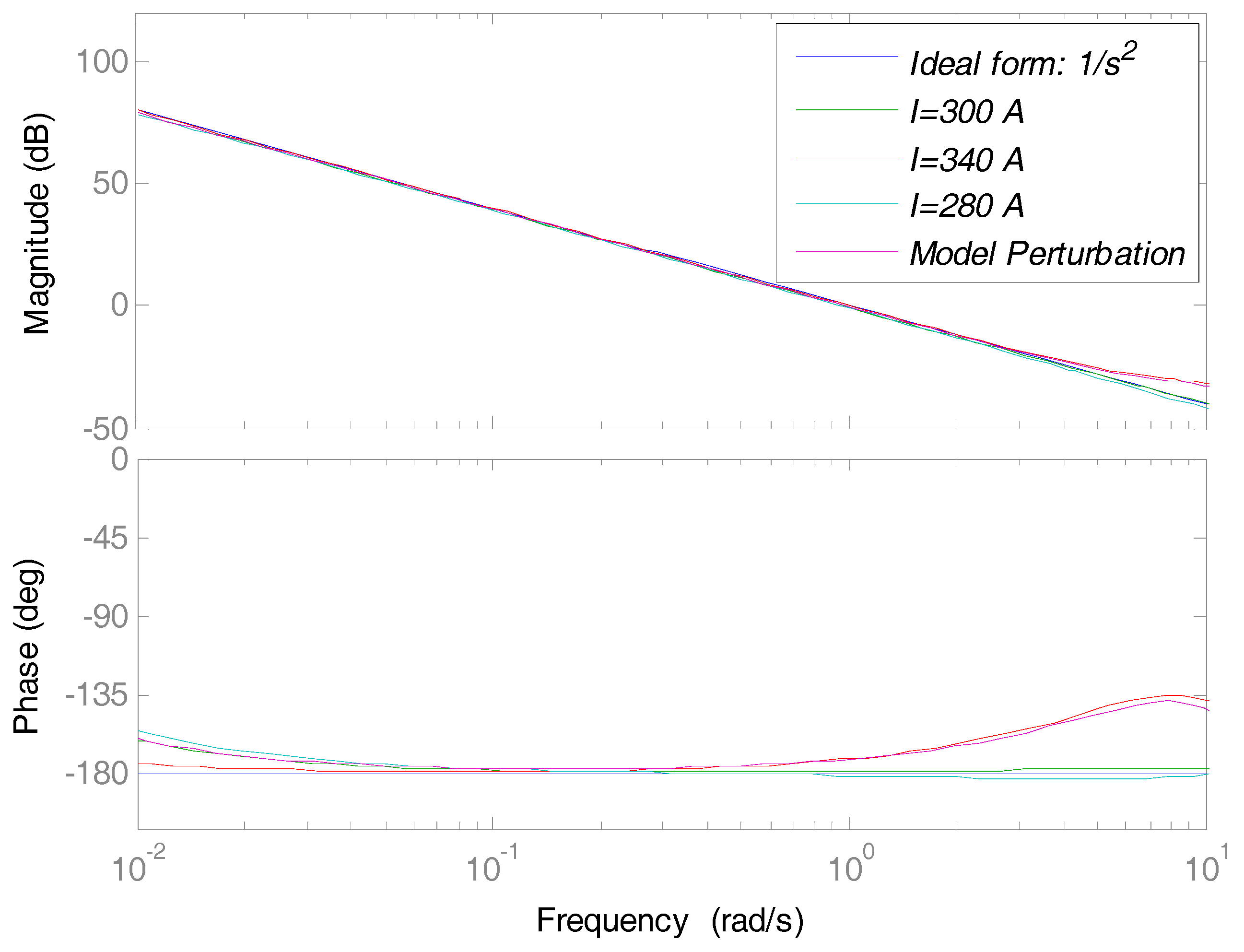
3.2. Parameter Tuning and Verification
3.3. The Comprehensive Control Strategy
- The rising command of the voltage requires the increment of the fuel feed, which would however decrease fuel utilization.
- The decreasing command of the voltage requires reducing the fuel feed, which would however increase fuel utilization.
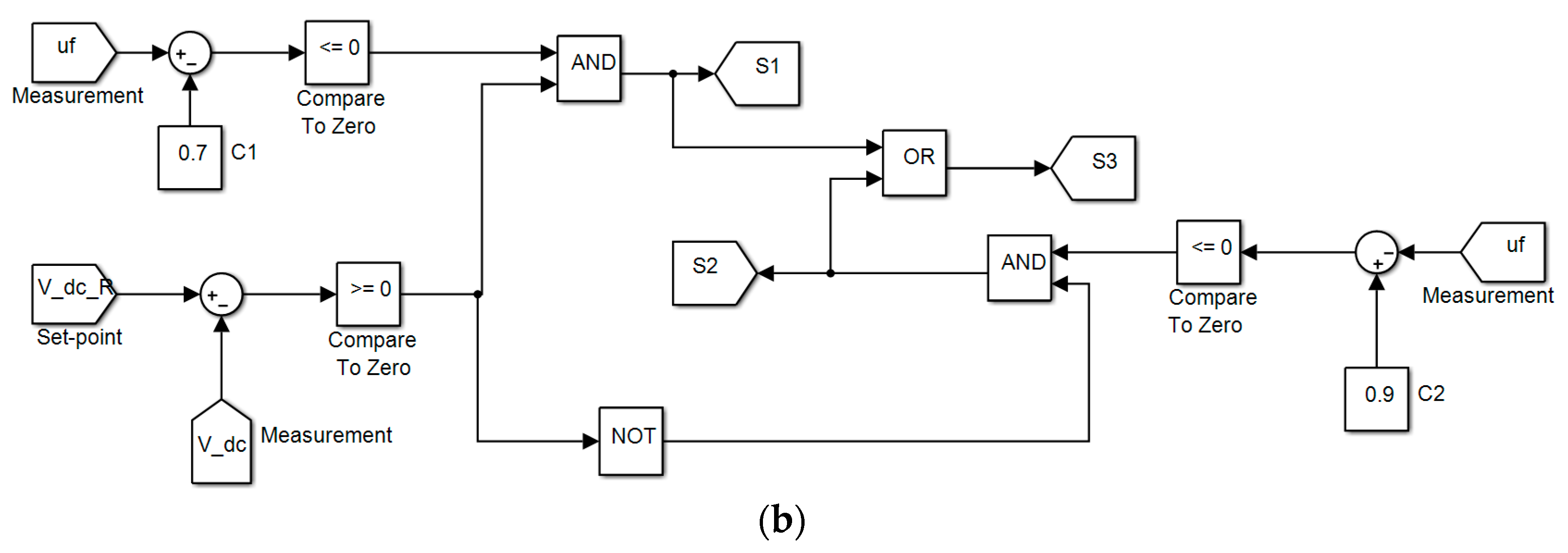
3.4. Bumpless Transfer
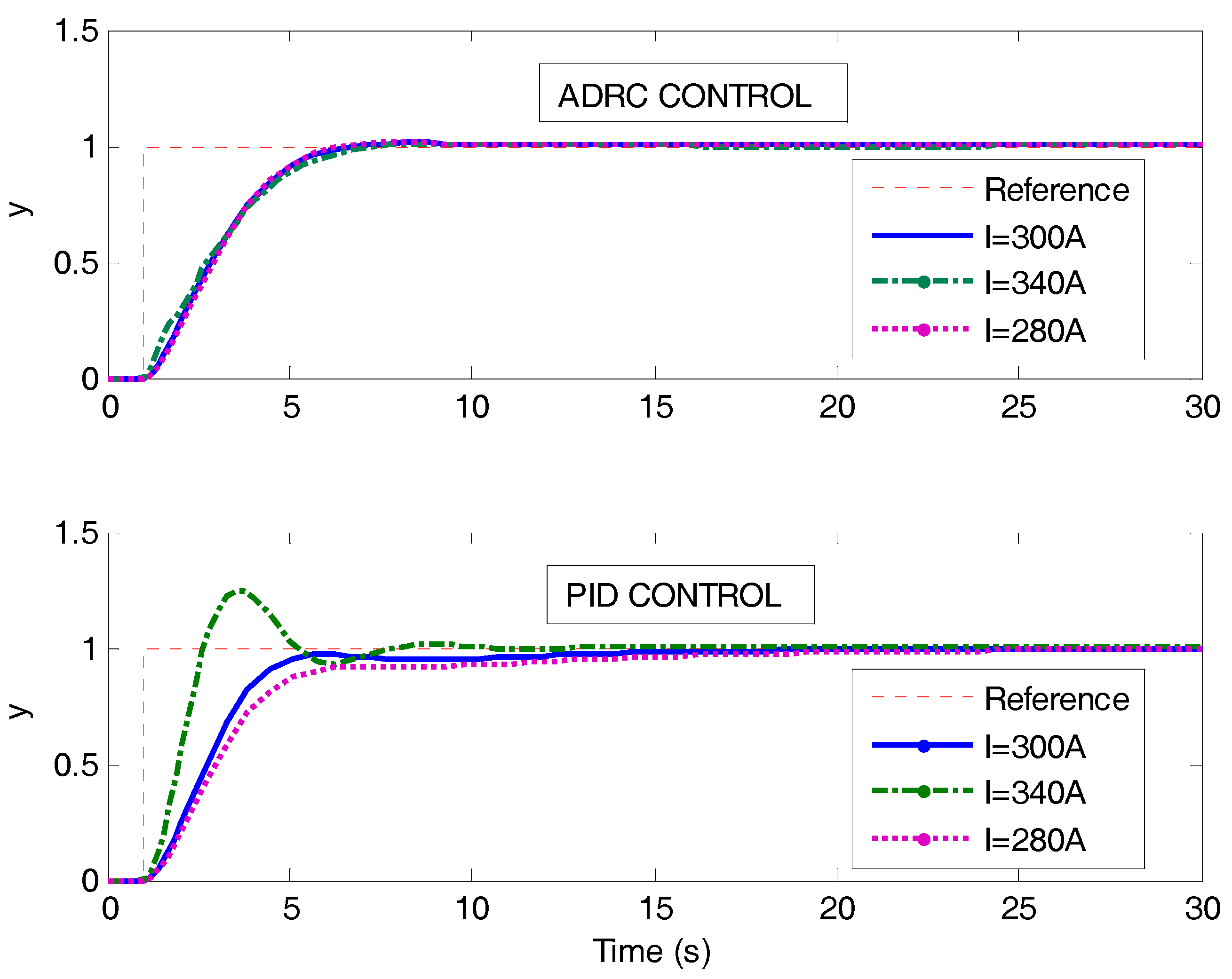
4. Comparative Simulation
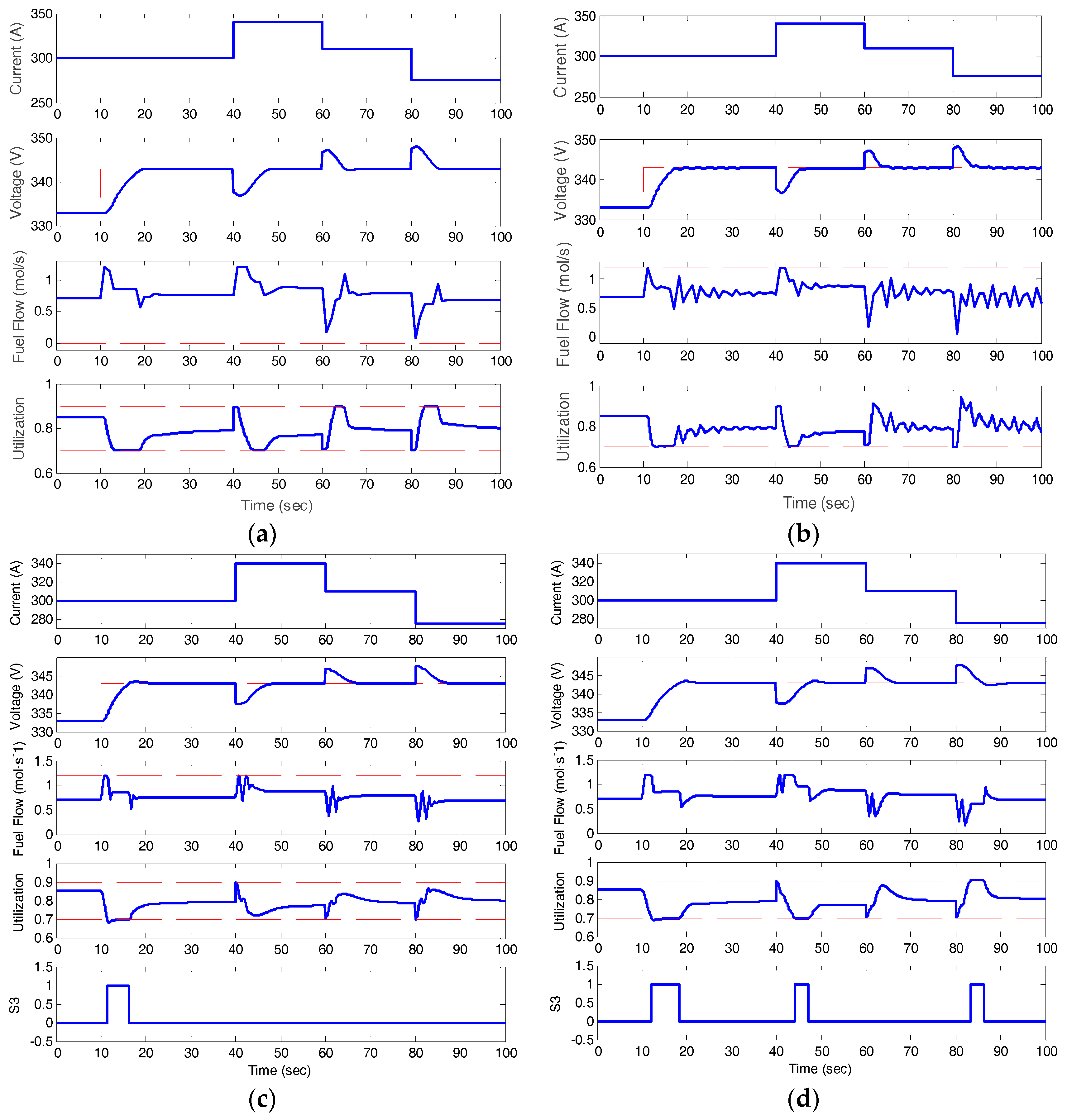
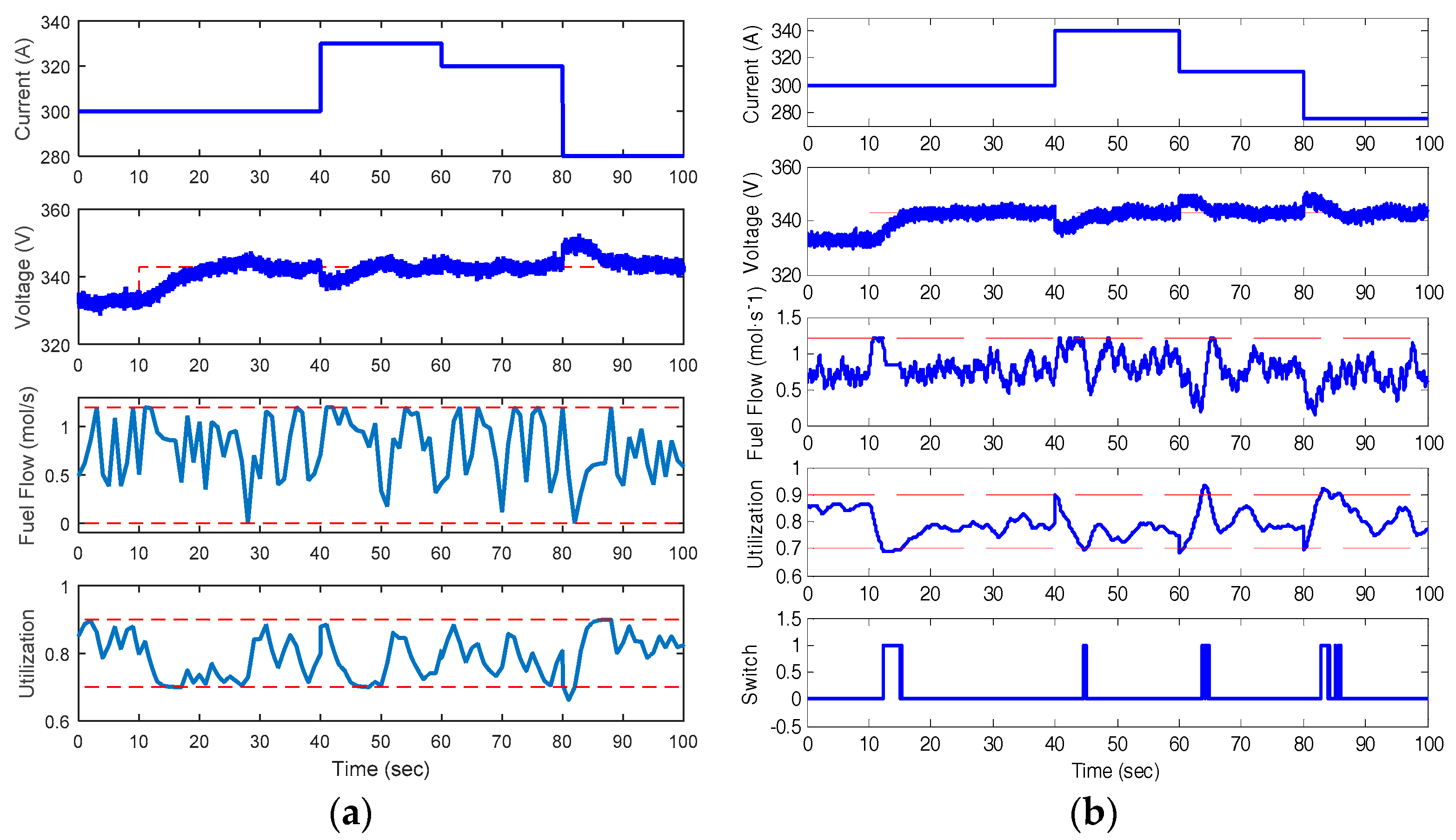
4.1. Simulation Results of MPC
4.2. Simulation Results of the Proposed Control
4.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cruz Rojas, A.; Lopez Lopez, G.; Gomez-Aguilar, J.; Alvarado, V.; Sandoval Torres, C. Control of the Air Supply Subsystem in a PEMFC with Balance of Plant Simulation. Sustainability 2017, 9, 73. [Google Scholar] [CrossRef]
- Suther, T.; Fung, A.; Koksal, M.; Zabihian, F. Macro level modeling of a tubular solid oxide fuel cell. Sustainability 2010, 2, 3549–3560. [Google Scholar] [CrossRef]
- Padulles, J.; Ault, G.W.; McDonald, J.R. An integrated SOFC plant dynamic model for power systems simulation. J. Power Sources 2000, 86, 495–500. [Google Scholar] [CrossRef]
- Li, Y.H.; Choi, S.S.; Rajakaruna, S. An analysis of the control and operation of a solid oxide fuel-cell power plant in an isolated system. IEEE Trans. Energy Convers. 2005, 20, 381–387. [Google Scholar] [CrossRef]
- Knyazkin, V.; Söder, L.; Canizares, C. Control challenges of fuel cell-driven distributed generation. In Proceedings of the 2003 IEEE Bologna Power Tech Conference Proceedings, Bologna, Italy, 23–26 June 2003; Volume 2, p. 2. [Google Scholar]
- Wang, X.; Huang, B.; Chen, T. Data-driven predictive control for solid oxide fuel cells. J. Process Control 2007, 17, 103–114. [Google Scholar] [CrossRef]
- Zhang, X.W.; Chan, S.H.; Ho, H.K.; Li, J.; Li, G.; Feng, Z. Nonlinear model predictive control based on the moving horizon state estimation for the solid oxide fuel cell. Int. J. Hydrog. Energy 2008, 33, 2355–2366. [Google Scholar] [CrossRef]
- Huo, H.B.; Zhu, X.J.; Hu, W.Q.; Tu, H.-Y.; Li, J.; Yang, J. Nonlinear model predictive control of SOFC based on a Hammerstein model. J. Power Sources 2008, 185, 338–344. [Google Scholar] [CrossRef]
- Wu, X.J.; Zhu, X.J.; Cao, G.Y.; Tu, H.-Y. Predictive control of SOFC based on a GA-RBF neural network model. J. Power Sources 2008, 179, 232–239. [Google Scholar] [CrossRef]
- Li, Y.; Shen, J.; Lu, J. Constrained model predictive control of a solid oxide fuel cell based on genetic optimization. J. Power Sources 2011, 196, 5873–5880. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Hierarchical optimization of boiler-turbine unit using fuzzy stable model predictive control. Control Eng. Pract. 2014, 30, 112–123. [Google Scholar] [CrossRef]
- Wade, H.L. Inverted decoupling: A neglected technique. ISA Trans. 1997, 36, 3–10. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.; Lee, K.Y. Optimal disturbance rejection for PI controller with constraints on relative delay margin. ISA Trans. 2016, 63, 103–111. [Google Scholar] [CrossRef] [PubMed]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Li, D.; Li, C.; Gao, Z.; Jin, Q. On active disturbance rejection in temperature regulation of the proton exchange membrane fuel cells. J. Power Sources 2015, 283, 452–463. [Google Scholar] [CrossRef]
- Huang, C.E.; Li, D.H.; Xue, Y. Active disturbance rejection control for the ALSTOM gasifier benchmark problem. Control Eng. Pract. 2013, 21, 556–564. [Google Scholar] [CrossRef]
- Liang, G.; Li, W.; Li, Z. Control of superheated steam temperature in large-capacity generation units based on active disturbance rejection method and distributed control system. Control Eng. Pract. 2013, 21, 268–285. [Google Scholar] [CrossRef]
- Li, D.; Li, Z.; Gao, Z.; Jin, Q. Active disturbance rejection-based high-precision temperature control of a semibatch emulsion polymerization reactor. Ind. Eng. Chem. Res. 2014, 53, 3210–3221. [Google Scholar] [CrossRef]
- Sun, L.; Dong, J.; Li, D.; Lee, K.Y. A practical multivariable control approach based on inverted decoupling and decentralized active disturbance rejection controller. Ind. Eng. Chem. Res. 2016, 55, 2008–2019. [Google Scholar] [CrossRef]
- Zheng, Q.; Chen, Z.; Gao, Z. A practical approach to disturbance decoupling control. Control Eng. Pract. 2009, 17, 1016–1025. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.H.; Gao, Z.; Yang, Z.; Zhao, S. Combined feedforward and model-assisted active disturbance rejection control for non-minimum phase system. ISA Trans. 2016, 64, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Guo, B.Z.; Zhou, H.C. The active disturbance rejection control to stabilization for multi-dimensional wave equation with boundary control matched disturbance. IEEE Trans. Autom. Control 2015, 60, 143–157. [Google Scholar] [CrossRef]
- Wu, G.; Sun, L.; Lee, K.Y. Disturbance rejection control of a fuel cell power plant in a grid-connected system. Control Eng. Pract. 2017, 60, 183–192. [Google Scholar] [CrossRef]
- Sun, L.; Wu, G.; Xue, Y.; Shen, J.; Li, D.; Lee, K.Y. Coordinated Control Strategies for SOFC Power Plant in a Microgrid. IEEE Trans. Energy Convers. 2017. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.; Wu, G.; Lee, K.Y.; Xue, Y. A Practical Compound Controller Design for Solid Oxide Fuel Cells. In Proceedings of the 9th IFAC Symposium on Control of Power and Energy Systems (CPES), Delhi, India, 9–11 December 2015; pp. 445–449. [Google Scholar]
- Sun, L.; Li, D.; Lee, K.Y. Enhanced decentralized PI control for fluidized bed combustor via advanced disturbance observer. Control Eng. Pract. 2015, 42, 128–139. [Google Scholar] [CrossRef]
- Schmid, C.; Biegler, L T. Quadratic programming methods for reduced hessian SQP. Comput. Chem. Eng. 1994, 18, 817–832. [Google Scholar] [CrossRef]
- Wang, L. Model predictive control: Design and implementation using MATLAB. In Proceedings of the 2009 American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 25–26. [Google Scholar]
- Li, M.; Li, D.; Wang, J.; Zhao, C. Active disturbance rejection control for fractional-order system. ISA Trans. 2013, 52, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Dong, J.; Li, D.H. Active disturbance rejection control for superheated steam boiler temperatures using the fruit fly algorithm. J. Tsinghua Univ. 2014, 54, 1288–1292. [Google Scholar]
- Zhang, Y.; Li, D.H.; Gao, Z.; Zheng, Q. On oscillation reduction in feedback control for processes with an uncertain dead time and internal-external disturbances. ISA Trans. 2015, 59, 29–38. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Li, D. Control design for the SISO system with the unknown order and the unknown relative degree. ISA Trans. 2014, 53, 858–872. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Gao, L.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar]
- Zhang, Y.; Li, D.; Xue, Y. Active disturbance rejection control for circulating fluidized bed boiler. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems (ICCAS), JeJu Island, Korea, 17–21 October 2012; pp. 1413–1418. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA—The Instrumentation, Systems, and Automation Society: Triangle Park, NC, USA, 2006. [Google Scholar]


| Parameter | Value | Unit | Representation |
|---|---|---|---|
| 1237 | Absolute temperature | ||
| 96,485 | Faraday’s constant | ||
| 8.314 | Universal gas constant | ||
| 1.18 | Ideal standard potential | ||
| 384 | Number of cells in series in the stack | ||
| 0.996 × 10−3 | Constant | ||
| 8.32 × 10−6 | Valve molar constant for hydrogen | ||
| 2.77 × 10−6 | Valve molar constant for water | ||
| 2.49 × 10−5 | Valve molar constant for oxygen | ||
| 26.1 | Response time of hydrogen flow | ||
| 78.3 | Response time of water flow | ||
| 2.91 | Response time of oxygen flow | ||
| 1.145 | Ratio of hydrogen to oxygen | ||
| 0.126 | Ohmic loss | ||
| 5 | Time constant of the fuel processor | ||
| 0.05 | Tafel constant | ||
| 0.11 | Tafel slope | ||
| 800 | Limiting current density |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Hua, Q.; Shen, J.; Xue, Y.; Li, D.; Lee, K.Y. A Combined Voltage Control Strategy for Fuel Cell. Sustainability 2017, 9, 1517. https://doi.org/10.3390/su9091517
Sun L, Hua Q, Shen J, Xue Y, Li D, Lee KY. A Combined Voltage Control Strategy for Fuel Cell. Sustainability. 2017; 9(9):1517. https://doi.org/10.3390/su9091517
Chicago/Turabian StyleSun, Li, Qingsong Hua, Jiong Shen, Yali Xue, Donghai Li, and Kwang Y. Lee. 2017. "A Combined Voltage Control Strategy for Fuel Cell" Sustainability 9, no. 9: 1517. https://doi.org/10.3390/su9091517
APA StyleSun, L., Hua, Q., Shen, J., Xue, Y., Li, D., & Lee, K. Y. (2017). A Combined Voltage Control Strategy for Fuel Cell. Sustainability, 9(9), 1517. https://doi.org/10.3390/su9091517








