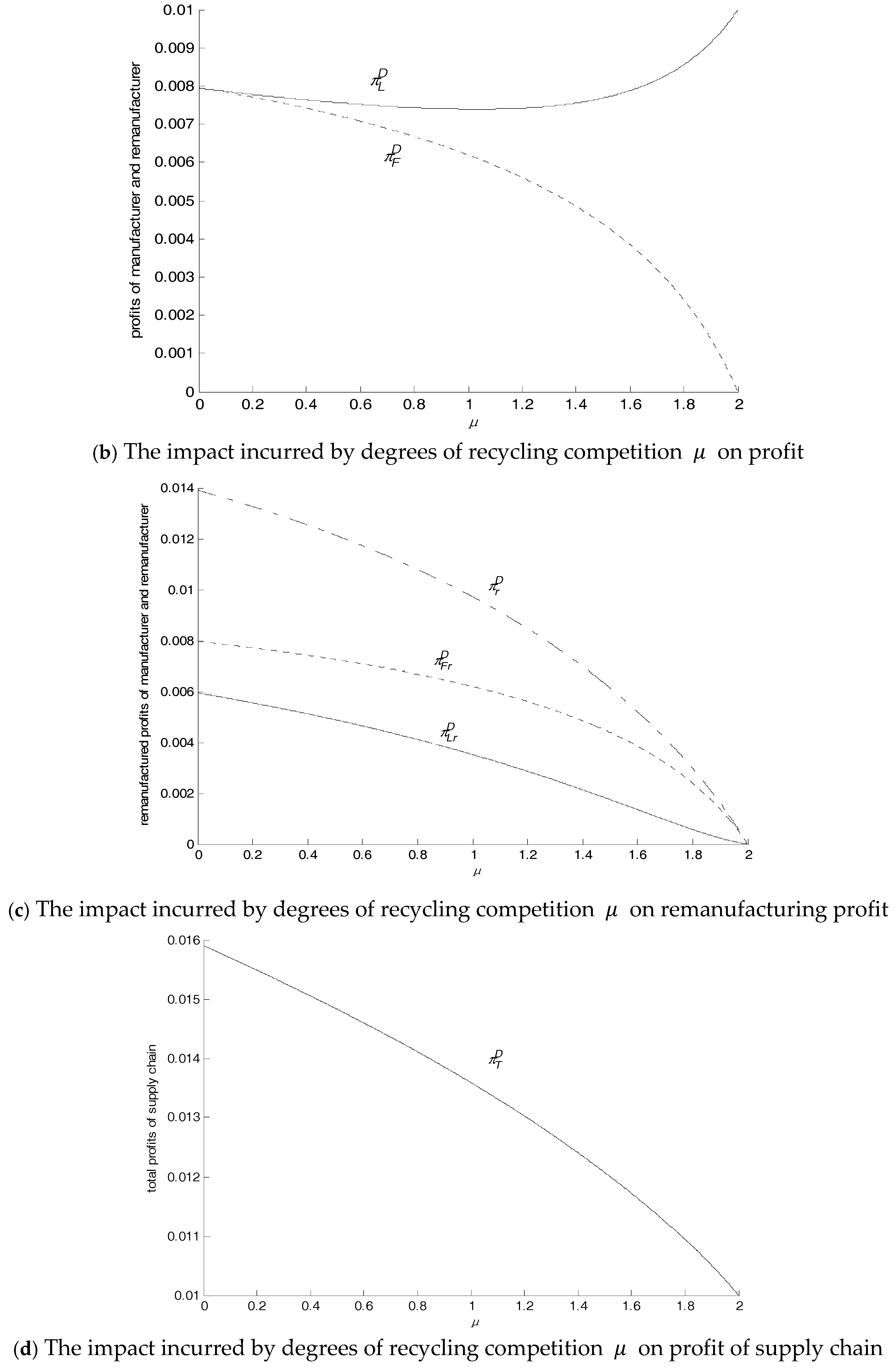1. Introduction
Remanufacturing is defined as a process of dismantling used products, whose components are repaired and then usedfor making new products. It is derived from repair; however, it is obviously different from repair or manufacturing [
1].
A number of researchers deployed principles of economics to investigate the remanufacturing supply chains, while some studies focused on how remanufacturing supply chain members chose channels and some on how channel structures could be optimized [
2,
3,
4,
5]. Nonetheless, some researchers centered on the optimization of operations in remanufacturing supply chains, and one example was that the system dynamics is applied to examining capacity planning in remanufacturing supply chains [
6,
7,
8,
9,
10].
Obviously, remanufacturing has captured growing attention in academia, and the advantage of remanufacturing is that remanufacturing can reduce resources consumption and production costs, contributing to the increasing attention on remanufacturing in terms of environmental and economic benefits. Therefore, a multitude of enterprises are likely to undertake remanufacture to satisfy the needs of consumers who pursue green consumption and respond to the relevant rules and regulations. Seeing the potential social, economic and environmental benefits of remanufacturing, nonlocal remanufacturers, with the advantage of their own technology and reputation, attempt to enter the local market to compete with local manufacturers. As a result, local enterprises face competition from remanufactured products by nonlocal remanufacturers in the market and the recycling market involved. For instance, Michelin Company started remanufacturing proactively when faced with competition from tire remanufacturers and produces new and remanufactured tires simultaneously to compete with other remanufacturers.
In reality, with advantages of remanufacturing technology, nonlocal remanufacturers are likely to enter the local remanufacturing market, if remanufacturing cost is relatively low or quality check is relatively strict. However, local manufacturers enjoy better brand equities among consumers. Generally, to respond to state policies and to enhance environmental benefits, local governments tend to subsidize remanufacturers to some extent to encourage enterprises to remanufacture.
Therefore, when there is one potential nonlocal remanufacturing competitor in the market, how can local manufacturers decide whether they engage in remanufacturing? Currently, the degrees of consumers’ acceptance of new and remanufactured products are inconsistent, while the degrees of accepting remanufactured products by local and nonlocal manufacturers do not conformeither. How do local and nonlocal manufacturers make decisions? What will happen when the government subsidies remanufacturing? When local and nonlocal remanufacturers are involved in remanufacturing, what is the competition in recycling market? When these problems are combined, how do market members respond? These are the research questions addressed by this article. In such supply chains, this study aims to explore how nonlocal and local manufacturers choose whether or not they recycle used products for remanufacturing. It is assumed that there is only one local manufacturer who makes new products and chooses whether to remanufacture and another nonlocal remanufacturer who considers whether to engage in the local market. At the same time, the recycling model is also considered, and the models are constructed to indicate four markets regarding whether local and nonlocal remanufacturers engage in remanufacturing. In addition, the correlations among the three production streams (brand-new products of local manufacturers, remanufactured products of nonlocal remanufacturers and remanufactured products of local manufacturers) are analyzed and profitabilityis derived with the four models. In addition, the impacts of government subsidies and of the degree of competition among enterprises that recycle products for these two manufacturers are discussed. Some concrete conclusions can be drawn from this study, which can provide some constructive suggestions for enterprises and governments in terms of policies and management.
The remainder of this article is organized as follows.
Section 2 of this article presents a review of the relevant literature. In
Section 3, fundamental problems are described and hypotheses are proposed, and the demand function of selling competition and the function of recycling quantity in recycling competition are provided.
Section 4 involves the solution and analysis of the four models. In
Section 5, profits in four market situations and the output of products are further compared and analyzed through numeric examples.
Section 6 concerns the conclusions and future research orientations.
2. Literature Review
Based on the research methods by Cerchioneand Esposito [
11], Centobelli et al. [
12] and Centobelli et al. [
13], the review of literature focuses on some fundamental concepts such as “remanufacturing”, “consumer willingness to pay”, “competition”, and“government subsidies”, to mention just a few. In the first part of the literature review, we present the relationship among remanufacturing supply chain members when consumer willingness to pay is considered. The second part involves the impact of competition in remanufacturing supply chains on their members, encompassing forward and reverse competition. The third part considers the effect of competition on supply chains when consumer willingness to pay is taken into account. In the fourth part, we investigate the influence of government subsidies on remanufacturing supply chains in the context of competition.
In the research on remanufacturing discussed in the introduction, the demand function involves the impact of price sensitivity coefficient on demand. Nevertheless, some researchers deploy consumer utility theory to investigate the demand changes brought by different degrees of consumer willingness to pay for new and remanufactured products and the gap between prices of the two. Ray et al. [
14] study durable goods involving two groups of consumers: new customers and trade-in customers, and pricing of remanufactured products and recyclingcosts. They show that durability of products, recycling profits, the degree of product depreciation and the scale of two types of consumers can have an effect on optimal pricing of recycled products. Debo and Wassenhove [
15] consider a gap betweenacceptabilityof new and remanufactured products, and it is important for manufacturers to determine the optimal price of new and remanufactured products and the enterprise’s level of remanufacturing when they are ready to remanufacture. More importantly, Abbey and Blackburn [
16] use experimentation to show that there are indeed two types of consumers: green consumers and consumers of new products in the market. They investigate how enterprises should determine the optimal price of new and remanufactured products by exploiting the theory of consumer effects in this type of market divisions. The result suggeststhat enterprises should increase the price of new products to offset cannibalization of remanufactured products in the market for new products.
The above studies are concerned with the impact of varying degrees of consumer willingness to pay for remanufactured products, whereas they fail to explore the effect of competition on remanufacturing supply chains. In terms of competition in remanufacturing system, Atasu et al. [
17] investigate the impact of green consumers and the product life cycle on remanufacturing profits when there is no competition and the manufacturer of brand-new products competes with the original manufacturers. Their results show that these factors can exert an enormous effect on remanufacturing profits; in the context of competition, remanufacturing can be an effective market strategy to suppress competition via prices. Based on product life cycle, Huang et al. [
18] examine product pricing and production strategy when manufacturers compete; competitors enter the market in the second cycle of products and compete with the original manufacturers of new products. Their results show that the original manufacturer should reduce the price of new products in two cycles, multiple cycles or infinite cycles so that there is sufficient volume of used products for recycling and remanufacturing in the second cycle to obtain competitive advantages via the low cost. In reality, there is competition among retailers. Savaskan and Van Wassenhove [
19] examine the manufacturer’s choice of recycling channels when there is competition among retailers. The manufacturer may choose to recycle alone or to delegate the retailer to recycle, and the result is that the profit of supply chain depends on recycling when the manufacturer recycles directly, while it depends on competition among retailers when the retailer recycles.
Östlin et al. [
20] list seven closed-loop structures of recycling used products in remanufacturing: ownership-based, service-contract, direct-order, deposit-based, credit-based, buy-back and voluntary-based relationships, and they discuss advantages and disadvantages of these seven recycling structures, in the hope that the research can enhance reader’s comprehension of remanufacturing close-loop supply chain. This demonstrates that the reverse supply chain plays a vital role in remanufacturing. However, the literature discussed above only focused on forward competition in closed-loop supply chains, while the reverse competition or recycling competition was not considered in the closed-loop supply chains. Jena and Sarmah [
21] explore how to determine the proportion of recycled products and the wholesale price of each manufacturer when the manufacturers are faced with selling and recycling competition. On this basis, they look at the competition between prices and services when random demand and random conditions of recycling products are added to the above structure [
22]. Bulmus et al. [
23] investigate the two-stage game model in which an original manufacturer and a remanufacturer compete in selling and recycling. In the first stage, the original manufacturer makes only new products; in the second stage, the remanufacturer engages in remanufacturing and competes with the original manufacturer in recycling and selling remanufactured products. The production strategy of the original manufacturer in the first period is thus examined. In addition, Wu [
24] examines the two-way competition between the original manufacturer and the remanufacturer, considering whether the manufacturer engages in remanufacturing and whether the remanufacturer enters the local market. Li and Li [
25] look at competition among multiple remanufacturers, and the quantity of recycled products by each remanufacturer depends on the price they offer, and thus remanufacturers compete in recycling. The study exploits the optimality theory and non-collaborative game theory and finds that the price at Nash equilibrium in competition is higher than incollaborative equilibrium. Chen and Chang [
26] examine competition and collaboration among original manufacturers and other supply chain members in remanufacturing supply chains when the random demand is considered. Their results show that original manufacturers are willing to remanufacture and collaborate with supply chain members when remanufacturing costs and the level of competition are lower. Otherwise, original manufacturers are more willing to make new products and remanufacture by introducing the third party, leading to competition.
However, the above studies did not integrate the impact of consumer willingness to pay on demand with competition. Hence, Li [
27] considers that with WTP as a premise, competition from nonlocal remanufacturers is introduced. In supply chains, the degree of consumer willingness to pay for products from two different manufacturers differs, while the willingness to pay for new and remanufactured products is identical. The result indicates that the original manufacturer can earn profits and also prevent the competitor from entering the market via remanufacturing. Based on the consumer willingness to pay, Guo et al. [
28] take the entry condition of remanufacturing for the original manufacturer into account when there is a gap between consumer awareness of new and remanufactured products, and introduce a remanufacturer as a competitor. They show that the market for new products can be squeezed if the original manufacturer gets into remanufacturing in certain conditions, whereas the low cost, the low price and a large quantity of remanufacturing can compensate for the loss caused by this squeezing. Likewise, based on consumer willingness to pay, Wu and Xiong [
29] investigate the two-stage model of competition among new and remanufactured products by the manufacturer and the remanufactured products (by the remanufacturer) when there is agap between consumer awareness about new and remanufactured products. They conclude that the manufacturer and the remanufacturer can have twelve choices based on remanufacturing cost, and involvement of the remanufacturer in remanufacturing can reduce the manufacturer’s profits, unless the manufacturer engages in remanufacturing. Nonetheless, when the production cost of new productsis extremely low, the manufacturer tends to choose not to remanufacture or to remanufacture partially, whereas the remanufacturer tends to choose recycled products and remanufacture completely.
The research below involves the impact of government subsidies on remanufacturing in the context of competition. Wang and Da [
30] investigate the impact of the mechanism of reward and punishment provides by the government on supply chains in which two manufacturers compete. One case is where one manufacturer chooses remanufacturing, and the other case is where two manufacturers are involved in remanufacturing. In the mechanism of reward and punishment, the recycle rate increases significantly and this effect is more apparent in competition; in this mechanism, the price of new products declines, which is conducive to consumers. Zhu and Zhou [
31] explore the influence of government subsidies on the supply chain system when manufacturers compete with remanufacturers in the industry of automobile parts, and they claim that government subsidies can facilitate the remanufacturing development effectively and boost remanufacturers’ earnings. Gong et al. [
32] consider closed-loop supply chain system consisting of one manufacturer, one retailer, and one recycling agent. The retailer sells and recycles products, and competes with the recycle agent who is not involved in sales. The results show that, in the context of recycling competition, the government subsidy increases the retailer’s and the recycling agent’s recycling volume, the recycling cost and the manufacturer’s, the retailer’s and the recycling agent’s profits.
The above literature has investigated the impact of WTP, forward competition, reverse competition and government subsidy on remanufacturing supply chains respectively (merely some studies integrate WTP with competition, and some research incorporates government subsidies with competition) but have failed to consider all the factors in one study. In comparison with the literature above, this article considers that: (1) Consumer willingness to pay for new and remanufactured products varies, and the willingness to pay for products of two enterprises differs. In other words, three types of heterogeneous demand streams are considered. (2) The competition for forward sales is generated because consumer willingness to pay is different, while this study considers recycling competition, namely reverse competition, when the local and nonlocal manufacturers engage in remanufacturing.
This study considers that consumer willingness to pay for new and remanufactured products varies, and also looks at consumer willingness to pay for different brands (local and nonlocal brands) which differs too. It comprehensively investigates the forward and reverse competition in the closed-loop supply chains. It explores four models regarding the impact of the production cost of new and remanufactured products, the coefficient of consumer willingness to pay, the coefficient of recycling competition and the government subsidy output and profits in terms of whether the local and nonlocal manufacturers engage in remanufacturing. Consequently, as opposed to the findings discussed above, this study comprehensively considers the forward and reverse competition in remanufacturing supply chains and differing consumer willingness to pay and other factors, resulting in more complex and intriguing findings through comparative analyses. This study can serve as a complement for the theory of remanufacturing and shed some light on the enterprises making relevant decisions.
4. Model Analysis
According to the strategy choice concerning whether the local manufacturer engages in remanufacturing in the market and whether the nonlocal remanufacturer involves remanufacturing in the local market, this study considers four models as follows: Models A–D.
Model A: When the nonlocal remanufacturer does not become involved in the local market, both nonlocal and local manufacturers do not engage in remanufacturing, and hence there are only new products from the local manufacturer.
Model B: When the nonlocal remanufacturer does not enter the local market and the local manufacturer engages in remanufacturing and gets government subsidy, there are two types of products in the market. The market is still dominated by the local manufacturer.
Model C: When the nonlocal remanufacturer recycles old products for remanufacturing and gets government subsidy, the local manufacturer does not remanufacture. Now, there are two types of products from two enterprises in the market, and the remanufactured products from the nonlocal remanufacturer compete with new products from thelocal manufacturer.
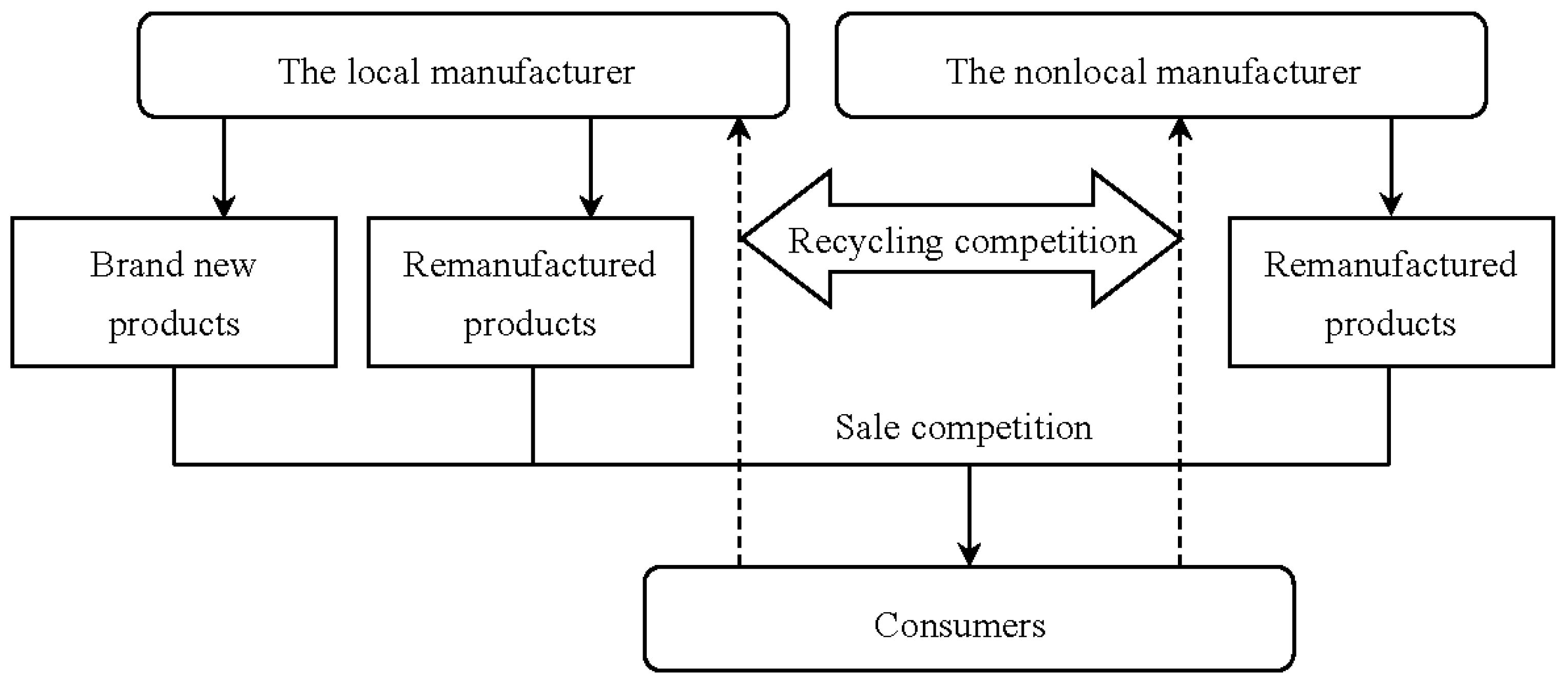
Model D: When the nonlocal remanufacturer enters the local market and the local manufacturer is involved in remanufacturing, both get government subsidy. Three types of products compete in the market. In addition, in Model D, the local manufacturer and nonlocal remanufacturer compete in recycling, and the recycling quantity is determined by their own recycling pricing and the consumer’s sensitivity to recycling price and the coefficient of recycling competition between the two enterprises. The structure of the closed-loop supply chain in Model D is shown in
Figure 1, and the structure of supply chains in other models can be understood by deletion based on
Figure 1.
4.1. Demand Function
It is assumed that the consumer scale in the market is 1, and each consumer can purchase only one product in each period, and the willingness to pay is assumed to be
, which is subject to uniform distribution
([
17,
29]). The utility varies when consumers purchase brand-new and remanufactured products of different brands. Here, the proof of the demand function in four different competition situations is presented.
In Model A, there is only one type of product: a new product by the local manufacturer, and thus the utility that the consumer buys this type of product is:
. Consumers have two choices: to buy or not to buy. The lowest willingness to buy is the critical point of buying or not buying, and the quantity is:
. The consumers’ utility at this critical point of buying or not buying is the same:
. As a result, the inverse demand function is:
In Model B, the market is dominated by the local manufacturer, while new products by the local manufacturer compete with remanufactured products internally. Consumers have three choices in this circumstance: they buy brand new products or remanufactured products or they do not buy products. The lowest consumer willingness to pay for brand new products is located at the critical point of buying brand new products and buying remanufactured products, and hence the purchasing quantity is:
, and their utility is the same as that of buying remanufactured products:
, and
is derived. The lowest consumer willingness to pay for remanufactured products is located at the critical point of not buying:
, and hence their utility is the same as that of not buying:
. To sum up, the inverse demand function is:
The circumstances in Model C are similar to those in Model B. In this mode, two products compete with each other. Remanufactured products are made not by the local manufacturer but by the nonlocal remanufacturer. Therefore, asimilar inverse demand function is as follows.
The circumstance of Model D is the most complicated, but the inferences of the inverse demand function are similar. In this circumstance, three products compete in the market. Consumers have four choices: they buy brand new products; they buy remanufactured products by the localmanufacturer; they buy remanufactured products by the nonlocal remanufacturer, and they do not buy. The lowest consumer willingness to pay for brand new products is located at the critical point of buying remanufactured products by the local manufacturer, and hence their utility is the same as that of buying the local remanufactured products.
can be derived. The lowest consumer willingness to pay for local remanufactured products is located at the critical point of buying nonlocal remanufactured products, and hence their utility is the same as that of buying nonlocal remanufactured products:
. Finally, the lowest consumer willingness to pay for nonlocal remanufactured products is located at the critical point of not buying products, and hence their utility is the same as that of not buying products:
. Below is the inverse demand function in this circumstance.
4.2. Function of Recycling Quantity
According to the description and proof [
25], if there is competition in the recycling market, the recycling quantity function has to satisfy the following hypotheses. Firstly, the recycling quantity increases with a rise in recycle price but decreases with a rise in competitors’ recycling price. Secondly, the ratio between the flexibility of recycle price and recycle price diminishes singly as regards recycle price but increases singly as regards competitors’ recycle price. Thirdly, the sum of all impacts of all recycle price on flexibility is less than or equal to the absolute flexibility. Assumption 6 shows that there are indefinite numbers of recyclable products in the market, and hence in Model D, the recycling quantity function can be expressed as below.
Here,
is the consumer sensitivity to price of recycled products, and
is the competition coefficient of recycle price. According to the proof [
25],
is required.
In Models B and C, there is no competition in recycling, with competition coefficients of
is 0, and thus the recycling quantity function is as follows.
4.3. Model A
In this model, the nonlocal manufacturer does not involve in the local market, and the local manufacturer does not engage in remanufacturing. This model serves as a reference, and there is neither remanufacturing nor recycling. As a result, the profit function of the local manufacturer is as below.
Together with the description of model A, the decision of Model A can be expressed in Equation (1) below:
Equation (1) is a concave function, and Conclusion 1 is drawn from the first-order condition.
Conclusion 1. In Model A, when the local manufacturer maximizes the profit, the output and pricing of brand-new products is:Below are the profits.
4.4. Model B
According to the setting of Model B, when the nonlocal remanufacturer does not involve in the local market, the local manufacturer remanufactures and recycles used products and obtains the government subsidy for remanufacturing. The profit function of the local manufacturer is:
In the profit function, the first part is the revenue of the brand-new product, and the second part is the revenue of remanufactured products.
The model shows that it is not necessary for the manufacturer to recycle old products which are not remanufactured, because extra recycling expenses are incurred but the manufacturer does not make profits. Hence, it is assumed that the enterprise remanufactures all recycled old products, and obtains not only sales profits but also government subsidy, namely, .
Therefore, based on the assumption, the inverse demand function and the recycling quantity function above, the decision of Model B is expressed in Equation (2) as below.
Equation (2) is the strict concave function of and , and there is only one maximal value. Thus, Conclusion 2 is drawn.
Conclusion 2. In Model B, when the profit of the local manufacturer is maximal, the output of new and remanufactured products is:
Now, if
, then it is necessary for the cost of new product to satisfy the following condition.
Next, for convenience, we assume:
It is clear from the above analysis that, when the production cost of the new product is , the local manufacturer is willing to remanufacture. In addition, when the production cost of the new product reaches a certain degree and exceeds , the local manufacturer will stop making new products.
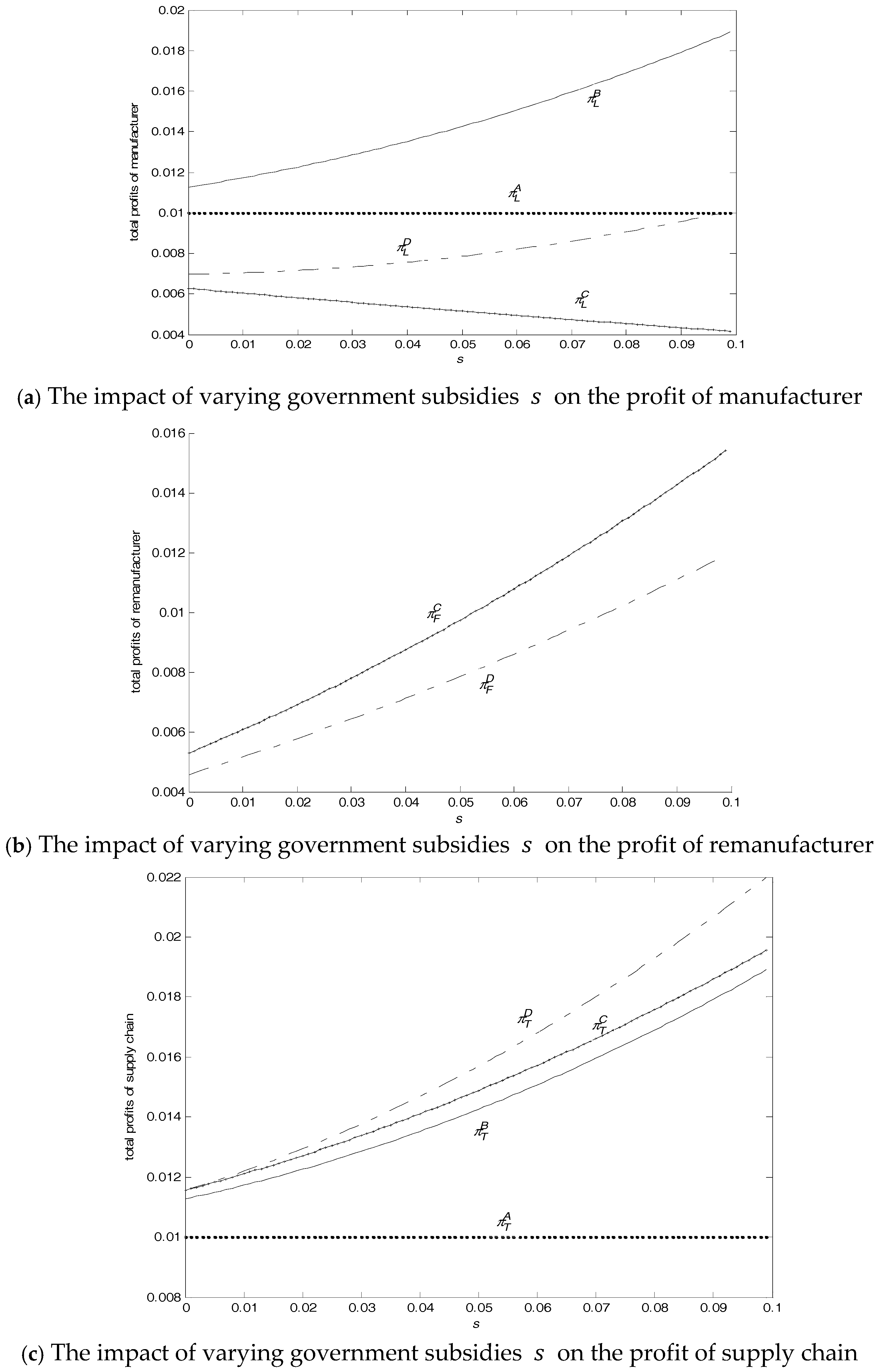
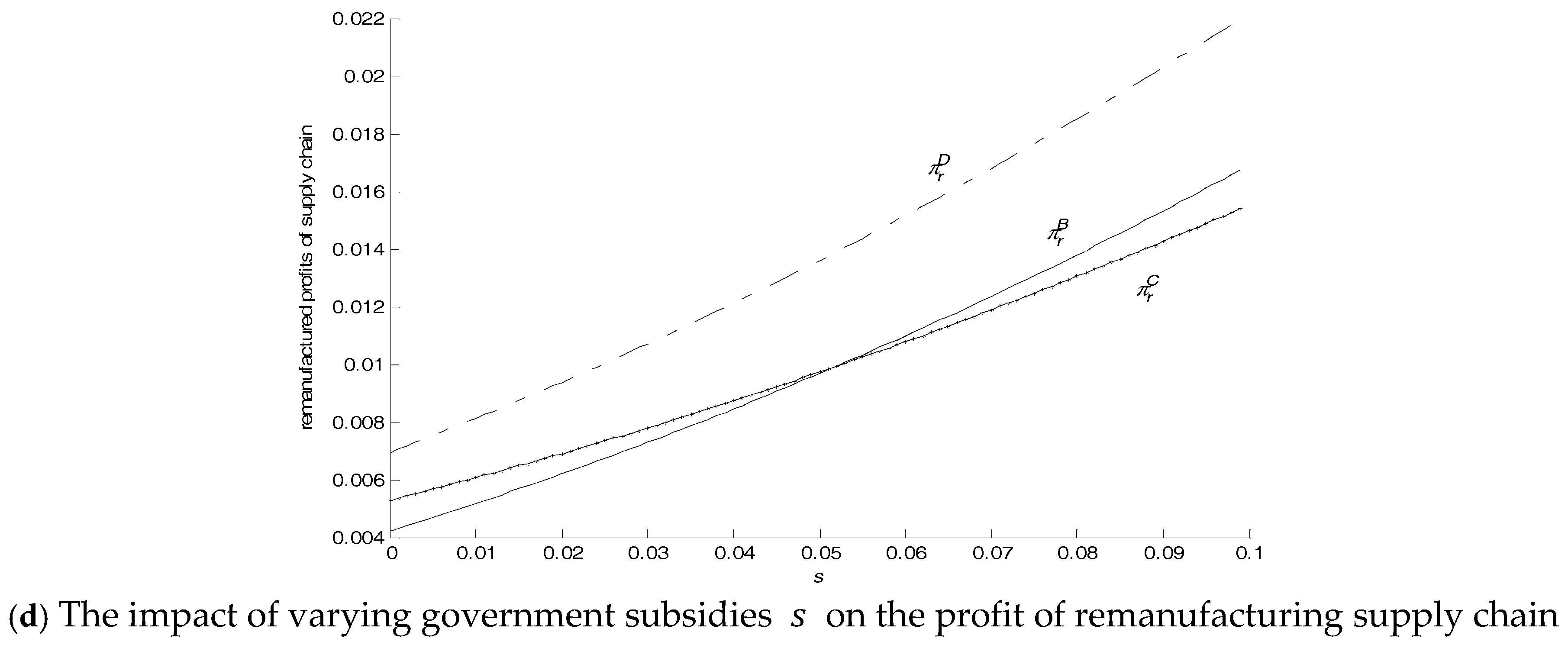
As , it is clear that when the government subsidizes remanufacturing, the value of declines, thus lowering the constraint for the local manufacturer to engage in remanufacturing. As such, the government subsidy boosts remanufacturing to some extent. In terms of , enterprises are more likely to stop making brand new products due to the government subsidy.
Certainly, when the cost of making brand-new products is less than (actually, it only necessarily amounts to ), the local manufacturer will not choose to remanufacture. This is identical to the case in Model A. Alternatively, if the consumer acceptance of the remanufactured products by the local manufacturer satisfies a certain condition, then the local manufacturer will think of remanufacturing.
The pricing of new and remanufactured products and the recycling cost can be derived in Model B from the conclusions above.
In addition, the maximal profit of the local manufacturer can be derived in Model B as follows.
4.5. Model C
In this model, the local manufacturer does not engage in remanufacturing, whereas the nonlocal remanufacturer is involved in remanufacturing for the local market and isobtaining government subsidy. As a result, in this model, the profit function of the local manufacturer is:
The profit function of nonlocal remanufacturers is as below.
Similarly, it is clear that the nonlocal remanufacturer will not recycle redundant old products according to the profit function of the nonlocal remanufacturer. The remanufacturer spends more on recycling and cannot obtain the reward, and therefore, is derived likewise.
Next, in the light of the function solved above, the decision of Model C can be made, as shown in Equation (3).
In Equation (3), the profit function of the two enterprises has the unique maximal value, and Conclusion 3 is drawn.
Conclusion 3. In Model C, to maximize their own profits, the local manufacturer and the nonlocal remanufacturer each determine the output of their respective products. If
, production cost of new productsmust satisfy the following condition.
Likewise, for convenience, we assume:
It is clear from the above condition that the government subsidy can also promote remanufacturing, lowering the constraints on enterprises involved in remanufacturing. In addition, the local manufacturer does not remanufacture, and thus declines because of the higher government subsidy. The local manufacturer is more likely to be squeezed by the nonlocal remanufacturer (). Now, since the production cost of brand new products is less than (actually it only needs to be equal), the nonlocal remanufacturer will not engage in remanufacturing in the local market. Here, the circumstance is consistent with that in Model A. Alternatively, if the consumer acceptance of the remanufactured products by the nonlocal manufacturer satisfies a certain condition, then the nonlocal remanufacturer will choose to enter the local market.
The pricing of new and remanufactured products and recycling price of nonlocal remanufactured products can be obtained from Conclusion 3.
The expression of the optimal profit of the two enterprises in this model is relatively complicated, and therefore it is not listed here. Details can be found in
Appendix B.
4.6. Model D
In this model, the nonlocal remanufacturer enters the local market and engages in remanufacturing. The local manufacturer is also involved in remanufacturing when the government subsidizes remanufacturing. In other words, the local manufacturer not only makes new products but also remanufactures. In addition, the local manufacturer and the nonlocal remanufacturer compete in recycling used products. In the market, now three products compete.
Hence, in this model, profit functions of the local manufacturer and the nonlocal remanufacturer are as follows.
This analysis shows that it is unnecessary for the two enterprises to recycle used products. Likewise, it is assumed that
and
. Based on the statements above, the decision of this model can be expressed in Equation (4).
Solving Equation (4), Conclusion 4 is drawn.
Conclusion 4. In this model, to maximize the profits, optimal results of the output of new products and remanufactured products by the local manufacturer and the nonlocal remanufacturer are as below.in which Now, to satisfy
, below is the condition that needs to be satisfied for the production cost of new products.
For convenience, the value of
is expressed by the result.
According to the range of , government subsidy can boost remanufacturing, and each enterprise can meet the requirements of engaging in remanufacturing. Additionally, within the range of cost of new products, it is noticeable that, when , some enterprises may choose not to remanufacture, and the circumstance is consistent with that in Models B and C. Likewise, when , the local manufacturer and nonlocal remanufacturer are not involved in remanufacturing, and the circumstance is the same as that in Model A.
Summarizing the conditions for the manufacturer to engage in remanufacturing from the above models, from an alternative perspective, if each enterprise is involved in remanufacturing, how does the remanufacturing cost vary according to the government subsidy? With the rise in government subsidy, the upper limit on and becomes higher. In other words, the loose constraint on remanufacturing makes remanufacturing profitable for enterprises.
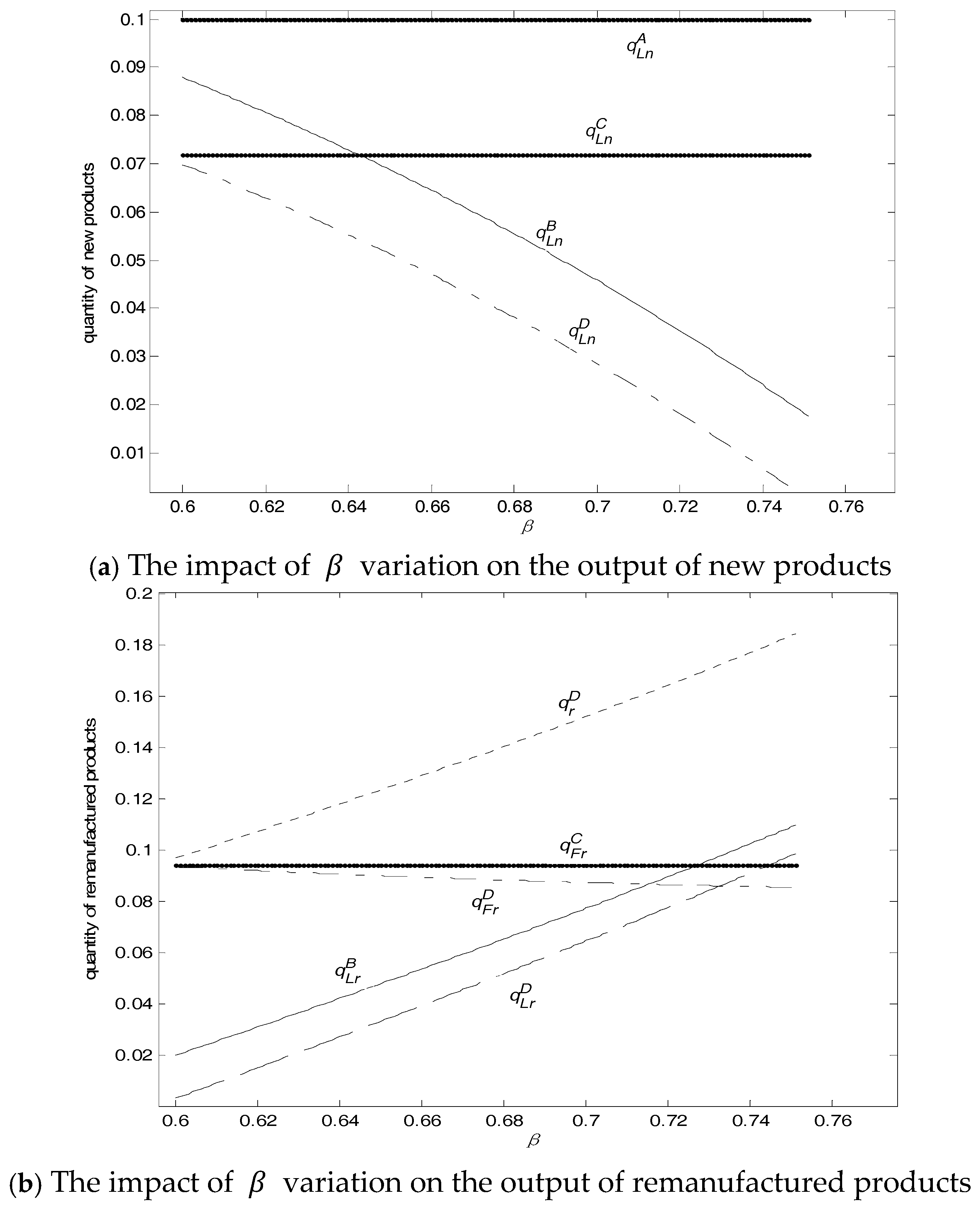
The expressions of the profit and price are complicated in Model D, and they are not listed here. In the four models, the profits of each enterprise, the output of remanufactured products of each enterprise, and the comparison of remanufacturing profit and the output of new products are analyzed in the following numeric examples due to the complexity of the results.
4.7. Some Corollaries
Before analyses of the numeric examples, calculations in
Section 4 can produce some corollaries. Nevertheless, the profits in Model D and the price expressions are too complex, which is not convenient for comparison. Hence, comparison and analyses are further provided after assignment.
Corollary 1. .
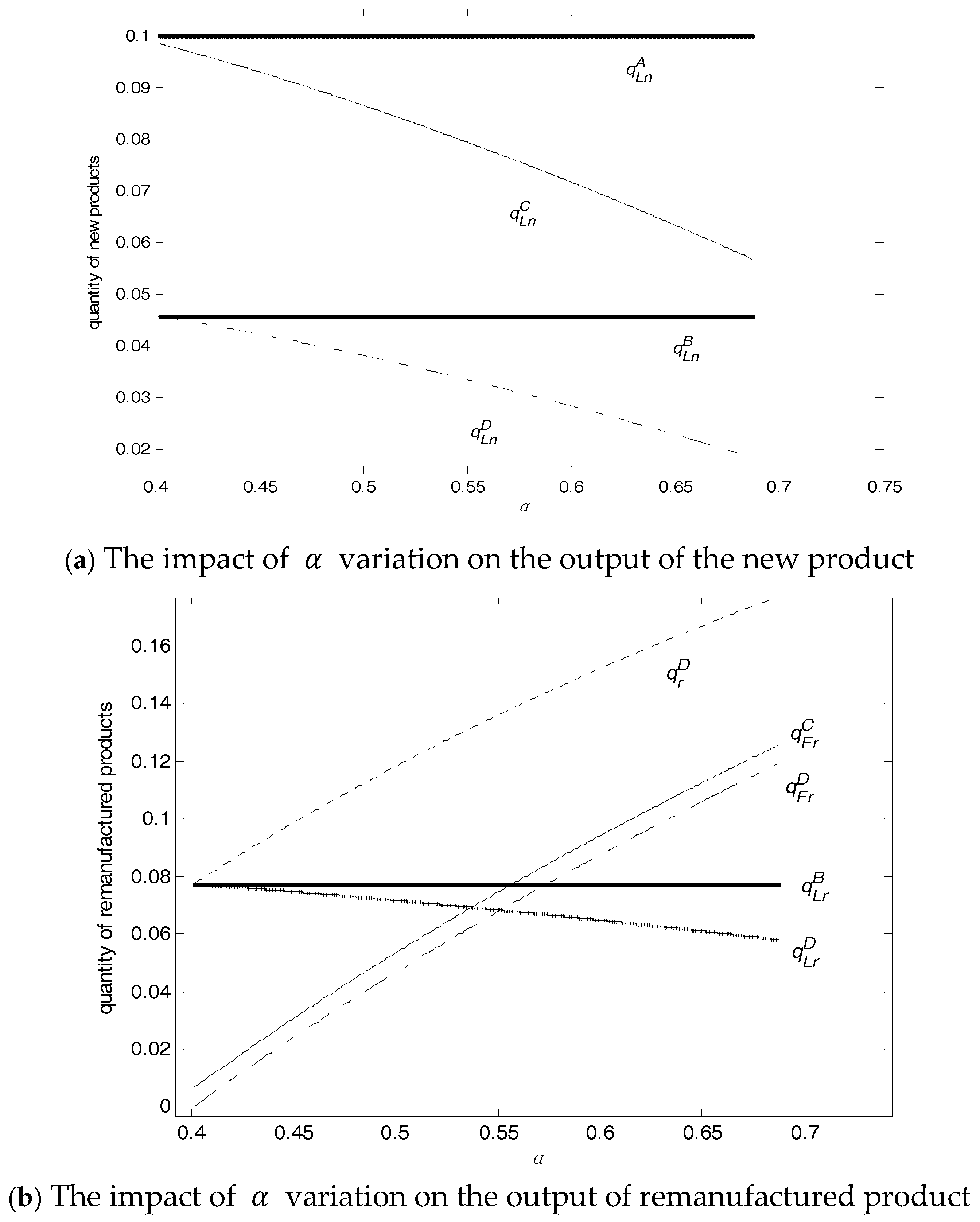
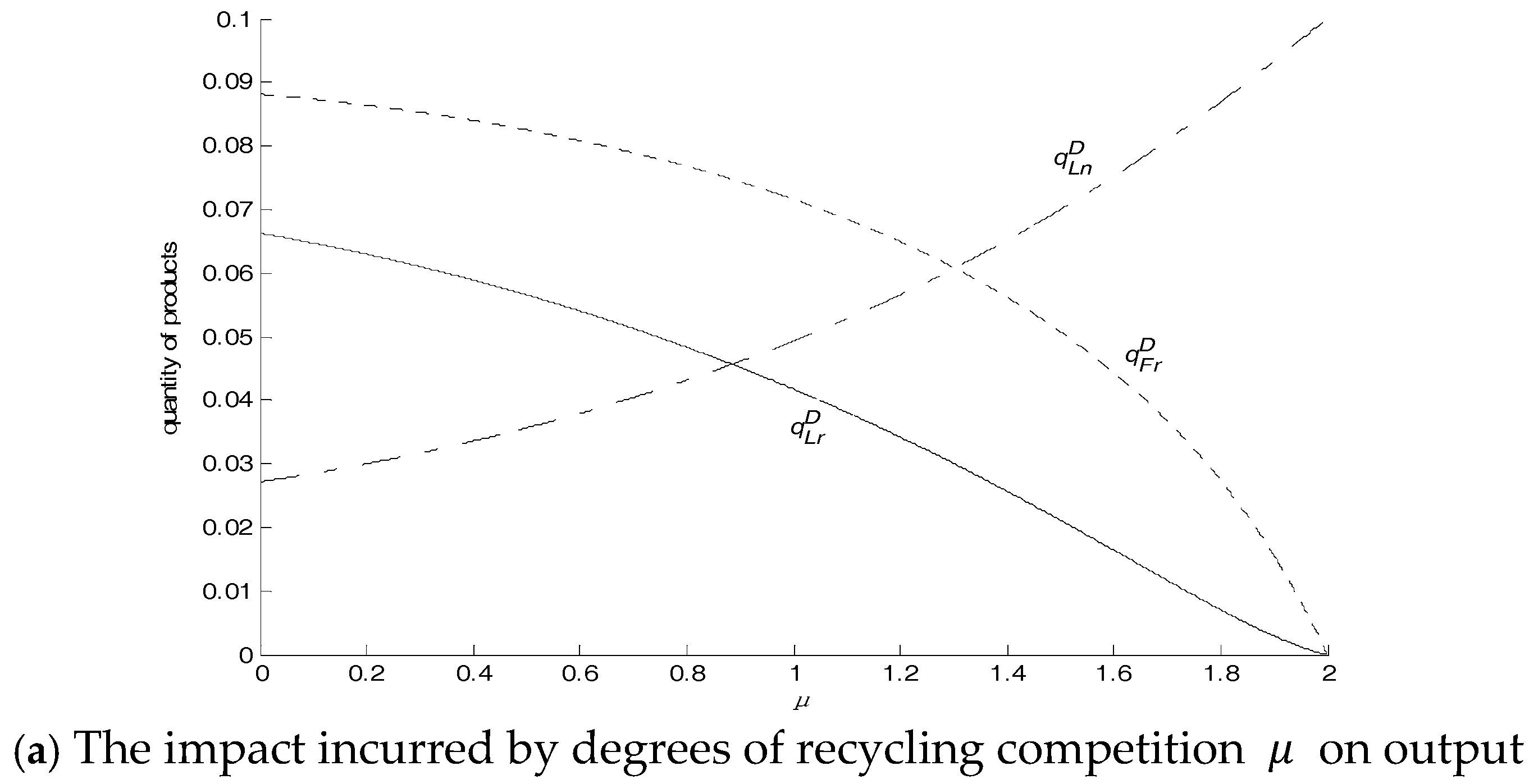
When the local manufacturer remanufactures, remanufactured products cannibalize and compete with new products in the market, leading to a decline in the output of new products. When only the nonlocal manufacturer remanufactures, remanufactured products produced by the nonlocal manufacturer will compete with brand-new products by the local manufacturer, thereby squeezing the market of brand-new products by the local manufacturer. Meanwhile, in Model D, according to , the output of new products by the local manufacturer is squeezed by remanufactured products both fromthe local manufacturer and nonlocalremanufacturer. Therefore, the output of new products declines further.
Corollary 2. .
Without competition, regardless of whether the local manufacturer is involved in remanufacturing, the pricing of new products is fixed. Conversely, when the local manufacturer is squeezed by the nonlocal remanufacturer, the local manufacturer wants to attract consumers through a lower price. However, the cost of new products cannot be advantageous to the remanufacturing cost of the nonlocal remanufacturer. Ultimately, the market is cannibalized by the nonlocal remanufacturer. Thus, in this circumstance, the local manufacturer is at a disadvantage and should avoid remanufacturing. When the nonlocal remanufacturer enters the market, the local manufacturer should take measures instead of being indifferent. For example, the local manufacturer can get involved in remanufacturing and compete with the nonlocal remanufacturer.
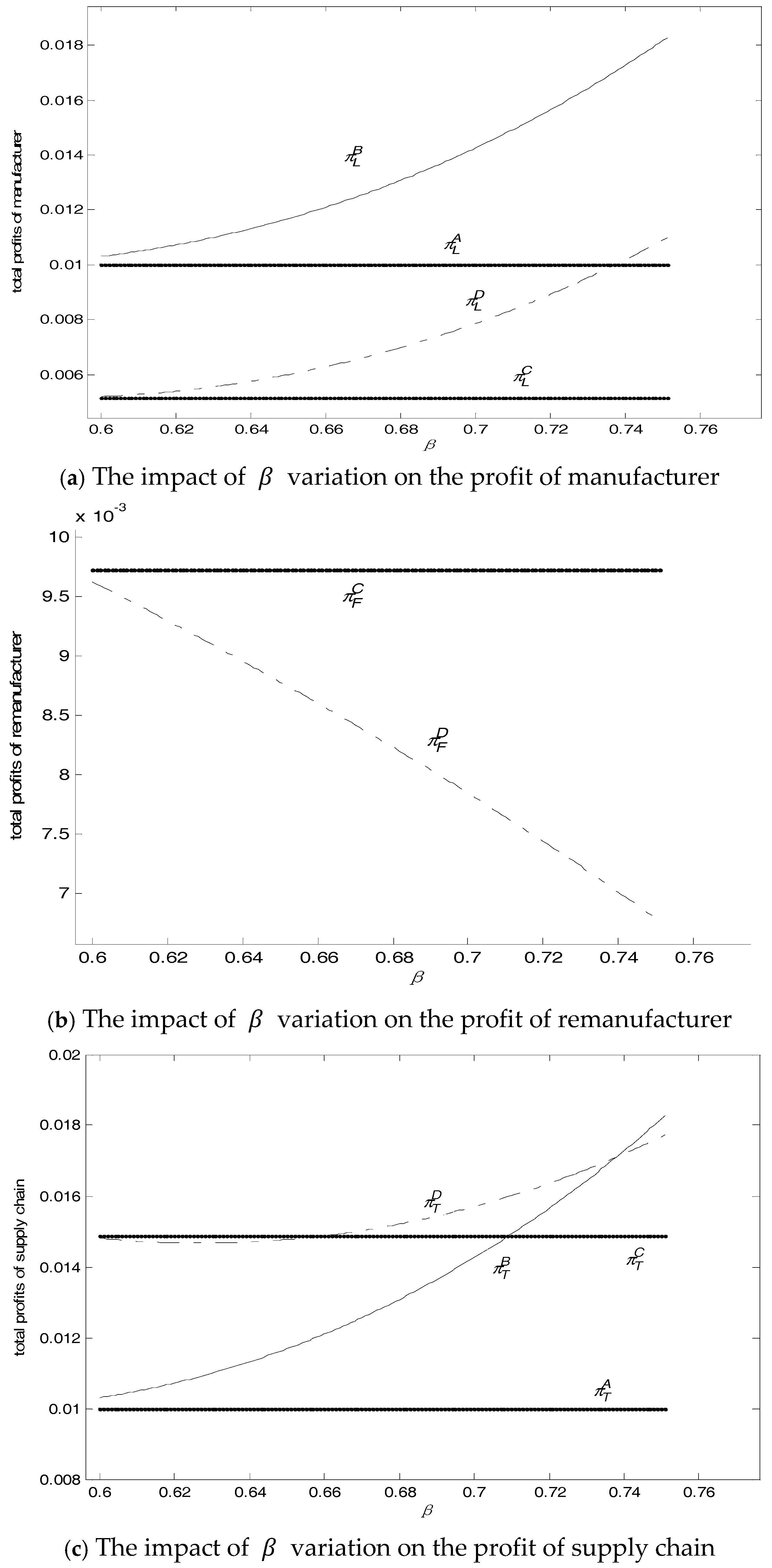
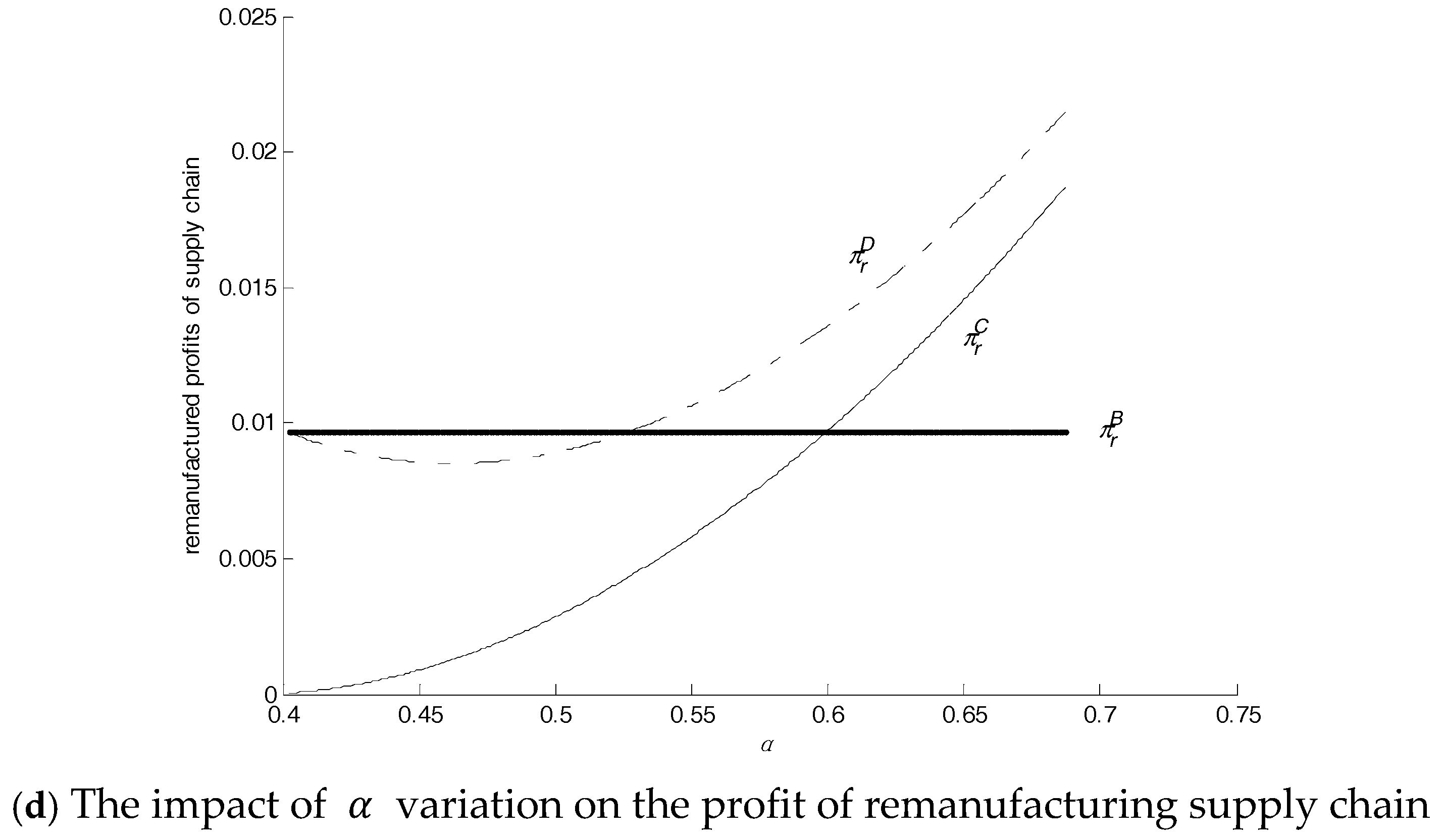
Corollary 3. .
When the local manufacturer engages in remanufacturing, remanufactured products compete with new products; remanufacturing is profitable, increasing the total profits of the local manufacturer. When only the local manufacturer remanufactures, the local remanufacturer gains more profits, whereas in Model C, profits of the local remanufacturer are minimum. It is easy to understand these two cases. In Model B, the local manufacturer’s remanufactured products compete with brand new products, whereas the local manufacturer still gets the remanufacturing profit. The remanufacturing cost is low, and, with government subsidy, the local manufacturer’s profits are maximal in Model B. In Model C, the nonlocal manufacturer makes remanufactured products, the market of brand new products that the local manufacture loses cannot be compensated for and the profits are lower than those in Models A and B.
6. Conclusions
This article examinesasupply chain consisting of one local manufacturer and one other nonlocal remanufacturer as a potential competitor. In this supply chain, enterprises can be both the manufacturer and the retailer. In remanufacturing, they can also be recycling agents. Consequently, considering the competition in sales and recycling, government subsidy and WTP gap, four models are designed and the corresponding models are built regarding whether the nonlocal remanufacturer engages in remanufacturing in the local market and whether the local manufacturer engages in remanufacturing and competes with the nonlocal remanufacturer. Ultimately, analyses of the four models and numerical examples are presented.
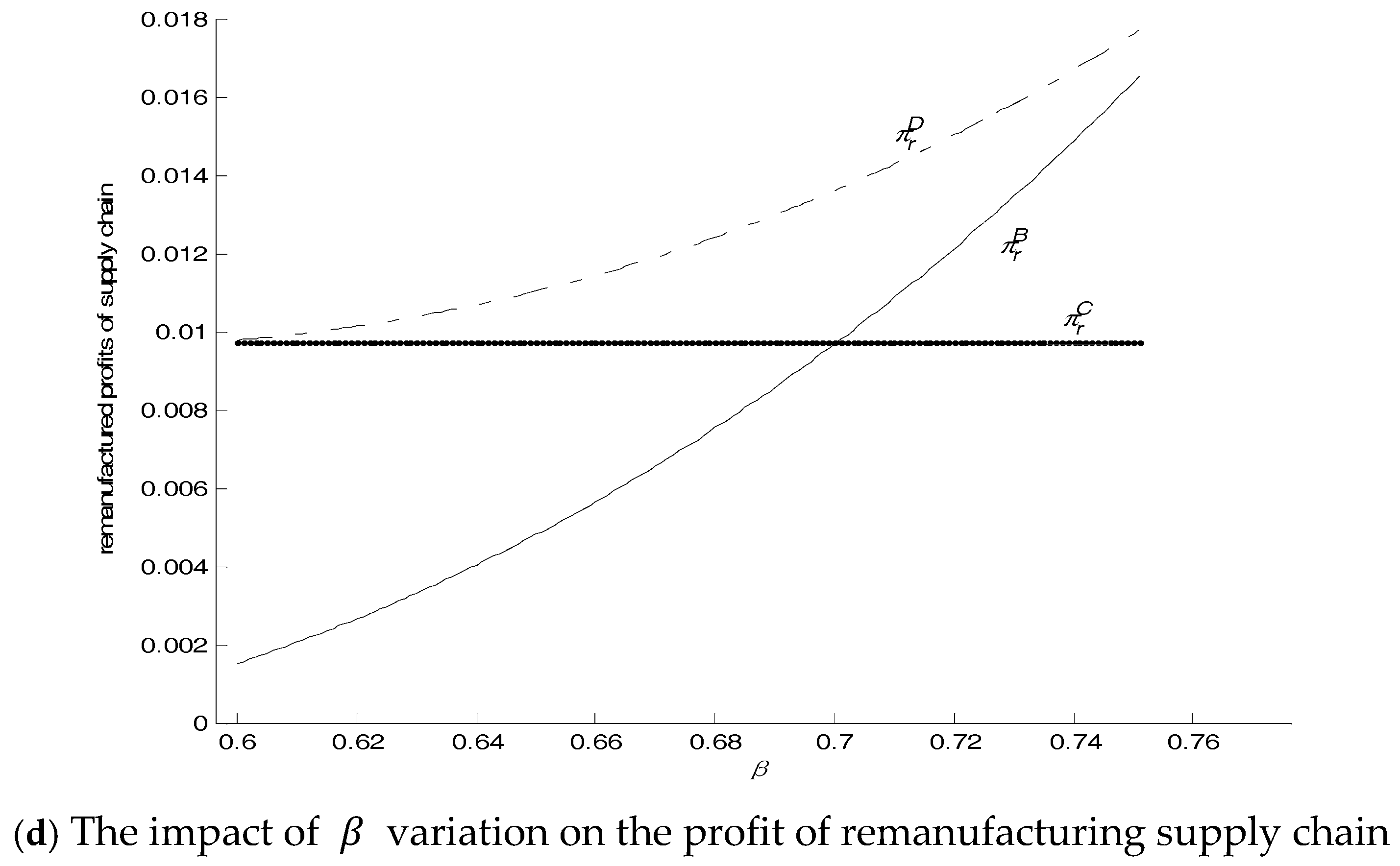
The analyses show the optimal output of new and remanufactured products and their maximal profits of the local manufacturer and nonlocal remanufacturer in the four circumstances. The analyses of the expressions of the optimal output define the boundary conditions for each enterprise to get involved in remanufacturing. Meanwhile, the numerical examples demonstrate the impacts of consumer acceptance of remanufactured products (), government subsidy and recycling competition degree to enterprises. Finally, the four circumstances are compared. Below are some findings: (1) Consumer acceptance of remanufactured products directly affects the remanufacturing activities of each enterprise and the profits of the overall supply chain. When consumer acceptance of remanufactured products increases, remanufacturers can obtain more profits and the local manufacturers are willing to give up the market of brand-new products for remanufactured products. Nonetheless, the profit rate of new products is huge and the acceptance of new products is high, thus the local manufacturer who makes new products should be prudent to decide whether to remanufacture by examining consumer acceptance of remanufactured products carefully. Otherwise, the extremely low acceptance of remanufactured products will result in earnings of remanufacturing being inadequate to compensate for the loss of the market of new products. (2) Consumer acceptance of remanufactured products varies, and therefore the market structure will change accordingly. When consumer acceptance of remanufactured products is medium, profits of supply chains in competition are higher than those without competition. As a result, when consumer acceptance of remanufactured products is medium, enterprises should allow or participate in competition in the market of remanufactured products. The government also should encourage enterprises to remanufacture to increase the total profits and boost remanufacturing. When the consumer acceptance is extremely high or there is a huge gap between consumer acceptance of remanufactured products of the two enterprises, remanufacturing competition will reduce the total profits of the overall supply chains. At this point, the enterprise with higher consumer acceptance can stop competition and monopolize the business. (3) The government subsidy can relax the boundary conditions for enterprises remanufacturing, and the government subsidy for remanufacturing can further increase the remanufacturer’s profits. This suggests that the government can provide some appropriate amounts of subsidies for remanufacturing enterprises so that they are more willing to engage in remanufacturing. (4) Recycling competition decreases the output of remanufactured products of local and nonlocal manufacturers, while it increases the output of remanufactured products significantly in the whole society. In addition, the increasingly intense recycling competition among enterprises leads to more harm in terms of the total profits of supply chains. Therefore, when the local and nonlocal manufacturers are all involved in remanufacturing, the government can supervise moderately to enable the recycling competition to be plausible. In this way, remanufacturing can be boosted and the initiative for remanufacturing will not be thwarted. Based on the above analyses, this study can provide some constructive managerial guidance for the potential nonlocal remanufacturers or the local manufactures. In the market, local and nonlocal manufacturers should investigate the consumer acceptance degrees towards their own and their competitors’ remanufactured products when they determine whether or not they involve remanufacturing. Thus, they would decide whether they avert competition passively, or they avoid competition by stopping competitors from entering the market through their own power, or they join competition proactively. At the same time, the manufacturer is supposed to understand the government’s policies to avert losing some opportunities. In addition, it is vital for the manufacturer to collaborate with the government’s regulation and supervision and lower the loss of profits through legitimate competition. This research can also shed some light on directions further research should take for providing a better understanding of remanufacturing.
One limitation of this study is that the design of the model is too complex, with a number of parameters, resulting in complex expressions of the ultimate results and non-intuitive conclusions. Future research can be extended further. This article focuses on the enterprise with fixed production cost. If the cost is the function of the remanufacturing technology, the results could be different. In addition, this study concerns a single period, and thus the recycling quantity of enterprises is infinite, which can be extended to two or multiple periods. The recycling quantity of enterprises can be finite, and thus the recycling quantity function is prone to changes. Moreover, in the competition between the local manufacturer and numerous nonlocal remanufacturers, how the market evolves can also be considered. Ultimately, further analyzing the total welfare including consumer’s surplus and environmental damage based on this study is of great significance in terms of making policies.