1. Introduction
‘Ambidexterity’ basically refers to a firm’s ability to be efficient in managing current business and to be adaptable to cope with changing demands in the future. By attaining ambidexterity, a firm can be sustainable in the business environment. Innovation is a must to achieve ambidexterity for most firms. Incremental innovations are basically exploitative and lay the foundation on existing organizational knowledge to meet the needs of existing customers. On the other hand, radical innovations are usually exploratory because they often demand new knowledge or departure from known skills, and they are often targeted at potential customers or emergent markets. It is found that a superior performance in innovation is positively correlated to a trade-off strategy between exploration and exploitation. However, few firms may succeed at managing the trade-offs in practice. This is because exploration and exploitation are based on fundamentally different logics and require very different strategies and structures [
1]. Nevertheless, some works have proposed that the two kinds of activity may not be in conflict but in harmony. While a positive interaction effect adopting a trade-off between them is theoretically predicted, there have been few empirical findings on how they are operated jointly in practice. An implicit meaning from the above arguments is that firms trying to pursue both activities may get worse results since the interaction effect between them could be negative [
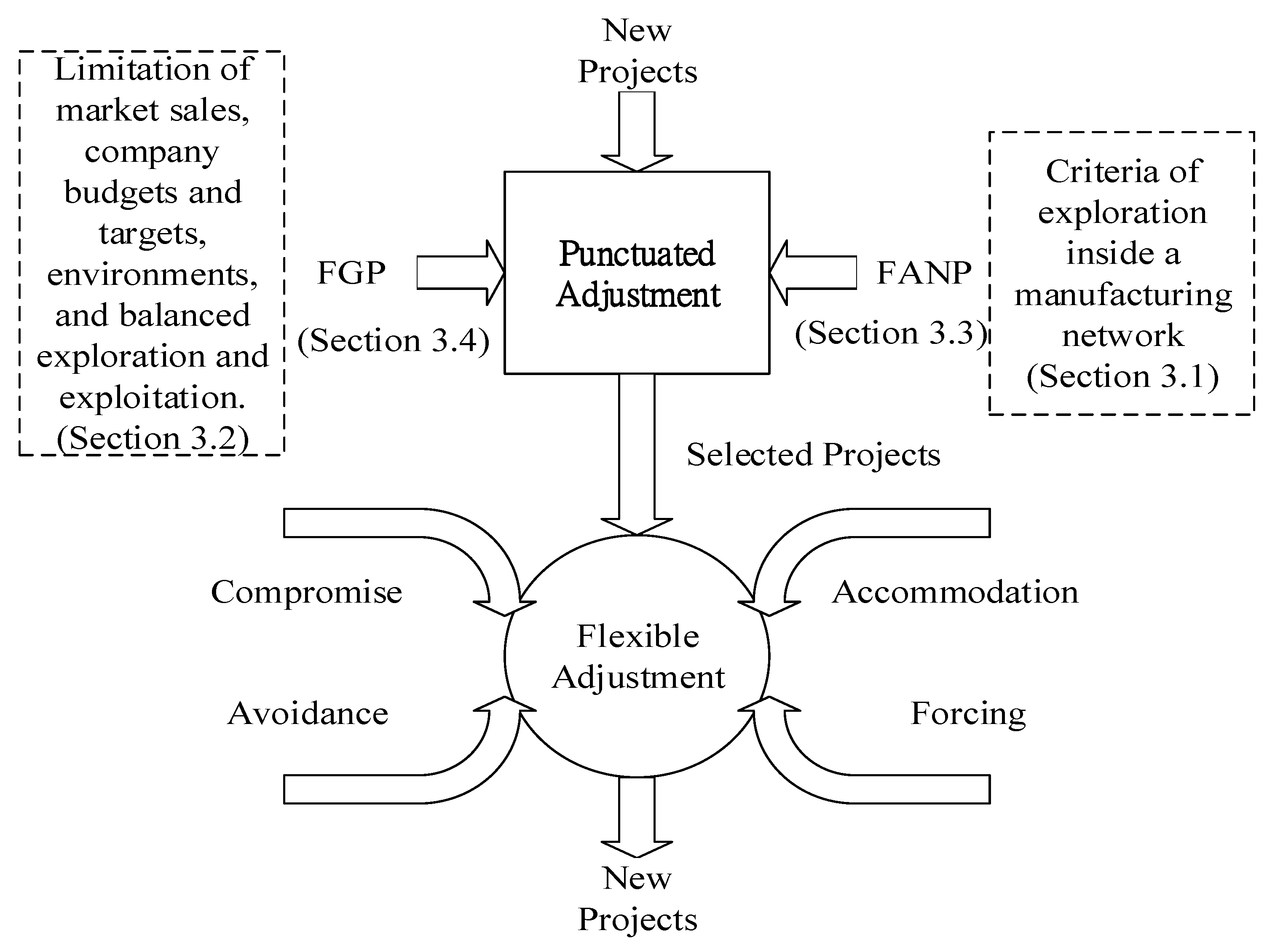
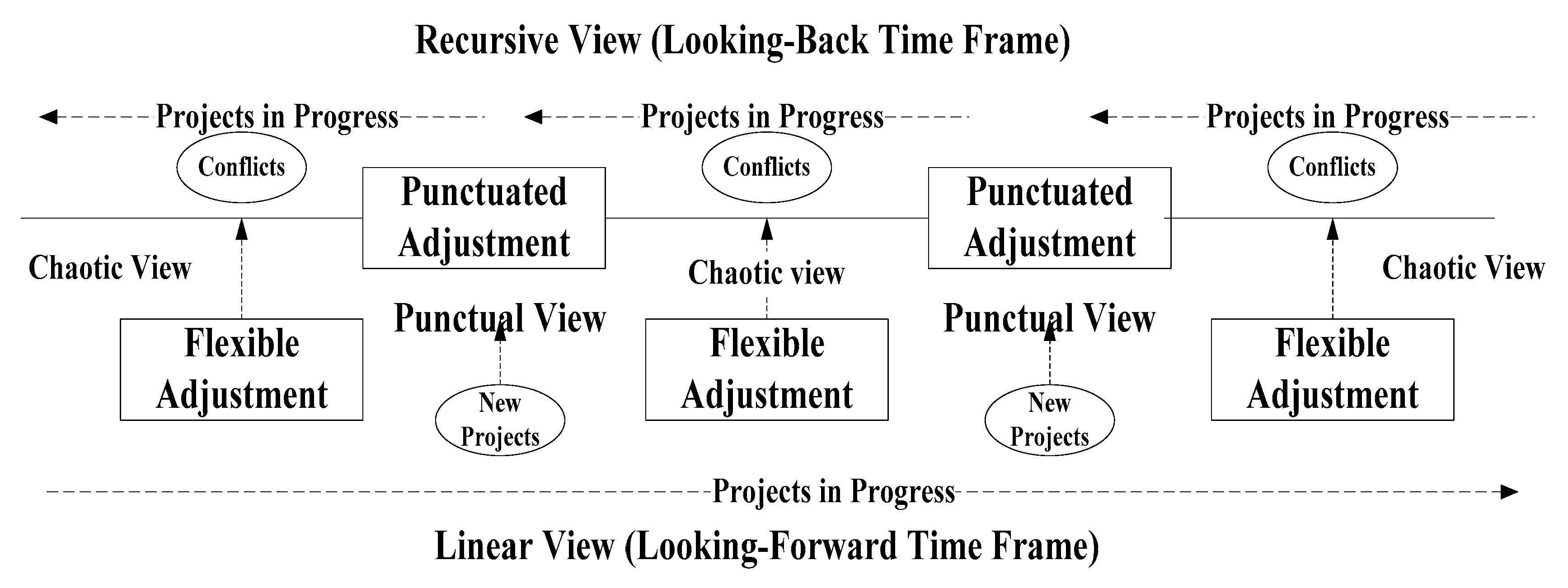
1]. In order to tackle such unstudied problems, a mathematical decision-making framework is constructed. The framework is a linear, recursive, and chaotic adaptive system and includes the two following parts.
First, a computer mediated social groupware (CMSG) with Delphi technique to manage conflicts such as collaboration, accommodation, compromise, forcing and avoidance is designed to flexibly allocate limited resources to the projects. The proposed model not only practically discusses balanced exploitation and exploration from the perspective of network collaboration, but also theoretically expands balanced and combined dimensions of ambidexterity [
2], manages structural ambidexterity [
1,
3], and contextual ambidexterity simultaneously [
4,
5,
6]. However, ambidexterity may result in path dependence or lock-in technologies. Second, in order to assist practitioners in selecting the most suitable projects under different resources, limitations and capabilities to balance exploitation and exploration in a long-term perspective, this paper develops a model by integrating a fuzzy analytic network process (FANP) [
7] with fuzzy goal programming (FGP) [
8].
The proposed model is applied to a photovoltaic (PV) manufacturer in China to practically investigate and theoretically analyze its previous experiences. The results show that a balanced exploration and exploitation can be achieved, and sustainable competitive advantage can subsequently be reached. With exploitative activities to meet the needs of existing customers and to maintain a stream of foreseeable income, the firm can also focus on some exploratory activities to target potential customers or emergent markets so that the firm can be sustainable in the future. The proposed model is recommended to managers for developing and implementing projects.
4. A FANP with FGP Model in a Case Study
The mathematical model is applied to a firm, which has been one of the main equipment providers in the flat panel display (FPD) industry in China for many years. In the beginning of a year, the company planned to become one of the main equipment providers in photovoltaic (PV) renewable energy enterprises in China. Simulators (SIM), automatic production equipment (APE), cutting machines (CM), plasma etching machines (PEM), wire sawing machines (WSM), plasma cleaning machines (PCM), crystalline furnaces (CF), plasma-enhanced chemical vapor deposition (PECVD), diffusion furnaces (DF), and laminators (LAM) are core equipment for the PV manufacturing industry. The firm tried to select suitable new projects for development from the above ten candidates, which are denoted by V1 to V10.
The procedure of the FANP and FGP model is summarized as follows [
7,
27,
28]:
1. Define the new product development project selection problem with the goal of selecting the most exploratory projects. Criterion organizational structure (C1) has detailed criteria (a) to (d). Detailed criteria (e), (f), and (g) are under the criterion functional item (C2). Under the criterion organizational environment (C3), detailed criteria (h) to (j) are included.
2. Pairwise compare the criteria.
Five experts in the company are asked to pairwise compare the importance of the criteria using six different linguistic terms, as shown in
Table 1.
After the linguistic variables are collected from each expert, they are transformed into triangular fuzzy numbers. The matrix (
) for expert
k for the pairwise comparison of criteria is:
where
m is the number of criteria.
For example, a matrix from one of the experts is:
3. Combine experts’ opinions and construct a combined pairwise comparison matrix.
If there are
k experts, there are
k triangular fuzzy numbers for each pairwise comparison. A geometric average approach is often used to combine experts’ responses [
7,
29]:
where
.
Use the comparison of the importance of
organizational structure (
C1) and
functional item (
C2) as an example. The triangular fuzzy numbers for each expert are (1/7, 1/5, 1/3), (1, 3, 5), (1/5, 1/3, 1), (1/5, 1/3, 1) and (1, 3, 5). The synthetic triangular fuzzy number is (0.36, 0.72, 1.53). The fuzzy combined pairwise comparison matrix is:
where
.
The center of gravity (COG) is one of the common methods applied to defuzzify the pairwise comparison. The defuzzification between criteria
i and
j is [
30]:
The defuzzified combined pairwise comparison matrix thus is:
4. Obtain the priority vector of the defuzzified combined pairwise comparison matrix.
A priority vector is calculated for the defuzzified combined pairwise comparison matrix by solving [
21,
22]:
where
is the defuzzified combined pairwise comparison matrix,
is the eigenvector, and
is the largest eigenvalue of
.
The priority vector and the
are calculated as:
5. Examine the consistency of the defuzzified combined pairwise comparison matrix.
The consistency of the defuzzified combined pairwise comparison matrix is checked by the consistency index (
CI) and consistency ratio (
CR) [
22]:
where
n is the number of items being compared in the matrix, and
RI is a random index [
22]. Usually, the threshold
CR value is 0.10, and a value exceeding the threshold implies that there is an inconsistent evaluation.
6. Calculate the priorities of detailed criteria with respect to their same upper-level criterion with the assumption that no dependence among detailed criteria exists.
Based on the experts’ opinions, the priorities are calculated by repeating step 2 to 5, and the priority vector with respect to the upper-level criterion (
n) is
. In the case study, the priority vector of detailed criteria with respect to
organizational structure (
C1),
functional item (
C2) and
organizational environment (
C3) are respectively as follows:
7. Calculate the priorities of alternatives with respect to each detailed criterion.
By repeating steps 2 to 5, the priority vector for alternatives with respect to each detailed criterion is calculated. Eigenvectors with respect to criterion n are combined into a matrix .
8. Analyze the interdependence among detailed criteria under the same upper-level criterion.
The interdependence among the detailed criteria under the same upper-level criterion is analyzed through the impact of each detailed criterion on other detailed criteria with the same upper-level criterion. After repeating steps 2 to 5, the interdependence matrix of detailed criteria with the same upper-level criterion is calculated:
9. Calculate the interdependence priorities,
, of the detailed criteria by synthesizing the results from Step 6 and Step 8:
10. Obtain the priorities of alternatives under the criteria.
The priorities of alternatives,
, with respect to criterion
n are calculated by synthesizing the results from Step 7 and Step 9:
for each
n. By grouping together the vectors of
for all
n’s, a matrix
is obtained:
11. Calculate the overall priorities for the alternatives. The overall priorities for the alternatives are obtained by synthesizing the results from Step 4 and Step 10:
12. Obtain the priorities of multiple goals.
The final goal of the case study is to maintain a balance between exploitative and exploratory activities. In order to reach the goal, in addition to the goal of selecting the most exploratory projects for the firm (G1), four other goals are: budget limit (G2), exploratory hours (G3), gross profit (G4) and exploitative hours (G5). A questionnaire is prepared to pairwise compare the importance of the goals in optimizing the ultimate goal of the problem. In addition, the expected performance of alternatives is pairwise compared with respect to each additional goal. The priorities of the five multiple goals are 0.299, 0.234, 0.155, 0.154 and 0.158, respectively.
13. Formulate and solve the FGP model.
The FGP model is formulated and solved to select the projects [
7,
12]. The objective is to maximize the satisfaction of the projects, and the goals are
,
, …,
, …,
GG.
In the case study, a new plan for year 1 to year 3 including
$180 million as the maximum budget, 7000 targeted exploratory hours,
$300 million minimum amount of gross profit, and 3000 targeted exploitative hours are set in year 1 and shown in
Table 2.
Because of limited resources, at most five projects can be implemented simultaneously. One of automatic production equipment (V2) and cutting machines (V3) needs to be carried out because the firm was doing well in these products in year 1 to year 3 and could take advantage of previous experience. Since the firm aimed to keep a balance among exploitative and exploratory activities, the experts agree that at least one project should be selected from V6 to V10, which are exploratory projects.
Based on the priorities obtained in Step 12 and the additional goals, the FGP formulation is:
Subject to:
for selecting the most exploratory projects
for budget limit
for exploratory hours
for gross profit
for exploitative hours
The allowable budget is set between
$170 million and
$190 million. The targeted exploratory hours are between 7000 and 8000 h. The gross profit is between
$300 million and
$400 million. The targeted exploitative hours are between 2000 and 3000 h. Then, we have the following limits:
where all variables are nonnegative.
5. Discussion
A FANP with FGP model can help managers to select the most appropriate projects while maintaining a balance between exploitation and exploration. In this study, a photovoltaic (PV) manufacturer in China has been selecting new products for development with the consideration of keeping exploitation and exploration balanced. In the beginning of year 1, the firm spent roughly the same amount of time and expense on developing exploitative and exploratory projects. While some projects performed better than expected, others did not. On top of that, no systematic method was available to transfer the limited resources from the failed projects to the successful.
To be exact, during year 1, the company selected automatic production equipment, cutting machines, small PECVD, and cleaning machines for development. In years 2 and 3, the development on exploration had not been as successful as that on exploitation. The developments of small PECVD and cleaning machines, which are exploratory innovation projects, were not very successful, and most of the profits were generated from the exploitative projects. The major reasons are that the accumulated exploratory hours were only 3200 h (targeted exploratory hours were 5000 h) and the accumulated exploitative hours were 5900 h (targeted exploitative hours were 5000 h), as shown in
Table 3. In addition, the exploitative projects were more successful at the end. Therefore, the firm needed to adopt the proposed model for the next three years (from year 4 through year 6) to balance its current plan by punctuated adjustment and execute new projects by flexible adjustment [
31].
After defining the NPD project selection problem and constructing the evaluation network, the authors invited senior managers to confirm the suitability of the network, which comprised three general criteria and ten detailed criteria. A pairwise comparison questionnaire was prepared based on the network. The managers were then asked to fill out the questionnaire. As listed in
Table 3, the results show that, among the three criteria, functional item (
C2), with a weight of 0.532, is the most important factor for balanced exploitation and exploration, in the opinion of the managers. The reason is that functional item, which indicates the functionality of members and departments in a firm, is very important for survival in a competitive market. Organizational structure (
C1) ranks second with a weight of 0.352. It indicates that the organizational structure with other partners in developing new products is rather important for the final success of products. Organization environment (
C3), which describes the environment the firm faces when developing new products, ranks last with a weight of 0.116.
The importance weights of detailed criteria under each criterion can also be found in
Table 3. Under the criterion of organizational structure (
C1), informal or formal organizational connection (d) is the highest concern of the experts, with a weight of 0.379, followed by cooperation with new or old partners (a), with a weight of 0.363. Under the criterion of functional item (
C2), cooperation with R & D or production/market functions (e) is the most important detailed criterion, with a weight of 0.488. It is followed by new projects having orthogonal or continuum relationships (f), with a weight of 0.359. Under the criterion of organizational environment (
C3), new projects within dynamic or competitive environments (h) garners the highest attention, with a very high weight of 0.643.
The integrated weights need to be observed to understand the overall importance of the detailed criteria for exploratory project selection. This is because an important detail criterion may not be very important overall if the weight of its upper-level criterion is not very high. The most important detailed criterion among all the ten detailed criteria is cooperation with R & D or production/market functions (e), with an integrated weight of 0.260. This is mainly because an exploratory NPD can only be successful if members in the R & D department can cooperate well with key members in other departments such as production and marketing. The second most important detailed criterion is new projects having orthogonal or continuum relationships (f), with an integrated weight of 0.191. This is because the knowledge and expertise obtained from previous products can be carried over to develop the new product. Informal or formal organizational connection (d) and cooperation with new or old partners (a) rank third and fourth with integrated weights of 0.133 and 0.128, respectively. This is because the firm needs to have some kind of connection and cooperation with other firms in the manufacturing network to expedite the information flow regarding the projects among the member firms.
After synthesizing the importance of the criteria and detailed criteria with the expected performance of the ten candidate projects, the FANP analysis shows that the most exploratory projects are diffusion furnaces (V9) (a final weight of 0.129), PECVD (V8) (0.125), crystalline furnaces (V7) (0.124) and laminators (V10) (0.116). Next, the company needs to evaluate the projects further based on resource limits and specific constraints, and this is done by the FGP model. While the company aims to select the most exploratory projects, budget limit, exploratory hours, gross profit and exploitative hours need to be considered in a comprehensive way. After calculations by the proposed model, four projects are finally selected: automatic production equipment (V2), cutting machines (V3), crystalline furnaces (V7) and diffusion furnaces (V9). These four projects should be selected to compensate for the changes from exploitative activities to exploratory activities in year 4. Even though PECVD (V8) and laminators (V10) have high priorities in the FANP analysis, they are not chosen in the FGP model, where additional goals and constraints are added. These two projects may be implemented in future periods after further studies.
In the beginning of year 4, new projects including automatic production equipment (V2), cutting machines (V3), crystalline furnaces (V7) and diffusion furnaces (V9) were chosen based on the proposed model for punctuated adjustment, and more effort was put on exploratory innovation to compensate for the low accumulated exploratory hours in previous years. From year 4 through year 6, ambidextrous adjustment was carried out to steadily shift the limited resources among projects. An accumulation of 7170 exploratory hours and 3200 exploitative hours were invested. Successful exploratory projects were developed, and a noticeable amount of profits were made. In the year of year 4, collaboration was stressed because it was important to generate maximum synergy by accelerating exploratory activities while maintaining previous successful projects. Projects V2 and V3 were retained while V7 and V9 were reinforced. In year 5, compromise was focused on because of imminent time pressure to develop some projects. Project V2 (reduced) transferred limited resources to project V3 (expedient) while project V7 (reduced) transferred limited resources to project V9 (expedient). In year 6, because the development of project V2 was behind schedule, forcing was applied to project V2 while accommodation was applied to project V7. At the same time, because it was important to accelerate project V9, collaboration was applied. Then, project V3 was retained while V9 was reinforced.
6. Conclusions
In order to be sustainably competitive, a firm needs to balance its exploratory and exploitative activities over the long run. However, past work and practice have not shown much evidence on whether these two activities can co-exist, why a firm should select one over the other, and whether exogenous or endogenous contextual factors could determine which activities should be focused on. Therefore, this paper aims to theoretically and practically propose a conceptual model that can help balance exploration and exploitation for a firm. In summary, this paper has some important contributions. First, this paper discusses the topic from the perspective of network collaboration. It is more practical for industries; second, this paper extends organizational ambidexterity into two dimensions, punctuated adjustment and flexible adjustment, so that a balanced exploitation and exploration can be attained in the long term; third, this paper extends ambidexterity into five situations, including collaboration, compromise, accommodation, forcing and avoidance. Basically, the members in a team will put their effort toward exploration or exploitation when collaboration among projects can be adopted to generate maximum synergy of the firm. Compromise should be adopted when different projects are desired by different members or when an expedient solution is necessary. Forcing or accommodation is recommended if a decisive action does not need to be made urgently, and a trade-off between exploitation and exploration should be adopted. Avoidance should be adopted when unpopular actions may result from a quick decision, and both exploration and exploitation activities may be reduced; fourth, the paper designs a platform, called CMSG with Delphi technique, to simultaneously break constraints from structural ambidexterity and facilitate stretch, support, discipline, and trust from contextual ambidexterity by timely communication; fifth, the conceptual model considers processes of projects from linear, recursive, chaotic, and punctually adjusted views, and thus the model is more comprehensive. Finally, the paper is the first one that aims to adjusted unbalanced exploitation and exploration under punctuated adjustment using a fuzzy analytic network process (FANP) with fuzzy goal programming (FGP) model.
After practically investigating the previous experiences of a flat panel display (FPD) manufacturer using the proposed model, this research concludes that balanced exploration and exploitation can be attained and sustainable competitive advantage can be subsequently obtained. The model is recommended to practitioners for selecting and implementing projects. By following the steps detailed in this paper, practitioners can adjust the model, with the incorporation of different factors and goals based on the specific environment, for sustainable project management.
For future studies, some other methodologies, such as self-organizing maps, neural networks and mixed linear programming (MLP), can be applied to solve the problem. These methodologies can be compared with the proposed FANP with FGP model to learn the advantages and disadvantages of the proposed model.