Sponsorship for the Sustainability of Historical-Architectural Heritage: Application of a Model’s Original Test Finalized to Maximize the Profitability of Private Investors
Abstract
:1. Introduction
2. State of the Art
2.1. The Evaluation of the Sponsorship's Optimal Level to Maximize Company Profits
2.2. The Static Investment Model in Sponsorship
→ π = Σi [pi (Qi, S) Kiα Liβ Sγ − (rKi + wLi + sS)].
3. The Application of the Static Investment Model in Sponsorship
3.1. Monumentando Napoli Project
3.2. The Application of the Model
- production value (PV) = €11,786,374
- production costs (PC) = €10,424,509
- operating income (OI) = PV − PC = €1,361,865
- depreciation and provisions costs (DC) = €1,494,146
- staff costs (CL) = €1,402,947
- number of employees (n) = 37.5.
- total assets (A) = €18,750,043.
- R = €11,786,374
- CT = €10,424,509
- π = €1,361,865
- CL = €1,402,947
- CS = €240,000
- CK = €1,494,146
- CV = = CT − CK − CL − CS = €7,287,416
- K = €18,750,043
- L = 37.5 employees
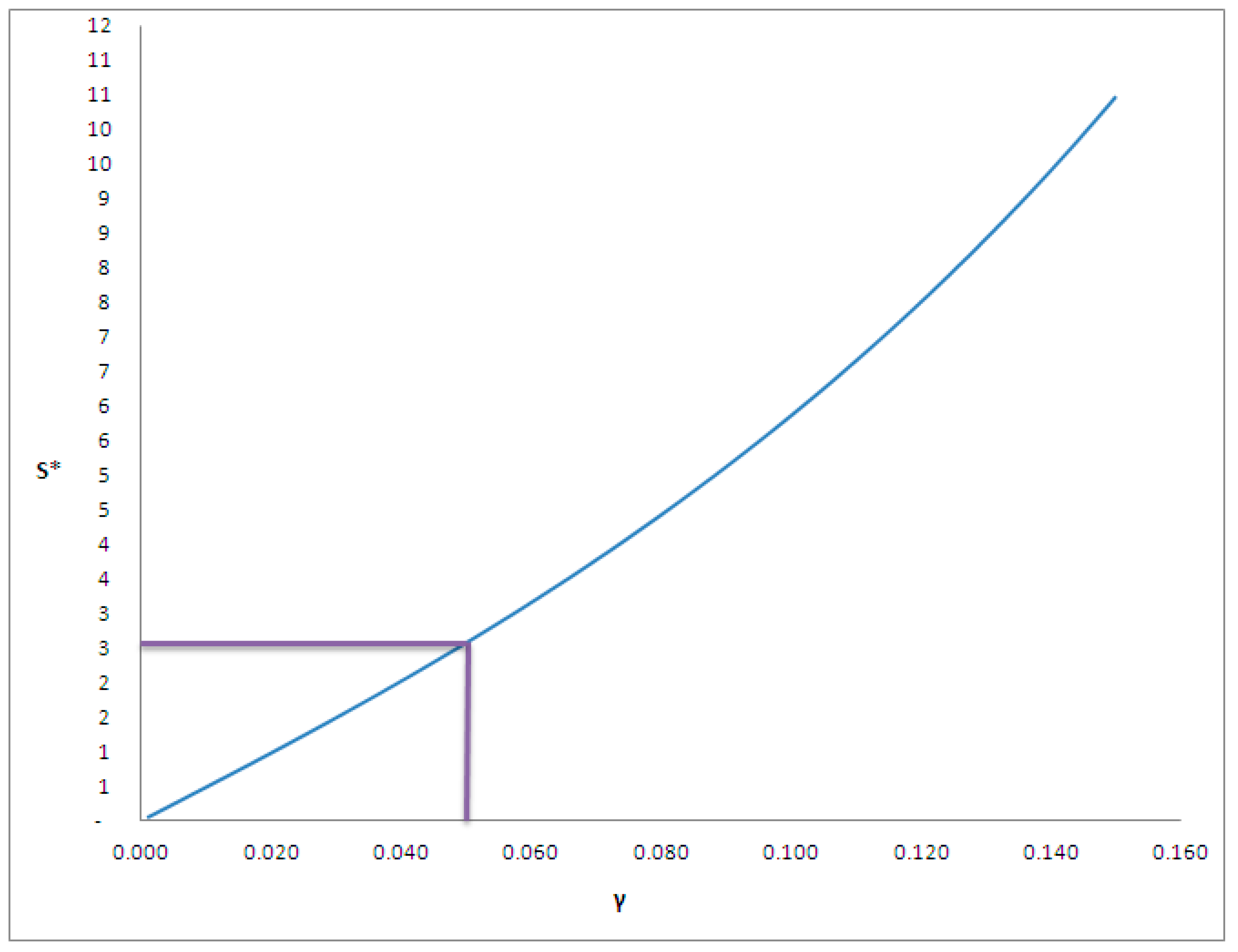
- S = 1 sponsorship
- p = €/kg 15
- r = CK/K ≅ 8%
- w = CL/L = €/employees 37,412
- s = €/sponsorships 240,000
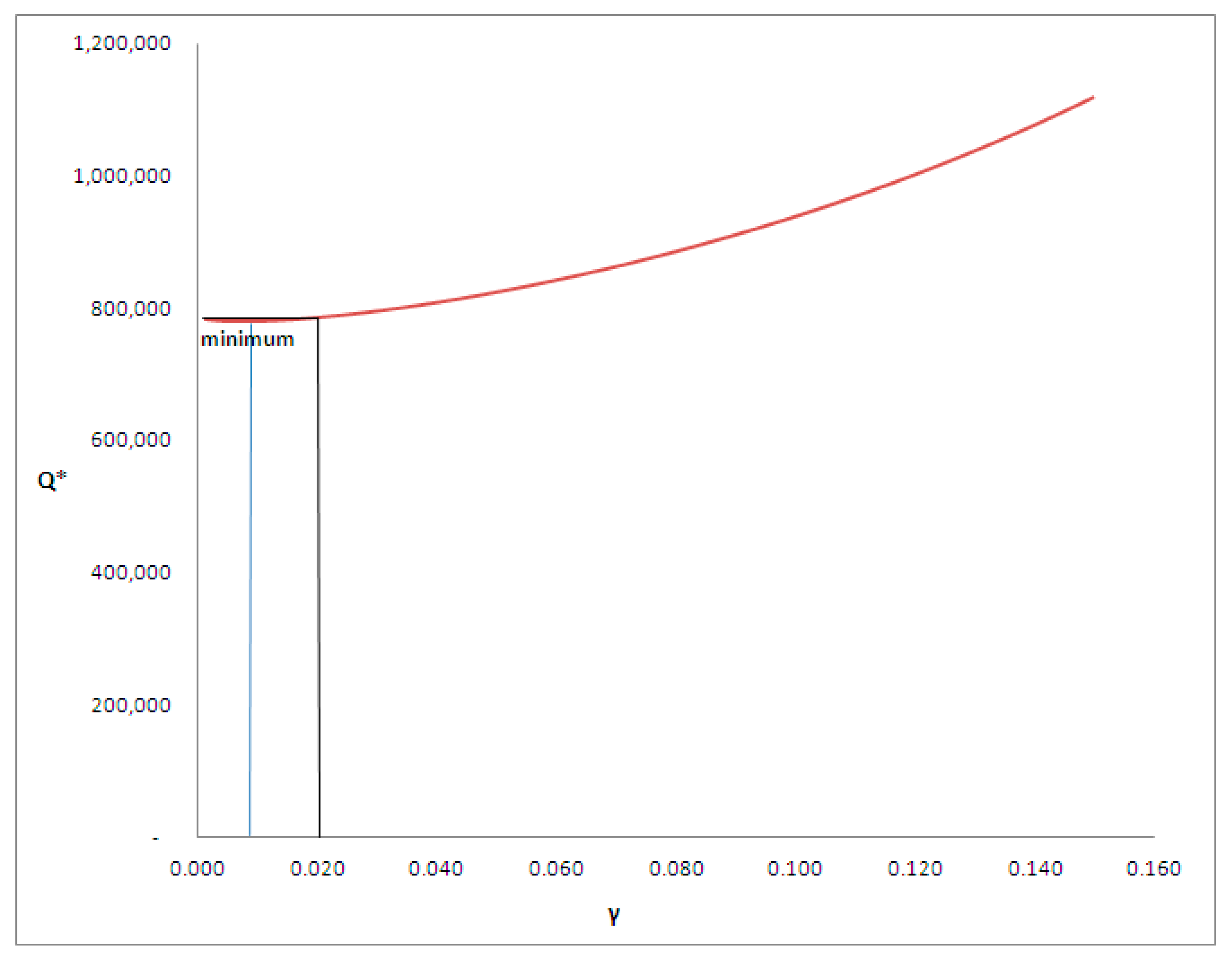
- Q = R/p = kg 785,758.
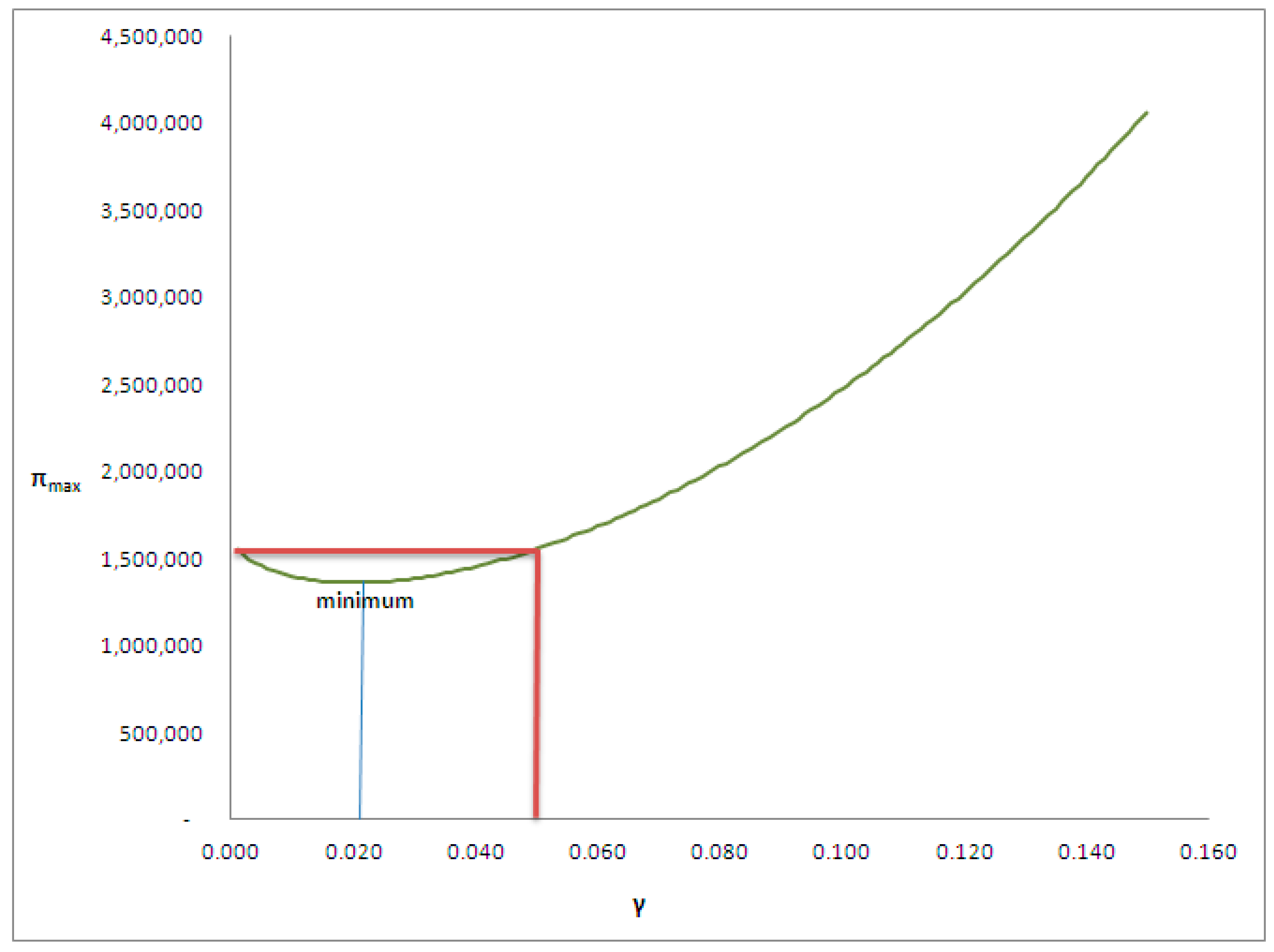
= 15 × 937,747 − 7,287,416 − 18,750,043 × 0.08 − 37,412 × 37.5 − 240,000 × 6 = ≅ €2,475,070.
4. Discussion
α’ = 0.7638764,
β’ = 0.2157608.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Report Bes-Istat 2016. Available online: https://www.istat.it/it/files/2016/12/BES-2016.pdf (accessed on 18 August 2017).
- Barbati, C.; Cammelli, M.; Sciullo, G. Diritto e Gestione dei Beni Culturali; Il Mulino: Bologna, Italy, 2011; p. 113. [Google Scholar]
- Cammelli, M. Pubblico e privato nei beni culturali: Condizioni di partenza e punti di arrivo. Aedon 2007, 2. Available online: http://www.aedon.mulino.it/archivio/2007/2/editoriale.htm (accessed on 8 July 2017).
- Mollica, A. L’Italia si aggrappa agli sponsor per salvare i suoi monumenti. Il Giornalettismo, 30 September 2004. [Google Scholar]
- 11th Annual Federculture Report. 2015. Available online: http://www.federculture.it/2015/06/xi-rapporto-annuale-federculture/ (accessed on 18 August 2017).
- Forte, F.; Rupe, M. Sponsorship in the enhancement of Cultural Heritage and the role of Creative Industry: Some evaluative aspects. In Heritage and Technology—Mind Knowledge Experience, Proceedings of the XIII International Forum Le Vie dei Mercanti, Aversa-Capri, Italy, 11–13 June 2015; La Scuola di Pitagora editrice: Napoli, Italy, 2015; p. 1805. [Google Scholar]
- Rupe, M. Moda e Beni Culturali: Il Meccanismo Della Sponsorizzazione. Bachelor’s Thesis, Second University of Naples, Caserta CE, Italy, 2014. [Google Scholar]
- Rappaport, A. Creating Shareholder Value: A Guide for Managers and Investors, 2nd ed.; Free Press: New York, NY, USA, 1999; p. 224. [Google Scholar]
- Ameels, A.; Bruggeman, W.; Scheipers, G. Value-Based Management: An Integrated Approach to Value Creation a Literature Review; Vlerick Leuven Gent Management School: Gent, Belgium, 2002. [Google Scholar]
- Bucci, A.; Castellani, M.; Figini, P. L’investimento in Sponsorizzazione delle Imprese: Un’analisi Economica in Termini Statici e Dinamici; Rivista di Politica Economica: Rome, Italy, 2003; Volume 93, pp. 183–224. [Google Scholar]
- Cornwell, T.B.; Maignan, I. An International Review of Sponsorship Research. J. Adv. 1998, 27, 1–21. [Google Scholar] [CrossRef]
- McDonald, C. Sponsorship and the Image of the Sponsor. Eur. J. Mark. 1991, 25, 31–38. [Google Scholar] [CrossRef]
- Eventi Aziendali: Italy Business Event. 2012. Available online: http://www.eventiaziendali.it/approfondimenti/view/la-sponsorizzazione-culturale-elementi-per-il-calcolo-dellefficacia/68 (accessed on 15 June 2017).
- Pham, M.T. The Evaluation of Sponsorship Effectiveness: A Model and Some Methodological Considerations; Gestion 2000: Brussels, Belgium, 1991; pp. 47–65. [Google Scholar]
- Ensor, R.J. The Corporate View of Sports Sponsorship. Athl. Bus. 1987, 9, 40–43. [Google Scholar]
- Hulks, B. Should the Effectiveness of Sponsorship be Assessed, and How? Admap 1980, 12, 623–627. [Google Scholar]
- Sparks, R.E.C. Rethinking Media Evaluation: Tobacco Sponsorship Messages and Narrative Conventions in Motorship Telecasts. In World Marketing Congress Proceedings; Grant, K., Walker, I., Eds.; Academy of Marketing Science: Melbourne, Australia, 1995; pp. 111–115. [Google Scholar]
- Douglas, P.H. The Cobb-Douglas Production Function Once Again: Its History, Its Testing, and Some New Empirical Values. J. Political Econ. 1976, 84, 903–916. [Google Scholar] [CrossRef]
- Cobb, C.W.; Douglas, P.H. A Theory of Production. Am. Econ. Rev. 1928, 18, 139–165. [Google Scholar]
- Monumentando Napoli. Available online: https://monumentandonapoli.com/ (accessed on 8 September 2017).
- Analisi Informatizzata Delle Aziende Italiane. Available online: https://aida.bvdinfo.com/Report.serv?_CID=61&context=2S5WC2KM1F60WAU (accessed on 8 December 2016).
- Fasulo, C. 7 Metodi per Calcolare il Marketing Budget. 2016. Available online: http://www.polkandunion.com/blog/7-metodi-calcolare-marketing-budget/ (accessed on 9 September 2017).
- Monier, J.H.; Gordon, J.; Ogren, P. How CMOs Can Get CFOs on Their Side. 2013. Available online: https://hbr.org/2013/11/how-cmos-can-get-cfos-on-their-side (accessed on 9 September 2017).
- Hipp, M. 9 Popular Ways to Determine Your Marketing Budget. 2017. Available online: http://www.smallfuel.com/blog/entry/popular-ways-to-determine-your-marketing-budget/ (accessed on 9 September 2017).
- Macchiaroli, M.; De Mare, G.; Nesticò, A. Significant appraisal issues in value estimate of quarries for the public expropriation. Valori Valutazioni 2017, 18, 17–23. [Google Scholar]
- Sraffa, P. Sulle relazioni fra costo e quantita’ prodotta. Annali Econ. 1925, II, 277–328. [Google Scholar]
- De Mare, G.; Granata, M.F.; Nesticò, A. Weak and strong compensation for the prioritization of public investments: Multidimensional analysis for pools. Sustainability 2015, 7, 16022–16038. [Google Scholar] [CrossRef] [Green Version]
- Nesticò, A.; Macchiaroli, M.; Pipolo, O. Costs and benefits in the recovery of historic buildings: The application of an economic model. Sustainability 2015, 7, 14661–14676. [Google Scholar] [CrossRef]
- Marella, G.; Canesi, R. Residential construction cost: An Italian survey. Data Brief 2017, 11, 231–235. [Google Scholar]
- D’Alpaos, C.; Marella, G.; Canesi, R. Foreclosed homes market in 580 Italy: Bases of value. Int. J. Hous. Sci. Appl. 2016, 40, 201–209. [Google Scholar]
- Nesticò, A.; Pipolo, O. A protocol for sustainable building interventions: Financial analysis and environmental effects. Int. J. Bus. Intell. Data Min. 2015, 10, 199–212. [Google Scholar] [CrossRef]
- Bentintendi, R.; De Mare, G. Upgrade the ALARP Model as a Holistic Approach to Project Risk and Decision Management; Hydrocarbon Processing: Houston, TX, USA, 2017. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dolores, L.; Macchiaroli, M.; De Mare, G. Sponsorship for the Sustainability of Historical-Architectural Heritage: Application of a Model’s Original Test Finalized to Maximize the Profitability of Private Investors. Sustainability 2017, 9, 1750. https://doi.org/10.3390/su9101750
Dolores L, Macchiaroli M, De Mare G. Sponsorship for the Sustainability of Historical-Architectural Heritage: Application of a Model’s Original Test Finalized to Maximize the Profitability of Private Investors. Sustainability. 2017; 9(10):1750. https://doi.org/10.3390/su9101750
Chicago/Turabian StyleDolores, Luigi, Maria Macchiaroli, and Gianluigi De Mare. 2017. "Sponsorship for the Sustainability of Historical-Architectural Heritage: Application of a Model’s Original Test Finalized to Maximize the Profitability of Private Investors" Sustainability 9, no. 10: 1750. https://doi.org/10.3390/su9101750





