Carbon Reduction Strategies Based on an NW Small-World Network with a Progressive Carbon Tax
Abstract
:1. Introduction
2. Literature Review
3. Research Method and Model Construction
3.1. Progressive Carbon Tax and Social Welfare Maximization Models
3.1.1. A Model of Progressive Carbon Tax Policy
3.1.2. Social Welfare Maximization Model
3.2. Evolutionary Model of Traditional Industrial Clusters Based on a Progressive Carbon Tax Policy in a NW Small-World Network
3.2.1. Evolutionary Game Learning Model
3.2.2. The Basic Premise of the Traditional Industrial Cluster Evolution Model
3.2.3. The Expected Earnings Setting in the Evolutionary Game
3.2.4. The Evolution Mechanism of Enterprises under the Progressive Carbon Tax Policy
4. Numerical Simulation and Results
4.1. The Solution of the Progressive Carbon Tax and Social Welfare Maximization Model
4.2. Evolution of Enterprises under the Progressive Carbon Tax Policy
4.2.1. Parameter Initialization Settings
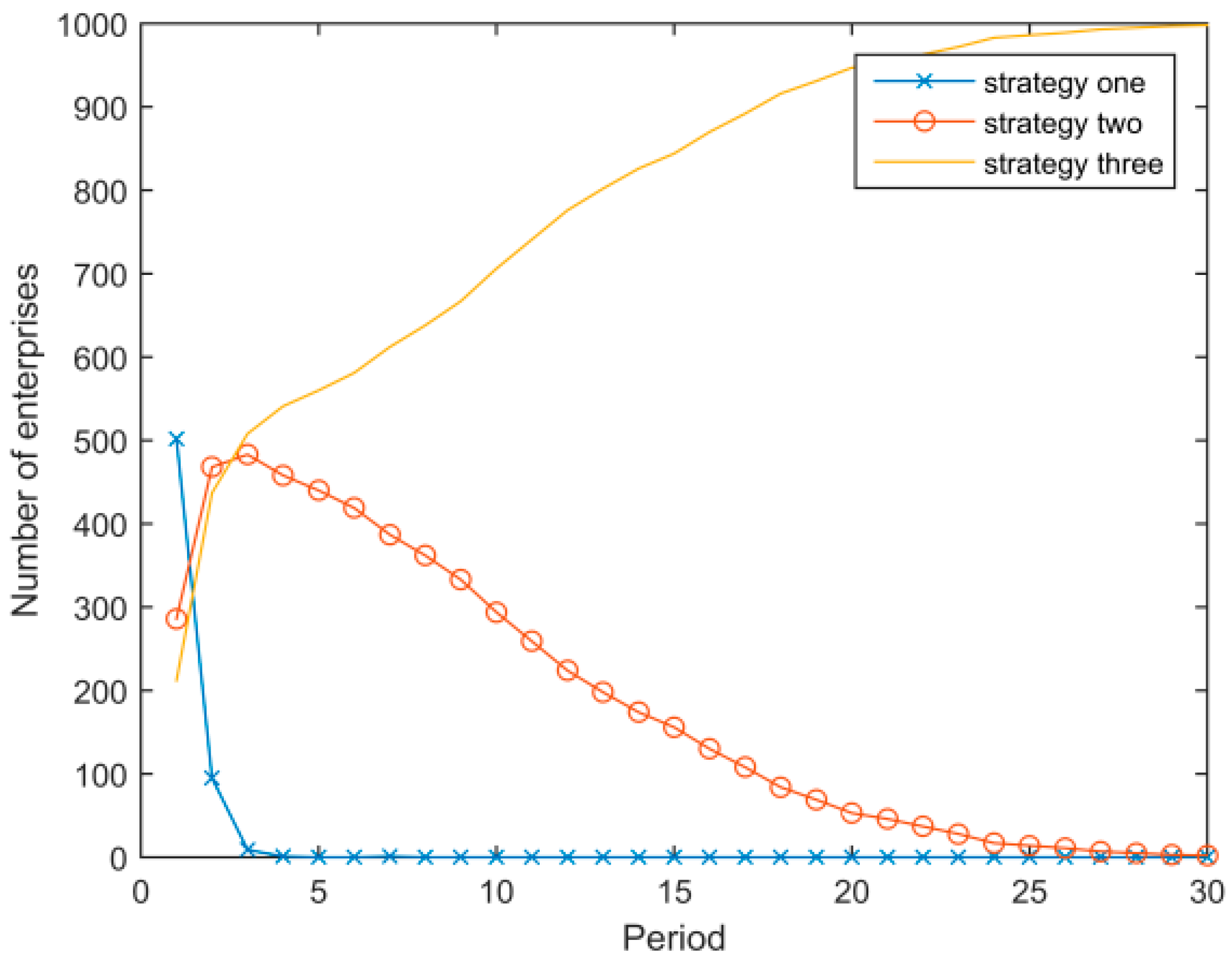
4.2.2. Evolution among Enterprises under the Benchmark Parameters
4.2.3. The Influence of Parameter Values
- (1)
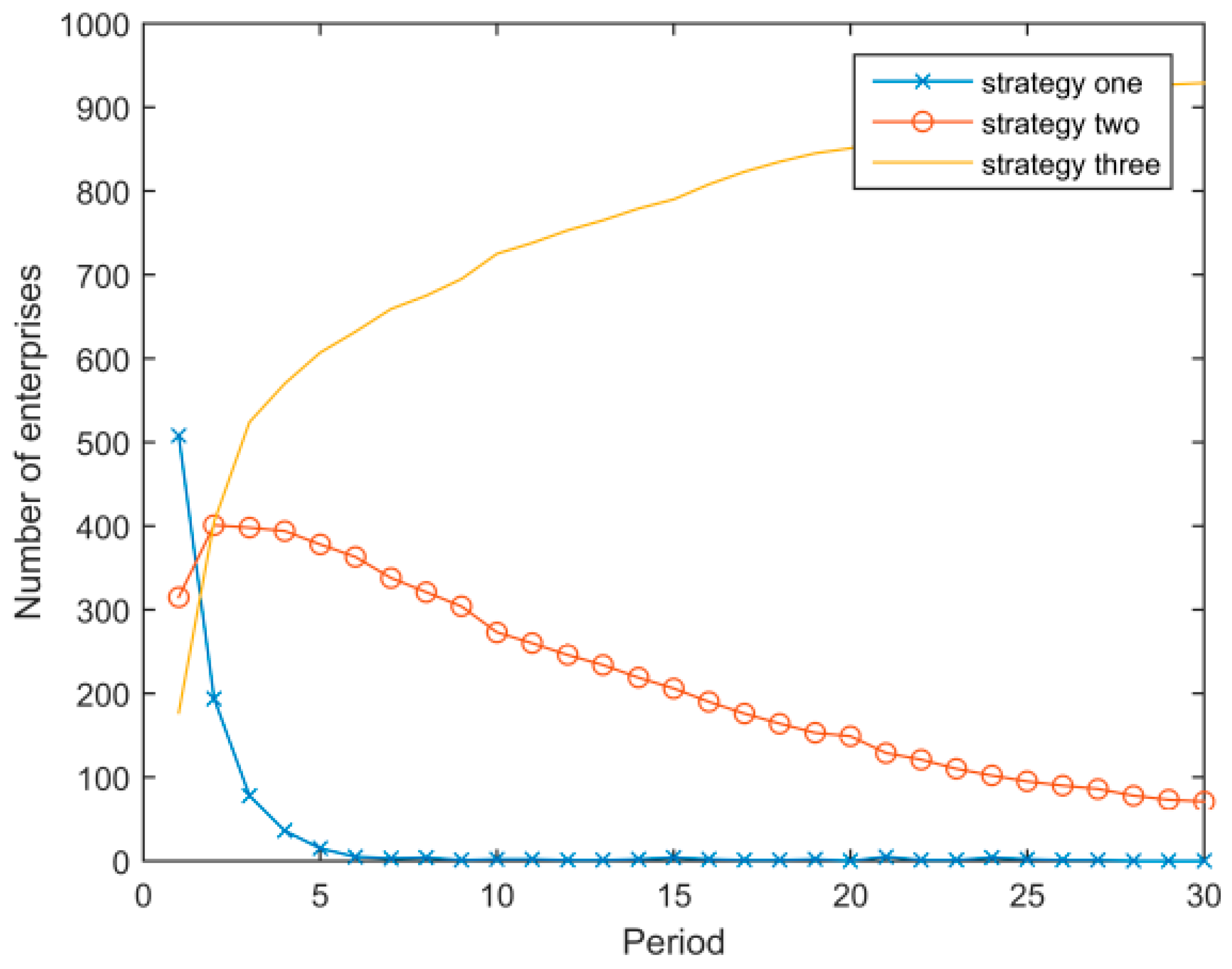
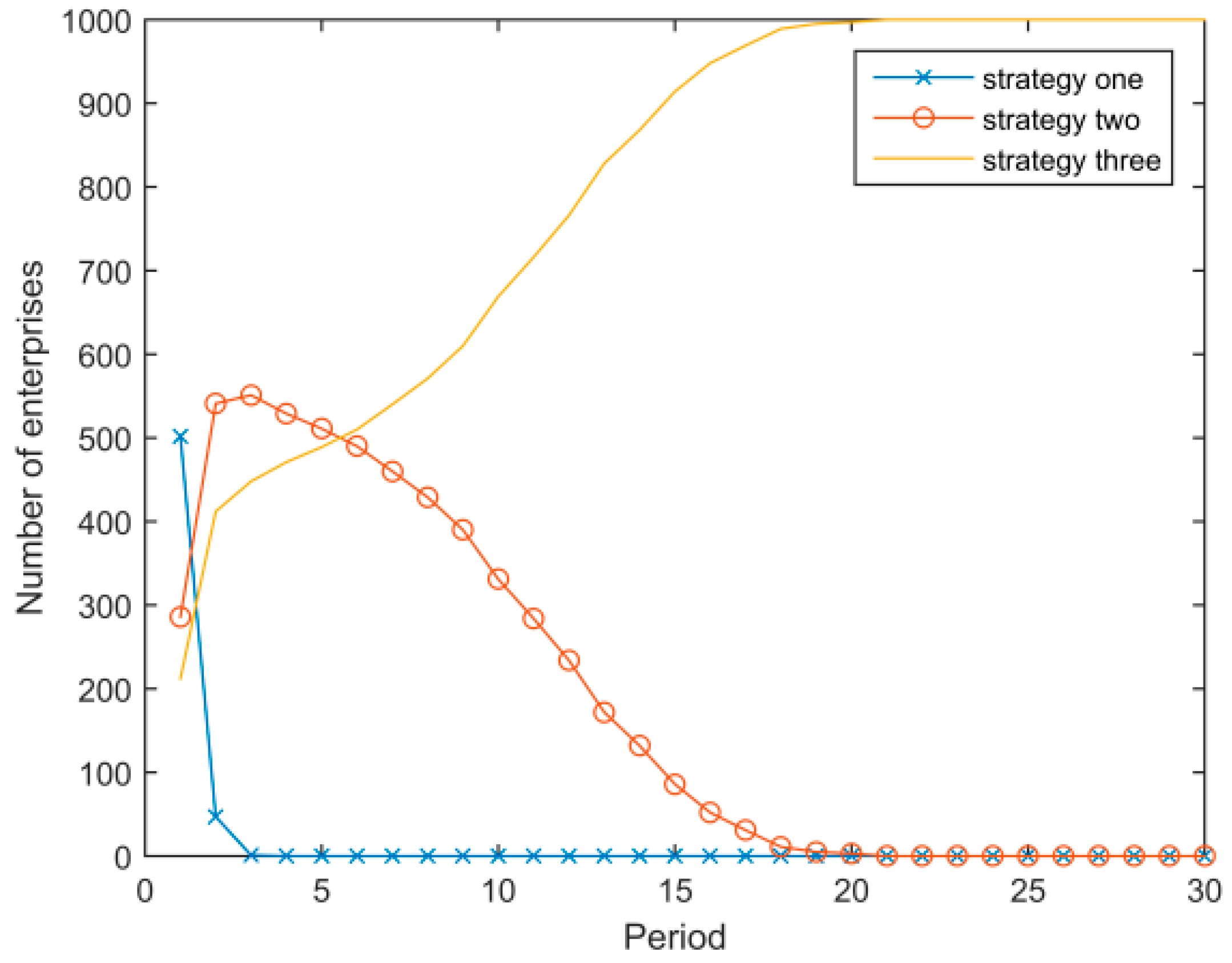
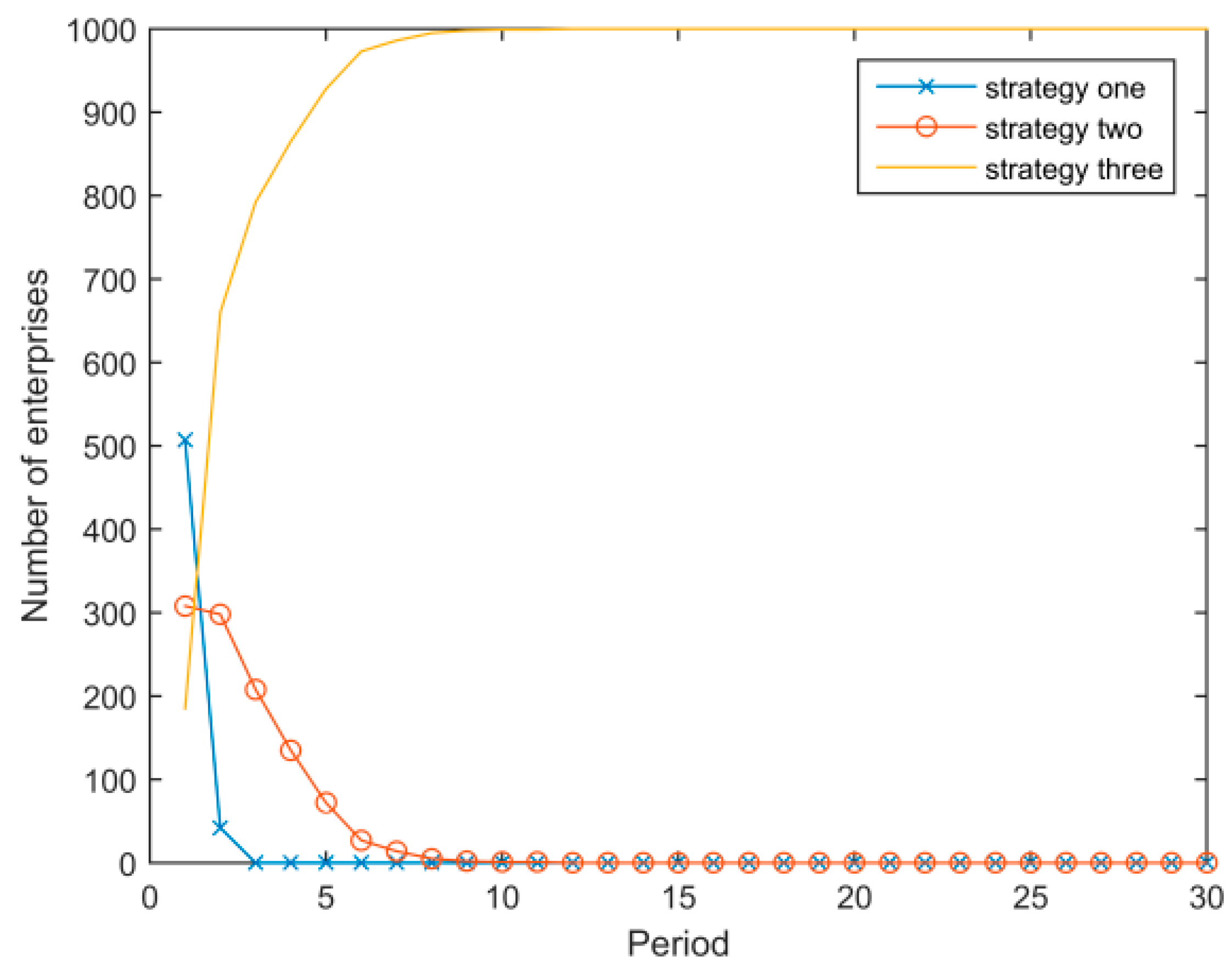
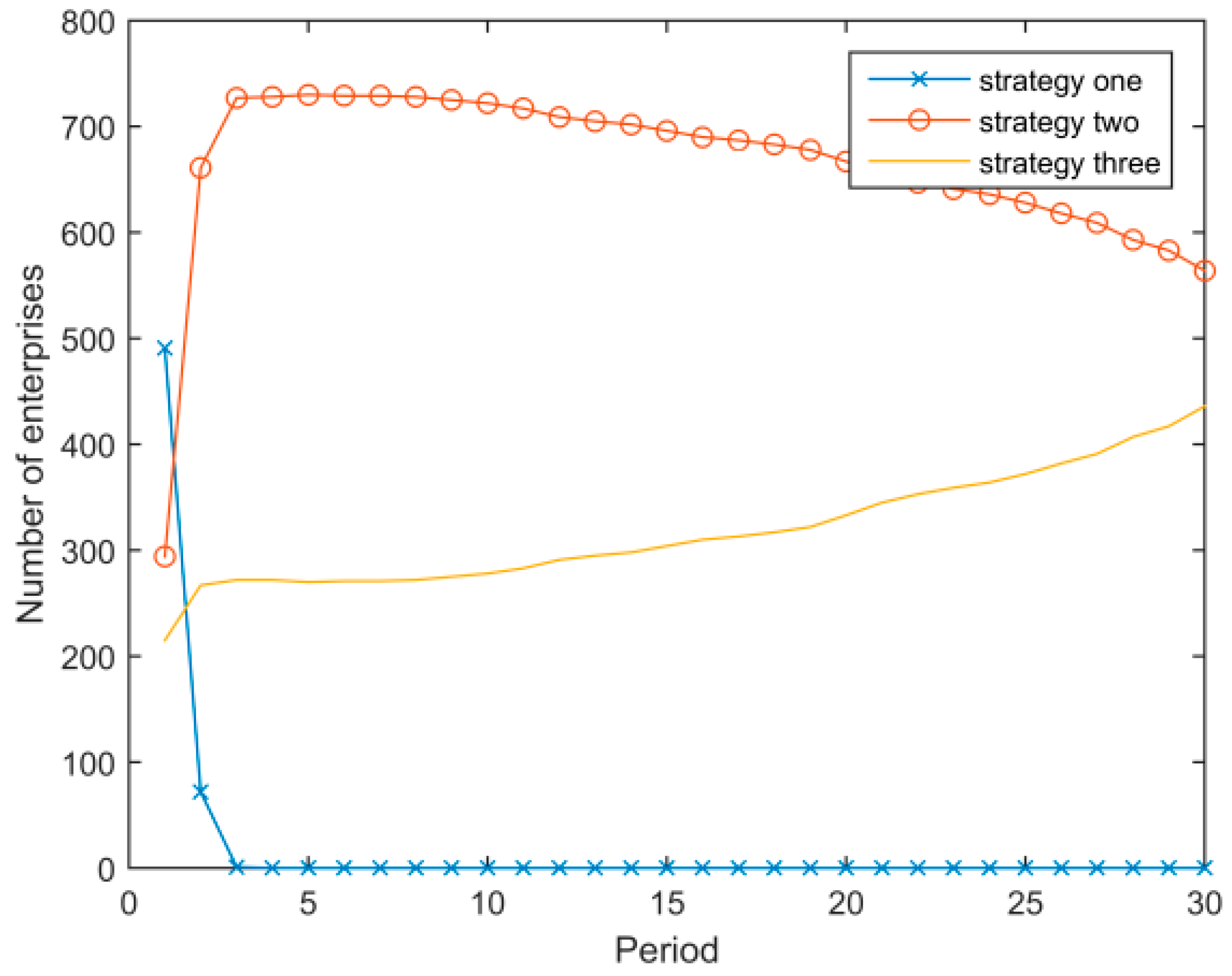
- Assuming that other parameters remain unchanged, Figure 5 and Figure 6 show the evolution results when the discount coefficient of enterprises is δ = 0.1 and δ = 0.9, respectively. Figure 5 illustrates that when δ = 0.1, the general evolutionary trend of the system remains unchanged, but the evolution is slower than with the baseline parameter (δ = 0.5). Figure 6 illustrates that when δ = 0.9, there is a “boom” phenomenon that diffuses the low energy consumption strategy to the whole system.
- (2)
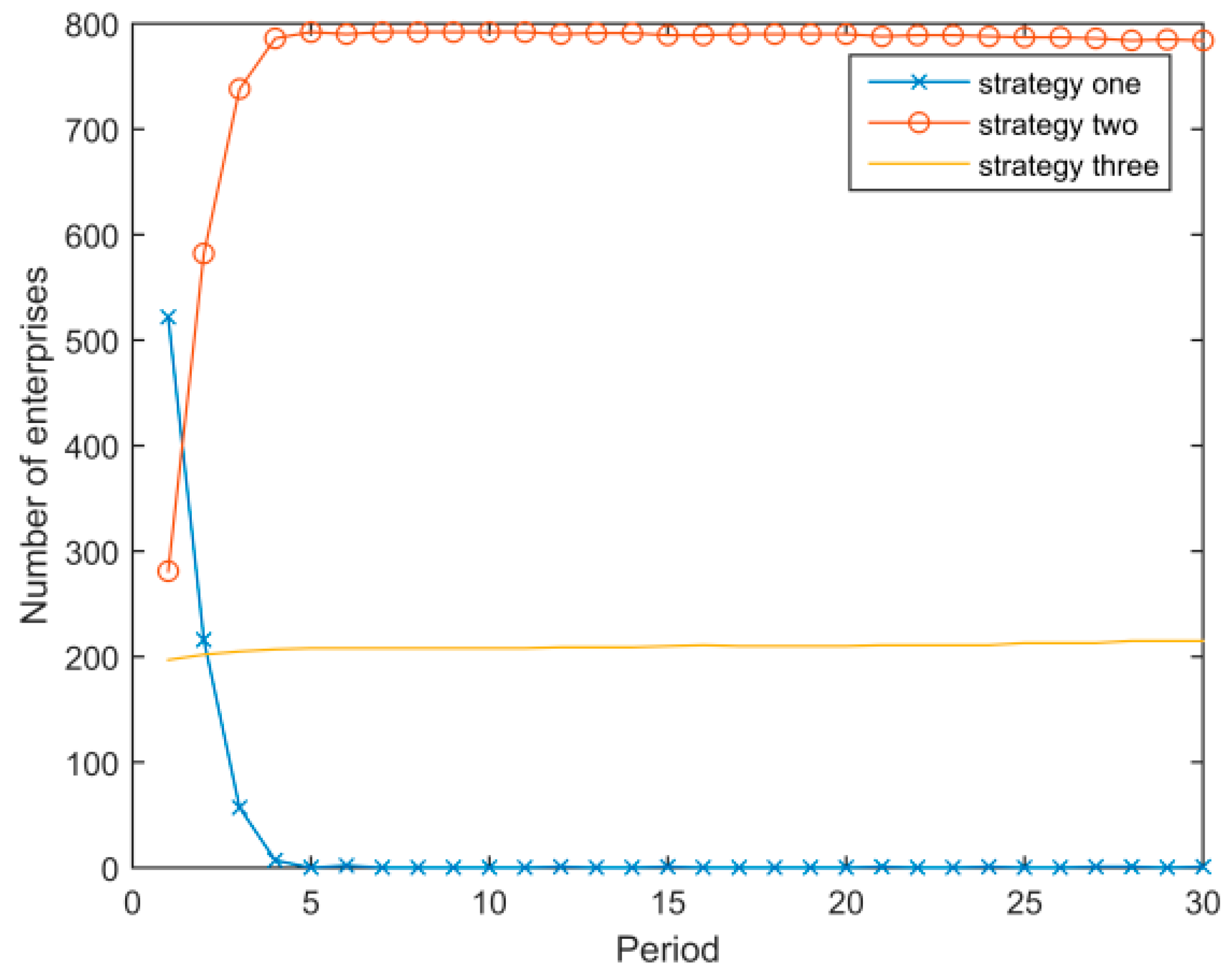
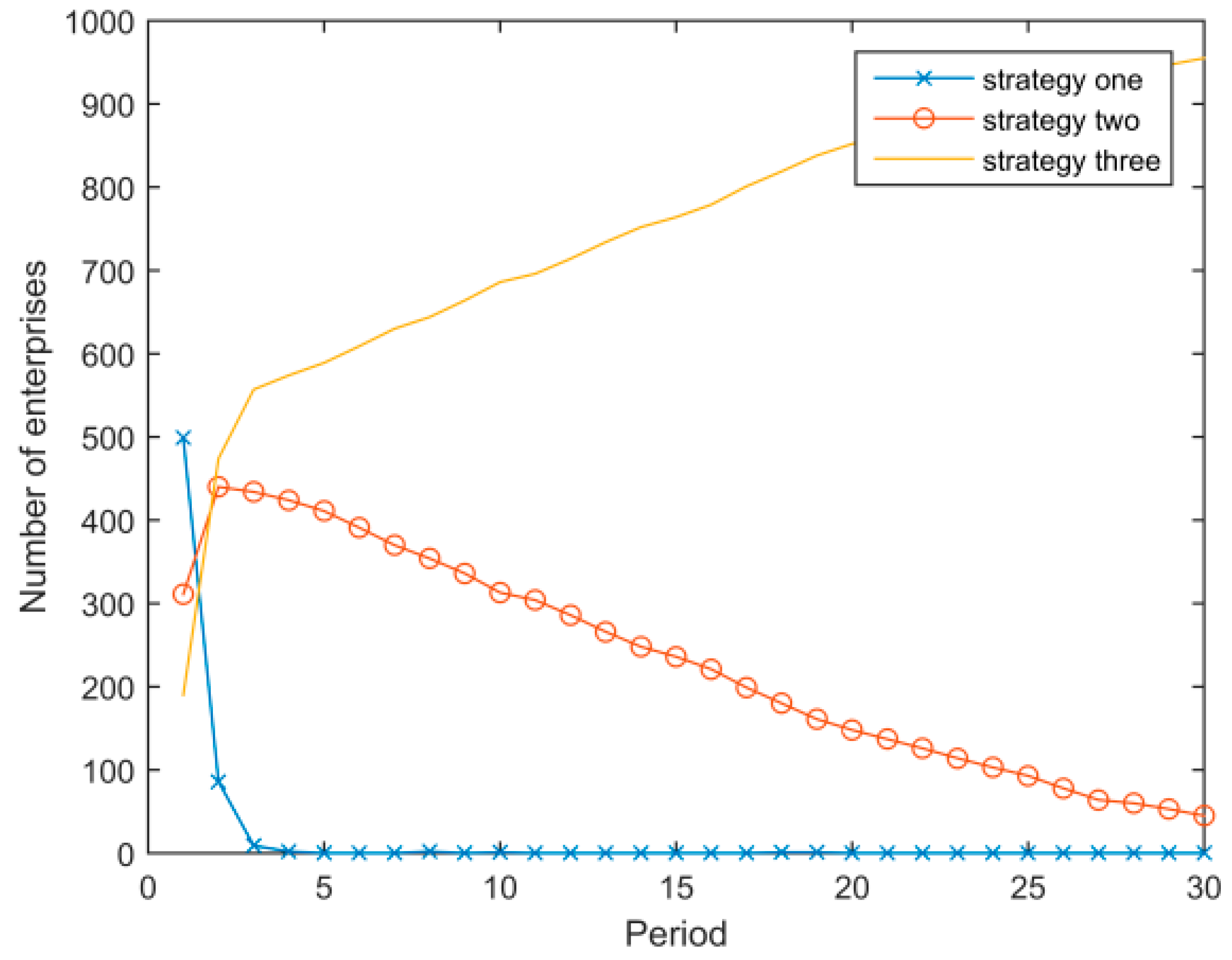
- Assuming that other parameters remain unchanged and only the price of the low energy consumption strategy changes, Figure 7 and Figure 8 show the evolutionary result when and , respectively. Figure 7 illustrates that when , the low energy consumption strategy is diffused much faster, and even the number of enterprises adopting the medium energy consumption strategy does not increase during the process of evolution. Figure 8 illustrates that when the price of the low energy consumption strategy is high, enterprises with a high energy consumption strategy initially convert to the medium energy consumption strategy, and the low energy strategy cannot spread across the system.
- (3)
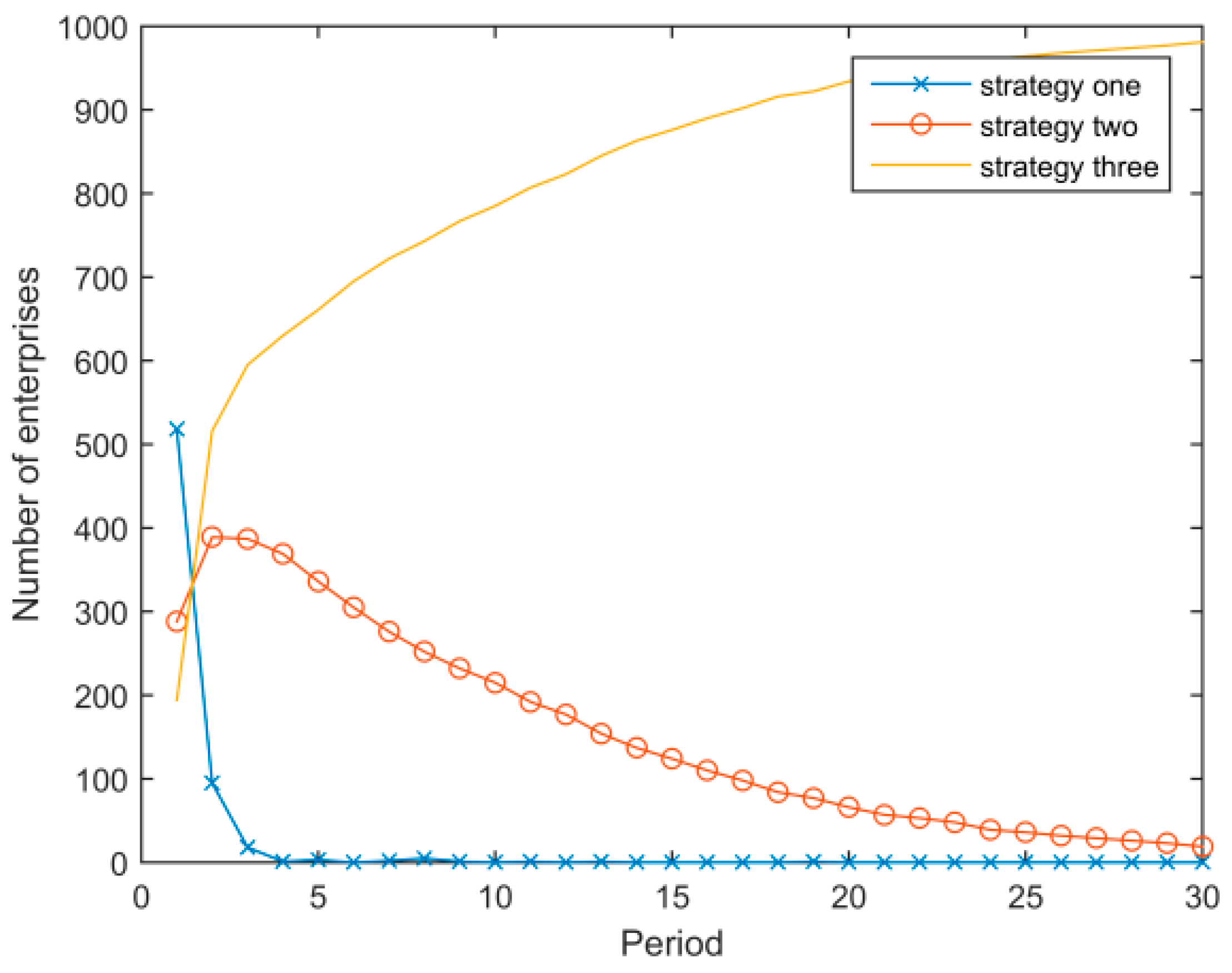
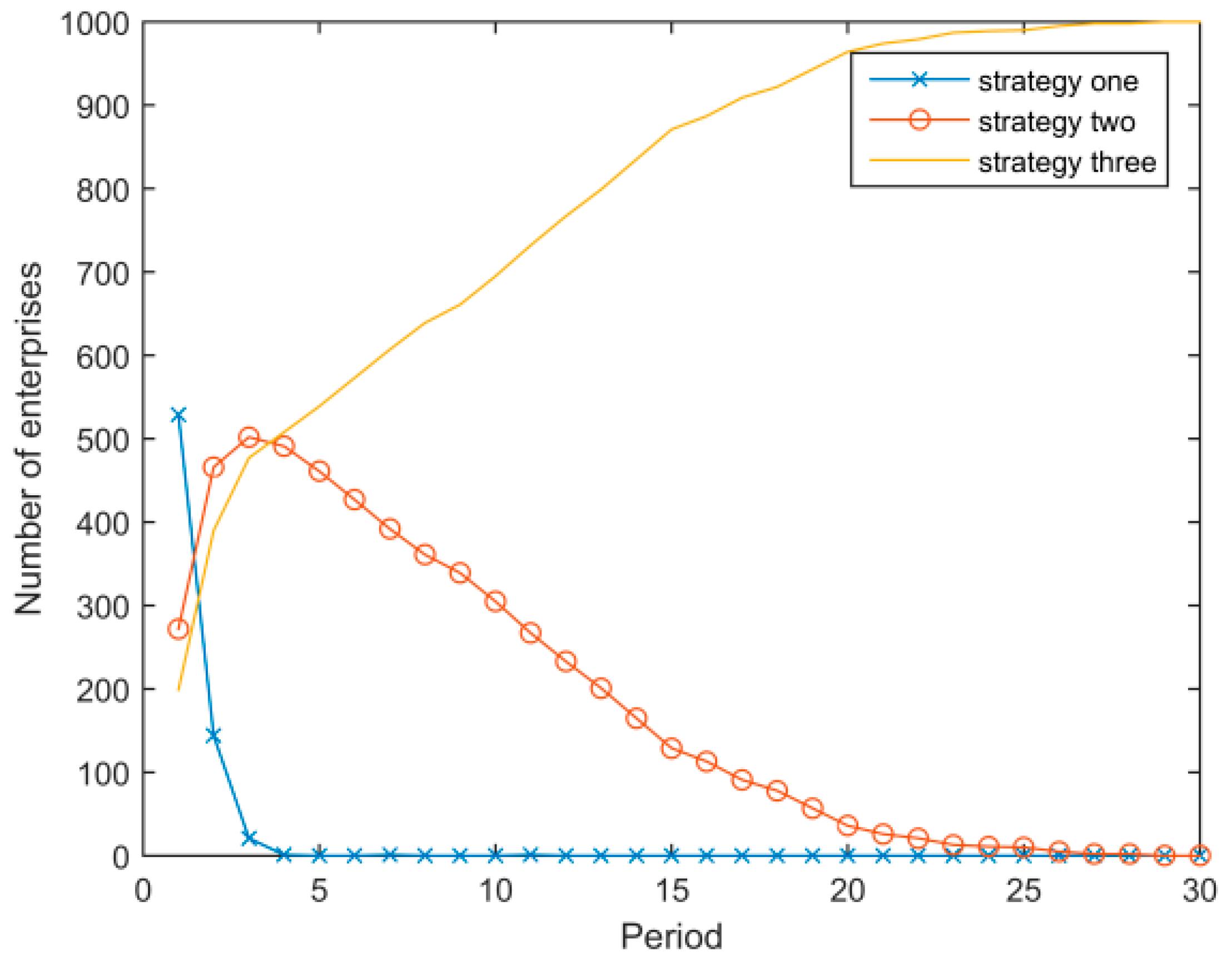
- Figure 9 shows the system evolutionary result when the network effect parameter is changed to , and Figure 10 when . Figure 9 illustrates that when the network externalities are small, the evolutionary trend is similar to that with the baseline parameter, but the speed is slower. Figure 10 illustrates that when the network externalities are large, the low energy consumption strategy eventually spreads to the whole system, but there is a period during which the medium energy consumption strategy dominates.
- (4)
- With other parameters unchanged, the expected adjustment factor ξ is set respectively to 0.1 and 0.9. The evolutionary results are shown in Figure 11 and Figure 12. Comparing these two figures with Figure 4, we conclude that the larger the expected adjustment factor, the higher the diffusion speed of the low energy consumption strategy. When the enterprises have a certain expectation for a standard, the faster adjustment quickly reduces the initially large number of enterprises adopting the high energy consumption strategy. The government should increase the publicity for successful examples of the transition to low energy consumption strategy, thereby making those high energy/medium energy enterprises become more confident in the transition to low energy consumption strategy, rather than let them think that it is a “difficult” process which requires significant time and money to complete.
5. Conclusions and Discussion
- (1)
- Under the progressive carbon tax system, enterprises initially adopt different energy consumption strategies and gradually switch to the low energy consumption strategy, which eventually spreads to the entire system. There are two reasons for this result. First, the low consumption strategy has higher profits and lower environmental costs, so the benefits cover the cost of transitioning from a high to a low energy consumption strategy. Second, due to the influence of network externalities, when a business entity chooses a low consumption strategy, neighboring enterprises increase their expected income from adopting a low energy consumption strategy, thus driving the agents in the neighborhood to adopt the strategy faster.
- (2)
- With other conditions remaining unchanged, the greater the discount coefficient of enterprises, the faster they will change to a low energy consumption strategy. Because companies pay more attention to future earnings, they pay more attention to how the environmental costs arising from production activities affect their profits.
- (3)
- The higher the cost of converting, the longer it takes for enterprises to change to a low energy consumption strategy. When the conversion cost is higher than a certain value, the low energy consumption strategy will not spread to the entire system because the cost is higher than the expected benefit. In this case, enterprises that previously adopted the high energy consumption strategy will change to the medium energy consumption strategy.
- (4)
- The network externality effect is positively associated with the diffusion speed of the low energy consumption strategy. When the network externality effect is large (but not too large), the advantages of the low energy consumption strategy gradually rise and the strategy quickly spreads to the whole system because of its higher profit and lower environmental costs.
- (5)
- The greater the expectation adjustment factor, the faster the diffusion speed of the low consumption strategy. This is due to the rapid reduction in the number of enterprises that initially adopt the high energy consumption strategy when the expectation adjustment speed is faster.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
- (1)
- To learn about the NW small-world network, let us start with the WS small-world network. The first small-world network model (WS small-world network model) was proposed by Watts and Strogatz [40]. Ordinarily, the connection topology is assumed to be either completely regular or completely random. However, many biological, technological, and social networks lie somewhere between these two extremes. Thus, they explored simple models of networks that can be tuned through this middle ground: regular networks ‘rewired’ to introduce increasing amounts of disorder. These systems can be highly clustered, like regular lattices, yet have small characteristic path lengths, like random graphs.
- (2)
- However, there is an obvious disadvantage of the WS small-world network: the process of random reconnection may destroy network’s connectivity, which means that isolated nodes may appear. Thus, Newman and Watts [41] developed the NW small-world network model in 1999 to improve the initial WS model. They pointed out that the NW small-world network model not only is more suitable for simulation analysis of the evolutionary game between individuals in the real world than the traditional regular or random networks, but also overcomes the disadvantage of the WS small-world network model.
Appendix B
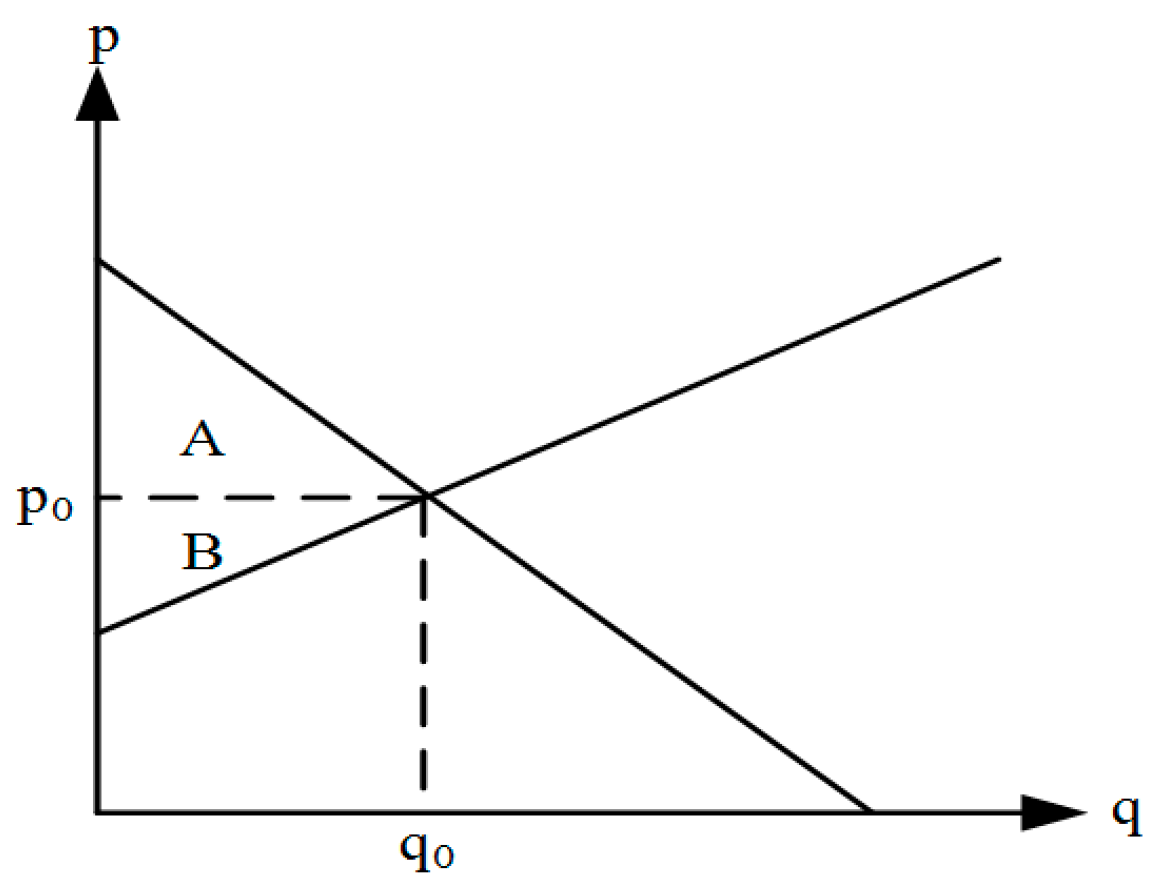
Appendix C
References
- Stavins, R.N. The problem of the commons: Still unsettled after 100 years. Am. Econ. Rev. 2011, 101, 81–108. [Google Scholar] [CrossRef]
- Bjorkegren, A.B.; Grimmond, C.S.B.; Kotthaus, S.; Malamud, B.D. CO2 emission estimation in the urban environment: Measurement of the CO2 storage term. Atmos. Environ. 2015, 122, 775–790. [Google Scholar] [CrossRef]
- Milliman, S.R.; Prince, R. Firm incentives to promote technological change in pollution control. J. Environ. Econ. Manag. 1989, 17, 247–265. [Google Scholar] [CrossRef]
- Montgomery, W.D. Markets in licenses and efficient pollution control programs. J. Econ. Theory 1972, 5, 395–418. [Google Scholar] [CrossRef]
- Tietenberg, T.H. Economic instruments for environmental regulation. Oxf. Rev. Econ. Policy 1990, 6, 17–33. [Google Scholar] [CrossRef]
- Agee, M.D.; Atkinson, S.E.; Crocker, T.D.; Williams, J.W. Non-separable pollution control: Implications for a CO2 emissions cap and trade system. Resour. Energy Econ. 2014, 36, 64–82. [Google Scholar] [CrossRef]
- Stavins, R.N. Market-based environmental policies: What can we learn from U.S. Experience (and related research)? Resour. Future 2003, 3–43. [Google Scholar] [CrossRef]
- Nordhaus, W.D. After Kyoto: Alternative mechanisms to control global warming. Am. Econ. Rev. 2005, 96, 31–34. [Google Scholar] [CrossRef]
- Wittneben, B.B.F. Exxon is right: Let us re-examine our choice for a cap-and-trade system over a carbon tax. Energy Policy 2009, 37, 2462–2464. [Google Scholar] [CrossRef]
- Herzog, T.; Baumert, K.A.; Pershing, J. Target: Intensity. An Analysis of Greenhouse Gas Intensity Targets, 1st ed.; World Resources Institute: Washington, DC, USA, 2006; pp. 15–24. ISBN 1-56973-638-3. [Google Scholar]
- Carayol, N.; Roux, P. Knowledge flows and the geography of networks: A strategic model of small world formation. J. Econ. Behav. Organ. 2009, 71, 414–427. [Google Scholar] [CrossRef]
- Hsu, C.-I.; Shih, H.-H. Small-world network theory in the study of network connectivity and efficiency of complementary international airline alliances. J. Air Transp. Manag. 2008, 14, 123–129. [Google Scholar] [CrossRef]
- Sheng, J. Effect of uncertainties in estimated carbon reduction from deforestation and forest degradation on required incentive payments in developing countries. Sustainability 2017, 9, 1608. [Google Scholar] [CrossRef]
- Liu, B.; Li, T.; Tsai, S. Low carbon strategy analysis of competing supply chains with different power structures. Sustainability 2017, 9, 835. [Google Scholar] [CrossRef]
- Li, W.; Li, G.; Zhang, R.; Sun, W.; Wu, W.; Jin, B.; Cui, P. Carbon reduction potential of resource-dependent regions based on simulated annealing programming algorithm. Sustainability 2017, 9, 1161. [Google Scholar] [CrossRef]
- Martin, R.; Muuls, M.; Wagner, U.J. The impact of the European Union emissions trading scheme on regulated firms: What is the evidence after ten years? Rev. Environ. Econ. Policy 2016, 10, 129–148. [Google Scholar] [CrossRef]
- Oestreich, A.M.; Tsiakas, I. Carbon emissions and stock returns: Evidence from the EU emissions trading scheme. J. Bank. Financ. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Q.; Liang, Q.-M.; Chen, H. A bibliometric analysis of research on carbon tax from 1989 to 2014. Renew. Sustain. Energy Rev. 2016, 58, 297–310. [Google Scholar] [CrossRef]
- Jaeger, W.K. Carbon taxation when climate affects productivity. Land Econ. 2002, 78, 354–367. [Google Scholar] [CrossRef]
- Bruvoll, A.; Larsen, B.M. Greenhouse gas emissions in Norway: Do carbon taxes work? Energy Policy 2004, 32, 493–505. [Google Scholar] [CrossRef]
- Floros, N.; Vlachou, A. Energy demand and energy-related CO2 emissions in Greek manufacturing: Assessing the impact of a carbon tax. Energy Econ. 2005, 27, 387–413. [Google Scholar] [CrossRef]
- Callan, T.; Lyons, S.; Scott, S.; Tol, R.S.J.; Verde, S. The distributional implications of a carbon tax in Ireland. Energy Policy 2009, 37, 407–412. [Google Scholar] [CrossRef]
- Bureau, B. Distributional effects of a carbon tax on car fuels in France. Energy Econ. 2011, 33, 121–130. [Google Scholar] [CrossRef] [Green Version]
- Wesseh, J.P.K.; Lin, B. Optimal emission taxes for full internalization of environmental externalities. J. Clean. Prod. 2016, 137, 871–877. [Google Scholar] [CrossRef]
- Liu, X.; Wang, C.; Niu, D.; Suk, S.; Bao, C. An analysis of company choice preference to carbon tax policy in china. J. Clean. Prod. 2015, 103, 393–400. [Google Scholar] [CrossRef]
- Yates, R. Universal health coverage: Progressive taxes are key. Lancet 2015, 386, 227–229. [Google Scholar] [CrossRef]
- Chiroleu-Assouline, M.; Fodha, M. From regressive pollution taxes to progressive environmental tax reforms. Eur. Econ. Rev. 2014, 69, 126–142. [Google Scholar] [CrossRef]
- Orsi, F. Environment: Progressive taxes for sustainability. Nature 2017, 541, 464. [Google Scholar] [CrossRef] [PubMed]
- Maynard Smith, J. The theory of games and the evolution of animal conflicts. J. Theor. Biol. 1974, 47, 209–221. [Google Scholar] [CrossRef]
- Smith, J.M.; Price, G.R. The logic of animal conflict. Nature 1973, 246, 15–18. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Ji, P.; Ma, X.; Li, G. Developing green purchasing relationships for the manufacturing industry: An evolutionary game theory perspective. Int. J. Prod. Econ. 2015, 166, 155–162. [Google Scholar] [CrossRef]
- Scrimgeour, F.; Oxley, L.; Fatai, K. Reducing carbon emissions? The relative effectiveness of different types of environmental tax: The case of New Zealand. Environ. Model. Softw. 2005, 20, 1439–1448. [Google Scholar] [CrossRef]
- Telli, Ç.; Voyvoda, E.; Yeldan, E. Economics of environmental policy in turkey: A general equilibrium investigation of the economic evaluation of sectoral emission reduction policies for climate change. J. Policy Model. 2008, 30, 321–340. [Google Scholar] [CrossRef] [Green Version]
- Timilsina, G.R.; Shrestha, R.M. General equilibrium effects of a supply side GHG mitigation option under the clean development mechanism. J. Environ. Manag. 2006, 80, 327–341. [Google Scholar] [CrossRef] [PubMed]
- Baron, D.P.; Meyerson, R.B. Regulating a monopolist with unknown costs. Econometrica 1982, 50, 911–930. [Google Scholar] [CrossRef]
- Gabriel, S.A.; Conejo, A.J.; Fuller, J.D.; Hobbs, B.F.; Ruiz, C. Complementarity Modeling in Energy Markets, 1st ed.; Springer: New York, NY, USA, 2013; pp. 72–476. ISBN 978-1-4419-6122-8. [Google Scholar]
- Ho, T.H.; Wang, X.; Camerer, C.F. Individual differences in EWA learning with partial payoff information. Econ. J. 2008, 118, 37–59. [Google Scholar] [CrossRef]
- Xian, Y.B.; Mei, L. Adaptive expectation, complex network and the dynamic of standard diffusion—Research based on computational economics. J. Manag. Sci. 2007, 20, 62–71. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J.; Watts, D.J. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
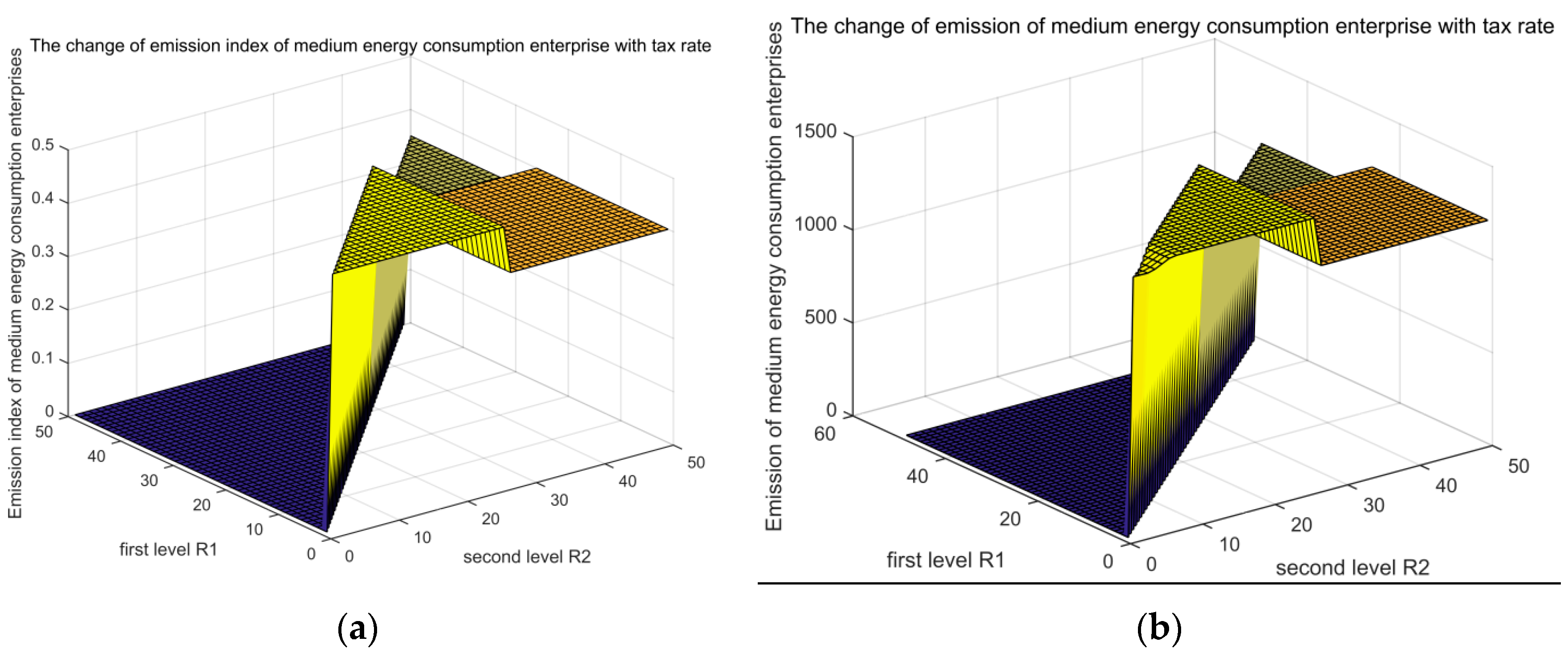
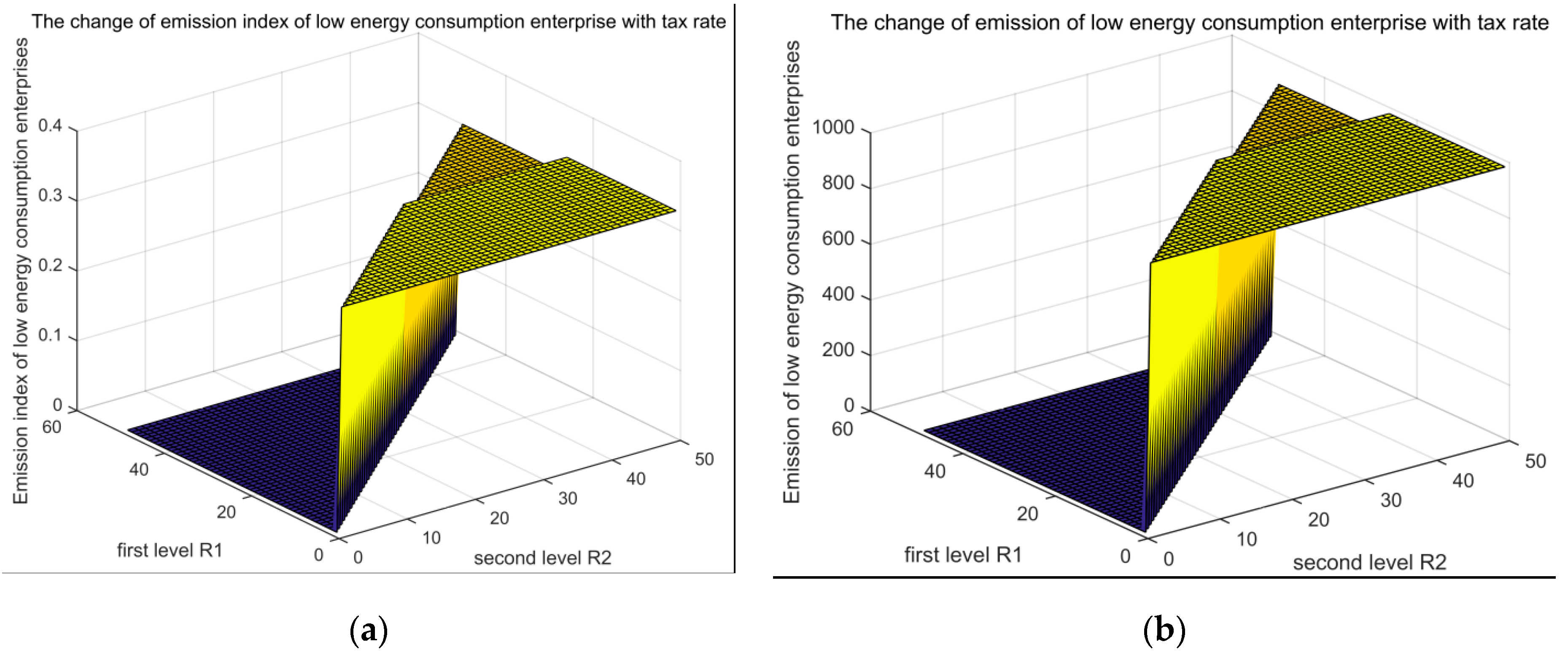
| Type of Fuel | Variable Cost (VC) | Energy | Emission Factor |
|---|---|---|---|
| wil | hl (US $/t 100 m3) | (GJ/t·100 m3) | el (t CO2/t·100 m3) |
| coal | 100 | 32.1 | 2.457 |
| petroleum coke | 50 | 23.3 | 2.53 |
| natural gas | 11 | 3.72 | 0.29 |
| Enterprise | Cost of Production | Limit of Production Capacity | Energy | ||
|---|---|---|---|---|---|
| ci ($/t) | ti | di | bi (GJ/t) | ||
| A | 22 | 0.001 | 3000 | 6 | |
| B | 26 | 0.001 | 3000 | 4.5 | |
| C | 29 | 0.001 | 3000 | 3 | |
| Emission Index | Emissions | Environmental Cost | Pre-Tax Profit | After-Tax Profit | |
|---|---|---|---|---|---|
| High energy consumption enterprise | 0.4677 | 1253.6 | 12,138 | 19,320.5 | 7182.5 |
| Medium energy consumption enterprise | 0.3508 | 1052.4 | 4115.3 | 33,973.3 | 29,858 |
| Low energy consumption enterprise | 0.3000 | 900 | 0 | 52,534 | 52,534 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Huang, W.; Liu, P. Carbon Reduction Strategies Based on an NW Small-World Network with a Progressive Carbon Tax. Sustainability 2017, 9, 1747. https://doi.org/10.3390/su9101747
Wu B, Huang W, Liu P. Carbon Reduction Strategies Based on an NW Small-World Network with a Progressive Carbon Tax. Sustainability. 2017; 9(10):1747. https://doi.org/10.3390/su9101747
Chicago/Turabian StyleWu, Bin, Wanying Huang, and Pengfei Liu. 2017. "Carbon Reduction Strategies Based on an NW Small-World Network with a Progressive Carbon Tax" Sustainability 9, no. 10: 1747. https://doi.org/10.3390/su9101747





