1. Introduction
Highly accurate forecasting of streamflow is critical for water resource management as fresh water shortages increase in arid and semi-arid regions [
1]. As an important component of the water budget, it is also critical for sustainable crop production, food security and social sustainability [
2,
3,
4]. With the data assimilation method and remotely sensed data, streamflow estimates can be improved a lot [
5,
6,
7,
8,
9]. However, most of these studies used remotely sensed soil moisture or snow; little attention has been focused on assimilating observed evapotranspiration (ET) data. In particular, evapotranspiration is the largest mode of water loss in arid and semi-arid regions [
2]. Streamflow estimates will benefit a lot from taking into account observed evapotranspiration from remote sensing in these areas.
Remote sensing-derived ET products have been used to evaluate or calibrate the hydrological model and improve streamflow forecasting [
10,
11,
12,
13]. However, such calibrations need a lot of time and labor or computing resources. Additionally, calibration is insufficient for streamflow forecasting when forcing input (i.e., precipitation) is not correct. Data assimilation as a complementary tool can be used to fill up the calibration deficiency in decreasing the discrepancy between streamflow prediction and observation. Pan et al. [
14] assimilated Moderate Resolution Imaging Spectroradiometer (MODIS)-derived ET into Variable Infiltration Capacity (VIC) and Surface Energy Balance System (SEBS) models to estimate water budget terms. However, ET was only a non-state variable in the model, which could not feed the assimilation effect back to the model and update the model’s state variables, so the other hydrological variables were not optimized as a whole and this method is not suitable for improving streamflow prediction.
ET-related data assimilation researches are still in the formative stage for most hydrological models [
15,
16]. For model state updating purposes, ET observation should be associated with the model state variable; considering ET as a state variable in a model (e.g., [
15]) or associating it with other state variables are two practical methods. Remotely sensed evapotranspiration can be used for hydrological model parameter calibration or estimation, which can affect the surface runoff generation [
10,
12,
13,
16,
17]. Parr et al. [
18] found that hydrological predictions may be subject to the bias in past ET modeling, leading to substantial uncertainties in the modeled hydrological trend. They replaced the simulated ET components (canopy evaporation, transpiration, bare ground evaporation, canopy sublimation, and surface sublimation) of the VIC model with the bias-corrected ET calculated from a simple bias-correction algorithm and historic remotely sensed ET. The streamflow estimation was improved due to the corrected ET components. This procedure can still be considered as a model bias correction method. Understanding historic evapotranspiration trends and high-quality forcing data are prerequisites, because the mass balance is the main constrain for ET components and runoff updating in VIC [
18]. Generally, monthly time scale water balance, including ET and streamflow, can be simulated well by well calibrated hydrological models. They are particularly valuable for applications where one is primarily interested in monthly, seasonal and annual streamflow volumes [
19]. While the flood risk warning and management need hydrological data at high spatiotemporal resolution, utilizing fresh incoming high-resolution ET data for hydrological forecasting simultaneously is still a big challenge.
It is a major challenge to relate surface runoff modeling to the ET modeling. The reports and literatures on the relationship among precipitation, ET and surface runoff will be useful for associating daily ET and surface runoff [
20]. Rawlins et al. [
21] found that simulations of arctic evapotranspiration and runoff are both strongly dependent on the quality of time series data used to drive the model. The uncertainty of model input (i.e., precipitation) can be the main factor to influence the simulation accuracy of both ET and surface runoff [
22]. The uncertainty of precipitation can be defined by a widely used multiplicative error model [
23,
24]. An estimated precipitation error can be obtained by analyzing observed and simulated ET. The error for simulated ET can be transformed to precipitation error based on the ET model. So using remotely sensed evapotranspiration to reduce input uncertainties and further to improve the hydrologic predictions is practical.
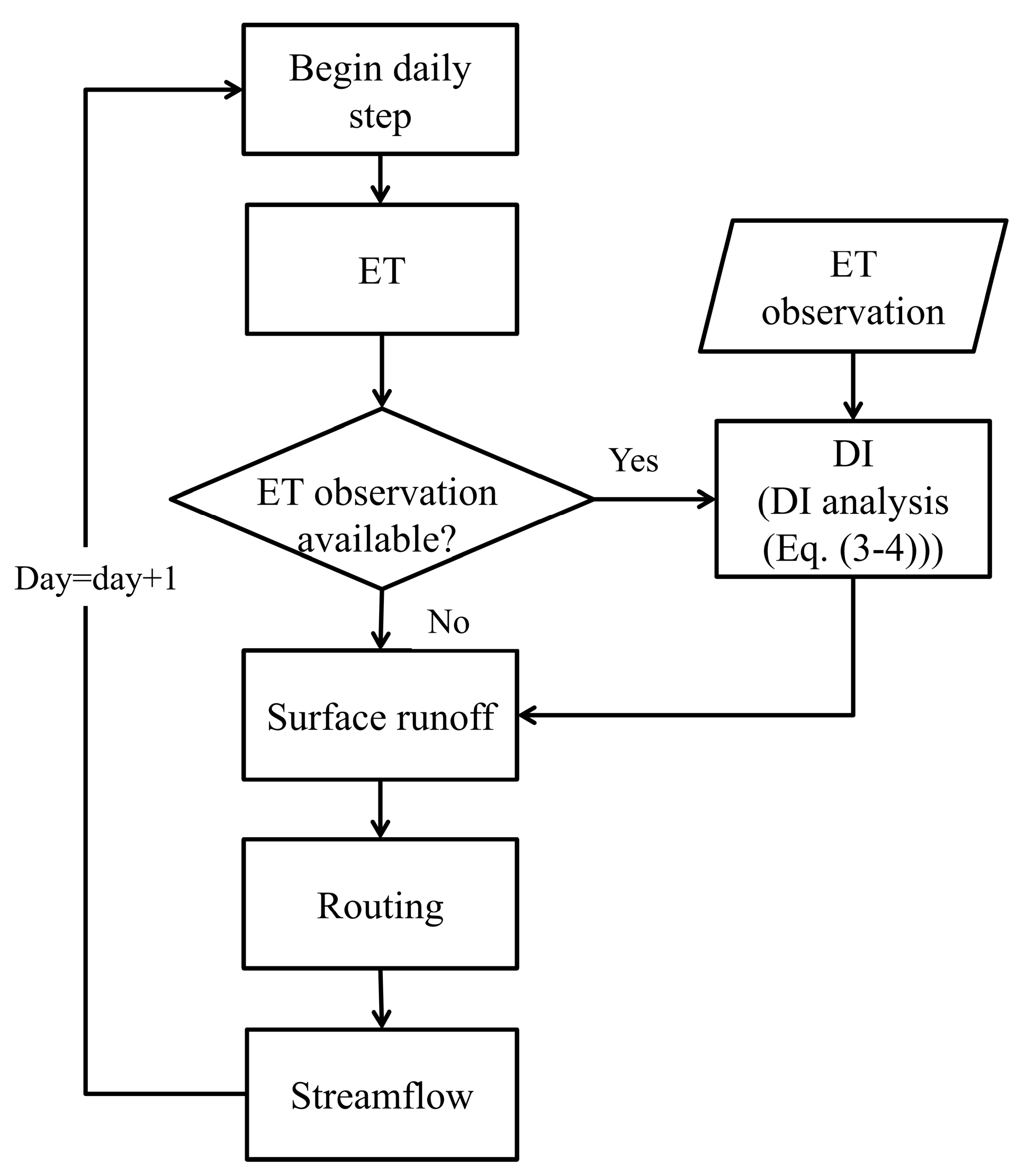
In this paper, we assess the performance of streamflow predictions with remote sensing-derived ET and state augmentation direct insertion method for a distributed hydrological model, SWAT. We have to solve two problems: (1) matching ET data with the modeling units efficiently; and (2) assimilating the ET into the model to update the streamflow estimates. In this way, a modified SWAT model and a state augmentation direct insertion assimilation method are designed to assimilate ET data.
The remainder of the paper is organized as follows.
Section 2 and
Section 3 provide background on hydrological models.
Section 4 describes the direct insertion data assimilation method. We describe case studies including the design of the synthetic and real-word data assimilation experiments in
Section 5.
Section 6 presents the results from two designed cases: (1) hydrological modeling scheme; and (2) evapotranspiration data assimilation scheme. Finally, conclusions and outlooks are summarized in
Section 7.
7. Summary and Outlooks
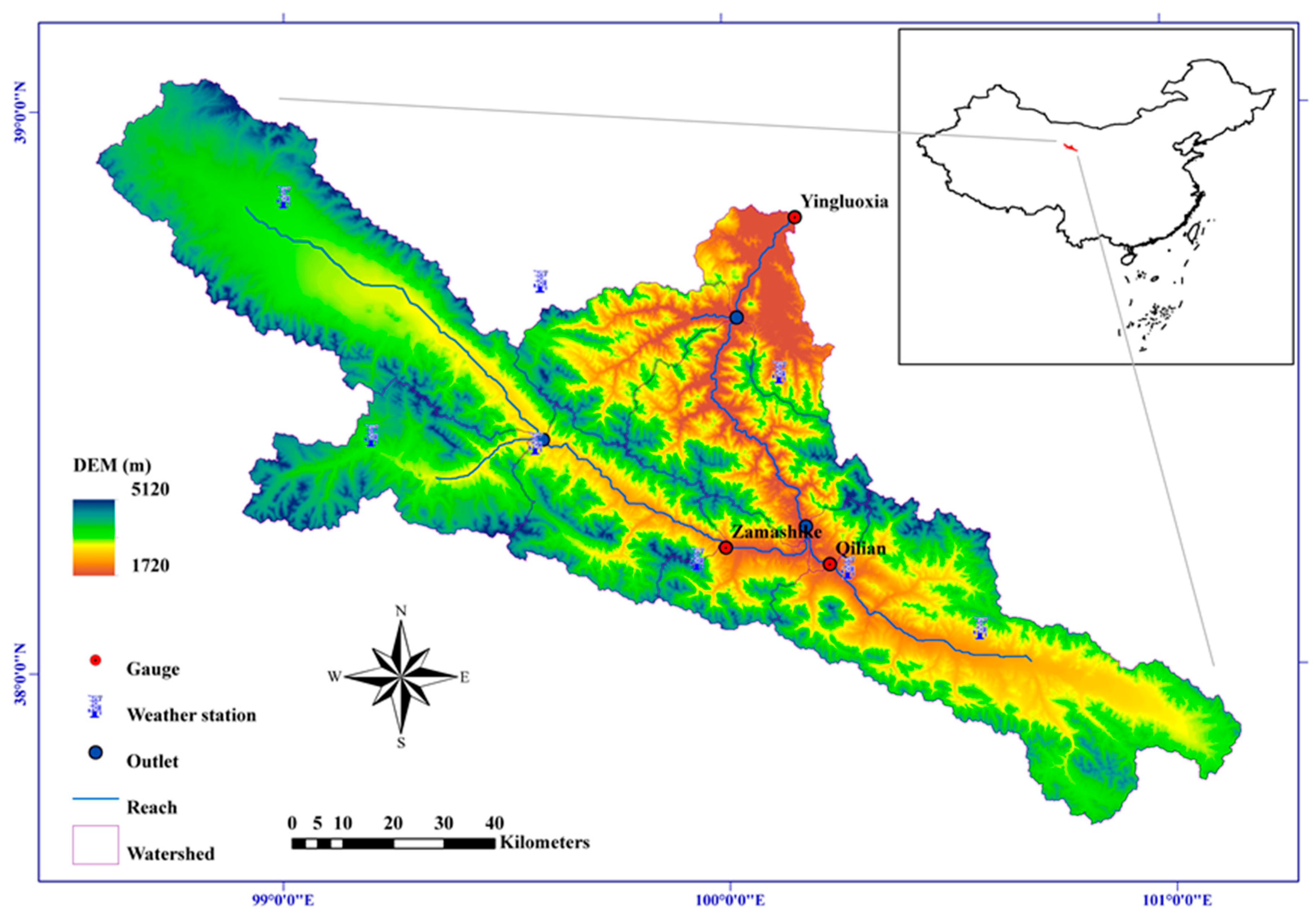
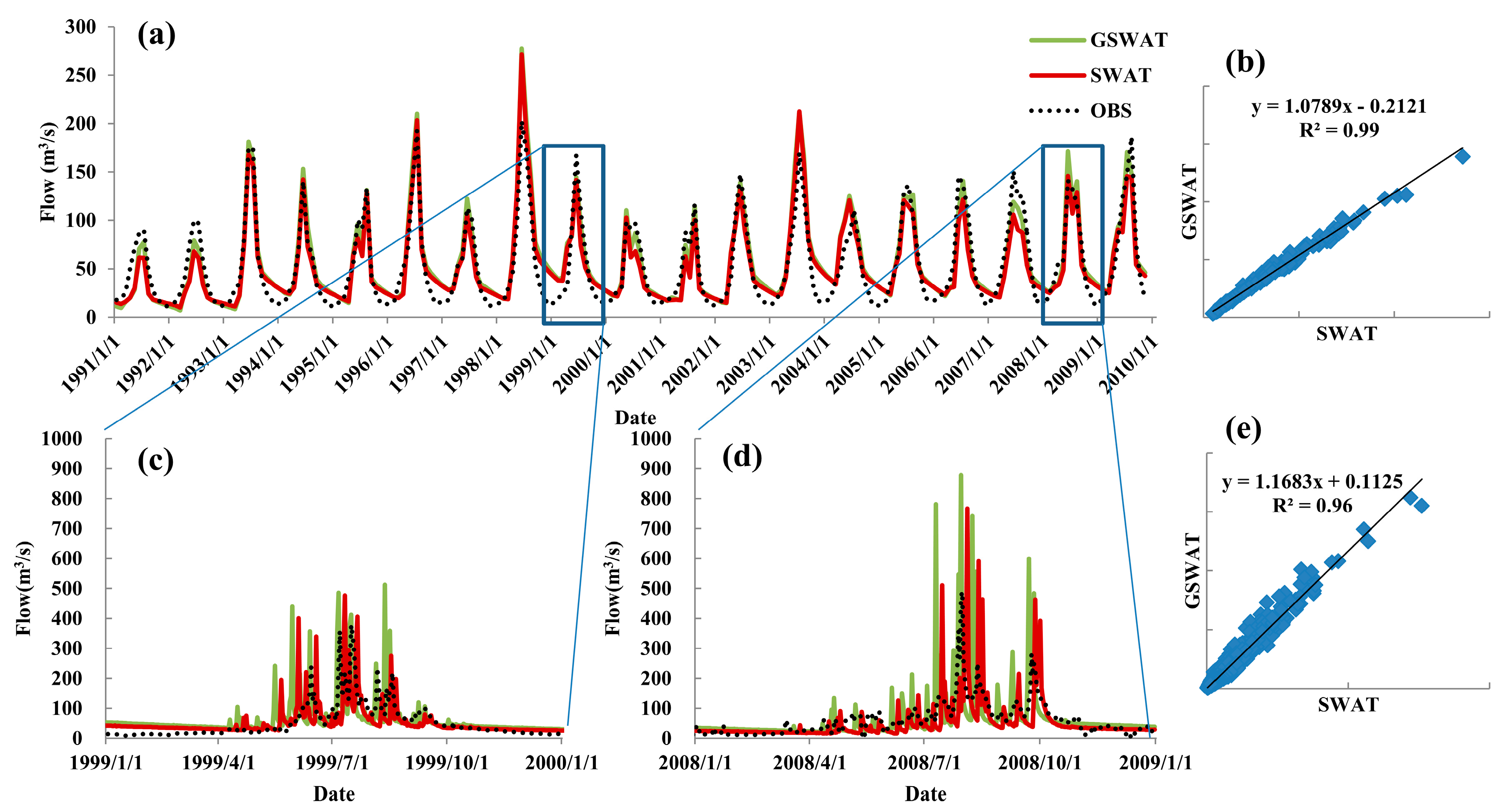
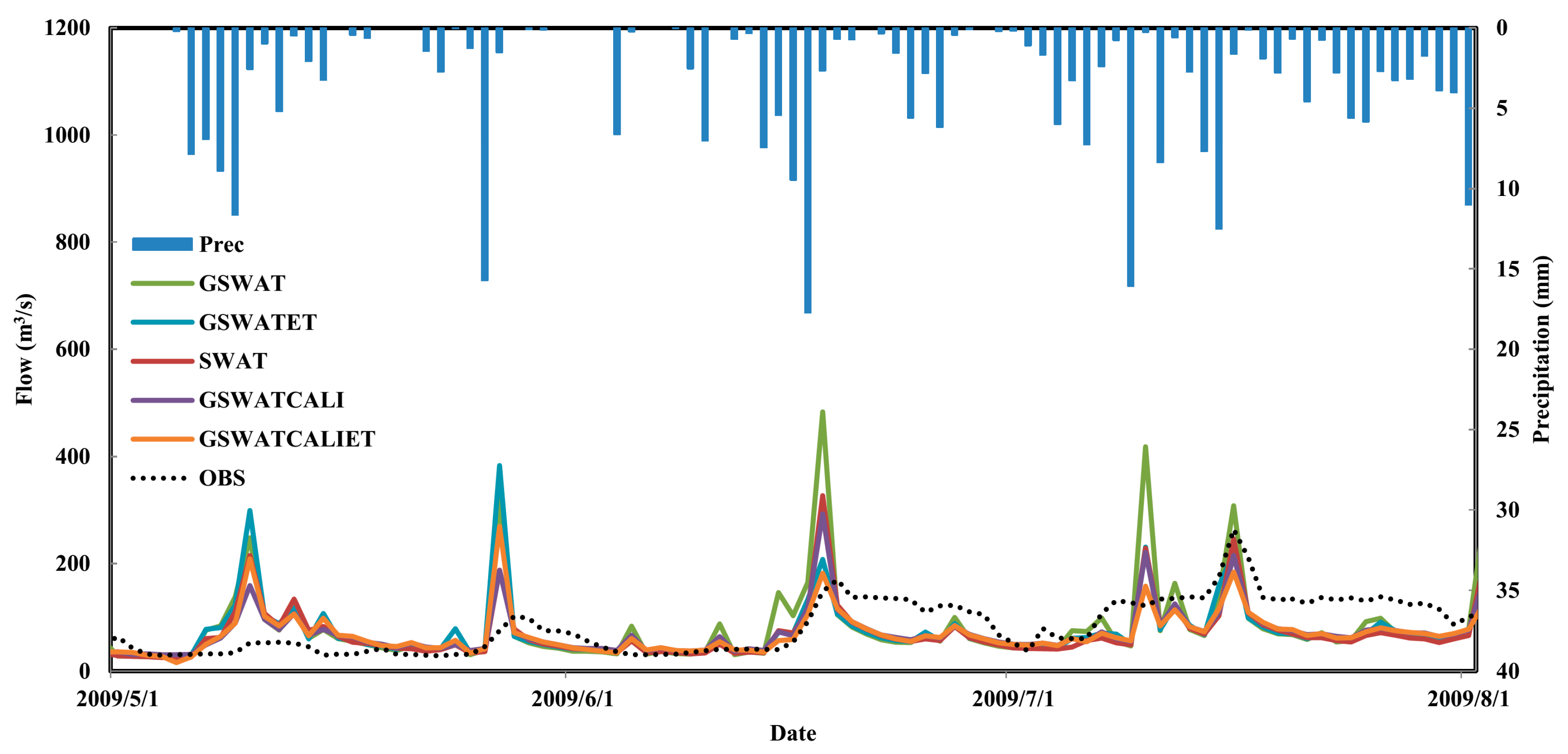
Streamflow is an important water resource for sustainable watershed management. To promote the accuracy of the streamflow estimation in a semi-arid basin, the evapotranspiration product was assimilated into the gridded SWAT (GSWAT) model using the direct insertion method. We first modified SWAT to incorporate grid format data and assessed its capability in hydrological modeling. Parameters were further calibrated to improve daily streamflow prediction for SWAT and GSWAT. We related the ET modeling uncertainty (mainly precipitation uncertainty) to surface runoff modeling and updated it with incoming ET observation at daily time scale. The observed ET along with modeled ET updated surface runoff by using correct coefficient. Correct coefficient was calculated based on the assumption of the precipitation uncertainty for surface runoff and evapotranspiration modeling is correlated. This kind of assumption can be further improved with deeper investigation. Updated fluxes enter into the reach and update the water storage, which will route to the outlet of the basin finally. A synthetic data experiment and a real data experiment were carried out for a semi-arid basin to validate the efficacy of the state augmentation direct insertion method. The results show that the state augmentation direct insertion (DI) assimilation method can achieve an acceptable streamflow estimation improvement with a reliable ET observation, which derived from the combination of multisource remote sensing data and ET model with multiple parameterizations [
37].
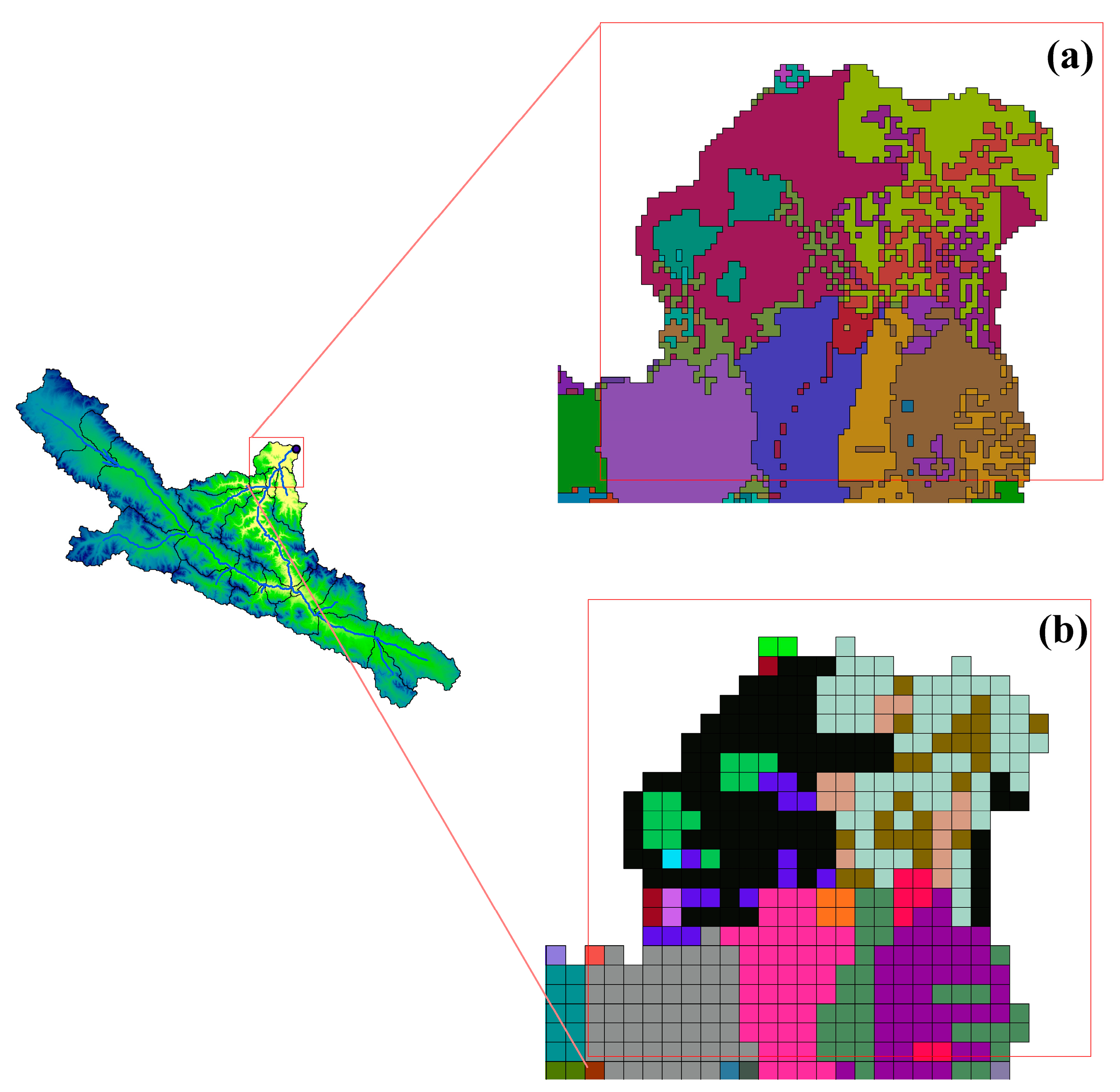
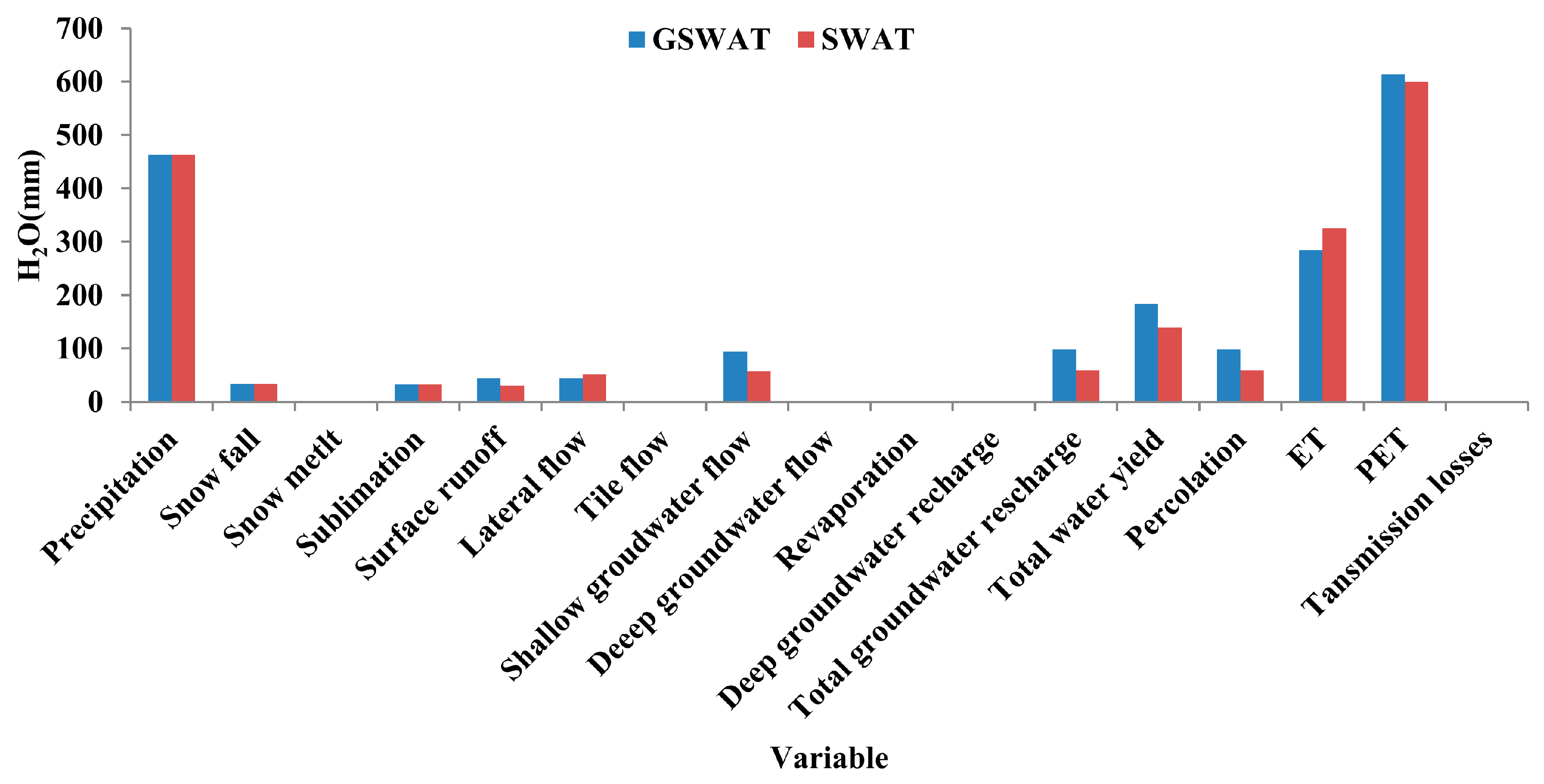
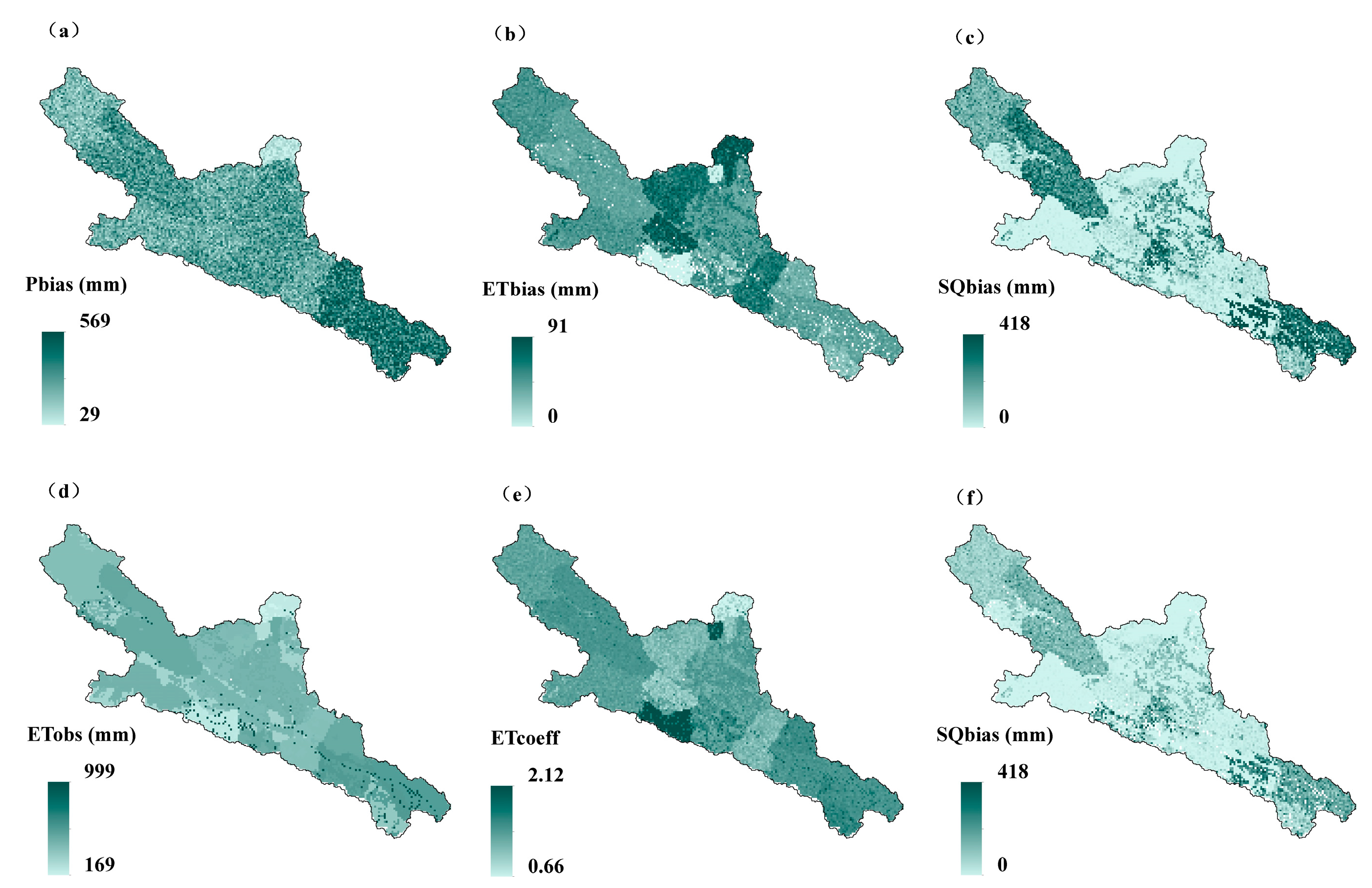
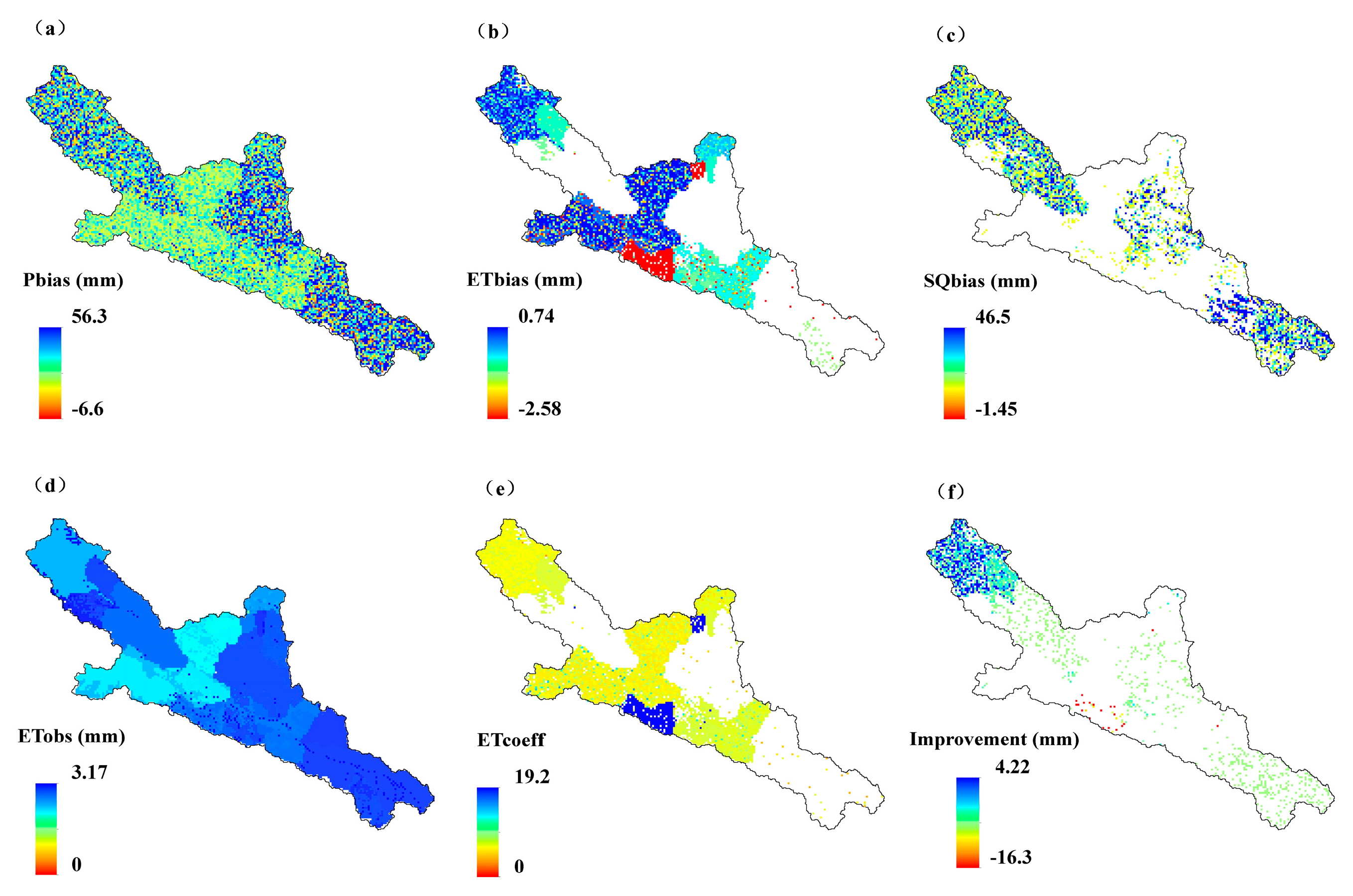
Parameters for models (SWAT, GSWAT and GSWATET) are calibrated against daily and monthly streamflow observations from 1990 to 1999 and validated from 2000 to 2009. Spatial domain and parameter mismatch between gridded and original HRU dominate the small discrepancies between basin variables simulated by GSWAT and SWAT. Spatial resolution of GSWAT can be matched with SWAT but will cost a lot of computational time. The detailed comparison between GSWAT and SWAT has been studied and will not be discussed in greater detail here [
28]. Toward perfect streamflow prediction, calibration and data assimilation are all necessary. When the calibration is not sufficient, the data assimilation method can be used as a complement tool to diminish forecasting errors sourced from model uncertainties. In this study, parameter optimization and data assimilation procedures are separate. The simultaneous optimization and data assimilation (SODA) method can be used for improving hydrological forecasting [
58,
59].
Not only streamflow but also other hydrological variables (e.g., soil moisture and snow water equivalent) can be updated by assimilating ET product into the model. We did not include this kind of study in this article to briefly highlight the possibility of improving streamflow estimation with ET assimilated. Different ET products generated from different methods (e.g., [
60]) can also be assimilated into the model to evaluate their effects on regional water balance simulation. Besides ET products, GSWAT can also assimilate other remote sensing data such as snow state products and soil moisture products from MODIS, AMSR-E, SMOS (Soil Moisture and Ocean Salinity) and SMAP (Soil Moisture Active and Passive) etc. Remotely sensed precipitation data can also be assimilated into GSWAT to decrease the forcing input uncertainty. The use of remote sensing data for hydrological model data assimilation has important implications to the catchments with sparse or no gauging. With more and more available remote sensing data, data assimilation technology will be a promising method to merge these data to provide more accurate land surface states and fluxes products for assisting watershed management and flood/draught prediction.