An Extended Input Output Table Compiled for Analyzing Water Demand and Consumption at County Level in China
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Water Consumption in Primary Industry
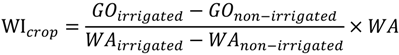
3.2. Water Usage in Other Industries
3.3. Mathematical Approach
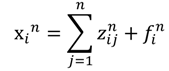
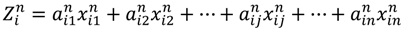
 ) of each sector, which would represent proportional changes in each sector by final demand changes at provincial level. According to Stone’s explanation,
) of each sector, which would represent proportional changes in each sector by final demand changes at provincial level. According to Stone’s explanation,  also indicates the economic phenomena of substitution effect and fabrication effect [32,33].
also indicates the economic phenomena of substitution effect and fabrication effect [32,33]. ;
;  is the total consumption by sector i in region r and
is the total consumption by sector i in region r and  is gross input of sector i in r at county level.
is gross input of sector i in r at county level.  is the total input by sector i and
is the total input by sector i and  is gross input of sector i at provincial level. In addition, when defining the regional fabrication effect for sector j in region r as
is gross input of sector i at provincial level. In addition, when defining the regional fabrication effect for sector j in region r as  ;
;  is the total value-added payment by sector j in region r and
is the total value-added payment by sector j in region r and  is gross output of sector j in r at county level.
is gross output of sector j in r at county level.  is the total value-added payments by sector j and
is the total value-added payments by sector j and  is gross output of sector j at provincial level. The regional fabrication effect gives the possibility changes in the proportion of value-added water demand in a sector’s output over iteration. Thereby, the expression of the technical coefficient (
is gross output of sector j at provincial level. The regional fabrication effect gives the possibility changes in the proportion of value-added water demand in a sector’s output over iteration. Thereby, the expression of the technical coefficient (  ) of each sector at the provincial level would also be derived in Equation (4), which also presents as initial value of the technical coefficient at county level.
) of each sector at the provincial level would also be derived in Equation (4), which also presents as initial value of the technical coefficient at county level.
 , is introduced, which is iteratively caused by cultivation and human activities intervention into sectoral outputs in Equation (5) when defining Equation (6) as a row of the total iteratively intermediate demand matrix Z rr at county level. Here, we designed local total final demand would be iterated and eventually burden on water consumption. In other words, we assumed other sectoral final demands would be driven by natural resource consumption.
, is introduced, which is iteratively caused by cultivation and human activities intervention into sectoral outputs in Equation (5) when defining Equation (6) as a row of the total iteratively intermediate demand matrix Z rr at county level. Here, we designed local total final demand would be iterated and eventually burden on water consumption. In other words, we assumed other sectoral final demands would be driven by natural resource consumption.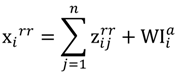
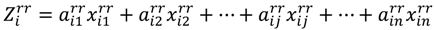
 as
as  ; here u and v is the convention in literature, and v’ represents the value-added vector. Then, an evolutionary equation would be reached in Equation (7), which is the original name of RAS-algorithm through a transaction as Equation (8).
; here u and v is the convention in literature, and v’ represents the value-added vector. Then, an evolutionary equation would be reached in Equation (7), which is the original name of RAS-algorithm through a transaction as Equation (8).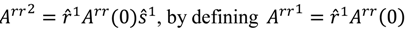
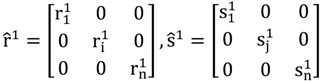 when ri1 = ui(1) /ui0 is the first of what will be a series of adjustment terms for the logic of the row adjustments; and when sj1 = vj(1) /vj0 is the first of what will be a series of adjustment terms for the logic of the column adjustments; Note that, if the ri1 < 1, the elements in ith row of Arr(0) are all reduced when multiply by ri1, and vice versa; if the sj1 < 1, the elements in jth column of Arr1 are all reduced when multiply sj1, and vice versa. By repetition of the RAS procedures over 1992–2007, a relative consistent technical coefficient matrix would be derived when the following Equation (9) can be held. It could also predict consistent-based structural changes in the future [33,34].
when ri1 = ui(1) /ui0 is the first of what will be a series of adjustment terms for the logic of the row adjustments; and when sj1 = vj(1) /vj0 is the first of what will be a series of adjustment terms for the logic of the column adjustments; Note that, if the ri1 < 1, the elements in ith row of Arr(0) are all reduced when multiply by ri1, and vice versa; if the sj1 < 1, the elements in jth column of Arr1 are all reduced when multiply sj1, and vice versa. By repetition of the RAS procedures over 1992–2007, a relative consistent technical coefficient matrix would be derived when the following Equation (9) can be held. It could also predict consistent-based structural changes in the future [33,34].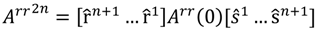
3.4. Non-Parameter Methodology for Missing Data Interpolation
4. Study Area
5. Data Collection
6. Empirical Comparison Results
| Primary Industry Total Output | Difference from county-level | Diff percentage |
|---|---|---|
| (Thousand CNY) | (%) | |
| Agriculture | −6317.9 | −17.1 |
| Forestry | 204.2 | 12.5 |
| Animal Husbandry | −14.5 | −3.2 |
| Fisheries | 0.0 | - |
| Others in Primary Industry | 0.0 | - |
| Ferrous Metal Smelting & Rolling | 0.0 | - |
| Other Non-metallic Mineral Mining | −0.4 | - |
| Chemical Raw Materials & Products Manufacturing | −43741.2 | −68.3 |
| Others in Secondary industry | −724.1 | −1.0 |
| Transportation and Warehousing Postal | −1822.0 | −92.2 |
| Wholesale and Retail trade | −500.2 | −89.5 |
| Others in Tertiary industries | −2658.4 | −76.7 |
| Sectoral Input for Total Output in Other Industries | Secondary Industry (%) | Tertiary Industry (%) |
|---|---|---|
| Agriculture | −92 | −91 |
| Forestry | - | - |
| Animal Husbandry | - | - |
| Fisheries | - | −99 |
| Others in Primary Industry | - | - |
| Ferrous Metal Smelting & Rolling | 56 | - |
| Other Non-metallic Mineral Mining | −93 | - |
| Chemical Raw Materials & Products Manufacturing | −34 | −93 |
| Others in Secondary industry | 160 | −16 |
| Transportation and Warehousing Postal | −93 | −69 |
| Wholesale and Retail trade | - | −99 |
| Others in Tertiary industries | −82 | −5 |
7. Conclusion and Discussion
Acknowledgments
Author Contributions
Appendix
Appendix A
| XWAT | XAGR | XFRT | XHCD | XFISH | XADS | XFSR | XONM | XCPM | XOSI | XTWP | XWRT | XOTI | XFD | GO | XIM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WATER | 133 | 548 | 174 | 1 | 0 | 0 | 1 | 1 | 1 | 99 | 3 | 1 | 85 | 6399 | 6142 | −1304 |
| AGR | 0 | 28,284 | 0 | 1090 | 0 | 1263 | 0 | 0 | 0 | 4955 | 1572 | 0 | 266 | 209,207 | 337,947 | 91,309 |
| FRT | 0 | 0 | 1833 | 0 | 0 | 0 | 0 | 0 | 0 | 136 | 0 | 0 | 1 | 10,327 | 13,807 | 1509 |
| HCD | 0 | 0 | 0 | 440 | 0 | 1 | 0 | 0 | 0 | 73 | 0 | 0 | 2 | 78,037 | 113,299 | 34,747 |
| FISH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30 | 4602 | 906 | −3726 |
| ADS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 36,571 | 12,261 | −24,314 |
| FSR | 0 | 0 | 0 | 0 | 0 | 0 | 577,990 | 0 | 306 | 16131 | 1 | 0 | 1 | 43,237 | 624,907 | −12,759 |
| ONM | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1271 | 13 | 897 | 4 | 0 | 2 | 10,475 | 20,266 | 7603 |
| CPM | 14 | 19,327 | 496 | 0 | 0 | 478 | 1459 | 22 | 63,219 | 6614 | 11 | 0 | 846 | 166,629 | 121,714 | −137,402 |
| OSI | 2534 | 29,375 | 5756 | 30506 | 2405 | 869 | 71,843 | 13,560 | 61,995 | 3,924,667 | 67,531 | 2069 | 148,177 | 1,460,661 | 2,514,478 | −3,307,470 |
| TWP | 13 | 44 | 32 | 5 | 3 | 69 | 440 | 82 | 119 | 3362 | 12,326 | 1811 | 1285 | 199,692 | 254,790 | 35,506 |
| WRT | 0 | 0 | 0 | 0 | 0 | 59 | 0 | 0 | 0 | 0 | 3 | 0 | 11 | 124,571 | 171,759 | 47,115 |
| OTI | 442 | 161 | 195 | 120 | 87 | 242 | 4380 | 453 | 697 | 17,789 | 4305 | 6368 | 155,123 | 1,043,561 | 896,549 | −337,374 |
| TVA | 6842 | 204,937 | 7345 | 92,221 | 5380 | 4692 | 201,792 | 9910 | 34,104 | 689,681 | 135,970 | 124,487 | 561,822 | 0 | 0 | 0 |
| TI | 9979 | 282,677 | 15,831 | 124,383 | 7875 | 7675 | 857,905 | 25,299 | 160,455 | 4,664,409 | 221,726 | 134,736 | 867,650 | 3,393,969 | 5,088,825 |
| XWAT | XAGR | XFRT | XHCD | XFISH | XADS | XFSR | XONM | XCPM | XOSI | XTWP | XWRT | XOTI | XFD | GO | XIM | ERR | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WATER | 129 | 12,402 | 1401 | 81 | 0 | 4 | 223 | 39 | 110 | 7090 | 308 | 130 | 6367 | 6399 | 6142 | −2264 | −26,276 |
| AGR | 0 | 25,343 | 0 | 8492 | 0 | 3120 | 0 | 0 | 0 | 59,236 | 15,132 | 0 | 6152 | 207,357 | 337,947 | −8151 | 21,266 |
| FRT | 0 | 0 | 1607 | 0 | 0 | 22 | 89 | 0 | 13 | 10,837 | 4 | 0 | 323 | 10,235 | 13,807 | −4686 | −4636 |
| HCD | 0 | 0 | 0 | 434 | 0 | 21 | 0 | 0 | 0 | 6857 | 0 | 0 | 309 | 77,347 | 113,299 | −1203 | 29,534 |
| FISH | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 172 | 0 | 0 | 4712 | 4561 | 906 | −3893 | −4647 |
| ADS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1803 | 0 | 0 | 0 | 36,248 | 12,261 | −32,200 | 6411 |
| FSR | 0 | 0 | 0 | 0 | 0 | 0 | 294,502 | 0 | 1776 | 84,927 | 17 | 0 | 10 | 338,223 | 624,907 | −138,662 | 44,115 |
| ONM | 0 | 0 | 0 | 0 | 0 | 0 | 53 | 1176 | 541 | 27,608 | 287 | 0 | 166 | 10,383 | 20,266 | −1334 | −18,613 |
| CPM | 82 | 59,662 | 1648 | 0 | 0 | 2733 | 13,775 | 208 | 40,308 | 53,905 | 170 | 0 | 12,523 | 165,156 | 121,714 | −131,423 | −97,033 |
| OSI | 1129 | 38,640 | 2974 | 27,127 | 212 | 682 | 82,531 | 7828 | 40,035 | 1,436,127 | 70,307 | 5703 | 183,543 | 1,414,133 | 2,514,478 | −736,680 | −59,813 |
| TWP | 67 | 1173 | 218 | 107 | 3 | 475 | 7938 | 667 | 1624 | 47,876 | 11,414 | 15,682 | 22,049 | 197,926 | 254,790 | −63,809 | 11,381 |
| WRT | 0 | 0 | 0 | 0 | 0 | 559 | 8 | 0 | 4 | 42 | 349 | 0 | 1451 | 123,469 | 171,759 | 0 | 45,877 |
| OTI | 599 | 1521 | 410 | 913 | 22 | 597 | 26227 | 1301 | 3572 | 100,547 | 22,686 | 26,774 | 124,480 | 1,034,332 | 896,549 | −499,866 | 52,434 |
| TVA | 4135 | 199,206 | 5549 | 76,144 | 668 | 4048 | 199,561 | 9048 | 33,733 | 677,453 | 134,117 | 123,469 | 534,466 | 0 | 0 | 0 | 0 |
| TI | 6142 | 337,947 | 13,807 | 113,299 | 906 | 12,261 | 624,907 | 20,266 | 121,714 | 2,514,478 | 254,790 | 171,759 | 896,549 | 3,393,969 | 5,088,825 | 0 | 0 |
Appendix B. GAMS codes used for correcting RAS-IO table of Shandan County.
- $SETGLOBAL PROGPATH E:\IGSSNR\Shandan\code
- *$SETGLOBAL DATAPATH E:\IGSSNR\Shandan\code\data\
- *$SETGLOBAL DATANAM Shandan
- SETS
- i SECTORS/
- WAT Water
- AGR Agriculture
- FRT Forestry
- HCD Animal Husbandry
- FISH Fisheries
- ADS Others in Primary Industry
- FSR Ferrous Metal Smelting & Rolling
- ONM Other Non-metallic Mineral Mining
- CPM Chemical Raw Materials & Chemical Products Manufacturing
- OSI Others in Secondary industry
- TWP Transportation and Warehousing Postal
- WRT Wholesale and Retail trade
- OTI Others in Tertiary industries
- TVA Value-added
- /,
- HH columns/
- XWAT water
- XAGR Agriculture
- XFRT Forestry
- XHCD Animal Husbandry
- XFISH Fisheries
- XADS Others in Primary Industry
- XFSR Ferrous Metal Smelting & Rolling
- XONM Other Non-metallic Mineral Mining
- XCPM Chemical Raw Materials & Chemical Products Manufacturing
- XOSI Others in Secondary industry
- XTWP Transportation and Warehousing Postal
- XWRT Wholesale and Retail trade
- XOTI Others in Tertiary industries
- * XIMP Imports
- XFD Final Demand
- /;
- * Program requires three different data inputs:
- * CONFLOW: the matrix of original flows
- * C0: column containing row sum controls
- * CON: column containing column sum controls
- TABLE CONFLOW(i,hh) INITIAL PRIVATE CONSUMPTION FLOWS
- * weighted privincial level IO table should be followed;
- PARAMETER c0(i) Control vector;
- c0("WAT") = 6141.94302;
- c0("AGR") = 337947.33512;
- c0("FRT") =13806.9385;
- c0("HCD") = 113299.11636;
- c0("FISH") = 905.8044;
- c0("ADS") = 12261.47662;
- c0("FSR") = 624906.5642;
- c0("ONM") = 20266.28528;
- c0("CPM") = 121714.10924;
- c0("OSI") = 2514477.82296;
- c0("TWP") = 254789.58278;
- c0("WRT") = 171758.5029;
- c0("OTI") = 896549.4087;
- c0("TVA") = 0.0;
- PARAMETER CON(hh) AGGREGATE INPUT CONSUMPTION LEVELS;
- CON("XWAT") = 6141.94302;
- CON("XAGR") = 337947.33512;
- CON("XFRT") = 13806.9385;
- CON("XHCD") = 113299.11636;
- CON("XFISH") = 905.8044;
- CON("XADS") = 12261.47662;
- CON("XFSR") = 624906.5642;
- CON("XONM") = 20266.28528;
- CON("XCPM") = 121714.10924;
- CON("XOSI") = 2514477.82296;
- CON("XTWP") = 254789.58278;
- CON("XWRT") = 171758.5029;
- CON("XOTI") = 896549.4087;
- CON("XFD") = 0.0;
- ALIAS(I,RR);
- ALIAS(HH,CC);
- PARAMETER a0(rr,cc) Initial coefficients matrix to RAS
- a1(rr,cc) Final coefficients matrix after RAS
- rasmat0(rr,cc) Initial flows matrix to RAS
- ct(cc) RAS column control totals
- rt(rr) RAS row control totals
- ratio Adjustment parameter on control totals
- checkcol Check sum of column control totals
- checkrow Check sum of row control totals
- sumccc Original column sums of RAS matrix
- sumrrr Original row sums of RAS matrix;
- VARIABLES
- DEV Deviations
- RASMAT(rr,cc) RASed matrix
- R1(rr) Rho of RAS matrix
- S1(cc) Sigma of RAS matrix
- LOSS Objective (loss) function value;
- * Parameter initialization
- sumccc(cc) = SUM(rr, conflow(rr,cc));
- sumrrr(rr) = SUM(cc, conflow(rr,cc));
- a0(rr,cc) = conflow(rr,cc) / sumccc(cc);
- rasmat0(rr,cc) = a0(rr,cc) * CON(cc);
- ct(cc) = CON(cc);
- rt(rr) = c0(rr);
- ratio = SUM(rr, rt(rr))/SUM(cc, ct(cc));
- ct(cc) = ct(cc) * ratio;
- checkcol = SUM(cc, ct(cc));
- checkrow = SUM(rr, rt(rr));
- display ratio, checkcol, checkrow;
- display conflow, a0;
- display con, ct;
- display c0, rt;
- * Variable initialization
- DEV.L = 0.0;
- R1.L(rr) = 1;
- S1.L(cc) = 1;
- RASMAT.L(rr,cc) = a0(rr,cc) * ct(cc);
- CON(cc) = ct(cc);
- EQUATIONS
- BIPROP(rr,cc) Bi-proportionality for RAS matrix
- DEVSQ Definition of squared deviations
- OBJ Objective function
- RCONST(rr) Row constraint
- CCONST(cc) Column constraint;
- BIPROP(rr,cc).. RASMAT(rr,cc) =E= R1(rr)*S1(cc)*rasmat0(rr,cc);
- CCONST(cc).. ct(cc) = E = SUM(rr, RASMAT(rr,cc));
- RCONST(rr).. rt(rr) = E = SUM(cc, RASMAT(rr,cc));
- DEVSQ.. DEV = E = SUM( (rr,cc)$rasmat0(rr,cc),
- SQR( (RASMAT(rr,cc) − rasmat0(rr,cc))/rasmat0(rr,cc)));
- OBJ.. LOSS = E = SUM(rr, R1(rr)**2 + (1/R1(rr))**2 )
- + SUM(cc, S1(cc)**2 + (1/S1(cc))**2);
- * Variable bounds
- RASMAT.LO(rr,cc) = 0.0;
- R1.LO(rr) = 0.01;
- S1.LO(cc) = 0.01;
- MODEL CONSUMERAS/BIPROP
- CCONST
- RCONST
- * DEVSQ
- OBJ/;
- *DEVSQ is commented out
- OPTIONS ITERLIM = 10000,LIMROW = 0,LIMCOL = 0,SOLPRINT=OFF;
- SOLVE CONSUMERAS USING NLP MINIMIZING LOSS;
- display rasmat.l, r1.l, s1.l;
- a1(rr,cc) = rasmat.l(rr,cc)/ct(cc);
- display a0, a1;
Conflicts of Interest
References
- Duarte, R.; Sánchez-Chóliz, J.; Bielsa, J. Water use in the Spanish economy: An input-output approach. Ecol. Econ. 2002, 43, 71–85. [Google Scholar]
- Ciscar, J.C.; Iglesias, A.; Feyen, L.; Szabó, L.; van Regemorter, D.; Amelung, B.; Soria, A. Physical and economic consequences of climate change in Europe. Proc. Nat. Acad. Sci. USA 2011, 108, 2678–2683. [Google Scholar] [Green Version]
- Xie, W.; Li, N.; Ji, Z.; Wu, J. Spatial and economic impacts analysis of an emergency event. In Proceedings of the Information Science and Service Science and Data Mining (ISSDM), 2012 6th International Conference on New Trends in, Taipei, Taiwan, 23–25 October 2012.
- Huang, J.; Liu, Y.; Martin, W.; Rozelle, S. Changes in trade and domestic distortions affecting China’s agriculture. Food Policy 2009, 34, 407–416. [Google Scholar] [CrossRef]
- You, F.; Tao, L.; Graziano, D.J.; Snyder, S.W. Optimal design of sustainable cellulosic biofuel supply chains: Multiobjective optimization coupled with life cycle assessment and input-output analysis. AIChE J. 2012, 58, 1157–1180. [Google Scholar] [CrossRef]
- Daniels, P.L.; Lenzen, M.; Kenway, S.J. The ins and outs of water use—A review of multi-region input-output analysis and water footprints for regional sustainability analysis and policy. Econ. Syst. Res. 2011, 23, 353–370. [Google Scholar] [CrossRef]
- Leontief, W.W. Quantitative input and output relations in the economic systems of the United States. Rev. Econ. Stat. 1936, 18, 105–125. [Google Scholar] [CrossRef]
- McMillan, H.K.; Krueger, T.; Freer, J.E.; Westerberg, I. Benchmarking observational uncertainties for hydrology. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 9–13 December 2013.
- Wu, F.; Zhan, J.; Shi, C.; Zhao, C. An extended input-output table for environmental and resources accounting. Chin. J. Popul. Resour. Environ. 2014, 12, 33–41. [Google Scholar] [CrossRef]
- Calzadilla, A.; Rehdanz, K.; Tol, R.S. The GTAP-W Model: Accounting for Water Use in Agriculture (No. 1745); Kiel Working Papers: Kiel, Germany, 2011. [Google Scholar]
- Titze, M.; Brachert, M.; Kubis, A. The identification of regional industrial clusters using qualitative input-output analysis (QIOA). Reg. Stud. 2011, 45, 89–102. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, M.; Yang, H.; Chapagain, A. An input-output analysis of trends in virtual water trade and the impact on water resources and uses in China. Econ. Syst. Res. 2011, 23, 431–446. [Google Scholar] [CrossRef]
- Leontief, W.W. Studies in the Structure of American Economy, 1919–1929; Harvard University Press: Cambridge, MA, USA, 1941. [Google Scholar]
- Leontief, W. Environmental repercussions and the economic structure: An input-output approach. Rev. Econ. Stat. 1970, 52, 262–271. [Google Scholar] [CrossRef]
- Lofting, E.M.; McGauhey, P.H. Economic Valuation of Water: An Input-Output Analysis of California Water Requirements; Water Resources Center, University of California: Oakland, CA, USA, 1968. [Google Scholar]
- Duchin, F. Input-output analysis and industrial ecology. In The Greening of Industrial Ecosystems; National Academy press: Washington, DC, USA, 1994; pp. 61–68. [Google Scholar]
- Baumol, W.J. Leontief’s great leap forward: Beyond Quesnay, Marx and von Bortkiewicz. Econ. Syst. Res. 2000, 12, 141–152. [Google Scholar] [CrossRef]
- Lange, G.M. Applying an integrated natural resource accounts and input-output model to development planning in Indonesia. Econ. Syst. Res. 1998, 10, 113–134. [Google Scholar]
- Kim, H.B.; Jin, S.Y.; Yun, K.S. Impact Analysis of a Water Quality Enhancing Policy: A Simple Input-Output Approach. Reg. Stud. 2001, 35, 103–111. [Google Scholar] [CrossRef]
- Velazquez, E. An input-output model of water consumption: Analysing intersectoral water relationships in Andalusia. Ecol. Econ. 2006, 56, 226–240. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, H.L.; Lu, M.F. Analysis of water consumption using a regional input-output model: Model development and application to Zhangye City, Northwestern China. J. Arid Environ. 2009, 73, 894–900. [Google Scholar]
- Stone, R. Input-Output and National Accounts; Organisation for European Economic Co-operation: Paris, France, 1961. [Google Scholar]
- Oosterhaven, J.; Piek, G.; Stelder, D. Theory and practice of updating regional versus interregional interindustry tables. Pap. Reg. Sci. 1986, 59, 57–72. [Google Scholar] [CrossRef]
- Ghahramani, Z.; Jordan, M.I. Learning from Incomplete Data. Available online: http://hdl.handle.net/1721.1/7202 (accessed on 24 January 1995).
- Kohn, R.; Ansley, C.F. Estimation, prediction, and interpolation for ARIMA models with missing data. J. Am. Stat. Assoc. 1986, 81, 751–761. [Google Scholar] [CrossRef]
- Deng, X.; Fang, Y.; Lin, Y.; Yuan, Y. Non-parametric method for filling in the missing value for cross-sectional dataset: A validation on the per capita GDP data at county level in China. J. Food Agric. Environ. 2012, 10, 1350–1354. [Google Scholar]
- West, G.R. Regional trade estimation: A hybrid approach. Int. Reg. Sci. Rev. 1990, 13, 103–118. [Google Scholar] [CrossRef]
- Van der Mensbrugghe, D.; Roson, R. Climate, Trade and Development; Centre for Trade and Economic Integration (CTEI): Geneva, Switzerland, 2010. [Google Scholar]
- Toh, M.H. The RAS approach in updating input-output matrices: An instrumental variable interpretation and analysis of structural change. Econ. Syst. Res. 1998, 10, 63–78. [Google Scholar] [CrossRef]
- Lahr, M.L. A review of the literature supporting the hybrid approach to constructing regional input-output models. Econ. Syst. Res. 1993, 5, 277–293. [Google Scholar] [CrossRef]
- Lahr, M.L. A Strategy for Producing Hybrid Regional Input-Output Tables; Center for Urban Policy Research, Rutgers, The State University: New Brunswick, NJ, USA, 1998. [Google Scholar]
- Miller, R.E.; Blair, P.D. Input-Output Analysis: Foundations and Extensions; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Kurz, H.D.; Dietzenbacher, E.; Lager, C. Input-Output Analysis, Volume 1; Edward Elgar Publishing: Cheltenham, UK, 1998. [Google Scholar]
- Rodriguez, A.; Dunson, D.B. Nonparametric Bayesian models through probit stick-breaking processes. Bayesian Anal. 2011, 6, 145–177. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China. Statistics Yearbook of Gansu Province; National Bureau of Statistics of China: Beijing, China; pp. 1992–2007.
- Smith, J.W.; Floyd, M.F. The urban growth machine, central place theory and access to open space. City Cult. Soc. 2013, 4, 87–98. [Google Scholar] [CrossRef]
- Van der Linden, J.A.; Dietzenbacher, E. The determinants of structural change in the European Union: A new application of RAS. Environ. Plan. A. 2000, 32, 2205–2230. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Deng, X.; Zhang, F.; Wang, Z.; Li, X.; Zhang, T. An Extended Input Output Table Compiled for Analyzing Water Demand and Consumption at County Level in China. Sustainability 2014, 6, 3301-3320. https://doi.org/10.3390/su6063301
Deng X, Zhang F, Wang Z, Li X, Zhang T. An Extended Input Output Table Compiled for Analyzing Water Demand and Consumption at County Level in China. Sustainability. 2014; 6(6):3301-3320. https://doi.org/10.3390/su6063301
Chicago/Turabian StyleDeng, Xiangzheng, Fan Zhang, Zhan Wang, Xing Li, and Tao Zhang. 2014. "An Extended Input Output Table Compiled for Analyzing Water Demand and Consumption at County Level in China" Sustainability 6, no. 6: 3301-3320. https://doi.org/10.3390/su6063301





