Heat Transmission Coefficient Measurements in Buildings Utilizing a Heat Loss Measuring Device
Abstract
:1. Introduction
1.1. Introduction to Energy Performance Upgrading
1.2. Introduction to U-Value Meter

- (1)
- If the Meter is taken outdoors from an indoor environment the Meter has to be acclimatized to the outdoor temperature for a minimum period of half an hour. The display will show “Waiting”, until the Meter is in thermal equilibrium with its surroundings. While waiting, the Meter can display the difference between the reference sensor and the heat absorption sensor temperatures.
- (2)
- After acclimatization the user is prompted to key in the indoor temperature. After that, the user is asked to hold the reference sensor up in the air, and the outdoor temperature is measured for half a minute. During data acquisition these temperature values are given as input to the main processor. In fact, the outdoor temperature is continuously measured by the reference sensor and can be displayed at any time while the apparatus is turned on.
- (3)
- When thermal equilibrium is reached, the display says “Ready” and the user can initiate the measurement. If the user, by accident, turns the Meter towards the sun or puts his hand on the heat absorption sensor, causing a thermal rise in the heat absorption sensor, the processor will show the message “Waiting…” again, indication lack of thermal balance. Thermal equilibrium is reached when the temperature difference between the heat absorption sensor and the reference sensor is below 0.3 ºC.
- (4)
- When the user holds the Meter against the test piece, the main processor starts to count the time and the measuring process is going on for the entire measuring period (20 seconds). The display shows “Measuring…” and displays the temperature rise of the heat absorption sensor, while the measurement goes on.
- (5)
- Immediately after the measurement is finished, the display says “Calculate…” for a few seconds and the U-value is presented afterwards.
- (6)
- The user can store the results in an internal memory by pressing the button “Memory”.
- (7)
- The Meter will display “Waiting…” until the heat absorption sensor is back in thermal equilibrium with the outdoor temperature, and after that a new measurement can begin.
1.3. Main Processor
2. EUDP Project
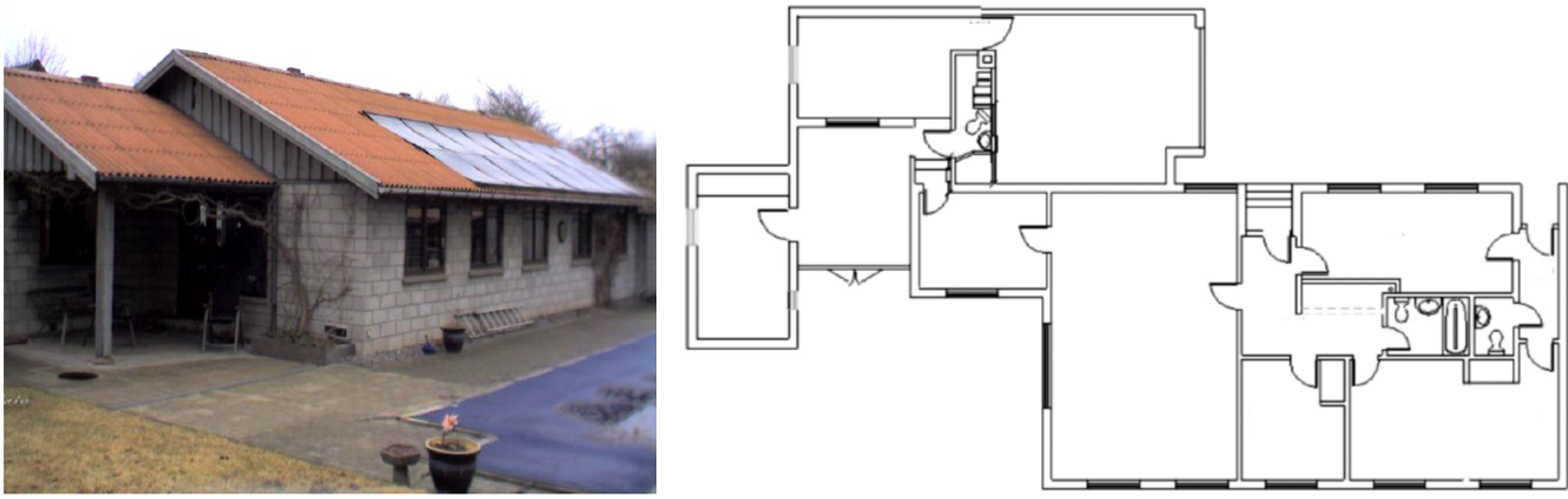



| Id | Object | Tin (°C) | Remark | U-value (W/m2K) |
|---|---|---|---|---|
| 1 | Parapet | 21.9 | 2 thin wooden boards with air/insulation between. 3 cm thick in total | 1.44 |
| 2 | Outer wall | 23.0 | Measured at 70 cm height | 0.80 |
| 3 | Outer wall | 22.4 | Measured at 1.5 m height | 0.84 |
| 4 | Outer wall | 23.3 | Measured at 1.5 m height | 0.88 |
| 5 | Pane | 23.3 | Measured at the middle of the pane | 1.24 |
| 6 | Outer wall | 23.3 | Measured at 1.5 m height | 0.87 |
| 7 | Outer wall | 23.5 | Measured at 1.5 m height | 0.81 |
| 8 | Outer wall | 23.5 | Measured at 1.5 m height | 0.85 |
| 9 | Exterior door | 22.0 | Door made of 4 cm thick wood (possibly teak) | 1.72 |
| 10 | Pane | 22.3 | Measured at the middle of the pane | 1.30 |
| 11 | Outer wall | 22.3 | Measured at 1.5 m height | 0.89 |
| 12 | Beam | 22.3 | Window lintel (lightweight concrete) | 1.12 |
| 13 | Edge of wall | 22.3 | No significant peripheral effects were measured | 0.91 |
| 14 | Exterior door | 22.0 | Door made of 4 cm thick wood (possibly teak) | 1.78 |
| 15 | Wall | 22.4 | Wall between the garage and living room | 0.32 |
| 16 | Outer wall | 20.5 | Outer wall of utility room/laundry room (facade) | 0.26 |
| 17 | Outer wall | 20.5 | Outer wall of utility room/laundry room (gable) | 0.29 |
| 18 | Outer wall | 20.5 | Outer wall of utility room/laundry room (gable) | 0.29 |
| 19 | Socket | 21.9 | Measured at the center of the base | 1.03 |
| 20 | Outer wall | 22.7 | Built-in cupboard stood up against this wall. Measured at 40 cm height | 0.36 |
| 21 | Pane | 22.7 | Measured at the middle of the pane | 1.16 |
| 22 | Outer wall | 22.7 | Measured at wall section below the window | 0.32 |
| 23 | Outer wall | 22.7 | Measured at 40 cm above socket level | 0.20 |
| 24 | Outer wall | 22.7 | Measured 80 cm above bottom of wall | 0.23 |
- Outer walls including sockets are insulated with 195 mm mineral wool which is plastered.
- One exterior door replaced by a modern entrance door with low U-value. The other exterior door is removed and the opening closed and insulated as the rest of the façade.
- House entrance was insulated with 100 mm insulation
- Gables and foot of roof were insulated with good connection to the ceiling insulation
- Digging up soil around the concrete foundation and in top, new foundation blocks made of lightweight concrete are established and insulated with phenolic foam (PF).
- The existing windows (with low-energy glazing) are moved out to align with the façade.
- Installation of mechanical ventilation (balanced) aggregate with heat recovery
- Air tightening of the ceiling and between ceiling and outer walls.
- Insulation of bedroom (previously insulated from inside to a certain level).
3. Limitations and Uncertainties
| Examples | Measuring Object | U1 | U2 | U3 | Expected U | Age |
|---|---|---|---|---|---|---|
| Example I | Terrace door | 1.35 | 1.33 | 1.31 | 1.20 | 6 years |
| Low E-glazed window | 1.24 | 1.27 | 1.30 | 1.20 | 6 years | |
| Outer wall | 1.04 | 0.97 | 0.94 | 0.90 | 32 years | |
| Example II | Double-glazed window | 3.00 | 3.12 | 2.80 | 36 years | |
| Outer wall | 0.41 | 0.42 | 0.40 | 36 years | ||
| Example III | Double-glazed window | 2.87 (average of 9 measurements) | 2.80 | 25 years |
4. Conclusions
References and Notes
- Sørensen, L.S. Varmeudveksling under brandforløb. In Brandfysik og Brandteknisk Design af Bygninger(in Danish), 1st ed.; Polyteknisk Forlag: Copenhagen, Denmark, 2004; pp. 167–198, 473–496. [Google Scholar]
- Sørensen, L.S. Energy Renovation of Buildings Utilizing the U-value Meter, a New Heat Loss Measuring Device. Sustainability 2010, 2, 461–474. [Google Scholar] [CrossRef]
- Sørensen, L.S. U-value Meter (Transmission Coefficient Measuring Apparatus). European Patent Application (EPA) 1,347,289, March 2003. [Google Scholar]
- Danish Meteorological Institute. Available online: http://www.dmi.dk (accessed on 15 March 2013).
- EUDP-2009-II: Development of standard solutions for energy-extensive building envelope renovation of existing buildings from the period 1960–1980. A project with financial support from the Energy Technological Development and Demonstration Program (EUDP), 2009.
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: Somerset, NJ, USA, 2006; Chapter 9, Table 13.3. [Google Scholar]
- Holman, J.P. Heat Transfer, 8th ed.; McGraw-Hill Inc: New York, NY, USA, 1997; pp. 123–158. [Google Scholar]
- Gerike, A. Portable temperature sensing device. U.S. Patent 4,173,894, 13 November 1979. [Google Scholar]
- Chuah, Y.K.; Sun, M.-T.; Huang, B.-J. Insulation measuring apparatus which forces heat flow in one direction with a constant temperature region. U.S. Patent 6,257,761, 10 July 2001. [Google Scholar]
- Szabo, P. Method of and apparatus for the determination of the thermal insulating properties of building walls. U.S. Patent 4,647,221, 8 November 1985. [Google Scholar]
- Poppendiek, H.F. Means and techniques useful in establishing R values in insulation. U.S. Patent 4,236,403, 2 December 1980. [Google Scholar]
- Marechal, J.-C. Device and method for thermal measurements on walls. E.P. Patent 0,065,433, 24 November 1982. [Google Scholar]
- DS/EN 12664. In Thermal Performance of Building Materials and Products-Dry and Moist Products of Medium and Low Thermal Resistance; DS/EN-Standard; 2001.
- DS/EN 12667. In Thermal Performance of Building Materials and Products-Products of High and Medium Thermal Resistance; DS/EN-Standard; 2001.
- Both, E.; Christiansen, G. Termodynamik(in Danish), 2nd ed.; Den Private Ingeniørfond: Lyngby, Denmark, 1995. [Google Scholar]
- Marsh, R. Arkitektur og Energi: Mod en 2020-Lavenergistrategi(in Danish), 1st ed.; Aalborg University: Hørsholm, Denmark, 2011. [Google Scholar]
- Munch-Andersen, J. Efterisolering af Etageboliger; (in Danish). Aalborg University: Hørsholm, Denmark, 2010. [Google Scholar]
- DS/EN ISO 10077–2. In Termisk ydeevne for vinduer, døre og skodder-Beregning af varmetrans-mission-Del 2: Numerisk metode for rammer; (in Danish). Dansk Standard: Charlottenlund, Denmark, 2004; p. 262.
- DS 452:1999. In Termisk isolering af tekniske installationer; (in Danish). Dansk Standard: Charlottenlund, Denmark, 1999.
- DS/EN ISO 10211:2008. In Kuldebroer i bygningskonstruktioner: Varmestrømme og overflade-temperaturer. Detaljerede beregninger; (in Danish). Dansk Standard: Charlottenlund, Denmark, 2008.
- Aggerholm, S.; Grau, K. Bygningers Energibehov; (in Danish). Aalborg University: Hørsholm, Denmark, 2005. [Google Scholar]
- DS 418:2002. In Beregning af bygningers varmetab; (in Danish). Dansk Standard: Charlottenlund, Denmark, 2002.
- SBi. In Anvisning om Bygningsreglement 2010; (in Danish). Aalborg University: Hørsholm, Denmark, 2010.
- Dampspærrer i klimaskærmen-fugttransport og materialer. (in Danish). Available online: https://byg-erfa.dk/dampspaerrer-fugttransport (accessed on 5 March 2013).
- DS 418:2011. In Beregning af bygningers varmetab; (in Danish). Dansk Standard: Charlottenlund, Denmark, 2011.
- 2002/91/EF. Direktiv om bygningers energimæssige ydeevne. (in Danish) Europaparlamentets og Rådets direktiv 2002/91/EF af 16/12/2002: De Europæiske Fællesskabers Tidende, 4.1.2003. 2003. Available online: http://eur-lex.europa.eu (accessed on 4 July 2013).
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sørensen, L.S. Heat Transmission Coefficient Measurements in Buildings Utilizing a Heat Loss Measuring Device. Sustainability 2013, 5, 3601-3614. https://doi.org/10.3390/su5083601
Sørensen LS. Heat Transmission Coefficient Measurements in Buildings Utilizing a Heat Loss Measuring Device. Sustainability. 2013; 5(8):3601-3614. https://doi.org/10.3390/su5083601
Chicago/Turabian StyleSørensen, Lars Schiøtt. 2013. "Heat Transmission Coefficient Measurements in Buildings Utilizing a Heat Loss Measuring Device" Sustainability 5, no. 8: 3601-3614. https://doi.org/10.3390/su5083601




