Economic Analysis of Climate Variability Impact on Malaria Prevalence: The Case of Ghana
Abstract
:1. Introduction
2. Malaria in Ghana: An Overview
3. Empirical Modeling and Data
Time Series Analysis
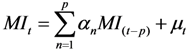
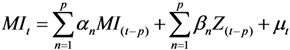
Cross-Sectional Analysis
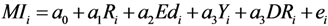
Generalized Maximum Entropy (GME)
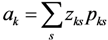
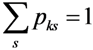 ; Zks constitutes a predetermined discrete support space ( s ) for the parameters; and ak is as defined in Equation 4. Furthermore, define the error term in Equation 3 as
; Zks constitutes a predetermined discrete support space ( s ) for the parameters; and ak is as defined in Equation 4. Furthermore, define the error term in Equation 3 as
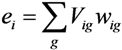
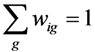 ; Vig constitutes an a priori discrete support space ( g ) for the errors; and ui is as defined in Equation 3. The GME estimator is specified as
; Vig constitutes an a priori discrete support space ( g ) for the errors; and ui is as defined in Equation 3. The GME estimator is specified as
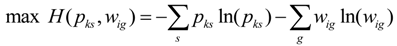
Data Types and Sources
4. Results and Discussions
| Variable | t-value | p-value | Lags |
|---|---|---|---|
| Malaria Incidence | −3.860 | 0.0137** | 3 |
| Humidity | −4.719 | 0.0006*** | 3 |
| Temperature | −3.965 | 0.0098*** | 3 |
| Rainy Days | −3.815 | 0.0158** | 3 |
| Wind speed | −3.434 | 0.0470** | 3 |
| Variables | # of Districts | Mean | Standard Deviation |
|---|---|---|---|
| Malaria Prevalence (Monthly)1 | 19 | 0.021 | 0.0082 |
| Rains (# of Yearly Rainy Days) | 20 | 104.050 | 19.7230 |
| No Formal Education (Proportion) | 20 | 0.722 | 0.2139 |
| Middle Income (Proportion) | 20 | 0.235 | 0.1967 |
| Eastern Region (1/0)2 | 20 | 0.150 | 0.3663 |
| VARIABLE | RRSS | URSS | F-stats |
|---|---|---|---|
| Humidity | 0.000445741 | 0.000384248 | 3.281** |
| Temperature | 0.000445741 | 0.000419099 | 1.303 |
| Rainy Days | 0.000445741 | 0.000312815 | 8.711*** |
| Wind speed | 0.000445741 | 0.000398086 | 2.454 |
| Varibale | Coefficient | Standard Error |
|---|---|---|
| Auto Rregresive (AR) | ||
| Lag 2 (L2). | 0.567 | (0.1707)*** |
| Moving Average (MA) | ||
| Lag 1 (L1) | 0.892 | (0.0994)*** |
| Constant | 0.029 | (0.0020)*** |
| Wald chi2(2) = 82.90: Prob > chi2 = 0.0000 | ||
| # of obs = 48 | ||
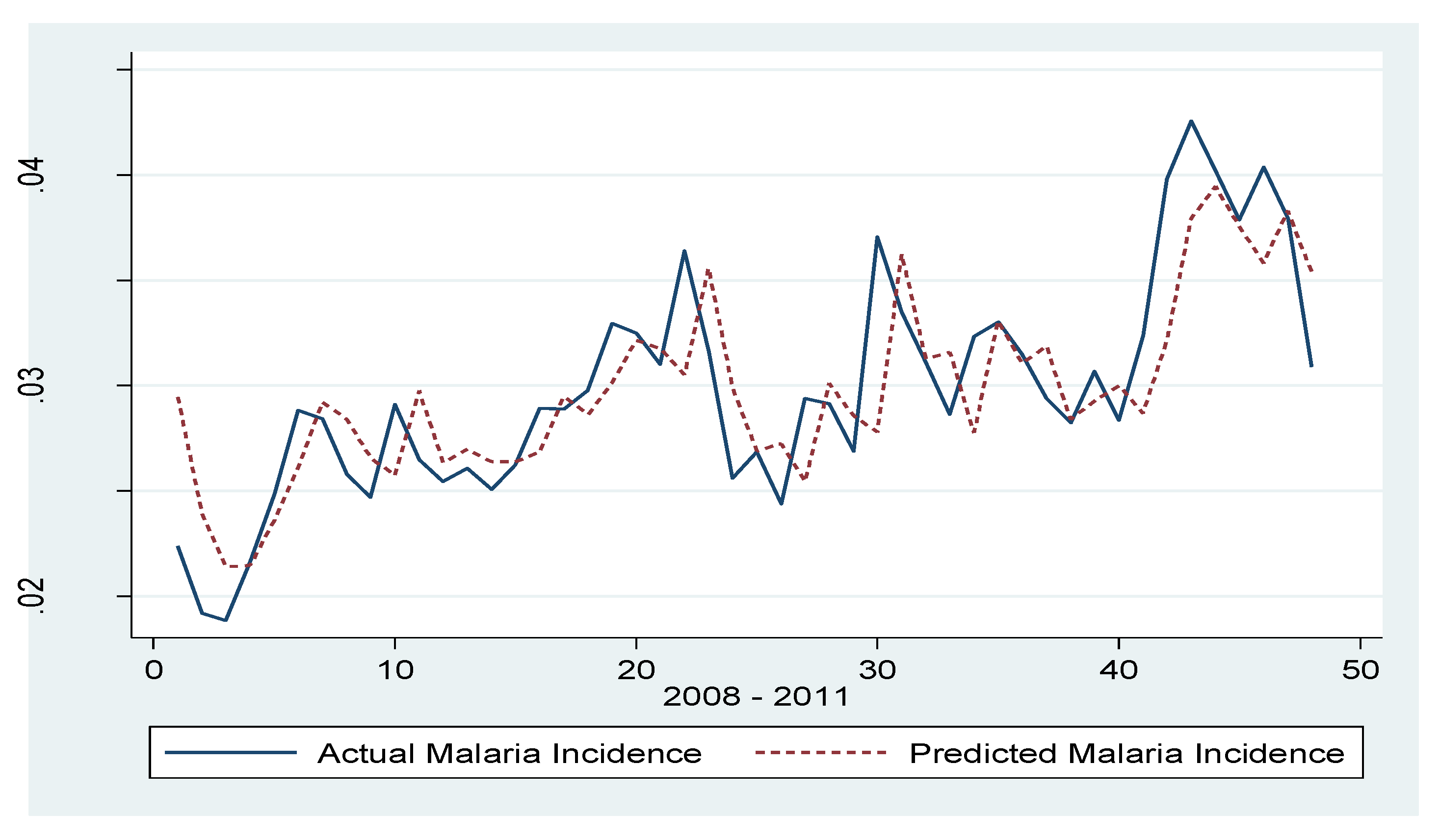
| Varibale | Coefficient | Standard Error |
|---|---|---|
| Auto Rregresive (AR) | ||
| Lag 1 ( L1) | 0.520 | (0.12219)** |
| Moving Average (MA) | ||
| Lag 1 (L1) | 0.301 | (0.2583) |
| Constant | 97.149 | (18.7753)*** |
| Wald chi2(2) = 22.62: Prob > chi2 = 0.0000 | ||
| # of Obs = 48 | ||
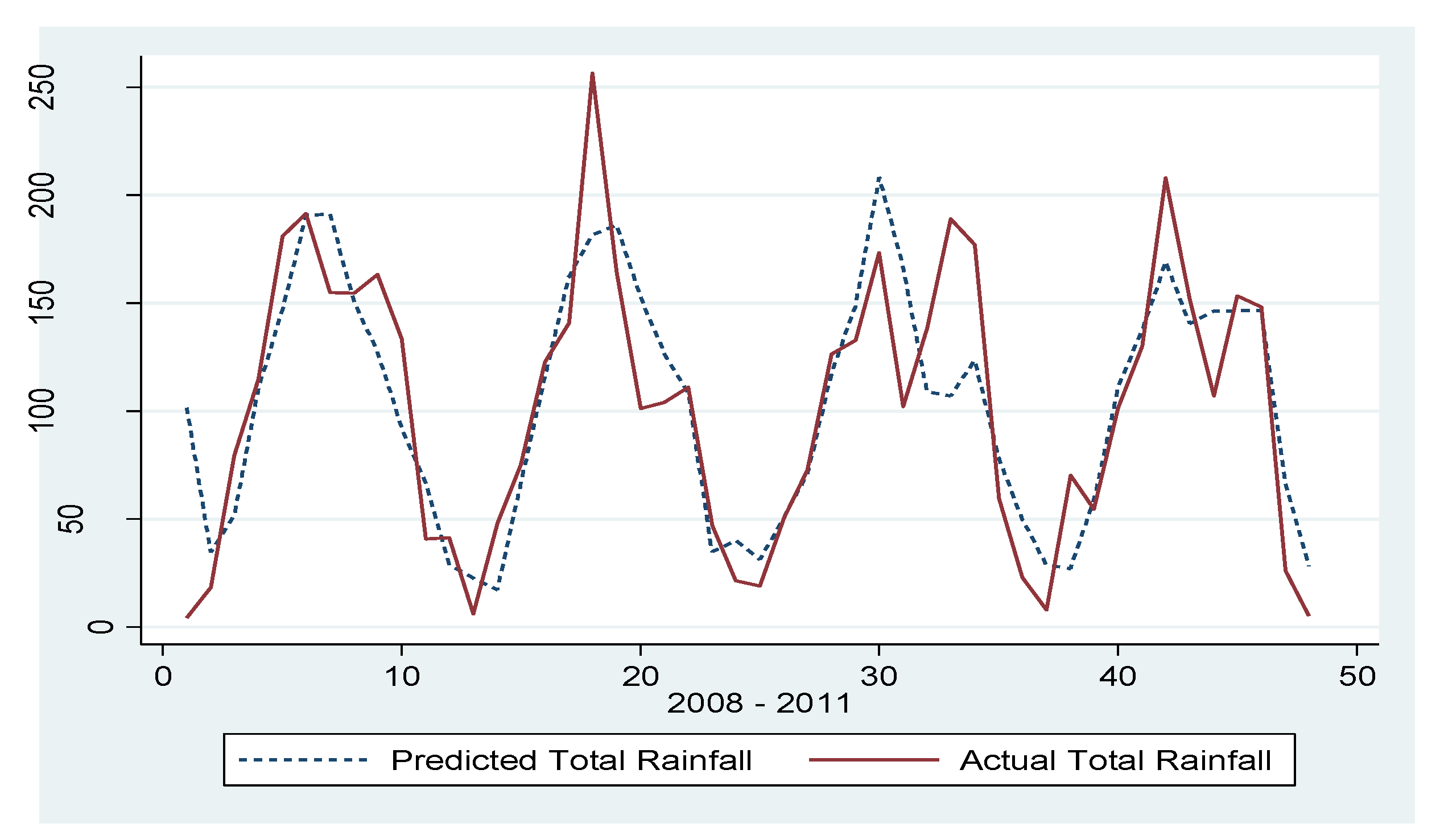
Cross-Sectional Analysis
| Variable | Regression 1
(Ordinary Least Square (OLS)) | Regression 2
(OLS: Bootstrap, 20 Replication) | Generalized Maximum Entropy (GME) Estimates | |||
|---|---|---|---|---|---|---|
| Coefficient | Elasticity | Coefficient | Elasticity | Coefficient | Elasticity | |
| Rains (# of rainy days) | 0.000136 (0.000065)** | 0.670 | 0.000136
(0.000058)** | 0.670 | 0.00022
(0.00006)*** | 1.113 |
| No Formal Education (Proportion) | 0.019026
(0.005969)*** | 0.661 | 0.019026
(0.006363)*** | 0.661 | 0.01999
(0.00922)*** | 0.702 |
| Middle Income (Proportion) | 0.010984
(0.004754)** | 0.124 | 0.010984
(0.00655)* | 0.124 | 0.01015
(0.0043) *** | 0.116 |
| Eastern Region (1/0) | 0.012654
(0.002463)*** | 0.065 | 0.012654
(0.002605)*** | 0.065 | −0.9909
(2.0045) | |
| Constant | −0.010702
(0.00680) | −0.010702
(0.006611) | −0.01934
(0.00914)*** | |||
| R-Squared | 0.65 | 0.65 | 0.61 | |||
5. Conclusions
Acknowledgements
Conflicts of Interest
References and Notes
- World Health Organization (WHO), World Malaria Report: 2010; World Health Organization: Geneva, Switzerland, 2010.
- World Health Organization (WHO), World Malaria Report: 2012; World Health Organization: Geneva, Switzerland, 2012.
- Murray, C.; Lopez, A.; Mathers, C.; Stein, C. The Global Burden of Disease 2000 Project, Aims, Methods, and Data Sources; World Health Organization: Geneva, Switzerland, 2001. [Google Scholar]
- Tanser, F.C.; Sharp, B.; le Sueur, D. Potential effect of climate change on malaria transmission in Africa. The Lancet 2003, 362, 1792–1798. [Google Scholar] [CrossRef]
- Patz, J.A.; Olson, S.H. Climate change and health: Global to local influences on disease risk. Ann. Trop. Med. Parasitol. 2006, 100, 535–549. [Google Scholar] [CrossRef]
- PEACE FM Online. Available online: http://news.peacefmonline.com/health/201304/162434.php (accessed on 1 September 2013).
- Ghana Demographic and Health Survey 2008. Available online: http://www.measuredhs.com/pubs/pdf/FR221/FR221%5B13Aug2012%5D.pdf (accessed on 1 September 2013).
- World Health Organization (WHO), World Malaria Report: 2009; World Health Organization: Geneva, Switzerland, 2009; pp. 1–33.
- Goodman, A.C.; Coleman, P.; Mills, A. Changing the first line drug for malaria treatment: Cost-effectiveness analysis with high uncertainty inter-temporal trade-offs. Health Econ. 2001, 10, 731–749. [Google Scholar] [CrossRef]
- Patz, J.A.; Epstein, P.R.; Burke, T.A.; Balbus, J.M. Global climate change and emerging infectious diseases. J. Am. Med. Assoc. 1996, 275, 217–223. [Google Scholar] [CrossRef]
- Gething, P.W.; Smith, D.L.; Patil, A.P.; Tatem, A.J.; Snow, R.W.; Hay, S.I. Climate change and the global malaria recession. Nature 2010, 465, 342–345. [Google Scholar] [CrossRef]
- Epstein, P.R.; Ferber, D. Changing Planet, Changing Health—How the Climate Crisis Threatens Our Health and What We Can Do about It; University of California Press: Berkeley, CA, USA, 2011. [Google Scholar]
- Ahern, M.J.; Kovats, R.S.; Wilkinson, P.; Few, R.; Matthies, F. Global health impacts of floods: Epidemiological evidence. Epidemiol. Rev. 2005, 27, 36–45. [Google Scholar] [CrossRef]
- Zhou, G.; Noboru, M.; Githeko, A.; Yan, G. Association between climate variability and malaria epidemic in the east African highlands. Proc. Natl. Acad. Sci. USA 2003, 101, 2375–2380. [Google Scholar]
- Ebi, K.; Hartman, J.; Chan, N.; McConnell, J.; Schlesinger, M.; Weyany, J. Climate suitability for stable malaria transmission in Zimbabwe under different climate change scenarios. Clim. Chang. 2005, 73, 375–393. [Google Scholar] [CrossRef]
- Thomson, M.C.; Mason, S.J.; Phindela, T.; Connor, S.J. Use of Rainfall and sea surface temperature monitoring for malaria early warning in Botswana. Am. J. Trop. Med. Hyg. 2005, 73, 214–221. [Google Scholar]
- Ndiaye, O.; le Hesran, J.-Y.; Etard, J.-F.; Diallo, A.; Simondon, F.; Ward, M.; Robert, V. Variations Climatiques Et Mortalité Attribuée Au Paludisme Dans La Zone De Niakhar, Sénégal De 1984 À 1996. Santé 2001, 11, 25–33. (in French). [Google Scholar]
- Jaenisch, T.; Patz, J. Assessment of association between climate and infectious diseases. Global Change Hum. Health 2002, 3, 67–72. [Google Scholar] [CrossRef]
- IPCC (Intergovernmental Panel on Climate Change), Climate Change 2007: Impacts, Adaptation and Vulnerability. In Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L.; Canziani, O.F.; Palutikof, J.P.; van der Linden, P.J.; Hanson, C.E. (Eds.) Cambridge University Press: Cambridge, UK, 2007; p. 976.
- IPCC (Intergovernmental Panel on Climate Change), Climate Change 2007: The Physical Science Basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S.; Qin, D.; Manning, M.; Chen, Z.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L. (Eds.) Cambridge University Press: Cambridge, UK, 2007.
- Martens, W. Health Impacts of Climate Change and Ozone Depletion: An Eco-Epidemiological Modelling Approach. Ph.D. Thesis, Ph.D. Thesis, Maastricht, The Netherlands, 1997. [Google Scholar]
- Egbendewe-Mondzozo, A.K.; Musumba, M.; McCarl, B.A.; Wu, X. Climate Change and Vector- borne Diseases: An Economic Impact Analysis of Malaria in Africa. Int. J. Environ. Res. Public Health. 2011, 8, 913–930. [Google Scholar] [CrossRef]
- Bomblies, A.; Eltahir, E.A.B. Assessment of impact of climate shifts on malaria. EcoHealth 2009, 6, 426–437. [Google Scholar] [CrossRef]
- Parham, P.; Michael, E. Modeling Climate Change and Malaria Transmission. Adv. Exp. Med. Biol. 2010, 673, 184–199. [Google Scholar] [CrossRef]
- Dadzie, S.K.; Brenyah, R.; Appawu, M.A. Role of species composition in malaria transmission by the Anopheles funestus group (Diptera: Culicidae) in Ghana. J. Vector. Ecol. 2013, 38, 105–110. [Google Scholar] [CrossRef]
- Reddy, M.R.; Overgaard, H.J.; Abaga, S.; Reddy, V.P.; Caccone, A.; Kiszewski, A.E.; Slotman, M.A. Outdoor host seeking behaviour of Anopheles gambiae mosquitoes following initiation of malaria vector control on Bioko Island, Equatorial Guinea. Available online: http://www.biomedcentral.com/content/pdf/1475-2875-10-184.pdf (accessed on 1 September 2013).
- President’s Malaria Initiative. Malaria Operational Plan FY 2013. Available online: http://pmi.gov/countries/mops/fy13/ghana_mop_fy13.pdf (accessed on 1 September 2013).
- United Nations Children’s Fund (UNICEF), UNICEF Ghana Fact Sheet Malaria; UNICEF: Accra, Ghana, 2007.
- Keba Africa. Available online: http://www.kebaafrica.org/malaria-prevention-2/ (accessed on 1 September 2013).
- Ministry of Health (MoH), Anti-Malaria: Drug Policy for Ghana; MoH: Accra, Ghana, 2009.
- President’s Malaria Initiative. Malaria operational plan—FY 2012 (5 years). Available online: http://pmi.gov/countries/mops/fy12/ghana_mop_fy12.pdf (accessed on 1 September 2013).
- Yilma, Z.; van Kempen, L.; de Hoop, T. Perverse ‘net’ effect? Health insurance and ex-ante moral hazard in Ghana. Soc. Sci. Med. 2012, 75, 138–147. [Google Scholar] [CrossRef]
- Baffoe, A.; Gbeve, K.; Ollenu, A.O. Home Management of Malaria, Acute Respiratory Infection & Diarrhoea in Ghana: Implementation Guidelines; Ministry of Health, Ghana Health Services: Accra, Ghana, 2009. [Google Scholar]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- The twenty weather stations are located at Abetifi, Accra, Ada, Akatsi, Akim-Oda, Axim, Akuse, Bole, Ho, Kete-Krachi, Koforidua, Kumasi, Navrongo, Sefwi-Bekwai, Saltpond, Sunyani, Takoradi, Tamale, Tema, Wa, Wenchi, and Yendi. As of 2008, Ghana had 170 districts
- Asante, F.A.; Asenso-Okyere, K. Economic Burden of Malaria in Ghana, A Technical Report for World Health Organization (WHO). 2003; unpublished work.
- Mba, C.J.; Aboh, I.K. Prevalence and Management of Malaria in Ghana: A Case Study of Volta Region. Afr. Popul. Stud. 2007, 22, 137–171. [Google Scholar]
Appendix
| Variable | District | t-value | p-value | lags |
|---|---|---|---|---|
| Malaria Incidence | Abetifi | −3.521 | 0.0372** | 0 |
| Accra | −16.414 | 0.0000*** | 3 | |
| Ada | −7.277 | 0.0000*** | 3 | |
| Akatsi | −3.820 | 0.0156** | 2 | |
| Akuse | −3.766 | 0.0184** | 1 | |
| Axim | −3.231 | 0.0784* | 0 | |
| Bole | −3.444 | 0.0458** | 0 | |
| Ho | −7.754 | 0.0000*** | 3 | |
| Koforidua | −3.383 | 0.0537* | 3 | |
| Krachi | −6.412 | 0.0000*** | 3 | |
| Kumasi | −3.903 | 0.0120** | 3 | |
| Navarongo | did not pass | |||
| Oda | −15.590 | 0.0000*** | 3 | |
| Saltpond | −3.609 | 0.0291** | 3 | |
| Sbekwai | −3.223 | 0.0799*** | 2 | |
| Sunyani | −3.267 | 0.0719*** | 3 | |
| Takoradi | −15.943 | 0.0000*** | 3 | |
| Tamale | −3.964 | 0.0099*** | 3 | |
| Tema | −6.985 | 0.0000*** | 3 | |
| Wa | −3.244 | 0.0759* | 3 | |
| Wenchi | −4.991 | 0.0002*** | 3 | |
| Yendi | −4.176 | 0.0049*** | 3 | |
| Humidity | Abetifi | −3.834 | 0.0149** | 3 |
| Accra | −4.347 | 0.0027*** | 3 | |
| Ada | −3.390 | 0.0528* | 1 | |
| Akatsi | −4.366 | 0.0025*** | 3 | |
| Akuse | −4.123 | 0.0058*** | 3 | |
| Axim | −3.738 | 0.0200** | 3 | |
| Bole | −5.400 | 0.0000*** | 3 | |
| Ho | −4.997 | 0.0002*** | 3 | |
| Koforidua | −4.607 | 0.0010*** | 3 | |
| Krachi | −4.670 | 0.0008*** | 3 | |
| Kumasi | −4.082 | 0.0067*** | 3 | |
| Navarongo | −6.275 | 0.0000*** | 3 | |
| Oda | −9.309 | 0.0000*** | 3 | |
| Saltpond | −4.742 | 0.0006*** | 3 | |
| Sbekwai | −6.224 | 0.0000*** | 3 | |
| Sunyani | −4.241 | 0.0039*** | 3 | |
| Takoradi | −7.003 | 0.0000*** | 3 | |
| Tamale | −4.457 | 0.0018*** | 3 | |
| Tema | −7.475 | 0.0000*** | 3 | |
| Wa | −5.731 | 0.0000*** | 3 | |
| Wenchi | −3.961 | 0.0100*** | 3 | |
| Yendi | −4.299 | 0.0032*** | 3 | |
| Temperature | Abetifi | −5.437 | 0.0000*** | 3 |
| Accra | −5.147 | 0.0001*** | 3 | |
| Ada | −4.025 | 0.0081*** | 3 | |
| Akatsi | −5.353 | 0.0000*** | 3 | |
| Akuse | −4.373 | 0.0024*** | 3 | |
| Axim | −4.508 | 0.0015*** | 3 | |
| Bole | −3.603 | 0.0296** | 3 | |
| Ho | −6.742 | 0.0000*** | 3 | |
| Koforidua | −3.580 | 0.0316** | 3 | |
| Krachi | −3.984 | 0.0093*** | 3 | |
| Kumasi | −4.871 | 0.0004*** | 3 | |
| Navarongo | −3.952 | 0.0103** | 3 | |
| Oda | −3.725 | 0.0208** | 3 | |
| Saltpond | −4.414 | 0.0021*** | 3 | |
| Sbekwai | −9.670 | 0.0000*** | 3 | |
| Sunyani | −5.998 | 0.0000*** | 3 | |
| Takoradi | −6.032 | 0.0000*** | 3 | |
| Tamale | −4.366 | 0.0025*** | 3 | |
| Tema | −3.921 | 0.0113** | 3 | |
| Wa | −4.195 | 0.0046*** | 3 | |
| Wenchi | −4.928 | 0.0003*** | 3 | |
| Yendi | −5.052 | 0.0002*** | 3 | |
| Rainy Days | Abetifi | −3.580 | 0.0316** | 3 |
| Accra | −4.349 | 0.0026*** | 3 | |
| Ada | −3.560 | 0.0334** | 3 | |
| Akatsi | −4.403 | 0.0022*** | 3 | |
| Akuse | −4.447 | 0.0018*** | 3 | |
| Axim | −3.503 | 0.0391** | 3 | |
| Bole | −3.653 | 0.0256** | 3 | |
| Ho | −3.583 | 0.0313** | 3 | |
| Koforidua | −4.399 | 0.0022*** | 3 | |
| Krachi | −5.168 | 0.0001*** | 3 | |
| Kumasi | −3.444 | 0.0458** | 3 | |
| Navarongo | −4.793 | 0.0005*** | 3 | |
| Oda | −3.581 | 0.0315** | 3 | |
| Saltpond | −4.900 | 0.0003*** | 3 | |
| Sbekwai | −3.643 | 0.0264** | 3 | |
| Sunyani | −3.437 | 0.0466** | 3 | |
| Takoradi | −3.910 | 0.0117** | 3 | |
| Tamale | −4.517 | 0.0014*** | 3 | |
| Tema | −3.717 | 0.0213** | 3 | |
| Wa | −3.962 | 0.0099*** | 3 | |
| Wenchi | −4.376 | 0.0024*** | 3 | |
| Yendi | −5.171 | 0.0001*** | 3 | |
| Wind Speed | Abetifi | −3.352 | 0.0581* | 3 |
| Accra | −4.396 | 0.0022*** | 3 | |
| Ada | −4.009 | 0.0085*** | 3 | |
| Akatsi | −4.019 | 0.0083*** | 3 | |
| Akuse | −4.059 | 0.0072*** | 3 | |
| Axim | −3.771 | 0.0181** | 3 | |
| Bole | −4.813 | 0.0004*** | 3 | |
| Ho | no observations | |||
| Koforidua | −3.504 | 0.0390*** | 3 | |
| Krachi | did not pass | |||
| Kumasi | −5.139 | 0.0001*** | 3 | |
| Navarongo | did not pass | |||
| Oda | −9.022 | 0.0000*** | 3 | |
| Saltpond | −3.906 | 0.0119** | 3 | |
| Sbekwai | −4.504 | 0.0015*** | 3 | |
| Sunyani | −5.391 | 0.0000*** | 3 | |
| Takoradi | no observations | |||
| Tamale | −4.670 | 0.0008*** | 3 | |
| Tema | −3.770 | 0.0181** | 3 | |
| Wa | no observations | |||
| Wenchi | −3.801 | 0.0165** | 3 | |
| Yendi | −3.617 | 0.0285** | 3 | |
| District | Humidity | Temperature | Rainy Days | Wind speed |
|---|---|---|---|---|
| Abetifi | No | No | No | No |
| Accra | No | Yes (***) | Yes (***) | No |
| Ada | Yes(**) | Yes (***) | No | Yes (***) |
| Akatsi | No | No | Yes(**) | No |
| Akuse | Yes (***) | Yes(**) | Yes (***) | No |
| Axim | Yes (***) | No | Yes (***) | No |
| Bole | No | No | No | No |
| Ho | Yes (***) | No | Yes(**) | No |
| Koforidua | Yes (***) | No | No | No |
| Krachi | Yes (***) | No | No | No |
| Kumasi | No | No | No | No |
| Navarongo | No | No | Yes (***) | No |
| Oda | No | No | No | No |
| Saltpond | No | Yes (***) | No | No |
| Sbekwai | No | No | No | No |
| Sunyani | No | No | No | No |
| Takoradi | Yes (***) | No | No | No |
| Tamale | Yes (***) | Yes (***) | Yes (***) | Yes (***) |
| Tema | No | Yes (***) | No | No |
| Wa | Yes (***) | No | Yes (***) | No |
| Wenchi | Yes (***) | No | No | Yes (***) |
| Yendi | Yes (***) | Yes (***) | Yes (***) | Yes (**) |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Akpalu, W.; Codjoe, S.N.A. Economic Analysis of Climate Variability Impact on Malaria Prevalence: The Case of Ghana. Sustainability 2013, 5, 4362-4378. https://doi.org/10.3390/su5104362
Akpalu W, Codjoe SNA. Economic Analysis of Climate Variability Impact on Malaria Prevalence: The Case of Ghana. Sustainability. 2013; 5(10):4362-4378. https://doi.org/10.3390/su5104362
Chicago/Turabian StyleAkpalu, Wisdom, and Samuel Nii Ardey Codjoe. 2013. "Economic Analysis of Climate Variability Impact on Malaria Prevalence: The Case of Ghana" Sustainability 5, no. 10: 4362-4378. https://doi.org/10.3390/su5104362




