Workspace Representation and Optimization of a Novel Parallel Mechanism with Three-Degrees-of-Freedom
Abstract
: The development of a new parallel mechanism based on simulation driven design is a rapid approach to discover the unique features or advantages of a conceptual model. In this research, one novel parallel mechanism which can generate three degrees-of-freedom translations is proposed. The kinematic model and Jacobian matrix is derived. The workspace generation and mapping is investigated based on simplified boundary searching method. The particle swarm algorithm is applied to search for the optimal volume of workspace.1. Introduction
The traditional parallel robots have proved their advantages in aspects of stiffness, rigidness, dexterity, reconfigurability, with the extensive applications in machine tools [1-3], motion simulators [4], picking and placing, sensors [5,6] and so on [7,8].
However, compared with the serial one, the drawbacks of the parallel robot is obvious [9,10]. Take its application in manufacturing as an example. The parallel robotic machines are usually composed with the active prismatic joint, the passive revolute joint, the passive universal joint or the passive spherical joint. According to the experience of real experiments, if the control system is broken or the vibration of the power supply, the unexpected motion will happen in these joints which may induce the permanent damage of the joints.
For the scenario of medical micromanipulation, the requirement of precision and safety is high. The compliant mechanism is fabricated with very flexible hinge or other flexure joint. The integration of compliant mechanism and parallel mechanism can provide an effective solution especially in precision and dexterity [11-14]. Besides, simulation driven design (SDD) as an effective method has been widely applied for the rapid prototype development. Based on SDD, the unique features or advantages of the conceptual model can be discovered in a high efficiency.
Many restriction factors of the parallel robot, including degree-of-freedom and configuration constraint of various joints, mechanical collision of different components, actuators stroke and singular limitations, affect the performances of workspace. Many scholars have developed different approaches and algorithms to investigate the features of workspace, especially its volume [15-27]. In [15], the joint workspace of a parallel kinematic machine (PKM) was calculated using the forward kinematic model. Since many PKMs are developed and fabricated based on decoupled kinematic structure, the single actuated joint usually cannot move dependently. Knowing the workspace of the active joints is important for motor selection and path planning. In [16], the relationship between task workspace and joint workspace was explained. In [18], the analogous symmetry characteristics of the reachable workspace for the symmetry group of the parallel mechanism were investigated. In [19], the reachable workspace was mapped without considering the joints limits and interferences between links. In [20], the path planning for singularity free route in a reachable workspace which was generated with a generic numerical algorithm was developed. In [21], the configuration optimization of a Delta-type parallel kinematic mechanism called Orthoglide was conducted based on a Cartesian workspace with prescribed kinetostatic performances. In [26], the modularity property of the parallel mechanism was utilized to calculate the volume of the workspace. In [27], the segmentation on the boundary curve of cross-section of a Stewart-Gough parallel manipulator was implemented to compute the size of the orientation workspace. In this research, the simplified workspace representation and optimization approaches are developed for a novel parallel mechanism. The proposed methods are generic and suitable for visual analysis, modeling and optimization of workspace for the different types of parallel manipulators.
In what follows, a new parallel mechanism that can generate three degrees-of-freedom translations is developed. Its kinematic model and Jacobian matrix is derived in Section 2. The workspace as the one of the most important indices of parallel mechanism is calculated and mapped in Section 3. The particle swarm algorithm based performance optimization is conducted to maximize the volume of workspace in Section 4. Section 5 gives the conclusions.
2. Conceptual Design and Kinematics Analysis
2.1. CAD Model
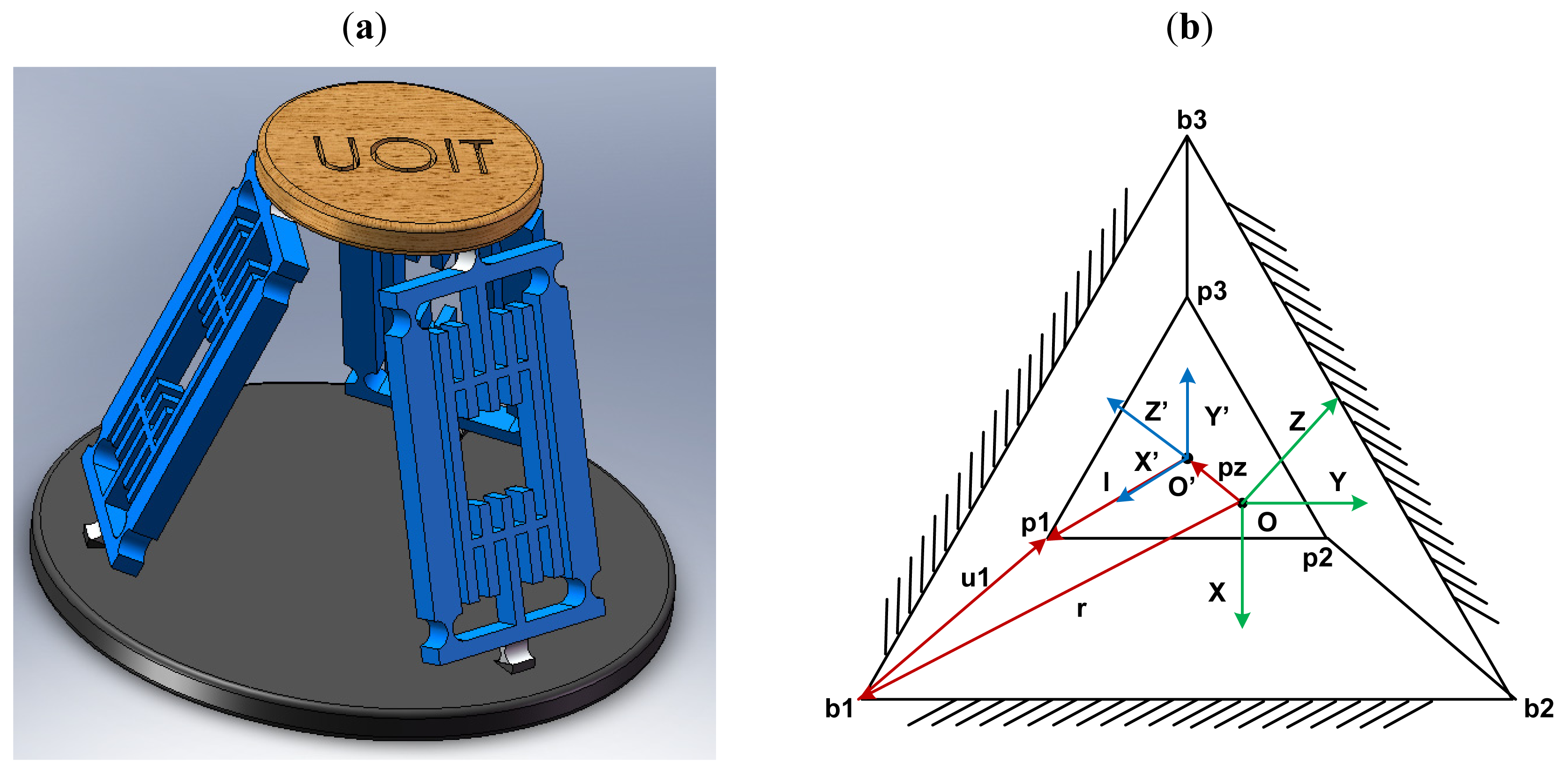
The novel parallel mechanism with three degrees-of-freedom translations is composed of a base structure, a moving platform and three legs connecting the base and platform. In each leg, a compliant revolute joint is attached to the moving platform. A four bar mechanism is hereafter connected to the revolute joint. The linear driven mechanism is embedded in the four bar mechanism which is actuated by a PZT. Another revolute joint which is perpendicular to the above-mentioned one is connected to the four bar mechanism and the base. The CAD model of the proposed 3-DOF parallel mechanism is shown in Figure 1.
2.2. Kinematics Analysis and Jacobian Matrix
Because of the nature of the compliant mechanism, generally speaking, the analysis of the parallel mechanism will be different to the conventional parallel mechanism. However, the detailed analysis will depend on the given case. Just like the traditional parallel manipulator, the proposed parallel mechanism has many performance indices, i.e., stiffness, dexterity, workspace, manipulability and so on. If the research topic is related to the stiffness of the parallel mechanism, the compliance of the flexure joint and link must be considered. Otherwise, the model would be inaccurate. Since in this case we would apply the PZTs as the actuators, the displacement of the moving platform will be mainly generated by the PZTs. Besides, in the research, the motion amplification effect produced by the PZTs is ignored. Based on these assumptions, the analysis of the proposed parallel mechanism can be simplified.
A kinematics model of the manipulator is shown in Figure 1(b). The vertices of the moving platform are pi (i = 1, 2, 3), and the vertices of the base are bi (i = 1, 2, 3). A global reference system O-XYZ is located at the center of the base. Another reference system O′-X′Y′Z′, called the moving frame, is located at the center of the moving platform. Note that Ob1 = Ob2 = Ob3 = r, and O′p1 = O′p2 = O′p3 = l.
The position vector of bi (i = 1, 2, 3) with respect to the global reference system is expressed as follows:
The position vector of pi (i = 1, 2, 3) with respect to the moving frame is expressed as below:
Thus, the position vector of pi (i = 1, 2, 3) with respect to the global reference system is derived as:
Thus, the inverse kinematics of the proposed parallel mechanism can be derived as:
Since the relationship of the differential for the input joints and the output displacements can be expressed as:
Thus, the Jacobian matrix of the proposed parallel mechanism is obtained as:
3. Workspace Mapping
As was defined in [15], generally, the workspace of a parallel mechanism can be roughly divided into task workspace and the joint workspace. The task workspace refers the motion scopes of the moving platform in two or three dimensions. The total area was calculated to describe the performance of a 2D task workspace. The total volume was calculated to describe the performance of a 3D task workspace.
The generation of workspace for the parallel mechanisms includes geometrical approach, numerical method and discretization method. With the integration of geometrical approach, discretization method and inverse kinematics model, a simplified boundary searching method (SBS) is developed to acquire the task workspace.
The calculating process of SBS method is described as follows:
s1: Define the input parameters of the proposed parallel mechanism. These parameters include l, r, dmin, dmax and h. Here, l and r are the radii of the moving platform and base, respectively. dmin and dmax are the motion scopes of the PZT. h is the height of the moving platform.
s2: Confirm the bounds of input parameters and other boundary conditions. Initially, the moving platform is located at the home position.
s3: Let counter = 0.
s4: Set the step-size for the movement of mobile platform in directions of x, y and z from initial pose. The step-size should be as small as possible to improve the calculation accuracy.
s5: Calculate the analytical solution of inverse kinematics model.
s6: The mobile platform transfers from the original/former position to the given position with the step-size.
s7: According to the bounds of input parameters and other boundary conditions, determining that whether the boundary conditions are exceeded when the mobile platform is located at a certain pose.
s8: If the answer to s7 is yes, then go to s9. Otherwise, counter = counter + 1, and jump back to s6.
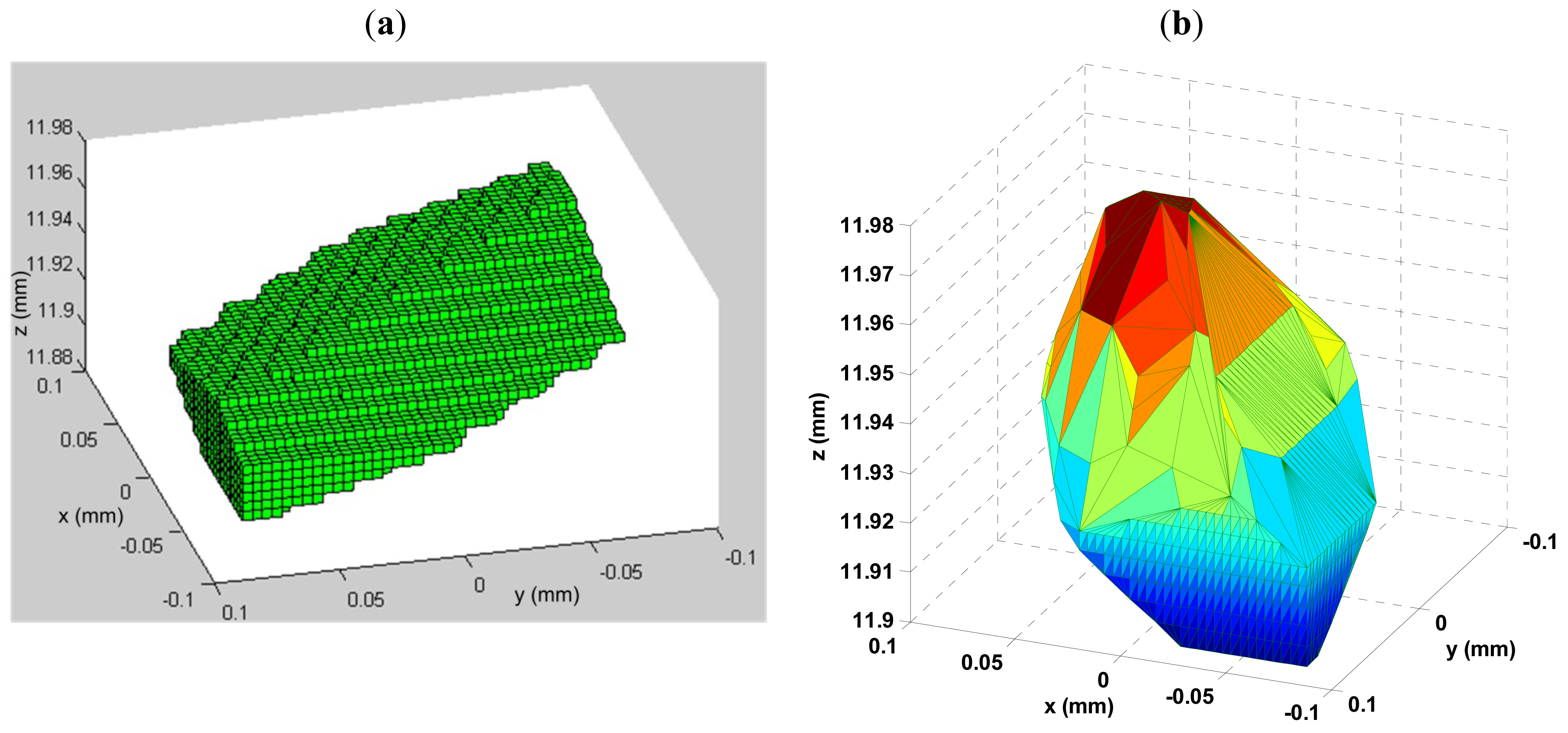
s9: In this step, since the moving platform is reaching the bound to the workspace, the algorithm terminates. Thus, generate and draw the workspace with the cubes (0.004 mm × 0.004 mm × 0.004 mm) in Cartesian coordinate system as shown in Figure 2(a).
s10: Plot the envelope of the workspace generated in s9, as shown in Figure 2(b).
The features of workspace including shape and volume are related with the dimensions of the proposed parallel mechanism. Figure 3 shows the different mapping of workspace when the two representative dimensions l and r are defined with the optional values.
4. Workspace Optimization
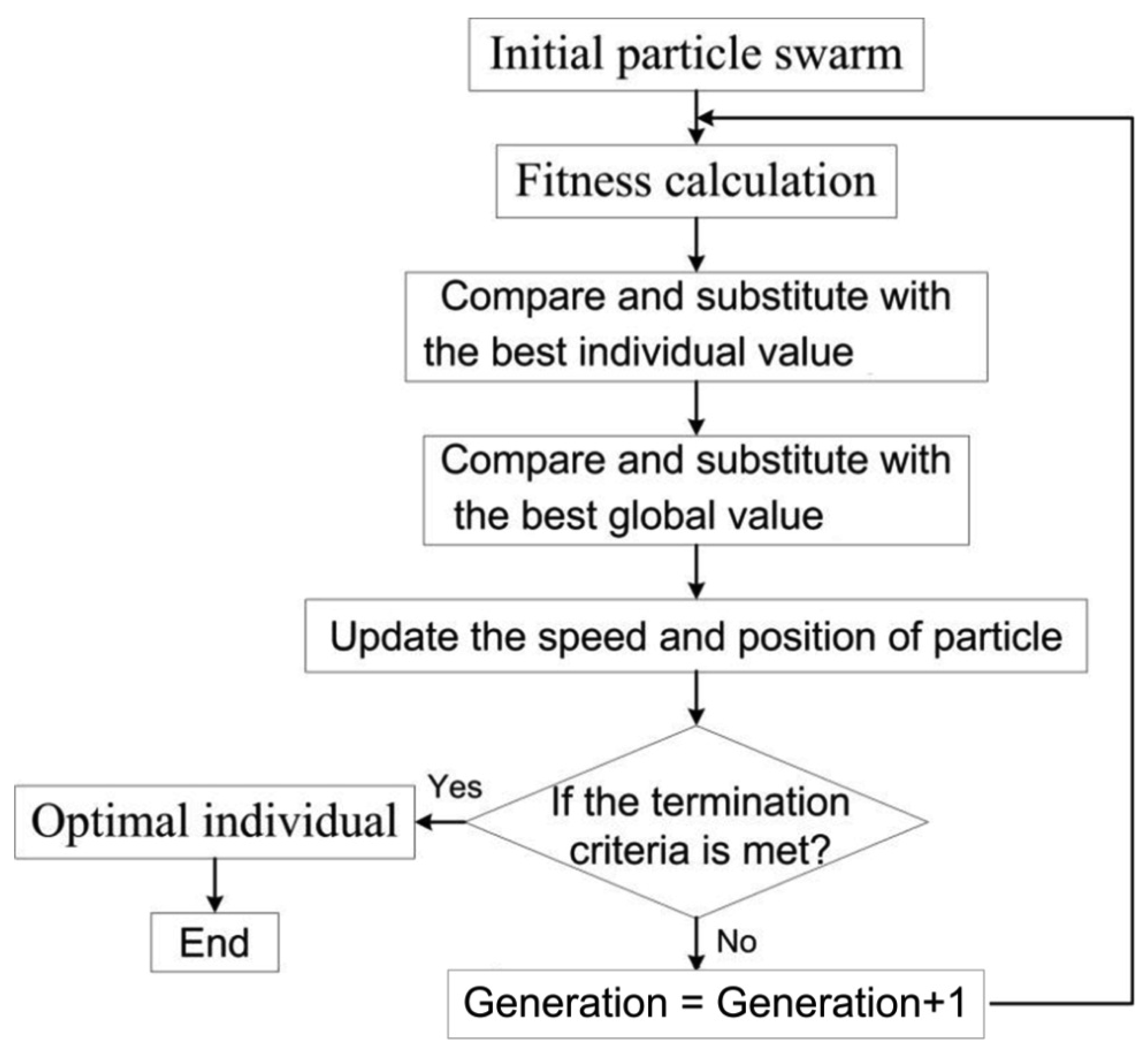
The traditional optimization methods usually adopt the local search by a convergent stepwise procedure which possibly falls into local optimal solution. If the complex function to be optimized does not possess convexity characteristics that essentially satisfy that the local extreme point is a global optimum, a global optimization algorithm is required. As an advanced computational intelligence method, particle swarm optimization (PSO) is inspired by simulating the swarm behavior such as bird flocking. Without the traditional evolution operators including crossover and mutation, PSO can be viewed as the extension and improvement of the working principle of genetic algorithm. Thus, the particle swarm algorithms will be used to search the overall optimal performance.
The general PSO algorithm is constituted with the following velocity and position [28]:
The mechanism parameters chosen for optimization are l, r, dmin, dmax and h. After considering the initial values and their possible changes, the ranges are set as
l ∈ [3.9, 4.5]mm,
r ∈ [7.7, 8.1]mm,
dmin ∈ [12.5, 12.58]mm,
dmax ∈ [12.58, 12.62]mm,
h ∈ [11.98, 12.02]mm.
In this scenario, the common PSO with inertia is utilized to perform the optimization process. The maximal velocity divisor is 2, the particles number is 100. Figure 5 illustrates the evolutionary process with PSO.
Before optimization, the value of objective function is equal to 5.42×10−4 mm3, with the initial parameters as follows:
l = 4 mm,
r = 8 mm,
dmin = 12.56 mm,
dmax = 12. 6 mm,
h = 12 mm.
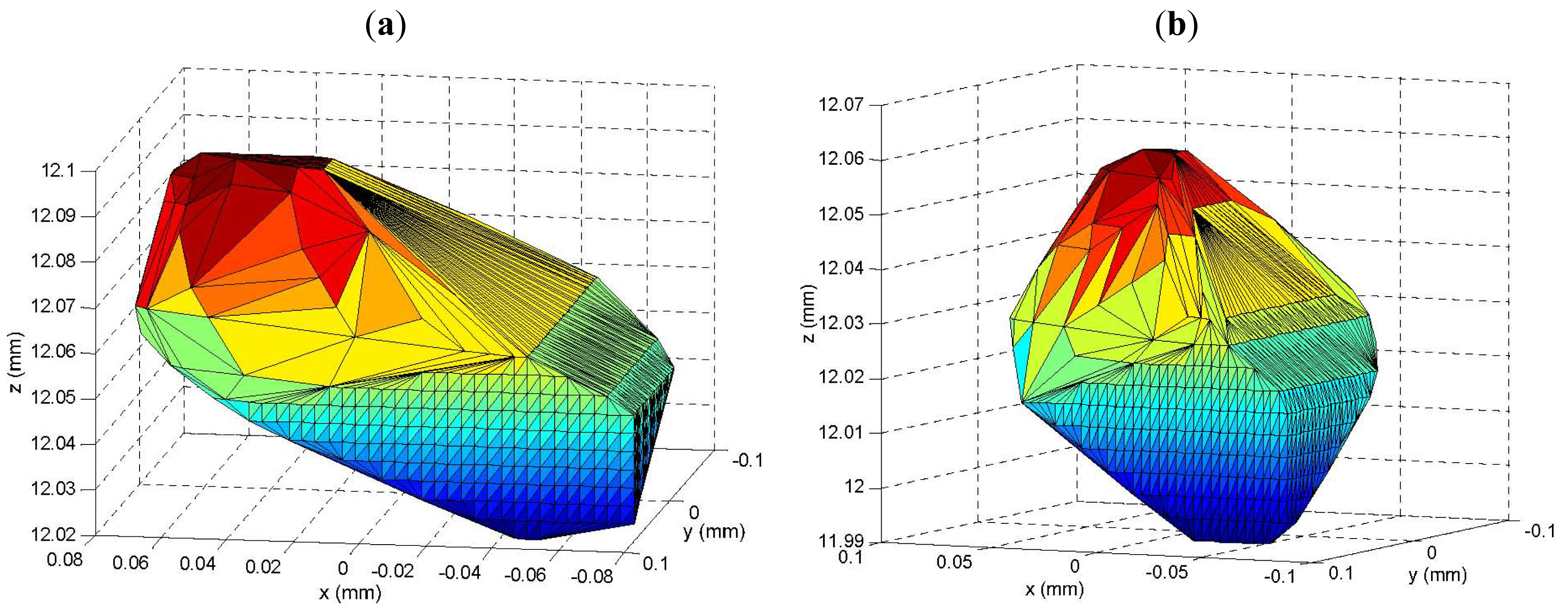
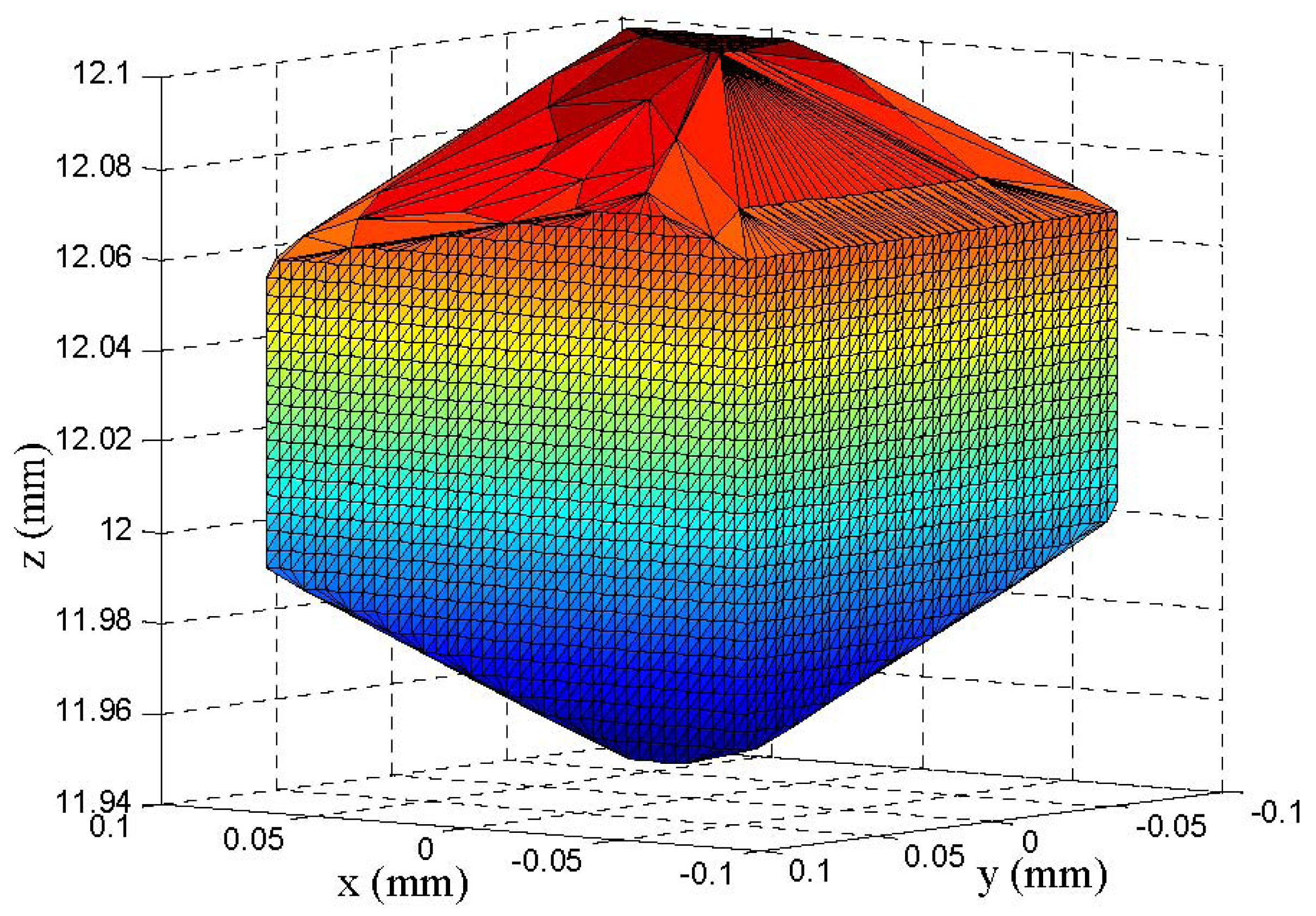
After optimization with 35 epochs, the volume of workspace is 2.82×10−3 mm3, improved by a factor of 5.2. The best individuals of the five parameters are:
L′ = 4.2854 mm,
R′ = 7.8943 mm,
d′min = 12.5 mm,
d′max = 12.62 mm,
h′ = 11.996 mm.
Figure 6 describes the envelope of the workspace with the maximal volume after optimization based on PSO.
5. Conclusions
The main contributions of this paper are summarized as follows:
A new parallel mechanism which can generate three degrees-of-freedom translations is designed. The related kinematics modeling is investigated.
A general approach called simplified boundary searching method is developed to generate the reachable workspace of the proposed parallel mechanism.
Optimization of the dimensional parameters is conducted to obtain the maximal volume of workspace based on particle swarm algorithm.
This research focuses on developing a generic and simplified method for the modeling, mapping, calculation and optimization of workspace for a parallel mechanism. Currently, the modeling and optimization of parallel mechanisms is still one open issue for the scholars and engineers in the world who are interested in or already investigating this topic. The newly developed method about workspace generation and improvement is presented in a clear and operational way. Through case study, it can be proved that this approach is very efficient in modeling and computing time. The proposed method is feasible as one efficient solution for the open issue of workspace.
This study has endeavored in design optimization of the workspace for a novel moving stage which can generate three degrees-of-freedom translations. The kinematic model and Jacobian matrix is derived. The simplified boundary searching method to generate the workspace of the proposed parallel mechanism is generic. The particle swarm algorithm is applied to improve the volume of workspace. For the future work, the prototype will be fabricated based on the proposed modeling and optimization approach.


Acknowledgments
The authors would like to thank the financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC). The authors gratefully acknowledge the financial support from Canada Research Chairs program, MITACS-NCE and ERA.
References and Notes
- Chen, S.; Chang, T.; Lin, Y. Applications of equivalent components concept on the singularity analysis of TRR-XY hybrid parallel kinematic machine tools. Int. J. Adv. Manuf. Technol. 2006, 30, 778–788. [Google Scholar]
- Refaat, S.; Herve, J.; Nahavandi, S. Two-mode overconstrained three-DOFs rotational translational linear motor based parallel-kinematics mechanism for machine tool applications. Robotica 2007, 25, 461–466. [Google Scholar]
- Gao, Z.; Zhang, D.; Hu, X.; Ge, Y. Design, analysis and stiffness optimization of a three-degree-of-freedom parallel manipulator. Robotica 2010, 28, 349–357. [Google Scholar]
- Hostens, I.; Anthonis, J.; Ramon, H. New design for a 6 dof vibration simulator with improved reliability and performance. Mech. Syst. Signal Process. 2005, 19, 105–122. [Google Scholar]
- Hou, Y.; Zeng, D.; Yao, J.; Kang, K.; Lu, L.; Zhao, Y. Optimal design of a hyperstatic Stewart platform-based force/torque sensor with genetic algorithms. Mechatronics 2009, 19, 199–204. [Google Scholar]
- Jin, Z.; Gao, F.; Zhang, X. Design and analysis of a novel isotropic six-component force/torque sensor. Sens. Actuators A 2003, 109, 17–20. [Google Scholar]
- Jensen, K.; Lusk, C.; Howell, L. An XYZ micromanipulator with three translational degrees of freedom. Robotica 2006, 24, 305–314. [Google Scholar]
- Palmer, J.; Dessent, B.; Mulling, J.; Usher, T.; Grant, E.; Eischen, J.; Kingon, A.; Franzon, P. The design and characterization of a novel piezoelectric transducer-based linear motor. IEEE/ASME Trans. Mechatron. 2004, 13, 441–450. [Google Scholar]
- Zhang, D.; Xi, F.; Mechefske, C.; Sherman, Y. Analysis of parallel kinematic machines with kinetostatic modelling method. Robot. Comput. Integr. Manuf. 2004, 20, 151–165. [Google Scholar]
- Zhang, D.; Bi, Z.; Li, B. Design and kinetostatic analysis of a new parallel manipulator. Robot. Comput. Integr. Manuf. 2009, 25, 782–791. [Google Scholar]
- Venanzi, S.; Giesen, P.; Parenti-Castelli, V. A novel technique for position analysis of planar compliant mechanisms. Mech. Mech. Theory 2005, 40, 1224–1239. [Google Scholar]
- Moon, Y. Bio-mimetic design of finger mechanism with contact aided compliant mechanism. Mech. Mech. Theory 2007, 42, 600–611. [Google Scholar]
- Gao, Z.; Zhang, D. Design and Implementation of a multidimensional acceleration sensor based on fully decoupled compliant parallel mechanism. Sens. Actuators 2010, 163, 418–427. [Google Scholar]
- Dong, W.; Sun, L.; Du, Z. Design of a precision compliant parallel positioner driven by dual piezoelectric actuators. Sens. Actuators 2007, 135, 250–256. [Google Scholar]
- Bi, Z.; Lang, S. Joint workspace of parallel kinematic machines. Robot. Comput. Integr. Manuf. 2009, 25, 57–63. [Google Scholar]
- Bi, Z.; Wang, L. Optimal design of reconfigurable parallel machining systems. Robot. Comput. Integr. Manuf. 2009, 25, 951–961. [Google Scholar]
- Bi, Z.; Jin, Y. Kinematic modeling of Exechon parallel kinematic machine. Robot. Comput. Integr. Manuf. 2011, 27, 186–193. [Google Scholar]
- Zhao, J.; Chu, F.; Feng, Z. Symmetrical characteristics of the workspace for spatial parallel mechanisms with symmetric structure. Mech. Mach. Theory 2008, 43, 427–444. [Google Scholar]
- Piccin, O.; Bayle, B.; Maurin, B.; Mathelin, M. Kinematic modeling of a 5-DOF parallel mechanism for semi-spherical workspace. Mech. Mach. Theory 2009, 44, 1485–1496. [Google Scholar]
- Dash, A.; Chen, I.; Yeo, S.; Yang, G. Workspace generation and planning singularity-free path for parallel manipulators. Mech. Mach. Theory 2005, 40, 776–805. [Google Scholar]
- Chablat, D.; Wenger, P. Architecture optimization of a 3-DOF translational parallel mechanism for machining applications, the Orthoglide. IEEE Trans. Robot. Autom. 2003, 19, 403–410. [Google Scholar]
- Pusey, J.; Fattah, A.; Agrawal, S.; Messina, E. Design and workspace analysis of a 6-6 cable-suspended parallel robot. Mech. Mach. Theory 2004, 39, 761–778. [Google Scholar]
- Jeong, J.; Kim, S.; Kwak, Y. Kinematics and workspace analysis of a parallel wire mechanism for measuring a robot pose. Mech. Mach. Theory 1999, 34, 825–841. [Google Scholar]
- Xu, B.; Li, T.; Liu, X.; Wu, J. Workspace analysis of the 4RRR planar parallel manipulator with actuation redundancy. Tsinghua Sci. Technol. 2010, 15, 509–516. [Google Scholar]
- Cervantes-Sanchez, J.; Rendon-Sanchez, J. A simplified approach for obtaining the workspace of a class of 2-dof planar parallel manipulators. Mech. Mach. Theory 1999, 34, 1057–1073. [Google Scholar]
- Brisan, C.; Csiszar, A. Computation and analysis of the workspace of a reconfigurable parallel robotic system. Mech. Mach. Theory 2011, 46, 1647–1668. [Google Scholar]
- Tsai, K.; Lin, J. Determining the compatible orientation workspace of Stewart-Gough parallel manipulators. Mech. Mach. Theory 2006, 41, 1168–1184. [Google Scholar]
- Birge, B. PSOt—A particle swarm optimization toolbox for use with Matlab. Proceedings of the 2003 IEEE Swarm Intelligence Symposium, Indianapolis, IN, USA, 24–26 April 2003; pp. 182–186.
- Conflict of Interest: The authors declare no conflict of interest.
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gao, Z.; Zhang, D. Workspace Representation and Optimization of a Novel Parallel Mechanism with Three-Degrees-of-Freedom. Sustainability 2011, 3, 2217-2228. https://doi.org/10.3390/su3112217
Gao Z, Zhang D. Workspace Representation and Optimization of a Novel Parallel Mechanism with Three-Degrees-of-Freedom. Sustainability. 2011; 3(11):2217-2228. https://doi.org/10.3390/su3112217
Chicago/Turabian StyleGao, Zhen, and Dan Zhang. 2011. "Workspace Representation and Optimization of a Novel Parallel Mechanism with Three-Degrees-of-Freedom" Sustainability 3, no. 11: 2217-2228. https://doi.org/10.3390/su3112217



