Dynamic Analysis of the Almagrera Tailings Dam with Dry Closure Condition
Abstract
:1. Introduction
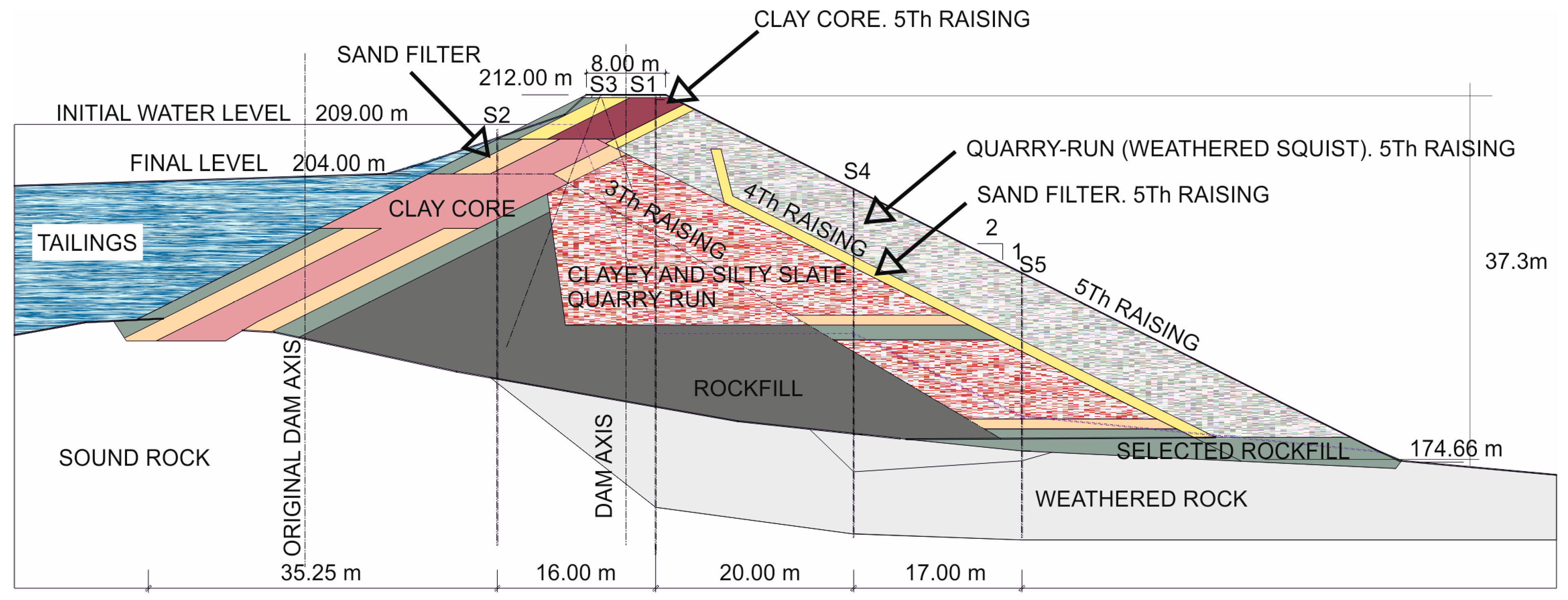
2. Location and Geology of the Almagrera Tailings Dam
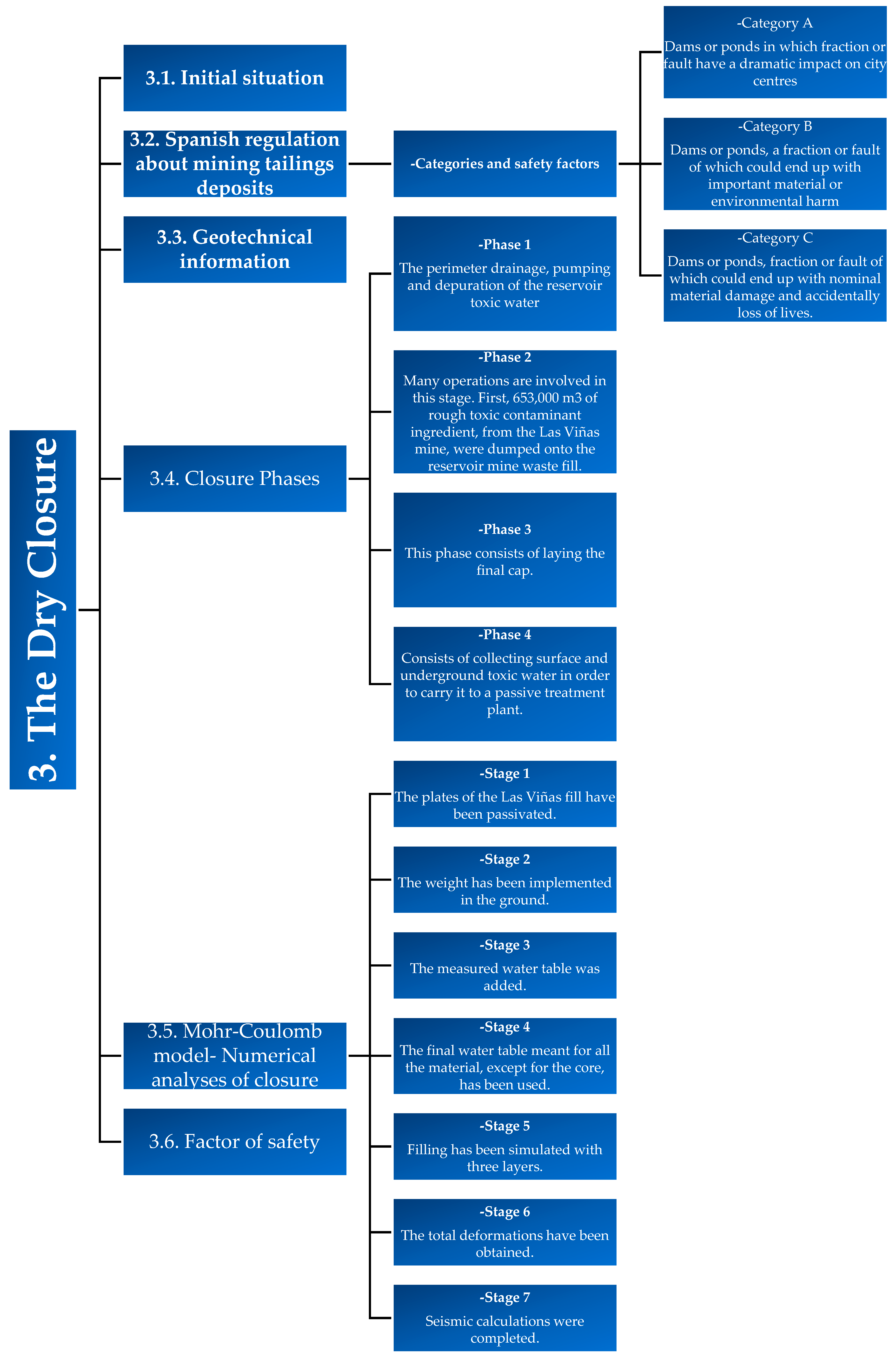
3. The Dry Closure
3.1. Initial Situation
3.2. Spanish Regulation about Mining Tailings Deposits
Categories and Safety Factors
- (a)
- If, in compliance with a hazard evaluation, a crucial incident may stem from a failure or malfunction; for instance, the demolishing of a mass or the fraction of a dam.
- (b)
- If it comprises substances categorized as hazardous under Directives 91/689 or 67/548/EEC over a definite level.
3.3. Geotechnical Information
3.4. Closure Phases
3.4.1. Phase 1
3.4.2. Phase 2
3.4.3. Phase 3
3.4.4. Phase 4
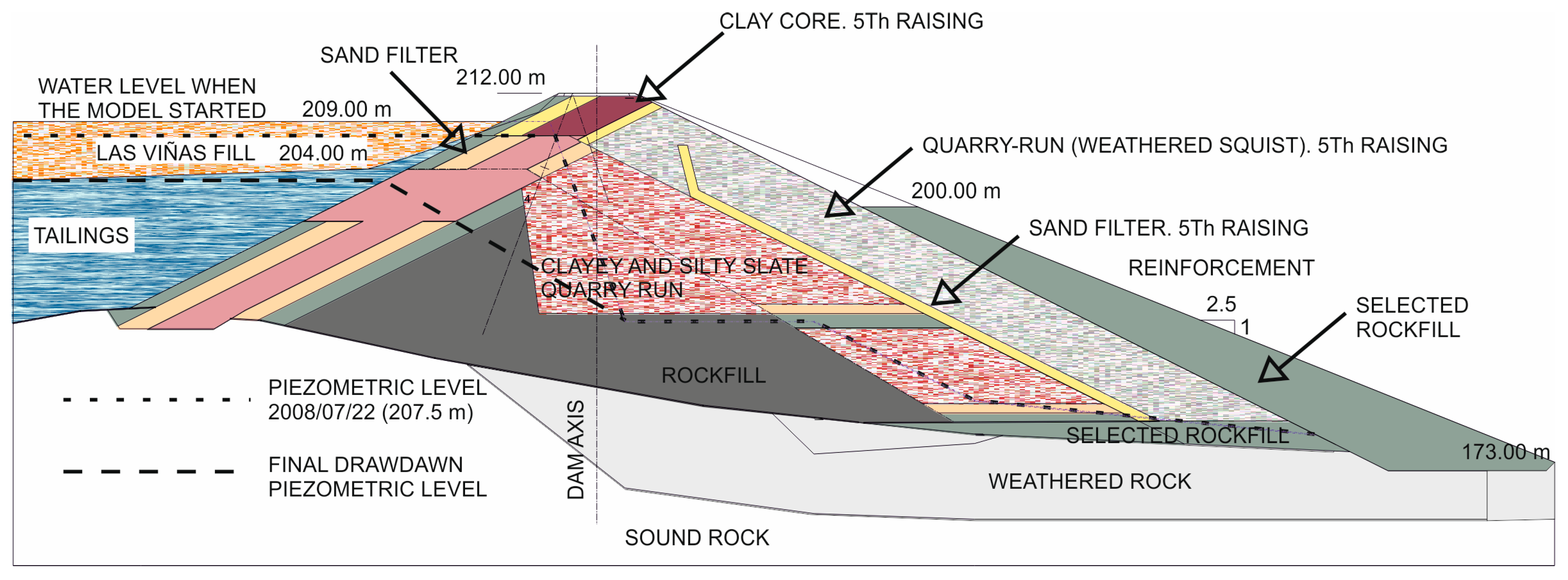
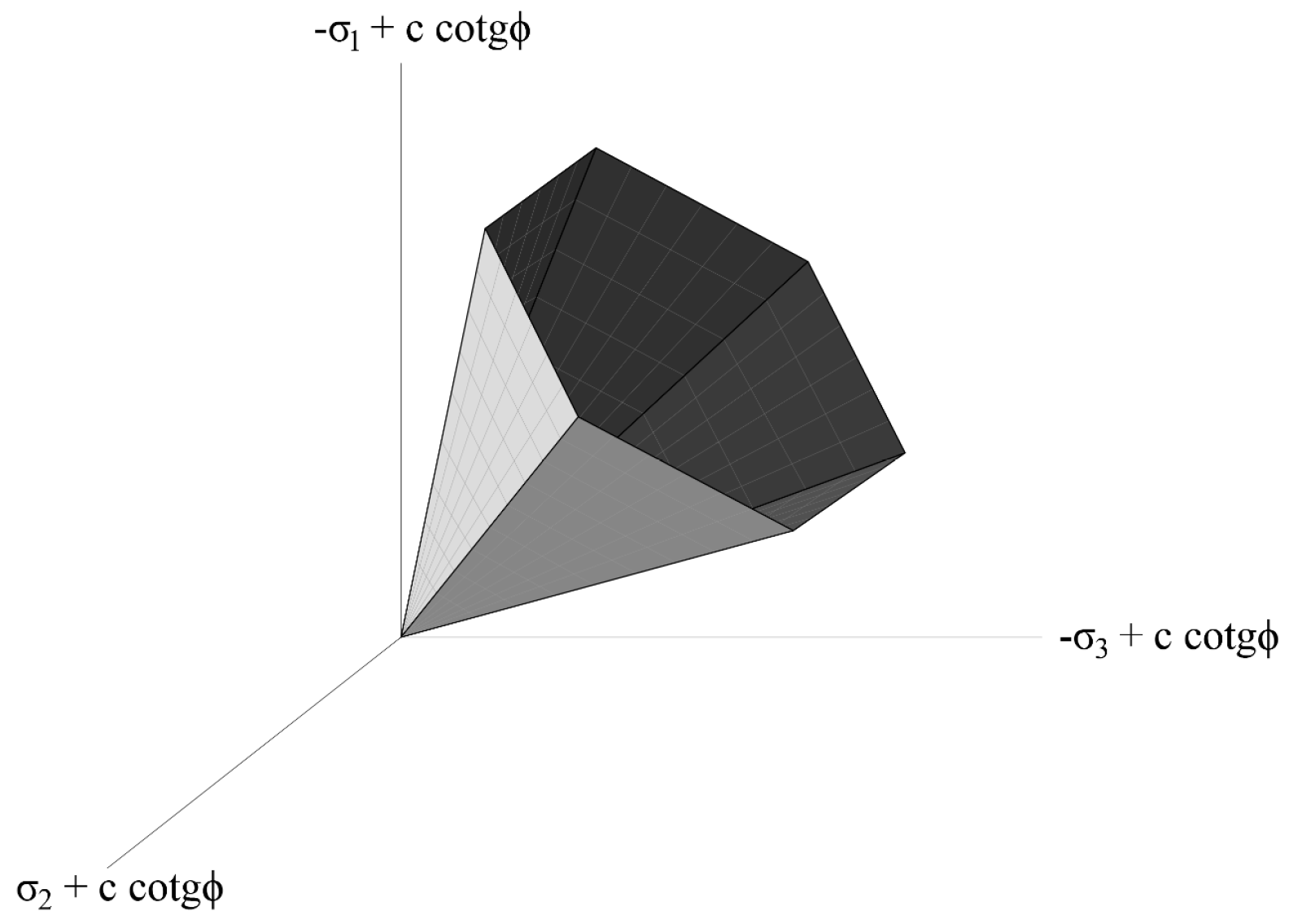
3.5. Mohr-Coulomb Model-Numerical Analyses of Closure
3.5.1. Stage 1
3.5.2. Stage 2
3.5.3. Stage 3
3.5.4. Stage 4
- (a)
- The final water table meant for all the material, except for the core, has been used. For the core, the initial water table reducing the water height over the upstream face has been estimated. The materials have been consolidated, initially undrained. As the total drawdown is supposed to be applied at the beginning, the time has been reduced to half (45 days).
- (b)
- From the initial water table the reservoir level reduction has been applied in the upstream face as a transient regime for 90 days through the PlaxFlow program.
3.5.5. Stage 5
3.5.6. Stage 6
- (a)
- Calculation with piezocone level.
- (b)
- Calculation with flow net.
3.5.7. Stage 7
3.6. Factor of Safety
4. Seismicity and Seismic Input Data
4.1. Seismic Properties of the Iberian Peninsula
4.2. Seismicity at the Almagrera Site
4.3. Spanish Regulation
- -
- : basic seismic acceleration.
- -
- : dimensionless coefficient which takes into account the return period. For constructions of special importance this is 1.3—which means a return period of 1000 years.
- -
- : soil amplification coefficient.
- -
- : Soil coefficient depending on the classifications of the soil (Table 4).
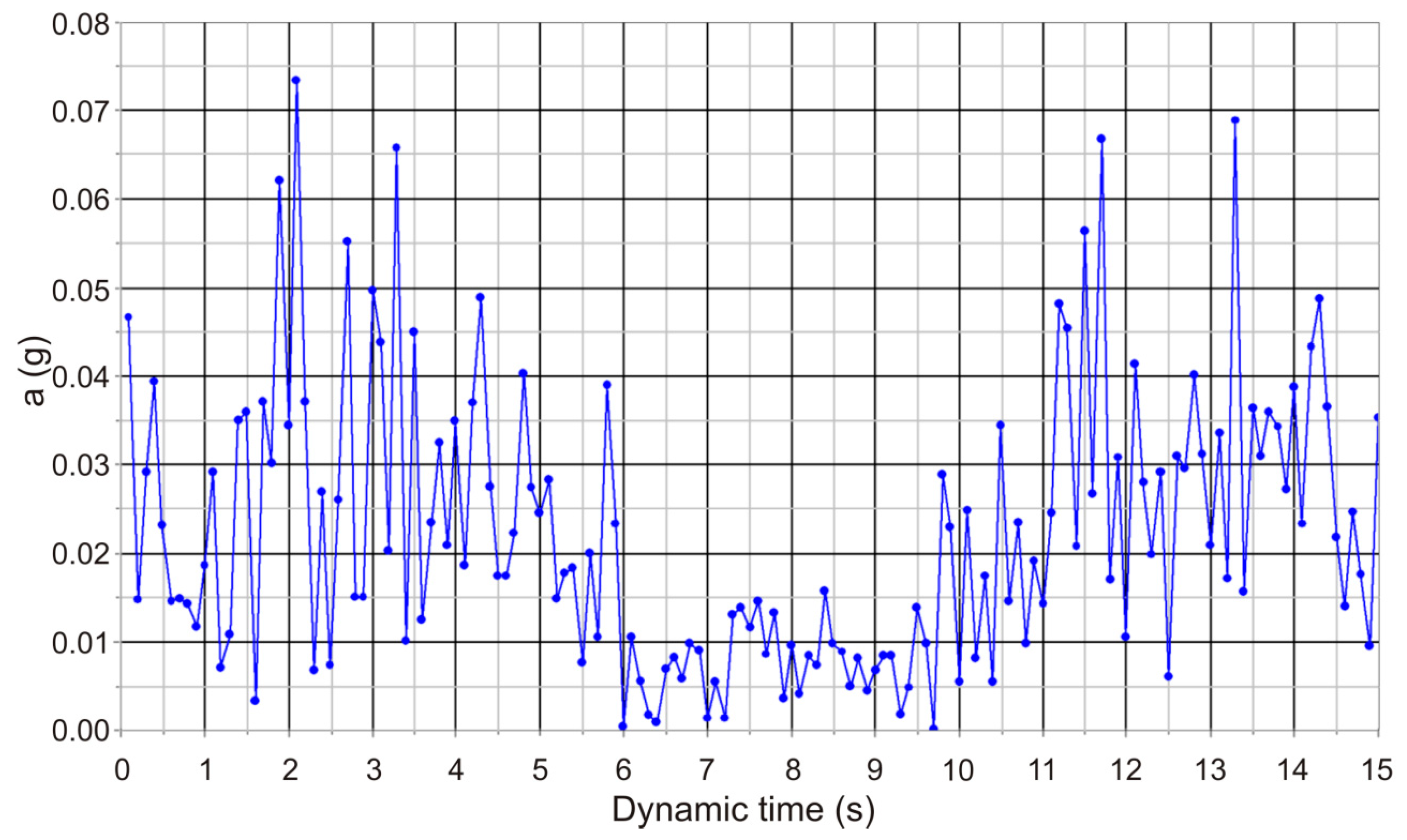
4.4. Definition of the Accelerograms
- -
- Founded on sound rock.
- -
- Repetition time shut to 1000 years.
5. Dynamic Calculation
5.1. The Safety of Dams during Earthquakes
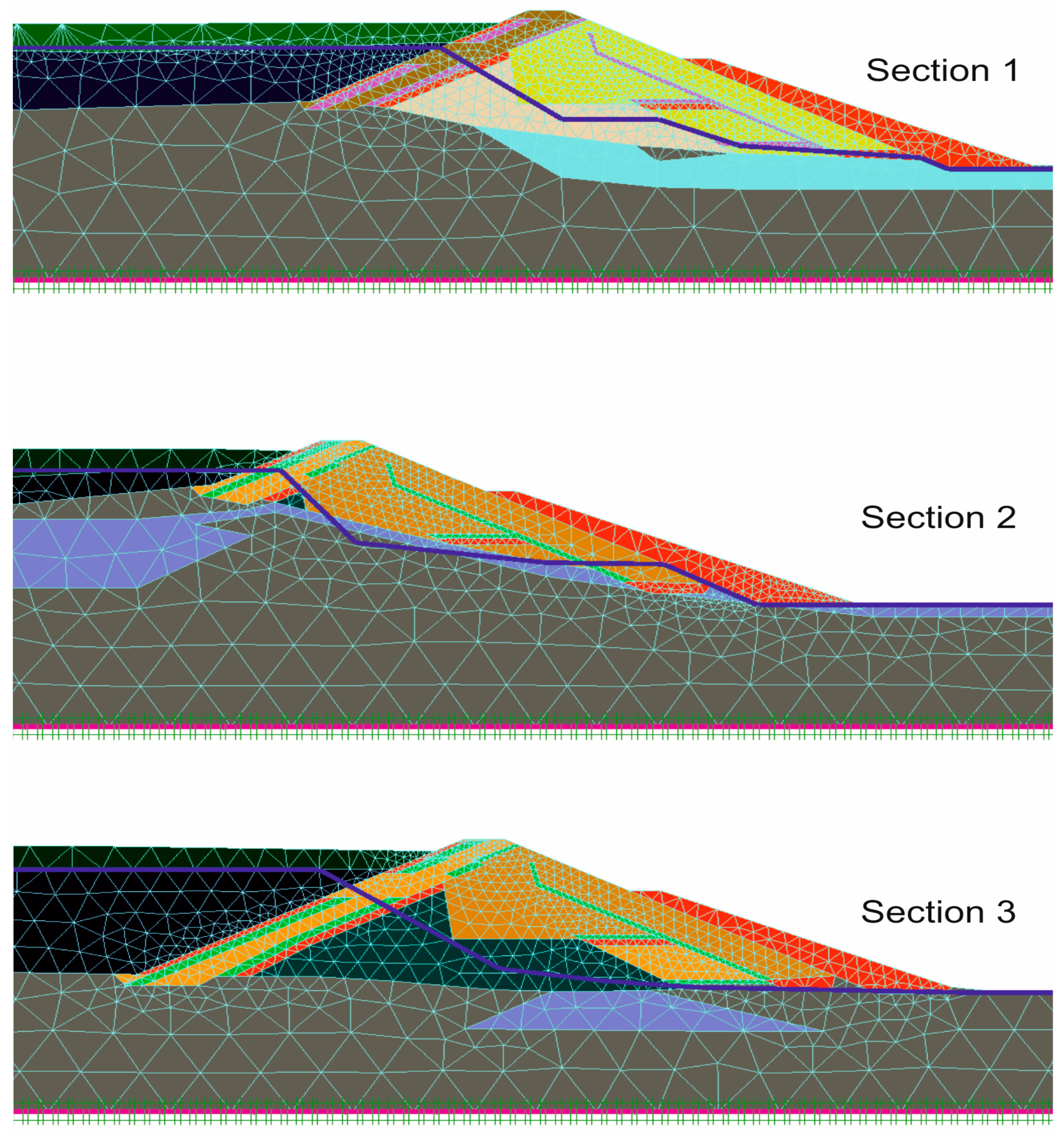
5.2. Finite Element Model
5.2.1. Material Models
5.2.2. Sources of Energy Dissipation
Material Damping
Numerical Damping
Boundary Cases
5.2.3. Calculation Steps
- (a)
- Self-weight.
- (b)
- Self-weight and accelerograms application.
6. Calculation Results
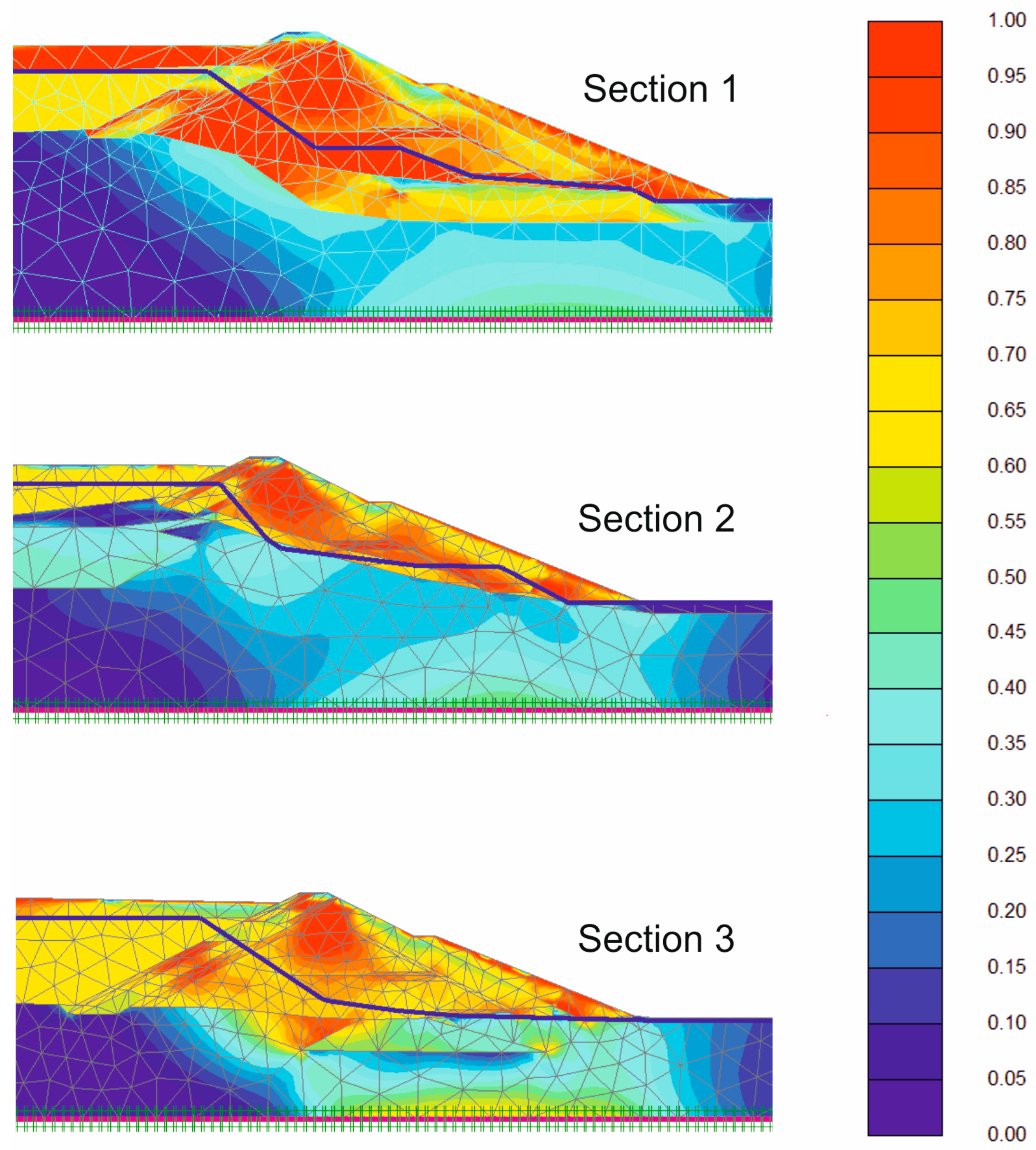
6.1. Analysis of Stress
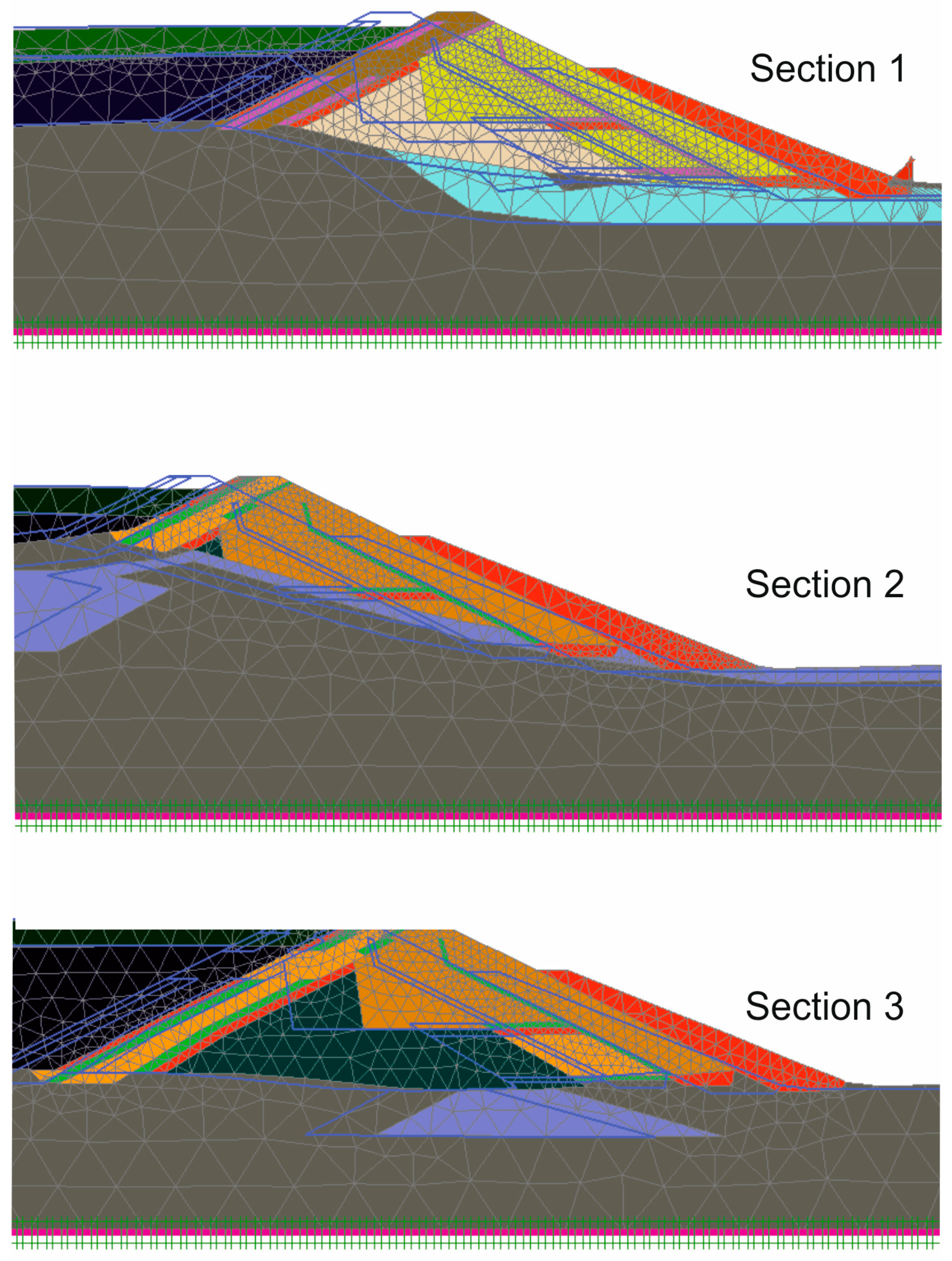
6.2. Analysis of Deformations
7. Analysis of Liquefaction
“An evaluation of the liquefaction susceptibility shall be made when the foundation soils include extended layers or thick lenses of loose sand, with or without silt/clay fines, beneath the water table level, and when the water table level is close to the ground surface. This evaluation shall be performed for the free-field site conditions (ground surface elevation, water table elevation) prevailing during the lifetime of the structure”.
8. Conclusions
- (1)
- A dynamic computation for the dry closure of the Almagrera’s tailings dam is presented herein.
- (2)
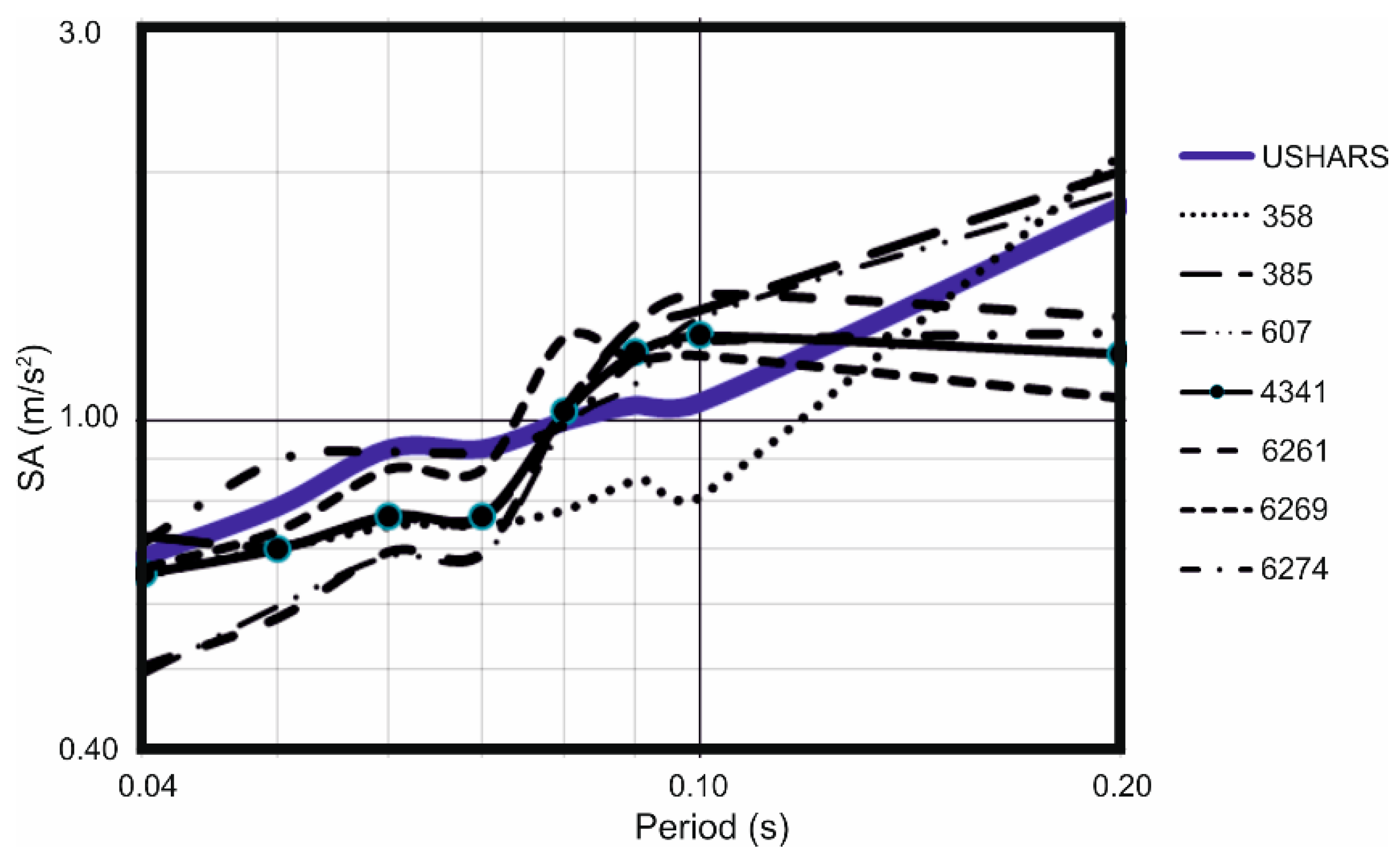
- In order to carry out a dynamic seismic analysis, a method for selecting real accelerograms has been presented. The method depends upon the construction of USHARS for the Almagrera site, considering the kind of ground at the foundation and the required hazard level. Up to seven accelerograms from the European Strong Motion data base have been selected.
- (3)
- The main advantage of using dynamic FE analysis is that it provides detailed information of the soil stress distribution and deformation. It should be noted that special care must be taken with the model. The material damping, the numerical damping and the boundary conditions have been configured to fit the dam’s real conditions. The HS-small model used allows calculating the residual deformation. The results show that the dam is safe enough.
- (4)
- The expected permanent displacement of the dam body after the maximum expected earthquake is acceptable, with Section 1 being the most critical. The results show that no continuous failure surface crosses the dam body for the maximum expected earthquake. Nonetheless, the results show that, at some short moments the dam body is close to collapse. Moreover, in some places, Las Viñas fill and the tailings may attain failure. This indicates a tailings displacement, but not a dam failure. The liquefaction that could suffer the fill upstream is unimportant.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alonso, E.E.; Gens, A. Aznalcóllar Dam Failure. Part 1: Field Observations and Material Properties. Géotechnique 2006, 56, 165–183. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A. Aznalcóllar Dam Failure. Part 3: Dynamics of the Motion. Géotechnique 2006, 56, 203–210. [Google Scholar] [CrossRef]
- Ministerio de Medio Ambiente. Plan Nacional de Residuos de Industrias Extractivas 2008–2015; Anexo 10 Del I; Ministerio del Medio Ambiente: Madrid, Spain, 2007; Volume 2015, pp. 11–210. [Google Scholar]
- Zandarín, M.T.; Oldecop, L.A.; Rodríguez, R.; Zabala, F. The Role of Capillary Water in the Stability of Tailing Dams. Eng. Geol. 2009, 105, 108–118. [Google Scholar] [CrossRef]
- Yin, G.; Li, G.; Wei, Z.; Wan, L.; Shui, G.; Jing, X. Stability Analysis of a Copper Tailings Dam via Laboratory Model Tests: A Chinese Case Study. Miner. Eng. 2011, 24, 122–130. [Google Scholar] [CrossRef]
- Yin, G.; Zhang, Q.; Wang, W.; Chen, Y.; Geng, W.; Liu, H. Experimental Study on the Mechanism Effect of Seepage on Microstructure of Tailings. Saf. Sci. 2012, 50, 792–796. [Google Scholar] [CrossRef]
- Rico, M.; Benito, G.; Díez-Herrero, A. Floods from Tailings Dam Failures. J. Hazard. Mater. 2008, 154, 79–87. [Google Scholar] [CrossRef]
- Van Niekerk, H.J.; Viljoen, M.J. Causes and Consequences of the Merriespruit and Other Tailings-Dam Failures. Land Degrad. Dev. 2005, 16, 201–212. [Google Scholar] [CrossRef]
- Rico, M.; Benito, G.; Salgueiro, A.R.; Díez-Herrero, A.; Pereira, H.G. Reported Tailings Dam Failures: A Review of the European Incidents in the Worldwide Context. J. Hazard. Mater. 2008, 152, 846–852. [Google Scholar] [CrossRef] [PubMed]
- Gachechiladze-Bozhesku, M. Learning from Transboundary Environmental Impact Assessment under the Espoo Convention: A Case of the Neman Hydropower Plant, Belarus. Impact Assess. Proj. Apprais. 2014, 32, 81–86. [Google Scholar] [CrossRef]
- Lin, P.; Huang, B.; Li, Q.; Wang, R. Hazard and Seismic Reinforcement Analysis for Typical Large Dams Following the Wenchuan Earthquake. Eng. Geol. 2014, 194, 86–97. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Z.; Yu, H.; Wen, R.; Lu, D.; Huang, M.; Zhou, Y.; Cu, J. Strong Motion Observations and Recordings from the Great Wenchuan Earthquake. Earthq. Eng. Eng. Vib. 2008, 7, 235–246. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, J.; Peng, Z.; Su, J. Seismic Velocity Changes in the Epicentral Region of the 2008 Wenchuan Earthquake Measured from Three-Component Ambient Noise Correlation Techniques. Geophys. Res. Lett. 2014, 41, 37–42. [Google Scholar] [CrossRef]
- Costa-Pierce, B.A. Constraints to the Sustainability of Cage Aquaculture for Resettlement from Hydropower Dams in Asia: An Indonesian Case Study. J. Environ. Dev. 1998, 7, 333–363. [Google Scholar] [CrossRef]
- Ambraseys, N.N. On the Shear Response of a Two-Dimensional Truncated Wedge Subjected to an Arbitrary Disturbance. Bull. Seismol. Soc. Am. 1960, 50, 45–56. [Google Scholar] [CrossRef]
- Marcuson, W.F., III; Hadala, P.F.; Franklin, A.G. Current Methods of Dynamic Analysis for Seismic Stability of Earth Dams. Eng. Geol. 1980, 60, 19–28. [Google Scholar] [CrossRef]
- Prevost, B.J.H.; Abdel-ghaffar, A.M.; Lacy, S.J. Nonlinear Dynamic Analyses of an Earth Dam. J. Geotech. Eng. 1985, 111, 882–897. [Google Scholar] [CrossRef]
- Kuwano, J.; Ishihara, K. Analysis of Permanent Deformation of Earth Dams Due To Earthquakes. Soils Found. 1988, 28, 41–55. [Google Scholar] [CrossRef]
- Elgamal, A.-W.M.; Gunturi, R.V. Dynamic Behaviour and Seismic Response of El Infiernillo Dam. Earthq. Eng. Struct. Dyn. 1993, 22, 665–684. [Google Scholar] [CrossRef]
- Woodward, P.K.; Griffiths, D.V. Influence of Viscous Damping in the Dynamic Analysis of an Earth Dam Using Simple Constitutive Models. Comput. Geotech. 1996, 19, 245–263. [Google Scholar] [CrossRef]
- Cascone, E.; Rampello, S. Decoupled Seismic Analysis of an Earth Dam. Soil Dyn. Earthq. Eng. 2003, 23, 349–365. [Google Scholar] [CrossRef]
- Khoei, A.R.; Azami, A.R.; Haeri, S.M. Implementation of Plasticity Based Models in Dynamic Analysis of Earth and Rockfill Dams: A Comparison of Pastor-Zienkiewicz and Cap Models. Comput. Geotech. 2004, 31, 384–409. [Google Scholar] [CrossRef]
- Wang, Z.L.; Makdisi, F.I.; Egan, J. Practical Applications of a Nonlinear Approach to Analysis of Earthquake-Induced Liquefaction and Deformation of Earth Structures. Soil Dyn. Earthq. Eng. 2006, 26, 231–252. [Google Scholar] [CrossRef]
- Rampello, S.; Cascone, E.; Grosso, N. Evaluation of the Seismic Response of a Homogeneous Earth Dam. Soil Dyn. Earthq. Eng. 2009, 29, 782–798. [Google Scholar] [CrossRef]
- Elia, G.; Amorosi, A.; Chan, A.; Kavvadas, M. Fully Coupled Dynamic Analysis of an Earth Dam. Géotechnique 2011, 61, 549–563. [Google Scholar] [CrossRef]
- Masini, L.; Rampello, S. Performance of Large Homogeneous Earth Dams during Strong Ground Motions. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Republic of Korea, 17–22 September 2017; pp. 2415–2420. [Google Scholar]
- Wei, K.; Chen, S.; Li, G.; Han, H. Application of a Generalised Plasticity Model in High Earth Core Dam Static and Dynamic Analysis. Eur. J. Environ. Civ. Eng. 2020, 24, 979–1012. [Google Scholar] [CrossRef]
- Pelecanos, L.; Kontoe, S.; Zdravković, L. The Effects of Dam–Reservoir Interaction on the Nonlinear Seismic Response of Earth Dams. J. Earthq. Eng. 2020, 24, 1034–1056. [Google Scholar] [CrossRef]
- Karabulut, M.; Geniş, M. Pseudo Seismic and Static Stability Analysis of the Torul Dam. Geomech. Eng. 2019, 17, 207–214. [Google Scholar] [CrossRef]
- Karabulut, M.; Kartal, M.E. Earthquake Response of Roller Compacted Concrete Dams Including Galleries. Struct. Eng. Mech. 2019, 72, 141–153. [Google Scholar] [CrossRef]
- Alsharedah, Y.A.; El Naggar, M.H.; Ahmed, A. Improving Tailings Dam Safety via Soil Treatment. Sustainability 2023, 15, 15276. [Google Scholar] [CrossRef]
- Luo, C.; Li, D.; Xu, B. Study on the Evolution of Tailings Dam Break Disaster under Complex Environment. Sustainability 2023, 15, 14728. [Google Scholar] [CrossRef]
- Li, Q.; Ma, G.; Lu, Y. An Experimental and Theoretical Study on the Tailings Dam with Geotextile Bags. Sustainability 2023, 15, 4768. [Google Scholar] [CrossRef]
- Dedring, T.; Graw, V.; Thygesen, K.; Rienow, A. Validation of an Empirical Model with Risk Assessment Functionalities to Simulate and Evaluate the Tailings Dam Failure in Brumadinho. Sustainability 2022, 14, 6681. [Google Scholar] [CrossRef]
- Yang, J.; Hu, J.; Wu, Y.; Zhang, B. Numerical Simulation of Seepage and Stability of Tailing Dams: A Case Study in Ledong, China. Sustainability 2022, 14, 12393. [Google Scholar] [CrossRef]
- Labanda, N.A.; Sottile, M.G.; Cueto, I.A.; Sfriso, A.O. Screening of Seismic Records to Perform Time-History Dynamic Analyses of Tailings Dams: A Power-Spectral Based Approach. Soil Dyn. Earthq. Eng. 2021, 146, 106750. [Google Scholar] [CrossRef]
- Da Silva, E.M.; Justo, J.L.; Durand, P.; Justo, E.; Vázquez-Boza, M. The Effect of Geotextile Reinforcement and Prefabricated Vertical Drains on the Stability and Settlement of Embankments. Geotext. Geomembr. 2017, 45, 447–461. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Li, J.; Xu, S. Seismic Response of Earth-Rock Dams with Innovative Antiseepage Walls on the Effect of Microscopic Fluid-Solid Coupling. Sustainability 2023, 15, 12749. [Google Scholar] [CrossRef]
- Chen, D.; Chen, H.; Zhang, W.; Tan, C.; Ma, Z.; Chen, J.; Shan, B. Buckling Failure Mechanism of a Rock Dam Foundation Fractured by Gentle Through-Going and Steep Structural Discontinuities. Sustainability 2020, 12, 5426. [Google Scholar] [CrossRef]
- Dong, K.; Mi, Z.; Yang, D. Comprehensive Diagnosis Method of the Health of Tailings Dams Based on Dynamic Weight and Quantitative Index. Sustainability 2022, 14, 3068. [Google Scholar] [CrossRef]
- Justo, J.L.; Morales-Esteban, A.; Justo, E.; Jiménez-Cantizano, F.A.; Durand, P.; Vázquez-Boza, M. The Dry Closure of the Almagrera Tailings Dam: Detailed Modelling, Monitoring Results and Environmental Aspects. Bull. Eng. Geol. Environ. 2019, 78, 3175–3189. [Google Scholar] [CrossRef]
- Justo, J.L.; Morales-Esteban, A.; Durand, P.; Vázquez-Boza, M.; Jiménez, F.A.; Rossi, E. Dynamic Calculation for the Dry Closure of Almagrera Tailings Dam. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013; pp. 1511–1514. [Google Scholar]
- Tornos, F. La Geología y Metalogenia de La Faja Pirítica Ibérica. Rev. La Soc. Española Mineral. 2008, 10, 13–23. [Google Scholar]
- Mellado, D.; Tornos, F. Geología y Estructura de La Mina de Río Tinto (Faja Pirítica Ibérica, España). Geogaceta 2006, 40, 231–234. [Google Scholar]
- Spain, G. (Ed.) Royal Decree, 975/2009 Real Decreto 975/2009, de 12 de Junio. Sobre Gestión de Los Residuos de Las Industrias Extractivas y de Protección y Rehabilitación Del Espacio Afectado Por Actividades Mineras; Ministerio: Madrid, Spain, 2009. [Google Scholar]
- Ministerio de Agricultura, Pesca, Alimentación y Medio Ambiente. Borrador de Norma Técnica de Seguridad Para La Clasificación de Las Presas y Para La Elaboración e Implantación de Los Planes de Emergencia de Presas y Embalses; Boletin Oficial del Estado: Madrid, Spain, 2011. [Google Scholar]
- Ministerio de Agricultura, Pesca, Alimentación y Medio Ambiente. Borrador de Norma Técnica de Seguridad Para El Proyecto, Construcción y Puesta En Carga de Presas y Llenado de Embalses; Boletin Oficial del Estado: Madrid, Spain, 2011. [Google Scholar]
- Álvarez-Valero, A.M.; Sáez, R.; Pérez-López, R.; Delgado, J.; Nieto, J.M. Evaluation of Heavy Metal Bio-Availability from Almagrera Pyrite-Rich Tailings Dam (Iberian Pyrite Belt, SW Spain) Based on a Sequential Extraction Procedure. J. Geochem. Explor. 2009, 102, 87–94. [Google Scholar] [CrossRef]
- Amouzou, G.Y.; Soulaïmani, A. Numerical Algorithms for Elastoplacity: Finite Elements Code Development and Implementation of the Mohr-Coulomb Law. Appl. Sci. 2021, 11, 4637. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J. Plaxis 2D Manual; Balkema Publishers: Delft, The Netherlands, 2012. [Google Scholar]
- Argus, D.F.; Gordon, R.G.; DeMets, C.; Stein, S. Closure of the Africa-Eurasia-North America Plate Motion Circuit and Tectonics of the Gloria Fault. J. Geophys. Res. 1989, 94, 5585–5602. [Google Scholar] [CrossRef]
- Kiratzi, A.A.; Papazachos, C.B. Active Crustal Deformation from the Azores Triple Junction to the Middle East. Tectonophysics 1995, 243, 1–24. [Google Scholar] [CrossRef]
- Jiménez-Munt, I.; Fernàndez, M.; Torne, M.; Bird, P. The Transition from Linear to Diffuse Plate Boundary in the Azores-Gibraltar Region: Results from a Thin-Sheet Model. Earth Planet. Sci. Lett. 2001, 192, 175–189. [Google Scholar] [CrossRef]
- Andeweg, B.; De Vicente, G.; Cloetingh, S.; Giner, J.; Muñoz Martin, A. Local Stress Fields and Intraplate Deformation of Iberia: Variations in Spatial and Temporal Interplay of Regional Stress Sources. Tectonophysics 1999, 305, 153–164. [Google Scholar] [CrossRef]
- Calvert, A.; Sandvol, E.; Seber, D.; Barazangi, M.; Roecker, S. Mourab Geodynamic Evolution of the Lithosphere and Upper Mantle beneath the Alboran Region of the Western Mediterranean: Constraints from Travel Time Tomography. J. Geophys. Res. 2000, 105, 10871–10898. [Google Scholar] [CrossRef]
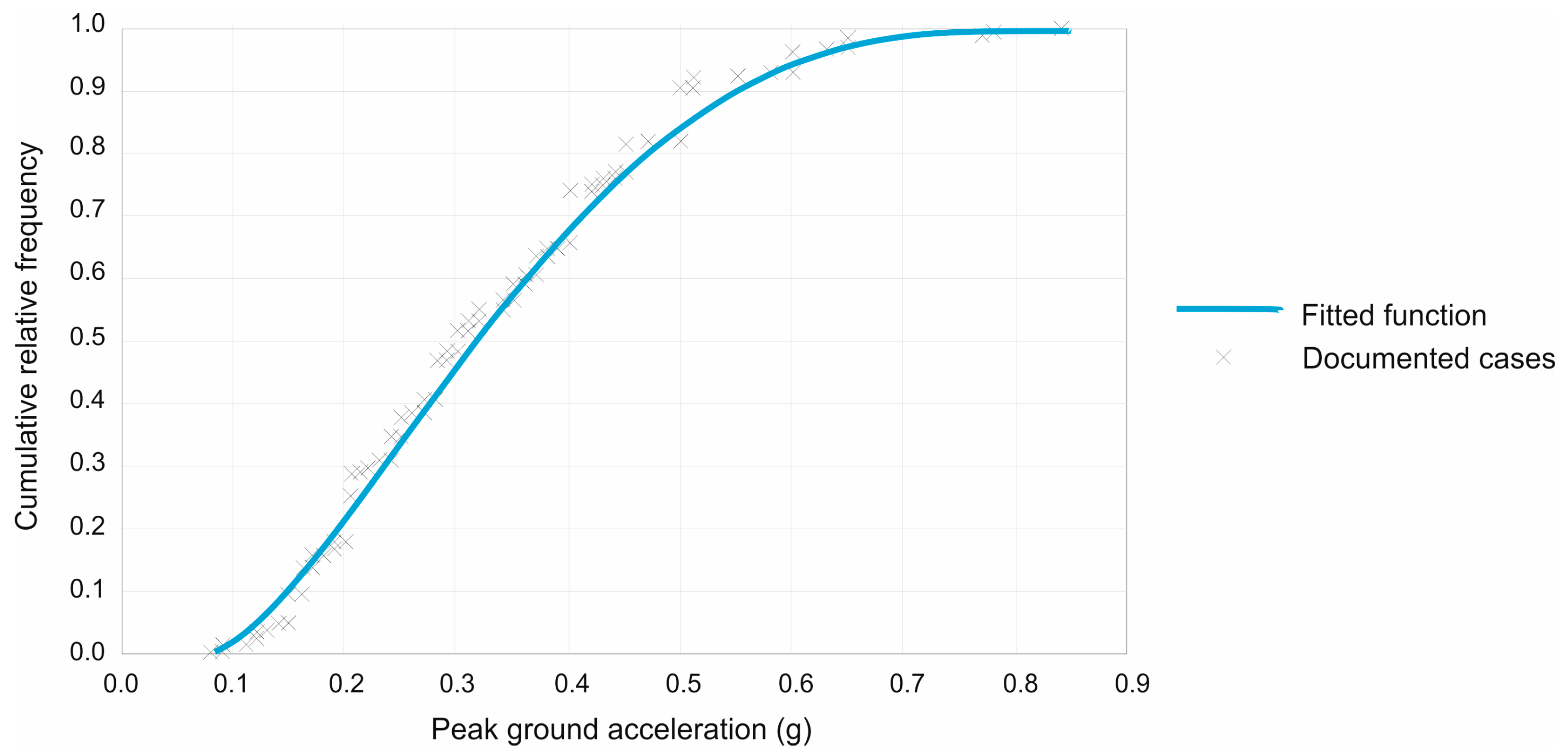
- Morales-Esteban, A.; de Justo, J.L.; Martínez-Álvarez, F.; Azañón, J.M. Probabilistic Method to Select Calculation Accelerograms Based on Uniform Seismic Hazard Acceleration Response Spectra. Soil Dyn. Earthq. Eng. 2012, 43, 174–185. [Google Scholar] [CrossRef]
- Ambraseys, N.N. The Seismic Stablity of Earth Dams; Imperial College London: London, UK, 1960; pp. 1345–1365. [Google Scholar]
- Finn, W.M.-H. Dynamic Response Analysis of Soil Structures. In Finite Element Handbook; Kardestunger, H., Norrie, D.H., Brezzi, F., Eds.; McGraw-Hill: New York, NY, USA, 1987; pp. 3168–3195. [Google Scholar]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Sarma, S.K. Seismic Stability of Earth Dams and Embankments. Géotechnique 1976, 13, 32. [Google Scholar] [CrossRef]
- Makdisi, F.I.; Seed, H.B. Simplified Procedure for Estimating Dam and Embankment Earthquake-Induced Deformations. J. Geotech. Eng. Div. 1978, 104, 849–867. [Google Scholar] [CrossRef]
- Makdisi, F.I.; Seed, H.B. Simplified Procedure for Evaluating Embankment Response. J. Geotech. Eng. Div. 1979, 105, 1427–1434. [Google Scholar] [CrossRef]
- Visone, C.; Bilotta, E.; Santucci De Magistris, F. One-Dimensional Ground Response as a Preliminary Tool for Dynamic Analyses in Geotechnical Earthquake Engineering. J. Earthq. Eng. 2010, 14, 131–162. [Google Scholar] [CrossRef]
- Charatpangoon, B.; Kiyono, J.; Furukawa, A.; Hansapinyo, C. Dynamic Analysis of Earth Dam Damaged by the 2011 Off the Pacific Coast of Tohoku Earthquake. Soil Dyn. Earthq. Eng. 2014, 64, 50–62. [Google Scholar] [CrossRef]
- Ebrahimian, B. Numerical Analysis of Nonlinear Dynamic Behavior of Earth Dams. Front. Archit. Civ. Eng. China 2011, 5, 24–40. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite Element Method Accuracy for Wave Propagation Problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Hardin, B.O.; Drnevich, V.P. Shear Modulus and Damping in Soil: Design Equations and Curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Iwasaki, T.; Takagi, Y. Hysteretic Damping of Sands under Cyclic Loading and Its Relation to Shear Modulus. Jpn. Soc. Soil Mech. Found. Eng. 1978, 18, 25–39. [Google Scholar] [CrossRef]
- Bardet, J.P.; Ichii, K.; Lin, C.H. EERA—A Computer Program for Equivalent-Linear Earthquake Site Response Analyses of Layered Soil Deposits; University of California: Los Angeles, CA, USA, 2000; p. 40. [Google Scholar]
- Hansen, R.H. Seismic Design for Nuclear Power Plants; M.I.T. Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Brinkgreve, R.B.J. Plaxis 2D v.8 Manual; Balkema Publishers: Delft, The Netherlands, 2002. [Google Scholar]
- Hilber, H.M.; Hughes, T.J.R.; Taylor, R.L. Improved Numerical Dissipation for Time Integration Algorithms in Structural Dynamics. Earthq. Eng. Struct. Dyn. 1977, 5, 283–292. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Lysmer, J.; Kuhlemeyer, R.L. Finite Dynamic Model For Infinite Media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar] [CrossRef]
- Morales-Esteban, A.; de Justo, J.L.; Reyes, J.; Miguel Azañón, J.; Durand, P.; Martínez-Álvarez, F. Stability Analysis of a Slope Subject to Real Accelerograms by Finite Elements. Application to San Pedro Cliff at the Alhambra in Granada. Soil Dyn. Earthq. Eng. 2015, 69, 28–45. [Google Scholar] [CrossRef]
- Santucci de Magistris, F.; Lanzano, G.; Forte, G.; Fabbrocino, G. A Database for PGA Threshold in Liquefaction Occurrence. Soil Dyn. Earthq. Eng. 2013, 54, 17–19. [Google Scholar] [CrossRef]
- de Justo, J.L.; Jiménez-cantizano, F.A.; de Justo Moscardó, E.; Vázquez-Boza, M.; Soriano-Cuesta, C.; Castilla-Freire, J. Estudio de Los Residuos Mineros de La Presa de Almagrera Por Medio de Piezoconos. Ing. Civ. 2014, 173, 43–45. [Google Scholar]

| Description | Classification (USCS) | c′ (kPa) | Φ′ (°) | γ (kN/m3) | K (m/s) | E (MPa) |
|---|---|---|---|---|---|---|
| Clayey and silty slate. Quarry run. | GC | 6 | 33 | 20.0 | 6.5 × 10−5 | 30 |
| Rockfill | SC | 15 | 31 | 21.9 | 9.5 × 10−7 | 60 |
| Sand filter. 5th raising | SP-SM | 1 | 35 | 20 | 10−5 | 50 |
| Quarry-run (weathered schist). 5th raising | GC | 6 | 33 | 20.2 | 6.5 × 10−5 | 30 |
| Sound rock | 250 | 20 | 21.4 | 1.3 × 10−7 | 104 | |
| Tailings (average) | ML | 8.8 | 31 | 28.8 | 1.4 × 10−8 | 2 |
| Clay core. 5th raising | SC | 18 | 30 | 19.8 | 10−8 | 50 |
| Sand filter | SP-SM | 1 | 35 | 20 | 10−5 | 50 |
| Selected rockfill | 1 | 35 | 20 | 5.1 × 10−3 | 60 | |
| Clay core | SC | 18 | 30 | 19.8 | 10−8 | 50 |
| Weathered rock | SC | 50 | 20 | 20.5 | 1.4 × 10−6 | 300 |
| “Las Viñas” fill | CL-ML | 32 | 26 | 22.3 | 5 × 10−7 | 12.6 |
| Type of Movement | Dam Category | |
|---|---|---|
| A or B | C | |
| Ordinary | 1.5 | 1.4 |
| Incidental | 1.3 | 1.2 |
| Extraordinary | 1.1 | >1.0 |
| Phase | δmax (mm) | Factor of Safety |
|---|---|---|
| First | 1.44 | |
| Reservoir at 207.5 level | 1.44 | |
| Drawdown | 350 | 1.34 |
| Fill | 1290 | 1.98 |
| Long term | 1610 | 2.74 |
| Long term extreme | 1730 | 1.31 |
| Type of Soil | Characteristics | |
|---|---|---|
| I | Vs > 750 m/s | 1.0 |
| II | 400 < Vs < 750 m/s | 1.3 |
| III | 200 < Vs < 400 m/s | 1.6 |
| IV | Vs < 200 m/s | 2.0 |
| Accelerograms | f |
|---|---|
| 358 | 1.08 |
| 385 | 0.915 |
| 607 | 1.043 |
| 4341 | 1.006 |
| 6261 | 1.050 |
| 6269 | 0.964 |
| 6274 | 0.923 |
| Section | S1. M-C. | S1. HS-S. | S2. M-C. | S2. HS-S. | S3. M-C. | S3. HS-S. |
|---|---|---|---|---|---|---|
| 1737.70 | 1737.70 | 2822.29 | 2822.29 | 1782.38 | 1782.38 | |
| 25 | 25 | 40 | 40 | 28 | 28 | |
| AESmin (m) | 8.69 | 8.69 | 8.82 | 8.82 | 7.95 | 7.95 |
| AESmodel (m) | 5.39 | 2.84 | 6.29 | 3.31 | 5.33 | 3.99 |
| Characteristics | Related Parameters |
|---|---|
| Stress subjected to stiffness as regards a power law | |
| Plastic straining on account of first deviatoric loading | |
| Plastic straining owing to first pressure | |
| Elastic reloading/unloading | , |
| Collapse as regards the MC failure criterion | , and |
| Sections | Section 1 | Section 2 | Section 3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Soil | H (m) | γ (kN/m3) | Vs (m/s) | H (m) | γ (kN/m3) | Vs (m/s) | H (m) | γ (kN/m3) | Vs (m/s) |
| Core | 3.30 | 19.80 | 95.74 | 3.9 | 19.8 | 95.74 | 3.9 | 19.8 | 95.74 |
| Filter | 1.10 | 20.00 | 95.26 | 1.1 | 20 | 95.26 | 2.06 | 20 | 95.26 |
| Quarry-run | 18.90 | 20.20 | 73.42 | 13.7 | 20.2 | 73.42 | 17.32 | 20.2 | 73.42 |
| Weathered Rock | 9.05 | 20.50 | 225.60 | 3.2 | 20.5 | 225.6 | 1.89 | 20.5 | 225.6 |
| Rockfill | 7.95 | 21.90 | 99.72 | - | - | - | 11.56 | 21.9 | 99.72 |
| Rock | 27.47 | 21.40 | 4118 | 46 | 21.4 | 4118 | 26.56 | 21.4 | 4118 |
| Equivalent layer | 67.77 | 20.90 | 1737.71 | 67.90 | 21.00 | 2822.30 | 63.29 | 20.99 | 1782.18 |
| Rayleigh Coefficients | Section 1 | Section 2 | Section 3 |
|---|---|---|---|
| 1.20831 | 1.95873 | 1.32696 | |
| 0.00025 | 0.00015 | 0.00023 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morales-Esteban, A.; Alpañés, J.L.d.J.; Castillo, P.; Karabulut, M. Dynamic Analysis of the Almagrera Tailings Dam with Dry Closure Condition. Sustainability 2024, 16, 1607. https://doi.org/10.3390/su16041607
Morales-Esteban A, Alpañés JLdJ, Castillo P, Karabulut M. Dynamic Analysis of the Almagrera Tailings Dam with Dry Closure Condition. Sustainability. 2024; 16(4):1607. https://doi.org/10.3390/su16041607
Chicago/Turabian StyleMorales-Esteban, Antonio, José Luis de Justo Alpañés, Pablo Castillo, and Muhammet Karabulut. 2024. "Dynamic Analysis of the Almagrera Tailings Dam with Dry Closure Condition" Sustainability 16, no. 4: 1607. https://doi.org/10.3390/su16041607






