Adaptive Equivalent Fuel Consumption Minimization Based Energy Management Strategy for Extended-Range Electric Vehicle
Abstract
:1. Introduction
2. Adaptive ECMS Energy Management Strategy
2.1. Mathematical Description of ECMS
2.2. Adaptive Adjustment of Equivalent Factor
2.3. Penalty Item for Frequent Start and Stop of Range Extender
3. Parameter Optimization of the A-ECMS
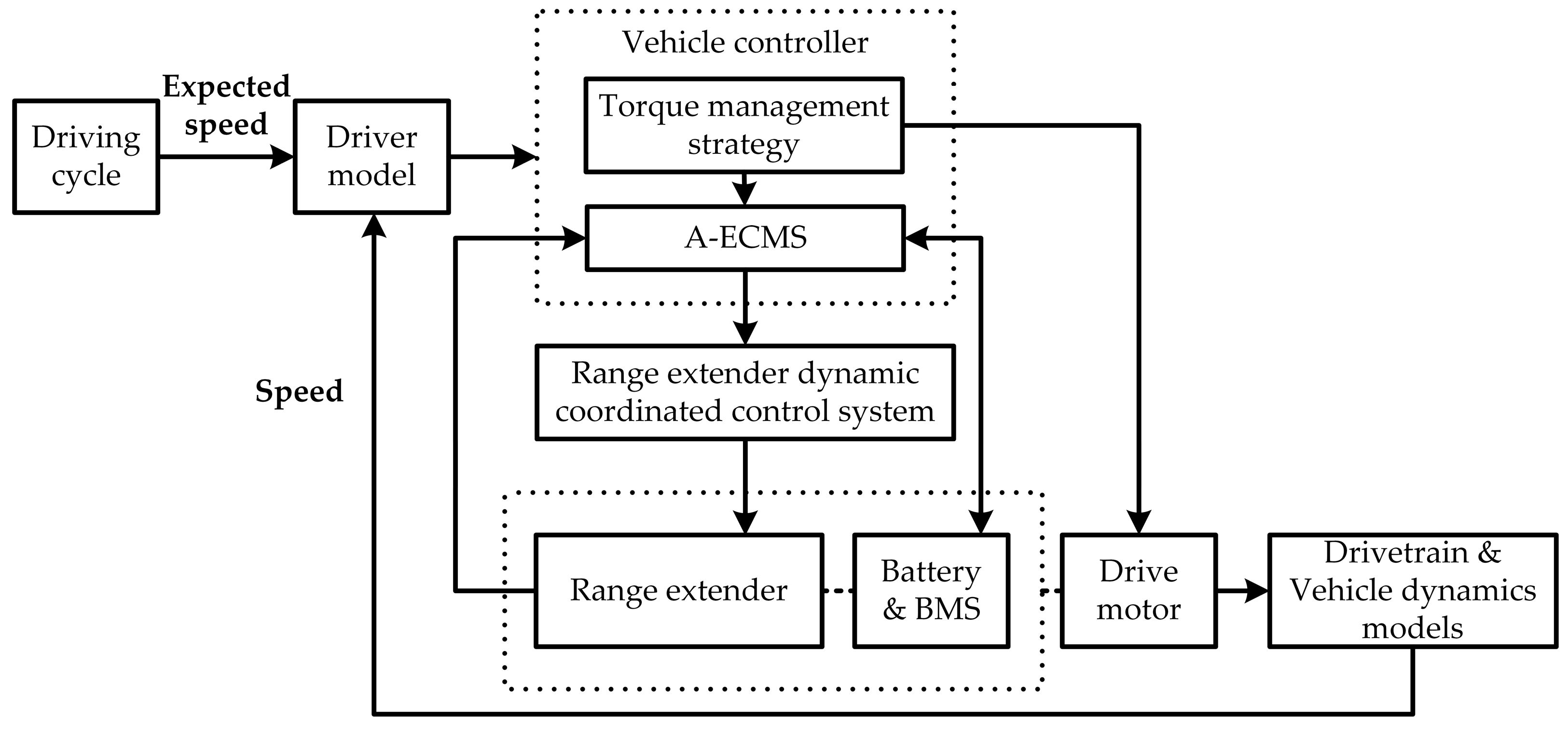
3.1. Vehicle Simulation Platform
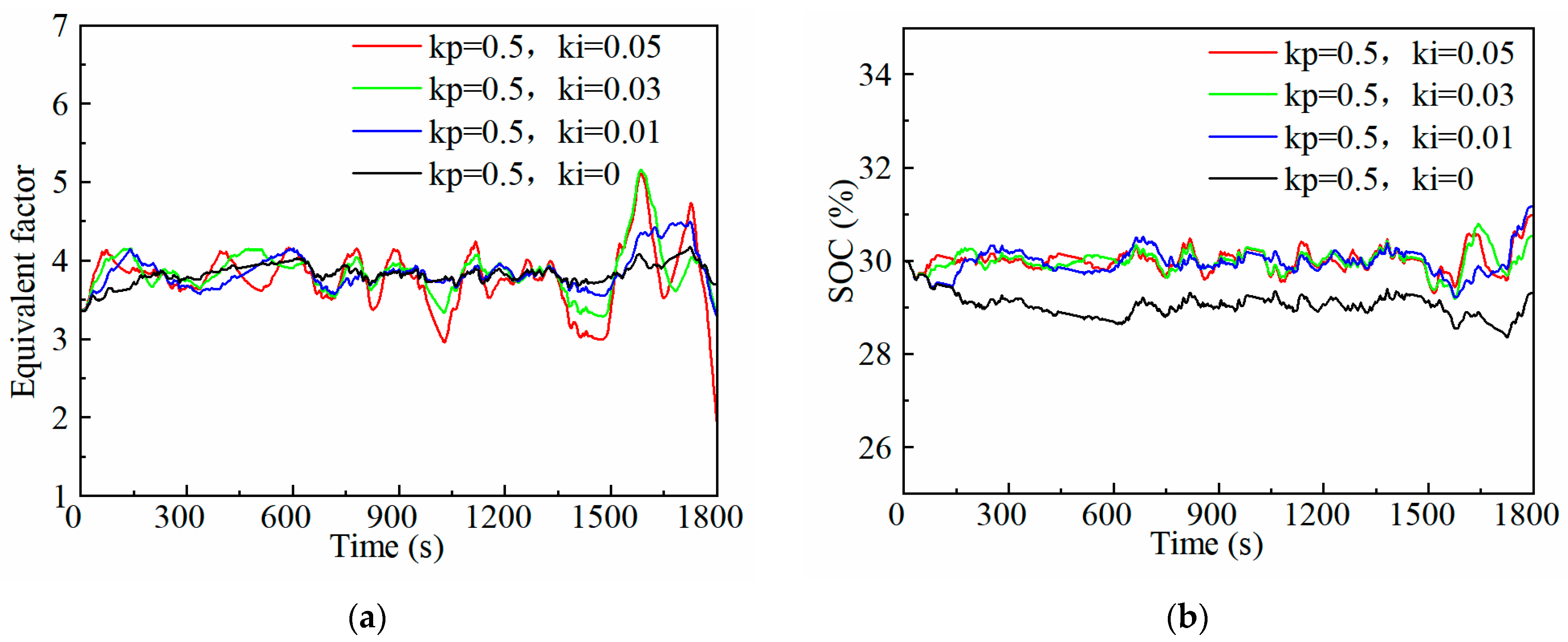
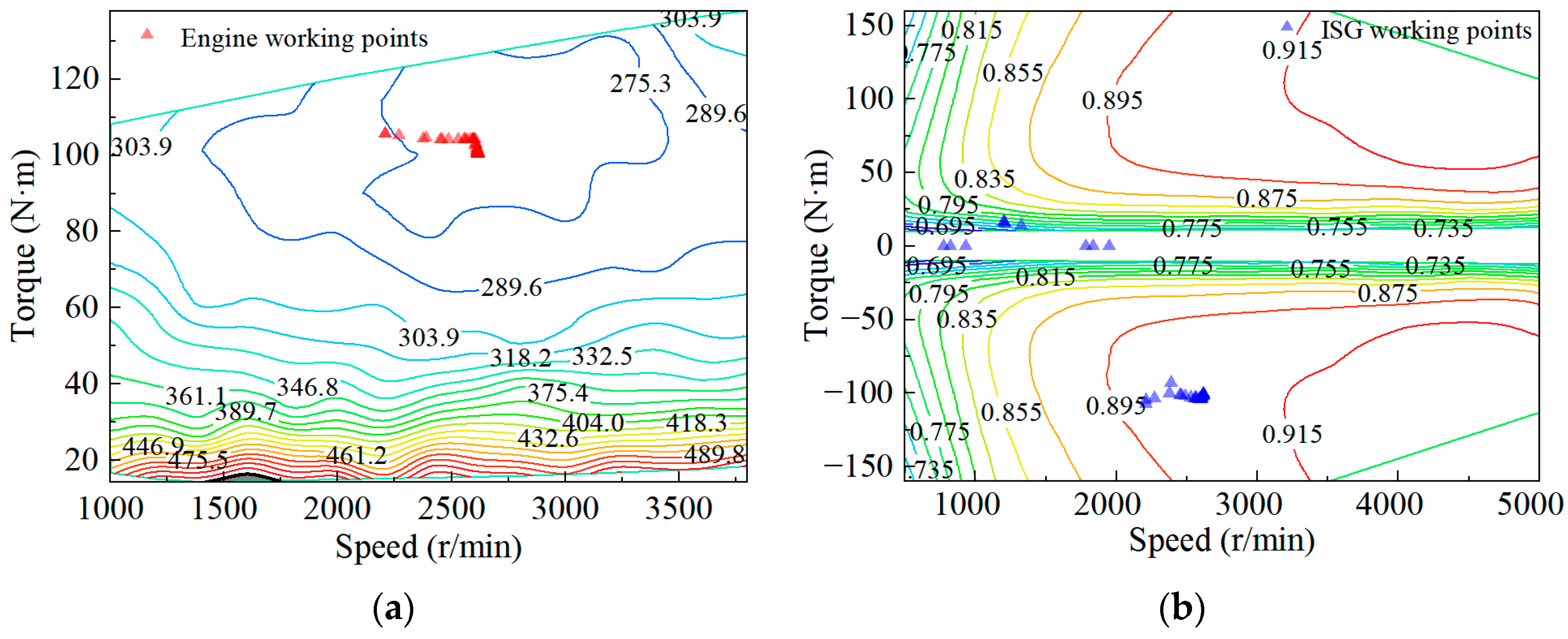
3.2. Adaptive Equivalent Factor Optimization
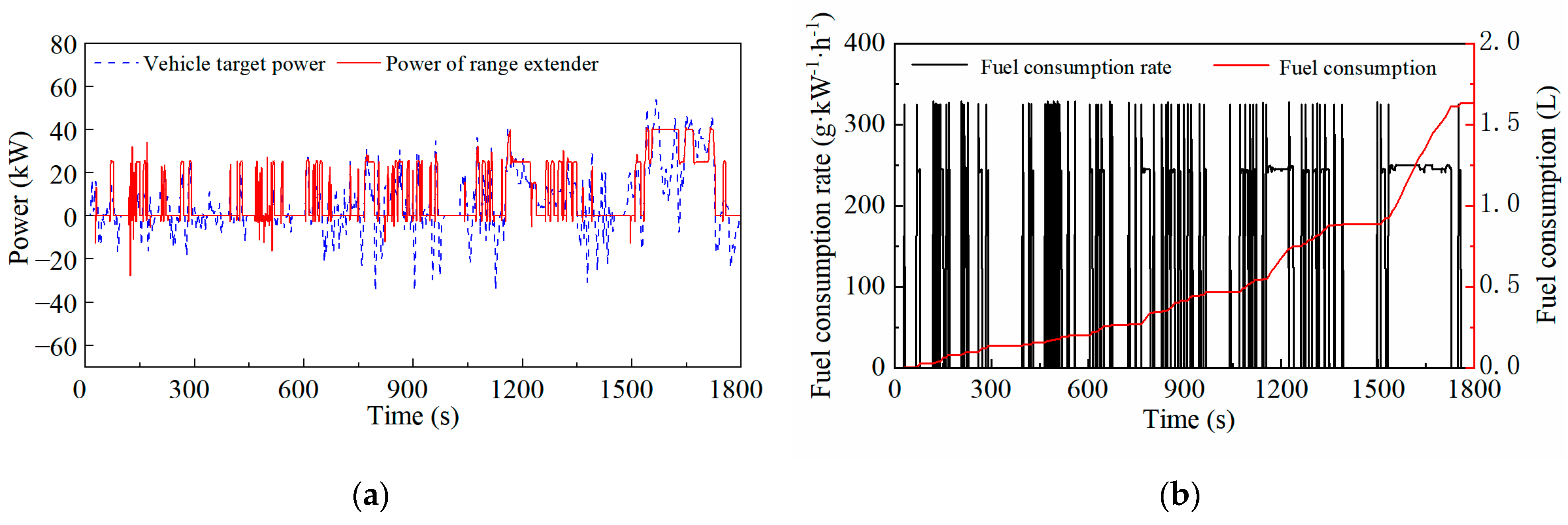
3.3. Start–Stop Penalty Factor Optimization
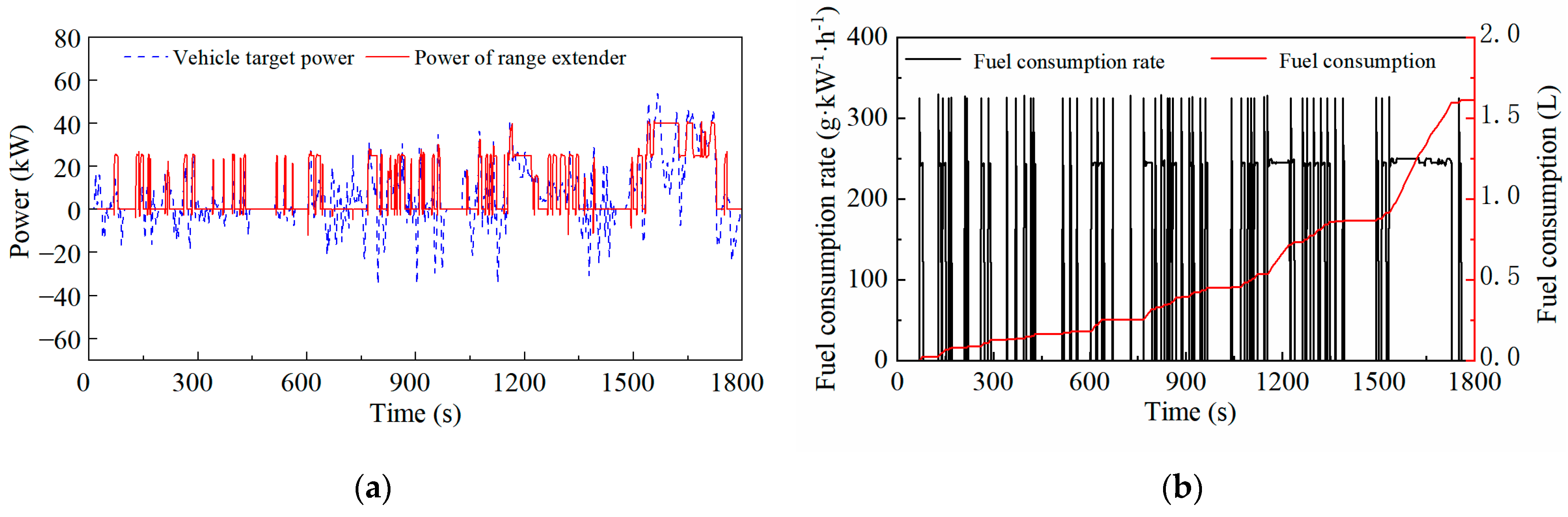
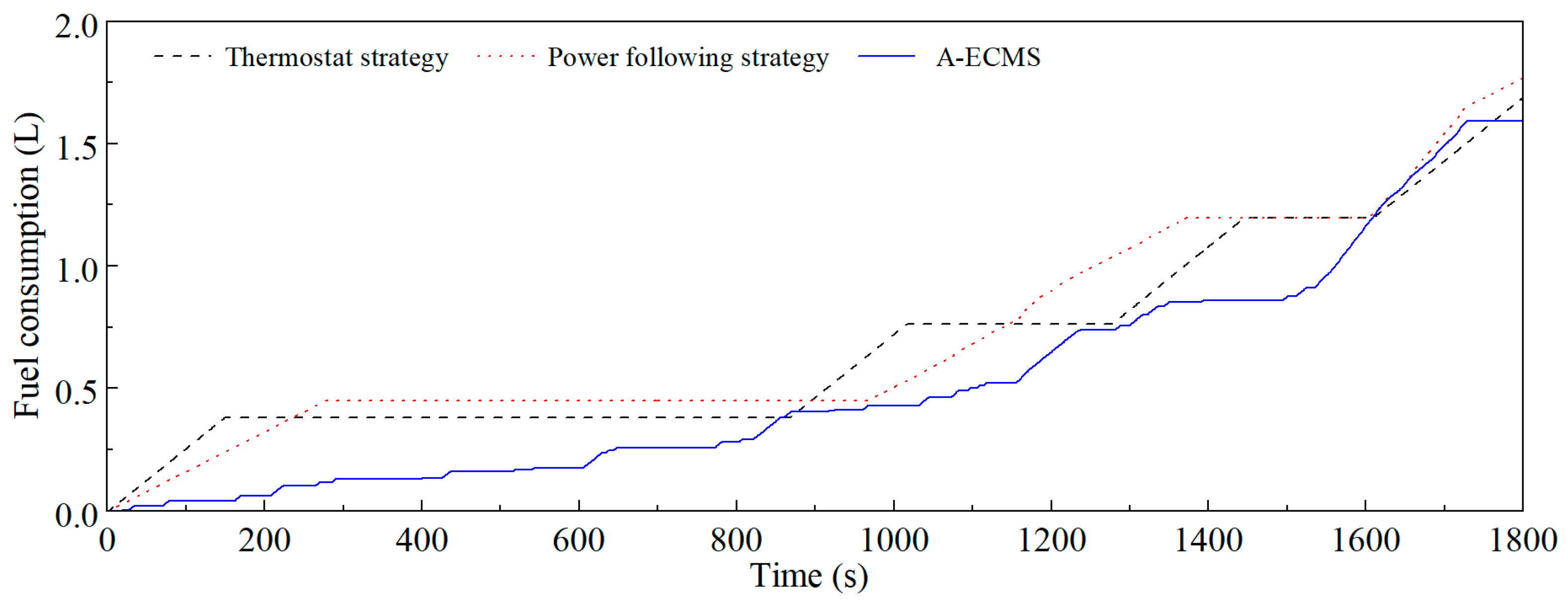
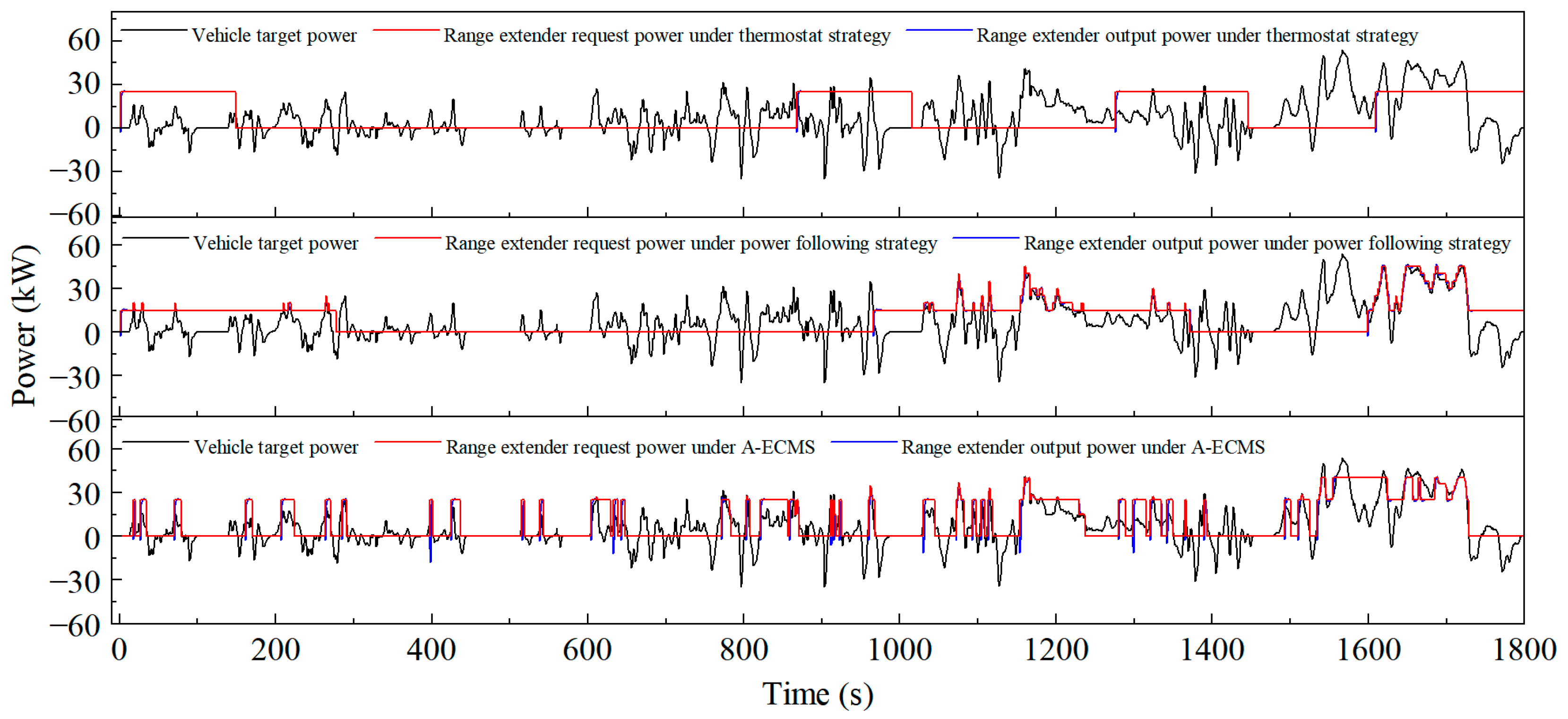
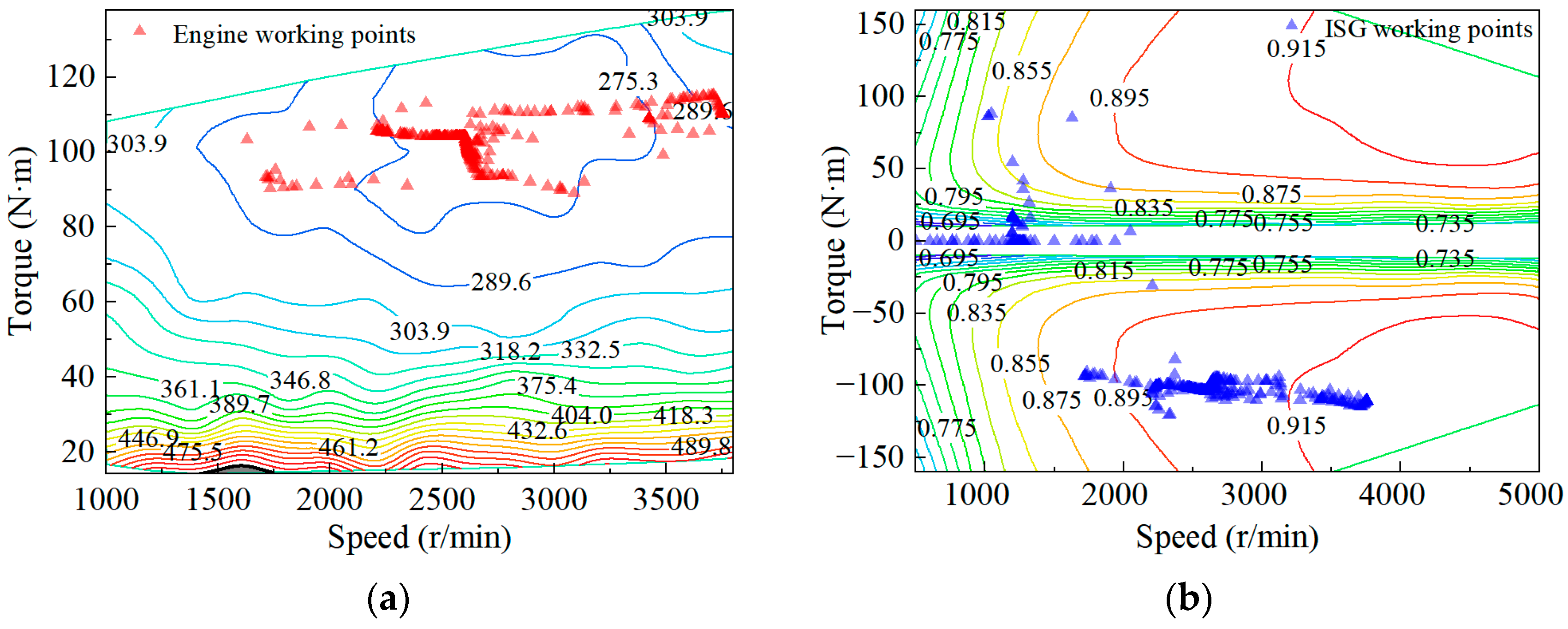
4. A-ECMS Strategy Verification
5. Conclusions
- The A-ECMS for extended-range electric vehicles, based on the adaptive equivalent factor of SOC feedback and a PI controller, is designed. After the tuning of the PI coefficients, the adaptive equivalent factor can not only make the final SOC reach the target SOC as close as possible at the end of the trip, but also keep the control system stable. From the verification results, the final SOC under the A-ECMS is 30.3%, and the deviation from the target SOC is only 0.3%.
- Considering the start–stop dynamic characteristics of the range extender, a start–stop penalty term for the range extender is added to the original Hamiltonian function. When a penalty start–stop factor of 0.02 is added, compared with the original A-ECMS, the start–stop times of the range extender are obviously reduced, and the fuel consumption during the entire trip drops from 1.631 L to 1.591 L.
- Based on the vehicle simulation platform, the proposed A-ECMS is verified under the WLTC. Compared with the thermostat and the power-following strategy, the A-ECMS shows a better fuel economy performance and lower battery ohmic losses. The comprehensive fuel consumption of the A-ECMS is 6.78 L/100 km, which is 6.2% lower than the thermostat strategy and 3.8% lower than the power following strategy. The ampere-hour flux of the battery of the A-ECMS is 10.78 Ah, which is 10.26 Ah lower than the thermostat strategy and 3.69 Ah lower than the power following strategy, which also proves that the A-ECMS is more conducive to prolonging the battery life.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EMS | Energy Management Strategy |
| A-ECMS | Adaptive Equivalent Fuel Consumption Minimization Strategy |
| ECMS | Equivalent Fuel Consumption Minimization Strategy |
| PMP | Pontryagin’s Minimum Principle |
| SOC | State Of Charge |
| PI | Proportional–Integral |
| ISG | Integrated Starter Generator |
| MPC | Model Predictive Control |
| ANN-ECMS | Artificial Neural Network Involved Equivalent Fuel Consumption Minimization Strategy |
| DP | Dynamic Programming |
| CS | Charge-Sustaining |
References
- Xue, Q.; Zhang, X.; Teng, T.; Zhang, J.; Feng, Z.; Lv, Q. A Comprehensive Review on Classification, Energy Management Strategy, and Control Algorithm for Hybrid Electric Vehicles. Energies 2020, 13, 5355. [Google Scholar] [CrossRef]
- Aslam, S.; Herodotou, H.; Mohsin, S.M.; Javaid, N.; Ashraf, N.; Aslam, S. A Survey on Deep Learning Methods for Power Load and Renewable Energy Forecasting in Smart Microgrids. Renew. Sustain. Energy Rev. 2021, 144, 110992. [Google Scholar] [CrossRef]
- Khattak, A.; Bukhsh, R.; Aslam, S.; Yafoz, A.; Alghushairy, O.; Alsini, R. A Hybrid Deep Learning-Based Model for Detection of Electricity Losses Using Big Data in Power Systems. Sustainability 2022, 14, 13627. [Google Scholar] [CrossRef]
- Yao, M. Adaptive Real-Time Optimal Control for Energy Management Strategy of Extended Range Electric Vehicle. Energy Convers. Manag. 2021, 234, 113874. [Google Scholar] [CrossRef]
- Huang, Y. Model Predictive Control Power Management Strategies for HEVs: A Review. J. Power Sources 2017, 341, 91–106. [Google Scholar] [CrossRef]
- Hou, J.; Yao, D.; Wu, F.; Shen, J.; Chao, X. Online Vehicle Velocity Prediction Using an Adaptive Radial Basis Function Neural Network. IEEE Trans. Veh. Technol. 2021, 70, 3113–3122. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, Y.; Dou, H.; Zou, R. Design of an Integrated Energy Management Strategy for a Plug-in Hybrid Electric Bus. J. Power Sources 2020, 448, 227391. [Google Scholar] [CrossRef]
- Han, L.; Jiao, X.; Zhang, Z. Recurrent Neural Network-Based Adaptive Energy Management Control Strategy of Plug-In Hybrid Electric Vehicles Considering Battery Aging. Energies 2020, 13, 202. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; He, R.; Sun, X.; Cai, Y.; Xu, Y. An ANFIS-Based ECMS for Energy Optimization of Parallel Hybrid Electric Bus. IEEE Trans. Veh. Technol. 2020, 69, 1473–1483. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, X.; Langari, R.; Wang, L.; Cui, Y.; Pang, H. Adaptive Energy Management in Automated Hybrid Electric Vehicles with Flexible Torque Request. Energy 2021, 214, 118873. [Google Scholar] [CrossRef]
- Zhang, Y.; Chu, L.; Fu, Z.; Xu, N.; Guo, C.; Zhao, D.; Ou, Y.; Xu, L. Energy Management Strategy for Plug-in Hybrid Electric Vehicle Integrated with Vehicle-Environment Cooperation Control. Energy 2020, 197, 117192. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Tsai, N.-C. Dual-Objective Energy Management Strategy for HEV. Int. J. Autom. Smart Technol. 2017, 7, 111–118. [Google Scholar]
- Rezaei, A.; Burl, J.B.; Zhou, B. Estimation of the ECMS Equivalent Factor Bounds for Hybrid Electric Vehicles. IEEE Trans. Control. Syst. Technol. 2018, 26, 2198–2205. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Qi, S.; Lang, K. An Artificial Neural Network-Enhanced Energy Management Strategy for Plug-in Hybrid Electric Vehicles. Energy 2018, 163, 837–848. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Zhang, J. An Energy Management of Plug-in Hybrid Electric Vehicles Based on Driver Behavior and Road Information. J. Intell. Fuzzy Syst. 2017, 33, 3009–3020. [Google Scholar] [CrossRef]
- Shen, Z.; Luo, C.; Dong, X.; Lu, W.; Lv, Y.; Xiong, G.; Wang, F.-Y. Two-Level Energy Control Strategy Based on ADP and A-ECMS for Series Hybrid Electric Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 13178–13189. [Google Scholar] [CrossRef]
- Choi, K.; Byun, J.; Lee, S.; Jang, I.G. Adaptive Equivalent Consumption Minimization Strategy (A-ECMS) for the HEVs with a Near-Optimal Equivalent Factor Considering Driving Conditions. IEEE Trans. Veh. Technol. 2022, 71, 2538–2549. [Google Scholar] [CrossRef]
- Zeng, T.; Zhang, C.; Zhang, Y.; Deng, C.; Hao, D.; Zhu, Z.; Ran, H.; Cao, D. Optimization-Oriented Adaptive Equivalent Consumption Minimization Strategy Based on Short-Term Demand Power Prediction for Fuel Cell Hybrid Vehicle. Energy 2021, 227, 120305. [Google Scholar] [CrossRef]
- Yang, S.; Wang, J. Self-Adaptive Equivalent Consumption Minimization Strategy for Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 189–202. [Google Scholar] [CrossRef]
- Deng, T.; Zhao, K.; Yu, H. An Adaptive Equivalent Consumption Minimization Strategy Considering Catalyst Temperature for Plug-in Hybrid Electric Vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 1375–1389. [Google Scholar] [CrossRef]
- Wang, Y.; Lou, D.; Xu, N.; Fang, L.; Tan, P. Energy Management and Emission Control for Range Extended Electric Vehicles. Energy 2021, 236, 121370. [Google Scholar] [CrossRef]
- Suzuki, S.; Tanaka, K.K.J.; Imagawa, H. Effect of Idling Stop at Traffic Signals on Fuel Consumption of Gasoline Engine Vehicles-Period of Idling Stop and Amount of Saved Fuel. J.-Jpn. Inst. Energy 2004, 83, 64–71. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Zhong, J.; Sha, F.; Zhong, Z. Research on Innovative Plug-in Hybrid Electric Vehicle Comprehensive Energy Consumption Evaluation Method Based on Statistic Energy Consumption. Sci. Prog. 2021, 104. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A Review on the Key Issues of the Lithium Ion Battery Degradation among the Whole Life Cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]










| Items | Parameter | Value |
|---|---|---|
| Vehicle | No-load mass/kg | 1740 |
| Wheel radius/m | 0.33 | |
| Windward area/m2 | 2.586 | |
| Air drag coefficient | 0.374 | |
| Rolling resistance coefficient | 0.01 | |
| Main reducer speed ratio | 8 | |
| Drivetrain efficiency | 90% | |
| Rotating mass conversion factor | 1.15 | |
| Engine | Type | Inline four-cylinder gasoline engine |
| Displacement/L | 1.5 | |
| Rated power/kW | 45 | |
| Maximum power/kW | 78 | |
| Maximum torque/(N·m) | 140 | |
| Maximum speed/rpm | 5200 | |
| ISG motor | Type | Permanent magnet synchronous motor |
| Maximum power/kW | 60 | |
| Maximum speed/rpm | 5000 | |
| Maximum torque/(N·m) | 167 | |
| Motor | Type | Permanent magnet synchronous motor |
| Maximum power/kW | 125 | |
| Maximum speed/rpm | 12,000 | |
| Maximum torque/(N·m) | 320 | |
| Battery | Type | Ternary polymer lithium battery |
| Capacity/Ah | 50 | |
| Number of series/parallels | 96/1 | |
| Nominal voltage/V | 345.6 |
| Start–Stop Penalty Factors | Fuel Consumption/L |
|---|---|
| 0 | 1.631 |
| 0.01 | 1.614 |
| 0.02 | 1.591 |
| 0.03 | 1.617 |
| 0.04 | 1.622 |
| 0.05 | 1.644 |
| Vehicle Demand Power (kW) | Working Point of Range Extender (kW) | The Minimum Specific Fuel Consumption (g·kW−1·h−1) |
|---|---|---|
| <15 | 15 | 277.8 |
| 15–20 | 20 | 271.5 |
| 20–25 | 25 | 262.1 |
| 25–30 | 30 | 269.2 |
| 30–35 | 35 | 271.2 |
| 35–40 | 40 | 270.8 |
| >40 | 45 | 273.9 |
| Energy Consumption Items | Thermostat Strategy | Power Following Strategy | A-ECMS |
|---|---|---|---|
| Final SOC (%) | 30.7 | 32.3 | 30.3 |
| Battery ohmic loss (kJ) | 751.7 | 454.8 | 217.4 |
| Ampere-hour flux (Ah) | 21.04 | 14.477 | 10.78 |
| Fuel consumption (L) | 1.708 | 1.768 | 1.591 |
| Comprehensive fuel consumption (L) | 1.679 | 1.639 | 1.574 |
| Comprehensive fuel consumption (L/100 km) | 7.23 | 7.05 | 6.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, D.; Lu, X.; Chao, X.; Zhang, Y.; Shen, J.; Zeng, F.; Zhang, Z.; Wu, F. Adaptive Equivalent Fuel Consumption Minimization Based Energy Management Strategy for Extended-Range Electric Vehicle. Sustainability 2023, 15, 4607. https://doi.org/10.3390/su15054607
Yao D, Lu X, Chao X, Zhang Y, Shen J, Zeng F, Zhang Z, Wu F. Adaptive Equivalent Fuel Consumption Minimization Based Energy Management Strategy for Extended-Range Electric Vehicle. Sustainability. 2023; 15(5):4607. https://doi.org/10.3390/su15054607
Chicago/Turabian StyleYao, Dongwei, Xinwei Lu, Xiangyun Chao, Yongguang Zhang, Junhao Shen, Fanlong Zeng, Ziyan Zhang, and Feng Wu. 2023. "Adaptive Equivalent Fuel Consumption Minimization Based Energy Management Strategy for Extended-Range Electric Vehicle" Sustainability 15, no. 5: 4607. https://doi.org/10.3390/su15054607






