Carbon Storage Estimation of Quercus aquifolioides Based on GEDI Spaceborne LiDAR Data and Landsat 9 Images in Shangri-La
Abstract
:1. Introduction
2. Materials and Methods
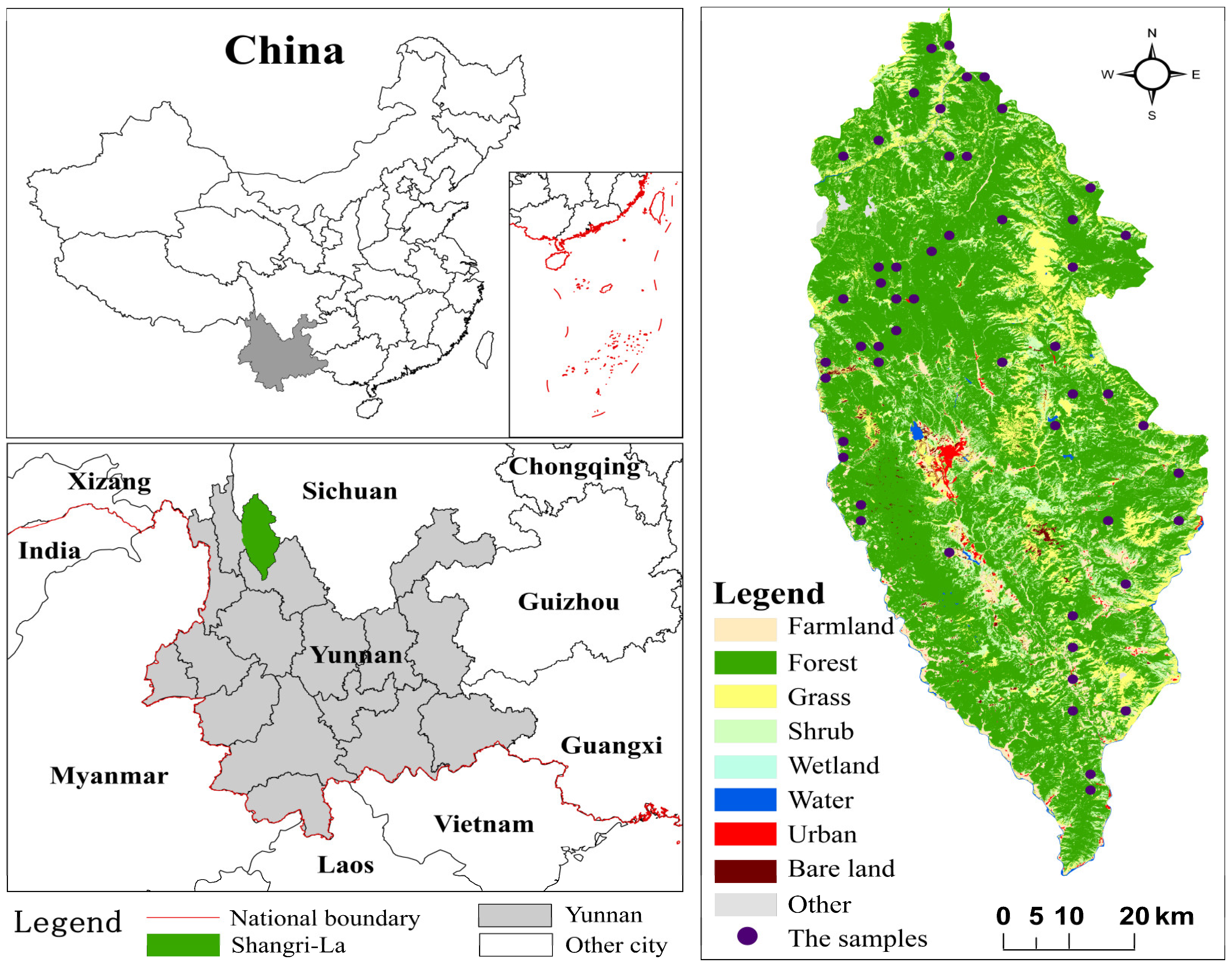
2.1. Study Area
2.2. Ground Survey Data Collection and Processing
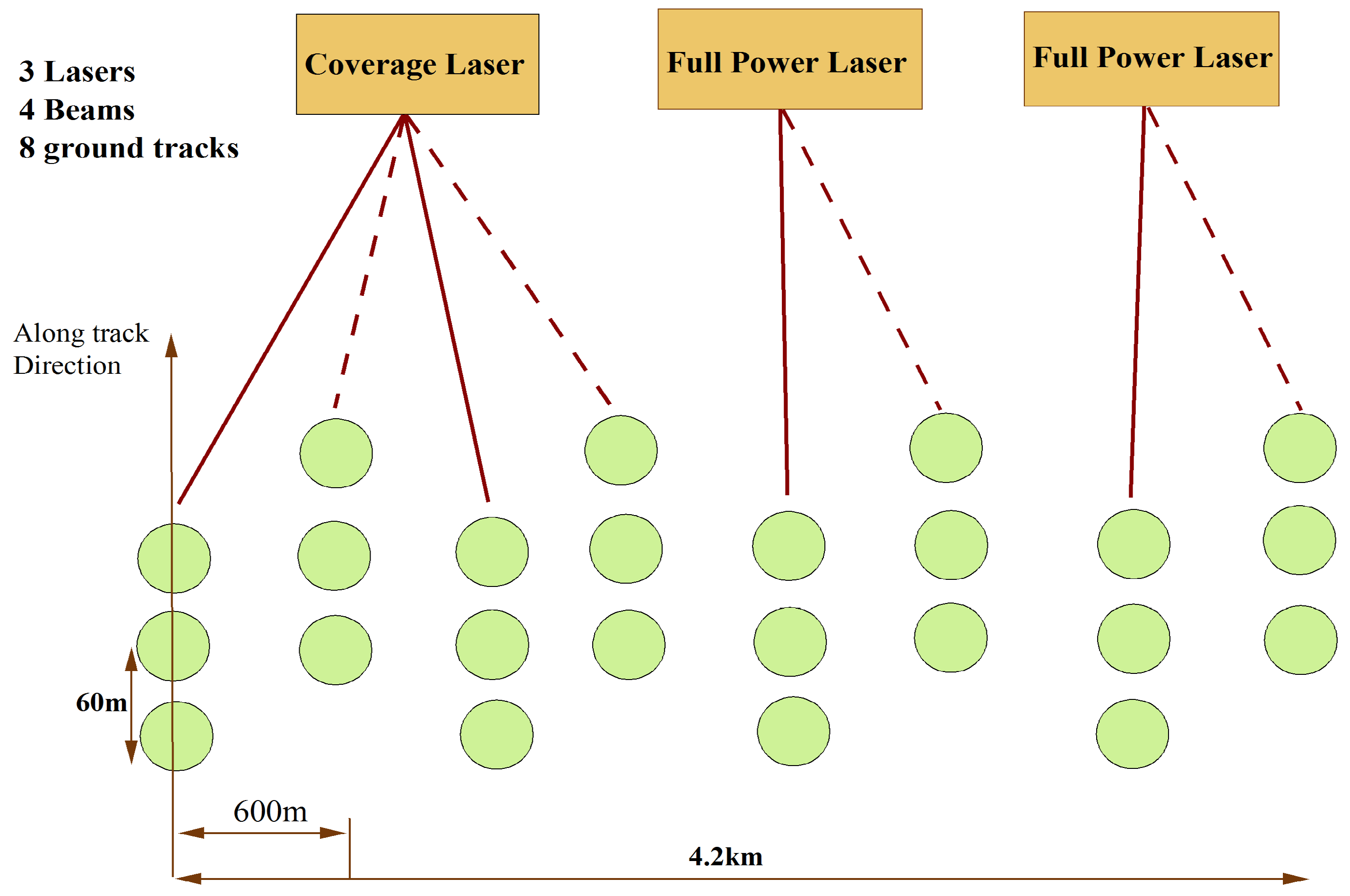
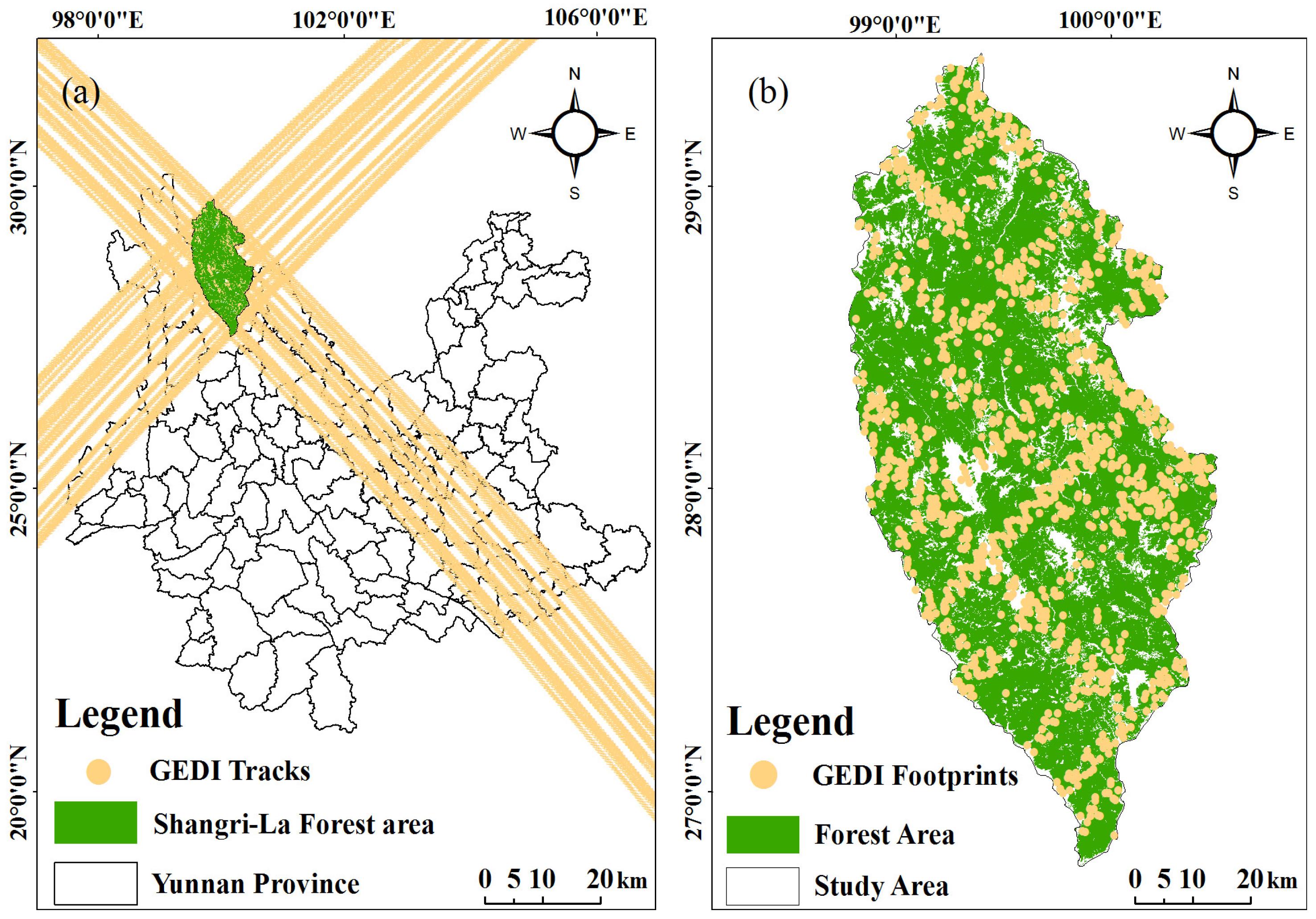
2.3. GEDI Data and Processing
2.4. Landsat 9 and Data Processing
2.5. Characteristic Variables Extraction and Selection
2.5.1. Optical Remote Sensing Independent Variable Factors
2.5.2. GEDI Parameters
2.6. Research Methods
2.6.1. Interpolation Method
- Variance Function
- 2.
- Kriging Interpolation
2.6.2. Carbon Storage Estimation Models
- Support Vector Machine
- 2.
- Bagging
- 3.
- Random Forest
2.7. Evaluation of Model Accuracy
3. Results
3.1. Selection of Variance Function Models
3.2. Variable Correlation Analysis
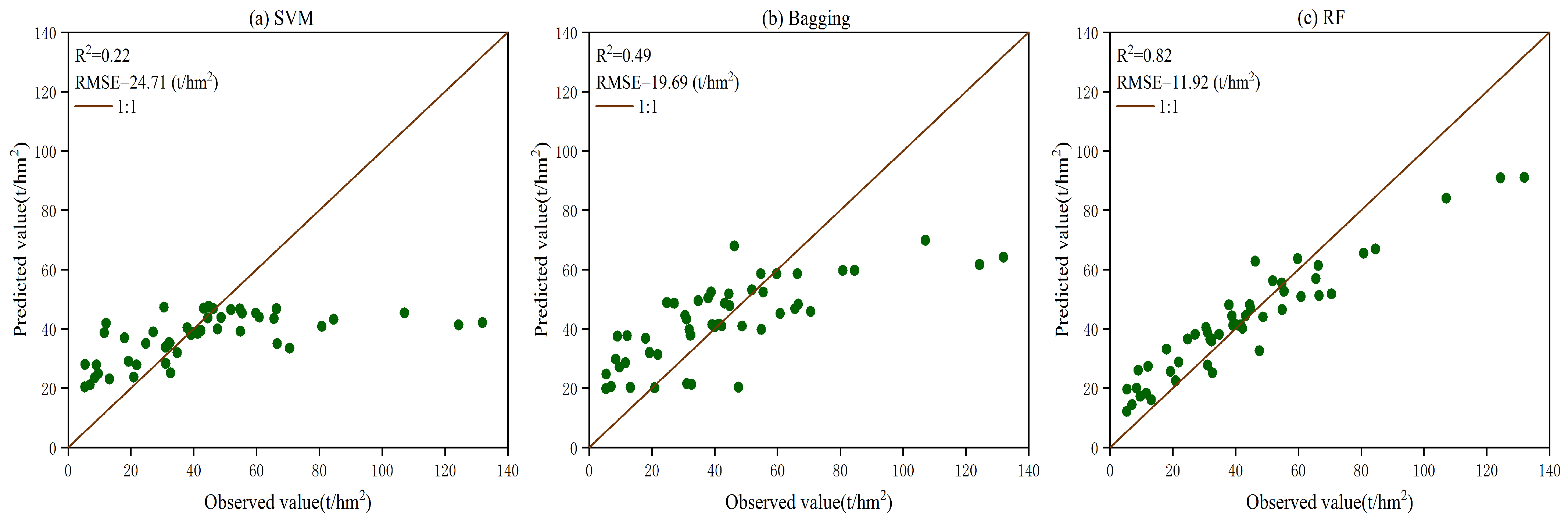
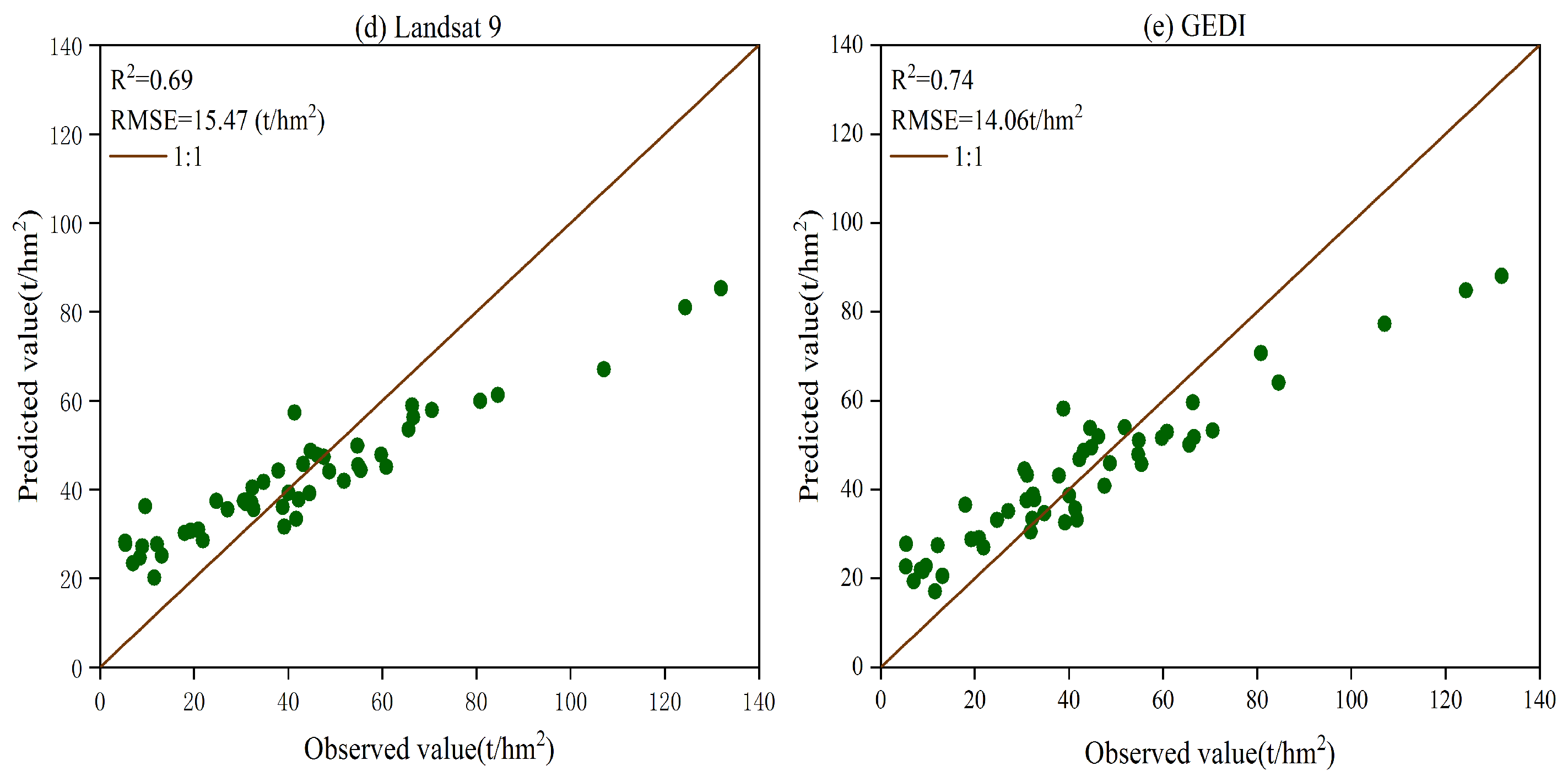
3.3. Comparison of Carbon Storage Estimation Results
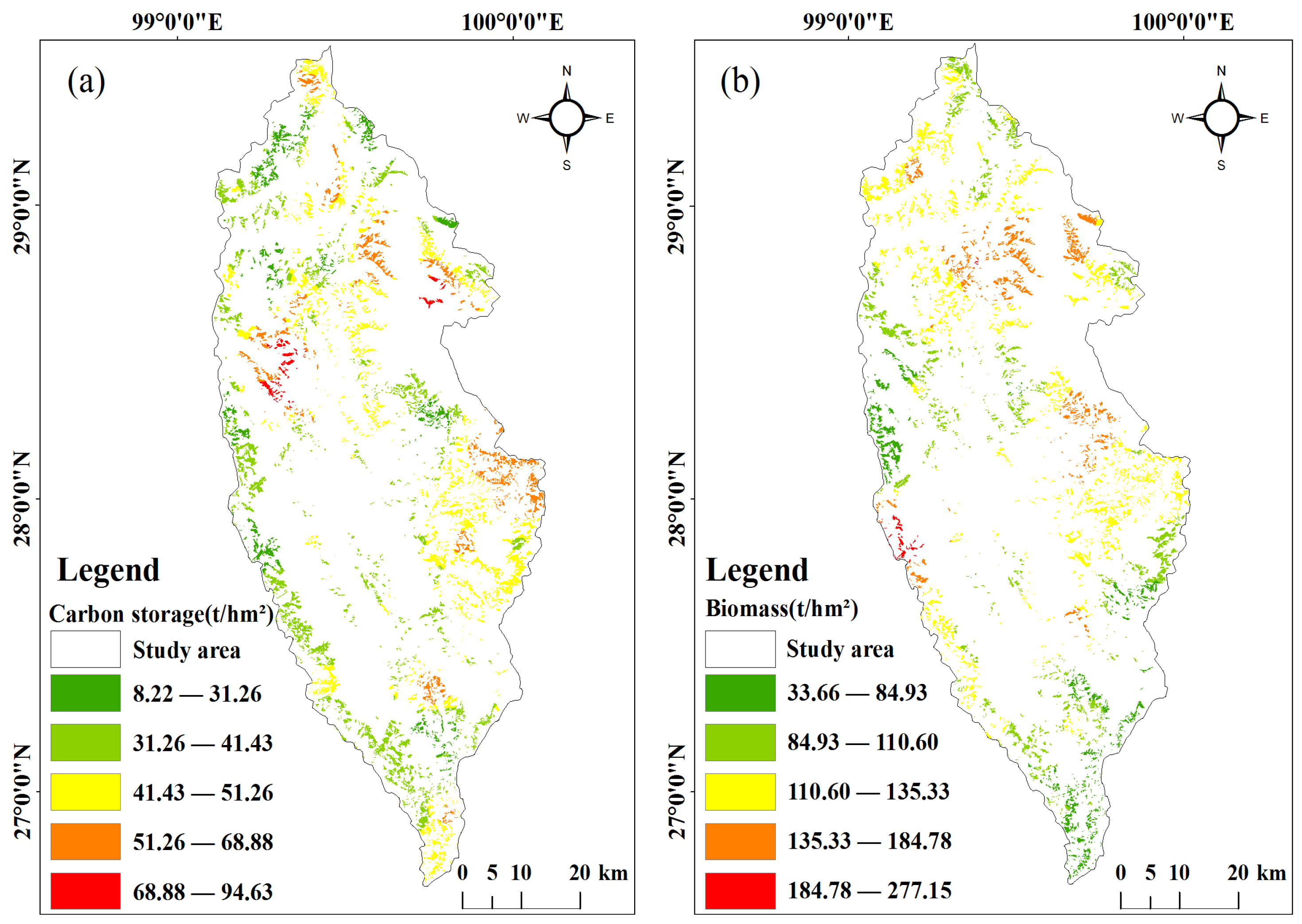
3.4. Spatial Distribution of Carbon Storage in Shangri-La
3.5. Distribution Regularity of Quercus aquifolioides Carbon Storage in Different Aspect
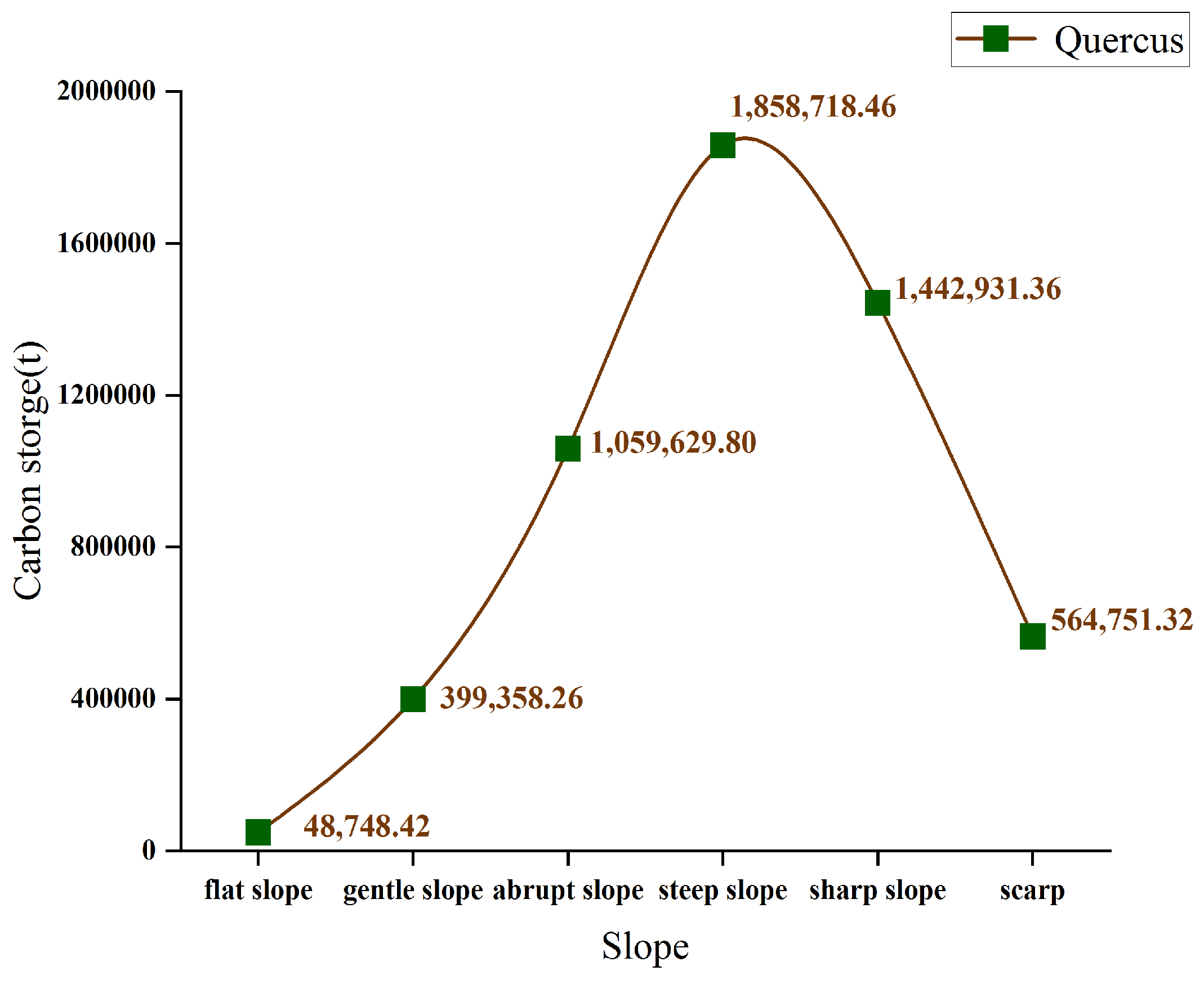
3.6. Distribution Regularity of Quercus aquifolioides Carbon Storage in Different Slopes
4. Discussion
4.1. Verifying Carbon Storage Estimation
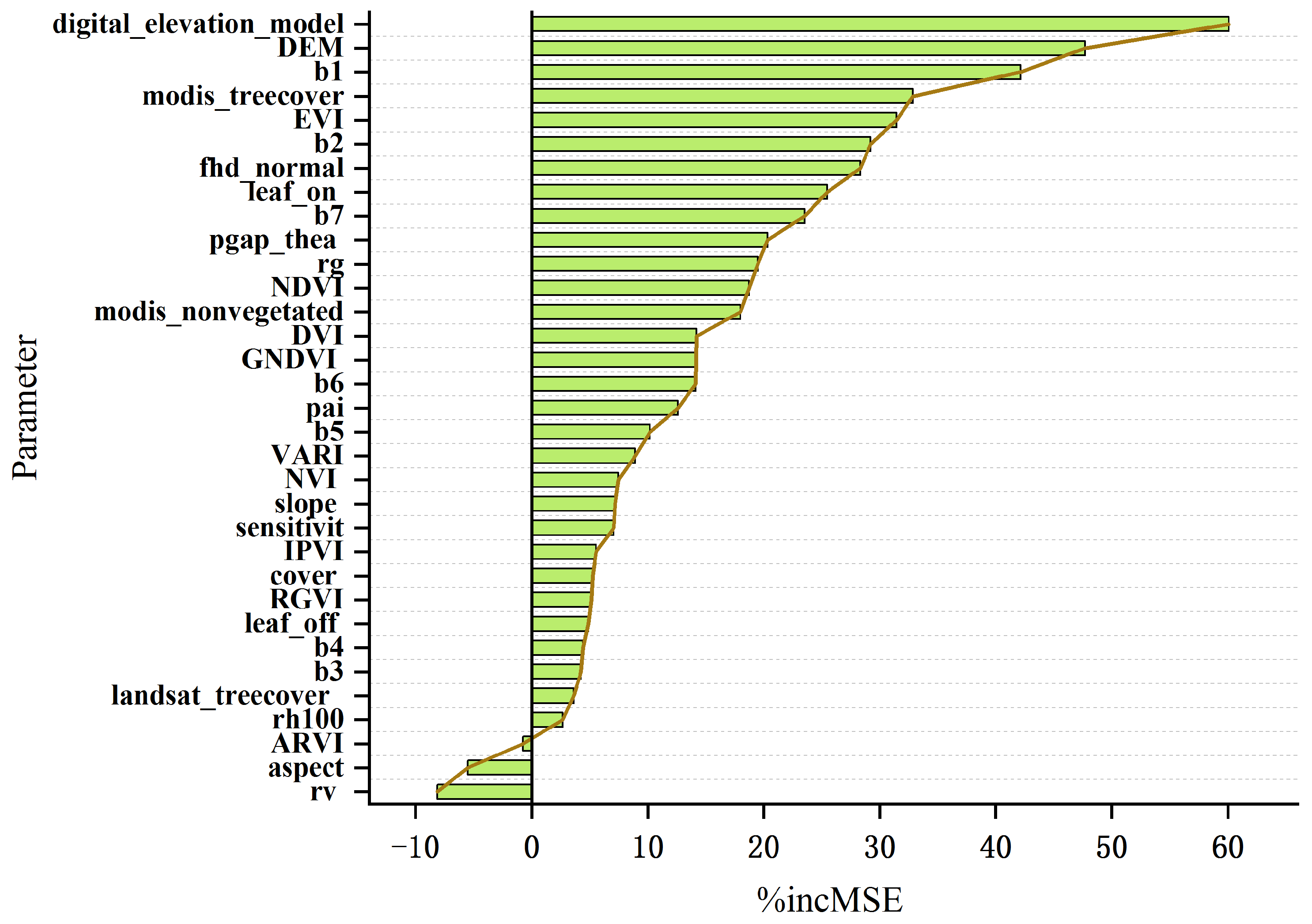
4.2. The Impact of Variable Selection on the Accuracy of Carbon Storage Estimation
4.3. The Influence of Different GEDI Algorithm Setting Groups for the Carbon Storage Estimation Accuracy
4.4. Limitations and Prospects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shao, W.; Cai, J.; Wu, H.; Liu, J.; Zhang, H.; Huang, H. An Assessment of Carbon Storage in China’s Arboreal Forests. Forests 2017, 8, 110. [Google Scholar] [CrossRef]
- Zhao, N.; Zhou, L.; Zhuang, J.; Wang, Y.; Zhou, W.; Chen, J.; Song, J.; Ding, J.; Chi, Y. Integration analysis of the carbon sources and sinks in terrestrial ecosystem, China. Acta Ecol. Sin. 2021, 42, 7648–7658. [Google Scholar] [CrossRef]
- Luo, Y.; Keenan, T.F.; Smith, M. Predictability of the terrestrial carbon cycle. Glob. Chang. Biol. 2015, 21, 1737–1751. [Google Scholar] [CrossRef] [PubMed]
- Amir, S.; Hormoz, S.; Scott, P.; Shaban, S. A comparative assessment of multi-temporal Landsat 8 and machine learning algorithms for estimating aboveground carbon stock in coppice oak forests. Int. J. Remote Sens. 2017, 38, 6407–6432. [Google Scholar] [CrossRef]
- Kaisheng, L. Spatial Pattern of Forest Carbon Storage in the Vertical and Horizontal Directions Based on HJ-CCD Remote Sensing Imagery. Remote Sens. 2019, 11, 788. [Google Scholar] [CrossRef]
- Long, Y.; Jiang, F.G.; Sun, H.; Wang, T.H.; Zou, Q.; Chen, C.S. Estimating vegetation carbon storage based on optimal bandwidth selected from geographically weighted regression model in Shenzhen City. Acta Ecol. Sin. 2022, 42, 4933–4945. [Google Scholar] [CrossRef]
- Yan, E.; Lin, H.; Wang, G.; Sun, H. Improvement of Forest Carbon Estimation by Integration of Regression Modeling and Spectral Unmixing of Landsat Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2003–2007. [Google Scholar] [CrossRef]
- Zhang, J.; Benoit, R.; Arturo, S.; Karen, C. Intra-and inter-class spectral variability of tropical tree species at La Selva, Costa Rica: Implications for species identification using HYDICE imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
- Svein, S.; Rasmus, A.; Terje, G.; Erik, N.; Dan, J.W. Estimating spruce and pine biomass with interferometric X-band SAR. Remote Sens. Environ. 2010, 114, 2353–2360. [Google Scholar] [CrossRef]
- Xi, Z.L.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods. Remote Sens. 2022, 14, 364. [Google Scholar] [CrossRef]
- Jiang, F.; Deng, M.; Tang, J.; Fu, L.; Sun, H. Integrating spaceborne LiDAR and Sentinel-2 images to estimate forest aboveground biomass in Northern China. Carbon Balance Manag. 2022, 17, 12. [Google Scholar] [CrossRef]
- Svetlana, S.; Sören, H.; Sean, P.H.; Hans-Erik, A.; Hans, P.; Wilmer, P.; Paul, L.P.; Erik, N.; Timothy, G.; Göran, S. Generalized Hierarchical Model-Based Estimation for Aboveground Biomass Assessment Using GEDI and Landsat Data. Remote Sens. 2018, 10, 1832. [Google Scholar] [CrossRef]
- Duncanson, L.; Neuenschwander, A.; Hancock, S.; Thomas, N.; Fatoyinbo, T.; Simard, M.; Silva, C.A.; Armston, J.; Luthcke, S.B.; Hofton, M.; et al. Biomass estimation from simulated GEDI, ICESat-2 and NISAR across environmental gradients in Sonoma County, California. Remote Sens. Environ. 2020, 242, 111779. [Google Scholar] [CrossRef]
- Dorado-Roda, I.; Pascual, A.; Godinho, S.; Silva, C.A.; Botequim, B.; Rodríguez-Gonzálvez, P.; González-Ferreiro, E.; Guerra-Hernández, J. Assessing the Accuracy of GEDI Data for Canopy Height and Aboveground Biomass Estimates in Mediterranean Forests. Remote Sens. 2021, 13, 2279. [Google Scholar] [CrossRef]
- Kanmegne, T.D.; Latifi, H.; Ullmann, T.; Baumhauer, R.; Bayala, J.; Thiel, M. Estimation of Aboveground Biomass in Agroforestry Systems over Three Climatic Regions in West Africa Using Sentinel-1, Sentinel-2, ALOS, and GEDI Data. Sensors 2022, 23, 349. [Google Scholar] [CrossRef]
- Shendryk, Y. Fusing GEDI with earth observation data for large area aboveground biomass mapping. Int. J. Appl. Earth Obs. 2022, 115, 103108. [Google Scholar] [CrossRef]
- Silva, C.A.; Duncanson, L.; Hancock, S.; Neuenschwander, A.; Thomas, N.; Hofton, M.; Fatoyinbo, L.; Simard, M.; Marshak, C.Z.; Armston, J.L.; et al. Fusing simulated GEDI, ICESat-2 and NISAR data for regional aboveground biomass mapping. Remote Sens. Environ. 2021, 253, 112234. [Google Scholar] [CrossRef]
- Liu, L. Inversion of Forest Canopy Height in Yunnan Province Based on Spaceborne Lidar Data and Optical Remote Sensing Data. Master’s Thesis, Yunnan Normal University, Kunming, China, 2022. [Google Scholar] [CrossRef]
- Sothe, C.; Gonsamo, A.; Lourenço, R.B.; Kurz, W.A.; Snider, J. Spatially Continuous Mapping of Forest Canopy Height in Canada by Combining GEDI and ICESat-2 with PALSAR and Sentinel. Remote Sens. 2022, 14, 5158. [Google Scholar] [CrossRef]
- Pascual, A.; Guerra-Hernández, J.; Armston, J.; Minor, D.M.; Duncanson, L.I.; May, P.B.; Kellner, J.R.; Dubayah, R. Assessing the performance of NASA’s GEDI L4A footprint aboveground biomass density models using National Forest Inventory and airborne laser scanning data in Mediterranean forest ecosystems. For. Ecol. Manag. 2023, 538, 120975. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, L. The characteristics and application prospects of the new generation Landsat satellite constellation. Urban Geotech. Investig. Surv. 2022, 5, 78–85. [Google Scholar]
- Li, C.; Chen, D.; Wu, D.; Su, X. Design of an EIoT system for nature reserves: A case study in Shangri-La County, Yunnan Province, China. Int. J. Sustain. Dev. World Ecol. 2015, 22, 184–188. [Google Scholar] [CrossRef]
- Song, F. Current status and characteristics of forest resources in Shangri-La County. J. West China For. Sci. 2008, 122, 124–128. [Google Scholar] [CrossRef]
- Shu, Q.; Xi, L.; Wang, K.; Xie, F.; Pang, Y.; Song, H. Optimization of Samples for Remote Sensing Estimation of Forest Aboveground Biomass at the Regional Scale. Remote Sens. 2022, 14, 4187. [Google Scholar] [CrossRef]
- State Forestry Administration of China (SFAC). Tree Biomass Models and Related Parameters to Carbon Accounting for Quercus; State Forestry Administration: Beijing, China, 2016. [Google Scholar]
- Xie, D.; Li, G.; Zhao, Y.; Yang, X.; Tang, X.; Fu, A.U.S. GEDI space-based laser altimetry system and its application. Space Int. 2018, 12, 39–44. [Google Scholar]
- Liang, M.; Duncanson, L.; Silva, J.A.; Sedano, F. Quantifying aboveground biomass dynamics from charcoal degradation in Mozambique using GEDI Lidar and Landsat. Remote Sens. Environ. 2023, 284, 113367. [Google Scholar] [CrossRef]
- Rajab, P.M.; Baghdadi, N.; Fayad, I. Comparison of GEDI LiDAR Data Capability for Forest Canopy Height Estimation over Broadleaf and Needleleaf Forests. Remote Sens. 2023, 15, 1522. [Google Scholar] [CrossRef]
- Masek, J.G.; Wulder, M.A.; Markham, B.; McCorkel, J.; Crawford, C.J.; Storey, J.; Jenstrom, D.T. Landsat 9: Empowering open science and applications through continuity. Remote Sens. Environ. 2020, 248, 111968. [Google Scholar] [CrossRef]
- NiroumandJadidi, M.; Bovolo, F.; Bresciani, M.; Gege, P.; Giardino, C. Water Quality Retrieval from Landsat-9 (OLI-2) Imagery and Comparison to Sentinel-2. Remote Sens. 2022, 14, 4596. [Google Scholar] [CrossRef]
- Gross, G.; Helder, D.; Begeman, C.; Leigh, L.; Kaewmanee, M.; Shah, R. Initial Cross-Calibration of Landsat 8 and Landsat 9 Using the Simultaneous Underflfly Event. Remote Sens. 2022, 14, 2418. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, H.; Li, C.; Ma, K.; Long, J.; Ren, L. Retrieving the forest aboveground biomass by combing the red edge bands of Sentinel-2 and GF-6. Acta Ecol. Sin. 2021, 41, 8222–8236. [Google Scholar] [CrossRef]
- Liu, S. Forest Biomass Estimation in Nanchuan District of Chongqing City Using a Combination of Sentinel-1 and Senyinel-2 Data. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2020. [Google Scholar] [CrossRef]
- Cai, C. Machine Learning Optimized Method for Spatial Estimation of Forest Biomass of Tianshan Spruce. Master’s Thesis, Xinjiang Agricultural University, Ürümqi, China, 2022. [Google Scholar] [CrossRef]
- Feng, Y. Spatial Statistics Theory and Its Application in Forestry; Chinese Forestry Publishing House: Beijing, China, 2008. [Google Scholar]
- Jiang, F.; Sun, H.; Chen, E.; Wang, T.; Cao, Y.; Liu, Q. Above-Ground Biomass Estimation for Coniferous Forests in Northern China Using Regression Kriging and Landsat 9 Images. Remote Sens. 2022, 14, 5734. [Google Scholar] [CrossRef]
- Zhou, R.; Zhao, T.; Wu, F. Aboveground biomass model based on Landsat 8 remote sensing images. J. Northwest For. Univ. 2022, 37, 186–192. [Google Scholar] [CrossRef]
- Xu, Z. Forest Biomass Retrieval Based on Sentinel-1A and Landsat 8 Image in Guidong County. Master’s Thesis, Nanjing Forestry University, Nanjing, China, 2020. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classifification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Liang, Z.; Li, Z.; Lai, Q.; Lin, Z.; Li, T.; Zhang, J. Application of 10-fold cross-validation in the evaluation of generalization ability of prediction models and the realization. Chin. J. Hosp. Stat. 2020, 27, 289–292. [Google Scholar] [CrossRef]
- Xu, L.; Shu, Q.; Fu, H.; Zhou, W.; Luo, S.; Gao, Y.; Yu, J.; Guo, C.; Yang, Z.; Xiao, J.; et al. Estimation of Quercus Biomass in Shangri-La Based on GEDI Spaceborne Lidar Data. Forests 2023, 14, 876. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Yue, C.; Xu, T.; Cheng, P. Carbon storage estimation of main forestry ecosystems in Northwest Yunnan Province using remote sensing data. In Remote Sensing of the Environment, Proceedings of the 18th National Symposium on Remote Sensing of China, Wuhan, China, 20 October 2012; SPIE: Washington, DC, USA, 2012; Volume 9158, pp. 176–183. [Google Scholar] [CrossRef]
- Cheng, P.; Wang, J.; Wang, X.; Yue, C.; Xu, T.; Chen, F.; Zhou, X.; Wang, X. Carbon storage and density of four main trees in Shangri-La based on plot data. For. Inventory Plan 2011, 36, 12–15. [Google Scholar] [CrossRef]
- Du, C. Estimation of Forest Aboveground Biomass and Determination of Its Saturation Values Based on Passive and Active Data. Ph.D. Thesis, Northeast Forestry University, Harbin, China, 2021. [Google Scholar] [CrossRef]
- Jiao, Y.; Wang, D.; Yao, X.; Wang, S.; Chi, T.; Meng, Y. Forest Emissions Reduction Assessment Using Optical Satellite Imagery and Space LiDAR Fusion for Carbon Stock Estimation. Remote Sens. 2023, 15, 1410. [Google Scholar] [CrossRef]
- Luo, H.; Shu, Q.; Wang, Q.; Wang, D.; Xie, F.; Zi, L. Estimation of above ground biomass of rubber forest with airborne lidar and Landsat8/OLI data. J. Northeast For. Univ. 2019, 47, 56–61. [Google Scholar] [CrossRef]
- Jiang, F.; Kutia, M.; Ma, K.; Chen, S.; Long, J.; Sun, H. Estimating the aboveground biomass of coniferous forest in Northeast China using spectral variables, land surface temperature and soil moisture. Sci. Total Environ. 2021, 785, 147335. [Google Scholar] [CrossRef]
- Adam, M.; Urbazaev, M.; Dubois, C.; Schmullius, C. Accuracy Assessment of GEDI Terrain Elevation and Canopy Height Estimates in European Temperate Forests: Influence of Environmental and Acquisition Parameters. Remote Sens. 2020, 12, 3948. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Liu, L.; Wang, C.; Nie, S.; Zhu, X.; Xi, X.; Wang, J. Analysis of the influence of different algorithms of GEDI L2A on the accuracy of ground elevation and forest canopy height. J. Univ. Chin. Acad. Sci. 2022, 39, 502–511. [Google Scholar] [CrossRef]
- Han, M.; Xing, Y.; Li, G.; Huang, J.; Cai, L. Comparison of the accuracy of the maximum canopy height and biomass inversion of the data of different GEDI algorithm groups. J. Cent. S. Univ. For. Technol. 2022, 42, 72–82. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural network guided interpolation for mapping canopy height of China’s forests by integrating GEDI and ICESat-2 data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]
- Tang, H.; John, A. Algorithm Theoretical Basis Document (ATBD) for GEDI L2B Footprint Canopy Cover and Vertical Profile Metrics; Goddard Space Flight Center: Greenbelt, MD, USA, 2019. [Google Scholar]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in Northeast China using SAR Sentinel-1B, multispectral Sentinel-2A, and DEM imagery. ISPRS J. Photogramm. 2019, 151, 277–289. [Google Scholar] [CrossRef]



| Species | Sample Size | Minimum | Maximum | Average | SD |
|---|---|---|---|---|---|
| Quercus aquifolioides | 52 | 5.36 | 131.98 | 41.79 | 30.23 |
| Vegetation Index | Full Name | Expression |
|---|---|---|
| Band reflectance | B1-Coastal, B2-Blue, B3-Green, B4-Red, B5-NIR, B6-SWIR 1, B7-SWIR 2 | - |
| NDVI | Normalized Difference Vegetation Index | NDVI = (NIR − R)/(NIR + R) |
| RVI | Ratio Vegetation Index | RVI = NIR/R |
| DVI | Difference Vegetation Index | DVI = NIR − R |
| RGVI | Red-green Vegetation Index | RGVI = (R − G)/(R + G) |
| GNDVI | Green Normalized Difference Vegetation Index | GNDVI = (NIR − G)/(NIR + G) |
| IPVI | Infrared Vegetation Index | IPVI = NIR/(NIR + R) |
| EVI | Enhanced Vegetation Index | EVI = (2.5 × (NIR − R))/(NIR + 6 × R − 7.5 × B + 1) |
| ARVI | Atmospherically Resistant Vegetation Index | ARVI = (NIR − (2 × R − B))/(NIR + (2 × R − B)) |
| VARI | Visible atmospherically resistant Index | VARI = (G − R)/(G + R−B) |
| Parameters | Description | Parameters | Description |
|---|---|---|---|
| cover | Total canopy cover | fhd_normal | Foliage height diversity index |
| pai | Total plant area index. | landsat_treecover | Landsat tree canopy cover |
| degrade_flag | Degrade flag | solar_elevation | Solar elevation |
| lon_lowestmode | Longitude of center of lowest mode | lat_lowestmode | Latitude of center of lowest mode |
| pgap_theta | Total gap between plant | modis_treecover | Percent tree cover from MODIS data |
| digital_elevation_model | Digital elevation model height above the WGS84 ellipsoid | modis_nonvegetated | Percent non-vegetated from MODIS data |
| leaf_off_doy | Leaf-off start day-of-year derived | leaf_on_doy | Leaf-on start day-of-year derived |
| rg | The ground energy value in the waveform | rv | The vegetation energy value in the waveform |
| rh100 | Height above the ground at the start of the waveform signal | sensitivity | The waveform penetrable to the largest tree covering in the canopy |
| leaf_off_flag | Indicating if the observation was recorded under deciduous forest conditions | quality_flag | Flag simplifying selection of most useful data |
| Parameter Name | Model | R2 | Residual SS | Nugget | Sill | Structural Ratio | Range |
|---|---|---|---|---|---|---|---|
| digital_elevation_model | Linear | 0.97 | 5.75 × 109 | 158,182.97 | 492,097.45 | 0.68 | 0.93 |
| Spherical | 0.96 | 6.02 × 109 | 151,000.00 | 647,400.00 | 0.77 | 1.91 | |
| Exponential | 0.95 | 7.56 × 109 | 130,000.00 | 671,000.00 | 0.81 | 2.86 | |
| Gaussian | 0.94 | 9.80 × 109 | 195,000.00 | 539,300.00 | 0.64 | 1.20 | |
| modis_treecover | Linear | 0.41 | 1.82 | 4.66 | 5.60 | 0.17 | 0.93 |
| Spherical | 0.60 | 1.23 | 0.18 | 5.24 | 0.97 | 0.07 | |
| Exponential | 0.72 | 0.88 | 0.61 | 5.28 | 0.88 | 0.11 | |
| Gaussian | 0.60 | 1.23 | 0.74 | 5.24 | 0.86 | 0.06 | |
| fhd_normal | Linear | 0.06 | 5.30 × 10−3 | 0.35 | 0.36 | 0.04 | 0.93 |
| Spherical | 0.44 | 3.18 × 10−3 | 0.02 | 0.36 | 0.95 | 0.06 | |
| Exponential | 0.42 | 2.94 × 10−3 | 0.04 | 0.36 | 0.89 | 0.07 | |
| Gaussian | 0.44 | 3.18 × 10−3 | 0.06 | 0.36 | 0.84 | 0.05 |
| Algorithm Setting Group | Smoothing Width (Noise) | Smoothing Width (Signal) | Waveform Signal Start Threshold | Waveform Signal end Threshold |
|---|---|---|---|---|
| 1 | 6.5σ | 6.5σ | 3σ | 6σ |
| 2 | 6.5σ | 3.5σ | 3σ | 3σ |
| 3 | 6.5σ | 3.5σ | 3σ | 6σ |
| 4 | 6.5σ | 6.5σ | 6σ | 6σ |
| 5 | 6.5σ | 3.5σ | 3σ | 2σ |
| 6 | 6.5σ | 3.5σ | 3σ | 4σ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Lai, H.; Yu, J.; Luo, S.; Guo, C.; Gao, Y.; Zhou, W.; Wang, S.; Shu, Q. Carbon Storage Estimation of Quercus aquifolioides Based on GEDI Spaceborne LiDAR Data and Landsat 9 Images in Shangri-La. Sustainability 2023, 15, 11525. https://doi.org/10.3390/su151511525
Xu L, Lai H, Yu J, Luo S, Guo C, Gao Y, Zhou W, Wang S, Shu Q. Carbon Storage Estimation of Quercus aquifolioides Based on GEDI Spaceborne LiDAR Data and Landsat 9 Images in Shangri-La. Sustainability. 2023; 15(15):11525. https://doi.org/10.3390/su151511525
Chicago/Turabian StyleXu, Li, Hongyan Lai, Jinge Yu, Shaolong Luo, Chaosheng Guo, Yingqun Gao, Wenwu Zhou, Shuwei Wang, and Qingtai Shu. 2023. "Carbon Storage Estimation of Quercus aquifolioides Based on GEDI Spaceborne LiDAR Data and Landsat 9 Images in Shangri-La" Sustainability 15, no. 15: 11525. https://doi.org/10.3390/su151511525








