A Spatial Decision Support System for Modeling Urban Resilience to Natural Hazards
Abstract
:1. Introduction
2. Materials and Methods
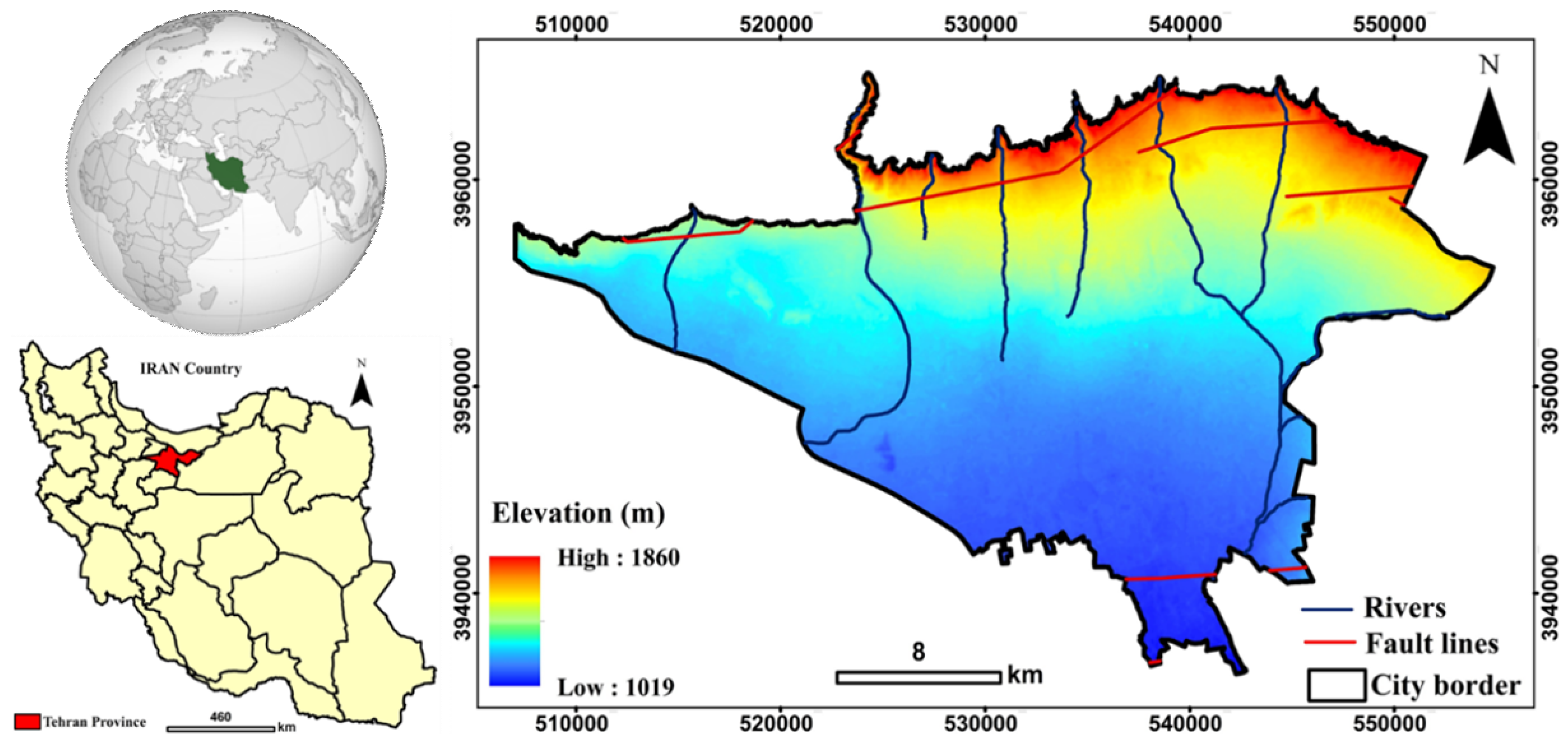
2.1. Study Area and Data Collection
2.2. Methodology
2.2.1. Standardization of Criteria
2.2.2. AHP
- Define the problem and express its goals in a clear manner (hierarchical tree design).
- Separate the defined problem into decision elements (criteria and options).
- Form a decision-making matrix using pairwise comparisons.
- Use the eigenvalue method to estimate the relative weight of decision-making criteria.
- Calculate the compatibility rate of matrices to ensure the compatibility of decision-makers’ judgments.
- Collect the decision weights for the overall ranking of the criteria.
2.2.3. OWA
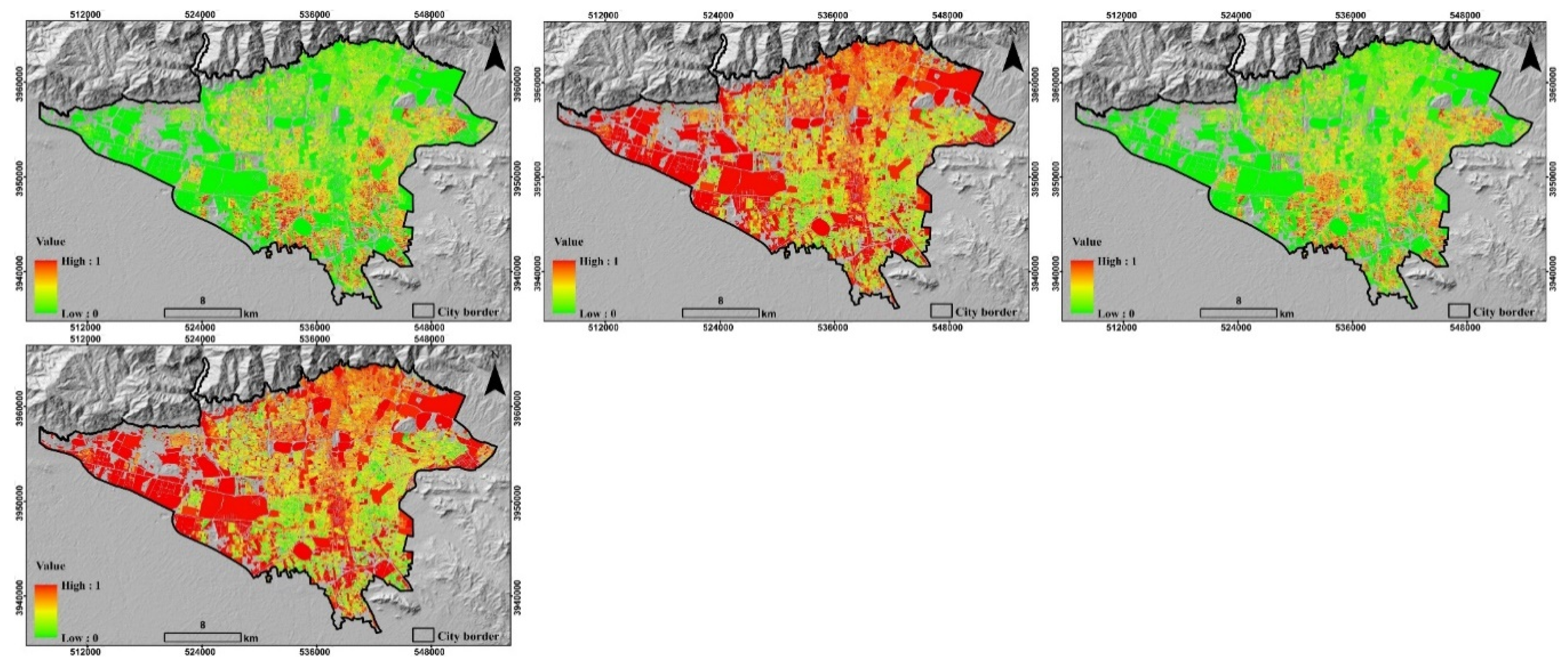
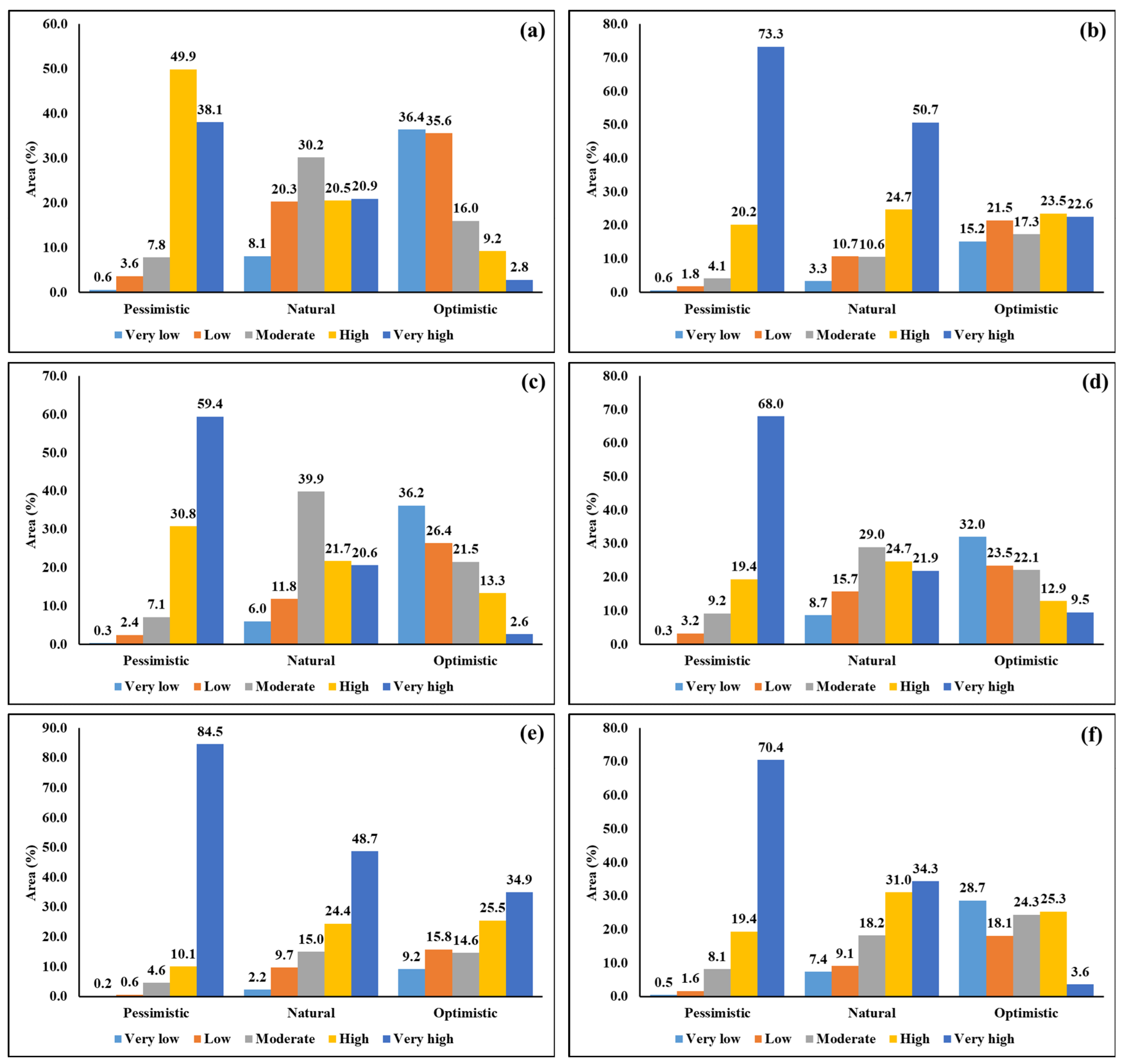
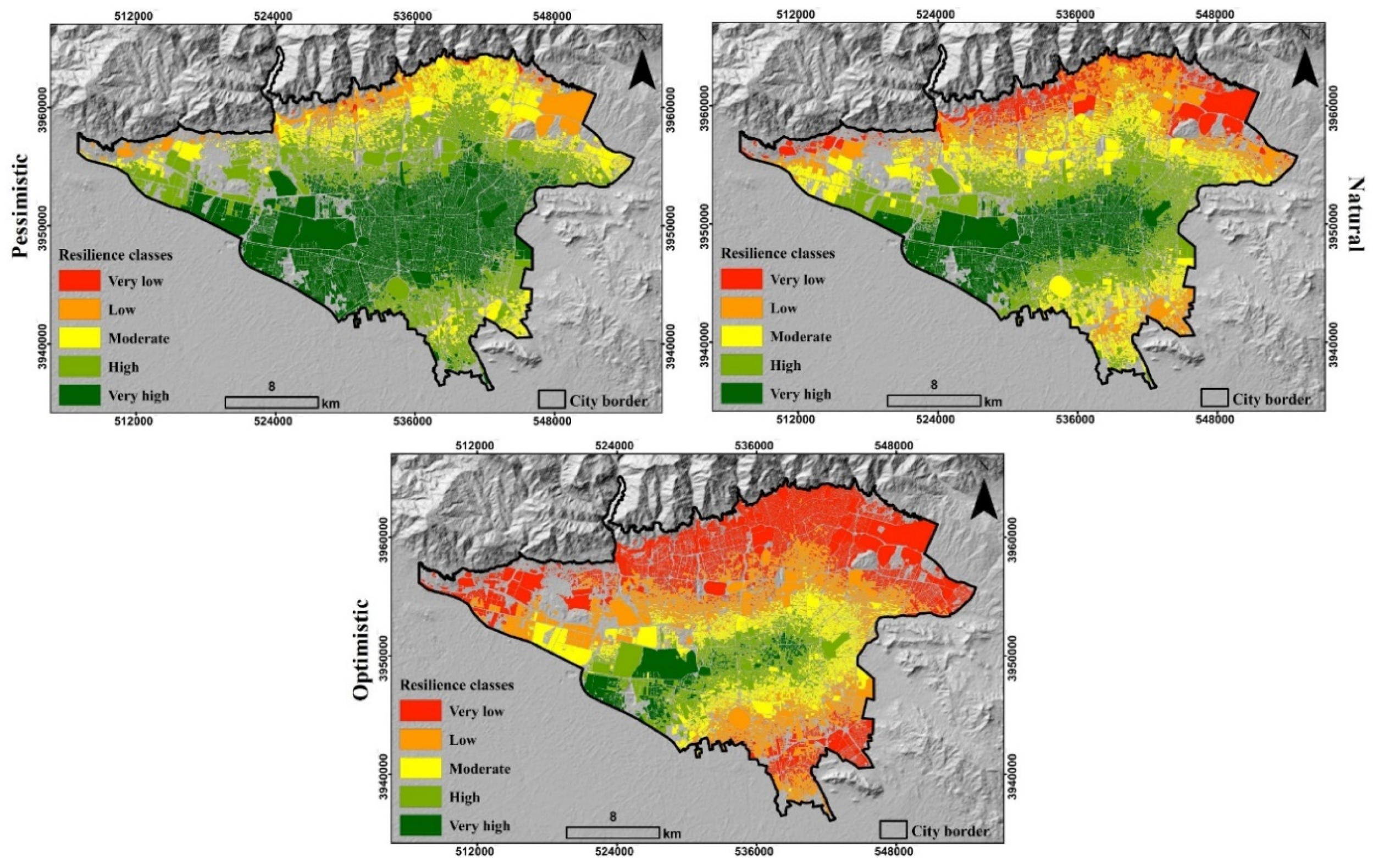
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Papathoma-Köhle, M.; Schlögl, M.; Fuchs, S. Vulnerability indicators for natural hazards: An innovative selection and weighting approach. Sci. Rep. 2019, 9, 15026. [Google Scholar] [CrossRef] [PubMed]
- Souissi, D.; Zouhri, L.; Hammami, S.; Msaddek, M.H.; Zghibi, A.; Dlala, M. GIS-based MCDM–AHP modeling for flood susceptibility mapping of arid areas, southeastern Tunisia. Geocarto Int. 2020, 35, 991–1017. [Google Scholar] [CrossRef]
- Afsari, R.; Nadizadeh Shorabeh, S.; Bakhshi Lomer, A.R.; Homaee, M.; Arsanjani, J.J. Using Artificial Neural Networks to Assess Earthquake Vulnerability in Urban Blocks of Tehran. Remote Sens. 2023, 15, 1248. [Google Scholar] [CrossRef]
- Boloorani, A.D.; Shorabeh, S.N.; Samany, N.N.; Mousivand, A.; Kazemi, Y.; Jaafarzadeh, N.; Zahedi, A.; Rabiei, J. Vulnerability mapping and risk analysis of sand and dust storms in Ahvaz, IRAN. Environ. Pollut. 2021, 279, 116859. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, S.A.; El-Raey, M.E. Vulnerability assessment for flash floods using GIS spatial modeling and remotely sensed data in El-Arish City, North Sinai, Egypt. Nat. Hazards 2020, 102, 707–728. [Google Scholar] [CrossRef]
- Nadizadeh Shorabeh, S.; Hamzeh, S.; Zanganeh Shahraki, S.; Firozjaei, M.K.; Jokar Arsanjani, J. Modelling the intensity of surface urban heat island and predicting the emerging patterns: Landsat multi-temporal images and Tehran as case study. Int. J. Remote Sens. 2020, 41, 7400–7426. [Google Scholar] [CrossRef]
- Şalcıoğlu, E.; Başoğlu, M. Psychological effects of earthquakes in children: Prospects for brief behavioral treatment. World J. Pediatr. 2008, 4, 165–172. [Google Scholar] [CrossRef]
- Rakhshani, T.; Taravatmanesh, S.; Khorramdel, K.; Ebrahimi, M. Social support for earthquake victims in East Azerbaijan, Iran. Arch. Psychiatry Psychother. 2017, 4, 66–72. [Google Scholar]
- Hadidi, A.; Holzbecher, E.; Molenaar, R.E. Flood mapping in face of rapid urbanization: A case study of Wadi Majraf-Manumah, Muscat, Sultanate of Oman. Urban Water J. 2020, 17, 407–415. [Google Scholar] [CrossRef]
- Afsari, R.; Nadizadeh Shorabeh, S.; Kouhnavard, M.; Homaee, M.; Arsanjani, J.J. A spatial decision support approach for flood vulnerability analysis in urban areas: A case study of Tehran. ISPRS Int. J. Geo-Inf. 2022, 11, 380. [Google Scholar] [CrossRef]
- Knaapen, A.M.; Seiler, F.; Schilderman, P.A.; Nehls, P.; Bruch, J.; Schins, R.P.; Borm, P.J. Neutrophils cause oxidative DNA damage in alveolar epithelial cells. Free Radic. Biol. Med. 1999, 27, 234–240. [Google Scholar] [CrossRef] [PubMed]
- Dimelli, D. Planning resilient cities: The case of Chania. UPLanD-J. Urban Plan. Landsc. Environ. Des. 2020, 5, 65–76. [Google Scholar]
- Cardona, O.D. The need for rethinking the concepts of vulnerability and risk from a holistic perspective: A necessary review and criticism for effective risk management. In Mapping Vulnerability; Routledge: Abingdon, UK, 2013; pp. 37–51. [Google Scholar]
- Chun, H.; Chi, S.; Hwang, B.-G. A spatial disaster assessment model of social resilience based on geographically weighted regression. Sustainability 2017, 9, 2222. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Doorga, J.R.; Magerl, L.; Bunwaree, P.; Zhao, J.; Watkins, S.; Staub, C.G.; Rughooputh, S.D.; Cunden, T.S.; Lollchund, R.; Boojhawon, R. GIS-based multi-criteria modelling of flood risk susceptibility in Port Louis, Mauritius: Towards resilient flood management. Int. J. Disaster Risk Reduct. 2022, 67, 102683. [Google Scholar] [CrossRef]
- Mayouf, Z.; Nouibat, B. Spatial Modeling for Urban Resilience Assessment: Using AHP and GUS (Case Study of Bou-Saada City, Algeria). Tech. Soc. Sci. J. 2022, 36, 607. [Google Scholar] [CrossRef]
- Duan, C.; Zhang, J.; Chen, Y.; Lang, Q.; Zhang, Y.; Wu, C.; Zhang, Z. Comprehensive Risk Assessment of Urban Waterlogging Disaster Based on MCDA-GIS Integration: The Case Study of Changchun, China. Remote Sens. 2022, 14, 3101. [Google Scholar] [CrossRef]
- Giovinazzi, S.; Marchili, C.; Di Pietro, A.; Giordano, L.; Costanzo, A.; La Porta, L.; Pollino, M.; Rosato, V.; Lückerath, D.; Milde, K. Assessing earthquake impacts and monitoring resilience of historic areas: Methods for GIS tools. ISPRS Int. J. Geo-Inf. 2021, 10, 461. [Google Scholar] [CrossRef]
- Bosisio, A.; Moncecchi, M.; Morotti, A.; Merlo, M. Machine learning and GIS approach for electrical load assessment to increase distribution networks resilience. Energies 2021, 14, 4133. [Google Scholar] [CrossRef]
- Shorabeh, S.N.; Firozjaei, H.K.; Firozjaei, M.K.; Jelokhani-Niaraki, M.; Homaee, M.; Nematollahi, O. The site selection of wind energy power plant using GIS-multi-criteria evaluation from economic perspectives. Renew. Sustain. Energy Rev. 2022, 168, 112778. [Google Scholar] [CrossRef]
- Firozjaei, M.K.; Nematollahi, O.; Mijani, N.; Shorabeh, S.N.; Firozjaei, H.K.; Toomanian, A. An integrated GIS-based Ordered Weighted Averaging analysis for solar energy evaluation in Iran: Current conditions and future planning. Renew. Energy 2019, 136, 1130–1146. [Google Scholar] [CrossRef]
- Qureshi, S.; Shorabeh, S.N.; Samany, N.N.; Minaei, F.; Homaee, M.; Nickravesh, F.; Firozjaei, M.K.; Arsanjani, J.J. A new integrated approach for municipal landfill siting based on urban physical growth prediction: A case study mashhad metropolis in Iran. Remote Sens. 2021, 13, 949. [Google Scholar] [CrossRef]
- Mijani, N.; Alavipanah, S.K.; Hamzeh, S.; Firozjaei, M.K.; Arsanjani, J.J. Modeling thermal comfort in different condition of mind using satellite images: An Ordered Weighted Averaging approach and a case study. Ecol. Indic. 2019, 104, 1–12. [Google Scholar] [CrossRef]
- Jelokhani-Niaraki, M.; Malczewski, J. A group multicriteria spatial decision support system for parking site selection problem: A case study. Land Use Policy 2015, 42, 492–508. [Google Scholar] [CrossRef]
- Tayyab, M.; Zhang, J.; Hussain, M.; Ullah, S.; Liu, X.; Khan, S.N.; Baig, M.A.; Hassan, W.; Al-Shaibah, B. Gis-based urban flood resilience assessment using urban flood resilience model: A case study of peshawar city, khyber pakhtunkhwa, pakistan. Remote Sens. 2021, 13, 1864. [Google Scholar] [CrossRef]
- Kaaviya, R.; Devadas, V. Water resilience mapping of Chennai, India using analytical hierarchy process. Ecol. Process. 2021, 10, 71. [Google Scholar] [CrossRef]
- He, Z.; Chen, H.; Yan, H.; Yin, Y.; Qiu, Q.; Wang, T. Scenario-based comprehensive assessment for community resilience adapted to fire following an earthquake, implementing the analytic network process and preference ranking organization method for enriched evaluation II techniques. Buildings 2021, 11, 523. [Google Scholar] [CrossRef]
- Xu, Z. An overview of methods for determining OWA weights. Int. J. Intell. Syst. 2005, 20, 843–865. [Google Scholar] [CrossRef]
- Nadizadeh Shorabeh, S.; Neysani Samani, N.; Jelokhani-Niaraki, M.R.J.-N. Determination of optimum areas for the landfill with emphasis on the urban expansion trend based on the combination of the Analytical Hierarchy Process and the Ordered Weighted Averaging model. J. Nat. Environ. 2017, 70, 949–969. [Google Scholar]
- Shorabeh, S.N.; Firozjaei, M.K.; Nematollahi, O.; Firozjaei, H.K.; Jelokhani-Niaraki, M. A risk-based multi-criteria spatial decision analysis for solar power plant site selection in different climates: A case study in Iran. Renew. Energy 2019, 143, 958–973. [Google Scholar] [CrossRef]
- Clements, A.C.; Pfeiffer, D.U.; Martin, V. Application of knowledge-driven spatial modelling approaches and uncertainty management to a study of Rift Valley fever in Africa. Int. J. Health Geogr. 2006, 5, 57. [Google Scholar] [CrossRef] [PubMed]
- Boroushaki, S.; Malczewski, J. Implementing an extension of the analytical hierarchy process using ordered weighted averaging operators with fuzzy quantifiers in ArcGIS. Comput. Geosci. 2008, 34, 399–410. [Google Scholar] [CrossRef]
- Rezvani, M.; Nickravesh, F.; Astaneh, A.D.; Kazemi, N. A risk-based decision-making approach for identifying natural-based tourism potential areas. J. Outdoor Recreat. Tour. 2022, 37, 100485. [Google Scholar] [CrossRef]
- Ozturk, D.; Kılıç-Gul, F. GIS-based multi-criteria decision analysis for parking site selection. Kuwait J. Sci. 2020, 47, 2–15. [Google Scholar]
- Aliniai, K.; Yarahmadi, A.; Zarin, J.Z.; Yarahmadi, H.; Lak, S.B. Parking lot site selection: An opening gate towards sustainable GIS-based urban traffic management. J. Indian Soc. Remote Sens. 2015, 43, 801–813. [Google Scholar] [CrossRef]
- Chen, H.; Wood, M.D.; Linstead, C.; Maltby, E. Uncertainty analysis in a GIS-based multi-criteria analysis tool for river catchment management. Environ. Model. Softw. 2011, 26, 395–405. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. GIS-multicriteria decision analysis for landslide susceptibility mapping: Comparing three methods for the Urmia lake basin, Iran. Nat. Hazards 2013, 65, 2105–2128. [Google Scholar] [CrossRef]
- Mokarram, M.; Pourghasemi, H.R.; Mokarram, M.J. A multi-criteria GIS-based model for wind farm site selection with the least impact on environmental pollution using the OWA-ANP method. Environ. Sci. Pollut. Res. 2022, 29, 43891–43912. [Google Scholar] [CrossRef]
- Chen, Y.; Paydar, Z. Evaluation of potential irrigation expansion using a spatial fuzzy multi-criteria decision framework. Environ. Model. Softw. 2012, 38, 147–157. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Donevska, K.R.; Mitrovski, C.D.; Frizado, J.P. Integrating multi-criteria evaluation techniques with geographic information systems for landfill site selection: A case study using ordered weighted average. Waste Manag. 2012, 32, 287–296. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Skilodimou, H.D.; Chousianitis, K.; Youssef, A.M.; Pradhan, B. Suitability estimation for urban development using multi-hazard assessment map. Sci. Total Environ. 2017, 575, 119–134. [Google Scholar] [CrossRef]
- Kaur, H.; Gupta, S.; Parkash, S.; Thapa, R. Application of geospatial technologies for multi-hazard mapping and characterization of associated risk at local scale. Ann. GIS 2018, 24, 33–46. [Google Scholar] [CrossRef]
- Araya-Muñoz, D.; Metzger, M.J.; Stuart, N.; Wilson, A.M.W.; Carvajal, D. A spatial fuzzy logic approach to urban multi-hazard impact assessment in Concepción, Chile. Sci. Total Environ. 2017, 576, 508–519. [Google Scholar] [CrossRef]
- Rahmati, O.; Yousefi, S.; Kalantari, Z.; Uuemaa, E.; Teimurian, T.; Keesstra, S.; Pham, T.D.; Tien Bui, D. Multi-hazard exposure mapping using machine learning techniques: A case study from Iran. Remote Sens. 2019, 11, 1943. [Google Scholar] [CrossRef]
- Mamdoohi, A.R.; Rezaei, H.; Irannezhad, E.; Saffarzadeh, A.; Abbasi, M. Hour and Period Based Congestion Pricing, Case of Tehran Mode Choice. Q. J. Transp. Eng. 2022, 14, 2233–2247. [Google Scholar] [CrossRef]
- Saffarzadeh, M.; Rezaei, H.; Majidi, M.Z. A Pricing Model for Freeway Tolls Based on the Share of Mode Shift, Route Shift, Travel Time Change and Users’ Willingness to Pay (Case study: Tehran_Saveh Freeway). J. Transp. Res. 2022, 19, 359–370. [Google Scholar]
- Rezaei, H.; Irannezhad, E.; Mamdoohi, A.R. Heterogeneous Analysis of Mode Choice Behavior Using Latent Class Model. J. Transp. Res. 2021, 18, 61–74. [Google Scholar] [CrossRef]
- Boloorani, A.D.; Kazemi, Y.; Sadeghi, A.; Shorabeh, S.N.; Argany, M. Identification of dust sources using long term satellite and climatic data: A case study of Tigris and Euphrates basin. Atmos. Environ. 2020, 224, 117299. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Z.; Tang, Z.; Zeng, G. A GIS-based spatial multi-criteria approach for flood risk assessment in the Dongting Lake Region, Hunan, Central China. Water Resour. Manag. 2011, 25, 3465–3484. [Google Scholar] [CrossRef]
- Saaty, T. The Analytic Hierarchy Process (AHP) for Decision Making; Kobe, Japan, 1980; p. 69. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Hierarchical analysis of behavior in competition: Prediction in chess. Behav. Sci. 1980, 25, 180–191. [Google Scholar] [CrossRef]
- Tripathi, A.K.; Agrawal, S.; Gupta, R.D. Comparison of GIS-based AHP and fuzzy AHP methods for hospital site selection: A case study for Prayagraj City, India. GeoJournal 2022, 87, 3507–3528. [Google Scholar] [CrossRef] [PubMed]
- Mallick, J. Municipal solid waste landfill site selection based on fuzzy-AHP and geoinformation techniques in Asir Region Saudi Arabia. Sustainability 2021, 13, 1538. [Google Scholar] [CrossRef]
- Saaty, T.L. An exposition of the AHP in reply to the paper “remarks on the analytic hierarchy process”. Manag. Sci. 1990, 36, 259–268. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Inconsistency and rank preservation. J. Math. Psychol. 1984, 28, 205–214. [Google Scholar] [CrossRef]
- Bakhshi Lomer, A.R.; Rezaeian, M.; Rezaei, H.; Lorestani, A.; Mijani, N.; Mahdad, M.; Raeisi, A.; Arsanjani, J.J. Optimizing Emergency Shelter Selection in Earthquakes Using a Risk-Driven Large Group Decision-Making Support System. Sustainability 2023, 15, 4019. [Google Scholar] [CrossRef]
- Malczewski, J.; Chapman, T.; Flegel, C.; Walters, D.; Shrubsole, D.; Healy, M.A. GIS–multicriteria evaluation with ordered weighted averaging (OWA): Case study of developing watershed management strategies. Environ. Plan. A 2003, 35, 1769–1784. [Google Scholar] [CrossRef]
- Mokarram, M.; Hojati, M. Using ordered weight averaging (OWA) aggregation for multi-criteria soil fertility evaluation by GIS (case study: Southeast Iran). Comput. Electron. Agric. 2017, 132, 1–13. [Google Scholar] [CrossRef]
- Zabihi, H.; Alizadeh, M.; Kibet Langat, P.; Karami, M.; Shahabi, H.; Ahmad, A.; Nor Said, M.; Lee, S. GIS Multi-Criteria Analysis by Ordered Weighted Averaging (OWA): Toward an integrated citrus management strategy. Sustainability 2019, 11, 1009. [Google Scholar] [CrossRef]
- Kazemi-Beydokhti, M.; Abbaspour, R.A.; Kheradmandi, M.; Bozorgi-Amiri, A. Determination of the physical domain for air quality monitoring stations using the ANP-OWA method in GIS. Environ. Monit. Assess. 2019, 191, 299. [Google Scholar] [CrossRef]
- Asadi, H.; Soffianian, A.; Hemami, M.-R.; Fakheran, S.; Akbari Feizabadi, H.; Corcoran, F. A hybrid GIS-OWA and DANP method for the identification and evaluation of ecotourism attractions: The case study of Abbas Abad Wildlife Refuge, Iran. GeoJournal 2022, 87, 5179–5196. [Google Scholar] [CrossRef]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Malczewski, J. Integrating multicriteria analysis and geographic information systems: The ordered weighted averaging (OWA) approach. Int. J. Environ. Technol. Manag. 2006, 6, 7–19. [Google Scholar] [CrossRef]

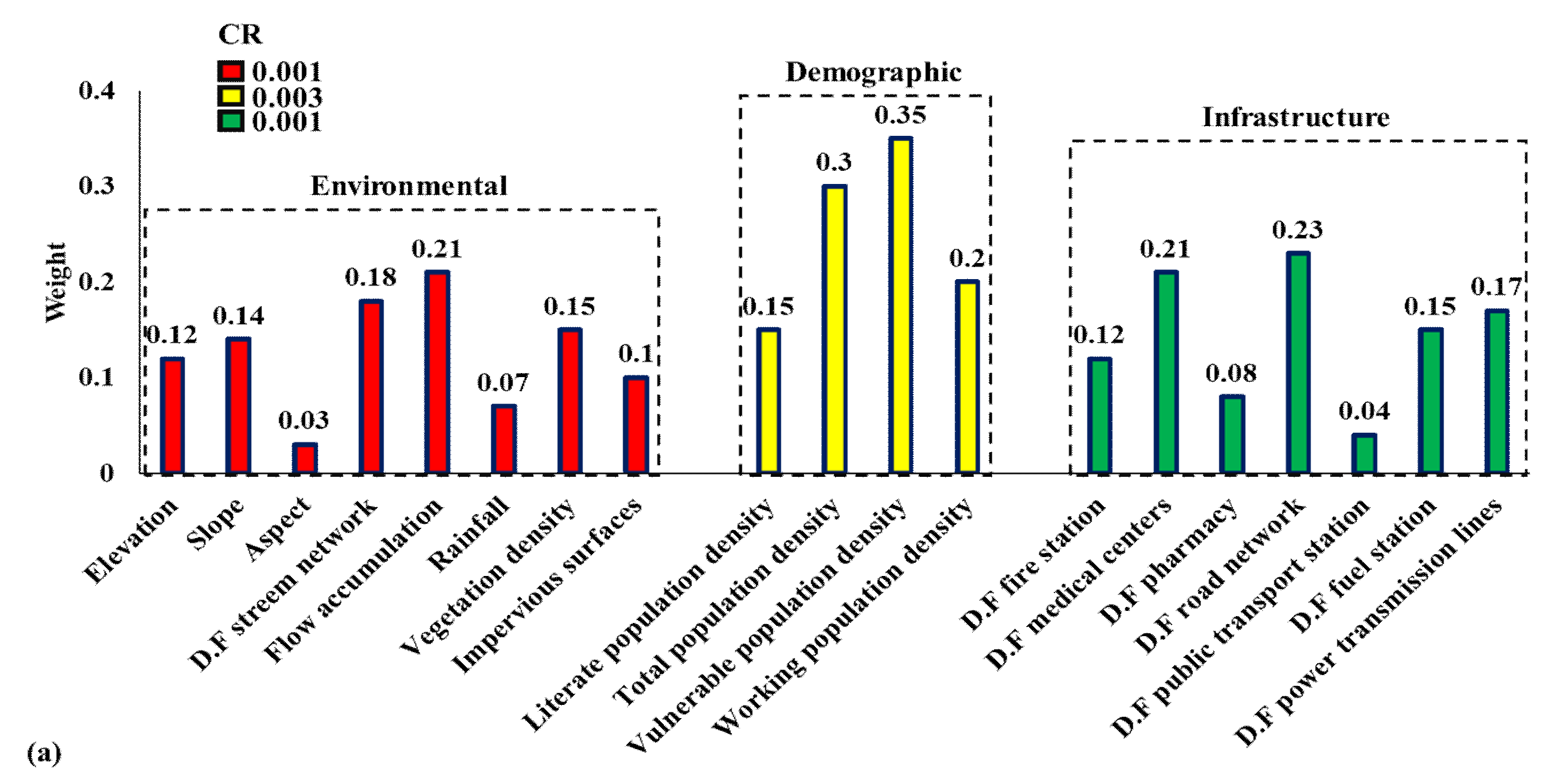
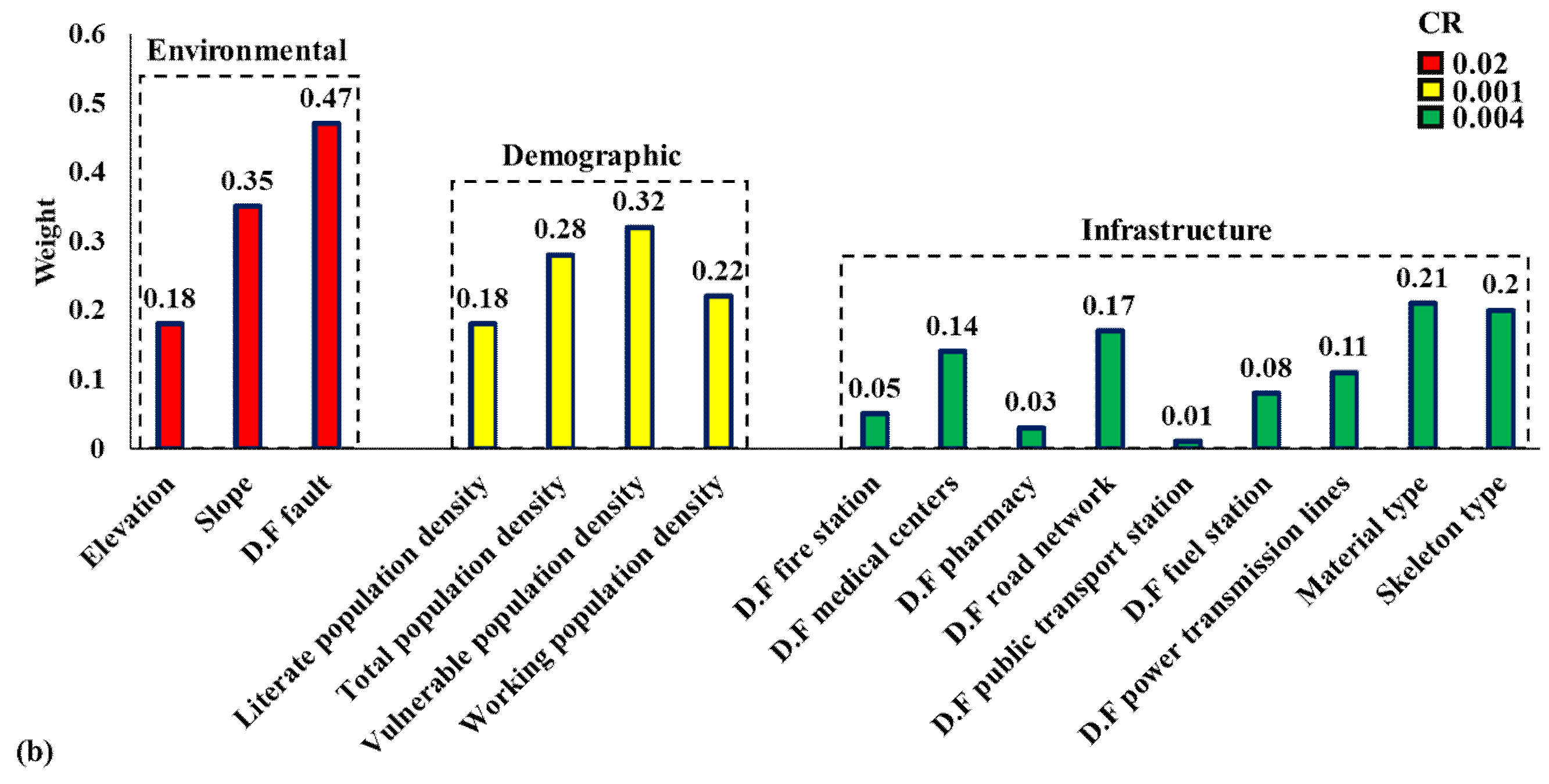



| Criterion | Sub-Criterion | Hazard Type | Format | Source |
|---|---|---|---|---|
| Environmental | Elevation | Flood/Earthquake | Raster | https://earthexplorer.usgs.gov/ (accessed on 25 December 2022) |
| Slope | Flood/Earthquake | Raster | Extracted from the Digital Elevation Model (DEM) | |
| Aspect | Flood | Raster | Extracted from the DEM | |
| Stream network | Flood | Vector | https://frw.ir/ (accessed on 18 November 2022) | |
| Flow accumulation | Flood | Raster | Extracted from the DEM | |
| Rainfall | Flood | Raster | https://wapor.apps.fao.org/ (accessed on 25 November 2022) | |
| Vegetation density | Flood | Raster | https://earthexplorer.usgs.gov/ (accessed on 25 November 2022) | |
| Impervious surfaces | Flood | Raster | https://earthexplorer.usgs.gov/ (accessed on 25 November 2022) | |
| Fault | Earthquake | Vector | https://gsi.ir/ (accessed on 18 November 2022) | |
| Demographic | Total population density | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 18 December 2022) |
| Vulnerable population density | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 18 December 2022) | |
| Working population density | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 18 December 2022) | |
| Literate population density | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 18 December 2022) | |
| Infrastructure | Power transmission lines | Flood/Earthquake | Vector | https://fa.ncc.gov.ir/ (accessed on 18 November 2022) |
| Fuel station | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 18 November 2022) | |
| Fire station | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 18 November 2022) | |
| Pharmacy | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 18 November 2022) | |
| Medical centers | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 05 November 2022) | |
| Road network | Flood/Earthquake | Vector | https://fa.ncc.gov.ir/ (accessed on 05 November 2022) | |
| Material type | Earthquake | Vector | https://www.tehran.ir/ (accessed on 05 November 2022) | |
| Skeleton type | Earthquake | Vector | https://www.tehran.ir/ (accessed on 05 November 2022) | |
| Public transport station | Flood/Earthquake | Vector | https://www.tehran.ir/ (accessed on 05 November 2022) |
| Scenarios | Very Low | Low | Moderate | High | Very High |
|---|---|---|---|---|---|
| Pessimistic | 1 | 8 | 18 | 31 | 42 |
| Neutral | 12 | 17 | 24 | 24 | 23 |
| Optimistic | 38 | 26 | 17 | 12 | 7 |
| Districts | Population Density | Pessimistic | Neutral | Optimistic |
|---|---|---|---|---|
| 1 | 10,270 | 2.716 | 48.298 | 99.235 |
| 2 | 14,999 | 0.975 | 21.397 | 55.791 |
| 3 | 11,986 | 0.010 | 10.531 | 47.347 |
| 4 | 15,710 | 0.090 | 22.507 | 68.240 |
| 5 | 15,337 | 1.531 | 19.753 | 52.506 |
| 6 | 12,643 | 0.006 | 0.018 | 3.310 |
| 7 | 20,374 | 0.000 | 0.000 | 0.000 |
| 8 | 35,806 | 0.000 | 0.000 | 0.137 |
| 9 | 9757 | 0.000 | 0.000 | 0.004 |
| 10 | 41,921 | 0.000 | 0.000 | 0.032 |
| 11 | 25,987 | 0.000 | 0.000 | 0.000 |
| 12 | 14,954 | 0.000 | 0.000 | 0.001 |
| 13 | 18,712 | 0.000 | 0.007 | 5.333 |
| 14 | 28,912 | 0.000 | 0.000 | 0.112 |
| 15 | 23,372 | 0.018 | 0.828 | 51.840 |
| 16 | 15,466 | 0.016 | 0.161 | 14.883 |
| 17 | 39,568 | 0.000 | 0.017 | 0.148 |
| 18 | 11,901 | 0.001 | 0.001 | 0.001 |
| 19 | 13,366 | 0.000 | 0.105 | 7.477 |
| 20 | 18,990 | 0.009 | 0.784 | 46.601 |
| 21 | 3887 | 0.000 | 0.688 | 16.370 |
| 22 | 3610 | 0.189 | 20.263 | 68.891 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaei, H.; Macioszek, E.; Derakhshesh, P.; Houshyar, H.; Ghabouli, E.; Bakhshi Lomer, A.R.; Ghanbari, R.; Esmailzadeh, A. A Spatial Decision Support System for Modeling Urban Resilience to Natural Hazards. Sustainability 2023, 15, 8777. https://doi.org/10.3390/su15118777
Rezaei H, Macioszek E, Derakhshesh P, Houshyar H, Ghabouli E, Bakhshi Lomer AR, Ghanbari R, Esmailzadeh A. A Spatial Decision Support System for Modeling Urban Resilience to Natural Hazards. Sustainability. 2023; 15(11):8777. https://doi.org/10.3390/su15118777
Chicago/Turabian StyleRezaei, Hamid, Elżbieta Macioszek, Parisa Derakhshesh, Hassan Houshyar, Elias Ghabouli, Amir Reza Bakhshi Lomer, Ronak Ghanbari, and Abdulsalam Esmailzadeh. 2023. "A Spatial Decision Support System for Modeling Urban Resilience to Natural Hazards" Sustainability 15, no. 11: 8777. https://doi.org/10.3390/su15118777







