Conflict Resolution Model of Automated Vehicles Based on Multi-Vehicle Cooperative Optimization at Intersections
Abstract
:1. Introduction
2. Related Work
3. Method
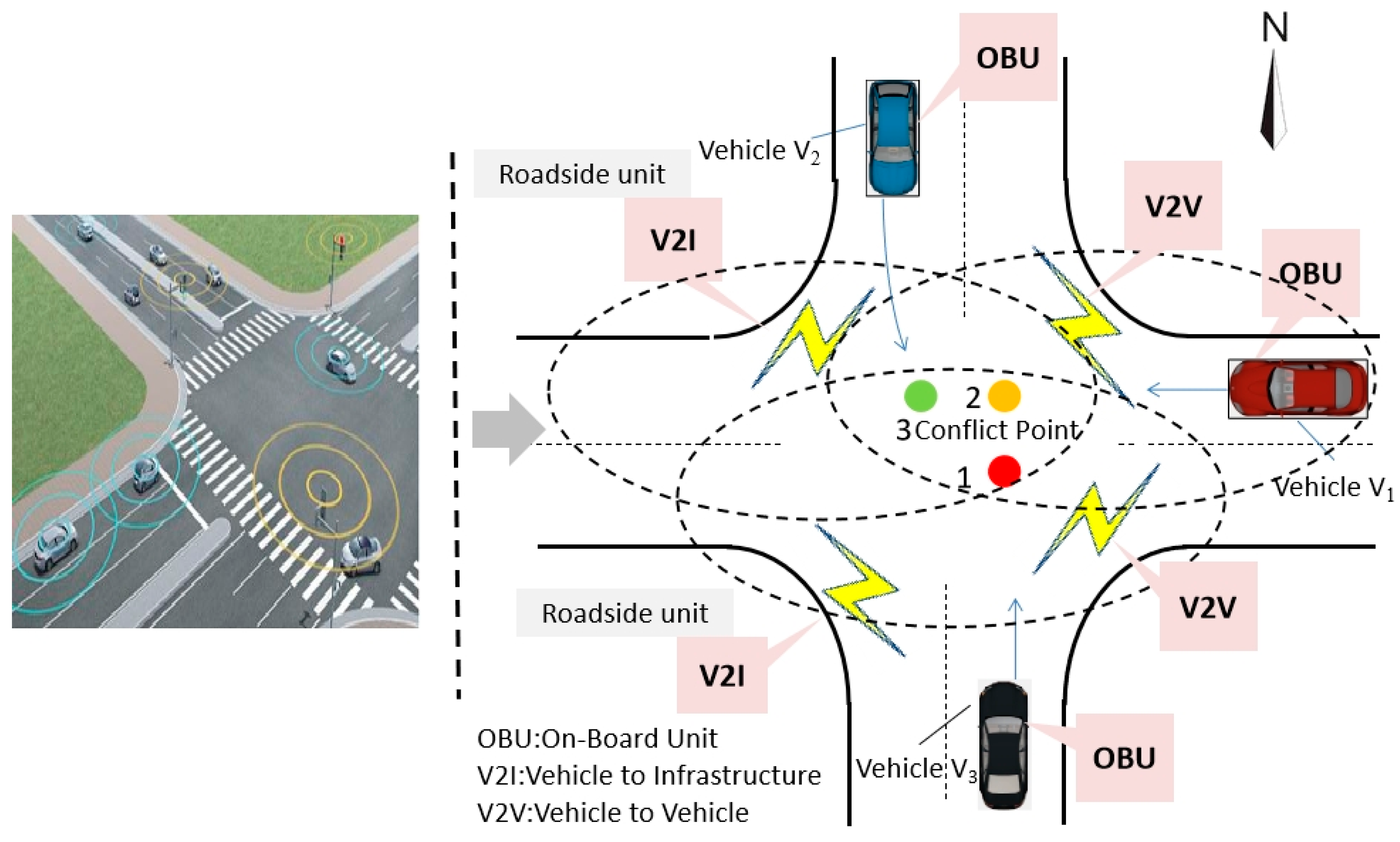
3.1. Vehicle Conflict Analysis
3.2. Decision-Making Process
3.3. Define Participants and Policies
3.4. Profit Indicators Selection
3.5. Model Objective Function
3.6. Model Solution
4. Results and Discussion
4.1. Simulation Scenarios
4.2. Results of Two-Vehicle Conflict
4.3. Results of Multi-Vehicle Conflict
4.4. The Results Analysis with Compared Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Aoude, G.S.; How, J.P. Using Support Vector Machines and Bayesian Filtering for Classifying Agent Intentions at Road Intersections; Technical Report ACL09-02; MIT Library: Cambridge, MA, USA, 2009; Available online: http://hdl.handle.net/1721.1/46720 (accessed on 10 February 2021).
- Wei, J.; Dolan, J.M.; Litkouhi, B. Autonomous vehicle social behavior for highway entrance ramp management. In Proceedings of the Intelligent Vehicles Symposium (IV), Broadbeach, Australia, 23–26 June 2013; pp. 201–207. [Google Scholar]
- Xiong, G.; Li, Y.; Wang, S.; Li, X.; Liu, P. HMM and HSS based social behavior of intelligent vehicles for freeway entrance ramp. Int. J. Control. Autom. 2014, 7, 79–90. [Google Scholar]
- Song, W.L.; Xiong, G.M.; Wang, S.Y.; Chen, H.Y. Decision making for intelligent vehicles based on driver type analyzing in an intersection. Trans. Beijing Inst. Technol. 2016, 36, 917–922. [Google Scholar]
- Kurt, A.; Yester, J.L.; Mochizuki, Y.; Özgüner, Ü. Hybrid-state driver/vehicle modelling, estimation andprediction. In Proceedings of the 13th International IEEE Annual Conference on Intelligent Transportation Systems, Madeira Island, Portugal, 19–22 September 2010; pp. 806–811. [Google Scholar]
- Correia, M.; Almeida, J.; Bartolomeu, P.C.; Fonseca, J.A.; Ferreira, J. Performance Assessment of Collective Perception Service Supported by the Roadside Infrastructure. Electronics 2022, 11, 347. [Google Scholar] [CrossRef]
- Abdelkader, G.; Elgazzar, K.; Khamis, A. Connected Vehicles: Technology Review, State of the Art, Challenges and Opportunities. Sensors 2021, 21, 7712. [Google Scholar] [CrossRef] [PubMed]
- Pang, W.; Gui, Y.; Yun, W.; Di, W. Cooperative active collision avoidance algorithm based on sliding mode control. J. Beijing Univ. Aeronaut. Astronaut. 2014, 40, 268–272. [Google Scholar]
- Levin, M.W.; Rey, D. Conflict-point formulation of intersection control for autonomous vehicles. Transp. Res. Part C Emerg. Technol. 2017, 85, 528–547. [Google Scholar]
- Fayazi, S.A.; Vahidi, A. Mixed integer linear programming for optimal scheduling of autonomous vehicle intersection crossing. IEEE Trans. Intell. Veh. 2018, 3, 287–299. [Google Scholar]
- Hideyuki, K. A merging-give way interaction model of cars in merging section: A game theoretic analysis. Transp. Res. Part A Policy Pract. 1999, 33, 305–312. [Google Scholar]
- Wang, M.; Hoogendoorn, S.P.; Daamen, W.; van Arem, B.; Happee, R. Game theoretic approach for predictive lane-changing and car-following control. Transp. Res. Part C 2015, 58, 73–92. [Google Scholar]
- Menendez-Romero, C.; Sezer, M.; Winkler, F.; Dornhege, C.; Burgard, W. Courtesy Behavior for Highly Automated Vehicles on Highway Interchanges. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV), Changshu, China, 26–30 June 2018. [Google Scholar]
- Nie, J.; Zhang, J.; Ding, W.; Wan, X.; Chen, X.; Ran, B. Decentralized Cooperative Lane-Changing Decision-Making for Connected Autonomous Vehicles. IEEE Access 2016, 4, 9413–9420. [Google Scholar] [CrossRef]
- Yang, Z.; Huang, H.; Wang, G.; Pei, X.; Yao, D.Y. Cooperative driving model for non-signalized intersections with cooperative games. J. Cent. South Univ. 2018, 25, 2164–2181. [Google Scholar]
- Elliott, D.; Keen, W.; Lei, M. Recent advances in connected and automated vehicles. J. Traffic Transp. Eng. 2019, 6, 7–29. [Google Scholar]
- Guan, Y.; Ren, Y.; Li, S.E.; Sun, Q.; Luo, L.; Li, K. Centralized Cooperation for Connected and Automated Vehicles at Intersections by Proximal Policy Optimization. IEEE Trans. Veh. Technol. 2020, 69, 12597–12608. [Google Scholar]
- Bashiri, M. Data-Driven Intersection Management Solutions for Mixed Traffic of Human-Driven and Connected and Automated Vehicles. arXiv 2012, arXiv:2012.05402. [Google Scholar]
- Ying, C.; Li, G.; Chen, X.M.; Zhao, Y. A driving game model for manned and unmanned vehicles at intersection. Trans. Beijing Inst. Technol. 2019, 9, 938–943. [Google Scholar]
- Aoude, G.S.; Luders, B.D.; Joseph, J.M.; Roy, N.; How, J.P. Problematically safe motion planning to avoid dynamic obstacles with uncertain motion patterns. Auton. Robot. 2013, 35, 51–76. [Google Scholar]
- Kim, C.; Langari, R. Game theory based autonomous vehicles operation. Int. J. Veh. Des. 2014, 65, 360–383. [Google Scholar]
- Li, S.E.; Xu, S.; Huang, X.; Cheng, B.; Peng, H. Eco-Departure of Connected Vehicles with V2X Communication at Signalized Intersections. IEEE Trans. Veh. Technol. 2015, 64, 5439–5449. [Google Scholar]
- Wang, Y.P.; Ge, G. Joint optimization of vehicle speed and traffic signals at a signalized intersection. Control Decis. 2019, 34, 2397–2405. [Google Scholar]








| Parameter | (m/s) | (m/s) | (m/s2) | (m/s2) | (m) | (m) | (m/s) | (m/s) | |
|---|---|---|---|---|---|---|---|---|---|
| Value | 16.7 | 0 | 2 | −2 | 140 | 125 | 13 | 10.5 | 0.4, 0.3, 0.3 |
| Parameter | (m) | (m) | (m/s) | (m) | (m) | (m/s) | (m) | (m) | (m/s) |
|---|---|---|---|---|---|---|---|---|---|
| Value | 200 | 180 | 16.7 | 150 | 160 | 13.3 | 140 | 100 | 11.1 |
| Conflict Resolution Strategy | Indicators | ||||||
|---|---|---|---|---|---|---|---|
| Average Revenue | Average Velocity (m/s) | Unreasonable Acceleration (m/s2) | Conflict Resolution Duration | Overall Revenue | |||
| Two-vehicle conflict | Cooperative driving | Vehicle C1 | 0.0880 | 14.024 | 2 | 18 | 0.1529 |
| Vehicle C2 | 0.0649 | 10.035 | 1 | ||||
| Non-cooperative driving | Vehicle C1 | 0.1279 | 9.060 | 1 | 22 | 0.1021 | |
| Vehicle C2 | −0.0258 | 12.250 | 0 | ||||
| Multi-vehicle conflict | Cooperative driving | Vehicle C1 | 0.1051 | 13.986 | 3 | 38 | 0.2332 |
| Vehicle C2 | 0.0846 | 16.972 | 1 | ||||
| Vehicle C3 | 0.0435 | 9.039 | 2 | ||||
| Non-cooperative driving | Vehicle C1 | −0.0859 | 14.879 | 4 | 45 | 0.1650 | |
| Vehicle C2 | 0.0971 | 12.989 | 0 | ||||
| Vehicle C3 | 0.1538 | 11.267 | 0 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Zhao, Y.; Zhang, R.; Gao, L. Conflict Resolution Model of Automated Vehicles Based on Multi-Vehicle Cooperative Optimization at Intersections. Sustainability 2022, 14, 3838. https://doi.org/10.3390/su14073838
Cheng Y, Zhao Y, Zhang R, Gao L. Conflict Resolution Model of Automated Vehicles Based on Multi-Vehicle Cooperative Optimization at Intersections. Sustainability. 2022; 14(7):3838. https://doi.org/10.3390/su14073838
Chicago/Turabian StyleCheng, Ying, Yanan Zhao, Rui Zhang, and Li Gao. 2022. "Conflict Resolution Model of Automated Vehicles Based on Multi-Vehicle Cooperative Optimization at Intersections" Sustainability 14, no. 7: 3838. https://doi.org/10.3390/su14073838







