Application of Acoustic Emission to Estimation of Strata Denudation: A Case Study from the Ordos Basin, China
Abstract
:1. Introduction
2. Analytical Methods
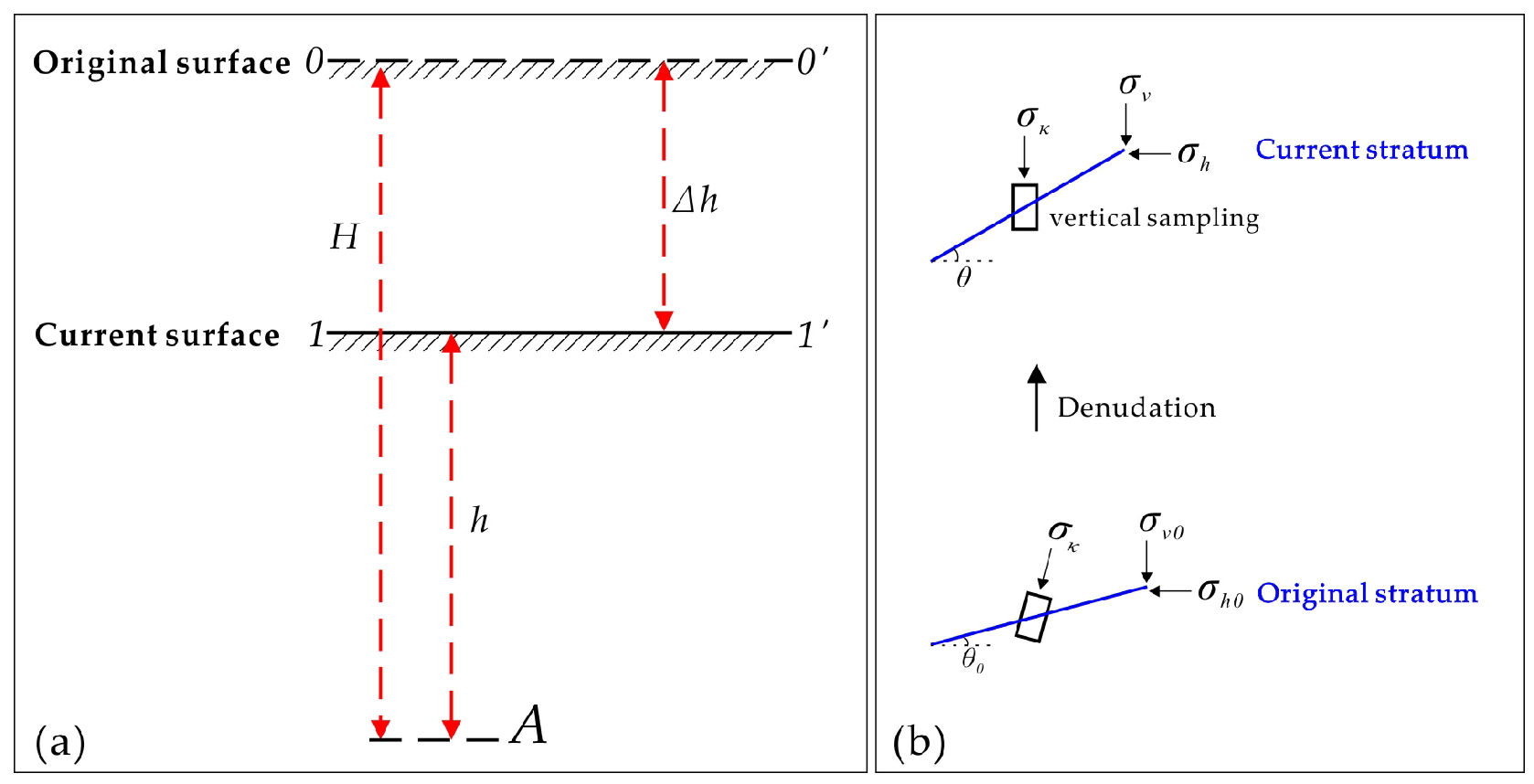
2.1. Principal of Acoustic Emission to Estimate the Denudation
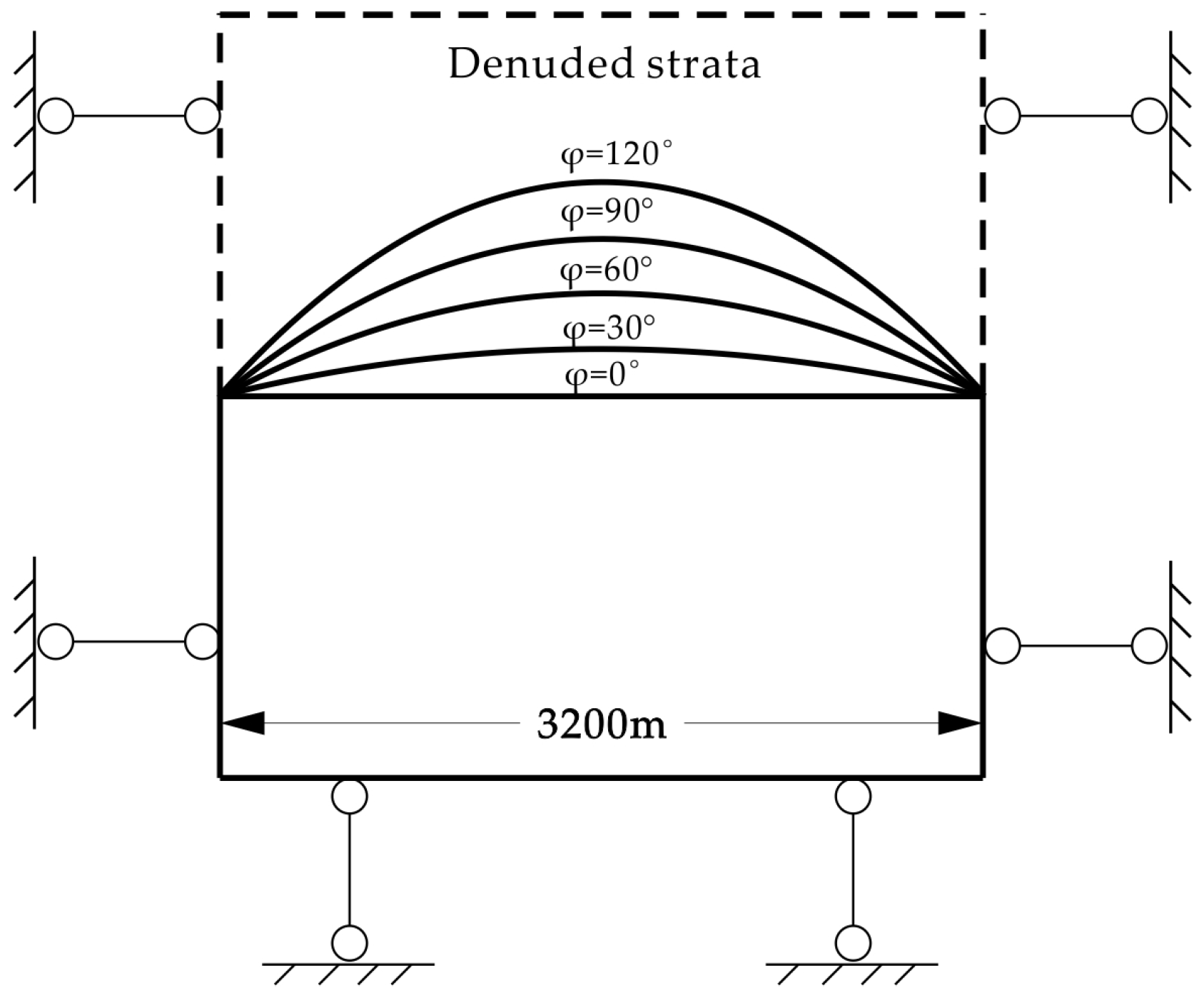
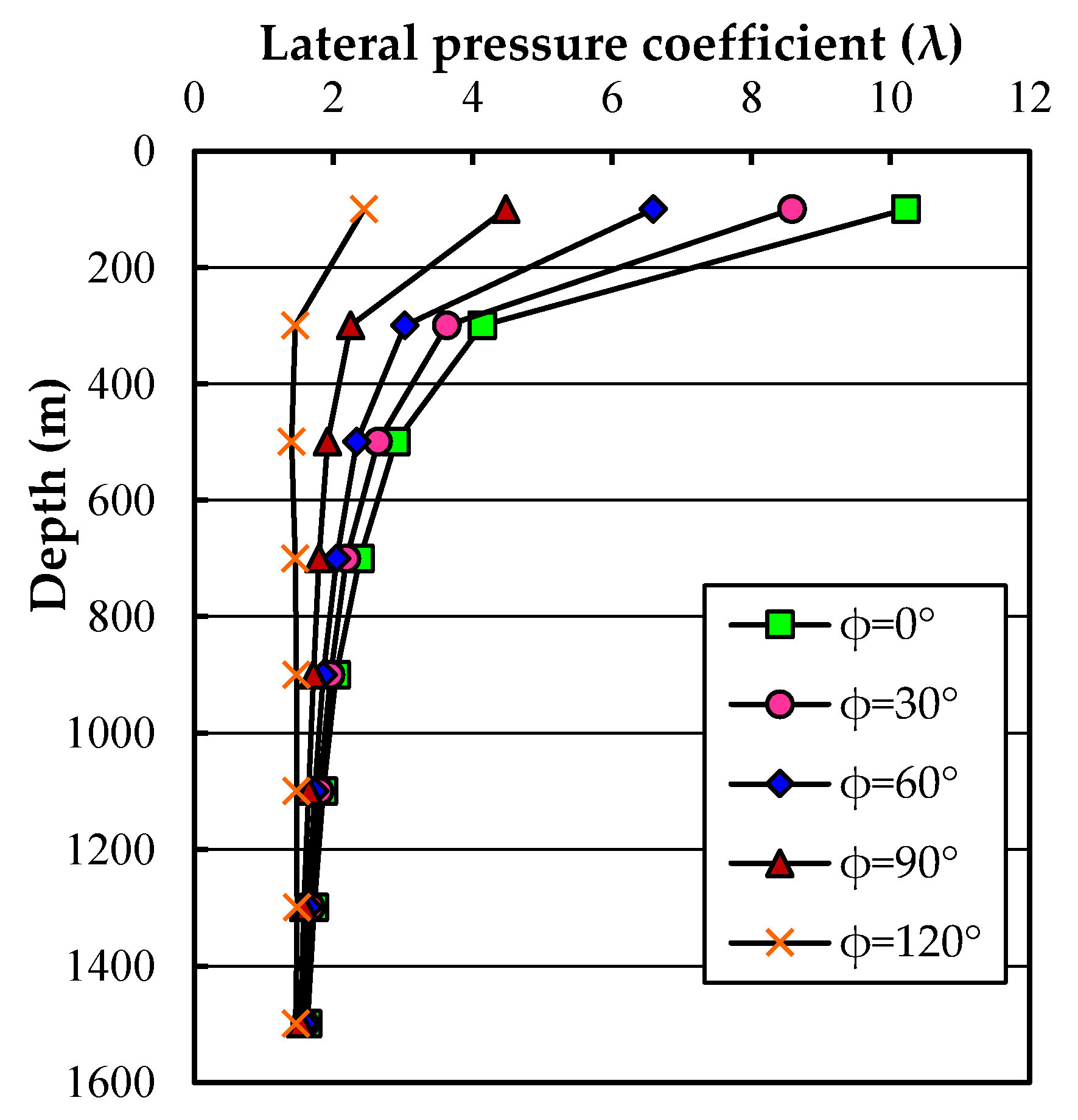
2.2. Influence of Stratum Denudation on In Situ Stress
3. Characteristics of the Study Area
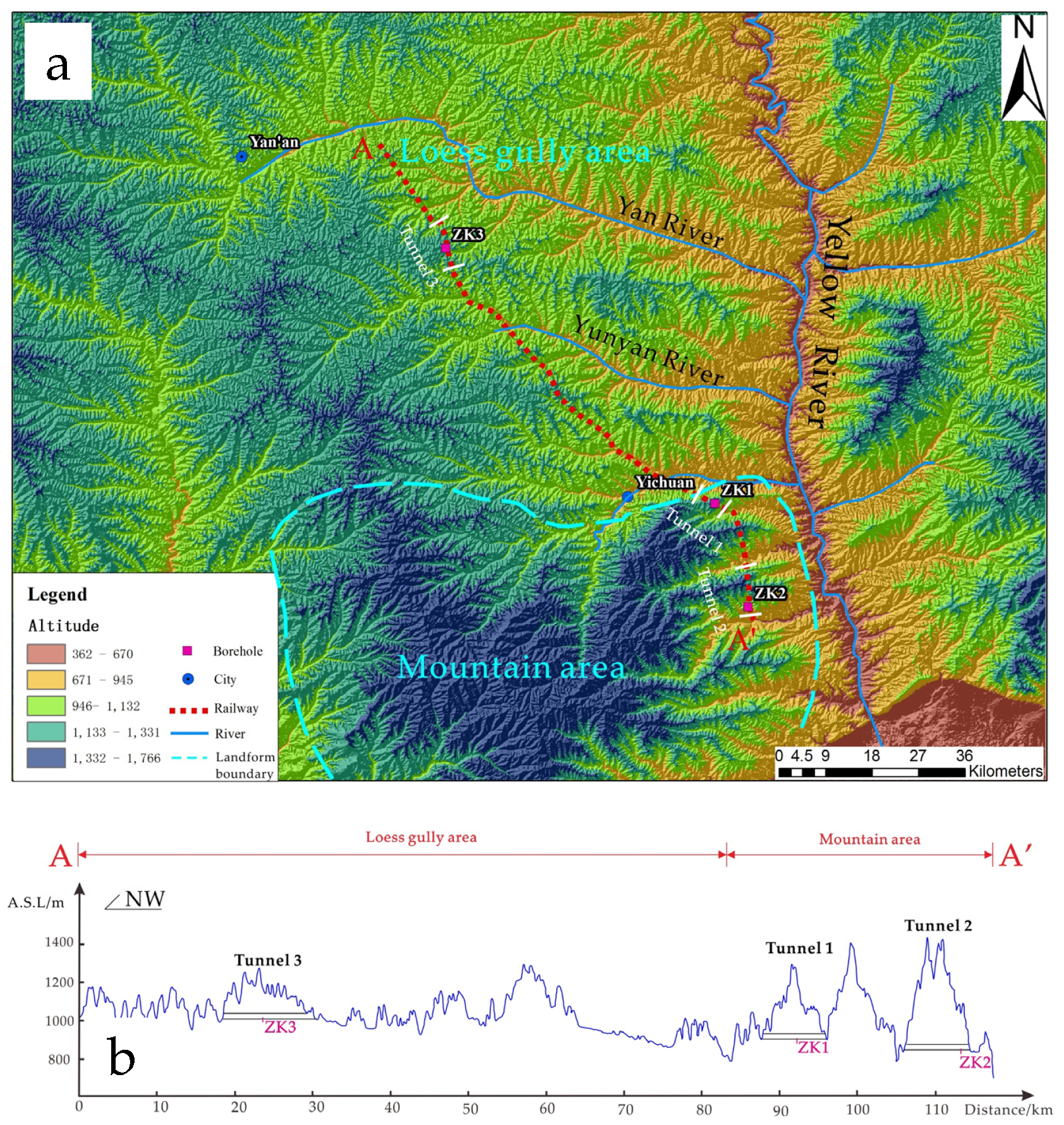
3.1. Geography and Tectonics
3.2. Engineering Situation
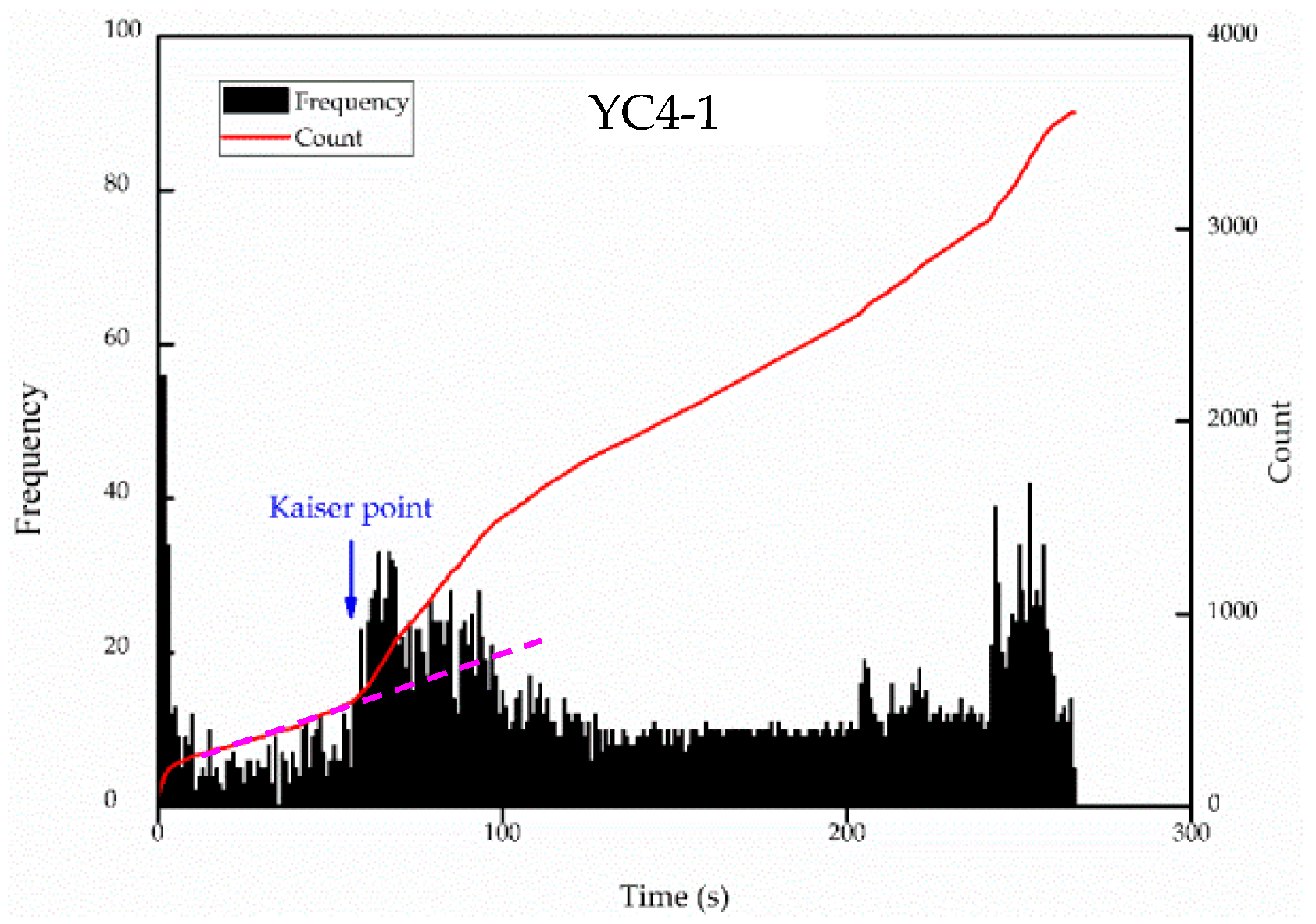
4. Sampling and Test Methods
5. Results and Discussion
5.1. Thickness of Denudation
5.2. Effect of Denudation on In Situ Stress
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hedberg, H.D. Relation of methane generation to undercompacted shales, shale diapirs, and mud volcanoes. AAPG Bull. 1974, 58, 661–673. [Google Scholar]
- Levine, J.R. Coalification: The Evolution of Coal as Source Rock and Reservoir Rock for Oil and Gas: Chapter 3; AAPG: Tulsa, OK, USA, 1993. [Google Scholar]
- Littke, R.; Urai, J.L.; Uffmann, A.K.; Risvanis, F. Reflectance of dispersed vitrinite in Palaeozoic rocks with and without cleavage: Implications for burial and thermal history modeling in the Devonian of Rursee area, northern Rhenish Massif, Germany. Int. J. Coal Geol. 2012, 89, 41–50. [Google Scholar] [CrossRef]
- Tissot, B.; Durand, B.; Espitalie, J.; Combaz, A. Influence of nature and diagenesis of organic matter in formation of petroleum. AAPG Bull. 1974, 58, 499–506. [Google Scholar]
- de Souza, V.L.; Rodrigues, K.R.; Pedroza, E.H.; Melo, R.T.d.; Lima, V.L.d.; Hazin, C.A.; de Almeida, M.G.; Nascimento, R.K.D. Sedimentation Rate and 210Pb Sediment Dating at Apipucos Reservoir, Recife, Brazil. Sustainability 2012, 4, 2419–2429. [Google Scholar] [CrossRef] [Green Version]
- Galloway, W.E. Genetic stratigraphic sequences in basin analysis I: Architecture and genesis of flooding-surface bounded depositional units. AAPG Bull. 1989, 73, 125–142. [Google Scholar]
- Guidish, T.; Kendall, C.S.C.; Lerche, I.; Toth, D.; Yarzab, R. Basin evaluation using burial history calculations: An overview. AAPG Bull. 1985, 69, 92–105. [Google Scholar]
- Van Hinte, J. Geohistory analysis--application of micropaleontology in exploration geology. AAPG Bull. 1978, 62, 201–222. [Google Scholar]
- Bierman, P.; Steig, E.J. Estimating rates of denudation using cosmogenic isotope abundances in sediment. Earth Surf. Process. Landf. 1996, 21, 125–139. [Google Scholar] [CrossRef]
- Dow, W.G. Kerogen studies and geological interpretations. J. Geochem. Explor. 1977, 7, 79–99. [Google Scholar] [CrossRef]
- Gallagher, K. Evolving temperature histories from apatite fission-track data. Earth Planet. Sci. Lett. 1995, 136, 421–435. [Google Scholar] [CrossRef]
- Katz, B.; Pheifer, R.; Schunk, D. Interpretation of discontinuous vitrinite reflectance profiles. AAPG Bull. 1988, 72, 926–931. [Google Scholar]
- Yin, T. A multi-information method for computing erosional thickness. Pet. Explor. Dev. 1992, 19, 42–47. [Google Scholar]
- Magara, K. Compaction and Fluid Migration; Elsevier: Amsterdam, The Netherlands, 1978; Volume 9. [Google Scholar]
- Chen, R.; Luo, X.; Chen, Z.; Yu, J.; Yang, Y. Restoration of burial history of four periods in Ordos Basin. Acta Pet. Sin. 2006, 27, 43–47. [Google Scholar]
- Liu, W.; Qin, M.; Qi, F.; Xiao, S.; Wang, Z. Analysis on the Meso-Neozoic subsidence and uplift history of the periphery of Ordos basin using apatite fission track. Uranium Geol. 2008, 24, 221–227. [Google Scholar]
- Ren, Z.; Zhang, S.; Gao, S.; Cui, J.; Xiao, Y.; Xiao, H. Tectonic thermal history and its significance on the formation of oil and gas accumulation and mineral deposit in Ordos Basin. Sci. China Ser. D Earth Sci. 2007, 50, 27–38. [Google Scholar] [CrossRef]
- Goodman, R.E. Subaudible noise during compression of rocks. Geol. Soc. Am. Bull. 1963, 74, 487–490. [Google Scholar] [CrossRef]
- Haider, M.F.; Giurgiutiu, V. A Helmholtz Potential Approach to the Analysis of Guided Wave Generation During Acoustic Emission Events. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2018, 1, 021002. [Google Scholar] [CrossRef]
- Haider, M.F.; Giurgiutiu, V. Analysis of axis symmetric circular crested elastic wave generated during crack propagation in a plate: A Helmholtz potential technique. Int. J. Solids Struct. 2018, 134, 130–150. [Google Scholar] [CrossRef]
- Hamstad, M. Frequencies and amplitudes of AE signals in a plate as a function of source rise time. In Proceedings of the 29th European Conference on Acoustic Emission Testing, Vienna, Austria, 8–10 September 2010; pp. 8–10. [Google Scholar]
- Lavrov, A. The Kaiser effect in rocks: Principles and stress estimation techniques. Int. J. Rock Mech. Min. Sci. 2003, 40, 151–171. [Google Scholar] [CrossRef]
- Zelenyak, A.-M.; Hamstad, M.A.; Sause, M.G. Modeling of acoustic emission signal propagation in waveguides. Sensors 2015, 15, 11805–11822. [Google Scholar] [CrossRef]
- Kaiser, J. Erkenntnisse und Folgerungen aus der Messung von Geräuschen bei Zugbeanspruchung von metallischen Werkstoffen. Arch. Eisenhüttenwes. 1953, 24, 43–45. [Google Scholar] [CrossRef]
- Kurita, K.; Fujii, N. Stress memory of crystalline rocks in acoustic emission. Geophys. Res. Lett. 1979, 6, 9–12. [Google Scholar] [CrossRef]
- Sun, B.; Ding, Y.; Shao, Z.; Zhou, X.; Wang, X. Application of acoustic emission technique in determination of fossil and present-day stresses in oil fields. J. Geomech. 1996, 2, 11–17. [Google Scholar]
- Xu, J.; Dai, J. Application of acoustic emission in the study of the number of Cenozoic tectonic phases in the Dongying Subbasin. J. Geomech. 2004, 10, 172–178. [Google Scholar]
- Yuanchen, D. Discussion on paleostress measurement by AE method. J. Geomech. 2000, 6, 45–52. [Google Scholar]
- Michihiro, K.; Fujiwara, T.; Yoshioka, H. Study on estimating geostresses by the Kaiser effect of AE. In Proceedings of the 26th US Symposium on Rock Mechanics (USRMS), Shanghai, China, 26–28 May 2006. [Google Scholar]
- Brown, E.; Hoek, E. Trends in relationships between measured in-situ stresses and depth. Int. J. Rock Mech. Min. Sci. 1975, 211–215. [Google Scholar] [CrossRef]
- Jing, F.; Sheng, Q.; Zhang, Y.; Luo, C.; Liu, Y. Research on distribution rule of shallow crustal geostress in China mainland. Chin. J. Rock Mech. Eng. 2007, 26, 2056–2062. [Google Scholar]
- Zhang, H.; He, Z.; Jin, X.; Zhang, P.; Meng, Z. Tectonic Evolution and Coal Accumulation of the Ordos Basin; Geological Publishing House: Beijing, China, 2005. [Google Scholar]
- Dai, J.; Li, J.; Luo, X.; Zhang, W.; Hu, G.; Ma, C.; Guo, J.; Ge, S. Stable carbon isotope compositions and source rock geochemistry of the giant gas accumulations in the Ordos Basin, China. Organ. Geochem. 2005, 36, 1617–1635. [Google Scholar] [CrossRef]
- Jiang, Z.; Mao, Z.; Shi, Y.; Wang, D. Multifractal Characteristics and Classification of Tight Sandstone Reservoirs: A Case Study from the Triassic Yanchang Formation, Ordos Basin, China. Energies 2018, 11, 2242. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Guo, Z.; Zhang, D. Sedimentary response of regional tectonic transformation in Late Triassic Yanchang period at the central and southern Ordos Basin. Earth Sci. Front. 2015, 22, 194–204. [Google Scholar]
- Huang, J. On Major Tectonic Forms of China; National Geological Survey of China under the Ministry of Economic Affairs: Taipei, Taiwan, 1945.
- Yang, Y.; Li, W.; Ma, L. Tectonic and stratigraphic controls of hydrocarbon systems in the Ordos basin: A multicycle cratonic basin in central China. AAPG Bull. 2005, 89, 255–269. [Google Scholar] [CrossRef]
- Li, S. Vortex structure and other problems relating to the compounding of geotectonic systems of northwestern China. Acta Geol. Sin. 2014, 34, 339–410. [Google Scholar]
- Zhao, M.; Behr, H.-J. Vitrinite reflectance in Triassic with relation to geothermal history of Ordos Basin. Acta Pet. Sin. 2007, 17, 15–23. [Google Scholar]
- Liu, C.; Zhao, H.; Wang, F. Attributes of the Mesozoic structure on the west margin of the Ordos Basin. Acta Geol. Sin. 2005, 79, 737–747. [Google Scholar]
- CRSRI. Menghua Railway In-Situ Stress Test Report; Changjiang River Scientific Research Institute of Changjiang Water Resources Commission: Wuhan, China, 2018. [Google Scholar]
- Yoshikawa, S.; Mogi, K. Experimental studies on the effect of stress history on acoustic emission activity—A possibility for estimation of rock stress. J. Acoust. Emiss. 1989, 8, 113–123. [Google Scholar]



| Site No. | Buried Depth | σH | σh | σv | λ=σH/σv | αH |
|---|---|---|---|---|---|---|
| /m | /MPa | /MPa | /MPa | /° | ||
| ZK1 | 290 | 12.9–15.8 | 7.4–9.4 | 7.8–8.8 | 1.7–1.9 | N79°E |
| ZK2 | 110 | 4.9–6.5 | 2.7–4.9 | 3.2–3.9 | 1.5–1.9 | N75°E |
| ZK3 | 180 | 13.4–15.9 | 8.7–9.6 | 4.9–5.9 | 2.6–2.8 | N74°E |
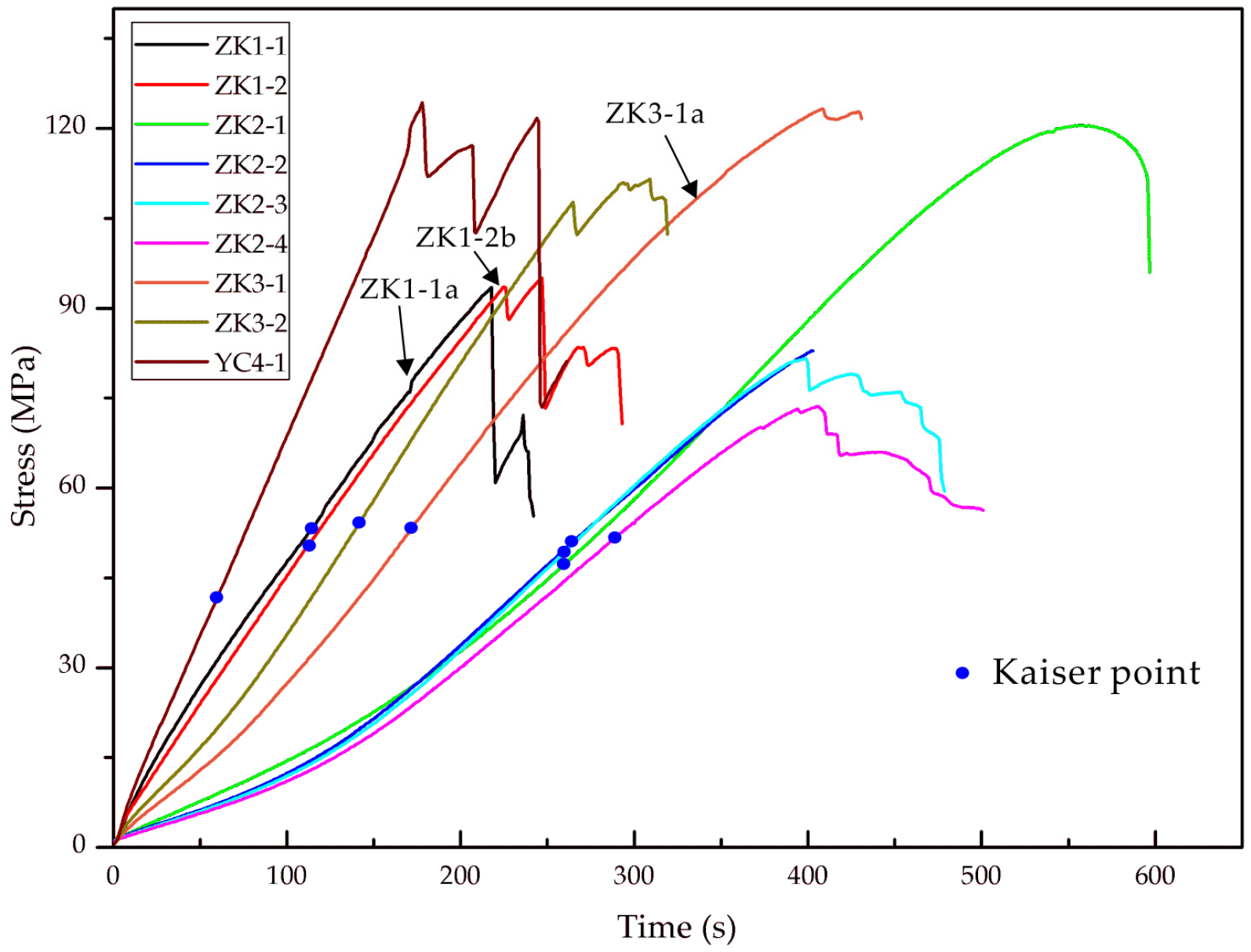
| Sample ID | Kaiser Point /s | Memorized Stress /MPa | H /m | h /m | Δh /m | Average Δh /m |
|---|---|---|---|---|---|---|
| ZK1-1 | 115 | 53.3 | 1977.8 | 290.0 | 1687.8 | 1608.1 |
| ZK1-2 | 109 | 49.1 | 1818.5 | 1528.5 | ||
| ZK2-1 | 260 | 50.0 | 1851.9 | 135.0 | 1716.9 | 1722.4 |
| ZK2-2 | 265 | 50.6 | 1874.1 | 1739.1 | ||
| ZK2-3 | 260 | 45.0 | 1666.7 | 1531.7 | ||
| ZK2-4 | 290 | 55.0 | 2037.0 | 1902.0 | ||
| ZK3-1 | 172 | 53.4 | 1977.8 | 200.0 | 1727.8 | 1794.4 |
| ZK3-2 | 142 | 54.3 | 2011.1 | 1761.1 | ||
| YC4-1 | 60 | 42.5 | 1574.1 | 0.0 | 1574.1 | 1574.1 |
| Methods | Geological Ages | Values/m |
|---|---|---|
| Vitrinite reflectance [17] | Middle Jurassic | 1800–2000 |
| Stratigraphic comparison [15] | Late Cretaceous | 1600–1800 |
| Apatite fission track [16] | Late Cretaceous | 1500–2000 |
| Acoustic emission (this study) | Late Cretaceous | 1574–1794 |
| Site ID | Depth /m | λ | λ′ |
|---|---|---|---|
| ZK1 | 310 | 4.0 | 1.7–1.9 |
| ZK2 | 135 | 8.3 | 1.5–1.9 |
| ZK3 | 200 | 6.1 | 2.6–2.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, S.; Shang, Y.; Li, Y. Application of Acoustic Emission to Estimation of Strata Denudation: A Case Study from the Ordos Basin, China. Sustainability 2019, 11, 861. https://doi.org/10.3390/su11030861
Wei S, Shang Y, Li Y. Application of Acoustic Emission to Estimation of Strata Denudation: A Case Study from the Ordos Basin, China. Sustainability. 2019; 11(3):861. https://doi.org/10.3390/su11030861
Chicago/Turabian StyleWei, Siyu, Yanjun Shang, and Yanyan Li. 2019. "Application of Acoustic Emission to Estimation of Strata Denudation: A Case Study from the Ordos Basin, China" Sustainability 11, no. 3: 861. https://doi.org/10.3390/su11030861




