Improvement of Ecological Footprint Model in National Nature Reserve Based on Net Primary Production (NPP)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
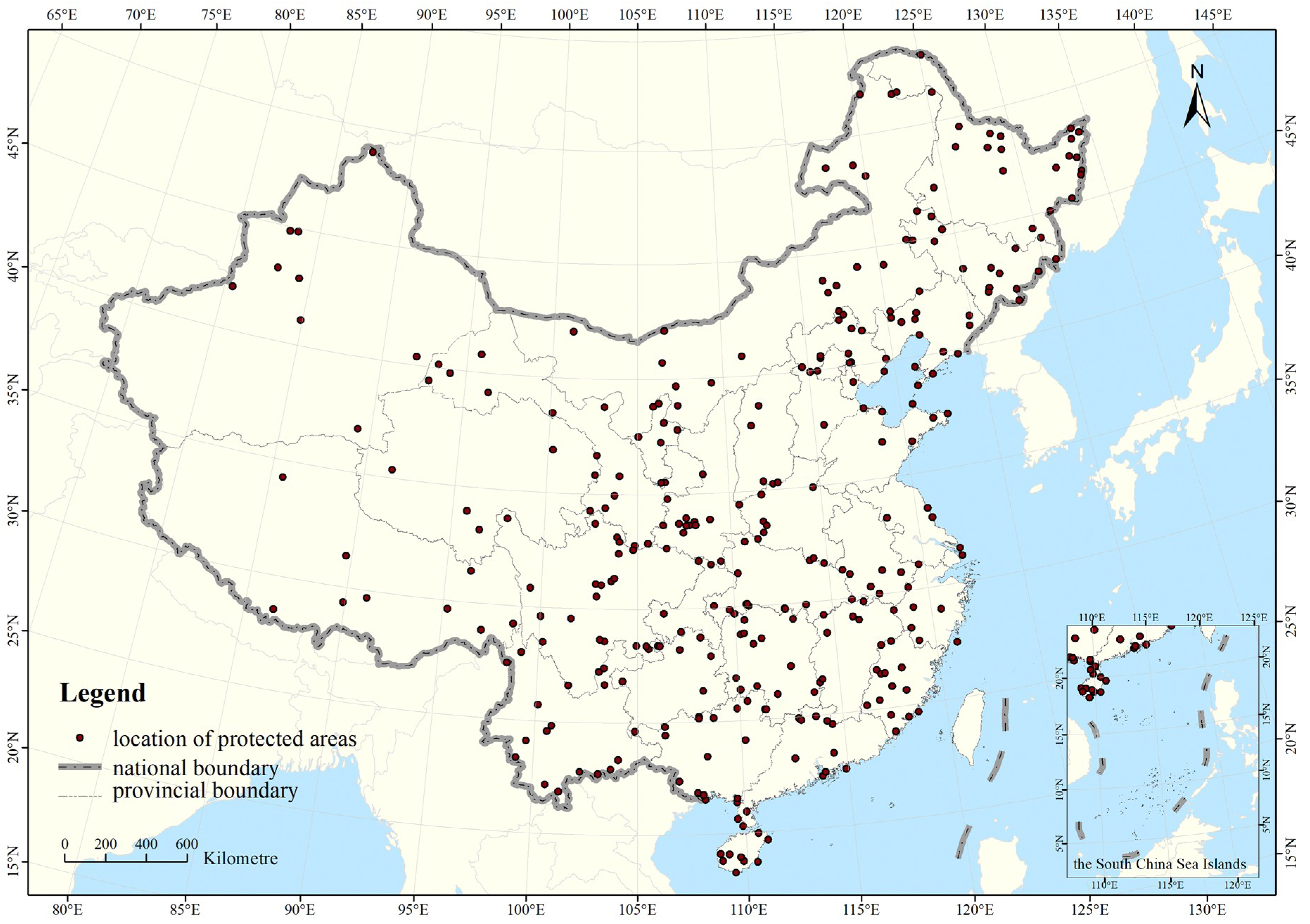
2.1.1. Nature Reserve Data
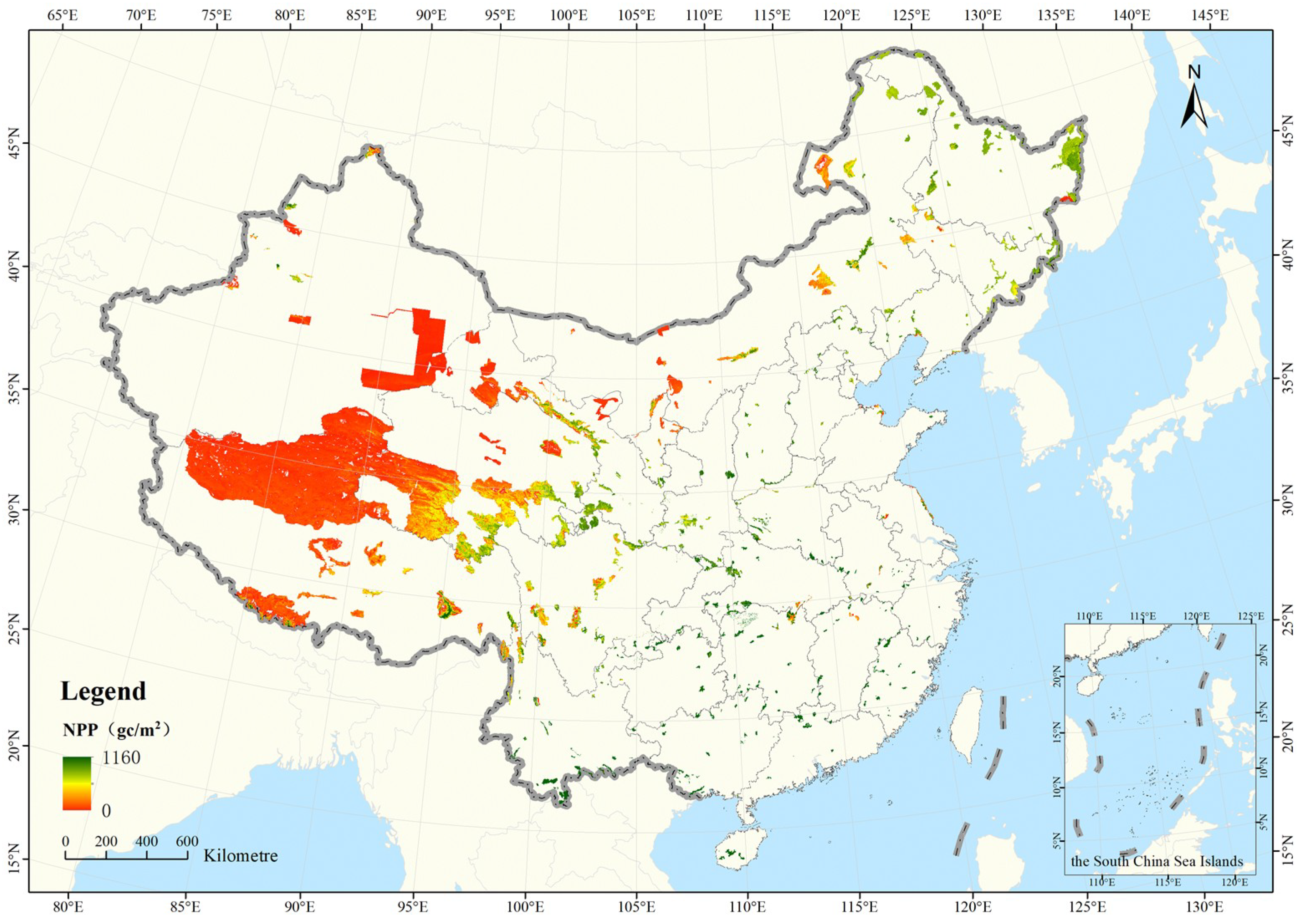
2.1.2. NPP Data
2.2. Methods
2.2.1. NPP Estimation Model
2.2.2. Improvement of the EF-NPP Model
2.2.3. Establishment of Equivalence Factor and Yield Factor in EF-GAEZ
2.2.4 Average Ecological Footprint Model
2.2.5. Calculation of the Average Ecological Footprint in the National Wilderness Preservation System
2.2.6. Correlation Analysis Method
3. Result and Analysis
3.1. Acquisition of NPP at National Nature Reserves
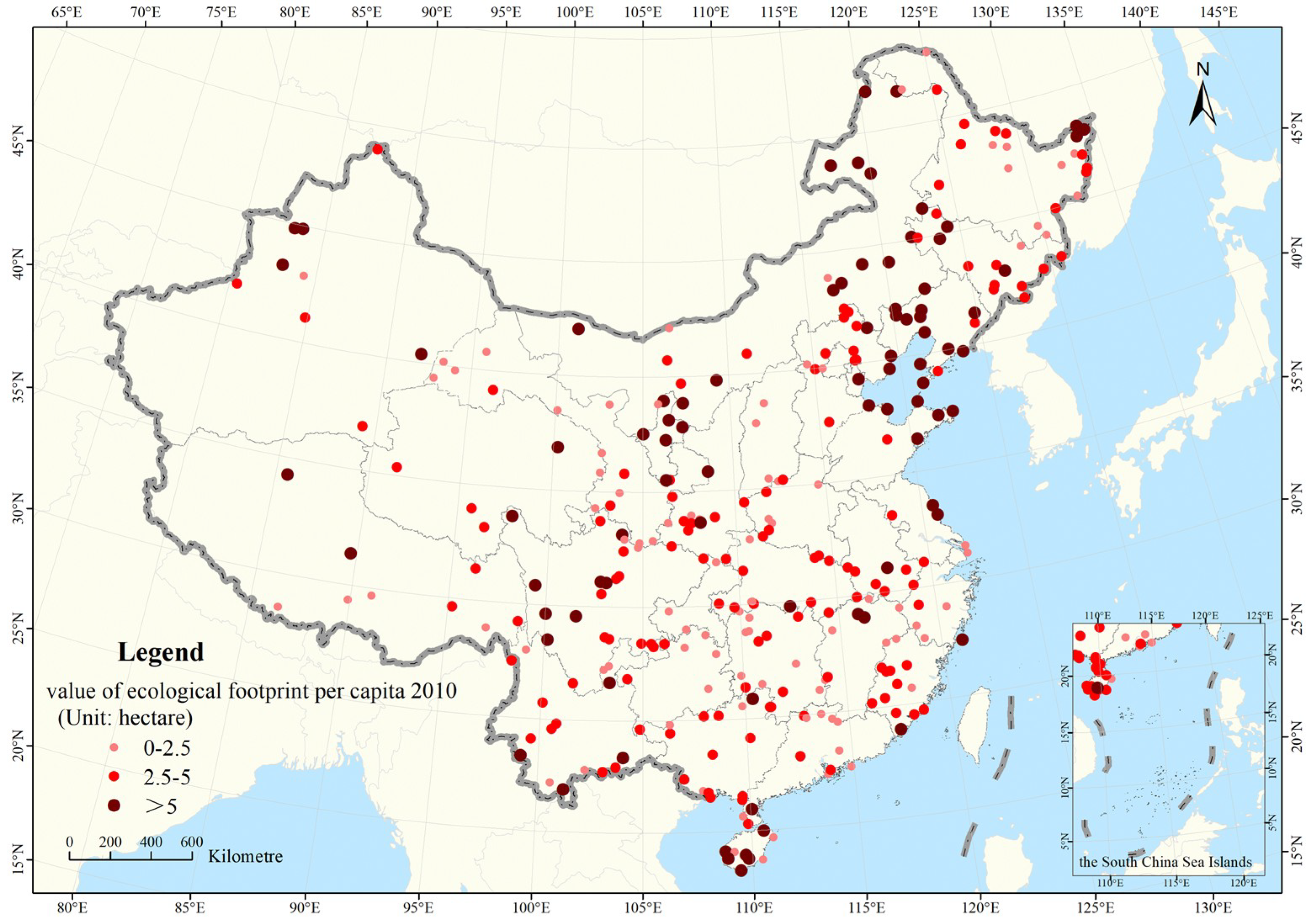
3.2. Spatial Distribution of Average Ecological Footprint in National Nature Reserves
3.3. Comparison of Equivalence Factor and Yield Factors in the EF-GAEZ Model and EF-NP Model
3.3.1. Equivalence Factor Comparison
3.3.2. Comparison of Yield Factors
3.4. Correlation Analysis of the Ecological Footprint per Capita between the EF-GAEZ and EF-NPP Models
3.4.1. Correlation Analysis of Ecological Footprint per Capita in 2000
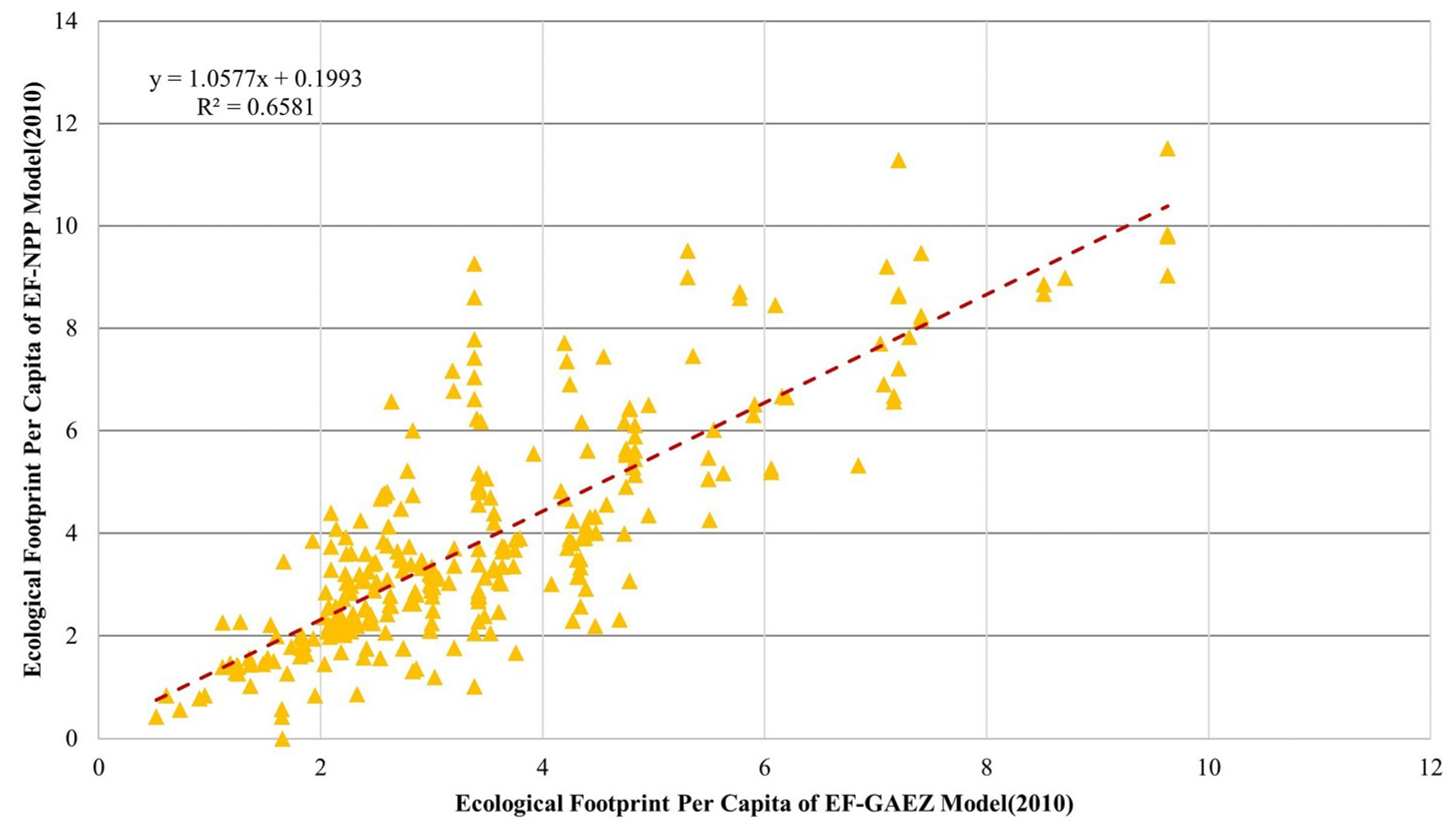
3.4.2. Correlation Analysis of the per Capita Ecological Footprint in 2010
3.5. Consistency Analysis of Ecological Footprint per Capita between the EF-GAEZ and EF-NPP Models
3.5.1. Comparison of the Ecological Footprint per Capita in 2000
3.5.2. Comparison of the Ecological Footprint per Capita in 2010
4. Discussion
4.1. Uncertainty and Sensitivity Analysis
4.2. The Advantage of the EF-NPP Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ciftcioglu, G.C. Revealing major terrestrial- and marine species-based provisioning ecosystem services provided by the socio-ecological production landscapes and seascapes of Lefke Region in North Cyprus. Environ. Dev. Sustain. 2018, 20, 197–221. [Google Scholar] [CrossRef]
- Fan, M.M.; Li, W.J. Research progress and debate on the theory of payment for ecosystem services: Based on the relationship between ecology and society. China Popul. Resour. Environ. 2017, 27, 137. [Google Scholar] [CrossRef]
- Holden, E.; Linnerud, K. The sustainable development area: Satisfying basic needs and safeguarding ecological sustainability. Sustain. Dev. 2010, 15, 174–187. [Google Scholar] [CrossRef]
- Velis, M.; Conti, K.I.; Biermann, F. Groundwater and human development: Synergies and trade-offs within the context of the sustainable development goals. Sustain. Sci. 2017, 12, 1007–1017. [Google Scholar] [CrossRef]
- Wood, S.L.; Jones, S.K.; Johnson, J.A.; Brauman, K.A.; Chaplin-Kramer, R.; Fremier, A.; Girvetz, E.; Gordon, L.J.; Kappel, C.V.; Mandle, L.; et al. Distilling the role of ecosystem services in the Sustainable Development Goals. Ecosyst. Serv. 2018, 29, 70–82. [Google Scholar] [CrossRef]
- Zagonari, F. Using ecosystem services in decision-making to support sustainable development: Critiques, model development, a case study, and perspectives. Sci. Total Environ. 2016, 548, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Osio, N.; Yanagihara, K.; Tani, Y. A Study on On-the-Machine Tool Re-Generation Technology: Process development for grinding tools with rapid baking system(Grinding technology). Nat. Genet. 2017, 10, 188–195. [Google Scholar] [CrossRef]
- Boucher, M.; Turcotte, N.; Guillemette, V.; Lantagne, G.; Chapotot, A.; Pourcelly, G.; Sandeaux, R.; Gavach, C. Recovery of spent acid by electrodialysis in the zinc hydrometallurgy industry: Performance study of different cation-exchange membranes. Hydrometallurgy 2018, 45, 137–160. [Google Scholar] [CrossRef]
- Fairhurst, C.W.; Ryge, G. The effectiveness of China’s National Forest Protection Program and National-level Nature Reserves, 2000 to 2010: PREPRINT. Biorxiv 2013. [Google Scholar] [CrossRef]
- Wang, L.; Pan, Y.; Cao, Y.; Li, B.; Wang, Q.; Wang, B.; Pang, W.; Zhang, J.; Zhu, Z.; Deng, G. Detecting early signs of environmental degradation in protected areas: An example of Jiuzhaigou Nature Reserve, China. Ecol. Indicat. 2018, 91, 287–298. [Google Scholar] [CrossRef]
- Senczyno, M.; Gerlée, A. Land use change impact on the nature reserves located in urban development areas: The case of the Natolin Forest and the Stefan Starzyński Kabacki Forest. Prace I Stud. Geogr. 2017, 62, 31–51. [Google Scholar]
- Ma, P.; Ye, G.; Peng, X.; Liu, J.; Qi, J.; Jia, S. Development of an index system for evaluation of ecological carrying capacity of marine ecosystems. Ocean Coast. Manag. 2017, 144, 23–30. [Google Scholar] [CrossRef]
- Ramirez-Acosta, J.; Castellanos, A.; Arnaud, G.; Breceda, A.; Rojas-Soto, O. Conservation of endemic terrestrial vertebrates in the protected areas of the Baja California Peninsula, Mexico. Nat. Areas J. 2017, 32, 15–30. [Google Scholar] [CrossRef]
- Nakajima, E.S.; Ortega, E. Carrying capacity using emergy and a new calculation of the ecological footprint. Ecol. Indicat. 2016, 60, 1200–1207. [Google Scholar] [CrossRef]
- Wang, S.; Yang, F.L.; Xu, L.; Du, J. Multi-scale analysis of the water resources carrying capacity of the Liaohe Basin based on based on ecological footprints. J. Clean. Prod. 2013, 53, 158–166. [Google Scholar] [CrossRef]
- Świąder, M.; Szewrański, S.; Kazak, J.; van Hoof, J.; Lin, D.; Wackernagel, M.; Alves, A. Application of ecological footprint accounting as a part of an integrated assessment of environmental carrying capacity: A case study of the footprint of food of a large city. Resources 2018, 7, 52. [Google Scholar] [CrossRef]
- Lin, D.; Hanscom, L.; Murthy, A.; Galli, A.; Evans, M.; Neill, E.; Mancini, M.; Martindill, J.; Medouar, F.Z.; Huang, S.; et al. Ecological footprint accounting for countries: Updates and results of the national footprint accounts. 2012–2018. Resources 2018, 7, 58. [Google Scholar] [CrossRef]
- Astles, K.L.; Holloway, M.G.; Steffe, A.; Green, M.; Ganassin, C.; Gibbs, P.J. An ecological method for qualitative risk assessment and its use in the management of fisheries in New South Wales, Australia. Fish. Res. 2006, 82, 290–303. [Google Scholar] [CrossRef]
- Dai, L.; Xu, B.; Wu, B. Assessing sustainable development of a historic district using an ecological footprint model: A case study of Nanluoguxiang in Beijing, China. Area 2017, 49, 94–105. [Google Scholar] [CrossRef]
- Ghita, S.; Saseanu, A.; Gogonea, R.M.; Huidumac-Petrescu, C.E. Perspectives of ecological footprint in European context under the impact of information society and sustainable development. Sustainability 2018, 10, 3224. [Google Scholar] [CrossRef]
- Lyon, S.W.; Desilets, S.L.E.; Troch, P.A. Characterizing the response of a catchment to an extreme rainfall event using hydrometric and isotopic data. Water Resour. Res. 2008, 44, 214. [Google Scholar] [CrossRef]
- Wackernagel, M.; Monfr, C.; Er, K.H. Ecological footprint time series of Austria, the Philippines, and South Korea for 1961–1999: Comparing the conventional approach to an ‘actual land area’ approach. Land Use Policy 2004, 21, 261–269. [Google Scholar] [CrossRef]
- Rees, W.; Wackernagel, M. Urban Ecological Footprints: Why Cities Cannot be Sustainable—And Why They are a Key to Sustainability. Environ. Impact Assess. Rev. 1996, 16, 223–248. [Google Scholar] [CrossRef]
- Kalbar, P.P.; Birkved, M.; Karmakar, S.; Nygaard, S.E.; Hauschild, M. Can carbon footprint serve as proxy of the environmental burden from urban consumption patterns? Ecol. Indicat. 2017, 74, 109–118. [Google Scholar] [CrossRef]
- Lanouar, C. The impact of energy consumption and economic development on Ecological Footprint and CO2 emissions: Evidence from a Markov Switching Equilibrium Correction Model. Energy Econ. 2017, 65, 355–374. [Google Scholar]
- He, J.; Wan, Y.; Feng, L.; Ai, J.; Wang, Y. An integrated data envelopment analysis and emergy-based ecological footprint methodology in evaluating sustainable development, a case study of Jiangsu Province, China. Ecol. Indicat. 2016, 70, 23–34. [Google Scholar] [CrossRef]
- Morgan, J. Ecological Footprints: An Essential Franciscan Guide for Faith and Sustainable Living. J. Soc. Christ. Ethics 2016, 36, 219–221. [Google Scholar] [CrossRef]
- Fan, Y.; Qiao, Q.; Xian, C.; Xiao, Y.; Fang, L. A modified ecological footprint method to evaluate environmental impacts of industrial parks. Resour. Conserv. Recycl. 2017, 125, 293–299. [Google Scholar] [CrossRef]
- Monfreda, C.; Wackernagel, M.; Deumling, D. Establishing national natural capital accounts based on detailed Ecological Footprint and biological capacity assessments. Land Use Policy 2004, 21, 231–246. [Google Scholar] [CrossRef]
- Reznichenko, N.; Davies, T.; Shulmeister, J.; McSaveney, M. Effects of debris on ice-surface melting rates: An experimental study. J. Glaciol. 2017, 56, 384–394. [Google Scholar] [CrossRef]
- Oku, E.E.; Ojikpong, T.; Yakubu, A.; Ezeaku, P. Soil Carbon Dynamics and Soil Properties Influenced by Different Types of Agronomic Land Use in the Forest Zone of Nigeria. J. Environ. Agric. Sci. 2015, 2, 1–5. [Google Scholar]
- Johannesen, A.B.; Nielsen, A.; Skonhoft, A. Livestock management at northern latitudes. Potential economic effects of climate change in sheep farming. Ecol. Econ. 2013, 93, 239–248. [Google Scholar] [CrossRef]
- Kitzes, J.; Galli, A.; Rizk, S.M.; Reed, A.; Wackernagel, M. Guidebook to the National Footprint Accounts; Global Footprint Network: Oakland, CA, USA, 2008. [Google Scholar]
- Laššák, P.; Labovský, J.; Jelemenský, Ĺ. Influence of parameter uncertainty on modeling of industrial ammonia reactor for safety and operability analysis. J. Loss Prev. Process Ind. 2010, 23, 280–288. [Google Scholar] [CrossRef]
- Tolk, A.; Bair, L.J.; Diallo, S.Y. Supporting Network Enabled Capability by extending the Levels of Conceptual Interoperability Model to an interoperability maturity model. J. Defense Model. Simul. 2013, 10, 145–160. [Google Scholar] [CrossRef]
- Wang, M.L.; Xu, F.L.; Lloyd, G.M. Results and implications of the damage index method applied to a multi-span continuous segmental prestressed concrete bridge. Struct. Eng. Mech. 2000, 10, 37–51. [Google Scholar] [CrossRef]
- Trousdale, W.; Gregory, R. Property evaluation and biodiversity conservation: Decision support for making hard choices. Ecol. Econ. 2004, 48, 279–291. [Google Scholar] [CrossRef]
- Urban, N.A.; Swihart, R.K.; Malloy, M.C.; Dunning, J.B., Jr. Improving selection of indicator species when detection is imperfect. Ecol. Indicat. 2012, 15, 188–197. [Google Scholar] [CrossRef]
- Tikabo, M.O.; Holden, S.T.; Bergland, O. Factor market imperfections and the land rental market in the highlands of Eritrea: Theory and evidence. Available online: http://www.umb.no/statisk/ior/discpaper/tenancy5_final5.pdf (accessed on 18 December 2018).
- Zhu, F.W.; Jin, Z.F.; Cui, F.F.; Lv, L.G.; Wang, J. Analysis of Land-Use Temporal and Spatial Pattern in Southern Jiangsu. Resour. Environ. Yangtze Basin 2015, S1, 23–29. [Google Scholar]
- Venetoulis, J. Assessing the ecological impact of a university: The ecological footprint for the University of Redlands. Int. J. Sustain. Higher Educ. 2001, 2, 180–197. [Google Scholar] [CrossRef]
- Talberth, J. By the Numbers: Economic Impacts of Climate Change in the Lower Mekong Basin. Available online: https://www.wri.org/blog/2015/02/numbers-economic-impacts-climate-change-lower-mekong-basin (accessed on 18 December 2018).
- Siche, R.; Agostinho, F.; Ortega, E. Emergy Net Primary Production (ENPP) as basis for calculation of Ecological Footprint. Ecol. Indic. 2010, 10, 475–483. [Google Scholar] [CrossRef]
- Liu, M.C.; Li, W.H. The calculation of China’s equivalence factor under ecological footprint mode based on net primary production. J. Nat. Resour. 2009, 24, 1550–1559. [Google Scholar] [CrossRef]
- Zhou, N.; Li, Y.C. Study on the ecological carrying capacity of Chongqing city Based on the ecological footprint improved model. J. Chongqing Normal Univ. 2018, 35, 56–63. [Google Scholar]
- Newsted, J.L.; Nakanishi, J.; Cousins, I.; Werner, K.; Giesy, J.P. Predicted distribution and ecological risk assessment of a “segregated” hydrofluorrother in the Japanese environment. Environ. Sci. Technol. 2002, 36, 4761–4769. [Google Scholar] [CrossRef] [PubMed]
- Penela, A.C.; Villasante, C.S. Applying physical input–output tables of energy to estimate the energy ecological footprint (EEF) of Galicia (NW Spain). Energy Policy 2008, 36, 1148–1163. [Google Scholar] [CrossRef]
- Gholkar, M.D.; Goroshi, S.; Singh, R.P.; Parihar, J.S. Influence of agricultural developments on net primary productivity (NPP) in the semi-arid region of India: A study using GloPEM Model. In Proceedings of the The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-8, 2014 ISPRS Technical Commission VIII Symposium, Hyderabad, India, 9–12 December 2014. [Google Scholar]
- Van Vuuren, D.P.; Smeets, E.M.W. Ecological footprints of Benin, Bhutan, Costa Rica and the Netherlands. Ecol. Econ. 2000, 34, 115–130. [Google Scholar] [CrossRef]
- Haberl, H.; Erb, K.H.; Krausmann, F. How to calculate and interpret ecological footprints for long periods of time: The case of Austria 1926–1995. Ecol. Econ. 2001, 38, 25–45. [Google Scholar] [CrossRef]
- Venetoulis, J.; Talberth, J.J.E. Refining the ecological footprint. Environ. Dev. Sustain. 2008, 10, 441–469. [Google Scholar] [CrossRef]



| Counties Involved by National Nature Reserves | Number of National Nature Reserves |
|---|---|
| 1 | 227 |
| 2–5 | 81 |
| 5–10 | 10 |
| >10 | 1 |
| Type | 2010 | 2000 |
|---|---|---|
| Farmland | 1.19 | 1.40 |
| Forest | 1.16 | 1.08 |
| Grassland | 0.85 | 0.77 |
| Water Area | 0.73 | 0.66 |
| Type | 2010 | 2000 |
|---|---|---|
| Farmland | 0.88 | 0.88 |
| Forest | 0.89 | 0.88 |
| Grassland | 1.39 | 1.77 |
| Water Area | 1.05 | 1.13 |
| Comparison Value | Parameter | EF-GAEZ2000efpc | EF-NPP2000efpc |
|---|---|---|---|
| EF-GAEZ2000efpc | Pearson correlation | 1 | 0.804 ** |
| P-value | - | 0.000 | |
| EF-NPP2000efpc | Pearson correlation | 0.804 ** | 1 |
| P-value | 0.000 | - |
| Comparison Value | Parameter | EF-GAEZ2010efpc | EF-NPP2010efpc |
|---|---|---|---|
| EF-GAEZ2010efpc | Pearson correlation | 1 | 0.811 ** |
| P-value | 0.000 | ||
| EF-NPP2010efpc | Pearson correlation | 0.811 ** | 1 |
| P-value | 0.000 |
| Ecological Footprint per Capita 2000 | EF-NPP model | EF-GAEZ model | Same Number of Protection Zones | ||
|---|---|---|---|---|---|
| Number | Percentage | Number | Percentage | ||
| 0–2.5 | 208 | 65% | 247 | 77% | 185 |
| >2.5 | 111 | 35% | 72 | 23% | 44 |
| Ecological Footprint per Capita 2010 | EF-NPP model | EF-GAEZ model | Same Number of Protection Zones | ||
|---|---|---|---|---|---|
| Number | Percentage | Number | Percentage | ||
| 0–2.5 | 98 | 31% | 103 | 32% | 71 |
| >2.5 | 221 | 69% | 216 | 68% | 146 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Fu, J.; Jiang, D.; Luo, J.; Sun, C.; Liu, H.; Wen, R.; Wang, X. Improvement of Ecological Footprint Model in National Nature Reserve Based on Net Primary Production (NPP). Sustainability 2019, 11, 2. https://doi.org/10.3390/su11010002
Liu X, Fu J, Jiang D, Luo J, Sun C, Liu H, Wen R, Wang X. Improvement of Ecological Footprint Model in National Nature Reserve Based on Net Primary Production (NPP). Sustainability. 2019; 11(1):2. https://doi.org/10.3390/su11010002
Chicago/Turabian StyleLiu, Xiaoman, Jingying Fu, Dong Jiang, Jianwu Luo, Chenxi Sun, Huiming Liu, Ruihong Wen, and Xuefeng Wang. 2019. "Improvement of Ecological Footprint Model in National Nature Reserve Based on Net Primary Production (NPP)" Sustainability 11, no. 1: 2. https://doi.org/10.3390/su11010002





