The Sustainable Characteristic of Bio-Bi-Phase Flow of Peristaltic Transport of MHD Jeffrey Fluid in the Human Body

Abstract

This study deals with the peristaltic transport of non-Newtonian Jeffrey fluid with uniformly distributed identical rigid particles in a rectangular duct. The effects of a magnetohydrodynamics bio-bi-phase flow are taken into account. The governing equations for mass and momentum are simplified using the fact that wavelength is much greater than the amplitude and small Reynolds number. A closed-form solution for velocity is obtained by means of the eigenfunction expansion method whereby pressure rise is numerically calculated. The results are graphically presented to observe the effects of different physical parameters and the suitability of the method. The results for hydrodynamic, Newtonian fluid, and single-phase problems can be respectively obtained by taking the Hartmann number (M = 0), relaxation time (${\lambda }_1=0$), and volume fraction (C = 0) as special cases of this problem.

1. Introduction

The transport of fluid due to wave propagation along the flexible wall of a channel, duct, or pipe is called peristalsis. Peristalsis is naturally found in the food or blood transport in living bodies. Inspired by this phenomenon, many engineering appliances in medical and other fields use peristalsis. Most of the fluid flowing has solid, liquid, or gaseous impurities that hinder the accurate calculation of results. The theory of particulate suspension has adequately described biological flows, like blood and food through the oesophagus. Moreover, in biological systems such as blood, particles in the respiratory tract, and transport of proteins and microorganisms in liquids are some cases where the assumption of multiphase liquids is effectively described. Other areas in which such flows are similarly helpful and have significant importance are lunar ash flows, powder innovation, burning, fluidization, filtration with aerosol, and rock sedimentation. If liquids have addons or impurities, traditional modelling may also not result in accurate or close-to-accurate outcomes. Hence, considering its applications and significance, the field is actively pursued by scientists and engineers. Ishii and Mishima [1] presented a two-fluid model for biphase fluids. They described the model time and area average and introduced an interfacial term to develop the link. Dukowicz [2] developed a new numerical model for particle fluids in liquid sprays. The model is also useful for general incompressible flows containing particles or droplets. The numerical scheme used a fully interacting combination of Eulerian fluid and Lagrangian particles. Tsuji et al. [3] compared the discrete particle model versus the two-fluid model. They also simulated the discrete model using Monte Carlo Simulations. Results show that the cluster population was much larger in the discrete particle model than in the two-fluid model. While discussing the peristaltic transport, Srivastava and Srivastava [4] devoted their efforts on identical rigid spherical particles suspended uniformly in a viscous fluid. They found the perturbation solution of the problem. Further, Misra and Pandey [5] reported a study on two-phase solid–liquid fluid flowing through a barrel-shaped cylinder. Bhatti et al. [6] discussed heat transfer in two-phase liquids with nonconducting solid spherical particles. They concluded that heat transfer would reduce with the inclusion of particles. Mekheimer et al. [7] worked with solid particles through a uniform channel. They found an analytic solution using the perturbation method. Many more significant studies on particle–fluid and peristaltic flows can be seen in References [8,9,10,11,12].

Utilization of non-Newtonian liquid in industry and engineering appliances spurred researchers around the globe to find new properties and the rheology of such fluids. A living body is made of different organic liquids that proliferate through its entirety. The transport of such fluids is usually performed by the process of peristalsis. Peristalsis is the automatic contraction and unwinding of smooth muscles. In the mechanical industry, the systems that develop the inspiration from such biological propulsion models are at present attracting a lot of interest, resulting in the development of machines like the heart–lung machine, roller pumps, and finger pumps [13]. Likewise, in different commercial ventures, pumping liquids is roused by this procedure. More importantly, human operating systems, like the digestive, circulatory, excretory, and even the reproductive system of both men and women, employ the concept of peristalsis at different stages of transport [14]. The importance of peristalsis in humans can be observed by the fact that one of the factors for infertility in human is a nonuniform peristaltic wave [15]. Peristalsis is also seen in the locomotion of earthworm, spermatozoa, snakes, and microorganisms [16]. An excellent summary of the mechanism of the peristaltic wave in fluid mechanics was reviewed by Fung [17]. Magnetohydrodynamics (MHD) is the flow of conducting liquid through an applied external magnetic field. The idea of MHD is very important in biomedical engineering. These days, an important development in drugging is the concept of targeted drugging; such drugs are controlled using a magnetic field that is helpful in cancer treatment. MRI is another application of MHD in biomedical engineering. Scientists effectively combined MHD and peristalsis to reap the advantages of their combined effects. For example, Kothandapani and Srinivas [18] probed the influence of MHD on the peristaltic transportation of viscous fluid through a porous channel. They also discussed heat transfer and the effects of elastic walls. Tripathi and Bég [19] studied the peristaltic transport of nanofluid through uniform transverse magnetic field. The Buongiorno formulation was assumed and results showed good agreement with Shapiro et al. [20]. A few other studies on the said area in the existing literature can be found in References [21,22,23,24,25,26,27,28,29,30,31,32].

Keeping in mind the applied nature of the study, MHD peristalsis flow of Jeffrey fluid with suspended particles in a rectangular duct is discussed.

Motivated by the developments in the present article, the influence of a magnetic field has been studied on the laminar, incompressible peristaltic driven flow of a non-Newtonian Jeffrey fluid with solid particles through a rectangular duct. The fluid is electrically conducting, and a constant static magnetic field is applied transverse to the flow direction. The governing flow problem was described using continuity and momentum equations with appropriate boundary conditions which are simplified with the assistance of long wavelength and low Reynolds number approximations. The boundary value problem was then reduced using nondimensional variables and the resulting system of reduced ordinary differential equations is solved analytically. The subsequent mathematical statements for the fluid and particulate phases were diagnostically analysed. A closed-form solution was obtained while the graphical results were displayed and examined in detail.

2. Modelling

Consider a rectangular duct, saturated by particle-laden Jeffrey fluid. The flow was induced due to a symmetric peristaltic wave transmitted in a positive x-axis, while walls in the xz-plane were stationary, as shown in Figure 1. The speed of the wave is “c”, wave length “$\Lambda$” with an amplitude of “b” units.

The wave propagation in the wall as displaced in Figure 1 can be mathematically expressed as [33]:

$$Z=H(X,t)=\pm a\pm b\cos \left[\frac{2\pi }{\Lambda }\left(X-ct\right)\right]$$

(1)

The flow is governed by the law of conservation of mass and momentum, along with the Lorentz force as a constant, and a transverse magnetic field is applied on the perpendicular to the flow direction. The flow velocities of fluid and particle phase are (U_f(X,Y,Z,t),0, W_f(X,Y,Z,t)) and (U_p(X,Y,Z,t),0, W_p(X,Y,Z,t)). Consequently, the governing equations take the following form:

$$\frac{\partial U_f}{\partial X}+\frac{\partial W_f}{\partial Z}=0$$

(2)

$$\begin{array}{l}(1-C){\rho }_f\left(\frac{\partial U_f}{\partial t}+U_f\frac{\partial U_f}{\partial X}+W_f\frac{\partial U_f}{\partial Z}\right)=\\ -(1-C)\frac{\partial P}{\partial X}+(1-C){\mu }_s\left(\frac{\partial }{\partial X}{T}_{XX}+\frac{\partial }{\partial Y}{T}_{XY}+\frac{\partial }{\partial Z}{T}_{XZ}\right)+C{S}^{\prime }\left(U_p-U_f\right)-\sigma B_0^{2}U\end{array}$$

(3)

$$\begin{array}{l}(1-C){\rho }_f\left(\frac{\partial W_f}{\partial t}+U_f\frac{\partial W_f}{\partial X}+W_f\frac{\partial W_f}{\partial Z}\right)=\\ -(1-C)\frac{\partial P}{\partial Z}+(1-C){\mu }_s\left(\frac{\partial }{\partial X}{T}_{ZX}+\frac{\partial }{\partial Y}{T}_{ZY}+\frac{\partial }{\partial Z}{T}_{ZZ}\right)+C{S}^{\prime }\left(W_p-W_f\right)\end{array}$$

(4)

$$\frac{\partial U_p}{\partial X}+\frac{\partial W_p}{\partial Z}=0,$$

(5)

$$C{\rho }_p\left(\frac{\partial U_p}{\partial t}+U_p\frac{\partial U_p}{\partial X}+W_p\frac{\partial U_p}{\partial Z}\right)=C\frac{\partial P}{\partial X}+C{S}^{\prime }\left(U_f-U_p\right)$$

(6)

$$C{\rho }_p\left(\frac{\partial W_p}{\partial t}+U_p\frac{\partial W_p}{\partial X}+W_p\frac{\partial W_p}{\partial Z}\right)=C\frac{\partial P}{\partial Z}+C{S}^{\prime }\left(W_f-W_p\right)$$

(7)

Equations (2)–(4) are describing continuity and momentum equations for the fluid phase, whereas Equations (5)–(7) are for the solid phase. It was assumed that all the particles had the same average size and shape. The distribution of the particles was also uniform. The drag coefficient $S^{\prime }$ can be described as

$$S^{\prime }=\frac{9{\mu }_0}{2{\check{a}}^2}\tilde{D}\left(C\right)$$

(8)

$$\tilde{D}\left(C\right)=\frac{C+1.33+\sqrt{C\left(8-3C\right)}}{3{\left(0.67-C\right)}^2}$$

(9)

The viscosity of the suspension ${\mu }_s$ expressed by the relation

$${\mu }_s=-\frac{{\mu }_f}{\Delta C-1}$$

(10)

$$\Delta =\frac{7}{1000}\exp (\frac{249}{100}C+\frac{1107}{T}\exp (-\frac{169}{100}C))$$

(11)

For Jeffrey base fluid tensor T in Equations (2) and (3) is [34]

$$T=\frac{{\mu }_f}{1+{\lambda }_1}\left(\dot{\gamma }+{\lambda }_2\ddot{\gamma }\right)$$

(12)

Using Galilean principal variables in fixed frame are transformed to wave frame by taking velocity of wave frame equals to “c” moving horizontally in x-axis direction. The involved velocities and pressure become

$$u=U-c,w=W,p\left(x,z\right)=P\left(X,Z,t\right).$$

(13)

Introducing

$$\begin{array}{c} \overline{x}=\frac{x}{\lambda },\overline{y}=\frac{y}{d},\overline{z}=\frac{z}{a}\overline{u}=\frac{u}{c},\overline{w}=\frac{w}{c\delta },\overline{t}=\frac{ct}{\lambda },\overline{h}=\frac{H}{a},\phi =\frac{b}{a},\overline{p}=\frac{a^{2}p}{\mu c\lambda },\delta =\frac{a}{\lambda },\beta =\frac{a}{d},\mathrm{Re}=\frac{\rho ac\delta }{\mu },M_1=\frac{S^{\prime }{a}^2}{\left(1-C\right){\mu }_s}, \\ M=\sqrt{\frac{\sigma }{\mu }}a{B}_0,{\overline{T}}_{\overline{x}\overline{x}}=\frac{a}{\mu c}{T}_{xx},{\overline{T}}_{\overline{x}\overline{z}}=\frac{a}{\mu c}{T}_{xz},{\overline{T}}_{\overline{x}\overline{y}}=\frac{d}{\mu c}{T}_{xy},{\overline{T}}_{\overline{y}\overline{z}}=\frac{d}{\mu c}{T}_{yz},{\overline{T}}_{\overline{z}\overline{z}}=\frac{\lambda }{\mu c}{T}_{zz},{\overline{T}}_{\overline{y}\overline{y}}=\frac{\lambda }{\mu c}{T}_{yy.}\end{array}\}$$

(14)

Equations (2)–(7) reduce to the following two nondimensional equations after employing Equations (13) and (14).

$$\frac{dp}{dx}=\frac{{\beta }^2}{1+{\lambda }_1}\frac{{\partial }^2{u}_f}{\partial y^2}+\frac{1}{1+{\lambda }_1}\frac{{\partial }^2{u}_f}{\partial z^2}-M^2\left(u_f+1\right)+C{M}_1\left(u_p-u_f\right)$$

(15)

$$\frac{dp}{dx}=(1-C)M_1(u_f-u_p)$$

(16)

The velocity at all four walls is

$$\begin{array}{lll}u(x,y,z)=-1, & \mathrm{at}& y=\pm 1,\\ u(x,y,z)=-1, & \mathrm{at}& z=\pm h\left(x\right)=\pm (1+\phi \cos 2\pi x),\end{array}$$

(17)

3. Exact Solutions

Eigenfunction expansion method is used to find the solution as defined in [34] to solve the coupled PDEs in (15) and (16) by taking $\frac{dp}{dx}$ constant.

$$\begin{array}{l}{u}_f=\frac{A_1}{M^2}-\frac{4\mathrm{Cos}({\theta }_{2}z)\mathrm{Cosh}\left(\raisebox{1ex}{${\theta }_1$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.y\right)\left(1+\frac{A_1}{M^2}\right)\mathrm{Sech}\left(\frac{{\theta }_1}{\beta }\right)\mathrm{Sin}\left({\theta }_2\right)}{\left(\pi -2n\pi \right)\left(h+\frac{\mathrm{Sin}\left(2h{\theta }_2\right)}{\pi -2n\pi }\right)}\\ A_1=-M^2-\frac{\frac{dp}{dx}\left(1-{\lambda }_1\right)}{1-C}+\frac{\frac{dp}{dx}\left(1-{\lambda }_1\right)}{1-C}\mathrm{Cos}(Mz)\mathrm{Sec}(hM)\\ {\theta }_1=\sqrt{M^2+{\theta }_2{}^2},\text{}{\theta }_2=\frac{1}{2}\left(1-2n\right)\pi \end{array}$$

(18)

$$u_p=\frac{1}{M_1(1-C)}\frac{dp}{dx}-(1-C)M_1{u}_{f.}$$

(19)

The flow rate of fluid and particle are given by

$$Q_f=\left(1-C\right){{\displaystyle \int }}_0^h{u}_{f}dy$$

(20)

$$Q_p=C{{\displaystyle \int }}_0^h{u}_{p}dy$$

(21)

and

$$Q=Q_f+Q_p$$

(22)

$dp/dx$ is calculated in terms of Q using Equation (22).

$$\begin{array}{l}\frac{dp}{dx}=\frac{A_2}{M^3}\left(hM-\tan \left(hM\right)\right)+\frac{32A_2\beta \left(2M\sin \left(h{\theta }_2\right)-{\theta }_{2}cos\left({\theta }_2\right)\tan \left(hM\right)\right)}{-8M{\theta }_2\left(M^2-{\theta }_2{}^2\right)\sqrt{{\theta }_1}\left(2h{\theta }_2+\sin \left(2h{\theta }_2\right)\right)}\mathrm{sech}\left(\raisebox{1ex}{${\theta }_1$}\!\left/ \!\raisebox{-1ex}{$\beta $}\right.\right)\\ A_2=-Q\frac{\left(-1+{\lambda }_1\right)}{(-1+C)}\end{array}$$

(23)

The change in pressure $\Delta P$ along x-axis can be evaluated numerically using

$$\Delta p=\underset{0}{\overset{1}{{\displaystyle \int }}}\frac{dp}{dx}dx.$$

(24)

4. Validation of Results

The obtained results are compared with the existing literature (Ijaz et al [35] and Ellahi and Farooq [36]) as a limiting case of the reported problem and are found in good agreement as indicated in

Table 1. The comparison between the obtained results with the existing literature [35,36] as a limiting case of problem under consideration.

z	C	M	β	λ1	Ijaz et al. [35]	Ellahi and Farooq [36]	Present solution
0	0	0	0.2	0	0.4934	0.4788	0.478898
0.5					0.3824	0.3638	0.363826
0	0	0	0.2	5	-	0.3145	0.31468
0.5					-	0.2727	0.272837
0	0	0	0.4	5	-	0.2598	0.259948
0.5					-	0.2476	0.247785
0	0	1	0.4	5	-	0.2293	0.229664
0.5					-	0.2164	0.216551

, i.e.,

• the problem under consideration reduces to a hydrodynamic case, if Hartmann number M = 0.
• The results for Newtonian fluid can be recovered if relaxation time ${\lambda }_1=0$.
  This study leads to a single-phase problem if volume fraction C = 0.

5. Results and Discussion

The equations describing the particle-laden flow in a rectangular duct are modeled and solved analytically. The effects of involving parameters, such as aspect ratio of duct $\beta$, Jeffrey fluid parameter ${\lambda }_1$, Hartmann number M, concentration of solid particles in fluid C, and drag coefficient M1 are shown using 2D and 3D plots for velocities of fluid and particles. Some important features of peristaltic transport were also observed using graphical results of pressure gradient and pressure rise.

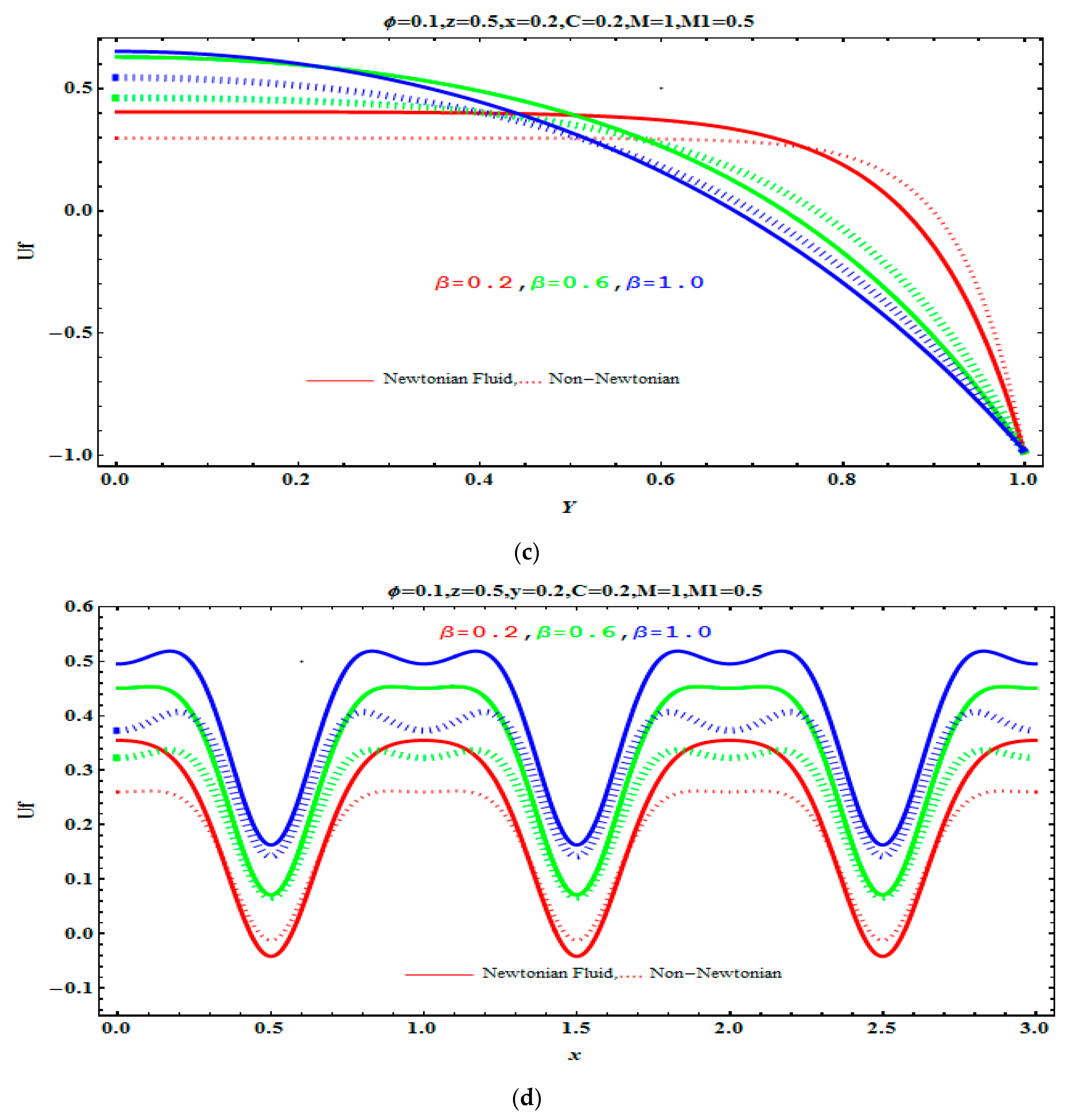
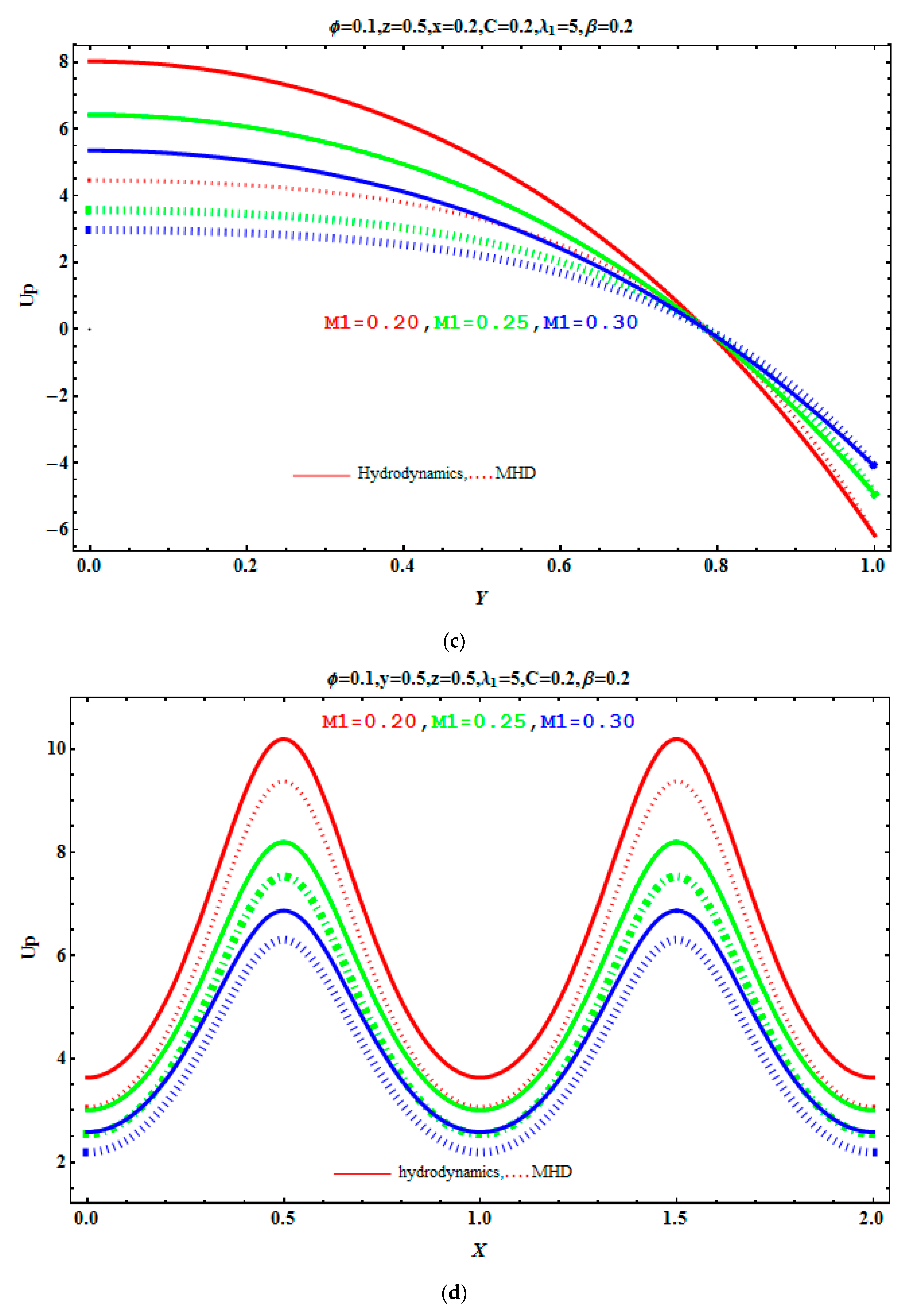
5.1. Velocity Profile

Figure 2, Figure 3, Figure 4 and Figure 5 are drawn to show variation in the velocity profile for various values of emerging parameters. The two- and three-dimensional analysis is submitted in these figures for all the observing parameters $\beta$, ${\lambda }_1$, M, M1, and C. Each figure contains four subfigures: (a) 3D plot for velocity profiles in uyz-axis; (b) 2D analysis of velocity profiles vs. z-axis; (c) 2D analysis of velocity profiles vs. y-axis; and (d) 2D analysis of velocity profiles vs. x-axis. Due to the symmetry of the geometry and flow, we assume only half channels to show the graphs, and the range for all independent parameters is taken as $x\in \left[0, 2\right], y\in \left[0, 1\right], z\in \left[0, h\right]$.

The variation in fluid velocity with respect to different values of aspect ratio of duct $\beta$ for Newtonian and non-Newtonian cases is displayed in Figure 2. It is noticed that velocity shows reductions in the central region of fluid as $\beta$ tends to 1, i.e., square duct but velocity increases close to walls for larger values of $\beta$. As $\beta$ displays, the ratio of length to width of the rectangular duct flow tends to slow down through the centre as duct width is increased. As relaxation time ${\lambda }_1=0$, the results reduce to Newtonian fluid case. It is shown that the flow of Newtonian fluid is faster as compared to non-Newtonian fluid, irrespective of aspect ratio of the duct, because of an increase in resistance by the non-Newtonian fluid. Figure 3 shows fluid velocity decreases with an increase in the values of Hartmann number $M$ for both the single- and two-phase model. The flow supresses as Lorentz force resists the motion of the fluid. Variation in fluid velocity was also observed as the concentration of particle $C$ changes. If C = 0, then the resulting equations are reduced to a single-phase model. It is observed that the velocity single-phase fluid is greater than the particle-laden fluid that has approximately 20% particles. This is due to the fact that particles are heavier and have a tendency to resist the flow and hence decrease the momentum of the fluid.

The particles are carried to the base fluid; hence, in most cases, particle velocity is proportional to fluid velocity. Particle velocity inside Newtonian and non-Newtonian base fluid is shown in Figure 4. Same graphs show the effects of variation of aspect ratio of duct $\beta .$ Considerably lower velocity of particles is noticed in non-Newtonian fluids when compared to Newtonian cases, which is evident of the fact that non-Newtonian fluid offers greater resistance to particle flow. Velocity shows reductions in the central region of duct for values of $\beta$ closer to 1. Figure 5 shows that particle velocity displays minor reduction in MHD vs. hydrodynamic cases. As particles are nonconducting, the reduction observed here is due to fact that fluid velocity decreases. Again, velocity decreases with the increase of drag force.

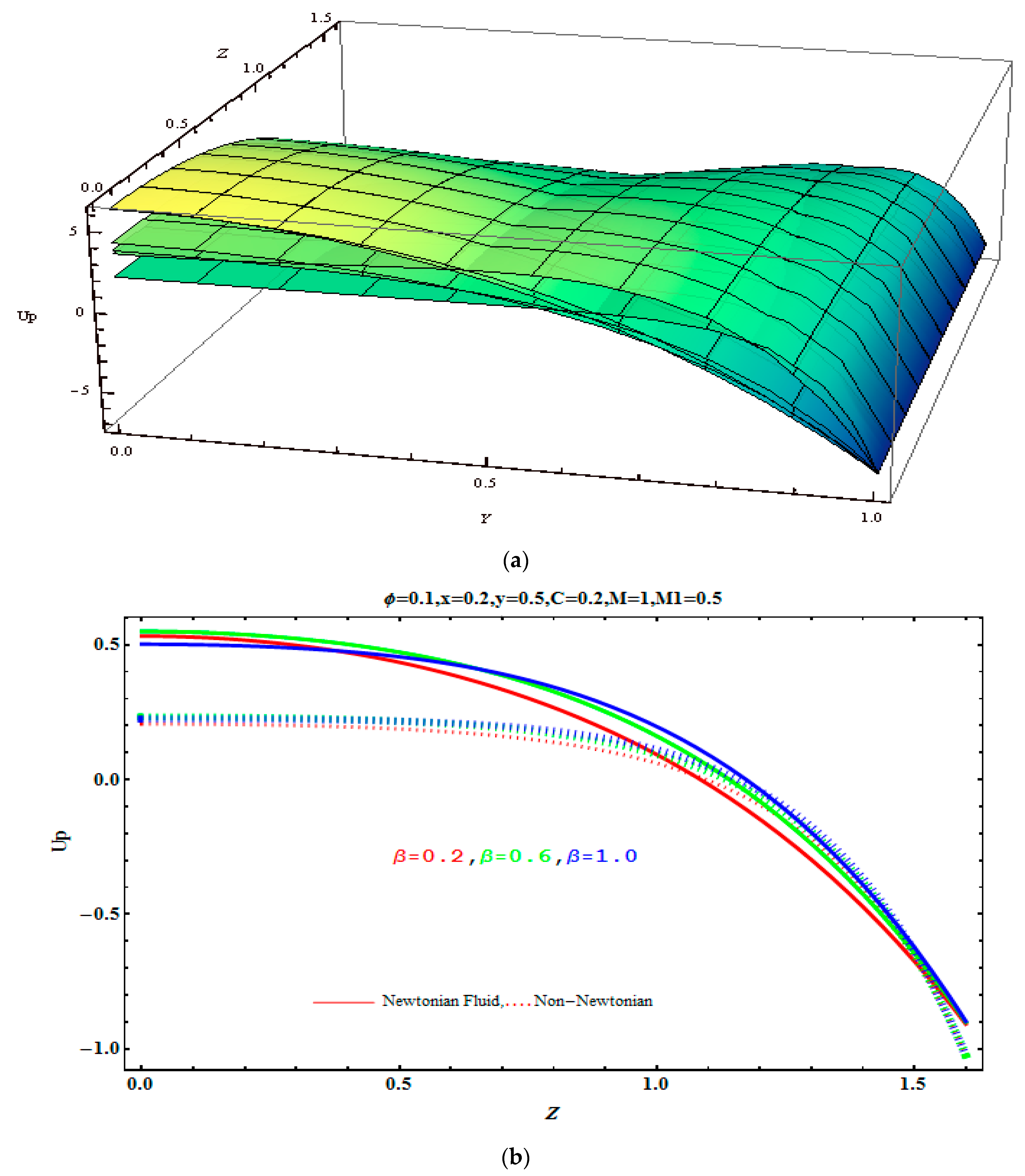
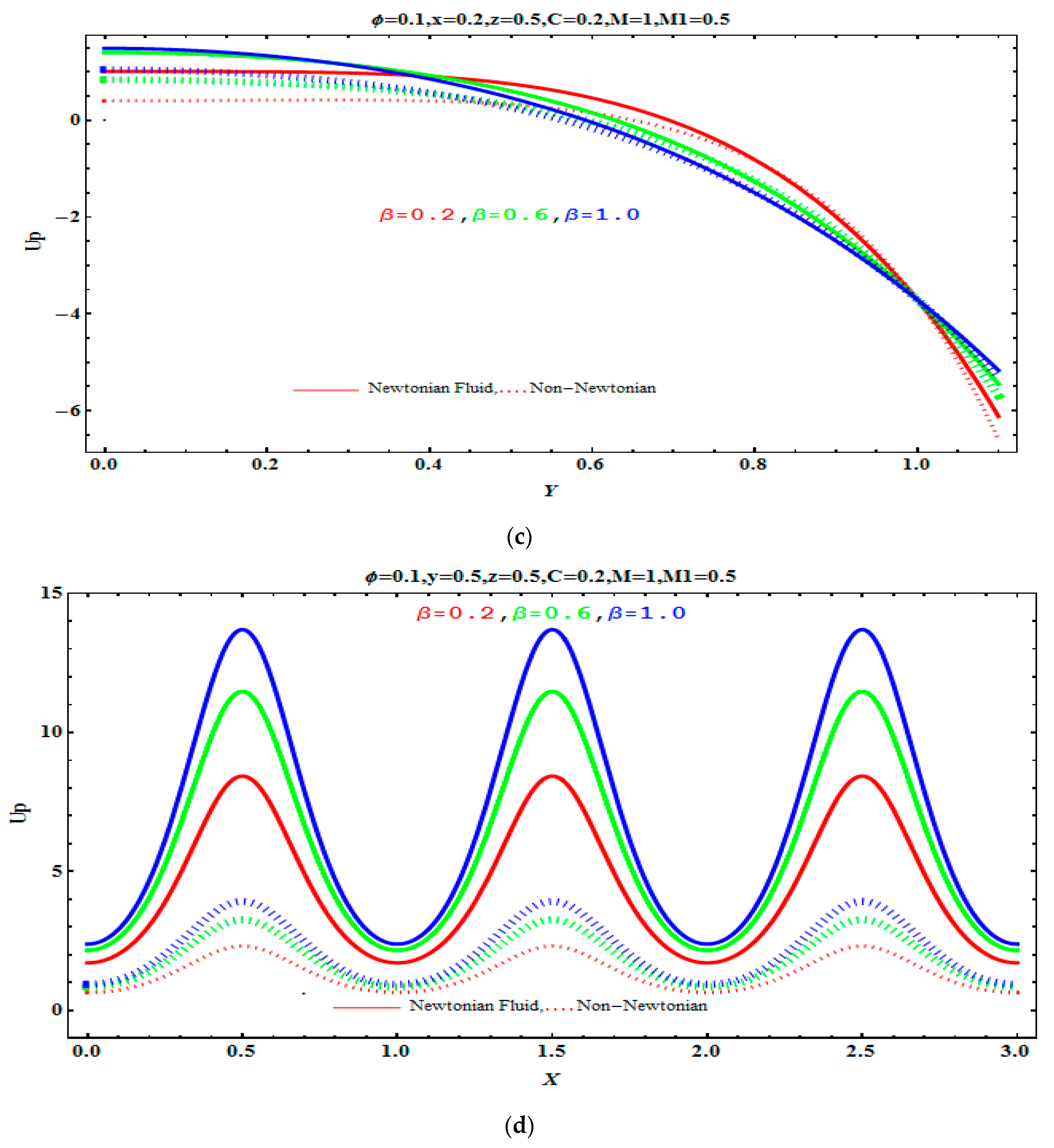
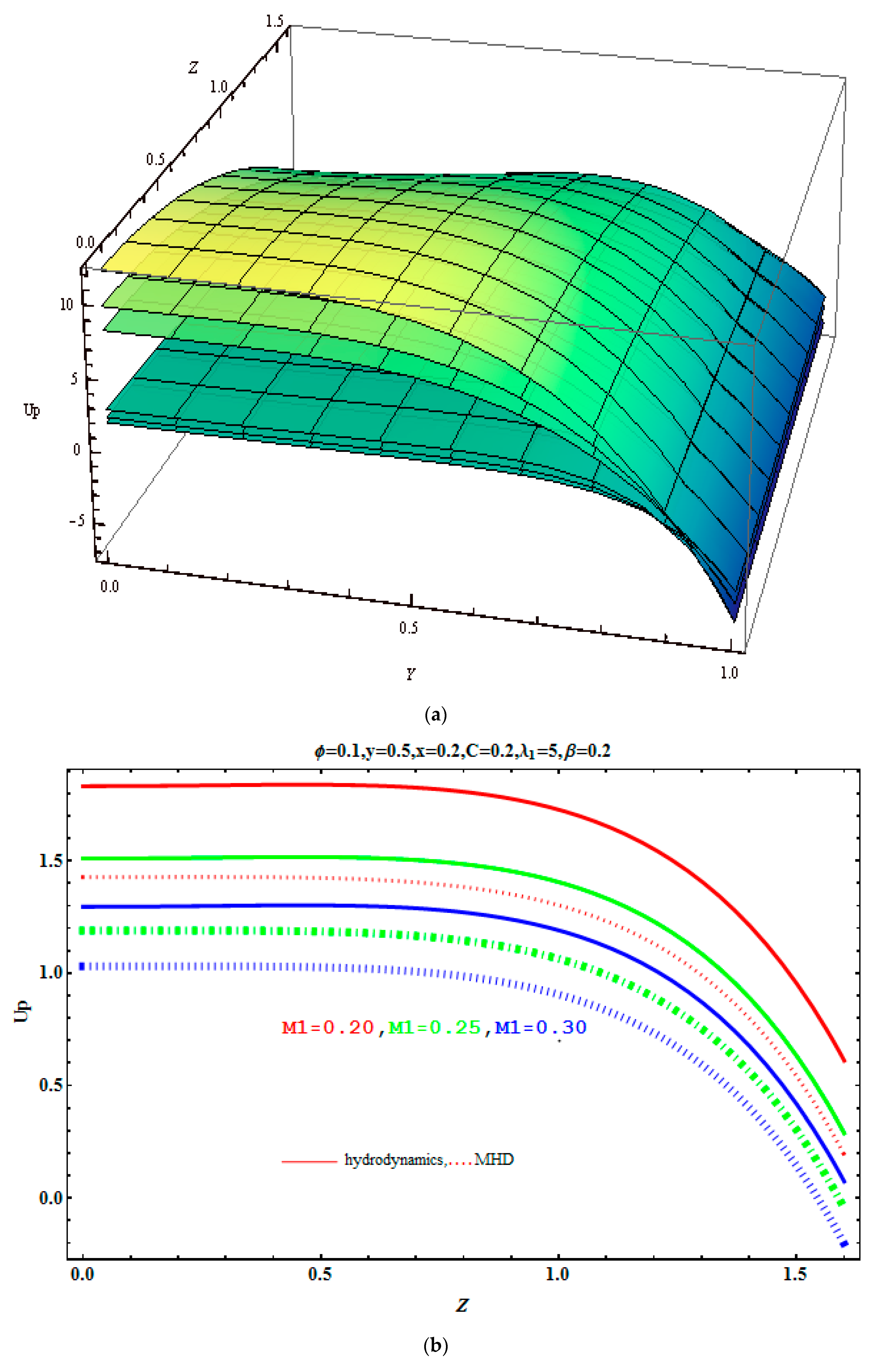
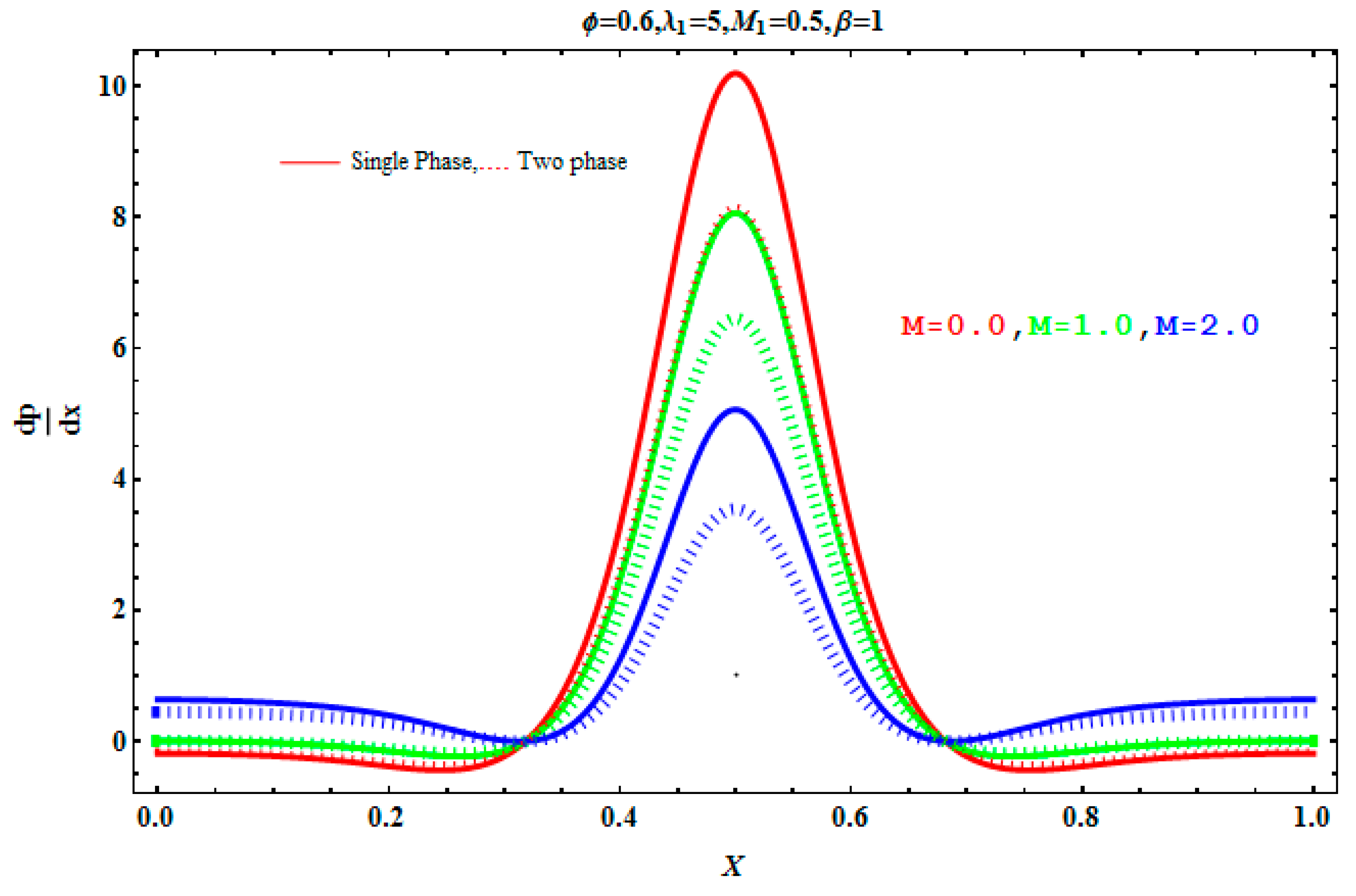
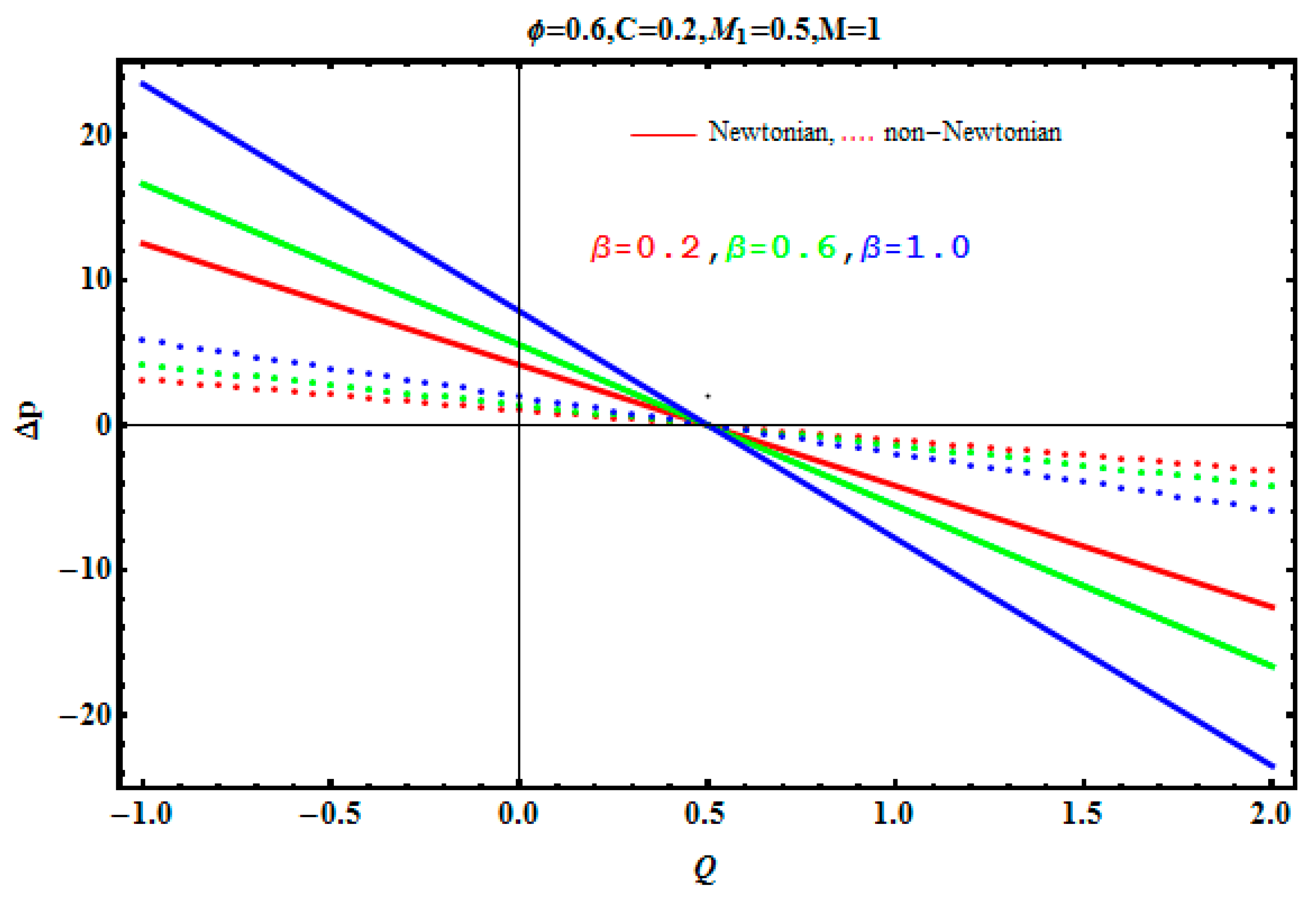
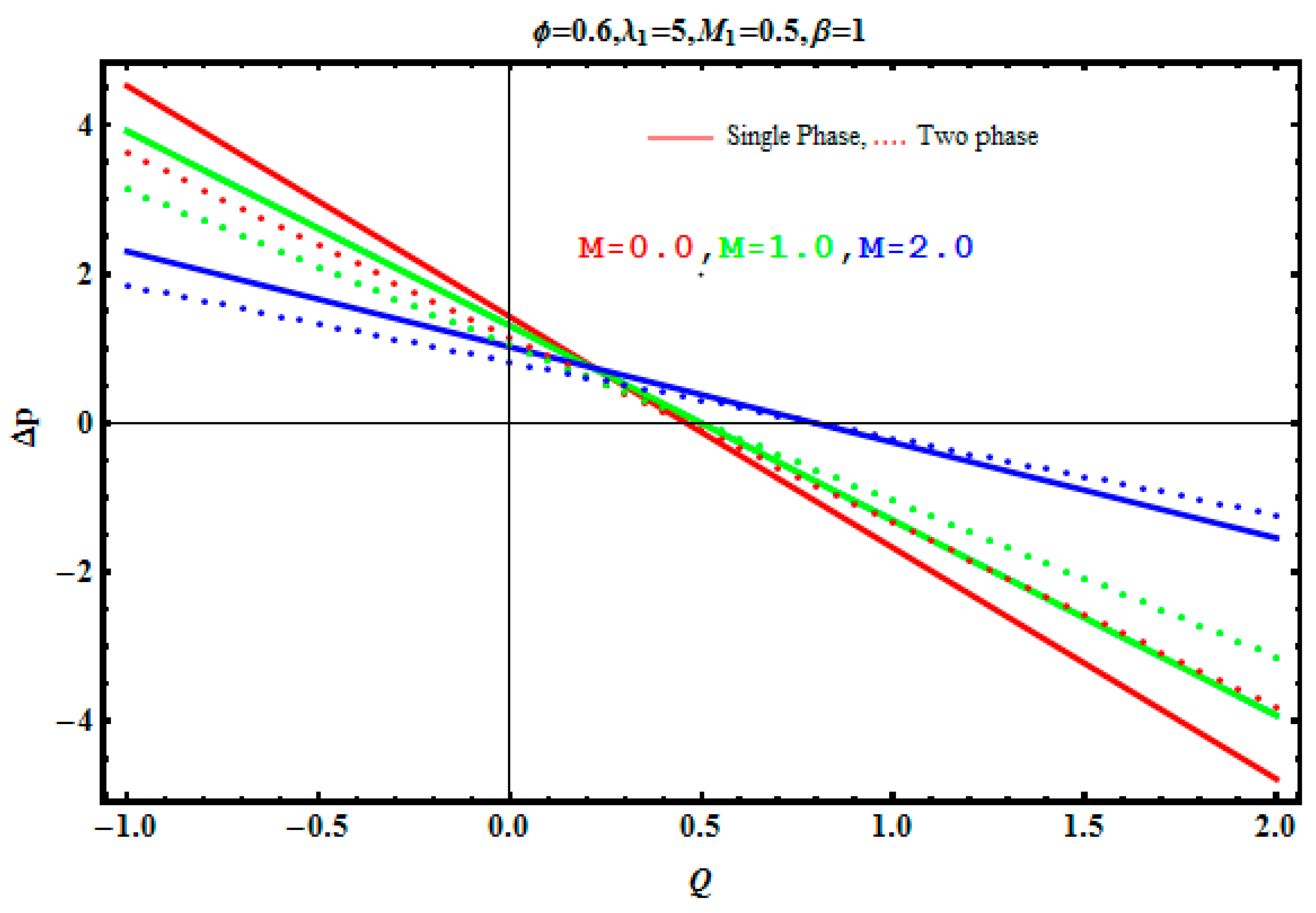
5.2. Pressure Gradient and Pressure Rise

Figure 6 and Figure 7 are drawn to demonstrate the influence of evolving parameters on pressure gradient along x-axis. It is perceived that the pressure gradient slightly decreases at the endpoint and achieves maximum value in the middle of the duct. Figure 6 is drawn to identify the variation in pressure gradient for different values of duct aspect ratio $\beta$, for both Newtonian and non-Newtonian cases. When the value of $\beta$ increases the pressure, it also rapidly increases along the duct length $x$. The pressure gradient attains even higher values for non-Newtonian fluid cases, whereas the behaviour of pressure gradient reverses as the concentration of particles in fluid $C$ increases (Figure 7). It is due to that decrease in velocity that pressure is increased. In Figure 7, pressure gradient was also decreasing for various values of Hartman number $M$.

Figure 8 and Figure 9 are drawn to show variation in pressure rise per unit wavelength Δp against the mean flux Q. Graphical results are plotted for Δp against Q. Here, the flow can be classified into three parts depending on position of graphical results. If the graph is in Quadrant (I), i.e., flow rate Q > 0 and pressure change Δp > 0, the region is called a peristaltic pumping region; for Quadrant (II), the flow rate is positive, but pressure rise/loss is negative, and the region is known as an augmented flow region; and, finally, Quadrant (IV), in which Q < 0 and Δp > 0, is known as backward pumping. If Δp = 0, it is called free pumping. It is clear that with the increase of flow rate, Δp decreases as flow rate is directly related to velocity and an increase in velocity decreases pressure. Figure 8 indicates that pressure falls as $M$ increases for single- and multiphase fluids. Free pumping is obtained at Q > 0.5. Same results are obtained for two values of C. It is also seen from Figure 9 that pressure rises for an increase in various values of ${\lambda }_1 \mathrm{and} \beta$. Free pumping in these figures is observed in the varsity of Q = 0.5.

6. Conclusions

The magnetodynamics of peristaltic flow of particle–fluid suspension in a rectangular duct is inspected. The flow problem of particle-laden Jeffrey fluid is solved analytically using eigenfunction expansion methods. It is assumed that the fluid moves slowly due to the wave on the wall having a large wavelength as compared to its amplitude. The resulting differential equations are solved analytically for velocity.

• It is found that velocity of the fluid decreases when the Hartmann number, Jeffreys’ parameter, and aspect ratio increased.
• Velocity decreases by increasing the value of volume fraction.
• Negative effects are observed on a pressure gradient due to Jeffrey fluid parameter λ₁, Hartmann number M, and concentration fraction C.
• The rise in pressure is observed due to augmentation in aspect ratio.
• A pressure drop is observed for the increasing values of a magnetic field parameter, Jeffrey fluid parameter, and volume fraction.