3.1. The Distance Frontier Model
The data are given as joint input-categories but two separate outputs for agricultural production and diversification activities. Taking this data-structure with multiple outputs, we choose the distance frontier framework [
37,
38]. We accommodate to the different economic, structural and legal environments in the three countries by estimating a separate distance frontier for each country, followed by a metafrontier, which envelopes the three country frontier [
39,
40].
Denote with
xt the set of inputs, and with
P(x) the output set, i.e., all feasible output vectors
given
xt. Then, a technology can be described with an output distance function [
37]
for all
. The distance function
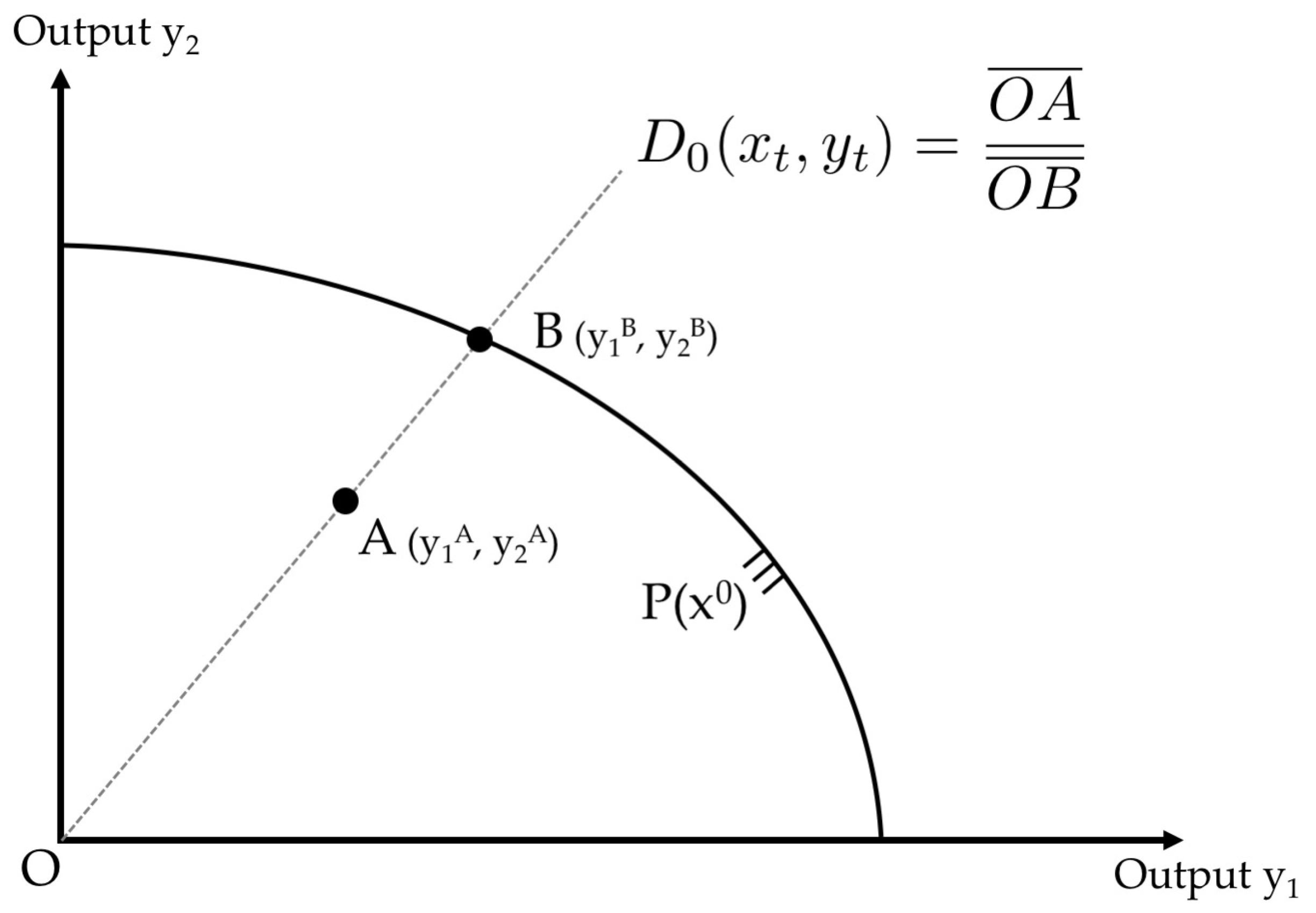
is nondecreasing, convex and linearly homogeneous in outputs, and decreasing and quasi-concave in inputs. The model is schematically described in
Figure 1.
The boundary of the output set is equivalent to the production possibility curve. The distance function
gives the relation of a given output vector (
in
Figure 1) to the maximal feasible output with unchanged input mix (
).
One challenge in estimating the distance frontier econometrically is that the distance frontier under technical efficiency is equal to one. In our model, we have to consider two types of output, agricultural output and para-agricultural output. Hence, we derive the model with two outputs, agricultural output (
y1) and para-agricultural output (
y2). Taking logarithms, we can write our model in a simplified form:
describes the relative distance between observed and maximal feasible output with given inputs, which leads to
. In contrast, the efficiency measure of Farrell describes the maximal radial expansion of an output with inputs fixed (i.e., TE
Farrell > 1) [
41]. So we can replace
D0 by the measure 1/
TEF:
We replace the term
1/TEF by an exponential error-term
exp(u) [
38]. For the purpose of simplification, we rescale
TEi as a reciprocal of Farrell’s measure of TE such that
and
.:
Reformulation and introduction of a white noise error term
v brings a form quite close to a stochastic production frontier [
42]:
represents the functional form that has to be determined. We started with a translog functional form and we tested for a Cobb-Douglas functional form. The first step is the estimation of group-specific frontier for the groups G = 1,2,3 which are Austria, Switzerland, and Germany.
The estimation of the parameters of the stochastic frontier model can be based on maximum-likelihood estimates. The first error-term
describes stochastic effects that are beyond the farmer’s control and are defined as independently and identically distributed as
[
42]. The inefficiency term
u is a non-negative amount that describes the inefficiency that is under the farmer’s control. This term
u has a half-normal distribution
this assumption allows the estimation of the heteroscedasticity model, which captures the impacts of a set of explanatory
j variables
z for technical efficiency.
The model is defined as follows:
with
zj as a set of explanatory variables, which explain technical (in)efficiency [
43,
44]. If the estimated parameter
is positive (
negative), the corresponding variable has a negative (
positive) influence on technical efficiency.
Since we are estimating the efficiency of farms in three countries we apply the stochastic meta-frontier model by firstly estimating group efficiency (TE) within the three countries and then estimating a joint deterministic metafrontier, which envelope the country-frontiers [
45,
46]. The metafrontier is defined as follows:
with the outputs
y and inputs
x of the metafrontier *. The model is a deterministic model, since we already consider stochastic effects in the group-frontiers. The parameters are produced by a linear optimization. In the final estimation of the metafrontier, we use a translog functional form as presented in Equation (10).
The model is a deterministic model and the parameters are produced by a linear optimization. We use two methods to estimate the parameters of the metafrontier, namely (1) the optimization by minimizing the absolute deviation, and (2) the minimization of the squared deviation [
45].
The combination of group-frontiers (
G = 1,2,3) and the metafrontier* allows to estimate the general differences in technology, which are captured by the model output, the ‘Meta-Technology Ratio’ (MTR). The MTR describes the technological differences of the group-frontiers used in the three countries to the joint technology (represented by the metafrontier). The total efficiency TE
* is defined as a product of the group- or country-specific efficiency TE
G, produced by the distance frontier model and the MTR:
The distance function and metafrontier are estimated using
sfamb [
47] for
OxMetrics 7.1 [
48], the metafrontier is simulated by 5000 times bootstrapping to generate estimates of the standard-errors.
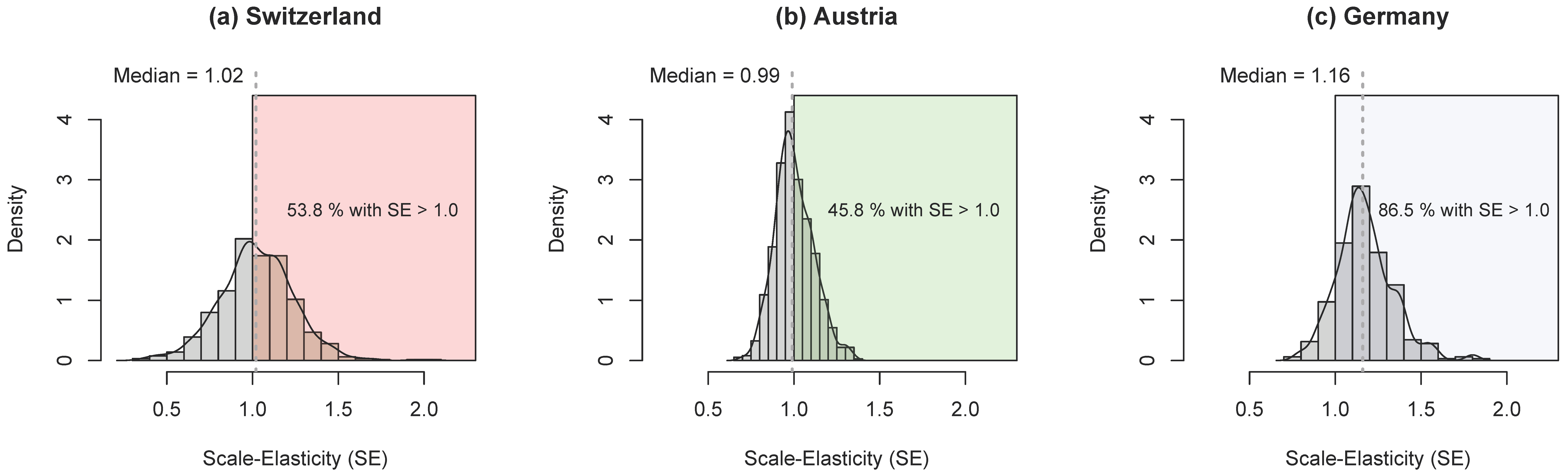
Based on the estimation results we can calculate the potential effect of a 1%-increase of para-agriculture, which is usually followed by an adjustment of the optimal input mix of the farms. Following Brümmer et al. (2006) [
49], we assume simple static profit maximizing behavior, the resulting optimization exercise involves
, subject to the frontier technology
, where
p and
w are the vectors of product prices and input prices, respectively. The first order conditions of the corresponding with respect to a specific input
j yields
, where
is the Lagrangian multiplier. Summing up over all
j first order conditions for the inputs, we have
. The summand corresponds to the
, the
jth input elasticity of the output distance function DO. The summation of the input distance elasticities over
j yields the (negative of the) scale elasticity,
. The cost share of input j is defined as
. Substituting the above first order conditions in both numerator and denominator of the cost share definition gives the shadow cost share
of input k:
.
Assuming a static profit-maximization, the adjustment is expressed as the change of the shadow cost shares followed by a relative change in the revenue from para-agriculture
y2 (Equation (9)):
In Equation (9), denotes the shadow cost share of input j, εj the input distance elasticity of input xj, and ε the scale elasticity.
3.2. Data Description and Adjustment
We use bookkeeping data from organic mixed and grassland-Farms in the years 2003, 2004, and 2005. In Germany the data refer to the bookkeeping period from July to June of the following year in the respective years 2003/04, 2004/05, and 2005/06, in Switzerland and Austria the data are organized in calendar years. The German data contains bookkeeping data from 106 farms in Bavaria and Baden-Württemberg, which was provided by Land Data GmbH. The Swiss data is taken from the Farm Accounting Data Network (F.A.D.N.) in Switzerland and contains 213 organic farms. The Austrian data is taken from the voluntarily bookkeeping farm network of the Ministry for Agriculture, Forestry, Environment and Water in Austria (BMLFUW) and contains 244 organic farms. As ‘outliers’ we define farms with any input or output value greater than the mean value plus three standard-deviations. This leads to a balanced panel data-set of 1689 observations, outliers are deleted from the data.
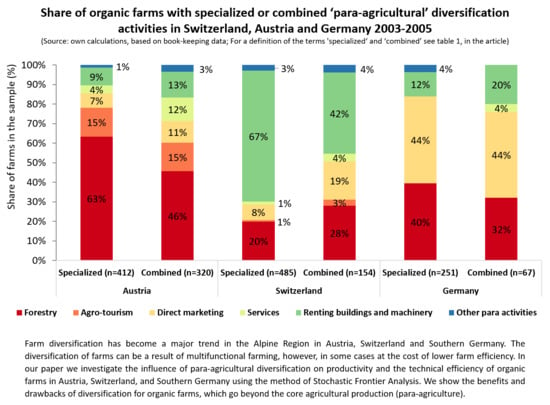
In Switzerland, para-agriculture describes activities, which are near to the agricultural production process and make a yearly revenue between 5000 and 250,000 Swiss Francs [
4,
5]. In order to ensure comparability between German, Austrian, and Swiss bookkeeping’s accountancy, rules were harmonized by using the same output-categories: Agricultural output (
y1) contains all revenues from plant and animal production while para-agricultural output (
y2) contains revenues from activities closely related to agriculture, such as direct marketing, agro tourism, wine production, services or renting out land, machinery or buildings. Furthermore, we include aggregated payments for organic farming and other ecological objectives in the three countries as ‘environmental payments’ (
z2). We summarized the remaining types of the agricultural payments as ‘other payments’ (
z3), which are mainly the per-hectare and per-animal direct payments.
In the Swiss F.A.D.N. data, farm and residential buildings are regarded as part of the farm enterprise, i.e., also the assets and costs of the residential buildings have to be included in the accounting. This unique characteristic of the Swiss data inflates the contribution of para-agricultural output to farm income compared with German and Austrian data. About 52% of the output of para-agriculture stems from artificial rent payments of the farmer’s family to the farm, the remaining 48% of para-agricultural revenue can be interpreted as para-agriculture activities that create farm income. We eliminate this effect from the Swiss data to ensure consistency by subtracting imputed rental payments from the farmer’s family to the farm in order to compensate for all costs that arise from residential buildings.
The data are deflated using the base year 2000 and official price indices from each country. Since trade for inputs and outputs are subject to tariffs between the EU and Switzerland, the exchange-rate might in some cases not fully reflect scarcities or input shadow-prices in Switzerland. Therefore, price adjustments are done for the single inputs and outputs of the Swiss data-set in order to reflect not only the currency exchange but also the diverging shadow-prices for different inputs in Switzerland.
The applied output distance-function is defined as follows:
with the output
y with
m = 1 for agricultural output and
m = 2 for output from para-agriculture, and the
x inputs
j = 1, 2, 3, 4 for variable costs, capital, labor and land and with
t for the year. The parameters
are to be estimated. The parameter
describes the contribution of the outputs from para-agriculture to the agricultural output. The parameter
describes the impact of the inputs
j on the agricultural output. The parameter
describes the influence of the interaction of
and the inputs
on the agricultural output.
represents the technical change over time-periods
t = 1, 2, 3 in the years from 2003 to 2005.
We assume that farm structure is fixed or quasi fixed in the short run, since labor is a given factor for family farms and the structure of farm-capital cannot be changed without substantial costs of adjustment. Kumbhakar [
50] shows that with a completely flexible input choice, endogeneity is one problem to be addressed for the model choice. However, this is not the case for our group of farms and our very short panel data-set. Therefore, we do not apply a model capturing a potential endogeneity.
Table 2 presents the summary of statistics:
The statistical summary in
Table 2 of the data shows a similar farm structure in Austria and Switzerland, in contrast to the farms structures in Southern Germany. Similarities between means can be found for the total output from para-agriculture, labor units per farm, agricultural land and the animal-units per hectare. The output from agriculture is highest in Southern Germany and significantly smaller in Switzerland and Austria. The relative contribution of para-agriculture (
z1) is highest in Austria with 34% of the total farm revenue and moderate in Switzerland with 22%, but still substantially higher than the share of para-agriculture in the Swiss conventional sector, where the average share is about 3.2% [
19]. The average contribution of para-agriculture in Germany is low in comparison, at roughly 6% of the total farm revenue.