Effect of Species Complementarity on Financial Return in Mixed Stands of European Beech and Scots Pine in Northern Spain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Target Species
2.2. Data Sets
- The calculation of overyielding in mixed stands was carried out by means of one of the models developed by Sterba et al. [34] that used 695 permanent plots from the third and fourth Spanish National Forest Inventory (SNFI) located in the region of Navarre. Sixty nine out of the 695 plots were located in mixed stands of P. sylvestris and F. sylvatica. The remaining plots corresponded to monospecific pine or beech stands. A summary table of the database as well as a map showing the location of the plots can be respectively found in Sterba et al. [34] (p. 551) and Condés et al. [23] (p. 88).
- A data series on average stumpage price for both species covering the period 1976–2004 was obtained from the official forest statistics data [35]. It must be mentioned that the yearbooks published by the Ministry of Agriculture until 1976 did not collect data on stumpage price and since 2005 this information is not included in the official statistics.
2.3. Growth and Yield Assessment
2.4. Stumpage Price Scenarios
2.5. Financial Return and Risk Assessment
- is simulated pine price for rotation i in scenario j (€/m3).
- is pine timber stock in the mixed stand at age T (m3/ha).
- is simulated beech price for rotation i in scenario j (€/m3).
- is beech timber stock in the mixed stand at age T (m3/ha).
- T is rotation age in years
- cr is regeneration cost (€/ha).
- r is discount rate
- is average pine price (€/m3).
- is average beech price (€/m3).
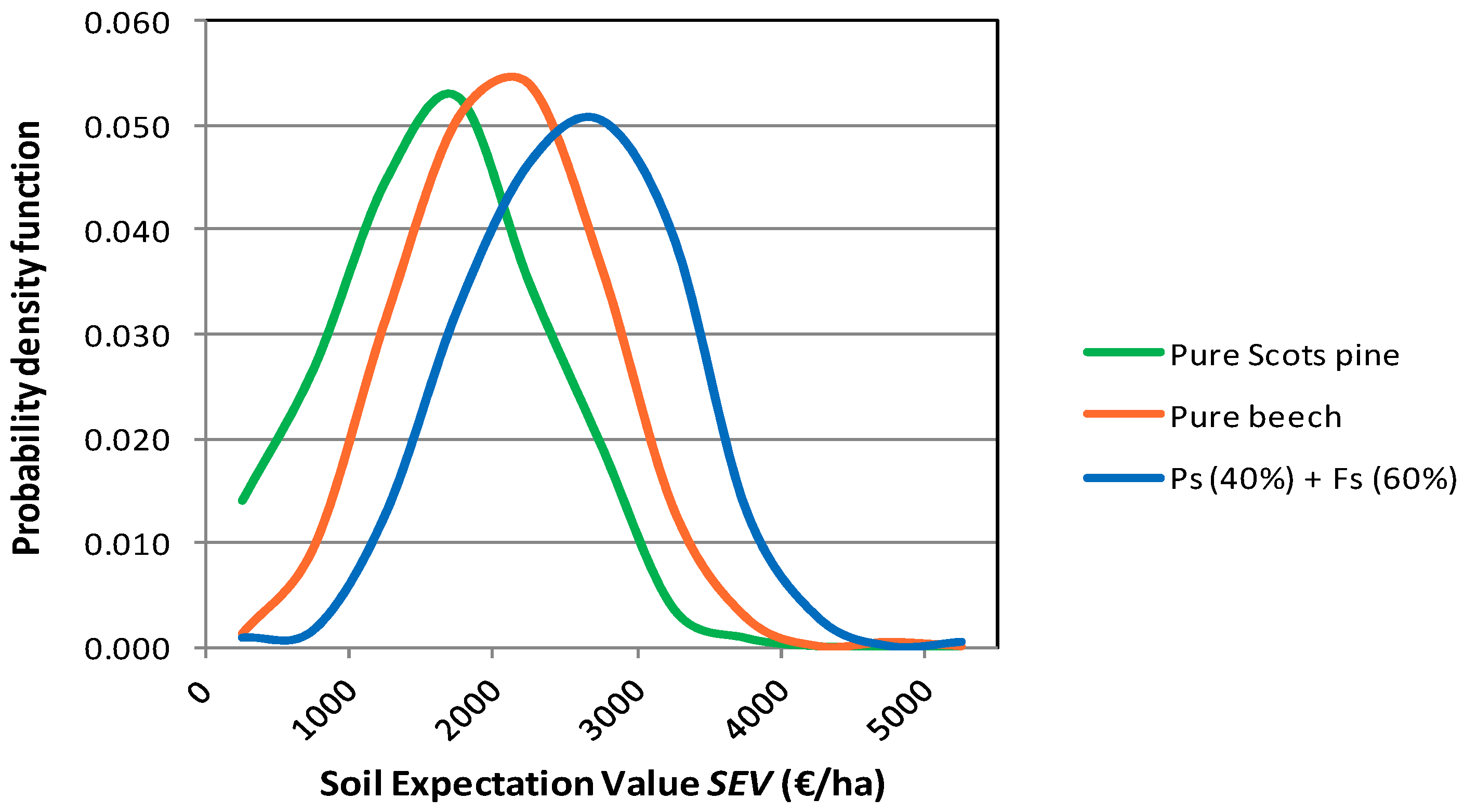
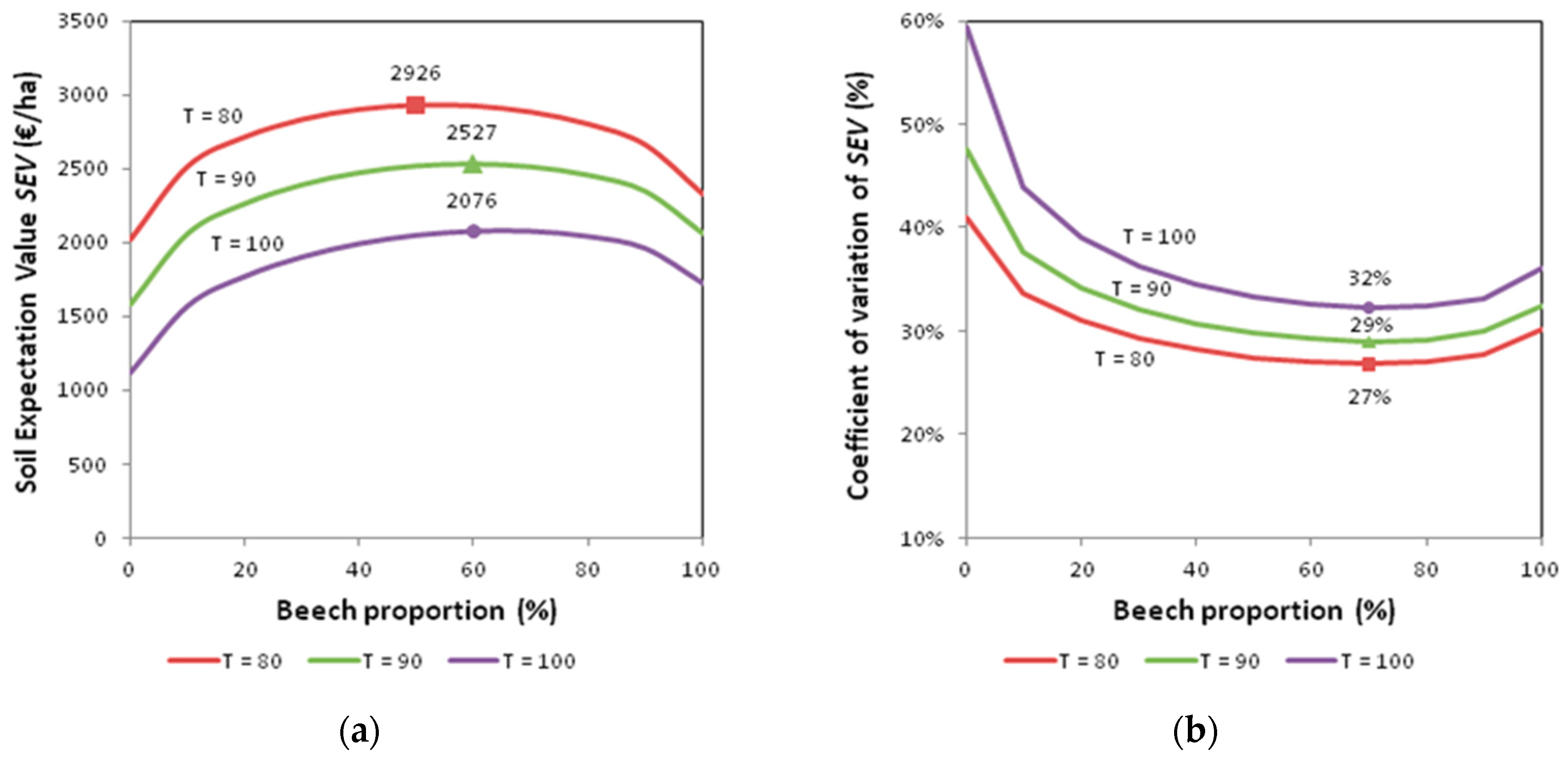
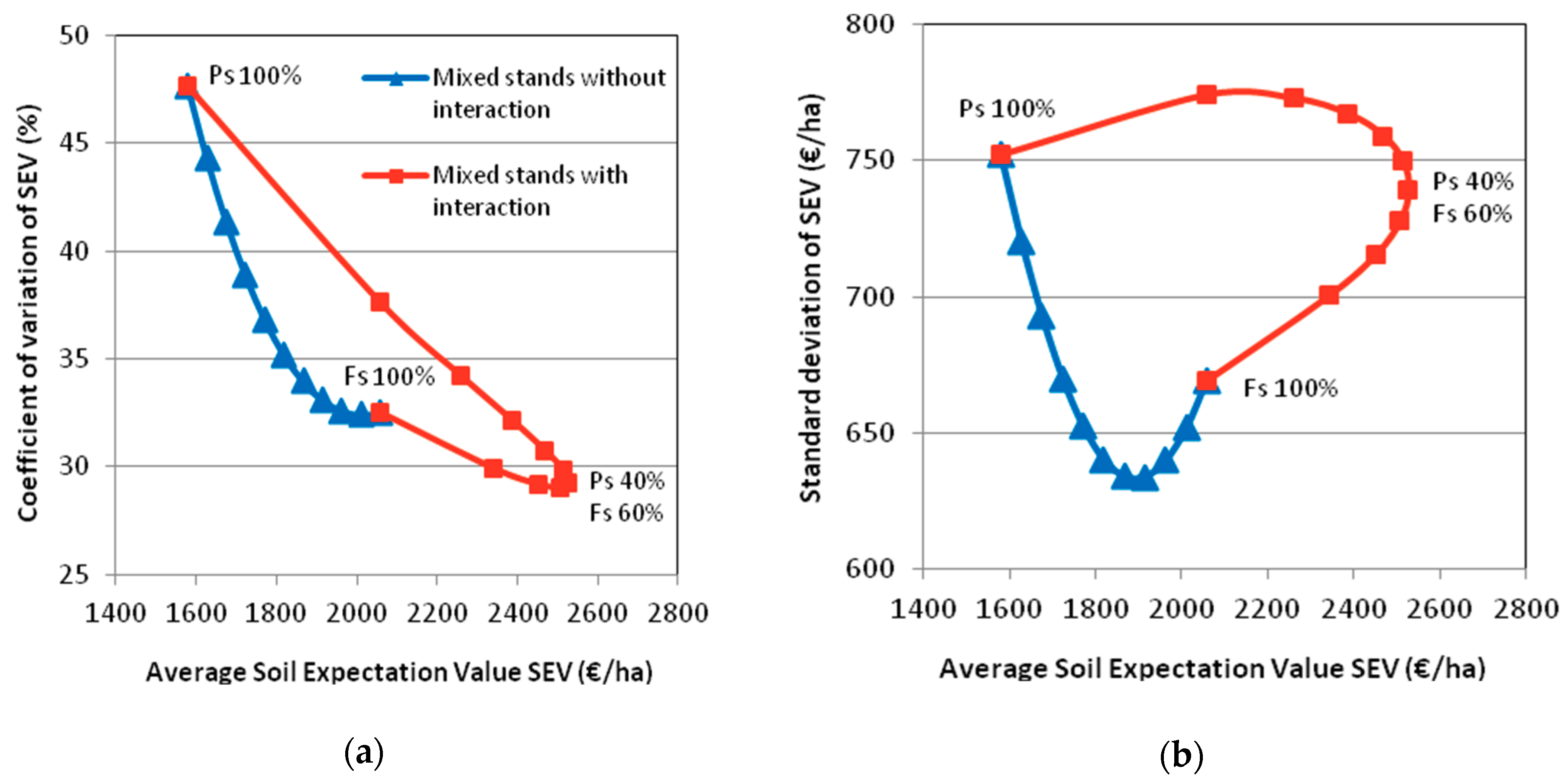
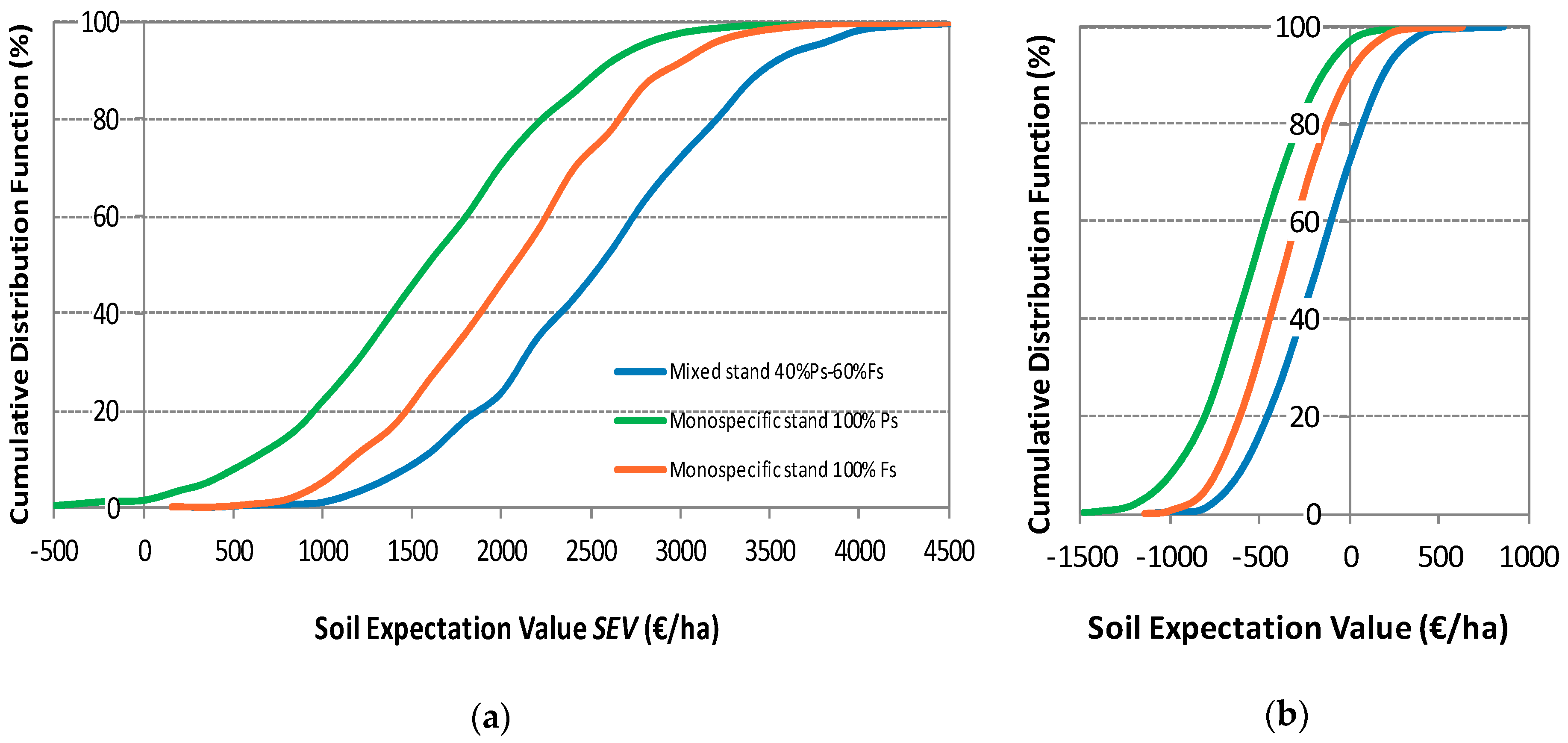
3. Results
3.1. Timber Yield
3.2. Financial Return and Risk
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Knoke, T.; Stimm, B.; Ammer, C.; Moog, M. Mixed forests reconsidered: A forest economics contribution on an ecological concept. For. Ecol. Manag. 2005, 213, 102–116. [Google Scholar] [CrossRef]
- Knoke, T.; Ammer, C.; Stimm, B.; Mosandl, R. Admixing broadleaved to coniferous tree species: A review on yield, ecological stability and economics. Eur. J. For. Res. 2008, 127, 89–101. [Google Scholar] [CrossRef]
- Kelty, M.J. Comparative productivity of monocultures and mixed-species stands. In The Ecology and Silviculture of Mixed-Species Forests; Kelty, M.J., Larson, B.C., Oliver, M.J., Eds.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 125–141. ISBN 978-94-015-8052-6. [Google Scholar]
- Wen, L.; Lei, P.F.; Xiang, W.H.; Yan, W.D.; Liu, S.T. Soil microbial biomass carbon and nitrogen in pure and mixed stands of Pinus massoniana and Cinnamomum camphora differing in stand age. For. Ecol. Manag. 2014, 328, 150–158. [Google Scholar] [CrossRef]
- Jactel, H.; Nicoll, B.C.; Branco, M.; Gonzalez-Olabarria, J.R.; Grodzki, W.; Langstrom, B.; Moreira, F.; Netherer, S.; Orazio, C.; Piou, D.; et al. The influences of forest stand management on biotic and abiotic risks of damage. Ann. For. Sci. 2009, 66, 701. [Google Scholar] [CrossRef]
- Cavard, X.; Macdonald, S.E.; Bergeron, Y.; Chen, H.Y.H. Importance of mixedwoods for biodiversity conservation: Evidence for understory plants, songbirds, soil fauna, and ectomycorrhizae in northern forests. Environ. Rev. 2011, 19, 142–161. [Google Scholar] [CrossRef]
- Oxbrough, A.; French, V.; Irwin, S.; Kelly, T.C.; Smiddy, P.; O’Halloran, J. Can mixed species stands enhance arthropod diversity in plantation forests? For. Ecol. Manag. 2012, 270, 11–18. [Google Scholar] [CrossRef] [Green Version]
- Gamfeldt, L.; Snäll, T.; Bagchi, R.; Jonsson, M.; Gustafsson, L.; Kjellander, P.; Ruiz-Jaen, M.C.; Fröberg, M.; Stendahl, J.; Philipson, C.D.; et al. Higher levels of multiple ecosystem services are found in forests with more tree species. Nat. Commun. 2013, 4, 1340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maraseni, T.N.; Pandey, S.S. Can vegetation types work as an indicator of soil organic carbon? An insight from native vegetations in Nepal. Ecol. Indic. 2014, 46, 315–322. [Google Scholar] [CrossRef]
- Nichols, J.D.; Bristow, M.; Vanclay, J.K. Mixed-species plantations: Prospects and challenges. For. Ecol. Manag. 2006, 233, 383–390. [Google Scholar] [CrossRef] [Green Version]
- Neuner, S.; Beinhofer, B.; Knoke, T. The optimal tree species composition for a private forest enterprise—Applying the theory of portfolio selection. Scand. J. For. Res. 2013, 28, 38–48. [Google Scholar] [CrossRef]
- Neuner, S.; Knoke, T. Economic consequences of altered survival of mixed or pure Norway spruce under a dryer and warmer climate. Clim. Chang. 2017, 140, 519–531. [Google Scholar] [CrossRef]
- Brunette, M.; Dragicevic, A.; Lenglet, J.; Niedzwiedz, A.; Badeau, V.; Dupouey, J.L. Biotechnical portfolio management of mixed-species forests. J. Bioecon. 2017, 19, 223–245. [Google Scholar] [CrossRef]
- Dragicevic, A.; Lobianco, A.; Leblois, A. Forest planning and productivity-risk trade-off through the Markowitz mean-variance model. For. Policy Econ. 2016, 64, 25–34. [Google Scholar] [CrossRef]
- Maraseni, T.N.; Cockfield, G. The financial implications of converting farmland to state-supported environmental plantings in the Darling Downs region, Queensland. Agric. Syst. 2015, 135, 57–65. [Google Scholar] [CrossRef]
- Vettenranta, J. Effect of species composition on economic return in a mixed stand of Norway spruce and Scots pine. Silva Fenn. 1996, 30, 47–60. [Google Scholar] [CrossRef]
- Lu, F.D.; Gong, P.C. Adaptive thinning strategies for mixed-species stand management with stochastic prices. J. For. Econ. 2005, 11, 53–71. [Google Scholar] [CrossRef]
- Griess, V.C.; Knoke, T. Bioeconomic modeling of mixed Norway spruce-European beech stands: Economic consequences of considering ecological effects. Eur. J. For. Res. 2013, 132, 511–522. [Google Scholar] [CrossRef]
- Kelty, M.J.; Cameron, I. Plot designs for the analysis of species interactions in mixed stands. Commonw. For. Rev. 1995, 74, 322–332. [Google Scholar]
- Pretzsch, H.; Block, J.; Dieler, J.; Dong, P.H.; Kohnle, U.; Nagel, J.; Spellmann, H.; Zingg, A. Comparison between the productivity of pure and mixed stands of Norway spruce and European beech along an ecological gradient. Ann. For. Sci. 2010, 67, 712. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schutze, G. Transgressive overyielding in mixed compared with pure stands of Norway spruce and European beech in Central Europe: Evidence on stand level and explanation on individual tree level. Eur. J. For. Res. 2009, 128, 183–204. [Google Scholar] [CrossRef]
- Forrester, D.I.; Kohnle, U.; Albrecht, A.T.; Bauhus, J. Complementarity in mixed-species stands of Abies alba and Picea abies varies with climate, site quality and stand density. For. Ecol. Manag. 2013, 304, 233–242. [Google Scholar] [CrossRef]
- Condés, S.; Del Río, M.; Sterba, H. Mixing effect on volume growth of Fagus sylvatica and Pinus sylvestris is modulated by stand density. For. Ecol. Manag. 2013, 292, 86–95. [Google Scholar] [CrossRef] [Green Version]
- Río, M.; Condés, S.; Sterba, H. Productividad en masas mixtas vs. masas puras: Influencia de la espesura en la interacción entre especies. In Proceedings of the Actas del 6º Congreso Forestal Español, Vitoria-Gasteiz, Spain, 10–14 June 2013; Sociedad Española de Ciencias Forestales: Madrid, Spain, 2013. ISBN 978-84-937964-9-5. [Google Scholar]
- Pukkala, T.; Vettenranta, J.; Kolstrom, T.; Miina, J. Productivity of mixed stands of Pinus-sylvestris and Picea-abies. Scand. J. For. Res. 1994, 9, 143–153. [Google Scholar] [CrossRef]
- Jonsson, B. Om Barrblandskogens Volymproduktion; English Summary: Yield of Mixed Coniferous Forest; Meddelanden från Statens Skogsforskningsinstitut; Statens Skogsforskningsinstitut: Stockholm, Sweden, 1962; Volume 50, 143p. [Google Scholar]
- Kerr, G.; Nixon, C.J.; Matthews, R.W. Silviculture and yield of mixed-species stands: The UK experience. In The Ecology of Mixed-Species Stands of Trees; Cannel, M.G.R., Malcolm, D.C., Robertson, P.A., Eds.; Blackwell Scientific Publications: Oxford, UK, 1992; pp. 35–51. [Google Scholar]
- Lu, H.C.; Condés, S.; del Río, M.; Goudiaby, V.; den Ouden, J.; Mohren, G.M.J.; Schelhaas, M.J.; de Waal, R.; Sterck, F.J. Species and soil effects on overyielding of tree species mixtures in the Netherlands. For. Ecol. Manag. 2018, 409, 105–118. [Google Scholar] [CrossRef]
- Maraseni, T.N.; Son, H.L.; Cockfield, G.; Duy, H.V.; Nghia, T.D. Comparing the financial returns from acacia plantations with different plantation densities and rotation ages in Vietnam. For. Policy Econ. 2017, 83, 80–87. [Google Scholar] [CrossRef]
- Ministerio de Medio Ambiente. Tercer Inventario Forestal Nacional: Navarra, Organismo Autónomo Parques Nacionales: Madrid, Spain, 2002; 340p.
- ADEMAN (Wood Producers Association of Navarre). Mercado de la madera. Revista Más Madera 2017, 11, 2–3. [Google Scholar]
- Madrigal, A.; Puertas, F.; Martínez-Millán, F.J. Tablas de Producción Para Fagus sylvatica L. en Navarra; Serie Agraria nº 3; Departamento de Agricultura, Ganadería y Montes, Gobierno de Navarra: Pamplona, Spain, 1992; p. 122. [Google Scholar]
- García-Abejón, J.L.; Tella-Ferreiro, G. Tablas de Producción de Densidad Variable Para Pinus sylvestris L. en el Sistema Pirenaico; Comunicaciones INIA, Serie: Recursos Naturales; Ministerio de Agricultura, Pesca y Alimentación: Madrid, Spain, 1986; Volume 43, pp. 1–28. [Google Scholar]
- Sterba, H.; del Río, M.; Brunner, A.; Condés, S. Effect of species proportion definition on the evaluation of growth in pure vs. mixed stands. For. Syst. 2014, 23, 547–559. [Google Scholar] [CrossRef]
- MAPAMA (Ministry of Agriculture, Fisheries, Food and Environment). Anuario de Estadística Agraria (1977–2005); Ministerio de Agricultura, Pesca, Alimentación y Medio Ambiente: Madrid, Spain, 2018; Available online: https://www.mapama.gob.es/es/estadistica/temas/publicaciones/anuario-de-estadistica/ (accessed on 3 July 2018).
- Instituto Nacional de Estadística (Spanish Statistical Office). Anuario Estadístico de España (1977–2005); Instituto Nacional de Estadística, Ministerio de Economía, Industria y Competitividad: Madrid, Spain, 2018; Available online: www.ine.es/prodyser/pubweb/anuarios_mnu.htm (accessed on 7 May 2018).
- González de Andres, E.; Seely, B.; Blanco, J.A.; Imbert, J.B.; Lo, Y.H.; Castillo, F.J. Increased complementarity in water-limited environments in Scots pine and European beech mixtures under climate change. Ecohydrology 2017, 10, e1810. [Google Scholar] [CrossRef]
- Pretzsch, H.; del Rio, M.; Ammer, C.; Avdagic, A.; Barbeito, I.; Bielak, K.; Brazaitis, G.; Coll, L.; Dirnberger, G.; Drossler, L.; et al. Growth and yield of mixed versus pure stands of Scots pine (Pinus sylvestris L.) and European beech (Fagus sylvatica L.) analysed along a productivity gradient through Europe. Eur. J. For. Res. 2015, 134, 927–947. [Google Scholar] [CrossRef] [Green Version]
- Houpert, L.; Rohner, B.; Forrester, D.I.; Mina, M.; Huber, M.O. Mixing Effects in Norway Spruce-European Beech Stands Are Modulated by Site Quality, Stand Age and Moisture Availability. Forests 2018, 9, 83. [Google Scholar] [CrossRef]
- Pandey, S.S.; Cockfield, G.; Maraseni, N. Dynamics of carbon and biodiversity under REDD+ regime: A case from Nepal. Environ. Sci. Policy 2014, 38, 272–281. [Google Scholar] [CrossRef]
- Maraseni, T.N.; Phimmavong, S.; Keenan, R.J.; Vongkhamsao, V.; Cockfield, G.; Smith, H. Financial returns for different actors in a teak timber value chain in Paklay District, Lao PDR. Land Use Policy 2018, 75, 145–154. [Google Scholar] [CrossRef]
- Roessiger, J.; Griess, V.C.; Knoke, T. May risk aversion lead to near-natural forestry? A simulation study. Forestry 2011, 84, 527–537. [Google Scholar] [CrossRef] [Green Version]
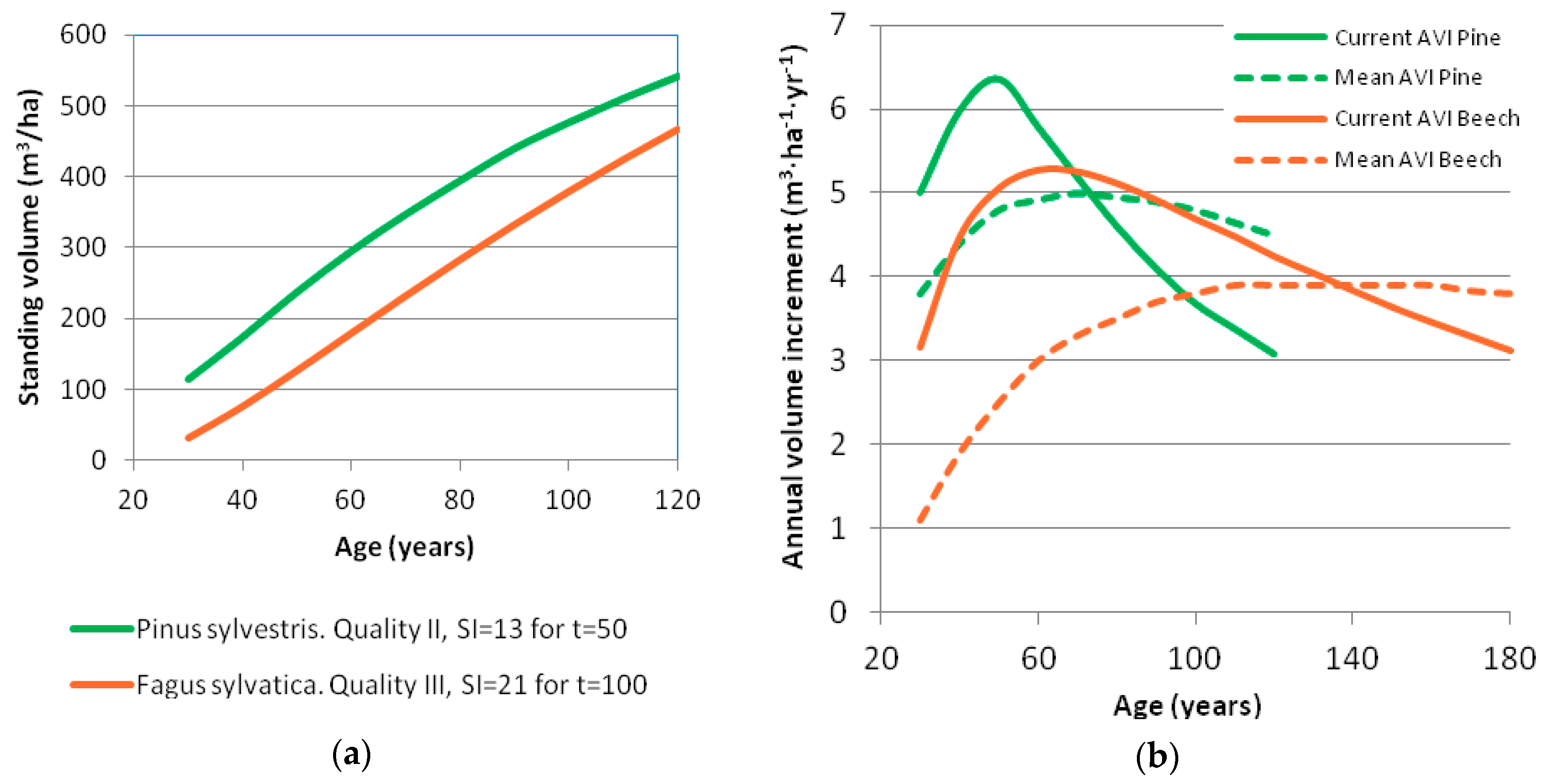
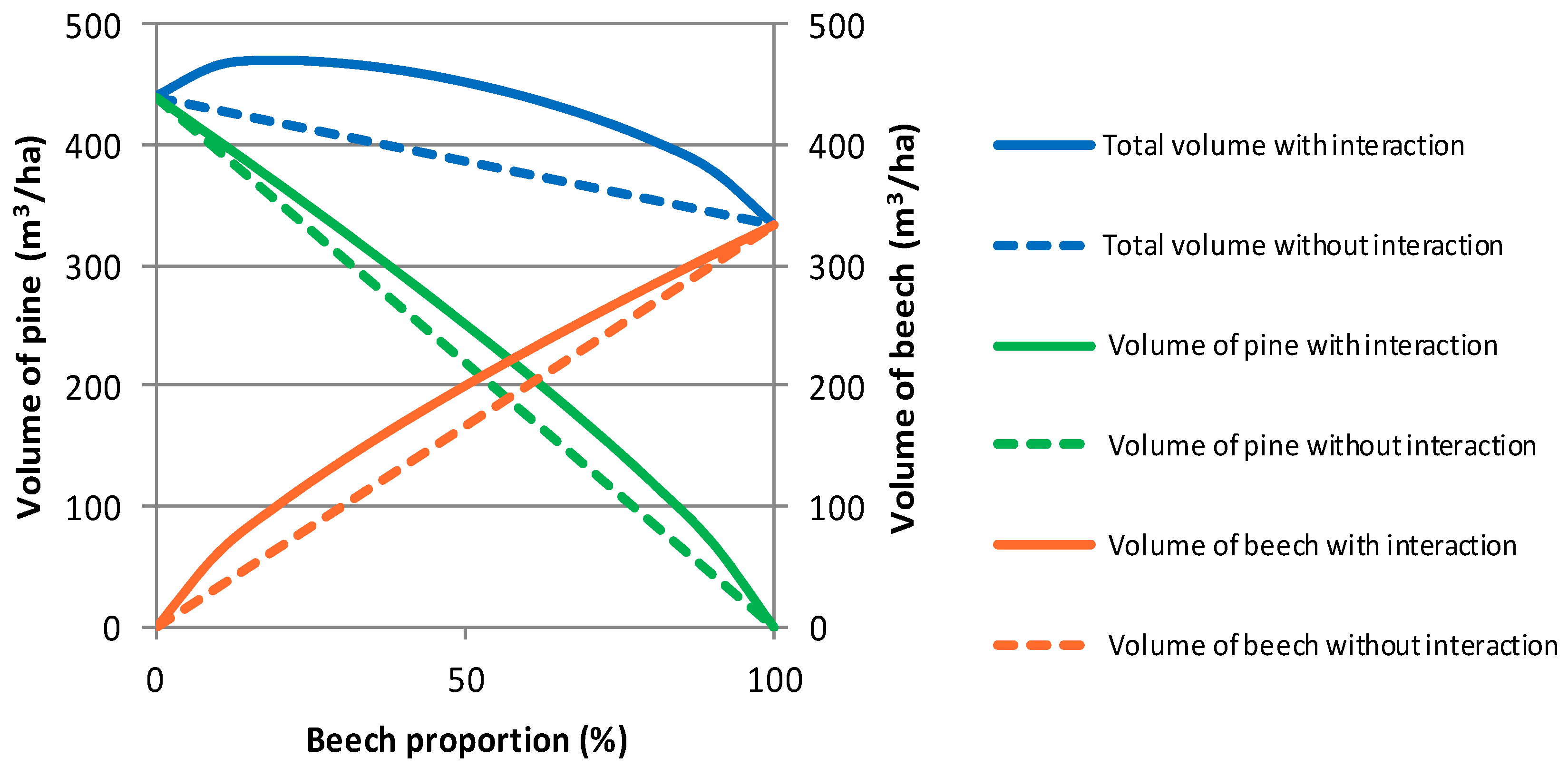
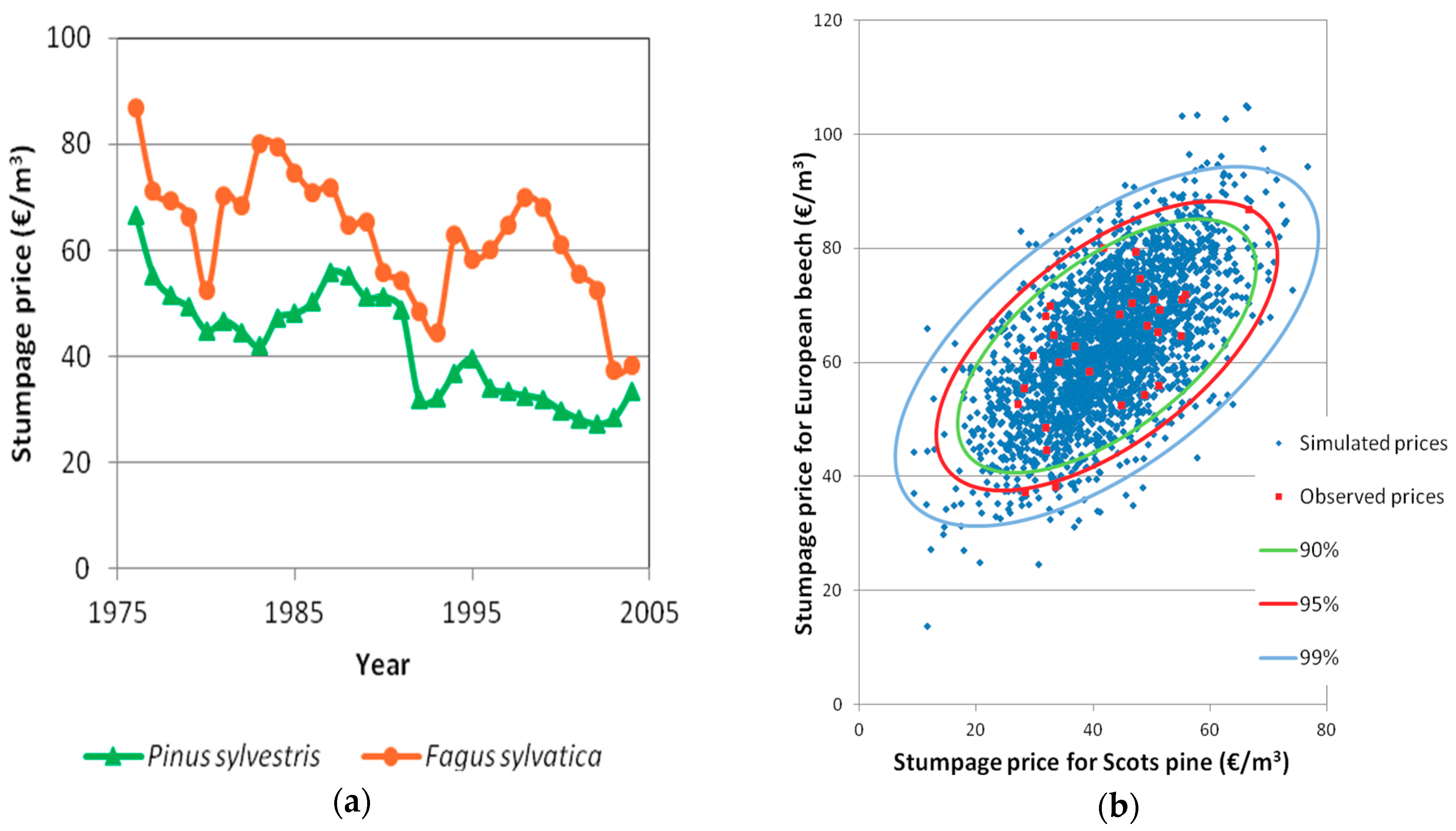
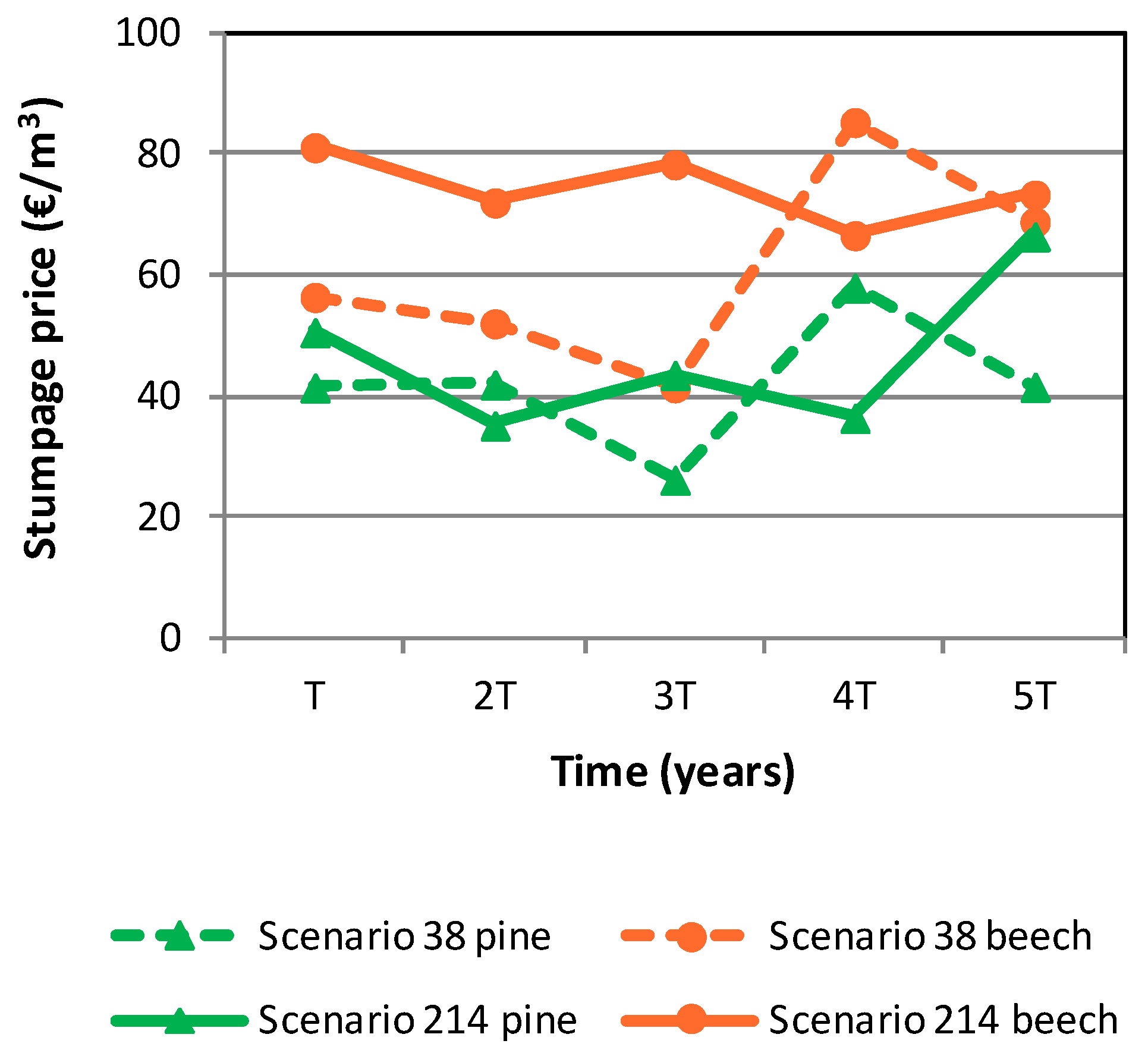
| Pine Proportion (%) | Beech Proportion (%) | Timber Stock at Age t (m3/ha) | |||||
|---|---|---|---|---|---|---|---|
| t = 70 | t = 80 | t = 90 | t = 100 | t = 110 | t = 120 | ||
| 100 | 0 | 347.6 | 395.1 | 440.5 | 477.3 | 511.1 | 541.9 |
| 90 | 10 | 360.8 | 414.7 | 466.3 | 509.4 | 549.4 | 586.1 |
| 80 | 20 | 359.3 | 415.9 | 470.1 | 516.2 | 559.1 | 598.7 |
| 70 | 30 | 353.8 | 412.0 | 467.7 | 515.9 | 560.9 | 602.5 |
| 60 | 40 | 345.5 | 404.7 | 461.4 | 511.1 | 557.6 | 600.7 |
| 50 | 50 | 335.0 | 394.7 | 451.9 | 502.5 | 550.1 | 594.4 |
| 40 | 60 | 322.4 | 382.1 | 439.3 | 490.6 | 538.8 | 583.9 |
| 30 | 70 | 307.5 | 366.7 | 423.5 | 475.0 | 523.6 | 569.1 |
| 20 | 80 | 290.0 | 348.1 | 403.8 | 455.0 | 503.4 | 548.9 |
| 10 | 90 | 268.2 | 324.3 | 378.2 | 428.4 | 476.1 | 521.0 |
| 0 | 100 | 232.2 | 283.4 | 332.6 | 379.5 | 424.3 | 466.7 |
| Pine Proportion | Beech Proportion | SEV | Cv | SEV | Cv | SEV | Cv |
|---|---|---|---|---|---|---|---|
| T = 80 Years | T = 90 Years | T = 100 Years | |||||
| (%) | (%) | (€/ha) | (%) | (€/ha) | (%) | (€/ha) | (%) |
| 100 | 0 | 2022 | 40.94 | 1579 | 47.62 | 1120 | 59.43 |
| 90 | 10 | 2514 | 33.65 | 2057 | 37.62 | 1571 | 43.91 |
| 80 | 20 | 2711 | 30.99 | 2259 | 34.21 | 1770 | 39.12 |
| 70 | 30 | 2829 | 29.32 | 2387 | 32.13 | 1902 | 36.32 |
| 60 | 40 | 2897 | 28.19 | 2469 | 30.75 | 1992 | 34.50 |
| 50 | 50 | 2926 | 27.43 | 2514 | 29.82 | 2048 | 33.29 |
| 40 | 60 | 2920 | 26.98 | 2527 | 29.25 | 2076 | 32.55 |
| 30 | 70 | 2879 | 26.82 | 2508 | 29.03 | 2075 | 32.23 |
| 20 | 80 | 2797 | 27.00 | 2452 | 29.19 | 2040 | 32.36 |
| 10 | 90 | 2657 | 27.70 | 2342 | 29.91 | 1959 | 33.15 |
| 0 | 100 | 2327 | 30.10 | 2058 | 32.51 | 1724 | 36.15 |
| Pine Proportion (%) | Beech Proportion (%) | Internal Rate of Return (IRR) % | ||
|---|---|---|---|---|
| T = 80 | T = 90 | T = 100 | ||
| 100 | 0 | 2.81 | 2.62 | 2.44 |
| 50 | 50 | 3.06 | 2.88 | 2.70 |
| 40 | 60 | 3.06 | 2.88 | 2.70 |
| 30 | 70 | 3.05 | 2.87 | 2.70 |
| 0 | 100 | 2.90 | 2.76 | 2.61 |
| Pine Proportion | Beech Proportion | SEV | Cv | SD | VaR |
|---|---|---|---|---|---|
| (%) | (%) | (€/ha) | (%) | (€/ha) | (€/ha) |
| 100 | 0 | 1579 | 47.62 | 752 | 338 |
| 50 | 50 | 2514 | 29.82 | 750 | 1277 |
| 40 | 60 | 2527 | 29.25 | 739 | 1307 |
| 30 | 70 | 2508 | 29.03 | 728 | 1307 |
| 0 | 100 | 2058 | 32.51 | 669 | 954 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García-Robredo, F. Effect of Species Complementarity on Financial Return in Mixed Stands of European Beech and Scots Pine in Northern Spain. Forests 2018, 9, 559. https://doi.org/10.3390/f9090559
García-Robredo F. Effect of Species Complementarity on Financial Return in Mixed Stands of European Beech and Scots Pine in Northern Spain. Forests. 2018; 9(9):559. https://doi.org/10.3390/f9090559
Chicago/Turabian StyleGarcía-Robredo, Fernando. 2018. "Effect of Species Complementarity on Financial Return in Mixed Stands of European Beech and Scots Pine in Northern Spain" Forests 9, no. 9: 559. https://doi.org/10.3390/f9090559





