Next Article in Journal
Failure to Communicate: Inefficiencies in Voluntary Incentive Programs for Private Forest Owners in Michigan
Next Article in Special Issue
Enhancing Forest Growth and Yield Predictions with Airborne Laser Scanning Data: Increasing Spatial Detail and Optimizing Yield Curve Selection through Template Matching
Previous Article in Journal
Genetic Diversity of the Black Mangrove Avicennia germinans (L.) Stearn in Northwestern Mexico
Previous Article in Special Issue
Object-Based Tree Species Classification in Urban Ecosystems Using LiDAR and Hyperspectral Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 7
Issue 9
10.3390/f7090198
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Full-Waveform Airborne Laser Scanning in Vegetation Studies—A Review of Point Cloud and Waveform Features for Tree Species Classification

by
Kristina Koenig
1,* and
Bernhard Höfle
1,2
1
Institute of Geography, Heidelberg University, Heidelberg 69120, Germany
2
Heidelberg Center for the Environment (HCE), Heidelberg University, Heidelberg 69120, Germany
*
Author to whom correspondence should be addressed.
Forests 2016, 7(9), 198; https://doi.org/10.3390/f7090198
Submission received: 19 May 2016 / Revised: 15 August 2016 / Accepted: 31 August 2016 / Published: 6 September 2016
(This article belongs to the Special Issue LiDAR Remote Sensing of Forest Resources)
Browse Figure
Versions Notes

Abstract

:
In recent years, small-footprint full-waveform airborne laser scanning has become readily available and established for vegetation studies in the fields of forestry, agriculture and urban studies. Independent of the field of application and the derived final product, each study uses features to classify a target object and to assess its characteristics (e.g., tree species). These laser scanning features describe an observable characteristic of the returned laser signal (e.g., signal amplitude) or a quantity of an object (e.g., height-width ratio of the tree crown). In particular, studies dealing with tree species classification apply a variety of such features as input. However, an extensive overview, categorization and comparison of features from full-waveform airborne laser scanning and how they relate to specific tree species are still missing. This review identifies frequently used full-waveform airborne laser scanning-based point cloud and waveform features for tree species classification and compares the applied features and their characteristics for specific tree species detection. Furthermore, limiting and influencing factors on feature characteristics and tree classification are discussed with respect to vegetation structure, data acquisition and processing.

Graphical Abstract

1. Introduction

In recent years, small-footprint full-waveform (FWF) airborne laser scanning (ALS) has become readily available and established for vegetation studies. This kind of data facilitates better sampling of the lower parts of tree crowns compared to data from discrete ALS and consists of the complete backscattered waveform information. Several geometric as well as radiometric features can be derived from these datasets. Geometric features are related to the XYZ coordinates of the point cloud and radiometric features refer to specific echo parameters that are extracted from the received waveform [1]. Such enriched point clouds offer an added value to features from discrete ALS for vegetation and forest mapping and for individual tree identification and classification [2,3]. Since 2004, FWF ALS systems are increasingly used for object detection and classification [4,5], and for the derivation of vegetation characteristics in forestry [6,7,8,9,10,11], agriculture [12], and in urban areas [13]. Research efforts focusing on vegetation are expanding due to an increasing need to quantify vegetation characteristics and to model environmental dynamics [14]. In particular, tree species information and the accurate identification of single trees is of great significance for sustainable forest management, ecosystem investigations and climate-vegetation relationships on the one hand, and for tree-related scientific research on the other [15].
The majority of vegetation studies with FWF ALS data input are conducted in the context of forestry research, aiming at a more accurate estimation of tree and forest stand parameters. The potential applicability of FWF ALS for estimating forest and tree characteristics has been shown for the derivation of forest and tree structure [16,17,18], canopy profile [19], leaf area index (LAI) [20,21], volume and above ground biomass [9,22,23], as well as for tree species classification [24,25,26,27].
Apart from forestry applications, 3D mapping of vegetation has gained increasing interest in urban data management as well as in ecological studies for monitoring and inventory issues. The richer spatial and radiometric information about the volumetric structure of trees from FWF data and the involvement of taxonomic information can assist in the assessment of biodiversity [2,28,29], animal ecology [30] or in the detection of invasive species [31]. Information on different tree species and their characteristics is also needed in urban environments [32], where both the presence and spatial variation of vegetation have a direct impact on radiation penetration and solar energy flux [33], evapotranspiration, microclimate and air circulation [34], and thus influence temperatures and air quality [2,35]. Many practical applications such as noise mitigation, reduction of air pollution, energy management and management of recreation areas rely on detailed up-to-date data sources. However, capturing detailed and classified data is challenging in urban environments, as these are associated with a high structural complexity involving different object types and a variety of geometric shapes. In contrast to closed forest stands, urban trees are characterized by large species diversity within small areas and a complex (typically anthropogenic) shape [13]. Here, FWF data can support the derivation of urban tree structure and species information [13,36].
Common to each study and application is the use of laser scanning features to capture the target object and its characteristics (e.g., tree species). Laser scanning features describe an observable characteristic of the returned laser signal (e.g., signal amplitude) or a quantity of an object (e.g., height-width ratio of the tree crown). Such features are available from the waveform and the point cloud directly or need to be derived by further processing (e.g., the backscatter cross-section by radiometric calibration [1]). Several studies and review papers on the use of FWF ALS data have been published and several of them deal with vegetation investigation and tree species classification, discussing the derivation and use of features for this purpose [37,38,39,40,41]. However, an extensive overview, categorization and comparison of FWF ALS-based point cloud and waveform features for tree species classification and how these features relate to specific tree species is still missing.
This review aims to fill this gap by identifying and evaluating frequently used and indicative point cloud and waveform features for tree species classification, which are derived from decomposed and partly radiometrically calibrated FWF ALS data. The focus here is on features, which are derived from data of previously detected/segmented single tree objects. Three key questions are addressed:
  • Which point cloud and waveform features have been used to classify trees into species classes?
  • How accurate are the classification strategies based on the derived features, and what are their limitations?
  • Which point cloud and waveform features have emerged as indicative features for a specific tree species?
This paper reviews peer-reviewed journal papers that investigate FWF ALS for tree species classification with special emphasis on derived FWF features. In order to form a comprehensive review, publications of international conferences (such as ISPRS Archives/Annals and SilviLaser) with a focus on tree species classification using FWF ALS data are regarded as well. The paper is divided into the following three sections: (1) overview of the derived and applied features for tree species classification (Section 2); (2) discussion of factors that limit and influence feature characteristics and tree species specific feature characteristics (Section 3); and (3) final conclusion and tabular summary of point cloud and waveform features (Section 4).

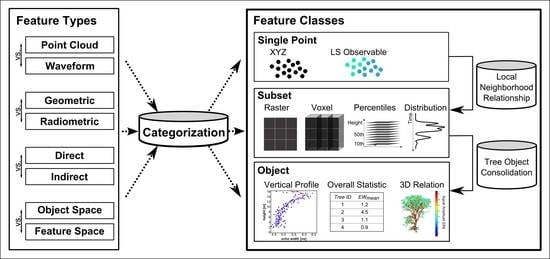
2. Derived and Applied Features for Tree Species Classification

Studies dealing with FWF ALS data and tree classification in particular, have varying terminology to describe the observables of the returned laser signal. Their terminology differs with respect to naming and abbreviation of the observables. For example, the received signal amplitude is defined as an attribute of the data in one study, while in others it is defined as a feature or parameter. The same applies for the combination of the observables for classification, which is described as model, feature set or saliency. Furthermore, varying abbreviations such as A, S1 or A0 for the received signal amplitude are used. These varieties hamper the comparability of results and discussion. Therefore, the terms feature and feature set are used to describe the observables of the returned laser signal and their combination for classification. The abbreviations refer to frequently used abbreviations within the studies or to acronyms of the feature naming in case of diverse abbreviations (Table A1 and Table A2).

2.1. Full-Waveform Data and Single Tree Classification

Information about the individual tree species and the subsequent estimation of species-specific derivatives is (among other parameters) required for forest management and is one of the biggest challenges in ALS-based inventories [42]. In contrast to discrete return laser scanners, full-waveform laser scanners record the complete backscattered waveform [5,43]. Instead of singular return locations, the FWF data reveal the detailed time-dependent distribution of the targets in the beam path and their physical backscattering properties of the transmitted laser pulse collected during its trip to the object surface and back [4,44].
Since the recorded waveform of highly vegetated areas is usually composed of several backscattered echoes, signal decomposition is performed in order to extract the different distinct targets along the path. To reconstruct the position, size, orientation and reflectance characteristics of scattering targets, [45] identify the following general tasks: (1) determination of the number of scatterers and (2) calculation of their distance from the scanner; (3) decomposition of waveform into single echoes; (4) calculation of additional echo parameters; and (5) radiometric calibration.
Most studies dealing with tree species classification perform the detection and extraction of single trees in a first step. Only laser scanning data associated with a detected tree are used for feature derivation and classification. The detection of single trees in general is conducted by considering the canopy height model [46,47,48] or the 3D point distribution within a defined neighborhood [49,50,51], as well as by adding pre-filtering steps and a hierarchical or a non-hierarchical rule base of further feature types. Most pre-filtering steps serve to exclude noisy data or to detect structure related characteristics. Commonly applied filters are the minimum height (Hmin) threshold and the number and index of return [13,27,52,53,54,55] as well as the features echo width [13,56,57,58,59,60,61,62,63,64,65], backscatter cross-section and backscatter coefficient [13,56,58,64,65].
Based on these detected single tree objects, different feature types are derived and combined to feature sets, which are then used for tree species classification. The features derived from FWF data cover features related to the point cloud and features related to the waveform. Due to the limited discussion of species-specific feature behavior and of single feature performance in tree species classification within the majority of reviewed studies, a general reflection of used features, successfully applied for classification (Section 2.2 and Section 2.3), is separated from a discussion of feature characteristics in relation to single tree species. The assignment of single features and their characteristic to a specific species is discussed in Section 3.2.

2.2. Derived Features for Tree Species Classification

The classification into tree species is achieved using laser scanning features. A laser scanning feature describes an observable characteristic of the returned laser signal. These features can be categorized into different types and the types can be assigned into two classes. A first distinction is made between the types geometric, radiometric and waveform features. Geometric features describe/represent the geometry of the tree object or of a part of the tree, e.g., a conical or rounded crown shape. Radiometric features describe/represent radiometric characteristics like the backscatter cross-section. While radiometric features are assigned to the single points of the point cloud, waveform features, in contrast, refer to the whole received waveform (e.g., the distance between two waveform echoes and the skewness of the waveform peaks). Secondly, these feature types can be assigned up to two classes, considering the different level of spatial correlation/aggregation. A distinction is made here between the class subset feature, which comprises/correlates a feature within a certain spatial subunit of the tree object (Table 1), and the class object feature, which comprises/correlates a feature with regard to the entire tree object (Table 2). The subunit is defined by a spatial neighborhood in 3D or 2D within the entire tree object (grid, raster, voxel, height layer bins and neighboring points). Subset and object features often reflect the statistics of a feature, like the mean echo amplitude of all echoes located within a single voxel cell and the mean height difference of the 10 nearest points of one point. In the following, the derived features of the studies are categorized by these feature types (geometric, radiometric and waveform) and assigned to the two classes (subset and object features).
Since the FWF systems measure the time-varying signal of the laser pulse, a theoretically unlimited number of returns per pulse and a higher point density can be achieved. Thus, the FWF ALS data may provide richer spatial information about the tree characteristics compared to discrete ALS data. Therefore, successfully derived and applied geometric features of discrete data are transferred to FWF data for tree species classification. For example, the number of echoes (TNo) within defined subsets of different height layers (TNorast,stats,filter [25,66]) and voxels (TNovoxel,column [55]) are used for a classification. These density measures are often normalized by the total number of echoes of the tree object (Pdens,bin,norm) [52]) or are compared with other density subsets, e.g., the ratio of number of echoes within a given search radius in 3D and 2D (ER3D/2D [26]). In addition, distance measures are derived for classification, like the mean horizontal distance of height layer points to the previously detected tree trunk (ΔDtrunk-dist,horiz) [52,53,66]. A different approach for considering the point neighborhood is chosen by [67]. The authors use the Haralick’s texture features (HTi) [68], and features which depend on the L-function (L(t)) and Delaunay triangulation. The Haralick’s texture features are calculated from the 3D gray level co-occurrence matrix which is based on the number of points per voxel in different XYZ directions. The L-function method is defined to derive K-function’s deviations from its expected value in a circle (with radius t) and to derive features from the L(t) curve. One example is the number of echoes, which are determined by the number of local minimums per height layer (Pdens,L-func_Npeak). The Delaunay feature (PTIN,Edge) defines the variance of edge lengths from triangulated points per height layer and their frequency distribution.
Besides considering geometric features, the statistics of waveform and radiometric features (e.g., echo amplitude and width, backscatter cross-section) are also calculated within a subunit [25,66]. The echo width is dependent on the amount, distribution and orientation of scattering elements along the laser beam direction. The height variations of small scatterers like needles of coniferous trees tend to broaden the echo width and groups of small scatterers are not separable anymore in the echo waveform [57,69,70]. Accordingly, a separation of different trees with varying structure can be expected by using the feature echo width. For instance, larch trees show higher averages in echo width compared to oaks (Quercus robur and Quercus petraea) and beeches (Fagus sylvatica) [47] and a higher standard deviation compared to spruce trees (Picea abies) [26] in particular in the upper crown layers (EWstats,h-layer).
The object feature class comprises/correlates the features with regard to the entire tree object. The object features are calculated from individual detected echoes [24,52,53,73], the complete recorded waveforms [24,55] and from prior aggregated subsets like raster cells [25], voxels [55] and metric or percentage height layers [11]. A summary of all regarded object features is shown in Table 2.
Geometric object features derived by fitting forms to the shape of point clouds are usually applied to prior detected crown echoes and forms like ellipsoids [73], parabolic surfaces [52,66,73], convex hull [49] and alpha shape [66,74]. Derived features are the vertical length (Zobj,ellip, PSheight) and radius (PSradius) of the fitted surface and subsequent function parameter (PSa, PSb). Applied crown features for species classification are the ratio of crown length and tree height (CRlt), the ratio of crown length and width (CRlw) and the crown volume (CRvol). Such geometric features were already applied for discrete echo data to classify pine, poplar and maple trees with an overall accuracy of 88.8% [75]. In particular, maples are classified with a high producer’s accuracy (95.9%). However, pine and poplar trees have similar CRlw.
Applied object features of radiometric and waveform features are the statistics of the number of returns of all waveforms (TNowave,stats), the amplitude (Astats,obj), the echo width (EWstats,obj), the backscatter cross-section (σstats,obj) and of the product of echo amplitude and width (EAW). The waveform-related object statistics RWE and Hm,energy of the returned waveform energy are used to differentiate between pine, spruce, linden and fir [24] and between pine, spruce and birch [76]. These two features are supplemented by the total pulse length for classifying Scots pine, Norway spruce and birch [27]. The distance between two waveform echoes are calculated by time difference (ΔTij, in ns) [55] and by difference in range (ΔRij, in m) [76]. The distances between waveform metrics such as the distance between waveform beginning and centroid to ground (ΔWRij) are among other features applicable for classifying different coniferous and broadleaved species of subtropical forest [15].
In addition to statistical measures, features with regard to the spatial distribution of radiometric characteristics of the entire tree are used for classification. Frequently analyzed vertical distribution curves are the number of echoes per height layer (VH) and the values of amplitude (VA), echo width (VEW) and backscatter cross-section (Vσ) over tree height [47]. As an example, the needles of larch trees (Larix decidua) induce higher echo width values in the upper canopy in comparison to the foliage of oak trees (Quercus robur and Quercus petraea), which have relatively constant values over tree height [47].

2.3. Applied Feature Sets for Tree Species Classification

The above discussed feature types and classes are usually combined for tree species classification (Table A3). The combined object statistics of (range corrected) amplitude, echo width, the product of echo amplitude and width and the number of echoes are suitable to classify Scots pine (Pinus sylvestris), Norway spruce (Picea abies), red oak (Quercus rubra) and European beech (Fagus sylvatica) of a German forest [25] and red pine (Pinus koraiensis), Koyama spruce (Picea koraiensis), Dahurian larch (Larix gmelinii), fir (Abies nephrolepis), white and ribbed birch (Betula platyphylla Suk. and Betula Costata), linden (Tilia Mandschurica) and Mongolian oak (Quercus Mongolica) of a forest in north-east China [24]. Higher accuracies are achieved at tree class level at both sites (Germany: 91.7% vs. 80.4%, China: 85.7% vs. 55.1%), and at the Chinese forest site, the corrected amplitude showed a six percent higher accuracy for corrected than for uncorrected amplitude data.
The proposed feature set in the study of [66] is supplemented by statistics per height percentile of elevation values, A, EAW and EW and filtered by the index of return. The classification of spruce (Picea abies), beech (Fagus sylvatica), fir (Abies alba) and maple trees (Acer pseudoplatanus) achieves an overall accuracy of 95% (leaf-on) and 94% (leaf-off) and higher accuracy for the lower height layers in a leaf-off condition (95%) than in leaf-on (86%). The most important feature under both conditions is the mean EAW per tree. The mean echo width works better for leaf-off data. The percentiles of the number of ALS echoes and the percentage of echoes in a specific tree layer have little impact on the classification.
Waveform features proved to be appropriate for the classification of Scots pine (Pinus sylvestris) when distinguishing between Norway spruce (Picea abies) and birch (Betula sp.), achieving a producer’s accuracy of 85.9% and an overall accuracy of 71.5% [76]. Birch and spruce tend towards higher misclassification. The most important features are the range difference between echoes (ΔR1st/last), the height of received waveform energy (Hm,energy) and the sum of peak amplitudes (Asum,obj) per waveform. The combination of these waveform features with the statistics of peak amplitudes, the full-width-half-maximum, the total length of a pulse and the height at which 50% of the waveform energy is received classify the three tree species as well [27]. Most important for classification is the energy of single returns.
A further approach to waveform feature derivation is taken by [55]. They compute the Principal Components (PC) of Fourier variables, which result from discrete Fourier transformation of each waveform. By adding these features to geometric subset features, the overall classification improves by 6% up to 85.4%. In particular, the differentiation between Douglas fir (Pseudotsuga menziessi (Mirb.) Franco) and red cedar (Thuja plicata Donn ex D. Don) benefits from PC-Fourier features. The coniferous (Pinus massoniana Lamb. and Pinus elliottii Engelm., Cunninghamia lanceolate (Lamb.) Hook.) and broadleaved species (Quercus acutissima Carruth., Liquidambar formosana Hance, Ilex chinensis Sims.) at a subtropical forest site are classified by [15] by using only features of an aggregated distribution function (ΔWRcentroid,ground, ΔWRbeginning,ground, ΔWRbeginning,1stpeak, TNowave,stats, FS, RWE). All waveforms belonging to a detected tree are incorporated into distribution functions (the authors call it ‘composite waveforms’) utilizing a voxelized tree space on the waveform parameters (peak value and peak width). These features achieve an overall accuracy of 86.2% at the class level and of 68.6% at the species level. The distance between the centroid of the distribution and the ground (ΔWRcentroid,ground) is proven to be very useful for discriminating tree species.
For classifying Norway spruce (Picea abies (L.)), Scots pine (Pinus sylvestris (L.)) and birch (Betula pendula (L.) and Betula pubescens (L.)) in a Swedish forest, the statistics of amplitude, echo width and number of echoes per waveform are supplemented by geometric subset features from deduced ellipsoid fittings (Zobj_ellip, PSheight, PSradius) to the tree crown’s point cloud [73]. The combination of statistical measures and geometric features achieves an overall accuracy of 71% and an accuracy of 60% when using geometric features only. However, the ellipsoidal tree crown model fails for trees with understory and leads to erroneous fitted forms. The effectiveness of geometric subset features in regard to tree structure is tested by [67]. They derive features from point distribution in vertical and horizontal dimensions within previously detected tree crowns. Four types are distinguished: (1) 3D texture features based on calculation of Haralick’s texture features (HTi) of voxels, which are averaged over varying directions in space; (2) relative degree of foliage clustering defined by gridded height layer number and its point pattern (e.g., Pgrid,VTMR); (3) relative scale of foliage clustering calculated from the L-Function of the 2D density layer (e.g., Pdens,L-func); and (4) gap distribution in horizontal and vertical direction (e.g., edge statistics of calculated TIN, PTIN,Edge). Those features achieve an overall accuracy of 82.2% at the class level and of 77.5% at the species level for classifying jack pine (Pinus banksiana Lamb.), eastern white pine (Pinus strobus L.), sugar maple (Acer saccharum Marsh.) and trembling aspen (Populus tremuloides Michx.). The major structural difference among the species occurs at the top crown layer rather than middle and low stem layers. For example, aspen trees tend to exhibit clumped crowns at the top layers compared to other species. These clumped crowns have higher variance-to-mean ratio (VTMR) of echo pattern and negative value of L(t) in comparison to the distributed foliage along the stem of maple trees (VTMR < 1, positive L(t)).

3. Discussion

3.1. Influencing and Limiting Factors on Feature Characteristic and Tree Classification

The variety of features that can be derived from FWF ALS data enables the classification of tree species. However, the feature characteristics are affected by (1) factors related to vegetation structure (e.g., species stand age and forest stand structure); (2) technical factors related to the sensor settings, flight and data acquisition parameters (e.g., flying altitude and illuminated target size) and (3) factors related to data processing (e.g., waveform decomposition, crown delineation and data filtering) [27,77,78].

3.1.1. Factors related to Vegetation Structure

The crown shape differs according to tree species, local tree competition and growth age as well as treatment history [79,80]. For example, Scots pine trees tend towards a conical shape when young and a rounded and irregular shape as they mature [81]. Beeches, by contrast, respond rapidly to varying light conditions, which lead to a modified unstable relation between crown dimension and stem volume [15,66]. Hovi et al. [27] point out that such tree effects explain the majority (>44%) of the within species variance of waveform energy, pulse length and peak amplitude. For example, suppressed pine trees tend to slender trunks and lower foliage mass and density, as they try to reach the dominant canopy and thus show a lower waveform energy and peak amplitude compared to dominant pine trees. Suppressed broadleaved trees grown below the general level of crown cover reveal a generally lower classification accuracy [15]. In particular, the canopy openness and the vertical arrangement of canopy elements affect the penetration depth and thus the variation of waveforms within the tree crown. Tree crowns with densely packed woody materials and foliage reduce the number of pulses that can penetrate and reach the ground and increase ΔWRcentroid,ground, whereas for more transparent crowns, more pulses can pass through and decrease ΔWRcentroid,ground. This is also connected to the time of data acquisition, as no or only a few leaves enable a higher penetration rate and cause differences in amplitude and width of the waveform peaks. For instance, the simulation of scanning a broadleaf deciduous tree stand of Acer rubrum and Quercus rubra demonstrated much a larger amplitude and width of the peak for the leaf-on case and wavelength of 1064 nm [82]. This vertical arrangement of scattering elements influences the backscattered echo width, and height variations of small scatterers tend to broaden the return pulse [70].

3.1.2. Technical Factors related to Data Acquisition and Processing

Furthermore, technical factors such as flying height, scanning angle as well as the waveform sampling and processing affect the usability of features and hamper the transferability of derived feature thresholds.
A low point density due to a high flying height above ground level and a low sampling rate results in a varying (geometric) representation of vertical profile features and classification accuracy for the same tree. The same feature derivation and classification step for decreased point density and increased voxel size, respectively, is applied by [67], and shows a positive linear correlation (R2 = 0.88) between point density and classification accuracy. A minimum point density of 50 points per square meter is required to achieve a classification accuracy higher than 70%, but 5 points per square meter are enough to achieve an accuracy of 50% (original 90 points m-2 flown at 300 m above ground level with a Riegl LMS-Q560). Although the used vertical profile features are still effective at lower point densities, the authors state that higher densities are necessary to extract structural parameters.
Besides this point density effect, the range and beam divergence determine the size of the laser footprint area. The laser beam diverges from its nominal direction with range and creates a narrow conic shape. The transmitted energy is spread over the footprint area and its intensity decreases towards the edges of the beam. Within the footprint area, a variable amount of scatterers is encountered. These scatterers, mostly with different sizes and orientations in the case of vegetation, affect the power and shape of the backscattered waveform and consequently the derived features.
A further influencing factor is the derivation of normalized height values. The tree height and crown shape are often delineated by finding the local maxima and the connected points. The height normalization by subtracting the DTM from the non-ground elevation might be straightforward in flat areas, but in the presence of slope, this leads to a horizontal displacement of tree location and a local distortion of the point cloud geometry within the tree crown. Therefore, [81] and [83] accordingly recommend a normalization considering the slope. One possible approach is normalization after point-based segmentation for each detected tree [84]. The tree’s point cloud is normalized using the ground elevation under the highest point of the crown as a reference for the rest of the point cloud.
The representation of vertical profile features and vegetation metrics in forested areas is also influenced by the scan angle [15,17,85]. In particular, a difference in canopy penetration depth due to varying incidence angles has been observed in areas with a large variation in tree height. While larger incidence angles (>10°) provide more information about the lower parts of the canopy, narrower scan angles increase the likelihood of obtaining returns from the ground [86]. With more detailed capturing of the lower layers, a precise derivation of the crown base becomes possible. This enhances the correctness of crown-related features and their applicability for subsequent classification. However, a more detailed representation of the lower layers increases the detection of understory as well. The understory included in the dataset may affect and distort the feature calculation, and thus further pre-processing is needed to remove it. The effect of the scan angle on waveform-based features (like ΔWRij) on classification accuracy is evaluated by [15], revealing no significant difference (~2%) in the overall accuracy when comparing the same features for waveforms of scan angles of <15° and of 15–30°.
When using features extracted from waveforms, several studies assume a perfectly nadir perspective of the laser beam and do not account for a slanted penetration of the laser beam in feature derivation. Subsequently, the information derived from the waveform is supposed to describe the tree crown vertically. However, off-nadir measurements and varying trajectories of overlapping strips may lead to uncertainties in spatiotemporal analyses due to the influence of the scan angle on the recorded signal strength. The signal strength and the receiver’s sampling rate and sensitivity induce relative shape differences in the waveforms, especially in fast rising 4 ns pulses [27]. To overcome these effects, a waveform normalization step is needed, comparable to radiometric calibration. The few studies dealing with such normalization (prior classification) combine all waveforms to distribution functions (DF). The pseudo-vertical waveform, as [87] call them, can result from the computation of cumulative waveforms from the sum of all signals falling within a tree crown boundary [22] or the voxel-based derivation and calculation of the mean and maximum waveform amplitude in each voxel [15,87,88,89]. Hermosilla et al. [87] state that such waveform distribution functions provide denser and more continuous coverage and enhance the characterization of vegetation. Thus, more crown structure information is retrieved and a more consistent response at adjacent height levels is provided. However, the voxel size has to be carefully selected and should consider the laser footprint size, crown diameter, and average ground spacing of pulses [15]. If the horizontal voxel size is lower than the laser footprint, many incomplete DF of waveforms are produced and the number of newly formed DFs is much higher than the directly observed raw waveforms. In contrast, a larger voxel size tends to produce over-synthesized DFs and consequently, a loss of detailed geometric and radiometric information.
The occurrence of multiple echoes and the number of echoes in general depends on certain sensor settings (e.g., beam width and waveform sampling interval) and waveform processing [90]. A larger beam width and a higher waveform sampling interval increase the chance of multiple echoes. Further, a more sensitive waveform decomposition algorithm may lead to a higher number of echoes [5]. However, single objects (e.g., branches and leaves) can only be detected as separate objects if their distance is larger than the half of the pulse length. For example, this distance is 0.6 m for a pulse length of 4 ns (recorded by the Riegl LMS-Q680).
This is also connected to the echo width and subsequent feature derivation and threshold transferability. Values have to be considered carefully, since the width depends on the strength of the received pulse [60,65]. To tackle this problem, [60] and [63] apply a normalization procedure in an urban environment, receiving an overall classification accuracy (>93%) and correctness (93%) for trees. Lin [60] uses the concept of Fuzzy Small membership functions in a defined neighborhood and [63] normalize the echo width by its minimum EW and maximum EW, which is found by using quantiles of the distribution of echo width. Such approaches improve the transfer of thresholds of normalized echo width from region A to region B.
Vegetation is usually represented by heterogeneous targets within the illuminated footprint with diverse geometric representation (e.g., area, orientation) and reflectance properties (e.g., leaves or needles, thin and thick branches and tree trunk). The reflectance properties of the scattering elements differ between the commonly applied wavelengths of 1064 nm and 1550 nm and influence the intensities of the returned energy [27,91,92]. For example, the returned intensities from leaves are similar to trunks/branches at 1064 nm and lower at 1550 nm, where leaf scattering is strongly attenuated by liquid water absorption. Using the backscattered signal strength for purposes of detection and classification requires a radiometric calibration, since it depends on various factors such as emitted pulse, range, incidence angle and atmospheric conditions. Hence, the recorded amplitude values would vary for a given target, even within a single dataset, and require the values to be converted to absolute physical quantities especially for multi-temporal analysis and for data from different ALS systems. The physical principles of radiometric calibration of FWF ALS data are discussed in several studies [1,93]. The resulting physical quantity is the backscatter cross-section σ, which represents the characteristics of the reflecting target accounting for its size, reflectivity and directionality of scattering [43].
The backscatter cross-section constitutes a physical property and is independent from the transmitted laser pulse. It has shown good performance for vegetation classification [13,56,65]. Wagner et al. [65] recognize a variety of σ within forest canopies and identify an influence of tree species and tree structure. Furthermore, σ is affected by the beam width, the flying altitude and the resultant variation in energy of the returned signal and area of the laser beam footprint on the target. For example, [65] reveal a σ of <0.08 m2 for vegetation (flying altitude: 500 m, footprint: 0.25 m) whereas [64] reveal a σ of >0.6 m2 (flying altitude: 1900 m, footprint: 0.95 m). This makes it difficult to compare σ of targets with similar scattering properties. Therefore, the use of γ, defined as the normalized measure of σ regardless of the area of the footprint, is advantageous [56]. In the case of vegetation, where the target surface, e.g., leaves, is smaller than the laser footprint, the actual illuminated target area is unknown. However, γ depends on the number of echoes per laser shot from the trees [56,58]. For multiple returns, the γ is smaller than for single returns. Echoes with a single peak might represent extended targets and their parameters can be directly related to the target’s radiometric properties.
The selection and implementation of methods for feature derivation also have an impact on feature characteristics. Resulting errors in tree segmentation may increase the likelihood of outliers, which influence the feature statistics (e.g., Amean per tree). Hovi et al. [27] compare the features derived by watershed segmentation (WS) and manual tree segmentation (MS) and analyze the impact on classification. They show that echo width has a higher weighting for MS-based classification and lower weighting for WS-based classification. A prior detection and removal of outliers to derive a more robust classification is recommended [54].

3.2. Tree Species Specific Feature Characteristics

Full-waveform airborne laser scanning provides features for tree species classification at varying taxonomic levels. Depending on the species composition (coniferous and deciduous trees) and period of data acquisition (leaf-on and leaf-off), the applied features for species classification vary. Some features are better suited for certain species than for others. Table 3 summarizes these feature characteristics for the major tree species within the different studies.
For the differentiation between coniferous and deciduous trees, features related to the different crown shape and structure have to be used. The coniferous trees of the reviewed studies show a higher canopy density (TNoobj, Hmin) [26] and a higher ratio of single reflections (ERsingle/multiple,obj) [66] under leaf-off condition and more canopy gaps (PTIN,Edge) [67] under leaf-on condition compared to deciduous trees. Furthermore, coniferous trees tend to display a higher backscatter cross-section [47] and the usage of amplitude features is more suitable under leaf-off condition than under leaf-on [52,53,94]. Generally, higher accuracies have been achieved under leaf-off condition when classifying at class level (coniferous and deciduous) compared to leaf-on data.
Among tree species, major structural differences occur at the top crown layers and at the bases of the living crown. In particular, features related to penetration rate and biophysical properties of the top layers are advantageous for species classification. Pine trees show a lower mean amplitude and a lower mean echo width than the deciduous trees, as well as a lower number of echoes for each crown under leaf-on condition [27,73]. The lower amplitude may be due to the spectral and geometrical properties, meaning that pine trees reflect less light and have less tree crown density with fewer main branches [73]. Furthermore, pine trees have a higher proportion of single returns at the 90th height percentile, as shown by studies on discrete ALS data [75,95,96]. This difference in the spatial distribution enables the differentiation between pine and spruce [73]. Spruce trees show narrower echo widths and a lower standard deviation of echo width [26,27], which could be due to a dense surface of needles and rather horizontal branches, and the low height variation of the scatterers within the laser footprint. During leaf-off season, the surface of a larch is more heterogeneous than that of a spruce and therefore the height variation of the scatterers within the laser footprint is higher. The upper crown parts of larch trees have higher values of echo width and backscatter cross-section [26].
The features for deciduous tree species differ through the phenological cycle. Radiometric features of needles and leaves are less different in leaf-on than needles and bark in the leaf-off season [52]. The number of echoes (TNo) in the lower height layers is higher under leaf-off than under leaf-on conditions. The ratio of single and multiple echoes (ERsingle/multiple,obj) is the best feature for classification of beech and maple under leaf-off. The crown density varies between deciduous species in the same season and allows a classification by waveform-based features. Vaughn et al. [55] classify bigleaf maple by the small inter-peak distance (ΔRij) and differentiate red alder and black cottonwood with an 80% accuracy by relative height percentiles. A structural difference of maple, white pine, jack pine and aspen is recognizable at the 14th height layer (≈crown base) [67], where maple and white pine have more leaves and branches distributed randomly (positive L(t)) than aspen and jack pine (negative L(t)) in leaf-on season. Furthermore, growing understory is more often detected under maples trees than under coniferous trees, which makes the detection of the crown base more difficult. Comparing the penetration features, poplar trees have a higher number of last returns closer to ground level in foliated season.
The waveform and radiometric features have the strength to classify oak and beech species in leaf-off season [47]. Both species belong to the family of Fagaceae and show relatively constant average values for echo width (VEW) and decreasing backscatter cross-section (Vσ) over the height profile. Small oaks have a lower average value in backscatter cross-section compared to taller trees in the same area. The sparse and evenly distributed foliage of birch crowns in leaf-on season induces widened returns with lower peak amplitudes [27].

4. Conclusions

This review gives a detailed overview of derived point cloud and waveform features of small footprint full-waveform airborne laser scanning data for tree species classification. The advantage of full-waveform features compared to features derived from discrete returns is due to the available waveform information that can be either accessed directly or derived by further processing. Furthermore, a higher point density and a theoretically unlimited number of returns that are recorded for each emitted pulse are present. The reviewed literature clearly shows that these FWF features, which reflect the geometric and radiometric characteristics of single trees, have the potential to improve tree species classification accuracies. Moreover, geometric feature types, already successfully applied to discrete data, have been transferred to FWF point cloud data. All subset and object features used for classifications are shown in Table 1 and Table 2. Main species-specific feature characteristics are summarized in Table 3.
For the classification of trees, features related to the backscatter signal strength at the upper crown parts (e.g., echo width at 90th height percentile) and the vertical distribution of scatterers (e.g., ratio of crown length and width CRlw) and its backscatter characteristics (e.g., echo width VEW) are the most important. The classification at the tree species level needs varying feature compositions for classification, depending on the underlying species (coniferous and deciduous trees) and the time of data acquisition (leaf-on and leaf-off). For the differentiation between coniferous and deciduous trees, features related to different crown structures, like the proportion of echoes (ER3D/2D, ERsingle/multiple,obj), are used for classification. Coniferous trees tend to a higher ratio of single reflections compared to deciduous trees under leaf-off condition, and to a broadening of the echo width (EWstats,h-layer) particularly for upper crown parts. The usage of amplitude features is more suitable under leaf-off than under leaf-on condition for the classification, where amplitudes of needles differ more significantly from the amplitudes of bark than from leaves. The different tree species can be better distinguished from each other by subset features of waveform and radiometric features and their comparison over the vertical profile. The vertical echo width profile (VEW) of beeches shows relatively constant values, whereas its backscatter cross-section (Vσ) decreases with increasing height. Conversely, larch trees tend to higher values of echo width and backscatter cross-section at upper crown parts. Waveform features are sensitive to the canopy openness and the vertical arrangement of canopy elements and thus indicative for different species. The larger leaves of bigleaf maple trees cause more distinctive and noticeable peaks in the return signal, and shows a smaller inter-peak distance (ΔRij/ΔTij) unlike other hardwood species.
Higher overall classification accuracies have been achieved at the class level (>80%, up to ~97%) compared to a classification at the species level (>70%, up to ~88%), whereas the producer’s accuracy of different species ranges from low to high (>90%) levels depending on the species composition. However, a detailed discussion of species-specific feature behavior is limited within the studies. Furthermore, most of the research to date related to tree species classification by FWF ALS data has been conducted in temperate and boreal forests, whereas only a few number of studies from (sub-) tropical and urban sites are published. In particular the multitude of different trees (species and shape) densely growing in forested (sub-) tropical area affects the applicability of distinct features for species classification and requires a closer examination. In addition, the feature characteristics are affected by factors related to the vegetation structure and by technical factors related to data acquisition and data processing, which hamper the transferability of species-specific feature thresholds. Scots pine trees for example, tend towards a conical shape when young and a rounded and irregular shape as they mature. Beeches, by contrast, respond rapidly to varying light conditions, which lead to a modified unstable relation between crown dimension and stem volume. Technical factors like scanning range and beam divergence determine the size of the laser footprint area. Within the footprint area, a variable amount of scatterers is encountered. These scatterers, mostly with different sizes and orientations in the case of vegetation, affect the power and shape of the backscattered waveform and consequently the derived features. Such factors need to be taken into consideration when deriving features for classification and when transferring a feature threshold from one study area to another.
Investigations on species-specific feature characteristics and a detailed analysis of the influence of technical factors, methods for tree detection and varying growing conditions on the feature characteristics should be a focus of future work. Furthermore, the transferability of already successfully applied features from discrete ALS to FWF ALS data is to be investigated in more detail in further studies. Such comprehensive feature analysis and collection could enable the provision of a (tree) signature database of FWF ALS data. Such a signature database would simplify the feature derivation and the transferability as well as the understanding of species-specific behavior.

Acknowledgments

This work was funded by the Federal Ministry of Science, Research and Arts (MWK), Baden-Wuerttemberg, Germany, in the framework of the projects LS-VISA (FKZ 1222 TG 87) and 4DEMON. We acknowledge the financial support of the Deutsche Forschungsgemeinschaft and Ruprecht-Karls-Universität Heidelberg within the funding programme Open Access Publishing.

Author Contributions

Kristina Koenig designed and conducted a substantial part of the review and wrote the article. Bernhard Höfle improved the article at various stages of the reviewing and writing process.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table
Table A1. Common abbreviations.
Table A1. Common abbreviations.
Abbreviation
ALSAirborne Laser Scanning
CHMCanopy Height Model
DBHDiameter at Breast Height
DSMDigital Surface Model
DTMDigital Terrain Model
FWFFull-WaveForm
LAILeaf Area Index
MSManual tree Segmentation
nDSMNormalized Digital Surface Model
PCPrincipal Component
VTMRVariance-To-Mean-Ratio
WSWatershed Segmentation
Table
Table A2. The following feature abbreviations are used in this manuscript.
Table A2. The following feature abbreviations are used in this manuscript.
AbbreviationUnitDefinition
Astats,obj(DN)The statistics of amplitude A, e.g., mean A of tree object (Amean,obj).
Asum,obj(DN)Sum of all waveform’s amplitude peaks.
CRlt(m/m)(%)Ratio of crown length and tree height.
CRlw(m/m)Ratio of crown length and width.
CRvol(m³)Crown volume.
CRvol,derivatives(m³/m)(%)Crown volume derivatices, e.g., CRvol in relation to crown length (CRvol,l), width (CRvol,w) or to tree height (CRvol,t).
EAW(DN)The product of echo amplitude and width, e.g., mean EAW of tree object (EAWmean,obj).
ER3D/2D Echo ratio. The number of points in 3D in a fixed search distance is related to the number of points in 2D found in the same distance in 2D.
ERsingle/multiple,obj Ratio of the number of single echoes to the number of multiple echoes.
EWstats,obj(ns)The statistics of echo-width, e.g., mean EW of tree object (EWmean,obj).
EWstats,h-layer The statistics of echo width of a height layer, e.g., mean EW of the upper 2 m (EWmean,u2m).
FS(°)Front slope angle from waveform beginning to first peak.
Hm,energy(m)(%)Height, at which a specific amount of energy is reached, e.g., 50% of the returned energy.
Hmin(m)(%)Height threshold as the minimum height.
HTi Haralick’s texture features calculated from 3D grey level co-occurrence matrix based on number of points per voxel in different directions in the 3D space.
Pdens,bin,norm(%)The number of echoes normalized by the total number of echoes of the tree object at given height layer.
Pdens,L-func The L-function features of echo number.
Pdens,L-func_Npeak Number of echoes, that are determined by the number of local minimums per height layer of a L-function.
Pgrid,VTMR Variance-to-mean-ratio of number of echoes of gridded height layer.
PSa, PSb Function parameter of the parabolic surface fitted to the tree crown.
PSheight(m)(%)Vertical length of the parabolic surface fitted to the tree crown.
PSradius(m)Radius of the parabolic surface fitted to the tree crown.
PTIN,Edge(m)Variance of edge lengths from Delaunay triangulated points per height layer and their frequency distribution.
RWE(DN)Total returned waveform energy.
TNo Total number of echoes.
TNoobj,Hmin Number of points above a defined height threshold.
TNorast,stats,filter The number of echoes within a defined height layer based on raster-based calculations. For example TNorast,mean,single as the average of the number of single echoes of all raster cells at a defined height.
TNovoxel,column The number of echoes per voxel is related to the number of echoes of all subjacent voxels.
TNowave,stats The statistics of the number of echoes of all waveforms.
VA Vertical profile of amplitude values.
VEW Vertical profile of echo width values.
VH Vertical profile of number of echoes.
Vσ Vertical profile of backscatter cross-section values.
V*_derivative Derivative of the vertical profile of a feature, e.g., skewness of VEW (VEW_skewness).
Zobj,ellip(m)Vertical length of ellipsoid fitted to tree crown.
ΔDtrunk- dist,horiz(m)The mean horizontal distance of an echo to the previously detected tree trunk.
ΔRij(m)Distance between two waveform echoes i and j calculated by difference in range, e.g., the distance between the first and the last echo in meter (ΔR1st/last).
ΔTij(ns)Distance between two waveform echoes i and j calculated by time difference, e.g., the distance between the first and the last echo in nanoseconds (ΔT1st/last).
ΔWRij(m)(ns)Distance measure of a waveform, e.g., the distance between waveform centroid and ground (ΔWRcentroid,ground), waveform beginning to ground (ΔWRbeginning,ground) and beginning and first peak (ΔWRbeginning,1stpeak).
γstats,obj(m2/m2)The statistics of backscatter coefficient, e.g., mean γ of tree object.
σstats,obj(m2)The statistics of backscatter cross-section, e.g., mean σ of tree object.
Table
Table A3. Overview of applied feature sets for species classification and the overall accuracies achieved by different studies.
Table A3. Overview of applied feature sets for species classification and the overall accuracies achieved by different studies.
Dominant Species and Study Area (Number of Trees, if Given)Tree Detection and Classification MethodApplied FeatureOverall Accuracy (c: Class, s: Species Level)Reference
Masson pine (Pinus massoniana (Lamb.), 85), Chinese fir (Cunninghamia lanceolate (Lamb.), 82), Slash pines (Pinus elliottii Engelm., 71), Sawtooth oak (Querus acutissima Carruth., 73), Chinese sweet gum (Liquidambar formosana Hance, 74), Chinese holly (Ilex chinensis Sims., 52) [Yushan Forest, China, leaf-on]Local Maxima Algorithm on CHM; Random Forest with Mean Decrease Accuracy [2/3 for model training]ΔWRcentroid,ground, ΔWRbeginning,ground, ΔWRbeginning,1stpeak, TNowave,stats, FS, RWEc: 86.2%[15]
s: 68.6%
Red pine (Pinus koraiensis), Koyama spruce (Picea koraiensis), Dahurian larch (Larix gmelinii), fir (Abies nephrolepis), white birch (Betula platyphylla Suk.), ribbed birch (Betula Costata), Manchurian linden (Tilia Mandschurica), elm (Ulmus Laciniata), Mongolian oak (Quercus Mongolica); (in total: 1847 trees) [Forest, China, leaf-on]Watershed Segmentation on CHM; Support Vector MachineRange corrected Astats,obj, EAWstats,obj, EWstats,obj, TNostats,obc: 85.7%[24]
s: 55.1%
Scots pine (Pinus sylvestris), Norway spruce (Picea abies), sessile oak (Quercus petraea), red oak (Quercus rubra), European beech (Fagus sylvatica) [Forest, SW Germany, leaf-on]Linear Discriminant Analysis with 18-fold cross-validationAstats,obj, EAWstats,obj, EWstats,obj, TNostats,obc: 91.7%[25]
s: 80.4%
Spruce (Picea abies, 42), European larch (Larix decidua, 23), red beech (Fagus sylvatica, 76) [Forest, Austria, leaf-off]Edge-based segmentation on nDSM; FuzzyRule Set & Decision Tree [1/2 for model training]ER3D/2D, TNoHmin, EWmean, EWstddev, σmean, σstdev, Hmin > 50th heightc: 83%[26]
s: 75%
Scots pine (Pinus sylvestris L.), Norway spruce (Picea abies (L.) Karst.), birches (Betula pendula Roth and Betula pubescens Ehrh.); (in total: 9930 trees) [Forest, Hyytiälä, Finland, leaf-on]Watershed segmentation on CHM & delineation by cylinders; Quadratic Discriminant Analysis and leave-one-out cross validationAstats, FWHMstats, RWE, Hm,50%energy, pulse length84%–91%[27]
Red beech (Fagus sylvatica, 11), oaks (Quercus robur and Quercus petraea, 10), hornbeam, larch (Carpinus betulus, 4) [Vienna Woods, Austria, leaf-off]Edge-based segmentation on nDSM; Descriptive feature analysisEWmean, EWCV, σmean, σcv(exploratory analysis)[47]
Norway spruce (Picea abies, 256), European beech (Fagus sylvatica, 397), Sycamore maple (Acer pseudoplatanus, 20) [Mountainous, mixed forest, SE Germany]Watershed segmentation on CHM; k-Means clusteringleaf-on: ΔDtrunk dist, horiz., EAWobj,mean, EW mean_single, EW mean_first leaf-off: EWsingle, EWfirst, ERsingle/multiplec:[52]
leaf-on: 85.4%
leaf-off: 95.7%
Norway spruce (Picea abies, 688), European beech (Fagus sylvatica, 812), fir (Abies alba, 70), Sycamore maple (Acer pseudoplatanus, 71), Norway maple (Acer platanoides, 21), lime trees (Tilia Europaea, 2) [Mountainous, mixed forest, SE Germany]Normalized cut segmentation; Expectation-Maximization Algorithm & Maximum Likelihood Classification [1/5 for model training]ΔDtrunk dist,horiz., EAWobj,mean, EWmean_single, EWmean_first, ERsingle/multiplec: [53]
leaf-on: 95/97%
leaf-off: 94%
Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco), western redcedar (Thuja plicata Donn ex D.Don), black cottonwood (Populus balsamifera L. ssp. trichocarpa (Torr. & A. Gray ex Hook.) Brayshaw), bigleaf maple (Acer macrophyllum Pursh), red alder (Alnus rubra Bong.); (22 to 29 trees per species) [Arboretum, Seattle, USA, leaf-on]Voxel-based segmentation; Support Vector Machine with five-fold cross-validationVstats, ΔRij, EAWmean, Pstats,perc, TNostats, PCwave,Fouriers: 85.4%[55]
Norway spruce (Picea abies, 688), European beech (Fagus sylvatica, 812), fir (Abies alba, 70), Sycamore maple (Acer pseudoplatanus, 71), Norway maple (Acer platanoides, 21), lime trees (Tilia Europaea, 2) [Mountainous, mixed forest, SE Germany]Watershed segmentation & Normalized cut segmentation; Expectation Maximization Algorithm & Maximum LikelihoodPstats,perc, Astats, EAWstats, EWstats, filtered by the index of returnc:[66]
leaf-on: 95%
leaf-off: 94%
lower layers:
leaf-on: 86%
leaf-off: 95%
upper layers:
leaf-on: 97%
leaf-off: 94%
Jack pine (Pinus banksiana Lamb., 158), eastern white pine (Pinus strobus L., 106), sugar maple (Acer saccharum Marsh., 105), trembling aspen (Populus tremuloides Michx., 182) [Forest, Ontario, Canada, leaf-on]Individual tree crown delineation from optical imagery; Linear Discriminant Analysis with 10-fold cross validation [1/2 for model training]Pgrid,VTMR, Pdens,L-func, PTIN,Edgec: 82.2%[67]
s: 77.5%
Norway spruce (Picea abies (L.)), Scots pine (Pinus sylvestris, (L.)), birches (Betula pendula (L.) and Betula pubescens (L.)); (in total, 789 trees) [Forest, SW Sweden, leaf-on]3D ellipsoid clustering; Linear Discriminant Analysis with leave-one-out cross validationAstats,obj, EAWstats,obj, EWstats,obj, TNostats, Zobj_ellip, PSheight, PSradiuss: 71%[73]
Scots pine (Pinus sylvestris), Norway spruce (Picea abies), birch (Betula sp.); (in total, 3695) [Forest, South Finland, leaf-on]Minimum curvature-based region detector; Random Forest with cross validationΔR1st/last, RWE, TNo, A1st/2nd/rd/th, Hm,energys: 71.5%[76]
Norway spruce (Picea abies (L.), 209), birch (Betula spp., 203), aspen (Poplus tremula L.) [Forest, SE Norway, leaf-on]Mean crown radius; Linear Discriminant Analysis & ANCOVA with cross-validationVH_kurtosis, VH_skewness, VH_coeff.var., Aobj,mean, Aobj,max, Pdens,bins: 88%[97]

Supplementary Files

Supplementary File 1

References

  1. Wagner, W. Radiometric calibration of small-footprint full-waveform airborne laser scanner measurements: Basic physical concepts. ISPRS J. Photogramm. Remote Sens. 2010, 65, 505–513. [Google Scholar] [CrossRef]
  2. Anderson, K.; Hancock, S.; Disney, M.; Gaston, K.J. Is waveform worth it? A comparison of LiDAR approaches for vegetation and landscape characterization. Remote Sens. Ecol. Conserv. 2015, 2, 5–15. [Google Scholar] [CrossRef]
  3. Lin, Y.; Hyyppä, J. A comprehensive but efficient framework of proposing and validating feature parameters from airborne LiDAR data for tree species classification. Int. J. Appl. Earth Observ. Geoinf. 2016, 46, 45–55. [Google Scholar] [CrossRef]
  4. Hug, C.; Ullrich, A.; Grimm, A. Litemapper-5600—A waveform-digitizing LiDAR terrain and vegetation mapping system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, 24–29. [Google Scholar]
  5. Mallet, C.; Bretar, F. Full-waveform topographic LiDAR: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
  6. Balenović, I.; Alberti, G.; Marjanović, H. Airborne laser scanning—The status and perspectives for the application in the South-East European forestry. South-East Eur. For. 2013, 4, 59–79. [Google Scholar] [CrossRef]
  7. Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in forest inventory using airborne laser scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
  8. Næsset, E. Airborne laser scanning as a method in operational forest inventory: Status of accuracy assessments accomplished in Scandinavia. Scand. J. For. Res. 2007, 22, 433–442. [Google Scholar] [CrossRef]
  9. Pirotti, F.; Laurin, G.V.; Vettore, A.; Masiero, A.; Valentini, R. Small footprint full-waveform metrics contribution to the prediction of biomass in tropical forests. Remote Sens. 2014, 6, 9576–9599. [Google Scholar] [CrossRef]
  10. Woods, M.; Pitt, D.; Penner, M.; Lim, K.; Nesbitt, D.; Etheridge, D.; Treitz, P. Operational implementation of a LiDAR inventory in Boreal Ontario. For. Chron. 2011, 87, 512–528. [Google Scholar] [CrossRef]
  11. Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef]
  12. Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 083671. [Google Scholar] [CrossRef]
  13. Höfle, B.; Hollaus, M.; Hagenauer, J. Urban vegetation detection using radiometrically calibrated small-footprint full-waveform airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2012, 67, 134–147. [Google Scholar] [CrossRef]
  14. Borre, J.V.; Paelinckx, D.; Mücher, C.A.; Kooistra, L.; Haest, B.; De Blust, G.; Schmidt, A.M. Integrating remote sensing in Natura 2000 habitat monitoring: Prospects on the way forward. J. Nat. Conserv. 2011, 19, 116–125. [Google Scholar] [CrossRef]
  15. Cao, L.; Coops, N.C.; Innes, J.L.; Dai, J.; Ruan, H.; She, G. Tree species classification in subtropical forests using small-footprint full-waveform LiDAR data. Int. J. Appl. Earth Observ. Geoinf. 2016, 49, 39–51. [Google Scholar] [CrossRef]
  16. Latifi, H.; Fassnacht, F.E.; Müller, J.; Tharani, A.; Dech, S.; Heurich, M. Forest inventories by LiDAR data: A comparison of single tree segmentation and metric-based methods for inventories of a heterogeneous temperate forest. Int. J. Appl. Earth Observ. Geoinf. 2015, 42, 162–174. [Google Scholar] [CrossRef]
  17. Leiterer, R.; Furrer, R.; Schaepman, M.E.; Morsdorf, F. Forest canopy-structure characterization: A data-driven approach. For. Ecol. Manag. 2015, 358, 48–61. [Google Scholar] [CrossRef]
  18. Lindberg, E.; Olofsson, K.; Holmgren, J.; Olsson, H. Estimation of 3D vegetation structure from waveform and discrete return airborne laser scanning data. Remote Sens. Environ. 2012, 118, 151–161. [Google Scholar] [CrossRef]
  19. Fieber, K.D.; Davenport, I.J.; Tanase, M.A.; Ferryman, J.M.; Gurney, R.J.; Becerra, V.M.; Walker, J.P.; Hacker, J.M. Validation of Canopy Height Profile methodology for small-footprint full-waveform airborne LiDAR data in a discontinuous canopy environment. ISPRS J. Photogramm. Remote Sens. 2015, 104, 144–157. [Google Scholar] [CrossRef] [Green Version]
  20. Alonzo, M.; Bookhagen, B.; McFadden, J.P.; Sun, A.; Roberts, D.A. Mapping urban forest leaf area index with airborne LiDAR using penetration metrics and allometry. Remote Sens. Environ. 2015, 162, 141–153. [Google Scholar] [CrossRef]
  21. Fieber, K.D.; Davenport, I.J.; Tanase, M.A.; Ferryman, J.M.; Gurney, R.J.; Walker, J.P.; Hacker, J.M. Effective LAI and CHP of a single tree from small-footprint full-waveform LiDAR. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1634–1638. [Google Scholar] [CrossRef]
  22. Allouis, T.; Durrieu, S.; Véga, C.; Couteron, P. Stem volume and above-ground biomass estimation of individual pine trees from LiDAR data: Contribution of full-waveform signals. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2013, 6, 924–934. [Google Scholar] [CrossRef]
  23. Cao, L.; Coops, N.; Hermosilla, T.; Dai, J. Estimation of forest structural variables using small-footprint full-waveform LiDAR in a subtropical forest, China. In Proceedings of the 2014 3rd International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Changsha, China, 11–14 June 2014.
  24. Xu, G.; Pang, Y.; Li, Z.; Zhao, D.; Liu, L. Individual trees species classification using relative calibrated full-waveform LiDAR data. In Proceedings of the SilviLaser 2012: 12th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Vancouver, BC, Canada, 16–19 September 2012; Coops, N., Wulder, M., Eds.; pp. 163–174.
  25. Heinzel, J.; Koch, B. Exploring full-waveform LiDAR parameters for tree species classification. Int. J. Appl. Earth Observ. Geoinf. 2011, 13, 152–160. [Google Scholar] [CrossRef]
  26. Hollaus, M.; Mücke, W.; Höfle, B.; Dorigo, W.; Pfeifer, N.; Wagner, W.; Bauerhansl, C.; Regner, B. Tree species classification based on full-waveform airborne laser scanning data. In Proceedings of Silvilaser 2009: 9th International Conference on LiDAR Applications for Assessing Forest Ecosystems, College Station, TX, USA, 14–16 October 2009; pp. 54–62.
  27. Hovi, A.; Korhonen, L.; Vauhkonen, J.; Korpela, I. LiDAR waveform features for tree species classification and their sensitivity to tree- and acquisition related parameters. Remote Sens. Environ. 2016, 173, 224–237. [Google Scholar] [CrossRef]
  28. Mücke, W.; Hermann, A. Estimation of biodiversity relevant quantities from airborne laser scanning data. Österreichische Z. Vermess. Geoinfor. 2010, 4, 201–210. [Google Scholar]
  29. Müller, J.; Vierling, K. Assessing Biodiversity by Airborne Laser Scanning. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2014; pp. 357–374. [Google Scholar]
  30. Hyde, P.; Dubayah, R.; Peterson, B.; Blair, J.B.; Hofton, M.; Hunsaker, C.; Knox, R.; Walker, W. Mapping forest structure for wildlife habitat analysis using waveform LiDAR: Validation of montane ecosystems. Remote Sens. Environ. 2005, 96, 427–437. [Google Scholar] [CrossRef]
  31. Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Hughes, R.F. Invasive species detection in Hawaiian rainforests using airborne imaging spectroscopy and LiDAR. Remote Sens. Environ. 2008, 112, 1942–1955. [Google Scholar] [CrossRef]
  32. Dwyer, J.F.; McPherson, E.G.; Schroeder, H.W.; Rowntree, R.A. Assessing the benefits and costs of the urban forest. J. Arboric. 1992, 18, 227–234. [Google Scholar]
  33. Van Leeuwen, M.; Coops, N.C.; Hilker, T.; Wulder, M.A.; Newnham, G.J.; Culvenor, D.S. Automated reconstruction of tree and canopy structure for modeling the internal canopy radiation regime. Remote Sens. Environ. 2013, 136, 286–300. [Google Scholar] [CrossRef]
  34. Alexander, C.; Tansey, K.; Kaduk, J.; Holland, D.; Tate, N.J. An approach to classification of airborne laser scanning point cloud data in an urban environment. Int. J. Remote Sens. 2011, 32, 9151–9169. [Google Scholar] [CrossRef]
  35. Janhäll, S. Review on urban vegetation and particle air pollution—Deposition and dispersion. Atmos. Environ. 2015, 105, 130–137. [Google Scholar] [CrossRef]
  36. Koma, Z.; Koenig, K.; Höfle, B. Urban Tree Classification Using Full-Waveform Airborne Laser Scanning. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-3, 185–192. [Google Scholar] [CrossRef]
  37. Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens. 2008, 29, 1339–1366. [Google Scholar] [CrossRef]
  38. Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. 2003, 27, 88–106. [Google Scholar] [CrossRef]
  39. Maltamo, M.; Næsset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning—Concepts and Case Studies; Managing Forest Ecosystems; Springer Netherlands: Dordrecht, The Netherlands, 2014. [Google Scholar]
  40. Pirotti, F. Analysis of full-waveform LiDAR data for forestry applications: A review of investigations and methods. iForest—Biogeosci. For. 2011, 4, 100–106. [Google Scholar] [CrossRef]
  41. Yan, W.Y.; Shaker, A.; El-Ashmawy, N. Urban land cover classification using airborne LiDAR data: A review. Remote Sens. Environ. 2015, 158, 295–310. [Google Scholar] [CrossRef]
  42. Vauhkonen, J.; Ørka, H.O.; Holmgren, J.; Dalponte, M.; Heinzel, J.; Koch, B. Tree species recognition based on airborne laser scanning and complementary data sources. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer Science + Business Media: Dordrecht, The Netherlands, 2014; pp. 135–156. [Google Scholar]
  43. Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitising airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
  44. Wagner, W.; Ullrich, A.; Melzer, T.; Briese, C.; Kraus, K. From single-pulse to full-waveform airborne laser scanners: Potential and practical challenge. Int. Arch. Photogramm. Remote Sens. 2004, 35, 201–206. [Google Scholar]
  45. Roncat, A.; Morsdorf, F.; Briese, C.; Wagner, W.; Pfeifer, N. Laser pulse interaction with forest canopy: Geometric and radiometric issues. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2014; pp. 19–41. [Google Scholar]
  46. Eysn, L.; Hollaus, M.; Lindberg, E.; Berger, F.; Monnet, J.M.; Dalponte, M.; Kobal, M.; Pellegrini, M.; Lingua, E.; Mongus, D.; et al. A benchmark of LiDAR-based single tree detection methods using heterogeneous forest data from the Alpine space. Forests 2015, 6, 1721–1747. [Google Scholar] [CrossRef] [Green Version]
  47. Höfle, B.; Hollaus, M.; Lehner, H.; Pfeifer, N.; Wagner, W. Area-based parameterization of forest structure using full-waveform airborne laser scanning data. In Proceedings of the SilviLaser 2008: 8th International Conference on LiDAR Applications for Assessing Forest Ecosystems, Edinburgh, UK, 17–19 September 2008; pp. 227–236.
  48. Koch, B.; Kattenborn, T.; Straub, C.; Vauhkonen, J. Segmentation of forest to tree objects. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2014; pp. 89–112. [Google Scholar]
  49. Gupta, S.; Weinacker, H.; Koch, B. Comparative analysis of clustering-based approaches for 3-D single tree detection using airborne fullwave LiDAR data. Remote Sens. 2010, 2, 968–989. [Google Scholar] [CrossRef]
  50. Strîmbu, V.F.; Strîmbu, B.M. A graph-based segmentation algorithm for tree crown extraction using airborne LiDAR data. ISPRS J. Photogramm. Remote Sens. 2015, 104, 30–43. [Google Scholar] [CrossRef]
  51. Zhang, J.; Sohn, G.; Brédif, M. A hybrid framework for single tree detection from airborne laser scanning data: A case study in temperate mature coniferous forests in Ontario, Canada. ISPRS J. Photogramm. Remote Sens. 2014, 98, 44–57. [Google Scholar] [CrossRef]
  52. Reitberger, J.; Krzystek, P.; Stilla, U. Analysis of full waveform LIDAR data for the classification of deciduous and coniferous trees. Int. J. Remote Sens. 2008, 29, 1407–1431. [Google Scholar] [CrossRef]
  53. Reitberger, J.; Krzystek, P.; Stilla, U. Benefit of airborne full waveform LiDAR for 3D segmentation and classification of single trees. In Proceedings of the ASPRS 2009 Annual Conference, Baltimore, MD, USA, 9–13 March 2009; pp. 1–9.
  54. Rutzinger, M.; Höfle, B.; Hollaus, M.; Pfeifer, N. Object-based point cloud analysis of full-waveform airborne laser scanning data for urban vegetation classification. Sensors 2008, 8, 4505–4528. [Google Scholar] [CrossRef]
  55. Vaughn, N.R.; Moskal, L.M.; Turnblom, E.C. Tree species detection accuracies using discrete point LiDAR and airborne waveform LiDAR. Remote Sens. 2012, 4, 377–403. [Google Scholar] [CrossRef]
  56. Alexander, C.; Tansey, K.; Kaduk, J.; Holland, D.; Tate, N.J. Backscatter coefficient as an attribute for the classification of full-waveform airborne laser scanning data in urban areas. ISPRS J. Photogramm. Remote Sens. 2010, 65, 423–432. [Google Scholar] [CrossRef]
  57. Ducic, V.; Hollaus, M.; Ullrich, A.; Wagner, W.; Melzer, T. 3D Vegetation mapping and classification using full-waveform laser scanning. In Proceedings of the EARSeL/ISPRS 2006, Vienna, Austria, 14–15 February 2006.
  58. Fieber, K.D.; Davenport, I.J.; Ferryman, J.M.; Gurney, R.J.; Walker, J.P.; Hacker, J.M. Analysis of full-waveform LiDAR data for classification of an orange orchard scene. ISPRS J. Photogramm. Remote Sens. 2013, 82, 63–82. [Google Scholar] [CrossRef]
  59. Hollaus, M.; Wagner, W.; Molnar, G.; Mandlburger, G.; Nothegger, C.; Otepka, J. Delineation of vegetation and building polygons from full-waveform airborne LIDAR data using OPALS software. In Proceedings of the geospatial data and geovisualization: Environment, security, and society, special joint symposium of ISPRS technical commission IV and AutoCarto 2010 in conjunction with ASPRS/GaGIS speciality conference, Orlando, FL, USA, 15–19 November 2010.
  60. Lin, Y.-C. Normalization of echo features derived from full-waveform airborne laser scanning data. Remote Sens. 2015, 7, 2731–2751. [Google Scholar] [CrossRef]
  61. Mallet, C.; Bretar, F.; Soergel, U. Analysis of full-waveform LiDAR data for classification of urban areas. Photogramm. Fernerkund. GeoInf. 2008, 5, 337–349. [Google Scholar]
  62. Stilla, U.; Jutzi, B. Waveform analysis for small-footprint pulsed laser systems. In Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA, 2008; pp. 215–234. [Google Scholar]
  63. Tran, G.; Nguyen, D.; Milenkovic, M.; Pfeifer, N. Potential of full waveform airborne laser scanning data for urban area classification—Transfer if classification approaches between missions. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 1317–1323. [Google Scholar] [CrossRef]
  64. Tseng, Y.H.; Wang, C.K.; Chu, H.J.; Hung, Y.C. Waveform-based point cloud classification in land-cover identification. Int. J. Appl. Earth Observ. Geoinf. 2015, 34, 78–88. [Google Scholar] [CrossRef]
  65. Wagner, W.; Hollaus, M.; Briese, C.; Ducic, V. 3D vegetation mapping using small-footprint full-waveform airborne laser scanners. Int. J. Remote Sens. 2008, 29, 1433–1452. [Google Scholar] [CrossRef]
  66. Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
  67. Li, J.; Hu, B.; Noland, T.L. Classification of tree species based on structural features derived from high density LiDAR data. Agric. For. Meteorol. 2013, 171, 104–114. [Google Scholar] [CrossRef]
  68. Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef]
  69. Höfle, B.; Hollaus, M. Urban vegetation detection using high density full-waveform airborne LiDAR data-combination of object-based image and point cloud analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 38, 281–286. [Google Scholar]
  70. Hollaus, M.; Mücke, W.; Roncat, A.; Pfeifer, N.; Briese, C. Full-waveform airborne laser scanning systems and their possibilities in forest applications. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Næsset, E., Vauhkonen, J., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2014; pp. 43–61. [Google Scholar]
  71. Guo, B.; Huang, X.; Zhang, F.; Sohn, G. Classification of airborne laser scanning data using JointBoost. ISPRS J. Photogramm. Remote Sens. 2015, 100, 71–83. [Google Scholar] [CrossRef]
  72. Gross, H.; Jutzi, B.; Thoennessen, U. Segmentation of tree regions using data of a full-waveform laser. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2007, 36, 57–62. [Google Scholar]
  73. Lindberg, E.; Eysn, L.; Hollaus, M.; Holmgren, J.; Pfeifer, N. Delineation of tree crowns and tree species classification from full-waveform airborne laser scanning data using 3-D ellipsoidal clustering. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 3174–3181. [Google Scholar] [CrossRef]
  74. Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ. 2010, 114, 1263–1276. [Google Scholar] [CrossRef]
  75. Ko, C.; Sohn, G.; Remmel, T.K.; Miller, J. Hybrid ensemble classification of tree genera using airborne LiDAR data. Remote Sens. 2014, 6, 11225–11243. [Google Scholar] [CrossRef]
  76. Yu, X.; Litkey, P.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Assessment of low density full-waveform airborne laser scanning for individual tree detection and tree species classification. Forests 2014, 5, 1011–1031. [Google Scholar] [CrossRef]
  77. Englhart, S.; Jubanski, J.; Siegert, F. Quantifying dynamics in tropical peat swamp forest biomass with multi-temporal LiDAR datasets. Remote Sens. 2013, 5, 2368–2388. [Google Scholar] [CrossRef] [Green Version]
  78. Stereńczak, K. Factors influencing individual tree crowns detection based on airborne laser scanning data. For. Res. Pap. 2013, 74, 323–333. [Google Scholar] [CrossRef]
  79. Han, A.R.; Lee, S.K.; Suh, G.U.; Park, Y.; Park, P.S. Wind and topography influence the crown growth of Picea jezoensis in a subalpine forest on Mt. Deogyu, Korea. Agric. For. Meteorol. 2012, 166, 207–214. [Google Scholar] [CrossRef]
  80. Seidel, D.; Hoffmann, N.; Ehbrecht, M.; Juchheim, J.; Ammer, C. How neighborhood affects tree diameter increment—New insights from terrestrial laser scanning and some methodical considerations. For. Ecol. Manag. 2015, 336, 119–128. [Google Scholar] [CrossRef]
  81. Khosravipour, A.; Skidmore, A.K.; Wang, T.; Isenburg, M.; Khoshelham, K. Effect of slope on treetop detection using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]
  82. Romanczyk, P.; van Aardt, J.; Cawse-Nicholson, K.; Kelbe, D.; McGlinchy, J.; Krause, K. Assessing the impact of broadleaf tree structure on airborne full-waveform small-footprint LiDAR signals through simulation. Can. J. Remote Sens. 2013, 39, S60–S72. [Google Scholar] [CrossRef]
  83. Duan, Z.; Zhao, D.; Zeng, Y.; Zhao, Y.; Wu, B.; Zhu, J. Assessing and correcting topographic effects on forest canopy height retrieval using airborne LiDAR data. Sensors 2015, 15, 12133–12155. [Google Scholar] [CrossRef] [PubMed]
  84. Vega, C.; Hamrouni, A.; El Mokhtari, S.; Morel, J.; Bock, J.; Renaud, J.P.; Bouvier, M.; Durrieu, S. PTrees: A point-based approach to forest tree extraction from LiDAR data. Int. J. Appl. Earth Observ. Geoinf. 2014, 33, 98–108. [Google Scholar] [CrossRef]
  85. Molnar, B.; Laky, S.; Toth, C. Using full waveform data in urban areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 38, 203–208. [Google Scholar] [CrossRef]
  86. Hopkinson, C.; Chasmer, L.E.; Sass, G.; Creed, I.F.; Sitar, M.; Kalbfleisch, W.; Treitz, P. Vegetation class dependent errors in LiDAR ground elevation and canopy height estimates in a boreal wetland environment. Can. J. Remote Sens. 2005, 31, 191–206. [Google Scholar] [CrossRef]
  87. Hermosilla, T.; Coops, N.C.; Ruiz, L.A.; Moskal, L.M. Deriving pseudo-vertical waveforms from small-footprint full-waveform LiDAR data. Remote Sens. Lett. 2014, 5, 332–341. [Google Scholar] [CrossRef]
  88. Buddenbaum, H.; Seeling, S.; Hill, J. Fusion of full-waveform LiDAR and imaging spectroscopy remote sensing data for the characterization of forest stands. Int. J. Remote Sens. 2013, 34, 4511–4524. [Google Scholar] [CrossRef]
  89. Hermosilla, T.; Ruiz, L.A.; Kazakova, A.N.; Coops, N.C.; Moskal, L.M. Estimation of forest structure and canopy fuel parameters from small-footprint full-waveform LiDAR data. Int. J. Wildland Fire 2014, 23, 224–233. [Google Scholar] [CrossRef]
  90. Chauve, A.; Vega, C.; Durrieu, S.; Bretar, F.; Allouis, T.; Pierrot Deseilligny, M.; Puech, W. Advanced full-waveform LiDAR data echo detection: Assessing quality of derived terrain and tree height models in an alpine coniferous forest. Int. J. Remote Sens. 2009, 30, 5211–5228. [Google Scholar] [CrossRef]
  91. Lukeš, P.; Stenberg, P.; Rautiainen, M.; Mõttus, M.; Vanhatalo, K.M. Optical properties of leaves and needles for boreal tree species in Europe. Remote Sens. Lett. 2013, 4, 667–676. [Google Scholar] [CrossRef]
  92. Woolley, J.T. Reflectance and Transmittance of Light by Leaves. Plant Physiol. 1971, 47, 656–662. [Google Scholar] [CrossRef] [PubMed]
  93. Briese, C.; Pfennigbauer, M.; Lehner, H.; Ullrich, A.; Wagner, W.; Pfeifer, N. Radiometric calibration of multi-wavelength airborne laser scanning data. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2012, 1, 335–340. [Google Scholar] [CrossRef]
  94. Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 561–574. [Google Scholar] [CrossRef]
  95. Ko, C.; Sohn, G.; Remmel, T.K. The impact of LiDAR point density on classifying tree genus: Using geometric features and vertical profile features. In Proceedings of the SilviLaser 2012: 12th International Conference on LiDAR Applications for Assessing Forest, Vancouver, BC, Canada, 16–19 September 2012; Coops, N., Wulder, M., Eds.;
  96. Ko, C.; Sohn, G.; Remmel, T.K. A comparitive study using geometric and vertical profile features derived from airborne LIDAR for classifying tree genera. ISPRS Ann. Photogramm. Remote Sens. Spatial Inf. Sci. 2012, 1, 129–134. [Google Scholar] [CrossRef]
  97. Ørka, H.O.; Næsset, E.; Bollandsås, O.M. Classifying species of individual trees by intensity and structure features derived from airborne laser scanner data. Remote Sens. Environ. 2009, 113, 1163–1174. [Google Scholar] [CrossRef]
Table
Table 1. Subset features for classification differentiated by geometric and radiometric feature types and related to studies at taxonomic class and species level.
Table 1. Subset features for classification differentiated by geometric and radiometric feature types and related to studies at taxonomic class and species level.
TypeReferences (Applied at c: Class Level; s: Species Level)
Geometric
Point-assigned: Elevation difference ΔHij between echo i and reference echo j, Elevation variance of all echoes ΔHvar, Elevation difference between highest and lowest elevation value; Point density Pdens, Penetration Index PI, Echo Ratio ER3D/2D (slope adaptive) and ERME (echo index)c: [23,54,56,60,61,71,72]
Planarity: Plane residuals Ɽ, Deviation of local normal vector ηZ, Structure tensor planarity TP and omnivariance TOc: [54,60,61,72]
Height layer/bin/percentiles: Average echo number Navg,bin, Maximum echo number deviation from the average echo number Nnb,bin, Point density Pdens,bin, Graph features of connected height layers (e.g., top distance TD), Variance-to-mean-ratio of number (VTMR) of echoes of gridded height layer Pgrid,VTMR, Mean trunk distance ΔDtrunk dist, horiz., Statistics *1 of TIN edges PTIN,Edge, filtered *2 statistics *1 of height Hperc,stats,filter, L-function features of echo number Pdens,L-func *c: [50,71]
s: [52,55,66,67,73]
Raster Statistics *1 (and Additional Filters *2): Number of echoes TNorast,stats,filters: [25,66]
Voxel: Echo number voxel column ratio TNovoxel,column, echo number voxel area ratio ΔAreavoxel,ch, Haralick’s texture features of echo number voxels HTis: [55,67]
Radiometric
Point-assigned: Echo width EW, Fuzzy small membership of echo width FEWCV, Product of echo amplitude and width EAWc: [60]
s: [25,66]
Raster Statistics *1 (and Additional Filters *2): Amplitude Arast,stats,filter,s: [25,66]
Height layer/bin/percentiles: filtered *2 statistics *1 of amplitude Aperc,stats,filters: [66]
*1 Statistics: Arithmetic mean, median, variance, standard deviation, average deviation, coefficient of variation, skewness, kurtosis; *2 Filter: (a) regarding number of returns: only using single, first or multiple echoes; (b) regarding height: all echoes, step-off count Hmin, height layer.
Table
Table 2. Object features for classification differentiated by geometric, waveform and radiometric feature types and related to studies at taxonomic class and species level.
Table 2. Object features for classification differentiated by geometric, waveform and radiometric feature types and related to studies at taxonomic class and species level.
TypeReferences (Applied at c: Class Level; s: Species Level)
Geometric
Statistics *1 (and Additional Filters *2): Number of echoes TNostats,obj by index ERsingle/multiple,obj, normalized height values Znorm,stats,obj, Voxel neighborhood statistics Voxneighbor,statsc: [64]
s: [24,26,53,55,66,73,76]
Point distribution: Echo Ratio ER3D/2D (slope adaptive) and ERME (echo index), Height of center of gravity Hgravity, Percentage of laser echoes above step-off count TNoPerc,Hmin,obj, Sphere-based minimum projection area Areaproj, Crown related distributions (e.g., CRpdens,derivatives)c: [13,59]
Vertical profile: Height values VH,statss: [47]
Shape: Ellipsoid features (e.g., height Zobj_ellip), Parabolic features (e.g., radius PSradius), Crown features (e.g., crown length—tree height—ratio CRlt)s: [28,66,73]
Waveform
Statistics *1: Sum of waveform amplitude Asum,obj, Returned waveform energy RWE and the height value Hm,energy of e.g., 50% of the total energy, Number of echoes per waveform TNowave,stats and between peak indices ΔNoij, distance between peak indices in range ΔRij and time ΔTij, distance between waveform metrics in range ΔWRij and time ΔWTij, Overlap width of first and second echo ΔOW1st/2nd,stats, Front slope angle from waveform beginning to first peak FS, Product of echo amplitude and width EAWstats,obj, Echo width EWstats,obj, Shape parameter of Gaussian decomposition αdecomp,wave (e.g., skewness)c: [15,64]
s: [15,55,66,73,76]
Vertical Profile *1: Echo width VEWc: [13]
s: [47]
Radiometric
Statistics *1: Amplitude Astats,obj, Backscatter cross-section σstats,obj, Backscatter coefficient γstats,obj,c: [13,47,54,64]
s: [24,26,52,53,55,58,66,73]
Vertical Profile *1: Amplitude VA, backscatter cross-section Vγc: [13]
s: [47]
*1 Statistics: arithmetic mean, median, variance, standard deviation, average deviation, coefficient of variation, skewness, kurtosis; *2 Filter: (a) regarding number of returns: only using single, first or multiple echoes; (b) regarding height: all echoes, step-off count Hmin, height layer.
Table
Table 3. Summary of species-specific feature characteristics of the major tree species.
Table 3. Summary of species-specific feature characteristics of the major tree species.
Taxonomy (Tree Class and Species)Feature Characteristic
Coniferous trees (vs. deciduous trees)
■
higher canopy density (TNoobj, Hmin) [26]
■
higher ratio of single reflections (ERsingle/multiple,obj) under leaf-off [66]
■
more canopy gaps (PTIN,Edge) under leaf-on condition [67]
■
tend to display higher backscatter cross-section (σ) [47]
■
usage of amplitude features (A) is more suitable under leaf-off condition than under leaf-on [52,53,94]
■
broadening of echo width (EW) [57,69,70]
Larch
■
higher values of echo width at upper crown parts (VEW) [26,47]
■
higher backscatter cross-section at upper crown parts (Vσ) [26]
Pine (vs. deciduous trees)
■
lower mean amplitude (Amean,obj) and lower mean echo width (EWmean,obj) [27,73]
■
lower number of echoes (TNo) for each crown under leaf-on condition [27,73]
Spruce
■
narrower echo width and lower standard deviation of echo width [26,27]
Deciduous trees
■
features differ through the phenological cycle → radiometric features of needles and leaves tend to be less different in leaf-on than needles and bark in leaf-off season [52]
Aspen
■
negative L(t) in leaf-on season [67]
■
higher variance-to-mean-ratio (VTMR) of echo pattern [67]
Beech
■
relatively constant values of average echo width (of bins) over the height profile [47]
■
decreasing backscatter cross-section over the height profile (Vσ) [47]
Birch
■
widened echo width (EW) [27]
■
lower peak amplitude [27]
Maple
■
bigleaf maple: small inter-peak distance (ΔRij) [55]
■
positive L(t) in leaf-on season [67]
■
variance-to-mean-ratio (VTMR) lower than one of echo pattern [67]
Oak
■
relatively constant values of average echo width over the height profile (VEW) [47]
■
decreasing backscatter cross-section over the height profile (Vσ) [47]
■
small oaks, lower average in backscatter cross-section (σstats,obj)compared to taller trees [47]
Poplar
■
higher number of last returns (TNolast) closer to ground level in leaf-on season

Share and Cite

MDPI and ACS Style

Koenig, K.; Höfle, B. Full-Waveform Airborne Laser Scanning in Vegetation Studies—A Review of Point Cloud and Waveform Features for Tree Species Classification. Forests 2016, 7, 198. https://doi.org/10.3390/f7090198

AMA Style

Koenig K, Höfle B. Full-Waveform Airborne Laser Scanning in Vegetation Studies—A Review of Point Cloud and Waveform Features for Tree Species Classification. Forests. 2016; 7(9):198. https://doi.org/10.3390/f7090198

Chicago/Turabian Style

Koenig, Kristina, and Bernhard Höfle. 2016. "Full-Waveform Airborne Laser Scanning in Vegetation Studies—A Review of Point Cloud and Waveform Features for Tree Species Classification" Forests 7, no. 9: 198. https://doi.org/10.3390/f7090198

APA Style

Koenig, K., & Höfle, B. (2016). Full-Waveform Airborne Laser Scanning in Vegetation Studies—A Review of Point Cloud and Waveform Features for Tree Species Classification. Forests, 7(9), 198. https://doi.org/10.3390/f7090198

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop