2. The Framework
We consider a two-period economy in which a risk-averse private landowner wants to maximize the utility deriving from final wealth, by choosing how much to harvest and how much to invest on financial markets [
25]. The utility index is assumed to be exponential with constant risk-aversion
ρ:U = −
exp(−ρ
w), where
w represents wealth at time 2.
Harvesting occurs in both periods, while financial investment made at time 1 returns its payoff at time 2. In particular, denoting by xi the quantity harvested at time i, and by pi the price at which wood harvested at time i is sold on the wood market, we assume that timber revenues p1x1 are invested at time 1 on the financial market.
Two assets are available: a risk-free bond with gross return (1 + rf), and a risky asset that pays out a dividend d at time 2 per unit of investment at time 1. We denote by ϖ the fraction of p1x1 invested in the risk-free asset. Therefore, the investment portfolio will be generically indicated as (1 − ϖ,ϖ).
Finally, we denote by Q the initial forest endowment, and by g its growth function, with g satisfying standard properties, such as: (i) g(0) = 0, (ii) g′ > 0, (iii) g′′ < 0.
Given the amount harvested at time 1,
x1, the stock available at time 2 is uniquely defined by the growth function
g and the initial endowment
Q. In addition, since we are assuming that utility derives from final wealth only, and that the rotations beyond the second period are ignored, it also follows that such a stock will be entirely harvested at time 2, so that:
2.1. Uncertainty
When the landowner makes his harvesting-investment decision at time 1, the future timber price
p2 and the realized dividend of the asset
d are not known, however their respective distribution are. In particular,
d = m +
εa +
εi;
p2 =
m +
εa +
εf m,
m ∈
![Forests 04 01158 i001]()
,
εa ~
N(0,
σa2),
εi ~
N(0,
σi2),
εf ~
N(0,
σf2)
. m and m are the expected asset dividend and the expected future timber price, respectively, which are both known at time 1. We assume that m > 1 + rf.
The asset dividend d and the future timber price p2 have a common component εa that represents an aggregate shock affecting the entire economy, including financial markets and the forest sector. Therefore, the variance of εa, σa2, can be thought of as a measure of aggregate economic (or, equivalently, undiversifiable) risk.
The two shocks εi and εf are mutually independent, and in addition they are also independent from εa. Therefore, they represent specific shocks exclusively affecting financial markets (εi), and the forest sector (εf). Hence, σi2 and σf2 can be thought of as measures of idiosyncratic risk: financial risk (σi2), and forest sector risk (σf2), respectively.
2.2. Information Arrival
While uncertainty resolves by time 2, with the realizations of the asset dividend and the timber price, some news concerning the asset already arrives at time 1 through a signal
s. In particular,
where εs is a noise distributed according to εs ~N(0, σs2). Notice that the signal in itself is a random variable, however its realization becomes known one period ahead with respect to the asset’s dividend and the timber price (that is, at time 1 instead of time 2). The signal is already partially informative about the asset’s price because of the two components εi and (scaled) εa. However the information about the asset’s brought by the signal is disturbed by the presence of a noise, εs, which renders s imprecise depending on its variance σs2.
σs2 is a measure of the precision of the signal, since higher σs2 induces also higher variability of the signal and, therefore, lower precision. α ∈ [0,1] represents the degree to which the signal is specific to the asset. If α = 1, the signal is simply a noisy estimate of the dividend d, and therefore it is partially informative about the aggregate shock εa, and, consequently, about p2. In contrast, if α = 0, the signal exclusively brings information for the financial market and it cannot be used to infer the timber price at time 2. For clarity, one can imagine that, when the signal is announced, the forest owner estimates its degree of specificity to the asset.
The informativeness of the signal with respect to the dividend and the timber price respectively is defined usually as γd = (cov(s,d))/(var(s)) and γp2 = (cov(s,p2))/(var(s)). Notice that by construction the signal is less informative with respect to the future timber price as reflected in γd > γp2 is also important to notice that an increase in aggregate economic risk σa2 makes the signal more informative (higher) for the forest price, while the opposite holds for an increase in financial specific risk σi2.
Given our assumptions,
s,
p2|
s and
d2|
s are also normally distributed. In particular, standard Bayesian updating leads to:
Notice that, when the signal is specific to the asset only, that is, when α = 0, the expected conditional future price, E[p2|s], is equal to the unconditional one, E[p2] = m, while the conditional covariance between the dividend and the price, Cov(d, p2|s), is equal to σa2, since εi and εf are independent. For this reason, if not explicitly mentioned otherwise, in the following we will assume that α ≠ 0.
Also notice that conditional covariance increases as aggregate economic risk increases (i.e., the higher σa2 is), while it reduces the signal becomes more precise (i.e., the lower σs2 is, and/or less financially specific (i.e., the higher α) is. In addition, if the signal concerned aggregate economic risk only, that is, s = αεa + εs, covariance would be higher than in (5), provided that the signal is sufficiently precise (i.e., σs2 is sufficiently low).
3. The Model
At the beginning of period 1, the forest owner is endowed with a forest stock Q, characterized by growth function g. The current timber price is p1, while the future price p2 is known to be distributed according to p2~N(m, σa2 + σf2).
The revenues p1x1 from timbers harvested at time 1, x1, are invested on financial markets; more precisely, a fraction ϖ of p1x1 is invested in a risk-free bond with gross return 1 + rf, while the remaining fraction 1 − ϖ is invested in a risky asset that pays out a dividend d in the second period. At the beginning of period 1, d is known to be distributed according to d~N(m, σa2 + σi2).
Hence the agent’s maximization problem consists in choosing optimal current timber supply x1, and the investment portfolio (ϖ, 1 − ϖ) in order to maximize the utility from final wealth w.
Given harvesting level
x1 and the portfolio (
ϖ, 1
− ϖ), final wealth at time 2 is:
where
x2 is given by (1).
Before the harvesting and investment decisions are taken, the agent receives some news concerning the financial market by means of a signal
s =
αεa +
εi +
εs [
26]. This information is then used to update the priors of
p2 and
d, and henceforth to choose optimal contingent harvesting
x1 and the portfolio (
ϖ, 1
− ϖ). In particular, the maximization problem becomes:
under the constraint given by the growth function (1).
Since both
p2|
s and
d|
s are normally distributed, so is
w|
s. Further, the utility index is a standard CARA exponential utility [
27], so that the expected utility of
w given the signal
s is a strictly increasing transformation of the kernel
E[
w|
s] −
![Forests 04 01158 i003]() Var
Var[
w|
s], where
E[
w|
s] =
x2 (
m + γd s) +
ωp1x1 (1 +
rf) + (1 − ω)
p1x1(
m + γd s) and
Var[
w|
s] =
![Forests 04 01158 i004]()
+ [(1 − ω)
p1x1)]
2[
![Forests 04 01158 i018]()
].
3.1. First Order Conditions
The first order conditions associated to the maximization problem (7) yield:
where
x2 is given by (1).
Notice that,
∂x2/
∂x1 < 0, (9) holds only if
![Forests 04 01158 i007]()
3.1.1. Harvesting and Investment
When analyzing the relationship between the optimal short-run supply of timber,
x1, and the financial portfolio (
ϖ, 1
− ϖ), it is easy to notice that the investment in the risky asset (1
− ϖ)
p1x1 is not affected by the specific level of current harvesting
x1. Hence, if harvesting is increased at time 1, the extra-revenues from timber sales are invested into the risk-free asset, and not in the risky one. In a similar fashion, as long as the signal on the financial market is observable, even if the landowner was given the possibility to exclusively invest in the risk-free asset [
28], the optimal short-run supply of wood would be given by the same
x1 solving (9) [
29].
In general, there is a trade-off between investing in the risk-free asset and allowing the forest to grow to time 2. This immediately appears in the first order condition (9): If m falls, x1 (harvesting in the first period) increases and the total investment in the risk-free asset increases as well. Similarly, if p1 or rf increases, so do x1 and the investment in the risk-free asset.
3.1.2. Harvesting and Risk
The increase in aggregate economic risk and in the two idiosyncratic risks impacts the short-run supply of timber (x1), and therefore investment. In particular, if risk in the forest sector σf2 increases, so does current harvesting x1 and the investment in the risk-free asset, as can be expected. Similarly, if risk-aversion ρ increases, so does x1. The investment in the risk-free asset increases as well, but this time also because the investment in the risky asset (1 − ϖ) is reduced by the increase in risk-aversion.
Inspection of the first order condition (9) reveals an interesting result: when the asset specific risk
σi2 increases, this is transmitted to the optimal harvested quantity through the signal
s. In particular, the signal's informativeness is reduced as reflected in the decrease of
γp2. If the signal conveys good news, a higher financial risk
σi2 unequivocally increases short-run timber supply,
ceteris paribus. In case of a negative signal, instead, the effect is a priori ambiguous [
30]. However, for high risk aversion, again short run supply increases when asset specific risk increases,
ceteris paribus.
The effect of financial risk σi2 on optimal harvesting is due to the presence of the common aggregate economic component εa and the signal s on the asset's dividend. Further, as noted above, under these assumptions financial risk σi2 affects optimal harvest as long as the agent observes the signal, no matter if he is given the actual possibility to invest in the risky asset or not. On the contrary, if no signal was received, and/or p2, s and d had no common component, the first order condition associated to the optimal harvesting quantity would not depend on σi2.
To the best of our knowledge, our model is the first in the literature to suggest that financial idiosyncratic risk can have an impact on harvesting behavior. Despite the relative difficulty in providing an accurate empirical analysis of this claim, the observation of the patterns followed by timber markets during, in particular, the first phase of the recent financial downturn might support this idea, as discussed in more detail in
Section 4.
Finally, it is interesting to notice how harvesting and financial investment react differently to an increase in aggregate economic risk. For simplicity, consider the case
α = 1. An increase in the aggregate economic risk
σa2 will always reduce the investment in the risky asset (1
− ϖ), no matter what the realization of the signal and the level of risk-aversion
ρ are. The reaction of the harvesting schedule is instead ambiguous for a positive signal and it depends on risk-aversion,
ρ [
31] , if
ρ is quite low, an increase in aggregate economic risk could possibly lead to a reduction in current harvesting level
x1 [
32].
This result indicates that the forest owner is behaving differently when deciding about timber harvesting compared to the evaluation of financial assets. In particular, let us consider an alternative risky asset at the place of the forest, with dividend d = p2. The first order condition associated to this problem shows that, in case of a positive signal, the variation of the investment in the second asset in response to an increase in σa2, is ambiguous, but in this case the sign of the reaction depends on the relative magnitude of variances, expected dividend, risk-free rate and signal realization, but not on the level of risk-aversion.
Even if it is beyond the scope of this paper to empirically evaluate the validity of the framework proposed, these findings seem to suggest that timber prices and financial markets co-move in quite a complicated manner, presenting both significant and negligible correlation; as empirical evidence from the literature also seems to suggest (see
Section 4).
3.1.3. Harvesting and the Signal Realization
We next investigate how harvesting is affected by the “positivity” of the information conveyed by the signal.
Suppose that s = 0, so that the updated expected dividend and timber price after having observed the signal do coincide with the unconditional ones, namely, E[d|s] = m, and E[p2|s] = m.
Let us denote by x1° the solution to (9) when the realization of the signal is s = 0.
Next, we define the function
ϕ(
x1,
s), such that
ϕ(
m,
x1,
s,
α,
ρ,
p1,
rf)=
![Forests 04 01158 i009]()
× (
m +
γp2s −
ρx2[
![Forests 04 01158 i011]()
]) +
p1(1 +
rf). Hence,
ϕ(
m,
x1°,
s,
α,
ρ,
p1,
rf) = 0.
An increase of the signal to s > 0 (that is, the arrival of good news) translates into ϕ(m,x1°,s,α,ρ,p1,rf) < 0. Since, ∂x2/∂x1 < 0 and ∂2x2/∂2x1 < 0, the new equilibrium requires a lower x1, so that the short-run supply of wood is reduced. As a consequence, also the total investment in the financial market p1x1 is reduced. In addition, given the positivity of the signal, the investment portfolio (ϖ, 1 − ϖ) is tilted towards the risky asset.
Summarizing, the arrival of good news induces a reduction in current harvesting (which in turn translates in a decrease of current wealth) and in the proportion of current wealth invested in the risk-free bond in favor of the one in the risky investment. The opposite happens if the signal conveys bad news (that is if s < 0); in this particular instance, harvesting at time 1 is increased, and the financial portfolio is tilted towards the risk-free asset.
3.2. Information
The informativeness of the signal depends on risks σa2, σi2, precision σs2, and the specificity parameter, α. Higher precision (i.e., lower σs2) translates into higher informativeness for both the dividend and the price. Hence, the new equilibrium requires a lower x1 and an investment portfolio more tilted towards the risky investment (that is, higher (1 − ϖ)). Therefore the investment in the risk-free asset is reduced because of the reduction of x1, but also because of the change in the optimal portfolio composition.
If good news arrives (
s > 0), short-run supply reduces as
α increases [
33]. This simply means that the more the signal becomes informative about aggregate economic risk, the stronger the forest landowner reacts to it (reducing the short-run supply of wood). In case of a negative signal the result is ambiguous: on one side a very trustable negative signal would induce an increase in the current-supply of wood. On the other hand, the fact that the signal is less specific to financial markets reduces the conditional variance of future timber price (
i.e., its overall risk), and consequently short-run supply is reduced.
4. Discussion and Conclusions
In this paper we have presented a theoretical model of optimal harvesting-investment decision for a private forest owner who invests the revenues from timber sale on financial markets. The framework has two main characteristics: (i) the role of information and (ii) the way uncertainty is modeled. As far as it has been possible to ascertain, this is the first theoretical paper investigating the effect of information on harvesting decisions. When modeling uncertainty, we explicitly allow for a distinction between aggregate economic risk and sector specific risk, such as financial and forestry risk respectively. Obviously it is beyond the scope of this paper to try to establish a direct linkage between concrete empirical facts and the results of our model. Nevertheless, the particular structure used here permits financial specific risk to influence harvesting behavior (see
Section 3.1.2 above), and, along with the introduction of the information component, it furthers the understanding of recent trends in timber prices that are difficult to explain using standard models.
For example, when the housing sector collapsed in US, timber prices in Sweden plummeted dramatically, as expected. However, they dropped even further after Lehman Brothers’ bankruptcy [
16]. To make a parallelism with the framework presented above, the Lehman Brothers’ breakdown could be interpreted as the “arrival of a signal”, carrying information on both aggregate economic and financial risk, affecting economic operators (including those in the forest sector) all over the world. Indeed, though the growth forecasts had already been gradually corrected downward since August 2007 [
17], they dropped dramatically only with the collapse of Lehman Brothers’, an event which apparently took market participants by surprise and therefore induced a strong reaction in prices.
The presence of common aggregate economic risk (due to the potential occurrence of a shock,
εa) and the arrival of financial information make the way financial and timber markets interact non-trivial, reconciling the mixed empirical evidence reported in the literature. Indeed, there is no consensus on the way timber prices and financial markets co-move. On one side, some studies have found a positive correlation between timber and financial markets [
20,
21], while quite a few studies point out that forest investments are an attractive alternative for risk diversification, due to negligible correlation with financial assets (see, e.g., [
22,
23,
24]).
Even if ours is not an equilibrium model, so that both financial and timber prices are exogenous, observing the conditional covariance between timber price and asset dividend one could partially accommodate these contrasting findings. Indeed, conditional covariance varies in value depending on the severity of aggregate economic risk and the specific information received (see
Section 2.2). Finally, Heikkinen [
21]—using time series data for the period from January 1988 to September 1999—finds that the correlation between timber and financial markets increases over time. This finding seems to be consistent with the idea that harvesting decision-making adjusts to the arrival of new information. This is also why we contend that the role of information in harvesting decision should be further investigated.
The accommodation of the role played by information/news in the model—particularly information specific to timber markets—is of relevance from a policy perspective. Hence, information is a frequently used policy tool, and the way information affects harvesting decisions is thus of interest, especially in light of the efforts to increase wood mobilization in many European countries. As an example, information about timber markets, coupled with recommendations not to postpone harvest, features frequently in forest owner associations membership magazines, presumably partly with the objective to increase the short-run supply of timber (see, e.g., [
18]).
Thus the model presented here can be used as a starting point for exploring an area of forest economics well worth considering, not least from a policy perspective and with very concrete applications. For example, departing from the approach proposed here, it is possible to develop an alternative framework suitable for analyzing how different degrees of information penetration affect the equilibrium price of timber. Alternatively, one could investigate how the release of information could be used as a policy tool to optimally induce higher/lower levels of timber supply among forest owners, depending on their specific characteristics (e.g., stand characteristics related to the extent of non-timber forest values). These topics will be part of our future research.
 , εa ~N(0, σa2), εi ~N(0, σi2), εf ~N(0, σf2).
, εa ~N(0, σa2), εi ~N(0, σi2), εf ~N(0, σf2).  Var[w|s], where E[w|s] = x2 (m + γd s) + ωp1x1 (1 + rf) + (1 − ω)p1x1(m + γd s) and Var[w|s] =
Var[w|s], where E[w|s] = x2 (m + γd s) + ωp1x1 (1 + rf) + (1 − ω)p1x1(m + γd s) and Var[w|s] =  + [(1 − ω)p1x1)]2[
+ [(1 − ω)p1x1)]2[  ].
].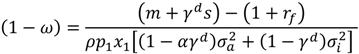
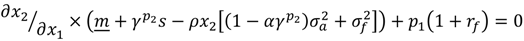

 × (m + γp2s − ρx2[
× (m + γp2s − ρx2[  ]) + p1(1 + rf). Hence, ϕ(m,x1°,s,α,ρ,p1,rf) = 0.
]) + p1(1 + rf). Hence, ϕ(m,x1°,s,α,ρ,p1,rf) = 0.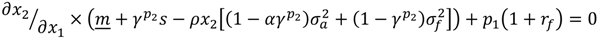
 .
.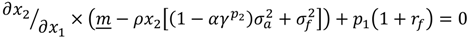
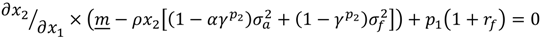
.




